Morphology mapping of platinum catalysts over the entire nanoscale

Abstract

Platinum nanoparticles are exceptional heterogeneous catalysts that play an important part in our existing and future energy economy. Understanding the size, shape and morphological transformations that may occur under different temperature conditions is vital to ensuring the long term stability of platinum-based technologies, or for planning ideal operating and storage conditions for platinum nanoparticles. In this paper we present a combination of experimental and theoretical results exploring the relationship between as-grown and thermodynamically preferred morphologies of platinum catalysts over the entire nanoscale. A shape-dependent thermodynamic model has been used to predict the stable morphology as a function of the size and temperature, and the first nanoscale phase diagram of platinum is constructed, by considering 15 different ideal and imperfect structures and shapes. This phase diagram is then discussed in relation to the experiments, to establish the relative stability of different shapes and the sizes at which they may be expected.

---

1 Introduction

To date, the most efficient heterogeneous catalysts have been made of platinum,¹ supported on carbon, aluminium oxide, or titanium oxide.^2,3 In addition to this, Pt is an important component in catalytic converters (in the automotive industry), as it facilitates the complete combustion of low concentrations of unburned hydrocarbons from the exhaust. However, platinum is extremely rare, occurring in only <0.003 ppm in the Earth's crust. Therefore, to achieve economic sustainability in combination with energy security, we must find intelligent ways of reducing the amount of Pt needed, increasing the number of cycles each catalyst can perform (recyclability) and increase efficiency by controlling the number of catalytically active sites (per particle). Nanosized heterogeneous catalysts show a considerable enhancement of catalytic activity and reactivity compared to macroscopic (planar) materials,^4,5 which affords us the opportunity to engineer more efficient materials at a lower cost. Motivated by this endeavour, recent studies have demonstrated that these differences are attributed to fundamental physical and chemical changes at the active sites, and not simply to the obvious increase in the surface area.^6–9 In particular, the shape of individual nanoparticles has an important influence on efficiency,^10,11 due to anisotropic adsorption of reactants at the exposed surface facets, edges and corners.¹² Therefore, considerable attention is being directed to engineering shapes to increase (or decrease) reactivity, depending upon the application in mind.¹³

The effects of particle shapes on catalytic performance were first reported by Narayanan and El-Sayed,^14–18 in which cubic, truncated octahedral and tetrahedral platinum nanocrystals were investigated for the electron transfer reaction between [Fe(CN)₆]³⁻ and S₂O²⁻₃ ions. It was found that the percentage of atoms located at corners and edges relative to the total surface atoms was highest for tetrahedral nanocrystals, followed by truncated octahedral and cubic nanocrystals, which lead to a decrease in the catalytic activity of cubic shapes (or conversely, an increase in reactivity).^17,18 For example, benzene hydrogenation has been investigated in the presence of a surface monolayer consisting of cubic and cuboctahedral Pt nanoparticles. It was shown that cyclohexane and cyclohexene product molecules were formed on cuboctahedral nanoparticles, whereas only cyclohexane was produced on cubic nanoparticles.¹⁹ Moreover, CO monolayer oxidation on quasi-spherical, cubic and “tetrahedral–hexagonal” platinum nanoparticles revealed a clear dependence between bidimensional (111) and (100) ordered domains present on the surface of the nanoparticles and their CO catalytic activity.²⁰ In regard to fuel cell applications, it has also been demonstrated that the specific activity of cubic platinum nanocrystals for oxygen reduction reactions can be as much as four times higher than those of truncated cubic and near-spherical polyhedral nanocrystals,²¹ and up to twice the activity of the commercial catalyst²² with a truncated octahedral morphology.

Given that the shape, and the long term stability of the shape under different thermal conditions, is critical to the performance of platinum nanocatalysts, we have undertaken predictive modeling (supported by first principles computer simulations) to identify the most stable shape and structure as a function of the particle size (N), or average diameter (D), and temperature (T). We have used an established theoretical nanomorphology model (that has been rigorously tested for nanogold²³), and included a large range of defect-free and twinned morphologies in the virtual sample set. The preferred shapes are then mapped in the 〈N,T〉 manifold, to generate the first complete nanoscale phase diagram of platinum. These predictions are then discussed in relation to our experiments, and others reported in the literature.

2 Experimental observations

The first step in the prediction of the thermodynamically preferred shape of platinum (under any conditions) is to identify the range of possible morphologies which are known to be observed experimentally.

Our Pt nanocrystals were prepared at 100 °C using L-ascorbic acid as the reducing agent following procedures by Meyer et al.²⁴ without any tri-sodium citrate added. A solution of 6.4% L-ascorbic acid was incubated in a boiling water bath. A solution consisting of 250 mM K₂PtCl₄ was prepared in a round-bottomed flask that was fitted to a water-jacketed condenser to maintain constant volume while heating. Once the contents of the flask had been brought to a rapid boil, the heated solution of L-ascorbic acid was rapidly injected to a final concentration of 0.3%. Solution samples at different annealing time periods (10 min, 30 min, and 5 h) were extracted using syringes and needles for Pt crystal size and shape analyses.

A drop of the sample suspension was placed on a holey carbon coated transmission electron microscopy (TEM) Cu grid and air-dried. All the TEM investigations were carried out by using an aberration-corrected FEG-(S)TEM (Titan 80–200) under TEM and STEM modes. Typical examples of TEM and high resolution TEM images of the samples grown over a 5 h period are shown in Fig. 1(a) and (b), respectively. Here we can see that the samples present a range of cross-sections, but have a narrow size distribution. Using this technique it is possible to determine the shapes of individual particles,^23,25 this is a very laborious and time consuming undertaking, which is significantly expedited by imaging in STEM mode. In Fig. 2 we can see some typical images of the larger samples taken in STEM mode, showing the cross-sectional outline, lattice planes, and contrast variations due to differences in particle thickness parallel to the beam. In general, both imaging modes reveal that the samples are fcc and dominated by a combination of octahedra and tetrahedra, which is consistent with other reported observations.^13,26–30 Some of the nanocrystals have their acute corners truncated, which will be referred to as minimally truncated octahedral and minimally truncated tetrahedra, respectively. Across this size domain, we find tetrahedra with edges 3–4 nm in length, octahedral with edges ∼3–5 nm in length, and minimally truncated octahedral with edges 8–10 nm in length.

Fig. 1 Transmission electron micrographs of platinum nanoparticles, showing (a) the diversity of cross-sections, and (b) the cross-sectional shapes of typical platinum nanoparticles produced in our experiments.

Fig. 2 Typical micrographs of platinum nanoparticles greater than ∼5 nm, taken in STEM mode. Greater intensity indicates greater thickness (perpendicular to the beam), and facilitates shape analyses, though some particles do not show lattice fringes due to the off zone axis.

In addition to this, at small sizes less than ∼3 nm, it was found that the platinum nanoparticles do not adopt a polyhedral crystalline morphology when growth is stopped after 30 min. At the lower end of this size regime <1 nm, the nanoparticles are generally amorphous (non-crystalline) and have a spherical appearance (Fig. 3), with highly mobile atoms at the surfaces. This can be seen in Fig. 3(a), but since they fall below the threshold of applicability for the theoretical modelling described in later sections, a detailed analysis and comparison to explicit computations will be reserved for future work. At the upper end of this size regime (∼1 nm to ∼3 nm) the particles are crystalline, but also display a quasi-spherical appearance (Fig. 3(b). In some cases these particles displayed symmetric contact twinning in the [111] direction, as shown in Fig. 4.

Fig. 3 STEM images showing (a) amorphous, non-crystalline Pt clusters, and (b) round (larger) Pt crystals. Note that the surface Pt on round crystals are less ordered (regular).

Fig. 4 A quasi-spherical twinned platinum nanoparticle, referred to as a truncated prism in the following sections, and shown in Fig. 7(d).

Fig. 5 The defect-free platinum nanomorphologies considered in this study. The first four shapes [(a), (b), (c) and (d)] are entirely enclosed by {111} facets, whereas the remaining shapes [(e), (f), (g) and (h)] are enclosed by an increasingly large fraction of {100} facets, until we reach the hexahedron (i) which is entirely enclosed by {100} facets.

While twinning is rare in platinum,²⁷ there are a number of twinned nanoparticle shapes that are consistently observed in particles produced using different techniques. For example, the symmetric contact twinning shown in Fig. 4 is consistent with the observations of Gontard et al.³¹ In addition to this, a range of shapes based on a twinned tetrahedral motif have also been proposed to explain particles that present a triangular cross-section.^27,28 Multiply twinned particles, such as truncated (Marks) decahedron and the well-known (Mackay) icosahedron, were first observed in platinum in the late 1990s,³² but subsequent reports of these shapes are limited. While it is possible to produce icosahedral platinum nanoparticles by reacting solutions of Pt(dba)₂ and toluene or triphenylphosphine with CO (in the absence of polymer stabilizers),³³ they are rarely observed in coexistence with other shapes, and hence the thermodynamic stability of these structures is questionable.

3 Theory and simulation

The shape-dependent model used here is based on a summation of the Gibbs free energy G(T) of a nanoparticle, and includes contributions from the particle bulk, surfaces, edges, corners,³⁴ and planar defects.^35,36 This model has previously been successfully used to examine the size- and temperature-dependent shape of gold nanoparticles³⁷ without necessitating a large number of explicit simulations of individual structures.³⁸ Here, since we are concerned with nanoparticles >3 nm in diameter we may use the expression:where M is the molar mass and ρ is the mass density, γ_i(T) is the temperature-dependent free energy of facet i, ν_θ(T) is the single stacking fault (or twin) energy in orientation θ, and η_ϕ(T) is the re-entrant line tension where the twin plane intersects with the free surface in the orientation ϕ. The volume dilation induced by the isotropic surface stresses σ_i and external pressure P_ex is included using the Laplace–Young formalism³⁵ using the bulk modulus B₀, and the average particle radius 〈R〉 calculated using a spherical approximation (which is consistent with the Laplace–Young formalism). In all cases atmospheric external pressure has been assumed (P_ex = 101.33 kPa). This version of the model requires the input of B₀, γ_i(T), σ_i(T), ν_θ(T) and η_ϕ(T), which must be calculated explicitly for all facets i, twin planes θ and line tensions ϕ of interest.

The calculations performed in this study were obtained from first principles using Density Functional Theory (DFT) within the Generalized-Gradient Approximation (GGA), with the exchange–correlation functional of Perdew–Burke–Ernzerhof (PBE).³⁹ This has been implemented via the Vienna Ab initio Simulation Package (VASP),^40,41 which spans reciprocal space with a plane-wave basis expanded to a given kinetic energy cut-off (in this case 230 eV), and utilizes an iterative self-consistent scheme to solve the Kohn–Sham equations using an optimized charge-density mixing routine. All calculations were performed using the Projected Augmented Wave (PAW) potentials,^42,43 with spin polarisation, to an energy convergence of 10⁻⁴ eV. Using this approach, the value of the bulk modulus was calculated to be 276 ± 12 GPa, which is in very good agreement with the value of 309 GPa⁴⁶ and 314 GPa⁴⁷ calculated using LDA, 246 GPa,⁴⁷ 241 GPa⁴⁸ and 246 GPa⁴⁹ calculated using GGA, and the experimental values measured at 278 GPa,⁵⁰ 283 GPa⁵¹ and 288 GPa.⁵²

In this paper the surfaces were modelled using periodic slabs generated by cleaving a three dimensional (periodic) super-cell along the crystallographic planes of interest, and adding a 15 Å layer of vacuum space. The periodic super-cell for the (111) surfaces contains 108 atoms, and the periodic super-cell for the (100) surfaces contains 128 atoms. In each of these structures, the surfaces were fully relaxed by optimizing the atoms in the 4 outer most atomic layers (the terminal plane, and three further planes beneath), which is consistent with the experimental observations.⁵³ The atomic planes in the center of the slabs were restricted to the bulk-like atomic positions. This has the advantage of providing more surfaces for analysis (both upper and lower facets), while still constraining the bulk like positions far from the surface. In addition to this, the 〈111〉 twinning (or stacking fault) energy was calculated with a 96 atom periodic super-cell, where all atoms were relaxed while the cell parameters were fixed to the bulk values.

The relaxations were performed using an efficient matrix-diagonalization routine based on a sequential band-by-band residual minimization method of single-electron energies^44,45 with direct inversion in the iterative subspace, without symmetry constraints. This methodology has previously been used successfully to model the surfaces of platinum.^53,54 This provides values of γ₁₁₁ = 1.26 J m⁻², γ₁₀₀ = 1.72 J m⁻²; σ₁₁₁ = 5.41 J m⁻², σ₁₀₀ = 3.40 J m⁻² and ν₁₁₁ = 0.13 J m⁻² (which compares well to the experimental values of 0.17 J m^−2 55 and 0.16 J m^−2 56). These values have been thoroughly compared with others reported in the literature in the ESI of ref. 54. The re-entrant line tensions of η₁₁₁ = 0.12 × 10⁻⁹ J m⁻¹ and η₁₀₀ = 0.02 × 10⁻⁹ J m⁻¹ were calculated using the above values, and fitting to the total energies of isolated (decahedral and icosahedral) platinum nanoparticles calculated with the same computational parameters and methods (above), using the same technique described for the case of gold in ref. 35.

Since these DFT calculations have been performed at T ≈ 0, a number of simple expressions have been used here to describe the temperature dependence. Firstly, we have used a semi-empirical expression for determining γ_i(T) proposed by Guggenheim:⁵⁷

where x is an empirical parameter (known to be unity for metals⁵⁸) and T_c is the critical temperature at which the structure of the surface deteriorates or changes significantly from the structure in the bulk (is not longer fcc).⁵⁹ The value of T_c is usually taken as the bulk surface melting temperature, but since this has been shown to be size-dependent in metallic nanoparticles,⁶⁰ the expression of Qi and Wang⁶¹ has also been employed:where T_m are the macroscopic surface melting temperatures, D is the average diameter of the nanostructure, r is the atomic radius of platinum, and Ω is a shape dependent factor defined as the ratio of the surface area of the particle divided by the surface area of a sphere of equivalent volume.⁶¹ Since σ = γ + A∂γ/∂A the temperature dependence of σ_i has been described in the same way. This method has previously proven successful in describing the temperature-dependent shape, stability and transformation in gold nanoparticles.^23,37 More useful equations for describing specific shapes are provided in ref. 62.

4 Results and discussions

4.1 Monocrystalline morphologies

Using the method described above, we began by modelling the temperature-dependent free energy for a range of defect-free monocrystalline nanoparticle morphologies (free of twin planes and stacking faults). The morphologies are displayed in Fig. 5, including the tetrahedron, the truncated tetrahedron, the regular octahedron, the truncated octahedron, the cuboctahedron, the truncated regular hexahedron (also known as a truncated cube) and the regular hexahedron (also known as a cube). In addition to this, we added two other shapes: one to the tetrahedral family called the minimally truncated tetrahedron (Fig. 5(b)) which is geometrically equidistant between the tetrahedron and truncated tetrahedron; and another to the octahedron-to-hexahedron geometric continuum called the minimally truncated octahedron (Fig. 5(e)), which is geometrically equidistant between the platonic octahedron and the Archimedean truncated octahedron. These shapes were included as they approximate some of the shapes observed in our (and other) experiments, and are complementary to the other shapes which have all been reported in the literature at one time or another.

Fig. 6 The calculated free energy for the nanoparticles morphologies shown in Fig. 5, as a function of the size (where N is the number of Pt atoms, so that 3 nm sizes appear to the right, converging to 100 nm on the left), for T = (a) 0 K, (b) 300 K, (c) 600 K, and (d) 900 K.

Even though all of these shapes are enclosed entirely by combinations of {100} and {111} facets, there is a distinct energetic order that depends on the relative surface-to-volume ratio (q), in addition to the orientation of the facets. At low temperature (T = 0 K) the minimally truncated octahedron, the truncated octahedron and the octahedron are the lowest energy shapes (in that order), but are very close in energy. This is consistent with previously reported results by Baletto et al.,⁶³ but is suggestive of a state of thermodynamic coexistence. The next highest energy morphology is the minimally truncated tetrahedron, then the truncated tetrahedron and cuboctahedron which are again in a state of thermodynamic coexistence (within the uncertainties of the model). At high energies the tetrahedron and truncated hexahedron are very close in energy, and the hexahedron is the most unstable shape of all. Overall the greater the fraction of {100} facets, the more unfavourable the shape is. For shapes with the same types (and relative areas) of facets, the higher the surface-to-volume ratio, the more unfavourable the shape is. For example, both the octahedron and the tetrahedron are enclosed exclusively with {111} facets, but the tetrahedron is significantly higher in energy and therefore unstable with respect to a morphological transformation to an octahedron or any of the other lower energy shapes. It is interesting to note that these general rules and energetic ordering are largely independent of size.

These results are plotted at T = 0 K as a function of the inverse cube of the volume (expressed as the total number of Pt atoms, N_Pt) in Fig. 6(a), followed by the results for the same shapes at 300 K, 600 K, and 900 K in Fig. 6(b)–(d), respectively. The sizes in these plots range from ∼2.5 nm to ∼100 nm in average diameter. By comparing these plots we can see that the relative free energy of different shapes changes with temperature, and in some cases, size-dependent crossovers have been introduced. Shapes enclosed by {111} facets shift to a lower position in the energetic ordering, irrespective of the surface-to-volume ratio, and those with the highest surface-to-volume ratio become even more energetically favourable at small sizes (indicated by crossovers). This is because the {111} surface has a lower characteristic melting temperature^64,65 than the {100} facets,⁶⁵ and this lowers the contribution of these surfaces to the total free energy. At 600 K we can clearly see that the tetrahedron is the lowest energy shape at small sizes, and the octahedron at large sizes. At 900 K the shapes enclosed by {111} facets have undergone surface melting at very small sizes (G < 0).

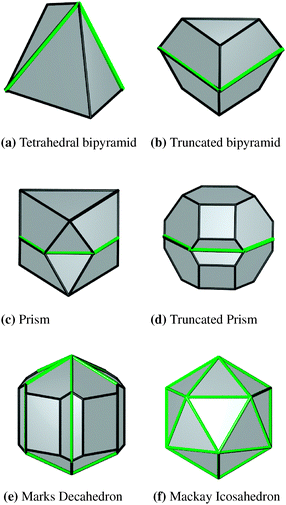Fig. 7 The twinned and multiply-twinned platinum nanomorphologies considered in this study. The location of the twin planes has been highlighted by marking the re-entrant edges around the circumference in green.

It is important to note that the hexahedron, truncated hexahedron and cuboctahedron are not thermodynamically preferred at any size or temperature (under these conditions), even though they are often produced in experiments,^28,68 indicating that their formation is either entirely kinetic in origin, or due to the inclusion of specific surfactants or precursors (or both).

4.2 Twinned morphologies

Given that the stacking fault energy is significant (being almost five times that of gold³⁵), and the re-entrant line tensions are all endothermic (while they are exothermic in gold³⁵), there is no energetic compensation to stabilise planar defects in platinum. A twin plane is never thermodynamically stable, but may be kinetically stable and be introduced if the synthesis environment is conducive. Therefore, in addition to the defect-free monocrystalline morphologies described above, we have also modelled the temperature-dependent free energy for a range of twinned nanoparticle morphologies, as displayed in Fig. 7. The shapes include the tetrahedral bipyramid, the truncated tetrahedral bipyramid (sometimes called a ‘trigon’), the symmetrically twinned octahedron which is referred to as the prism, the symmetrically twinned truncated octahedron which is referred to as the truncated prism, the multiply twinned Marks decahedron and the multiply twinned Mackay icosahedron. In the case of the singly twinned particles, each successive shape may be obtained by truncating the most acute corners from the preceding shape when following the progression from Fig. 7(a) to (d). However, only when we reach the truncated prism (Fig. 7(d)) do we finally introduce {100} facets.

Just as described above for the monocrystalline shapes, the specific free energy is plotted as a function of the inverse cube of the volume, for all of the shapes shown in Fig. 7 at T = 0 K, 300 K, 600 K, and 900 K in Fig. 8(a)–(d), respectively. In the case of the twinned morphologies the low temperature energetic order can depend on size. At small sizes the decahedron is most thermodynamically favourable (due to the low surface-to-volume ratio with respect to the alternative shapes), followed by the truncated prism (which also has a relatively low surface-to-volume ratio), prism, truncated bipyramid, icosahedron and tetrahedral bipyramid, respectively. In general, the higher the surface-to-volume ratio, the higher energy the free energy of the shape. The exception to this rule is the icosahedron, which has a very low surface-to-volume ratio, but has a large density of twin planes which represents a large energetic penalty. This is consistent with previously reported results by Baletto et al.⁶³ At larger sizes the decahedral motif becomes more unfavourable than the prism or truncated prism, and a crossover can be observed at ∼8.1 nm.

Fig. 8 The calculated free energy for the twinning nanoparticles morphologies shown in Fig. 7, as a function of size (where N is the number of Pt atoms, so that 3 nm sizes appear to the right, converging to 100 nm on the left), for T = (a) 0 K, (b) 300 K, (c) 600 K, and (d) 900 K.

As the temperature is increased, the prism (Fig. 7(c)) becomes the most thermodynamically stable among the twinned morphologies, and at high temperature we see a preference for the tetrahedral bipyramid emerging due to the combination of the high surface-to-volume ratio and low melting temperature of the {111} facets (as we did for the monocrystalline particles). At room temperature the multiply-twinned particles are not thermodynamically favourable, and at high temperatures they are very unstable with respect to transformations to any of the singly-twinned or monocrystalline (untwinned) structures. This is consistent with experimental observations, and the need for deliberate synthetic methods to be employed to produce these shapes.

4.3 Combined morphology map in 〈N,T〉 space

By combining all of these models, and systematically calculating the size-dependent free energy at 10 K intervals (from T = 0 K to T = 2300 K), it is possible to compare all shapes on the same 〈N,T〉 (or 〈D,T〉) manifold. At each stationary point there are a multitude of crossing points, indicating a change in the relative stability of different shapes, but it is the lowest energy shape at each 〈N,T〉 point that is of interest here. Using this technique, we have determined the lowest energy morphology at each point, and mapped the crossing points in Fig. 9. In addition to this, we have calculated the size-dependent melting temperature (using eqn (3)) for shapes that are stable at high temperature, and combined these results to provide the first phase diagram of platinum nanocatalysts.

Fig. 9 The equilibrium morphology map of nanoscale platinum. The grey regions are inaccessible to this theoretical treatment, and the corresponding average particle diameters at each size (N) increment are provided below the x-axis.

At high temperatures the “solid” region of the phase diagram is bounded by the size-dependent melting temperature, which is determined by calculating the size-dependent melting temperature for all of the shapes, and assigning the boundary to the shape with the highest value (that most resists melting). In this case, the icosahedron. Below this boundary is a region referred to as quasi-molten, in which all of the shapes start to melt, but may reorganise to form an icosahedron to preserve solidity. In this region the particles may appear quasi-spherical, but are not necessarily fluid. At lower temperatures we find a region referred to as roughened surfaces, where the surface melting temperatures have been breached, but the core (subject to the bulk size-dependent melting temperature) remains solid and crystalline. A similar region was observed, and confirmed experimentally, in the case of nanogold.²³

This phase diagram indicates that, at around room temperature, octahedral and minimally truncated octahedral are the thermodynamically preferred shapes (depending on the size). This is consistent with our experimental observations (above), the observations of others,⁶⁶ and the shape of commercial samples.^{53–54,67,68} In our experiments the smallest octahedron edge length was ∼4.6 nm, which (at 100 °C) resides just above the border with the minimally truncated octahedra. The existence of the decahedron at low temperature and small sizes is consistent with previously reported results by Baletto et al.⁶³ but, in general, at most industrially relevant sizes and temperatures, platinum nanocatalysts will prefer to adopt the monocrystalline (fcc) octahedral morphology.

In addition to the octahedron, the phase diagram predicted a region occupied by tetrahedra, which were also observed with great frequency in our experiments. However, here we observe some discrepancy. Although we observe more tetrahedra at small sizes, the phase diagram predicts that the tetrahedra should only occur at higher temperatures (between 600 K to 1200 K), but we routinely observe tetrahedra between 300 K and 400 K. In our experiments the largest tetrahedron has an edge length of ∼5.6 nm, and the smallest ∼3 nm. Converting between the edge lengths of an octahedron and a tetrahedron of equivalent mass is simply a matter of dividing (or multiplying) each length by the ratio of their surface-to-volume ratios (q_octahedron/q_tetrahedron = 1.26), so we find that the largest tetrahedron corresponds well with the smallest octahedron. The boundary is simply shifted to lower temperatures.

There are a number of reasons why the predicted octahedral/tetrahedral boundary differs from the experiment. Firstly, there are a number of subtle interactions that occur in the experiments which are absent from the version of the model applied herein. These include edge tensions and interactions with this substrate, which may only contribute minor perturbations to the specific free energy, but may have a more significant impact on the shape—particularly at higher temperatures. Alternative explanations include variations in the surface structure⁵⁴ or chemistry, or a deviation of the formation environment from ideal equilibrium conditions. This phase diagram maps the equilibrium structure, and does not take into account thermal fluctuations (such as edge diffusion⁶⁹) or non-equilibrium driving forces during formation. For example, both of the shapes participating in this boundary are enclosed by {111} surfaces, so it is entirely possible that shape selectivity is determined by coarsening kinetics and not thermodynamic stability. This is an important issue to be addressed, since the tetrahedron has been shown to exhibit higher catalytic activity.^17,18 Recently a kinetic theory of nanomorphology has been derived⁷⁰ and tested for the case of nanogold.⁷¹ This model confirmed that the frequent observation of gold icosahedral at thermodynamically forbidden sizes is due to their superior rate of coarsening and kinetic stability. A similar study of the shape- and time-dependent formation of platinum nanoparticles is planned for the future, to help uncover the reason for the frequent observation of platinum tetrahedra.

5 Conclusions

In this paper we present the first nanoscale phase diagram of isolated colloidal platinum nanoparticle catalysts, calculated using a shape-dependent thermodynamic model, and parameters obtained using first principles electronic structure simulations. The phase diagram predicts that, at low temperature, the octahedron or minimally truncated octahedron are the preferred morphologies, with the tetrahedron emerging only when the temperature is raised. The tetrahedron/octahedron boundary depends on both the size and temperature, but has been found to be inconsistent with experimental observations, which are shifted to lower temperatures, although the overall trend is remarkably consistent. At this stage it is assumed, since both shapes are enclosed entirely by {111} facets (and differ only by their surface-to-volume ratios), that this inconsistency may be related to dominant kinetic influences during coarsening, and future work is planned to test this hypothesis.

Acknowledgements

This project has been supported by the Australian Research Council (ARC) under grant number DP0986752, and the National Science Foundation (NSF) under grants 0810150 and 0824890. Computational resources for this project have been supplied by the National Computing Infrastructure (NCI) national facility under MAS Grant p00.

References

1. J. Hill, E. Nelson, D. Tilman, S. Polasky and D. Tiffany, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 11206.
2. Y. Suchorski and W. Drachsel, Top. Catal., 2007, 46, 201.
3. Catalysis and Electrocatalysis at Nanoparticle Surfaces, ed. A. Wieckowski, E. R. Savinova and C. G. Vayenas, Dekker, New York, 2003, pp. 455–500.
4. J. Meier, K. A. Friedrich and U. Stimming, Faraday Discuss., 2002, 121, 365.
5. H. Yano, J. Inukai, H. Uchida, M. Watanabe, P. K. Babu, T. Kobayashi, J. H. Chung, E. Oldfield and A. Wieckowski, Phys. Chem. Chem. Phys., 2006, 8, 4932.
6. B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71.
7. N. Lopez and J. K. Nørskov, J. Am. Chem. Soc., 2002, 124, 11262.
8. K. J. J. Mayrhofer, B. B. Blizanac, M. Arenz, V. R. Stamenkovic, P. N. Ross and N. M. Markovic, J. Phys. Chem. B, 2005, 109, 14433.
9. M. Arenz, K. J. J. Mayrhofer, V. Stamenkovic, B. B. Blizanac, T. Tomoyuki, P. N. Ross and N. M. Markovic, J. Am. Chem. Soc., 2005, 127, 6819.
10. P. J. F. Harris, Int. Mater. Rev., 1995, 40, 97.
11. T. S. Ahmadi, Z. L. Wang, T. C. Green, A. Henglein and M. A. El-Sayed, Science, 1996, 272, 1924.
12. K. J. J. Mayrhofer, M. Arenz, B. B. Blizanac, V. Stamenkovic, P. N. Ross and N. M. Markovic, Electrochim. Acta, 2005, 50, 5144.
13. S. Cheong, J. D. Watt and R. D. Tilly, Nanoscale, 2010, 2, 2045.
14. R. Narayanan and M. A. El-Sayed, J. Phys. Chem. B, 2003, 107, 12416.
15. R. Narayanan and M. A. El-Sayed, Nano Lett., 2004, 4, 1343.
16. R. Narayanan and M. A. El-Sayed, J. Am. Chem. Soc., 2004, 126, 7194.
17. R. Narayanan and M. A. El-Sayed, J. Phys. Chem. B, 2004, 108, 5726.
18. R. Narayanan and M. A. El-Sayed, Langmuir, 2005, 1, 2027.
19. K. M. Bratlie, H. Lee, K. Komvopoulos, P. Yang and G. A. Somorjai, Nano Lett., 2007, 7, 3097.
20. J. Solla-Gullón, F. J. Vidal-Iglesias, E. Herrero, J. M. Feliu and A. Aldaz, Electrochem. Commun., 2006, 8, 189.
21. C. Wang, H. Daimon, O. Onodera, T. Koda and S. Sun, Angew. Chem., Int. Ed., 2008, 47, 3588.
22. C. Wang, H. Daimon, Y. Lee, J. Kim and S. Sun, J. Am. Chem. Soc., 2007, 129, 6974.
23. A. S. Barnard, N. P. Young, A. I. Kirkland, M. A. van Huis and H. F. Xu, ACS Nano, 2009, 3, 1431.
24. D. A. Meyer, J. A. Oliver and R. M. Albrecht, Microsc. Microanal., 2010, 16, 33.
25. A. S. Barnard, R. R. Yeredla and H. Xu, Nanotechnology, 2006, 17, 3039.
26. L. C. Gontard, R. E. Dunin-Borowski and D. Ozkaya, J. Microsc., 2008, 232, 248.
27. J. Chen, B. Lim, E. P. Lee and Y. Xia, Nano Today, 2009, 4, 81.
28. Z. Peng and H. Yang, Nano Today, 2009, 4, 143.
29. V. Komanicky, H. Iddir, K. C. Chang, A. Menzel, G. Karapetrov, D. Hennessey, P. Zapol and H. You, J. Am. Chem. Soc., 2009, 131, 5732.
30. T. K. Sau and A. L. Rogach, Adv. Mater., 2010, 22, 1781.
31. L. C. Gontard, R. E. Dunin-Borkowski, M. H. Gass, A. L. Bleloch and D. Ozkaya, J. Electron Microsc. Tech., 2009, 58, 167.
32. D. Lu and K. Tanaka, Surf. Sci., 1997, 373, L339.
33. A. Rodriguez, C. Amiens and B. Chaudret, Chem. Mater., 1996, 8, 1978.
34. A. S. Barnard and P. Zapol, J. Chem. Phys., 2004, 121, 4276.
35. A. S. Barnard, J. Phys. Chem. B, 2006, 110, 24498.
36. A. S. Barnard, Rep. Prog. Phys., 2010, 73, 086502.
37. A. S. Barnard, X. M. Lin and L. A. Curtiss, J. Phys. Chem. B, 2005, 109, 24465; A. S. Barnard and L. A. Curtiss, J. Mater. Chem., 2007, 17, 3315; A. S. Barnard, J. Phys. Chem. C, 2008, 112, 1385.
38. A. S. Barnard and L. A. Curtiss, ChemPhysChem, 2006, 7, 1544.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
40. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, RC558.
41. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169.
42. P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953.
43. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
44. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
45. D. M. Wood and A. Zunger, J. Phys. A: Math. Gen., 1985, 18, 1343.
46. R. J. Needs and M. Mansfield, J. Phys.: Condens. Matter, 1989, 1, 7555.
47. M. Blanco-Rey and S. J. Jenkins, J. Phys.: Condens. Matter, 2010, 22, 135007.
48. J. L. F. Da Silva, C. Stampfl and M. Scheffler, Surf. Sci., 2006, 600, 703.
49. A. Khein, D. J. Singh and C. J. Umrigar, Phys. Rev. B: Condens. Matter, 1995, 51, 4105.
50. C. Kittel, Introduction to Solid State Physics, Wiley, New York, 5th edn, 1976.
51. CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, FL, 90th edn, 2009.
52. R. E. Macfarlane, J. A. Rayne and C. K. Jones, Phys. Lett., 1965, 18, 91.
53. L.-Y. Chang, A. S. Barnard, L. C. Gontard and R. E. Dunin-Borkowski, Nano Lett., 2010, 10, 3073.
54. A. S. Barnard and L. Y. Chang, ACS Catal., 2011, 1, 76.
55. Y. V. R. K. Prasad, D. H. Sastry and K. I. Vasu, J. Mater. Sci., 1970, 5, 495.
56. J. P. Hirth and J. Lothe, Theory of Dislocations, J. Wiley & Sons, New York, 2nd edn, 1982.
57. E. A. Guggenheim, Thermodynamics, North Holland, 4th edn, 1993.
58. A. V. Grosse, J. Inorg. Nucl. Chem., 1962, 24, 147.
59. G. A. Somorjai, Introduction to Surface Chemistry and Catalysis, John Wiley & Sons, Inc., New York, 1994.
60. P. Buffat and J. P. Borel, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 2287.
61. W. H. Qi and M. P. Wang, Mater. Chem. Phys., 2004, 88, 280.
62. A. S. Barnard, Comput. Phys. Commun., 2011, 182, 11.
63. F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, J. Chem. Phys., 2002, 116, 3856.
64. A. R. Sandy, S. G. J. Mochrie, D. M. Zehner, G. Grübel, K. G. Huang and D. Gibbs, Phys. Rev. Lett., 1992, 68, 2192.
65. H. B. Lyon and G. A. Somorjai, J. Chem. Phys., 1967, 46, 2539.
66. N. V. Long, N. D. Chien, T. Hayakawa, H. Hirata, G. Lakshminarayana and M. Nogami, Nanotechnology, 2010, 21, 035605.
67. L. C. Gontard, L.-Y. Chang, C. J. D. Hetherington, A. I. Kirkland, D. Ozkaya and R. E. Dunin-Borkowski, Angew. Chem., Int. Ed., 2007, 46, 3683.
68. L. Y. Chang and A. I. Kirkland, Microsc. Microanal., 2006, 12, 469.
69. M. Rajappan, W. Swiech, M. Ondrejcek and C. P. Flynn, J. Phys.: Condens. Matter, 2007, 19, 226006.
70. A. Seyed-Razavi, I. K. Snook and A. S. Barnard, Cryst. Growth Des., 2011, 11, 158.
71. A. S. Barnard and Y. Chen, J. Mater. Chem., 2011, 21, 12153.

---