Role of defects in propene adsorption and reaction on a partially O-covered Au(111) surface

Abstract

We investigate the role of defects—adatoms, vacancies, and steps—in the bonding and reaction of propene on Au(111) containing atomic oxygen, using density functional theory (DFT) calculations. The adsorption of propene is stronger on a surface containing defects compared to the flat, bulk-terminated surface, with the largest gain in binding (∼0.7 eV) on a surface with a 1/9 monolayer (ML) of Au adatoms. Charge-density difference plots reveal that the difference between defective surfaces and the bulk-terminated surface is a more pronounced depletion of electron density from the carbon–carbon π bond and a charge accumulation between the double bond and the gold atom to which the propene is bound. We calculate the energy barriers for two competing reactions that are important in determining the selectivity for propene oxidation. Allylic H abstraction by adsorbed O leads to combustion, whereas O addition to form an oxymetallacycle is the first step in propene epoxide formation. A comparison of the energetics of these two pathways on flat and defect-containing Au surfaces indicates that the reactivity depends on the nature and prevalence of surface defects. Both electronic and geometric factors, such as the path and the distance the oxygen must travel to meet the allylic hydrogen for abstraction, are important in explaining the reaction trends.

---

Introduction

The conversion of olefins to epoxides is an important reaction because epoxides are extensively used in the chemical industry as an intermediate for many synthetic processes.¹Gold-based catalysts are active for selective epoxidation of propene and other olefins at moderate temperatures, making them promising candidates for new catalytic processes. The development of new processes for epoxidation of propene is of particular interest because of the wide use of propene oxide for the production of polyether polyols, propene glycol, and propylene glycol ethers.²

There are many factors that contribute to the reactivity of a metal catalyst, a prominent one being its atomic-scale surface structure. Gold, in particular, has shown promise as a selective oxidation catalyst because of its high activity for CO oxidation^3–7 and for selective propene epoxidation⁸ at low temperatures. The effect of gold's surface structure on the reactivity is an intensely debated topic because there is evidence that the size of particles is critical in determining their activity.^9–13

Epoxidation of olefins over coinage metals (Cu, Ag, Au) is widely thought to proceed via an oxametallacycle intermediate formed from addition of O to the C=C bond (Scheme 1).^14,15 A major challenge to the selective epoxidation of propene specifically is that combustion often predominates over partial oxidation because of acidic, allylic C–H bonds (shown in Scheme 1). While ethene oxide is selectively produced using heterogeneous Ag catalysts,¹⁶propene is mainly combusted¹⁷ due to the efficient abstraction of allylic H in propene by O on Ag. These allylic hydrogens are acidic, labile, and can be more easily removed by oxygen bound to the noble metals (Au, Ag, and Cu) because oxygen acts as a Brønsted base. For gold or any other metal to be used as a catalyst for selective oxidation of olefins with allylic C–H bonds, oxametallacycle formation and subsequent ring closure must compete effectively with allylic hydrogen abstraction. The challenge is to determine the features of the catalyst that promote one or the other of these two reaction pathways.

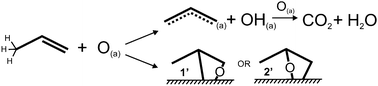Scheme 1 Schematic representation of the reactions of propene with adsorbed atomic oxygen on Au(111): allylic hydrogen abstraction to form allyl and hydroxyl (top) and oxygen insertion to form either a primary (1′) or secondary (2′) oxametallacycle (bottom). The reactive allylic hydrogens are drawn on propene.

These considerations motivated the present investigation of the activity of O bound to a metallic Au(111)^14,18,19 surface as a model system, similar to studies of olefin oxidation on O-covered Ag.^20–24 Previous studies have shown that atomic oxygen bound to metallic Au (O/Au(111)) is highly active for olefin partial oxidation, including the oxidation of propene.¹⁴Styrene epoxidation is promoted by O bound to Au(111) with a selectivity of ∼55%,¹⁸ remarkably similar to that reported for Au₅₅ clusters on inert supports.¹¹

Selective epoxidation is observed even under low-pressure conditions for phenyl substituted propenes, such as trans-β-methyl styrene and α-methylstyrene.^25,26 The selectivity for epoxidation depends on the gas-phase acidity of the C–H bonds in these reactant molecules.²⁶ In addition to combustion and epoxidation, there is a third pathway that is observed for propene and phenyl-substituted propenes—O insertion in the allylic C–H bond.^14,25,26 This pathway leads to acrolein from propene, and corresponding unsaturated aldehydes from the phenyl substituted propenes.

The selectivity for these competing oxidation pathways depends strongly on the morphology of the Au surface and the local bonding of O, both of which are affected by the oxygen coverage and surface temperature.^27,28 Our model studies show that gold atom release from the surface is induced by O bound to the surface and that atomic oxygen stabilizes gold adatoms resulting in a roughened surface.^29,30 The degree of long-range order, which can be tuned by changing the surface temperature and the rate of oxidation, substantially changes activity and selectivity towards propene oxidation on metallic Au.¹⁹ These morphological changes and changes in the surface order are associated with changes in the local bonding of O to the Au, suggesting that this is a key factor in determining chemical behavior towards propene oxidation.

There is also considerable experimental evidence that demonstrates the importance of surface morphology in determining reactivity and selectivity on Au nanoparticles. Defects, such as step-edge sites and other types of under-coordinated atoms, are ubiquitous on oxide-supported gold nanoparticles used as catalysts; under-coordinated gold atoms are thought to be one origin of gold activity,^31–33 which is also determined by the size and the morphology of the supported nanoparticles.^{7,8,11,34–36} The catalytic activity of gold nanoparticles on inert materials, e.g.boron nitride, silicon dioxide, and carbon, for styrene epoxidation using O₂ as an oxidant strongly depends on the particle size; smaller gold particles (∼1.4 nm in diameter) that have an irregular perimeter are most active, while larger particles (>2 nm) that have more regular shapes tend to be inactive.¹¹ Recent work on the reduction of resazurin on Au nanoparticles, studied by single-molecule techniques, likewise illustrates the importance of surface morphology, distribution of surface sites, and dynamic restructuring in nanocatalysis.^35,37,38

In the present work, we use density functional theory (DFT) to calculate the bond energies and barriers for allylic hydrogen abstraction and oxametallacycle formation of propene by oxygen on the Au(111) surface in order to understand the morphological and structural effects in olefin oxidation. While the oxidation of propene on the surface of gold has been the subject of several theoretical studies,^39–46 none of the previous studies considered the possible roles of defects in determining bonding and reactivity. We show that surface defects (such as steps, surface adatoms, and surface vacancies) significantly affect the adsorption properties of propene on gold. We also find that these defects change the reaction barriers for the two reactions we considered, which suggest that surface reactivity will generally depend on the presence of defects, consistent with experimental studies of catalytic behavior. Our results underscore the importance of including the effect of defects in models of catalytic behavior and surface reactivity when using electronic structure calculations to understand these phenomena.

Calculational details

For the DFT calculations, we used the VASP⁴⁷ code with the GGA-PW91⁴⁸ and LDA functionals⁴⁹ to describe electron exchange and correlation. The interaction of propene with the metal surface is mainly dispersive (van der Waals) in nature. We are fully aware of the limitations of the GGA functional in describing this type of interaction and the resulting underestimation of binding energies.⁵⁰ The LDA functional typically gives larger binding energies for dispersive systems which may be closer to actual bond energies, though not by virtue of providing a better physical description of dispersive forces.^51,52 Recent attempts have been made to create functionals that can accurately model dispersive forces,^53–55 with some success. Here we only report results obtained using the GGA functional since we are interested in qualitative trends and relative energies, which agree well between the two functionals. Moreover, much of the discussion focuses on reaction energy barriers, for which the GGA functional is generally used.

We use projector augmented wave pseudopotenitals^56,57 (cut-off: 400 eV) and a 4 × 4 × 1 Monkhorst-Pack k-point sampling of the reciprocal space. The electronic structure was converged to within 10⁻⁴ eV without spin treatment, and the geometries optimized until the forces were smaller than 0.02 eV Å⁻¹. The surface is modeled by a slab consisting of 4 layers in the (111) direction with a 3 × 3 supercell of the primitive unit cell in the lateral directions. Only the two uppermost layers of the slab were allowed to relax, with the rest being fixed at the ideal bulk positions. The bulk gold positions of the bottom two layers were determined using the calculated lattice constant (4.17 Å), which is in good agreement with the experimental value of 4.08 Å.⁵⁸

Reaction barriers were determined using the climbing nudged elastic band method (cNEB),^59–61 with three images between the two fixed end points at a reduced force threshold of 0.05 eV Å⁻¹. In a few cases, the calculation did not converge to a transition state, which required the use of additional images. To reduce computational costs, these calculations were preformed with a three layer slab, allowing the two uppermost layers to relax with 3 × 3 × 1 Monkhorst-Pack k-point sampling. An ensemble of starting points for each reaction was tested. We only report the energy of the pathway with the lowest barrier, defined as the difference in energy between the transition state and the lowest energy configuration from the ensemble of tested starting points. The lowest energy configuration was not always used as the starting point for performing the cNEB, since that configuration may not have the oxygen in close proximity to the allylic hydrogen or double bond. However, the difference in energy between the lowest energy configuration and that used as the starting configuration was always quite small (<0.1 eV).

Results

Equilibrium structures

Four different gold substrates were investigated to model the effects of under-coordinated gold atoms that may be responsible for activating gold: (1) the flat, defect-free (111) surface; (2) a (111) surface with 1/9 ML gold adatoms, that is, one extra Au atom per 3 × 3 (111) surface unit cell relative to the defect-free surface, which is placed at the FCC three-fold site; (3) a surface with 1/9 ML of vacancy defects, that is, one Au atom per 3 × 3 surface unit cell fewer than the defect-free surface; and (4) a stepped 〈110〉/{1,0,0} Au(211) surface, created by offsetting the lattice vectors by one gold layer, which results in a step and a (3 × 3) terrace. The Au(111) surface is the most thermodynamically stable surface of Au due to its hexagonal close-packed structure. The four surfaces were chosen to represent fundamentally every type of surface defect since most defects observed experimentally are likely combinations of those tested in this work.⁶²

The binding strength of propene on each of these surfaces is determined by its adsorption energy defined as:

E_ads = E_propene/Au − E_Au − E_propene

where E_propene/Au is the energy of a propene molecule bound to the gold substrate, E_Au is the energy of the gold substrate, and E_propene is the energy of a propene molecule in the gas phase. On each gold substrate many different adsorption structures of binding configurations were considered; the lowest energy configuration on the potential energy surface (PES) for each gold substrate was identified. In some cases more than one minimum on the PES exist with similar energies, which are briefly discussed, but we focus on the structure with the lowest energy.

Surface defects have a stabilizing effect on the relatively weak binding of propene to gold. The lowest energy configuration has an adsorption energy of −0.78 eV and has the C=C bond centered over a single under-coordinated gold adatom (Fig. 1). The overall trend is for the strongest binding on an adatom-covered surface, weakening with increasing coordination of the gold atom to which propene is bound. Therefore, the trend in adsorption strength for propene is:

defect-free < vacancy < step < adatom

as seen in Fig. 2. In the most extreme case, adsorption on the adatom-covered surface leads to a binding energy lower by 0.67 eV than the defect-free surface. This increase in binding strength is associated with a shorter carbon–gold distance. The sp²carbon–gold distance is 3.07 Å on the flat surface, but is 2.28 Å for the adatom-covered surface. The shorter bond length in conjunction with a stronger binding energy suggests that there is more electron density added between the carbon and gold atoms as the Au coordination number decreases. On the other defect surfaces, propene prefers adsorption to the gold atom with lowest coordination. In the case of vacancy defects, the double bond is situated on top of a gold atom neighboring a vacancy. Similarly, propene preferentially binds to the edge atoms of a step. On the flat defect-free surface, all the surface gold atoms have the same coordination, so adsorption is equally probable on top of any gold atom on the defect-free surface.

Fig. 1 Optimized geometries (top and side views) of propene on: (a) a gold surface with 1/9 ML of adatoms; (b) a gold surface with 1/9 ML vacancies; (c) a stepped gold surface. Gold adatoms, the first layer and the second layer of the gold surface are represented by orange, yellow, and brown spheres, respectively.

Fig. 2 Schematic representation of the adsorption energies and reaction barriers of propene with adsorbed atomic O on Au(111) for the “Flat”, “Vacancy”, “Step” and “Adatom” surfaces (all values in eV). The value under each black horizontal line indicates the adsorption energy for a propene molecule at this site in the presence of the O atom [the second value in square brackets corresponds to the adsorption energy in the absence of the O atom]. The barrier to the right (blue line) represents the allylic hydrogen abstraction reaction while the barrier to the left (red line) represents a secondary (2′) oxametallacycle reaction. The first four lowest effective-barrier reactions, labeled A, B, C, D, are indicated along with the effective barrier values (see the text for details).

Oxygen bound to gold in proximity to propene increases the adsorption energies for propene bound to surfaces both with and without defects. In Fig. 2, we summarize the adsorption energies (in eV), as obtained from the DFT-GGA calculations, in the presence of O atoms in the immediate neighborhood of the site where the reaction takes place (the adsorption energies in the absence of the O atoms are also given in square brackets in each case, for comparison). The adsorption energy for propene in the presence of a neighboring O atom is defined as:

E_ads = E_propene/Au/O − E_Au/O − E_propene

where E_Au/O is the energy of the gold substrate with oxygen at the same location as in the co-adsorbed system, E_propene/Au/O is the energy of the total system and E_propene is the energy of a single propene molecule in the gas phase. The preferred adsorption sites for oxygen on Au were established in previous work⁶² and were taken as the starting points for our investigation on propene adsorption. Atomic oxygen generally prefers to adsorb on a three-fold hollow site, binding away from an adatom, but neighboring a vacancy. On the stepped surface, binding to the three-fold site at the step edge or at a bridge site hanging over the step edge is essentially equal in energy.

We find that propene and oxygen bind in close proximity, yet they occupy the same sites that were preferred when adsorbed individually on each of the surfaces studied. This suggests that the interaction between propene and oxygen is weak relative to the binding strength of each component to the surface. Overall, the adsorption of propene is slightly stronger in the presence of oxygen (see Fig. 2). The increase in the magnitude of the adsorption energy is nearly the same for all the different substrates, with the average value being 0.13 eV. An oxygen atom binds preferentially near an allylic hydrogen of the propene on the defective surfaces, but not on the flat, defect-free surface. Oxygen atoms bind preferentially next to the hydrogen atom of the methylene on the defect-free surface. However, the difference in energy between this adsorption configuration and oxygen bound next to the allylic hydrogen is quite small (<0.05 eV), within the margin of error of our calculations.

Transition states for reactions

We investigated only two pathways, allylic hydrogen abstraction by oxygen to form adsorbed allyl and OH, and oxygen addition to one of the olefinic carbons to yield one of two possible oxametallacycles (Scheme 1), because they probe the competition between combustion and epoxidation, as previously established for Ag and Cu surfaces.⁴⁰ We also tested the transfer of hydrogen to Au, but found the energetic barrier to be much higher than the two previously mentioned pathways. While we use OH as one of the products for allylic hydrogen abstraction, experimentally OH is known to be unstable with respect to disproportionation on Au.⁶³ However, it is reasonable to expect that it is formed in the first step for allyl formation.

Allylic hydrogen abstraction is most facile when oxygen is present on the defect-free Au(111) surface and at vacancy defects. The calculated barrier for allylic hydrogen abstraction on the defect-free surface is 0.33 eV (Table 1), a value close to that (0.30 eV) calculated by Torres et al.⁴⁰ for hydrogen abstraction on flat O-covered Ag(111). The presence of under-coordinated atoms (steps and adatoms) leads to nearly twice the energy barrier for allylic C–H abstraction. The order of barrier heights is:

flat ≈ vacancy < adatom < step

as summarized in Table 1. The initial configuration for the cNEB calculations on all surfaces has oxygen in a three-fold FCC site in close proximity with the methyl group of propene rotated so that the allylic hydrogen is pointed toward the oxygen in the abstraction. This leads to a slight increase (<0.05 Å) in the O–Au separation.

Table 1 Reaction barriers (E_a) and change in energy (ΔE) for hydrogen abstraction of propene by oxygen (in the first two columns labeled by ‘H’) and propyl oxametallacycle with oxygen bonded to either the primary (1′) or secondary (2′) carbon. The ΔE for hydrogen abstraction is calculated with OH as the final step. As we explained in the text, OH is known experimentally to be unstable with respect to disproportionation on Au but is used since it is in the first step for allyl formation. Since it quickly disproportionates, this step is not a limiting reaction rate

Surface	E a H/eV	ΔE H/eV	E a 1′/eV	ΔE 1′/eV	E a 2′/eV	ΔE 2′/eV
Flat	0.33	−0.09	0.75	−0.39	0.51	−0.37
Vacancy	0.33	−0.07	0.89	−0.20	0.71	−0.31
Step	0.73	0.03	0.82	−0.32	0.62	−0.45
Adatom	0.65	0.08	0.87	0.16	0.65	−0.09

---

The final configuration contains the remaining allyl and an OH group (Fig. 3). The reaction pathway and geometry of the transition states are nearly the same on each of the other Au surfaces investigated. Further, the bond distances in all of the transition states are virtually identical (see Table 2).

Fig. 3 Atomic structures corresponding to different points along the two reactions: Allylic hydrogen abstraction by oxygen: (a) initial state; (b) transition state; (c) final state. Oxygen attaching to 2′ carbon to form an oxametallacycle on the defect-free Au(111) surface (d) initial state; (e) transition state; (f) final state. Brown, blue, red, and white spheres represent gold, carbon, oxygen, and hydrogen, respectively. The end point (c), which is not the global minimum since OH is not in its preferred bridging site, is used for the cNEB calculation because of its close proximity to the propene and transition state.

Table 2 Ground state and transition state distances in Angstroms for allylic hydrogen abstraction of propene by oxygen

Surface	Ground state			Transition state
	C–O	C–H	H–O	C–O	C–H	H–O
Flat	3.29	1.10	2.22	2.60	1.29	1.31
Vacancy	3.22	1.10	2.12	2.60	1.30	1.30
Step	3.74	1.10	2.64	2.61	1.30	1.33
Adatom	4.38	1.10	3.28	2.60	1.32	1.28

---

We considered the addition of adsorbed oxygen to propene to form the two possible oxametallacycle species, with oxygen being added to either the primary carbon (labeled 1′) or the secondary carbon (labeled 2′) (Scheme 1). The formation of the 2′ oxametallacycle is slightly preferred over the formation of the 1′ form on all surfaces investigated, based on the lower barriers and larger gains in energy calculated for the former (see Table 1).

There are also differences in the reaction barriers for oxametallacycle formation for the various types of defects, although the relative ordering and magnitudes of these differences are not the same as those calculated for hydrogen abstraction. The maximum difference in the energy barriers for oxametallacycle formation is 0.2 eV, approximately half of that for allylic C–H abstraction. The lowest barrier computed is 0.51 eV for formation of the 2′ oxametallacycle (addition to the C bound to the methyl group; Scheme 1) on the flat, defect-free surface, which is somewhat higher than the barrier computed for allylic hydrogen abstraction on the same surface (Table 1). The highest barrier for oxametallacycle formation is for the surface containing vacancy defects. Overall, the order of energy barriers for oxametallacycle formation is:

defect-free < step < adatom < vacancy

as seen from Table 1. This trend is the same for both the 1′ and 2′ oxametallacycle configurations. Interestingly, the Bell–Evans–Polanyi rule apparently does not hold,⁶⁴ since the reaction barrier (E_a) is not inversely proportional to the total change in energy (ΔE) during the reaction. This is likely a result of the other factors that have a greater effect on the reaction barrier and likely an expected result due to geometric differences.

The results of all the reaction barrier calculations are also included in Fig. 2, combined with the results for the adsorption energies at different sites.

Discussion

Our results indicate that adsorption of propene is enhanced on under-coordinated gold atoms: the gain in adsorption energy can be as large as 0.67 eV when the C=C double bond of propene is bound on top of an adatom compared to adsorption on the flat surface. This stabilization is ∼3 times greater than the overall binding energy of propene on the flat Au(111) surface (Fig. 2). This result is in agreement with previous reports by Chretien et al.⁶⁵ who found that propene binds most strongly on a gold cluster when the LUMO of the cluster “protrudes most in the vacuum”, which is usually at an under-coordinated gold atom. Similarly, Kokalj et al.⁶⁶ found that ethene binds stronger to defects on Ag(001) compared to adsorption on the flat surface. We elaborate below on the physical origin of these findings.

Physical origin of propene adsorption differences on Au(111) with defects

There is significant variation in charge distribution when propene is adsorbed on flat Au(111) compared to when either gold adatoms or oxygen atoms are present based on analysis of charge density difference plots (Fig. 4). We calculate the difference in electronic density between the combined system (propene adsorbed on the Au(111) surface) and the separate isolated components (free Au(111) surface and isolated propene molecule) with atomic positions frozen at the optimized surface geometry corresponding to the adsorbate system.

Fig. 4 Charge density difference contour plots for propene adsorbed on: (a) the clean, defect-free surface; (b) a surface with oxygen atoms; (c) a surface with Au adatoms and oxygen atoms. The plot is on the plane that connects the two carbon atoms that form the double bond in propene and the gold atom to which the propene is bound. In all three cases the carbon on the left is the one attached to the methyl group. In (b) the oxygen is neighboring to the allylic hydrogen. The labeled Au in (c) is the gold adatom while in (a) and (b) it is a gold atom in the first layer. Positive values (red) indicate accumulation of electronic charge; negative values (blue) correspond to depletion of charge.

There are only minor changes in the charge density difference for propene adsorbed on the flat, defect-free surface (Fig. 4a), consistent with the weak bonding of propene to clean, flat Au(111). Analogous to bonding models in organometallic compounds, propene bonding to a metal involves electron donation from the π orbitals of the C=C double bond to the d-band of the metal as well as donation of electrons from filled metal d states to the anti-bonding π* orbitals with a lengthening of the double bond.⁶⁷ Experimental studies of olefins on Au are also consistent with this bonding mode.^68,69 For Au(111), there are only minor changes in charge density when propene is bound to the surface, that is, a small depletion of electron density from vertical p-like orbitals of the two carbons that comprise the C=C double bond, and a very small increase in the electron density between the double bond and the Au atom, which most likely accounts for the slight attraction between propene and the surface. The plot also shows electron density addition to the σ-bond between the two carbon atoms.

There is more distortion of the charge density upon propene binding when oxygen is present on the gold surface (Fig. 4b). We find that the magnitude of these distortions depends on the location of the oxygen atom relative to the C=C double bond, with distortions being greater for oxygen adsorbed closer to the double bond.

The electronic configuration changes substantially for propene bound to the Au surface containing both Au adatoms and O: in this case, the electron density is much more localized between the Au and the C=C bond. This localization of charge occurs almost directly between each of the sp²-bonded carbons and the Au adatom, resulting in a stronger binding of propene to this surface. The C=C bond length correspondingly increases from 1.35 Å on the flat, defect-free surface to 1.39 Å on the adatom-covered surface. The localization of charge and more drastic electronic rearrangement are both attributed to the stronger adsorption of propene on the adatom-covered surface. In contrast to co-adsorption of oxygen and propene on the flat Au(111) surface, oxygen has little effect on the adsorption of propene on the adatom-covered surface, since oxygen does not prefer to bind close to the gold adatom (not shown).

Physical origin of reactivity differences in allylic hydrogen abstraction on Au(111)

Defects on the gold surface affect both the adsorption strength of propene and the barriers for reaction. The barrier for allylic hydrogen abstraction on the flat and vacancy surface is 0.33 eV, but on the stepped surface the barrier for hydrogen abstraction is 0.73 eV, more than twice that on the flat and vacancy surface.

The spatial arrangement of the allylic hydrogen of propene with respect to the atomic oxygen is one of the most important factors in determining the barrier height for allylic abstraction. During the reaction, both propene and oxygen must distort their equilibrium structures to meet at the transition state. The C–O distance is the same (∼2.61 Å) in all of the transition states for the four different surfaces, but is shorter than the relaxed C–O distance which was different on the four surfaces. For example, the equilibrium distance between the methyl carbon and oxygen in the starting configuration on the defect-free surface is 3.29 Å while on the adatom-covered surface it is 4.38 Å. This distance is also larger for the stepped surface (3.74 Å) and is similar to the adatom surface, which has a much higher barrier for allylic abstraction. The vacancy surface has a smaller starting C–O distance (3.22 Å) and a barrier lower than on the stepped and adatom surfaces, but closer to that on the flat, defect-free surface (0.33 eV).

Our calculations indicate that the oxygen atom moves to a less stable site during reaction with an allylic hydrogen leading to a slight deformation of the gold surface. The energy cost of this deformation correlates with the overall energy barrier and is at least partly responsible for the calculated differences between substrates. We calculated the difference in energy (ΔE_s) between oxygen adsorbed on the surface in its equilibrium position and oxygen and gold frozen in their positions from the transition state in the absence of propene. In all cases the oxygen atom moves from a three-fold site to a lower coordination site. The equilibrium coordination for oxygen in OH is on a two-fold site. In the transition state, the oxygen will have coordination somewhere in between a two-fold and three-fold site, since it is gaining a partial bond from hydrogen. Since the transition state in all four cases has nearly the same bond distances and the electronic structures are similar, we assume that this lower coordination with gold (the oxygen distortion which is the result of moving from a three-fold to two-fold site) should be the same on all four surfaces. Depending on the distance and the path along which the oxygen must travel to reach the C–O distance in the transition state (∼2.61 Å), this could place an extra strain on the oxygen in addition to the lower coordination, which can vary depending on the initial configuration. We find that ΔE_s is 0.19 eV, 0.18 eV, 0.55 eV, and 0.55 eV for the defect-free, vacancy-covered, adatom-covered, and stepped surfaces, respectively. Recall that the barriers on the four surfaces were 0.33 eV, 0.33 eV, 0.65 eV, and 0.73 eV, respectively, illustrating that the difference in energy between the equilibrium substrate and the substrate frozen in its transition state correlate well with the calculated barriers. A similar procedure was carried out for the 2′ oxametallacycle formation. We find that ΔE_s is 0.28 eV, 0.44 eV, 0.16 eV, and 0.08 eV for the defect-free, vacancy-covered, adatom-covered, and stepped surfaces, respectively. These energies do not correlate as well with the reaction barrier as was the case for the allylic hydrogen barrier, suggesting that other factors are important, including the distortion of propene and the electronic structure of the double bond, where we know the defect can have an impact (Fig. 4).

It is important to point out that the barrier for allylic hydrogen abstraction is not strictly correlated to the distance the oxygen needs to travel to meet the allylic hydrogen. We compared two different starting configurations for the reaction on the flat, defect-free surface. We found that the starting C–O distance was actually shorter for a reaction that ultimately resulted in a higher barrier. The higher barrier could be accounted for by the additional energy cost required to move the oxygen atom to its location in the transition state, ΔE_s. The energy barrier is also most likely correlated to propene distortion, since both the oxygen atom and propene can move to meet at the transition state. For simplicity, we only investigated the energy cost for oxygen distortion to illustrate the correlation to the energy barrier for allylic H abstraction.

It is worth exploring other factors that could affect the magnitude of the energy barrier on each type of surface. The basicity of atomic oxygen is generally thought to have a significant impact on its ability to abstract an allylic hydrogen⁴⁰ because a stronger base is expected to more easily react with the acidic hydrogen. Oxygen atoms are more electronegative than gold and are expected to redistribute electron density resulting in a partial negative charge on the oxygen and some small positive charge on the nearby Au atoms. A measure of the partial negative charge on the oxygen is a crude approximation for its basicity. To estimate the charge on the adsorbed oxygen atom, we use the Bader method which partitions the charge density into non-overlapping basins defined by hyper-surfaces where the electron density gradient vanishes.⁷⁰ The estimated charge on oxygen atoms is nearly the same on all of the four surfaces we considered (−0.81 e⁻). This result is expected since the binding of oxygen on all four of these surfaces is nearly the same; oxygen binds on a three-fold site in all cases. Previous work established that for the adsorption of electronegative atoms on gold, the partial negative charge on the adsorbate decreases only when the number of gold atoms to which the adsorbate atom is bound decreases.⁷¹

The binding strength of oxygen to the surface also does not solely explain the observed reaction trends. We could propose that the stronger the binding of oxygen to the gold surface, the harder it will be to react with hydrogen to form hydroxyls. In previous work, the adsorption of oxygen (at a coverage of 1/16 ML instead of the 1/9 ML used herein)⁶² was stronger at the edge of a step or adjacent to a vacancy compared to the flat, defect-free surface. While these results partly follow the proposed trend, the adatom-covered surface is a clear exception. The binding strength of oxygen on the adatom-covered surface is equal to or less (depending on its exact location) than on the flat surface yet the barrier for hydrogen abstraction is over two times higher on the adatom-covered surface in comparison to the flat, defect-free surface.

Changes in the bonding between the methyl carbon and the allylic hydrogen on the different surfaces also do not account for the calculated differences in barrier heights. The charge density difference plots in Fig. 4a and c show some electronic differences between the C=C double bond on the defect-free and the adatom-covered surfaces, but these differences do not extend to the allylic hydrogen. The electron densities between the methyl carbon and allylic hydrogen differ by no more than 0.02 e⁻ on the four different defect surfaces. The fact that bond distances are similar in the transition states for all four surfaces further suggests that the electronic structure of the reaction pathway is similar for all four cases.

Comparison to other DFT calculations of propene on Au

A recent report also investigated allylic hydrogen abstraction and oxygen insertion on the flat oxygen-covered Au(111) surface using DFT,⁷² but includes some important differences with our results. We have performed additional convergence tests, using a slab of thickness up to five layers and 7 × 7 × 1 Monkhurst-Pack k-point sampling, which gave energy barriers different by at most 0.1 eV but no change in the qualitative ordering of site reactivity. From these we conclude that the differences between our results and those of ref. 72 cannot be attributed to incomplete convergence.

Based on simple physical arguments, we argue that the results reported here are physically plausible. The barrier reported for allylic hydrogen abstraction in ref. 72 is smaller than our result and transition state geometries are different. In the work of Roldan et al.⁷² the distance between H and the accepting surface oxygen is 0.99 Å, which is very close to the equilibrium distance for a surface hydroxyl on Au (0.98 Å). We identified the transition state O–H distance to be 1.31 Å, with H nearly equally shared between the accepting oxygen and the carbon of the propene. Although we did find a transition state similar to the one reported in ref. 72, it seems that this transition state is associated with the hydroxyl group diffusing towards its final geometry. Our conclusion is that the transition state reported herein was missed in the prior work.

Another important difference between the present work and ref. 72 is the qualitative ordering of the energy barrier for the formation of the 1′ and 2′ oxametallacycles. In the work of Roldan et al.⁷² the barrier for forming the 1′ oxametallacycle is lower than 2′ formation, while the opposite is true in our work. As was the case in allylic hydrogen abstraction, the transition state geometries found by Roldan et al.⁷² differ from ours. During oxametallacycle formation an oxygen atom is added to the carbon–carbon double bond of the propene, effectively reducing the bond order from two to one. Indeed this carbon bond length increases from ∼1.36 Å to ∼1.52 Å from propene to the oxametallacycle. The carbon–carbon bond length in the transition state should lie somewhere between these values and, indeed, we find a value of 1.41 Å, while the work of Roldan et al.⁷² found a value of 1.35 Å, slightly less than the starting double bond length, which is implausible. A similar comparison cannot be made for the formation of the 2′ oxametallacycle since the previous studies did not report the carbon–carbon distance. We find similar trends for the 2′ oxametallacycle: the starting (propene), transition state, and end (2′ oxametallacycle) carbon–carbon distances were 1.36, 1.44, and 1.53 Å, respectively. Previous DFT calculations have investigated oxametallacycle formation on Ag(111) and Cu(111) and found on both surfaces that the primary oxametallacycle formation likewise had the lowest barrier.⁴⁰

Conclusions

Through an extensive investigation based on first-principles electronic structure calculations, we showed that the adsorption of propene on Au(111) can change significantly in the presence of defects. Of the different types of defects we considered, propene binds strongest on a single adatom-covered surface and binds stronger (compared to the flat, defect-free surface) on either vacancy-covered or stepped gold surfaces. Charge density difference plots reveal that the magnitude of the differences in the density, upon adsorption of propene, is greater on the defect-containing surfaces.

Our results also indicate that the reactivity of the gold surface changes in the presence of defects: for instance, the barrier for allylic hydrogen abstraction is smallest on the flat surface and highest on the adatom-covered surface. The difference in energy between the substrate in its equilibrium structure and the substrate frozen in its transition state configuration correlates well with the calculated energy barriers, suggesting that geometric and non-electronic factors account for most of the observed differences in the ability of oxygen to abstract allylic hydrogen.

Acknowledgements

The work was funded in part by a NSF graduate fellowship, a grant from NSF-NSEC (grant # CHE-0545335), and grants from Department of Energy (grant #ER25790). SCJ thanks the NSF for his GRFP fellowship. Computational resources were provided by the Faculty of Arts and Sciences Research Computing group and by the Instructional and Research Computing Services of the Harvard School of Engineering and Applied Sciences. We thank Dr Jan Haubrich, Dr Xiaoying Liu, and Dr Mark Hybertsen for helpful discussions.

Notes and references

1. J. A. Moulijin, P. W. N. M. van Leeuwen and R. A. Santen, Catalysis: an integrated approach to homogeneous, heterogeneous and industrial catalysis, Elsevier, New York, 1993.
2. T. A. Nijhuis, M. Makkee, B. M. Moulijn and B. M. Weckhuysen, Ind. Eng. Chem. Res., 2006, 45, 3447.
3. J. Schwank, Gold Bull., 1983, 16, 103.
4. M. Haruta and M. Date, Appl. Catal., A, 2001, 222, 427–437.
5. M. Haruta, Chem. Rec., 2003, 3, 75–87.
6. R. Meyer, C. Lemire, S. K. Shaikhutdinov and H. Freund, Gold Bull., 2004, 37, 72.
7. M. Haruta, N. Yamada, T. Kobayashi and S. Iijima, J. Catal., 1989, 115, 301–309.
8. T. Hayashi, K. Tanaka and M. Haruta, J. Catal., 1998, 178, 566–575.
9. M. Valden, X. Lai and D. W. Goodman, Science, 1998, 281, 1647–1650.
10. M. Valden, S. Pak, X. Lai and D. W. Goodman, Catal. Lett., 1998, 56, 7–10.
11. M. Comotti, W. C. Li, B. Spliethoff and F. Schuth, J. Am. Chem. Soc., 2006, 128, 917–924.
12. M. Haruta, Catal. Today, 1997, 36, 153–166.
13. M. Turner, V. B. Golovko, O. P. H. Vanghan, P. Abdulkin, A. Berenguer-Murcia, M. S. Tikhov, B. F. G. Johnson and R. M. Lambert, Nature, 2008, 454, 981.
14. X. Y. Deng, B. K. Min, X. Y. Liu and C. M. Friend, J. Phys. Chem. B, 2006, 110, 15982–15987.
15. S. Linic and M. A. Barteau, J. Am. Chem. Soc., 2002, 124, 310.
16. K. Weisermel and H. J. Arpe, Industrial Organic Chemistry,Wiley-VCH, Weinheim, 4th edn, 2003.
17. M. Akimoto, K. Ichikawa and E. Echigoya, J. Catal., 1982, 76, 333.
18. X. Y. Deng and C. M. Friend, J. Am. Chem. Soc., 2005, 127, 17178–17179.
19. B. K. Min, A. R. Alemozafar, D. Pinnaduwage, X. Deng and C. M. Friend, J. Phys. Chem. B, 2006, 110, 19833–19838.
20. A. Klust and R. J. Madix, Surf. Sci., 2006, 600, 5025.
21. J. W. Medlin and M. A. Barteau, Surf. Sci., 2002, 506, 105–118.
22. J. T. Roberts, A. J. Capote and R. J. Madix, J. Am. Chem. Soc., 1991, 113, 9848–9851.
23. J. T. Roberts, A. J. Capote and R. J. Madix, Surf. Sci., 1991, 253, 13–23.
24. J. T. Roberts and R. J. Madix, J. Am. Chem. Soc., 1988, 110, 8540–8541.
25. X. Y. Liu and C. M. Friend, J. Phys. Chem. C, 2010, 114, 5141–5147.
26. X. Y. Liu, T. A. Baker and C. M. Friend, Dalton Trans, 2010, 39, 36.
27. V. Zielasek, B. J. Xu, X. Y. Liu, M. Baumer and C. M. Friend, J. Phys. Chem. C, 2009, 113, 8924–8929.
28. B. K. Min, X. Y. Deng, X. Y. Li, C. M. Friend and A. R. Alemozafar, ChemCatChem, 2009, 1, 116–121.
29. J. Biener, M. M. Biener, T. Nowitzki, A. V. Hamza, C. M. Friend, V. Zielasek and M. Baumer, ChemPhysChem, 2006, 7, 1906–1908.
30. B. K. Min, X. Deng, D. Pinnaduwage, R. Schalek and C. M. Friend, Phys. Rev. B: Condens. Matter, 2005, 72, 4.
31. T. V. W. Janssens, A. Carlsson, A. Puig-Molina and B. S. Clausen, J. Catal., 2006, 240, 108–113.
32. C. Lemire, R. Meyer, S. K. Shaikhutdinov and H. J. Freund, Surf. Sci., 2004, 552, 27–34.
33. I. N. Remediakis, N. Lopez and J. K. Norskov, Appl. Catal., A, 2005, 291, 13–20.
34. N. Lopez, T. V. W. Janssens, B. S. Clausen, Y. Xu, M. Mavrikakis, T. Bligaard and J. K. Norskov, J. Catal., 2004, 223, 232–235.
35. W. Xu, J. S. Kong, Y. E. Yeh and P. Chen, Nat. Mater., 2008, 7, 992.
36. D. C. Lim, I. Lopez-Salido, R. Dietsche, M. Bubek and Y. D. Kim, Angew. Chem., Int. Ed., 2006, 45, 2413.
37. X. Zhou, W. Xu, G. Liu, D. Panda and P. Chen, J. Am. Chem. Soc., 2010, 132, 138.
38. W. Xu, J. S. Kong and P. Chen, Phys. Chem. Chem. Phys., 2009, 11, 2767.
39. S. Lee, L. M. Molina, M. J. Lopez, J. A. Alonso, B. Hammer, B. Lee, S. Seifert, R. E. Winans, J. W. Elam, M. J. Pellin and S. Vajda, Angew. Chem., Int. Ed., 2009, 48, 1467.
40. D. Torres, N. Lopez, F. Illas and R. M. Lambert, Angew. Chem., Int. Ed., 2007, 46, 2055.
41. D. Torres and F. Illas, J. Phys. Chem. B, 2006, 110, 13310.
42. A. M. Joshi, N. Delgass and K. T. Thomson, J. Phys. Chem. B, 2006, 110, 2572.
43. Y. Shimodaira and H. Kobayaski, J. Mol. Struct., 2006, 762, 57.
44. A. M. Joshi, W. N. Delgass and K. T. Thomson, J. Phys. Chem. C, 2007, 111, 7841–7844.
45. J. J. Bravo-Suarez, K. K. Bando, J. Q. Lu, T. Fujitani and S. T. Oyama, J. Catal., 2008, 255, 114–126.
46. J. J. Bravo-Suarez, K. K. Bando, T. Akita, T. Fujitani, T. J. Fuhrer and S. T. Oyama, Chem. Commun., 2008, 3272–3274.
47. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, 558–561.
48. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244–13249.
49. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
50. H. Rydberg, M. Dion, N. Jacobson, E. Schroder, P. Hyldgaard, S. I. Simak, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2003, 91, 126402.
51. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter, 1981, 23, 5048.
52. D. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566.
53. W. Kohn, Y. Meir and D. E. Makarov, Phys. Rev. Lett., 1998, 343, 4153.
54. Y. Andersson, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 1996, 76, 102.
55. E. Hult, H. Rydberg, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter, 1999, 59, 4708.
56. G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245–8257.
57. G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758.
58. in CRC Handbook of Chemistry and Physics, 77, ed. D. R. Lide, CRC Press, New York, 1996.
59. D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 134106.
60. G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901.
61. G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978.
62. T. A. Baker, C. M. Friend and E. Kaxiras, J. Phys. Chem. C, 2009, 113, 3232.
63. R. G. Quiller, T. A. Baker, X. Deng, M. E. Colling, B. K. Min and C. M. Friend, J. Chem. Phys., 2008, 129, 9.
64. C. Wentrup, Reactive Molecules, Wiley, New York, 1984.
65. S. Chretien, M. S. Gordon and H. Metiu, J. Chem. Phys., 2004, 121, 3756.
66. A. Kokalj, A. D. Corso, S. Gironcoli and S. Baroni, J. Phys. Chem. B, 2002, 106, 9839.
67. D. Shriver and P. Atkins, Inorganic Chemistry, W.H. Freeman and Company, New York, 1999.
68. H. M. Ajo, V. A. Bondzie and C. T. Campbell, Catal. Lett., 2002, 78, 359.
69. T. A. Nijhuis, E. Sacaliuc, A. M. Beale, A. M. J. van der Eerden, J. C. Schouten and B. M. Weckhuysen, J. Catal., 2008, 258, 256.
70. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford Science, Oxford, 1990.
71. T. A. Baker, C. M. Friend and E. Kaxiras, J. Chem. Phys., 2009, 130, 8.
72. A. Roldan, D. Torres, J. M. Ricart and F. Illas, J. Mol. Catal. A: Chem., 2009, 306, 6.

---