Correction for a possible reversible adsorption over an “inert” material†
Received
5th December 2010
, Accepted 12th January 2011
First published on 14th February 2011
Abstract
All TAP micro-reactor configurations contain inert particles which are used so that the catalyst zone can be maintained under isothermal conditions. Even on “inert” particles adsorption will occur to some degree; however, the extent to which this occurs has a critical influence on the analysis of the TAP data. In many cases the assumption that there is no interaction between probe molecules and inert particles is required as reversible adsorption over inert material is problematic when the TAP model has to be solved. Moreover, as the TAP pulse response experiments are designed to be conducted within the Knudsen diffusion regime, central to TAP data analysis is the characterization of the diffusional transport of reagent molecules through the micro-reactor, which is achieved via “diffusion only” experiments over an inert one zone packing. Therefore, if there are any processes occurring in addition to Knudsen diffusion over the inert material, such as reversible adsorption, it is important to factor these into the analysis. If these additional processes are not included, the entire data analysis would be questionable. The current work discloses the development of a function which accounts for the adsorption over the inert material, so that the TAP data analysis can be accurately determined. This newly developed analysis method has been exemplified using the selective reduction of oxygen in a hydrogen rich ethylene feed over silver catalysts as a case study.
Introduction
The Temporal Analysis of Products (TAP) reactor system has been designed for detailed kinetic characterization of various heterogeneous catalysts in the gas phase.1,2 The technique has been successfully applied to a wide range of reactions and catalysts.1–10 The TAP reactor operates on the premise of injecting a small gas pulse of very short duration into an evacuated micro-reactor containing a packed bed of particles. The duration of the inlet pulse is of the order of 250–500 μs, which provides the technique with a sub-millisecond time resolution. When the number of molecules in the pulse is sufficiently small (≈ 10−10 moles), the convective flow disappears and gas transport occurs by Knudsen diffusion. Due to the low inlet pulse intensity, the pulse-response TAP experiment provides an opportunity to control the catalyst composition.2 In a single-pulse TAP experiment, the changes in the catalyst composition during the experiment are very small compared with the amount of surface active sites due to the small pulse intensity. In a multi-pulse TAP experiment, the catalyst composition can be changed gradually, in a well-controlled manner.
It is a common practice when packing the TAP micro-reactor for kinetic catalyst characterization that the catalyst (active) zone is sandwiched between zones which are packed with inert material. The key advantage of such a reactor configuration is that it significantly improves temperature uniformity in the catalyst zone. In the case of the TAP technique this is known as a three-zone TAP reactor configuration. A limiting case of the three-zone configuration is a more advanced thin-zone TAP reactor (TZTR) configuration where the length of the active zone is much smaller than the length of the inert zones. The TZTR allows maintenance of nearly uniform concentration profiles in the thin catalyst zone during the vacuum pulse-response TAP experiment.11
Typical choices of inert material include silicon-carbide and quartz, with particles of approximately the same size as the catalyst. These materials typically have small surface area per volume compared with the catalyst under investigation and, therefore, are assumed to make little contribution to the adsorption processes. The assumption that there is no interaction between probe molecules and inert particles is critical in modelling TAP data (or data from any other transient experiments). Typically, this assumption is justified in a separate blank experiment. In TAP studies, such experiments involve pulsing various probe molecules over the reactor packed with inert material at various temperatures. Then, the responses are compared with theoretical curves calculated from the one-zone TAP Knudsen diffusion model. This model implies that the only process that takes place in the reactor is Knudsen diffusion. It is important to note that simple curve fitting of a few responses is not sufficient justification of Knudsen diffusion. It is well known that when adsorption/desorption are fast compared to the characteristic diffusion time, there is a contribution of the adsorption/desorption to the response shape. The contribution of fast adsorption/desorption appears as if the response corresponds to diffusion with a smaller diffusivity. Thus, an important part of the test for Knudsen diffusion is checking if observed diffusivities (D) or residence times (τres) follow the Knudsen diffusion law:
| |  | (1) |
The correct dependence of the Knudsen diffusivity or residence time on temperature (
T) and molecular weight (
Mw) of probe molecules can justify that none of probe molecules interact with the tested inert material in the studied temperature range.
Fig. 1 reports the correct dependence for helium, neon,
nitrogen and argon in the temperature range 50–300 °C over silicon carbide (particle size 500 μm). However, not all inert one-zone TAP tests produce such a clear dependence.
 |
| | Fig. 1 Residence time (first moment, M1) plotted vs. (molecular weight/temperature (K))1/2 for ( ) helium, ( ) helium, ( ) neon, ( ) neon, ( ) nitrogen and ( ) nitrogen and ( ) argon. ) argon. | |
There are four important factors that limit the inert behaviour of “inert material” in the pulse-response TAP experiment:
1. Very active molecules (e.g.ammonia or NOX) tend to adsorb on most surfaces;
2. In the low temperature range physical adsorption may be sufficiently strong to increase the residence time of the molecules to that comparable with the characteristic time of Knudsen diffusion (0.01–0.1 s);
3. Although surface impurities on the inert particles may be low compared with the number of active sites on the catalyst, a typical TAP pulse only contains a very small amount of molecules compared with the number of catalyst active sites. Hence, the quantity of impurities and number of pulsed molecules may be comparable.
4. Catalyst pre-treatment or activation using normal pressure flows often precedes kinetic tests. Such normal pressure treatments may significantly increase or activate the surface impurities on the inert particles.
It should be noted that temperature variation across the catalyst/inert bed is also important. A comparison of the profiles for argon as a function of catalyst bed configuration demonstrates that this is not an issue in the reactor shown here. In addition, this is much less problematic in the TZTR reactor configuration used here where only a very small amount of catalyst is used and the system is maintained under isothermal conditions.11
Reversible adsorption (likely physical adsorption) is the most typical process that occurs on “inert” surfaces. In this paper, theoretical tools to account for the reversible adsorption over “inert” particles in pulse-response TAP experiments and demonstration of the tools in practice are presented. First, the adsorption properties of the inert material are characterized in a series of one-zone TAP experiments. Second, the studied inert material is used for the thin-zone TAP reactor (TZTR) configuration, which includes catalyst and inert material.11 The theoretical tools allow the extraction of quantitative kinetic information about the interaction between probe molecules and catalyst in the form of basic kinetic coefficients.12 These basic kinetic coefficients were introduced previously as primary kinetic characteristics observed in the TAP experiment.12,13
In the TZTR, the concentration non-uniformity in the catalyst zone is negligible for a wide range of TAP conditions.14 These conditions are achieved when the length of the catalyst zone (or amount of catalyst) is much smaller than the length of the inert zones (amount of inert material). Hence, the amount (or volume) of inert material in the reactor is much greater than the amount of catalyst compared to the typical three-zone case. Thus, the adsorption over the inert material would produce a relatively greater contribution in the case of the TZTR, which makes the problem of reversible adsorption over the inert material especially relevant for this TAP reactor configuration.
One-zone model with reversible adsorption
The model of a single-pulse TAP experiment in a one-zone reactor can be expressed by a system of two partial differential equations for gas and surface concentrations:2| |  | (2) |
| |  | (3) |
where: ε is the bed voidage; Cg and Cθ are the gas and surface concentrations normalized per unit of reactor volume, respectively; D is the Knudsen diffusivity; x is the reactor axial coordinate; ka is the global adsorption rate constant (1/s); kd is the desorption rate constant (1/s).
Eqn (2) and (3) are subject to the ideal TAP initial and boundary conditions:15
| | | Zeroth initial condition: Cg|t=0 = 0, Cθ|t=0 = 0 | (4) |
| | | Vacuum condition at the exit: Cg|x=Lr = 0, | (5) |
| |  | (6) |
where:
Ar is the reactor cross-section area;
Din is the Knudsen diffusivity in the inert zone;
Lr is the length of the whole reactor and
Ng is the number of molecules in the inlet pulse.
The one-zone model can be solved using the Laplace transformation method, as detailed elsewhere.2 The Laplace solution for the exit flow time dependence (![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) exit) observed in the pulse-response TAP experiment was found as:
exit) observed in the pulse-response TAP experiment was found as:
| | 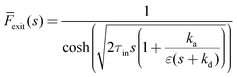 | (7) |
where the residence time in the inert one zone (
τin) is given by
eqn (8) and
s is the Laplace transform variable.
The Laplace solution from eqn (7) can be used to calculate moments (Mn) of the exit flow responses (Fexit) from the following equation:
| |  | (9) |
From
eqn (9), the following expressions for moments of the exit flow were determined:
| | 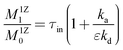 | (11) |
| |  | (12) |
where the upper index “1Z” denotes the moments measured in the inert one-zone TAP reactor.
Eqn (10) indicates that no conversion occurs in this case. Both eqn (11) and (12) can be used to determine the adsorption and desorption rate constants for an inert material from the moments of responses observed in the one-zone TAP experiment. They can also be used to calculate the following parameters:
| |  | (13) |
| |  | (14) |
The ratios
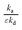
and

are explicitly present in the thin-zone solutions, as is discussed in the following section.
Thin-zone model with reversible adsorption over inert particles
The thin zone TAP reactor model includes partial differential equations for the inert zones and algebraic equations for matching the inert zone solutions in the centre of the catalyst zone (LTZ). The mass balance in the inert zones is described by eqn (2) and (3) from the previous section, which include the same diffusion, adsorption and desorption terms. Eqn (15) and (16) show the thin-zone matching conditions for the inert zone solutions (CI and CII):16| | | CI(t)|x=LTZ − CII(t)|x=LTZ = 0 | (15) |
| |  | (16) |
where LTZ is the axial position of the middle of the thin zone; Lcat is the length of the catalyst zone and RTZ is the spatial average reaction rate in the thin zone.
Eqn (15) ensures the continuity of concentration and is not related to the conversion or reaction rate.14 In general, the reaction rate for any reaction is taken into account in eqn (16), i.e. the difference between diffusional flows in/out of the thin zone is equal to the reaction rate.14 Thus the solutions that are presented (see eqn (19), (20) and (21)) describe all possible reactions between a probe molecule and catalyst.
The presented thin-zone model can be solved using the Laplace transformation method, subject to the initial and boundary conditions (eqn (4) to (6)). The Laplace solution for the exit flow was found as:
| |  | (17) |
where
r(
CCS,
s) is the Laplace reactivity that linearly relates the rate and the corresponding gas concentration in the Laplace domain.
12 The residence time in the
catalyst (
τcat) zone is given by
eqn (18):
Using eqn (9) and (17), the following expressions for moments of the exit flow were determined:
| | 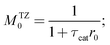 | (19) |
| |  | (20) |
| |  | (21) |
where
r0,
r1 and
r2 are basic kinetic coefficients (
sn−1).
Here, the upper index “TZ” denotes the moments that were measured in the thin-zone TAP reactor. In the case when no conversion occurs in the catalyst zone, eqn (19), (20) and (21) can be simplified as:
| |  | (23) |
| |  | (24) |
Here, the basic kinetic coefficients r0, r1 and r2 describe the catalyst,12 while the parameters ka and kd characterize adsorption/desorption over the inert material. The rate constants ka and kd are both present in eqn (19) to (24) in the form of either ratio  or
or 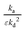 . The first and second moments observed in the one-zone experiment explicitly determine these ratios (eqn (11) to (14)). Consequently, in order to analyze thin-zone data, the ratios
. The first and second moments observed in the one-zone experiment explicitly determine these ratios (eqn (11) to (14)). Consequently, in order to analyze thin-zone data, the ratios  and
and 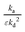 should merely be determined in the one-zone test, using eqn (13) and (14).
should merely be determined in the one-zone test, using eqn (13) and (14).
In particular, combining eqn (13) with eqn (23) and eqn (14) with eqn (24), it is possible to determine r1 and r2, respectively, in a step by step manner. Firstly, r1 can be calculated from eqn (25), using eqn (13) and (23):
| |  | (25) |
Then
r2 can be calculated using
eqn (14) and (24):
| |  | (26) |
Eqn (25) and (26) are then applied to the experimental data.
Application to the experimental data analysis: a case study with the selective reduction of oxygen in a hydrogen-rich ethylene feed over 2% Ag/γ-Al2O3 catalyst
This correction function has been utilised for TAP studies of the selective reduction of oxygen in a hydrogen-rich ethylene feed over a 2% Ag/γ-Al2O3 catalyst, which has been extensively characterised previously.17–19 High purity ethylene is required when used as a monomer for the production of polyethylene as trace amounts of oxygen in the parts per million range can deactivate the polymerization catalyst. Therefore, removal of oxygen without loss of ethylene is a key process step. Overall, the key requirement of the catalyst is to reduce oxygen selectively to water without oxidation or reduction of the ethylene.
Experimental
The TAP experiments studied the adsorption and the reaction properties of the main probe molecules (C2H4, O2 and H2) over the 2% Ag/γ-Al2O3 catalyst (particle size 150–250 μm), in the 100–200 °C temperature range. Details of the TAP system employed for the study can be found elsewhere.3,4,6,9 The thin zone TAP reactor (TZTR) approach11 was utilized for all the experiments, using silicon carbide (SiC) (non-porous, particle size 500 μm, VWR) as the inert packing material. All the gases (H2, O2, ethylene and Ar) used in the experiment had purity of >99%, and were supplied by BOC. In all experiments, the composition of the pulses from each valve consisted of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of reagent to Ar.
1 mixture of reagent to Ar.
Results
The preliminary experiments over the one-zone SiC reactor packing indicated that hydrogen or oxygen did not adsorb over this inert material, while, at temperatures ≤100 °C, ethylene showed significant adsorption over SiC.
Fig. 2 compares the residence time (first moment) observed for ethylene, oxygen and argon plotted versus the square root of the ratio of molecular weight to temperature. As clearly shown from the magnified scale, argon and oxygen follow the same linear Knudsen dependence given by eqn (1) and reported in Fig. 1. However, the residence time for ethylene shows a non-linear dependence with (temperature)−1 with a longer than expected residence time found at low temperatures, which is indicative of adsorption over the SiC. At higher temperatures (>150 °C), the binding of ethylene to SiC is sufficiently weak for it to follow a linear dependence expected for Knudsen diffusion. Consequently, in order to obtain detailed information about ethylene adsorption over the 2% Ag/γ-Al2O3 catalysts in the TZTR experiment, the one-zone data recorded over the SiC should be taken into account. Importantly, multi-pulse TAP experiments unravelled that the Ag/γ-Al2O3 catalyst did not convert ethylene to any product up to 200 °C (see Fig. S1 in ESI†). The pulse response intensity ratio of ethylene to argon was constant, fitting with the one-zone case, indicating that ethylene is adsorbed reversibly over the catalyst. This “zero-conversion” case is described by eqn (22) to (26). Using one zone and TZTR pulse response data and eqn (22) to (26), the following results were obtained.
 |
| | Fig. 2 Residence time (first moment, M1) plotted vs. (molecular weight/temperature (K))1/2 for ( ) argon, ( ) argon, ( ) oxygen, ( ) oxygen, ( ) ethylene observed over SiC one-zone packing. The inset reports a magnification of argon and oxygen residence times. ) ethylene observed over SiC one-zone packing. The inset reports a magnification of argon and oxygen residence times. | |
Influence of the catalyst treatment
The procedure for the TAP study of ethylene adsorption over the 2% Ag/γ-Al2O3 catalyst involved packing the reactor with a thin zone of the fresh catalyst (14 mg) followed by evacuation of the reactor and heating to 100 °C. Then a series of 100 pulse responses of 50/50 ethylene to argon mixture was recorded at 10 °C intervals over the temperature range 100–200 °C. Fig. 3 shows the subsequent evolution of the ethylene response.
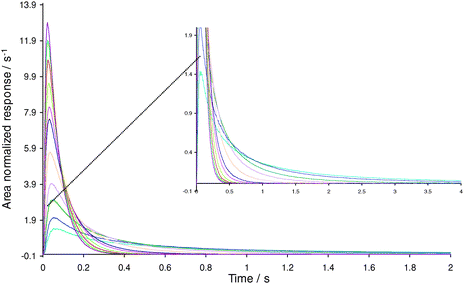 |
| | Fig. 3
Ethylene responses over oxidized 2% Ag/γ-Al2O3 catalyst. ( ) T = 200 °C, ( ) T = 200 °C, ( ) T = 190 °C, ( ) T = 190 °C, ( ) T = 180 °C, ( ) T = 180 °C, ( ) T = 170 °C, ( ) T = 170 °C, ( ) T = 160 °C, ( ) T = 160 °C, ( ) T = 150 °C, ( ) T = 150 °C, ( ) T = 140 °C, ( ) T = 140 °C, ( ) T = 130 °C, ( ) T = 130 °C, ( ) T = 120 °C, ( ) T = 120 °C, ( ) T = 110 °C, ( ) T = 110 °C, (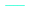 ) T = 100 °C (Broad tails are plotted on a magnified scale). ) T = 100 °C (Broad tails are plotted on a magnified scale). | |
Clearly, with increasing temperature, the experimental curves took a shorter time to reach the baseline. This is indicative of the faster diffusion as well as faster adsorption/desorption processes at high temperature, as would be expected. The reproducibility analysis showed that once the catalyst was heated above 150 °C and then cooled, the ethylene responses became broader than the corresponding responses observed during the heating of the fresh catalyst sample. As a result of this observation, the difference in behaviour of the fresh and the thermally treated catalyst was studied to understand the difference in adsorption/desorption characteristics as a function of the pre-treatment. It was also noted that the reduction by hydrogen and oxidation by oxygen produced changes in the adsorption behaviour of the catalyst. Hence, the experiments investigated four different variations of the catalyst, with the varying factor being the way in which the catalyst was treated. Details of these treated catalysts are provided in Table 1.
|
Catalysts (2% Ag/γ-Al2O3) |
Treatment process |
| Fresh |
— |
| Heated |
Heated above 150 °C |
| Reduced |
Reduced at 150 °C by H2/Ar multi-pulse |
| Oxidized |
Oxidized at 200 °C by O2/Ar multi-pulse |
Adsorption/desorption properties
Using eqn (25) the first basic kinetic coefficient, r1, was determined from the first moments which were observed in the one-zone and thin-zone TAP experiments. This coefficient is equal to the equilibrium adsorption rate constant when only reversible adsorption occurs over the catalyst:12| |  | (27) |
where Ka and Kd are the adsorption and desorption rate constants between ethylene and the catalyst. These are to be distinguished from the adsorption/desorption rate constants over the inert material (eqn (2)).
Fig. 4 and 5 show the uncorrected and the corrected equilibrium adsorption rate constants, r1, respectively. In each case, the observed r1 values of the four different catalyst treatments are plotted in the logarithmic scale. For both the uncorrected and corrected r1 values the slopes as a function of temperature are similar and the oxidation treatment resulted in the highest observed values of the equilibrium adsorption rate constant. It is clear from these results that the values of uncorrected r1 are significantly greater than those found following correction for the adsorption over the inert material. This is to be expected, given that there is a greater contribution of adsorption present in the uncorrected values as adsorption over the inert material has not been taken into account.
 |
| | Fig. 4 The uncorrected equilibrium adsorption constants, r1, of ethylene observed for ( ) fresh, ( ) fresh, ( ) heated, ( ) heated, ( ) oxidized, and ( ) oxidized, and ( ) reduced catalyst plotted in the logarithmic scale. ) reduced catalyst plotted in the logarithmic scale. | |
 |
| | Fig. 5 The corrected equilibrium adsorption constants, r1, of ethylene observed for ( ) fresh, ( ) fresh, ( ) heated, ( ) heated, ( ) oxidized, and ( ) oxidized, and ( ) reduced catalyst plotted in the logarithmic scale. ) reduced catalyst plotted in the logarithmic scale. | |
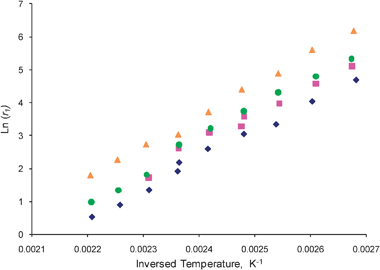
In order to extract the influence of different treatments on the adsorption and desorption rate constants, eqn (26) for the second moments can be used to determine second basic kinetic coefficients, r2. The coefficients r1 and r2 make it possible to determine both adsorption and desorption rate constants over the 2% Ag/γ-Al2O3 catalyst. It is also possible to express the desorption rate constant as a simple ratio:12
| | 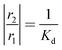 | (28) |
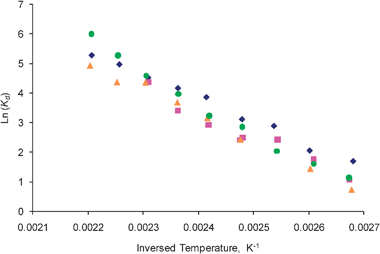
Thus, the adsorption rate constant can be easily obtained from eqn (27), as both r1 and Kd have been determined. The corrected desorption and adsorption rate constants were calculated from eqn (25) to (28), using the first and second moments observed in the one-zone and thin-zone TAP experiments. Fig. 6 and 7 show the uncorrected and the corrected desorption rate constants, respectively. Again, it is evident that the uncorrected results obtained are greater than the values corrected for the adsorption over the inert material.
 |
| | Fig. 6 The uncorrected desorption rate constants, Kd, of ethylene observed for ( ) fresh, ( ) fresh, ( ) heated, ( ) heated, ( ) oxidized, and ( ) oxidized, and ( ) reduced catalyst plotted in the logarithmic scale. ) reduced catalyst plotted in the logarithmic scale. | |
 |
| | Fig. 7 The corrected desorption rate constants, Kd, of ethylene observed for ( ) fresh, ( ) fresh, ( ) heated, ( ) heated, ( ) oxidized, and ( ) oxidized, and ( ) reduced catalyst plotted in the logarithmic scale. ) reduced catalyst plotted in the logarithmic scale. | |
Fig. 8 and 9 show the uncorrected and the corrected adsorption rate constants, respectively, for each of the pre-treated catalysts as well as the fresh material. In this case a substantial change in the variation with respect to temperature is observed with the corrected values showing the expected trend that the adsorption rate constant decreases with increasing temperature whilst the opposite is true for the uncorrected values. This non-Arrhenius behaviour is probably associated with changes in the surface structure of the adsorption sites due to the very labile silver species both in terms of oxidation state and structure of the particles which has been demonstrated in a number of studies.17–21
 |
| | Fig. 8 The uncorrected adsorption rate constants, Ka, of ethylene observed for ( ) fresh, ( ) fresh, ( ) heated, ( ) heated, (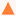 ) oxidized, and ( ) oxidized, and ( ) reduced catalyst. ) reduced catalyst. | |
 |
| | Fig. 9 The corrected adsorption rate constants, Ka, of ethylene observed for ( ) fresh, ( ) fresh, ( ) heated, ( ) heated, ( ) oxidized, and ( ) oxidized, and ( ) reduced catalyst. ) reduced catalyst. | |
This result emphasises the importance of the correction function, given that it is not only the values of adsorption rate constant that are influenced by the adsorption over inert material, but the entire trend. In this case, a conclusion on the elementary steps occurring in the process that is drawn from the uncorrected data would be clearly inaccurate.
From the slopes shown in Fig. 7, the activation energies for ethylene desorption were estimated, as reported in Table 2. While the desorption activation energies over fresh, heated and reduced samples were found to be in the similar range (920–960 J mol−1), the activation energy over the oxidized catalysts is significantly greater (1067 J mol−1).
|
Catalysts (2% Ag/γ-Al2O3) |
Desorption activation energy/J mol−1 |
| Fresh |
921 |
| Heated |
783 |
| Reduced |
960 |
| Oxidized |
1067 |
As a different desorption activation energy was observed for the oxidized catalysts, which could be attributed to the different types of ethylene adsorption sites, this was further investigated by a comparison of the diffuse reflectance UV-Vis (DRUV) results for the oxidized and reduced catalysts (Fig. 10). It is clear that significant differences exist between the DRUV spectra of the Ag/γ-Al2O3 catalyst oxidised at 200 °C and reduced at 150 °C in either He or H2. The absorption band in the 200–300 nm range (maximum at 225 nm) under oxidising conditions is attributed to Ag+ ions. In contrast, under the reducing atmosphere an absorption band forms at 324 nm attributed to silver clusters together with an absorption band at 410 nm which is attributed to silver particles. These data are consistent with previously reported EXAFS, UV-vis and electron microscopy results which show that even under mild reducing conditions silver is found to aggregate.19–21 Therefore, since the activation energy for desorption can be used as an indicator for the structure of the active sites, it is possible that both fresh and reduced catalysts may have a similar structure for the ethylene adsorption sites. This would suggest that the fresh catalyst may be partially reduced, possibly due to reduction under high vacuum in the TAP system. Importantly, the similarity between the reduced catalysts is reflected in the corrected values of the adsorption constant, for example, whereas significant variation was observed for the uncorrected values, demonstrating the importance of being able to take into account the adsorption over the inert material.
 |
| | Fig. 10
UV spectra of 0.5% Ag/γ-Al2O3 catalyst, under helium flow at 200 °C ( ), oxidized at 200 °C ( ), oxidized at 200 °C ( ) and reduced at 200 °C ( ) and reduced at 200 °C ( ). ). | |
In the context of the ability of this catalyst being able to selectively remove oxygen using hydrogen in the presence of ethylene, the corrected TAP data clearly demonstrate that the ethylene adsorption is very low over the catalyst even at low room temperature. This may be compared with oxygen which strongly adsorbs on the catalyst and, therefore, will undergo reaction with hydrogen in preference to the ethylene (see Fig. S4 in ESI†). Such a difference is not obvious from the uncorrected data due to the adsorption over the inert material.
Conclusions
In this paper the issue of adsorption on the inert material used as packing in the TAP micro-reactor is addressed. A theoretical tool which takes into account such adsorption is presented and thus provides a method by which TAP pulse response experimental data may be interrogated in order to extract detailed kinetic information about the interaction between probe molecules and the catalyst of interest.
The theoretical tool was applied to experimental TAP studies of reversible ethylene adsorption over 2% Ag/γ-Al2O3 catalyst. A contribution of ethylene adsorption on the silicon carbide (inert material) was identified below 150 °C. From the results obtained, the adsorption over inert material was found to have a significant impact on the values of adsorption and desorption rate constants. The corrected adsorption and desorption rate constants over the studied catalyst were calculated and then linked to the structure of the catalyst. In addition, from the corrected values it is clear that the high selectivity of the catalyst for the reaction of O2 with H2 as opposed to reactions with ethylene can be linked with the low adsorption strength of the ethylene on the silver catalyst.
Notation
|
A
r
| cross-sectional area of the reactor (m2) |
|
C
I, CII | concentrations in the first and second inert zones respectively |
|
C
CS
| set of catalyst state concentrations (mol m−3) |
|
C
g
| gas concentration (mol m−3) |
|
C
θ
| surface concentration (mol m−2) |
|
D
| Knudsen diffusivity (cm2s−1) |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) exit
exit
| dimensionless exit flow |
|
k
a
| adsorption rate constant over the inert material (cm3 of gas per mol s) |
|
K
a
| adsorption rate constant over catalyst (cm3 of gas per mol s) |
|
k
d
| desorption rate constant over the inert material (cm3 of gas per mol s) |
|
K
d
| desorption rate constant over catalyst (cm3 of gas per mol s) |
|
L
in, Lcat | length of the inert zone and catalyst zone respectively (m) |
|
L
r
| length of the reactor (m) |
|
L
TZ
| distance the middle of the thin zone is from reactor inlet |
|
M
n
| moment of nth order (mole sn) |
|
M
w
| molecular weight |
|
N
g
| pulse intensity (mol) |
|
r(CCS,s) | Laplace reactivities (1/s) |
|
R
TZ
| spatial average reaction rate in the thin zone |
|
r
n
| basic kinetic coefficient of nth order for ith probe molecule (sn−1) |
|
s
| Laplace variable |
|
t
| time coordinate (s) |
|
T
| temperature (K) |
|
x
| space coordinate (m) |
|
τ
res
| mean residence time (s) |
|
τ
in,τcat | mean residence time in inert and catalyst zones respectively (s) |
|
ε,(εin, εcat) | bed voidage (in inert and catalyst zone) |
Acknowledgements
Financial support from EPSRC under the CASTech project, and funding of studentships by the Thai government (BI) and DELNI (KM) are acknowledged.
References
- J. T. Gleaves, J. R. Ebner and T. C. Kuechler, Catal. Rev., 1988, 30, 49–116 CAS
 .
.
- J. T. Gleaves, G. S. Yablonskii, P. Phanawadee and Y. Schuurman, Appl. Catal., A, 1997, 160, 55–88 CrossRef CAS
 .
.
- A. Goguet, S. O. Shekhtman, R. Burch, C. Hardacre, F. C. Meunier and G. S. Yablonsky, J. Catal., 2006, 237, 102–110 CrossRef CAS
 .
.
- A. Goguet, C. Hardacre, N. Maguire, K. Morgan, S. O. Shekhtman and S. P. Thompson, Analyst, 2011, 136, 155–163 RSC
 .
.
- O. P. Keipert and M. Baerns, Chem. Eng. Sci., 1998, 53, 3623–3634 CrossRef CAS
 .
.
- K. Morgan, K. J. Cole, A. Goguet, C. Hardacre, G. J. Hutchings, N. Maguire, S. O. Shekhtman and S. H. Taylor, J. Catal., 2010, 276, 38–48 Search PubMed
 .
.
- M. Olea, M. Kunitake, T. Shido, K. Asakura and Y. Iwasawa, Bull. Chem. Soc. Jpn., 2001, 74, 255–265 CrossRef CAS
 .
.
- J. Pérez-Ramírez and E. V. Kondratenko, Catal. Today, 2007, 121, 160–169 CrossRef CAS
 .
.
- S. O. Shekhtman, A. Goguet, R. Burch, C. Hardacre and N. Maguire, J. Catal., 2008, 253, 303–311 CrossRef CAS
 .
.
- G. S. Yablonsky, M. Olea and G. B. Marin, J. Catal., 2003, 216, 120–134 CrossRef CAS
 .
.
- S. O. Shekhtman, G. S. Yablonsky, J. T. Gleaves and S. Chen, Chem. Eng. Sci., 1999, 54, 4371–4378 Search PubMed
 .
.
- S. O. Shekhtman, G. S. Yablonsky, J. T. Gleaves and R. Fushimi, Chem. Eng. Sci., 2003, 58, 4843–4859 Search PubMed
 .
.
- S. O. Shekhtman, N. Maguire, A. Goguet, R. Burch and C. Hardacre, Catal. Today, 2007, 121, 255–260 Search PubMed
 .
.
- S. O. Shekhtman and G. S. Yablonsky, Ind. Eng. Chem. Res., 2005, 44, 6518–6522 Search PubMed
 .
.
- D. Constales, S. O. Shekhtman, G. B. Marin, G. S. Yablonsky and J. T. Gleaves, Chem. Eng. Sci., 2006, 61, 1878–1891 Search PubMed
 .
.
- S. O. Shekhtman, G. S. Yablonsky, J. T. Gleaves and R. Fushimi, Chem. Eng. Sci., 2004, 59, 5493–5500 Search PubMed
 .
.
- B. Inceesungvorn, F. C. Meunier, C. Hardacre, R. Burch and K. Griffin, Chem. Commun., 2008, 6212–6214 RSC
 .
.
-
B. Inceesungvorn, Silver based heterogeneous catalysts for selective gas phase reactions, PhD thesis, Queen's University Belfast, 2009 Search PubMed
 .
.
- B. Inceesungvorn, J. López-Castro, J. Calvino, S. Bernal, F. C. Meunier, C. Hardacre, K. Griffin and J. J. Delgado, Appl. Catal. A, 2011, 391(1–2), 187–193 Search PubMed
 .
.
- J. P. Breen, R. Burch, C. Hardacre and C. J. Hill, J. Phys. Chem. B, 2005, 109(11), 4805–4807 CrossRef CAS
 .
.
- J. Shibata, K. I. Shimizu, S. Satokawa, A. Satsuma and T. Hattori, Phys. Chem. Chem. Phys., 2003, 5(10), 2154–2160 RSC
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c0cy00075b |
|
| This journal is © The Royal Society of Chemistry 2011 |
Click here to see how this site uses Cookies. View our privacy policy here. 

 ) helium, (
) helium, ( ) neon, (
) neon, ( ) nitrogen and (
) nitrogen and ( ) argon.
) argon.


![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) exit) observed in the pulse-response TAP experiment was found as:
exit) observed in the pulse-response TAP experiment was found as:

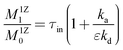



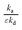 and
and  are explicitly present in the thin-zone solutions, as is discussed in the following section.
are explicitly present in the thin-zone solutions, as is discussed in the following section.


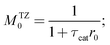




 or
or 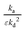 . The first and second moments observed in the one-zone experiment explicitly determine these ratios (eqn (11) to (14)). Consequently, in order to analyze thin-zone data, the ratios
. The first and second moments observed in the one-zone experiment explicitly determine these ratios (eqn (11) to (14)). Consequently, in order to analyze thin-zone data, the ratios  and
and 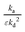 should merely be determined in the one-zone test, using eqn (13) and (14).
should merely be determined in the one-zone test, using eqn (13) and (14).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of reagent to Ar.
1 mixture of reagent to Ar.

 ) argon, (
) argon, ( ) oxygen, (
) oxygen, ( ) ethylene observed over SiC one-zone packing. The inset reports a magnification of argon and oxygen residence times.
) ethylene observed over SiC one-zone packing. The inset reports a magnification of argon and oxygen residence times.
 ) T = 200 °C, (
) T = 200 °C, ( ) T = 190 °C, (
) T = 190 °C, ( ) T = 180 °C, (
) T = 180 °C, ( ) T = 170 °C, (
) T = 170 °C, ( ) T = 160 °C, (
) T = 160 °C, ( ) T = 150 °C, (
) T = 150 °C, ( ) T = 140 °C, (
) T = 140 °C, ( ) T = 130 °C, (
) T = 130 °C, ( ) T = 120 °C, (
) T = 120 °C, ( ) T = 110 °C, (
) T = 110 °C, ( ) T = 100 °C (Broad tails are plotted on a magnified scale).
) T = 100 °C (Broad tails are plotted on a magnified scale).

 ) fresh, (
) fresh, ( ) heated, (
) heated, ( ) oxidized, and (
) oxidized, and ( ) reduced catalyst plotted in the logarithmic scale.
) reduced catalyst plotted in the logarithmic scale.
 ) fresh, (
) fresh, ( ) heated, (
) heated, ( ) oxidized, and (
) oxidized, and ( ) reduced catalyst plotted in the logarithmic scale.
) reduced catalyst plotted in the logarithmic scale.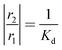

 ) fresh, (
) fresh, ( ) heated, (
) heated, ( ) oxidized, and (
) oxidized, and ( ) reduced catalyst plotted in the logarithmic scale.
) reduced catalyst plotted in the logarithmic scale.
 ) fresh, (
) fresh, ( ) heated, (
) heated, ( ) oxidized, and (
) oxidized, and ( ) reduced catalyst plotted in the logarithmic scale.
) reduced catalyst plotted in the logarithmic scale.
 ) fresh, (
) fresh, ( ) heated, (
) heated, ( ) oxidized, and (
) oxidized, and ( ) reduced catalyst.
) reduced catalyst.
 ) fresh, (
) fresh, ( ) heated, (
) heated, ( ) oxidized, and (
) oxidized, and ( ) reduced catalyst.
) reduced catalyst.
 ), oxidized at 200 °C (
), oxidized at 200 °C ( ) and reduced at 200 °C (
) and reduced at 200 °C ( ).
).![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) exit
exit
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
