Chirality transfer across length-scales in nematic liquid crystals: fundamentals and applications

Abstract

When a chiral dopant is dissolved in an achiral liquid crystal medium, the whole sample organizes into a helical structure with a characteristic length-scale of the order of microns. The relation between chirality at these quite different length-scales can be rationalized by a relatively simple model, which retains the relevant factors coming into play: the molecular shape of the chiral dopant, which controls the chirality of short range intermolecular interactions, and the elastic properties of the nematic environment, which control the restoring torques opposing distortion of the director. In this tutorial review the relation between molecular and phase chirality will be reviewed and several applications of the chiral doping of nematic LCs will be discussed. These range from the exploitation of the amplified molecular chirality for stereochemical purposes (e.g., the determination of the absolute configuration or the enantiomeric excess), to newer applications in physico–chemical fields. The latter take advantage of the periodicity of the chiral field, with length-scales ranging from hundreds to thousands of nanometres, which characterise the cholesteric phase.

---

Silvia Pieraccini

Silvia Pieraccini graduated in Medicinal Chemistry in 1996 and obtained her PhD degree in Pharmaceutical Science (major in organic chemistry) at the University of Bologna (2001). After a post-doc in the group of Prof. Spada, she was appointed Assistant Professor at the Department of Organic Chemistry of the University of Bologna (2005). Her research activity is in the fields of supramolecular chemistry and stereochemistry. In particular, her interests focus on the characterisation of self-assembled species and on the applications of liquid crystals in the stereochemical characterisation.

Stefano Masiero

Stefano Masiero graduated in Chemistry in 1985 and earned his PhD in Organic Chemistry in 1990. After a post-doctoral fellowship at the Italian Research National Council (CNR) he was appointed Assistant Professor at the Department of Organic Chemistry of the University of Bologna (1994). In 2007 he was promoted Associate Professor of Organic Chemistry. His research interests are in the supramolecular chemistry field, with focus on the design, synthesis and characterisation of self-assembling systems arising from guanylic and/or photoresponsive derivatives, for obtaining new functional materials, with emphasis on energy conversion.

Alberta Ferrarini

Alberta Ferrarini received her PhD in Chemical Sciences at the University of Padova, Italy, in 1989. She spent research periods at the Stuttgart University, Germany, with Prof. G. Kothe, and at Cornell University, USA, with Prof. J. H. Freed. Since 2000 she is Associate Professor of Physical Chemistry at the University of Padova. Most of her research has focused on the molecular interpretation of structural and dynamical properties of soft matter, by theoretical and computational methods.

Gian Piero Spada

Gian Piero Spada obtained his doctoral degree in Organic Chemistry in 1980 at the University of Bologna. After a research fellowship period, he joined the Faculty of Pharmacy of the University of Bologna in 1983 as Assistant Professor of Organic Chemistry and in 1992 he became Associate Professor. Since 2000 he has been full Professor of Organic Chemistry. Currently he is Director of the Graduate School of Chemical Science at the University of Bologna. His research activity is in the fields of stereochemistry and supramolecular chemistry.

---

1. Introduction

Liquid crystals (LCs) represent a state of matter intermediate between the solid and the liquid phase. LCs can flow, like liquids, but are anisotropic, like solids: properties like dielectric permittivity, magnetic susceptibility, heat and electric conductivity or light transmittance depend on the direction of measurement.^1,2 Several LC phases have been discovered, which differ in their symmetry and degree of order. Another distinction is usually made, between thermotropic and lyotropic liquid crystals. The former comprise low molar mass and polymeric organic compounds, typically containing anisotropic and fairly rigid units, which exhibit one or more LC phases upon cooling, below the isotropic liquid phase. Lyotropics include different systems, with the common feature that they are formed by solutions of molecules, mostly semi-flexible polymers or amphiphilic compounds, which undergo a transition to one (or more) ordered phase upon increasing concentration.

The transfer of chirality from the molecular to the mesoscopic scale in liquid crystals occurs through elasticity, which is intrinsically associated with the onset of orientational order, so, when a chiral dopant is dissolved in an achiral liquid crystal medium, the whole sample organizes into a helical structure with a characteristic length-scale of the order of microns. Solute effects on the structure of the solvation sphere, with some kind of “chiral imprinting” on the surrounding solvent, was observed also in isotropic liquids.³ What makes liquid crystals peculiar is their ability of transmitting torques over long distances, which depends on the presence of long-range orientational order.^1,2

This tutorial review deals with chirality in the thermotropic nematic phase formed from low molar mass compounds, and in particular we shall focus on the chirality induction by chiral solutes dissolved in achiral nematic LCs. This phenomenon has been extensively investigated and presently its main features are well understood. Cholesteric induction has moved from a specialistic topic to a subject of broader interest, usefully exploited for different applications, ranging from synthetic chemistry to photonics and materials science. In this paper the relation between molecular and phase chirality will be reviewed and several applications of the chiral doping of nematic LCs will be discussed. We shall also mention some aspects of chirality in other LC systems, which still await full understanding and wider application.

2. Chirality in liquid crystals

The behaviour of thermotropic LCs originates from the partial order at the molecular level: the molecular axes are not randomly distributed, as in ordinary liquids, but tend to lie parallel to each other. This leads to the definition of preferential alignment directions, which are known as directors.

2.1 The chiral nematic phase

The simplest example of LC is represented by the nematic phase (N), that has long range orientational order, but no translational order (the molecular centres of mass are randomly distributed in space).^1,2 The nematic phase is locally uniaxial, with the C_∞ axis coincident with the director. This is usually identified by a unit vector, n, with the specification that n and −n are equivalent; so the nematic phase has D_∞h symmetry. The formation of the nematic phase is driven by the anisotropy of intermolecular interactions, which in turn is related to the molecular structure: only system made of anisometric molecules can exhibit the nematic phase. In the presence of chiral molecules, which may be either introduced as solutes in LCs or coincide with the mesogens themselves, intermolecular interactions are not only anisotropic, but also chiral, and chirality is transferred to the phase organization.⁴ In the chiral nematic (N*) or cholesteric phase, the director rotates around a perpendicular axis in helical way, as shown in Fig. 1. The phase chirality is then defined by the pitch (p) and handedness of the helix. By convention, p is taken with sign, positive and negative values being associated with right-handed and left-handed helices, respectively. The magnitude of the helical pitch may range from hundreds of nanometres to micrometres, depending on the chemical constituents, but it is much longer than the molecular size anyway. The achiral nematic phase N, can be viewed as the limit case of a cholesteric with infinitely long pitch. The helical handedness is determined by the absolute molecular configuration: oppositely handed cholesterics are generated by enantiomers. Enantiomeric pairs compensate each other effects and the pitch goes to infinity in the case a racemic mixture. Thus, the cholesteric structure may be viewed as the molecular chirality brought to the observable scale and the helical pitch can be seen as a measure of chirality; actually, as will be explained below, the helical organization embodies more than chirality factors.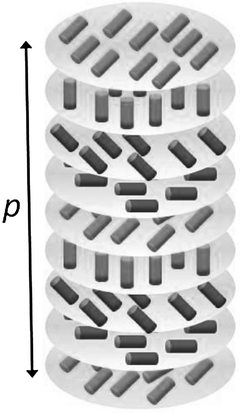

Fig. 1 Helical organization in the chiral nematic (N*) phase. Cylinders indicate director orientations.

Orientational order introduces a mesoscale variable, the director; it is this scale, rather than the molecular one, which is appropriate for describing most phenomena in LCs. An important concept associated with the director is that of elasticity: the director opposes deformation with a restoring force, which is proportional to the deformation itself. Director deformations are conveniently treated by the elastic continuum theory. Symmetry consideration lead to the identification of three basic deformation modes in nematics, which are denoted as twist, splay and bend, respectively.¹ Disregarding the two latter, which are not directly involved in the formation of the cholesteric phase, and indicating by q = 2π/p the helix wavenumber, the density of deformation free energy is expressed as:

f_el = k₂q + ½K₂₂q² (1)

where K₂₂ is the twist elastic constant and k₂ is the chiral strength. The former quantifies the elastic torque opposing twist deformation and is related to the anisotropy of intermolecular interactions. The latter is determined by the chirality of intermolecular interactions, as averaged out by molecular motions in the nematic environment, and vanishes in a system made of achiral (or chiral racemic) molecules. The equilibrium state of a free sample, in the absence of external constraints, corresponds to the minimum of the free energy; under this conditions, the helical wavenumber is obtained as:

q = −k₂/K₂₂. (2)

Thus, the magnitude of the cholesteric pitch is determined by the competition between chiral strength, which promotes twist deformation, and elastic restoring torque. For achiral systems the equilibrium configuration is that of uniform director (q = 0 or p → ∞), whereas spontaneous twist deformation of the director occurs in the presence of molecular chirality.

2.2 Other chiral LC phases

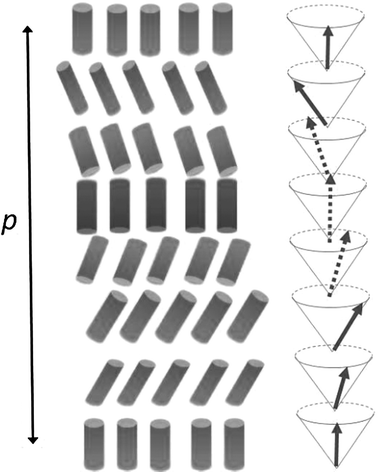
In the cholesteric phase, chiral intermolecular interactions result in a phase structure characterized by torsion along one axis; chiral interactions would be optimized if torsion were extended to any directions, as in what is known as the double twist structure, as sketched in Fig. 2. This organization, which brings about the presence of defects and then an increase of energy, may be found in the so called Blue Phases (BP). These, unlike cholesteric phases, are chiral at the mesoscale, but not macroscopically, since double twist cylinders are ordered in cubic arrangements, which can be seen as fluid lattices of defects.^1–2,4 BPs are generally stable under very special conditions; only recently, systems exhibiting wide temperature range BPs were found.^5–7

Fig. 2 Schematic representation of director organization in nematics (N), chiral nematics (N*) and Blue Phases (BP). Cylinders indicate director orientations.

Other examples of chiral LC phases are presented by smectics, wherein molecules, in addition to long range orientational order, also possess some degree of translational order:^1,2 the centres of mass are preferentially located in planes, so that layered structures are formed. According to their symmetry, we can distinguish smectic A, where the director is perpendicular to layers, and smectic C phases, in which the director is tilted. Molecular chirality has spectacular effects in the latter (smectic C*): in analogy with cholesterics, the director rotates from layer to layer, forming a helix as sketched in Fig. 3. Interestingly, this structure encompasses spontaneous polarization: each layer has a dipole moment, perpendicular to the plane defined by the layer normal and the local director.^4,8 The description of the many interesting chirality-dependent properties of smectic LCs is beyond the scope of this tutorial review and has been reviewed elsewhere.^2,9–11

Fig. 3 Sketch of the layered organization of the smectic C* phase. Cylinders indicate director orientations.

3. Molecular structure and cholesteric induction

Mesogen chirality is not a necessary requirement for the appearance of chiral liquid crystal phases; these can also be induced by chiral non-racemic compounds dissolved in non-chiral LC solvents.^12,13 Even a small amount of solute is sufficient to break the chiral symmetry of the phase. At low dopant concentrations, the inverse pitch of induced cholesterics is proportional to the amount of chiral solute:

1/p = β c r for c → 0 (3)

where c and r are the concentration (mole fraction) and the enantiomeric excess of the dopant, respectively. The factor β, usually denoted as the helical twisting power, quantifies the ability of a chiral dopant to induce twist deformation of the director. For a given nematic solvent, this is a specific property of each solute. As a first approximation, we can assume that non-chiral solvent properties, like the twist elastic constant, are unaffected by a small amount of solute; so, considering eqn (2), the different twisting ability of solutes in the same N solvent can be traced back to differences in the induced chiral strength k₂.

3.1 Experimental determination of the helical twisting power

The quantification of β requires the determination of the magnitude of the cholesteric pitch and of the handedness of the cholesteric helix.¹³ This can be obtained with spectroscopic or non-spectroscopic methods. The former techniques are based on typical optical properties of the cholesterics. In particular,¹⁴ in their planar texture (i.e. with the cholesteric axis parallel to the light propagation direction) the cholesteric helix reflects circular polarised light (CPL) of the same handedness and transmits CPL of the opposite handedness, when the wavelength is close to λ₀ = n p (where n is the mean refractive index); as a result, a P-cholesteric displays an intense negative CD at λ₀. Hence, this spectroscopic technique allows the simultaneous determination of pitch and sign of the induced cholesteric.

The non-spectroscopic methods are usually based on the observation of the cholesteric phase with an optical microscope in linearly polarised light. Some of these are modification of the Grandjean-Cano method¹⁵ based on the observation of the disclination lines that appear when a cholesteric is inserted in a variable-pathlength cell whose windows are appropriately rubbed to obtain the necessary alignment. The lens version is illustrated in Fig. 4. From the distance between these lines one can obtain the cholesteric pitch. The sense of the cholesteric can be obtained either modifying the geometry of the cell (e.g. modifying the rubbing directions of the windows surfaces or rotating one window—the lens—with respect to the other—the plate), or from the observation of the rotatory power originated by the helicoidal molecular order.¹⁴

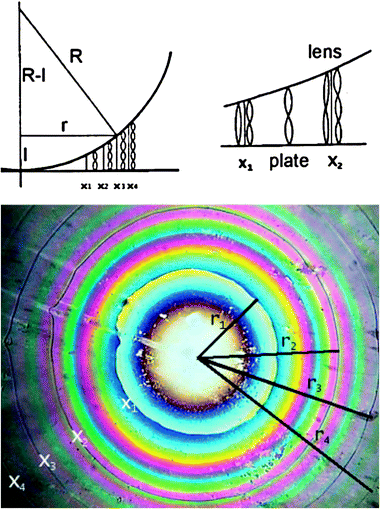Fig. 4 A schematic representation of the origin of the Grandjean–Cano disclination lines which form when a cholesteric is inserted between a plano-convex lens and a glass plate (a) and a typical texture (b). The surfaces of both lens and plate are rubbed to produce grooves along which the director is aligned; the rubbing directions of the top and bottom surfaces lie parallel to each other. In correspondence of the x's, the number of half-turns changes by one and this causes defects which are visible as sharp lines of circular shape. The radii r of the circular Grandjean–Cano disclinations are a function of only the curvature radius R of the lens and of the pitch of the cholesteric phase. (Reprinted with permission from ref. 16. Copyright 2008 John Wiley and Sons).

Another non-spectroscopic technique widely used to measure the cholesteric pitch is based on the Bragg scattering of monochromatic light obtained with a He–Ne laser: its angular dependence is related to the cholesteric pitch.¹⁷

Recently, a new technique based on the use of twisted nematic (TN) cells has been reported by Raynes;¹⁸ it provides a more sensitive measurements of large helical pitches.^19,20 TN cells are commercially available from LCD device manufacturers; they are generally constructed from ITO-glass with the inner surfaces coated with polyimide which is buffed. The surfaces are arranged so that the buffed directions are perpendicular to one another. When an achiral nematic is introduced into the cell, these directions determine the orientation of the director at the surfaces; then, to comply the anchoring conditions, the director must twist to form a quarter-helix between the two surfaces. For an achiral (or racemic chiral) material both left- and right-handed quarter helices can be formed. The two domains are separated by disclination defect lines which can be observed by transmitted polarized-light optical microscopy (Fig. 5).

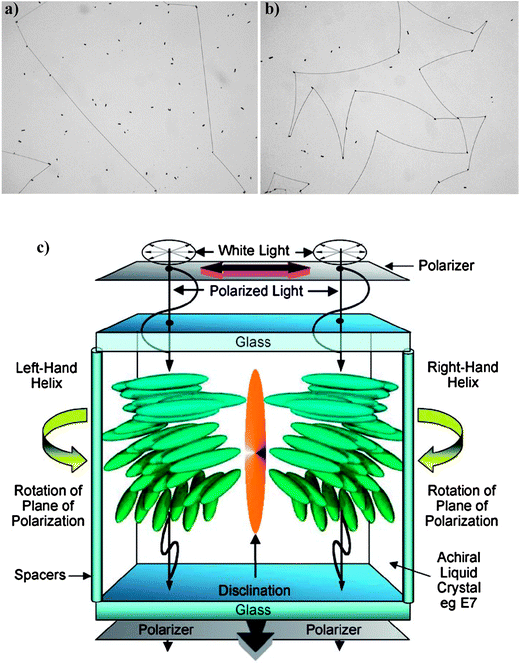Fig. 5 (a) Disclination lines separating left- and right-quarter helical domains in E7 achiral liquid crystal (the black dots are the spacers of the TN cell). (b) Bowed disclination lines in a TN device containing E7 doped with the chiral dopant CB15 (pitch 0.4 mm), (c) Arrangement of degenerate left- and right-hand quarter helical domains in the TN cell. (Adapted with permission from ref. 19. Copyright 2008 Wiley-VCH Vrlag GmbH & Co. KGaA.)

If the material filling in the cell is a cholesteric, the presence of a chirality bias breaks the degeneracy: in the TN cell one twist area is favored and grows at the expense of the other. For pitches greater than approximately 0.5 mm two domains are obtained with bowed (curved) disclination lines separating the domains.^18–20 The bowing will be related to the cholesteric pitch length. Making reasonable approximations it can be shown that the radius of curvature R, is related to the pitch length p, of the chiral nematic material as p = 2 R.

3.2 Molecular determinants of cholesteric induction: theoretical models

Since the discovery of the phenomenon of cholesteric induction, there have been attempts to unveil the puzzling relation between dopant and phase chirality, by empirical and theoretical models. The latter start from a molecular expression for the free energy density in the presence of twist deformation and the cholesteric pitch is obtained by minimization of the free energy. In principle, a molecular expression for the free energy can be derived from intermolecular interactions, using methods of statistical mechanics; in practice, this is feasible only for simple molecular models, at the cost of a number of approximations.^21–23 Thus, this kind of approach can provide general rules and predict trends, but cannot deal with the atomistic detail, which is important to rationalize the effects of the chemical structure of chiral dopants on their helical twisting power. In fact, the chiral contribution is only a tiny part of the whole intermolecular interactions and bears a subtle dependence on the molecular structure.²⁴ Prediction of helical twisting power is a challenge also for computer simulations: special strategies have to be devised to detect small free energy differences and the presence of twist deformation may conflict with straightforward periodic boundary conditions.^25,26 In the attempt to relate molecular geometry and helical twisting power, several descriptors of the intrinsic dopant chirality have been proposed. One of the earliest suggestions is due to Osipov, Pickup and Dunmur, who proposed a chirality tensor calculated from the atomic coordinates, in a form derived from the theory of optical activity.²⁷ From this tensor, two chirality indices were obtained, describing respectively the isotropic and the anisotropic contribution to the chirality of the nuclear skeleton in a molecule. Subsequently, other chirality indices were proposed;^28,29 these are general geometric parameters, which quantify the chirality of the molecular shape on the basis of the atomic positions or of the molecular surface, but the connection with the phenomenon of cholesteric induction may be loose.

3.2.1 The surface chirality model. The use of a simple yet realistic representation of the molecule is shared by the so called surface chirality (SC) model wherein, however, an expression for the helical twisting power is derived from a physical model of cholesteric induction.³⁰ This method has been very useful to elucidate the relationship between structure and twisting ability of chiral dopants, therefore it will be described in some detail. The starting point is an expression for the orienting mean field experienced by a molecule in the nematic environment: renouncing a detailed representation of the solvent, which is approximated as an elastic continuum, the structure of the solute is explicitly taken into account by parameterising the chirality and anisotropy of intermolecular interactions according to the molecular surface. It is assumed that, as a consequence of the interactions with the surrounding molecules in the ordered environment, each element of the molecular surface of the dopant, dS, experiences an orienting mean field of the form: dU = k_BTξP₂(n·s)dS, where s is a unit vector normal to the surface element and P₂ is the second Legendre polynomial, P₂(x) = 1.5 x² − 0.5. Thus, the preferred orientation is that with n⊥s (P₂(n·s) = −0.5), whereas n//s corresponds to the less favoured orientation (P₂(n·s) = 1). This is the simplest form to introduce the alignment tendency, taking into account the symmetry of the nematic environment. The (positive) parameter ξ, with dimension of inverse square length, specifies the orienting strength of the medium and is related to its degree of order. The orienting mean field experienced by a molecule in the uniaxial nematic phase is then obtained by integrating the elementary contribution over the whole molecular surface.‡

Given the orienting potential, a molecular expression for the Helmholtz free energy difference between the nematic and the isotropic phase is derived, as usual in molecular field theories.³⁰ In a twisted nematic phase the vector n changes, although slightly, with the positions on the molecular surface, therefore the orienting potential, and then the Helmholtz free energy, are implicit functions of the director distortion. By minimizing this free energy with respect to the twist distortion wavenumber q, a molecular expression for the helical twisting power is obtained, which can be put in the simple form β = AQ , where A is a quantity which only depends on the nematic solvent and Q, denoted as surface chirality parameter, is a solute property that depends on the chirality of the molecular surface and on the orientational order in the LC phase. This is defined as:

Q = −(2/3)^1/2(Q_xxS_xx + Q_yyS_yy + Q_zzS_zz) (4)

where i = x, y, z are the principal ordering axes of the solute, Q_ii represents the helicity of the molecular surface along the i-th axis and S_ii is the corresponding element of the Saupe ordering tensor.¹ The order parameter S_ii specifies the degree of alignment to the director of the i-th axis and takes values in the ranges −0.5 ≤ S_ii ≤ 1, with the extremes for the i-th axis perfectly ordered parallel (S_ii = 1) and perpendicular (S_ii = −0.5) to the director. It can be easily shown that S_zz = −(S_xx + S_yy) and Q_zz = −(Q_xx + Q_yy). Eqn (4) clearly shows that the surface chirality parameter Q is determined not only by the chirality of a solute, but also by its average orientation with respect to the local director.

The helicity of the molecular surface depends on the direction which is considered. Fig. 6 shows two views of the molecular surface of biphenyl with twist angle ϕ = π/4 (P*-enantiomer)§: in one case the helicity of the molecular surface along the axis perpendicular to the plane of the figure is right-handed (Q_ii > 0), in the other it is left-handed (Q_ii < 0).

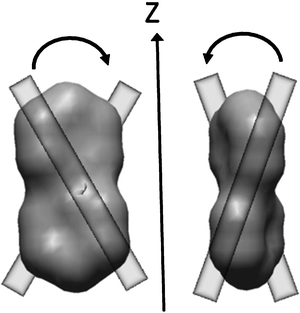Fig. 6 Molecular surface of P*-biphenyl with a twist angle ϕ = π/4 between the phenyl moieties. The vertical arrow is parallel to the molecular axis (z) with the highest tendency to lie parallel to the local director in the N* phase. Reddish segments are introduced to show the right-handed helicity along the y-axis perpendicular to the ‘molecular plane’ (left side) and the left-handed helicity along the x-axis (right side).

Two limiting cases can be considered: (i) a rod-like solute, which tends to align its long axis (z) to the local director and (ii) a disc-like solute, which tends to keep the molecular plane (xy) parallel to the local director. In both cases the relation S_zz ∼ −S_xx/2 ∼ −S_yy/2 holds, but S_zz is positive in the former and negative in the latter. For a rod-like solute Q ∼ (3/2)^1/2(Q_xx + Q_yy)S_zz is obtained: the induced director twist is determined by the average surface helicities along the short molecular axes (Q_xx and Q_yy), which tend to lie perpendicular to the director. For a disc-like solute it is convenient to write Q ∼ −(3/2)^1/2Q_zzS_zz , i.e. the induced phase helicity is dictated by the molecular helicity along the direction which is preferentially oriented perpendicular to the director (Q_zz). Examples of the two kinds of behaviour are provided by bridged biphenlys with long 4,4′-substituents³¹ and helicenes,³² respectively. These examples will be recalled in section 4.1; for more detailed analysis of the relation between molecular structure and helical twisting power the reader is referred to ref. 16 and 30.

The surface chirality parameter Q for a given dopant can be easily evaluated at negligible computational cost; only the atomic coordinates are needed, from which the molecular surface is calculated.³³ Solute flexibility is easily introduced into the SC model: the Q value for a flexible dopant is obtained by averaging over all the conformers: Q = Σ_αp^(α)Q^(α) where p^(α) and Q^(α) are the probability and the chirality parameter of the α conformer.³⁴

The proportionality factor between helical twisting power and surface chirality parameter is defined as A = N_Aξ/2πK₂₂v_m, with N_A being the Avogadro number, K₂₂ and v_m the twist elastic constant and the molecular volume of the liquid crystal solvent, respectively. The value of A for a given solvent is a function of temperature; it bears a dependence on the structure of the solvent, mainly through the twist elastic constant, which generally increases with the rigidity of the constituent molecules. When comparing different dopants in the same nematic solvent A can be taken as a scaling factor, identical for all solutes; usual values are of the order of magnitude of a few μm⁻¹ Å⁻³. In most cases the handedness of the induced cholesteric phase is characteristic of a given dopant and is maintained irrespectively of the chemical structure of the nematic solvent and of the temperature; these have the only effect of scaling the magnitude of the pitch, according to the expression reported above. However, in some cases changes of handedness with solvent and temperature have been observed, mostly for solutes with a modest twisting ability. This can be explained as the result of a change in the orientational behaviour and/or in the conformational distribution of the dopant.³⁵

One may ask why a simple approach like the SC model is successful. The reason is that, although in an approximate way, it catches the main physical determinants of cholesteric induction in thermotropic LCs. The atomistic representation of solute, with the proper account of flexibility, allows the introduction into the model of the necessary molecular details, whereas the elastic continuum description is sufficient for an approximate treatment of the response of the environment. The molecular surface is suitable to account for the short range interactions, controlled by the molecular shape, which dominate in thermotropic LCs. Phenomenological expressions scaling with the molecular surface are widely used in other contexts, e.g. in models for implicit solvation, with the underlying reason that short range interactions can be related to the amount of surface of a solute accessible to the surrounding molecules.³⁶ The same approach cannot be used for systems where other interactions play a role; for instance it would not be appropriate for the cholesteric phase of DNA, where electrostatic interactions between double helices are involved.³⁷ The quality of the SC predictions depends on the use of realistic atomic coordinates; nowadays, fairly good estimates of the latter can be obtained by standard quantum chemistry calculations, and this should probably be included among the reasons for the success of the SC approach. We must also mention that, due to its inherent approximations, the SC method has relatively low resolution; therefore its predictions must be taken with prudence for solutes with very low twisting ability (of the order of 1 μm⁻¹ or less).

3.3 Structural features associated to high twisting powers

Compounds with high helical twisting powers allow the control of the cholesteric pitch by doping the nematic phase with a small amount of solute. This is important for most applications, e.g. for those requiring a pitch in the range of the visible wavelength (vide infra): in these cases the solubility of the dopant could represent a limit. This motivated the search for the actual molecular features responsible for high twisting ability. Reliable estimates of twisting power can be obtained using the SC model with an atomistic solute representation. However some general rules can be given. In general, we can predict that molecules with reduced flexibility which exhibit clear orientational preferences and, as a result of chirality, a twisted shape, should have a strong twisting ability, not dramatically affected by substituents.³⁸ On the contrary, as a general rule, flexibility in solutes is associated with a decrease of their helical twisting power.³⁴ Calculations have shown that different conformers of a given compound may have strongly different order parameters and chirality and even opposite twisting ability, which leads to lowering of the net twisting power after averaging over the whole ensemble of conformers.

As anticipated above, chiral dopants can exhibit a different ability to twist the nematic phase spanning from weak inducers (β < 1 μm⁻¹) to strong inducers (β > 20 μm⁻¹); to our knowledge, the strongest chiral dopants investigated is a TADDOL derivative (534 μm⁻¹).³⁹ In the last decades, a high number of chiral dopants with quite different chemical structures were tested in order to evaluate their efficiency in twisting nematic phases. Many of such investigations have been recently reviewed by Feringa⁴⁰ and Spada.¹⁶ From the analysis of the experimental results in the literature, it was observed that most dopants with high twisting power are characterized by the presence of two (or more) (quasi-)planar moieties twisted one with respect to the other(s) and that the ability to twist the nematic phase depends on the structural similarity between dopant and solvent and on the conformational mobility of the host (in a rigid core solvent the values of β are generally smaller).^13,16,40

When the helical twisting power is very low (as often observed for molecules whose chirality is due to stereogenic centres), different approaches have been used to improve the ability of the molecule to express its chirality at the mesophase level.⁴⁰ One possibility is to adopt a “mesogenic functionalisation” of the chiral dopant. The introduction of a group resembling the structure of the nematic host enhances the solubility and the solute–solvent interactions and this leads to an enhancement of the dopant twisting ability (see section 4.2 below).

The interaction of a chiral dopant with a nematic host may be improved also by metal coordination.⁴¹Tris(pyridyl)amine-based ligands show negligible to small helical twisting powers in the most common nematic solvents, whereas complexation with Cu(I) or Cu(II) greatly increases β as a consequence of the reduced conformational flexibility and of the (quasi)propeller-like shape of the complexes. Furthermore, changes in overall shape of the complexes induced by different metals and counterions are transferred to the supramolecular level and proportional changes of the helical twisting powers are observed.

A third approach to enhance the chirality employs a co-solute that binds to the low-β dopant. Eelkema and Feringa proposed a “double amplification” approach which employs dinamically chiral biphenol or biphenyl phosphoric acid receptors for amplifying the chirality of simple amines and aminoalcohols. As an example, the binding between the dopant D and the receptorR (see chart 1) through H-bonding, selects a chiral conformation of the biphenyl receptor which, in turn, induces more efficiently a cholesteric.⁴²

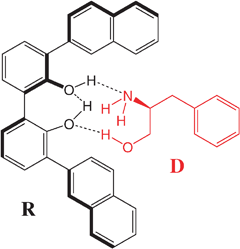Chart 1

4. Stereochemical applications

In cholesteric induction experiments, the molecular chirality is mapped onto an achiral (nematic) phase to yield a superstructural phase chirality which can be measured. With a model which relates the molecular chirality to the mesophase chirality one could infer stereochemical information about the dopant (e.g. the absolute configuration, the preferred conformation, the enatiomeric excess of the dopant, etc.). In 1984 Solladié published the first review summarising the state of the art at that time.¹³

4.1 Determination of the absolute configuration

The first empirical correlation between the cholesteric handedness and the solute configuration was described by Gottarelli et al. in 1975.⁴³ They reported that a series of homochiral benzyl alcohols in MBBA induces cholesterics of the same handedness. A few years later, Korte reported⁴⁴ the first attempt to find a general correlation between the configuration of a stereocenter and the handedness of the induced cholesteric. He related the handedness of the cholesteric to a stereochemical descriptor of the dopant based on the effective volume of the substituents. This relation is followed by more than one hundred compounds, as claimed by Korte, but also exceptions were reported. In these early empirical approaches proposed, the solvent molecules are considered as achiral rigid rods and the role of the chiral dopant is to prevent their parallel alignment, leading to the helicoidal arrangement. This model, which has been used to assign the configuration of a few series of compounds,^43–45 cannot account for the dependence of the value of β (and sometimes its sign) on the nature of the solvent.¹⁶

Only when, at the beginning of the 1980s, the structural features of dopant and solvent associated to high values of β were identified,^16,40 a more refined model, although of empirical nature, was proposed for the prediction of the sense of the induced cholesteric. According to this model (sketched in Fig. 6 in the case when both nematic host and chiral guest have a biaryl structure)⁴⁶ typical nematogenic molecules are flexible and can exist in chiral enantiomorphic conformations of opposite helicity in fast interconversion. The chiral dopant has a well defined molecular helicity (P* in Fig. 7)§ and stabilizes the homochiral conformation of the solvent: in this way, the P*-chirality is transferred from the dopant to the neighbouring molecule of the solvent and from this to the next-neighbouring one and so on. This leads to a deracemisation of the nematic solvent and its transformation into a P-cholesteric.⁴⁷

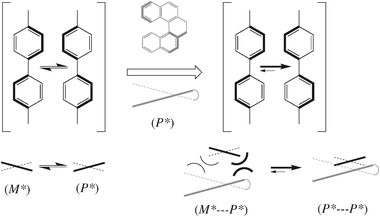Fig. 7 The chirality transfer from the dopant to the solvent. A chiral inducer with a (P*)-helicity aligned with its biaryl axis parallel to the biphenyl core of the nematogenic solvent can have close contact only with solvent molecules adopting the same (P*)-helicity.

The mechanism of Fig. 7, proposed also in ferroelectric LCs,⁴⁸ has been supported by rotatory power measurements in isotropic solutions.³ The rotatory power in dynamically chiral non mesogenic solvents (e.g.biphenyls) is increased or decreased in comparison to ordinary solvents (e.g.acetonitrile) in relation to the sign of twisting power of the solute. These data can be interpreted assuming that the right-handed twisting compounds induce in biaryl solvents an excess of solvent molecules in the P*-conformation: molecular statistical calculations support this chirality transfer.

Several stereochemical applications of cholesteric induction have been described; reliable results are obtained especially when the dopant has a high twisting power. One of the molecular fragments associated to a high value of twisting power is, as anticipated above, the biaryl unit; therefore many experiments have been done on compounds containing this unit.

The main factor in determining the handedness of the cholesterics induced by bridged 1,1′-binaphthyls is the helicity (P* or M*) of the solute and this observation is the basis of many configurational studies of chiral binaphthyls. All the homochiral (aR)-binaphthyls BN-1, BN-2 and BN-3 (see chart 2) have an M*-helicity of the core, and all induce, in biphenyl nematics, M-cholesterics.^38,46 By systematic structural variations of the covalent bridge, it is possible to obtain 1,1′-binaphthalenes with dihedral angles ranging from 60° to 96°; the handedness of the cholesteric phase always matches the helicity of the binaphthyl unit (see Table 1).³⁸ It should be noticed that derivatives BN-5 and BN-6 have helicity (P*, s-trans) opposite to BN-1—BN-4, hence they induce opposite-handed cholesterics.

Table 1 Helical twisting powers of (aR)-BN-1—BN-6¹⁶

	β	C1–C1′ conformation	Core helicity
BN-1	−85	s-cis	M*
BN-2	−80	s-cis	M*
BN-3	−79	s-cis	M*
BN-4	−33.6	s-cis	M*
BN-5	+40.0	s-trans	P*
BN-6	+95.2	s-trans	P*

---

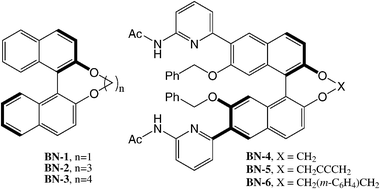Chart 2

This finding allows one to obtain useful information also on the conformation of non-bridged binaphthyls in solution.⁴⁹ In the case of (aS)-binaphthyls, s-cis and s-trans conformations are characterized by opposite helicities along the biaryl axis. Therefore one may expect the induction of left-handed or right-handed cholesterics, depending on the dominant conformation in solution. In fact, binaphthyls with substituents able to stabilize the s-cis conformation exhibit oppositely-signed β values with respect to binaphthyls with the bulkiest substituents stabilizing the s-trans conformation.

Though empirical models can help to rationalise the relationship between configuration and helical twisting power for certain classes of chiral compounds, a more general tool is needed for systematic assessment of the absolute configuration. Excellent results have been provided by coupling β measurements and predictions based on the SC model, whose main features have been outlined in the section 3.2.1. Biphenyl, whose structure is chiral for twist angles between the phenyl moieties ϕ ≠ nπ/2 (with n integer), is a simple case, yet sufficient to illustrate how subtle effects arise, which cannot be simply described in terms of empirical chirality descriptors, but are accounted for by the SC method. Order parameters and surface chirality components of biphenyl change as a function of the twist angle; accordingly, also the chirality parameter Q changes.^16,33 For P*-helicity of biphenyl (ϕ < π/2) a positive helical twisting power is predicted, as a result of the strong tendency of the y axis, characterized by high positive helicity (see Fig. 6), to lie perpendicular to the director.³⁰

Chart 3

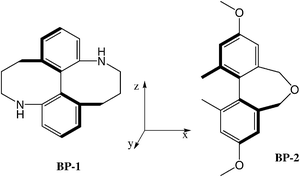
A relatively high and positive twisting power (+20 μm⁻¹) was measured for the (aR)-biphenyl derivative BP-1 (see chart 3), which is characterised by P*-helicity along the biphenyl axis.§ However there are counterexamples, like the derivative BP-2 which, although sharing the same P*-helicity at the molecular level (despite IUPAC notation for the stereoaxis is opposite), have negative twisting power (−11.4 μm⁻¹).^31,50 Calculations performed with the SC method show that these differences between the dopants can be mainly traced back to their different orientational behaviour, induced by the substitution in the central biphenyl core (see the examples of a rod-like and a disc-like solute in section 3.2.1). Whereas compound BP-1, like unsubstituted biphenyl, has a definite preference for keeping what we have denoted as the y axis perpendicular to the director, compound BP-2, which is more elongated, behaves more as a rod, with a small difference in the degree of alignment between the x and y axes. It follows that in the first case the y-helicity (right-handed) is imparted to the nematic host, whereas in the latter there is a significant contribution of the left-handed x helicity.³¹ It is worth singling out the difference from binaphthyl, where the y axis has significantly higher propensity than the x axis to lie perpendicular to the director, irrespectively of the presence of substituents: therefore P*-enantiomers almost invariably induce right-handed cholesterics.

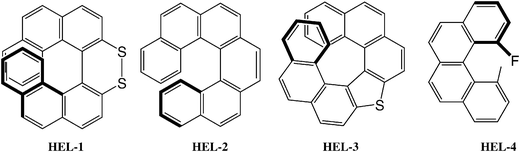
Another interesting example is represented by helicenes and related molecules. Homochiral P-helicenes very different spectroscopically, such as HEL-1, HEL-2, HEL-3 and HEL-4 (see chart 4), and hence hardly comparable by chiroptical techniques, are very similar in shape and give helical twisting powers of the same sign and of comparable intensity (−13, −55, −20, and −9, respectively);³² the twisting powers of helicenes is explained by the SC model.

Chart 4

4.2 Determination of the enantiomeric excess

The cholesteric pitch, for a given nematic LC doped with a chiral solute at a fixed concentration depends only on the ee of the dopant (see eqn (3)). This property, therefore, can be used as a measure of the enantiomeric purity of any chiral compound.

In principle, any method giving the pitch length of a cholesteric phase can be used to obtain the ee (see section 3.1). The standard method for measuring pitch lengths from several micrometres up to 0.5–1 mm is based on the Grandjean–Cano wedge¹⁵ and most of the β values reported in the literature are obtained in this way.

However, if the β or the ee or the solubility of a chiral analyte is very small, the induced cholesteric has a very long pitch, even higher than 1 mm, and Grandjean–Cano technique cannot be used for practical reasons. In these cases, the technique proposed by Raynes and based on the use of TN cells can be used.¹⁸ In ideal circumstances, pitch lengths up to 50 mm can be measured. This means that only small amounts of the dopant are required to evaluate the helical twisting power and then the enantiomeric excess.

An alternative approach for measuring the ee of dopants with low β has been adopted by Feringa and co-workers and is based on the reflection of visible light by aligned films of cholesteric phases with short pitch lengths matching the visible wavelength.⁵¹

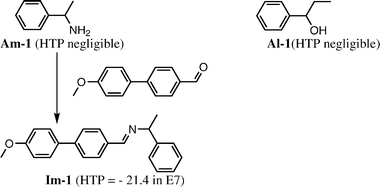
As mentioned in section 3.1 the colour generation originates from the selective reflection of circularly polarized light with the same handedness as that of the cholesteric phase and the wavelength of the order of the pitch. The wavelength of the reflected light must be tuned within the visible spectrum by a carefully choice of the chiral dopant and its concentration. The problem to overcome is that the β or solubility of chiral dopants are often not sufficiently high to induce a cholesteric with a reflection in the visible spectrum. Feringa approach is based on a simple functionalisation of an analyte with a mesogenic unit to increase the structural analogy with the nematic phase and hence its solubility and β. While simple amines (e.g.Am-1, see chart 5) or alcohols (e.g.Al-1) show small β values (and solubility) and therefore form long-pitch cholesteric phases, the simple derivatisation as imines (e.g.Im-1) or esters, respectively, forms compounds whose β values and solubilities are sufficiently high to give visible colour reflection and hence allows a visual estimation of the ee (Fig. 8).⁵¹

Chart 5

Fig. 8 Colour of the reflection of doped E7 samples with different enantiomeric excesses for Im-1. The colours shown are photographs of the aligned LC films taken perpendicular to the surface. (Adapted with permission from ref. 51. Copyright 2001 Wiley-VCH Vrlag GmbH & Co. KGaA.)

4.3 Asymmetric polymerization in a chiral liquid crystal field

The chiral environment of cholesteric liquid crystals has also been exploited for asymmetric synthesis. A remarkable example is given by polymerization to give helical polyacetylene, the simplest representative of conducting polymers; the combination of high electrical conductivity and chiral helicity is promising for novel electromagnetic and optical applications.⁵² Helical polyacetylene provides a spectacular case of hierarchical organization: films are formed by clockwise or counter-clockwise helical fibrils, which in turn are bundles of helical polyene chains. The morphology and the screw sense of fibrils are determined by the helical organization of the N*-LC. Thus, synthesis can be controlled by the choice of chiral dopants and operating temperature. Interestingly, it was found that chiral titanium complexes, having binaphthyl or other groups as coordination ligands, can play the twofod role of chiral dopants and catalysts. The method was extended to other polymers: recently, different helical conjugated polymers, including poly(bithiophene) and poly(ethylenedioxythiophene) derivatives as well as phenylene-thiophene copolymers were synthesized by chemical and/or electrochemical polymerization in N*-LCs environments.⁵³

5. Applications in nanoscience and in information technology

In recent years many reports on the applications of LCs (and in particular cholesteric phases) in advanced materials for information technologies and nanostructured systems have appeared but an exhaustive list of references is well beyond the scope of this tutorial review. In the following sections, only a few notable examples are reported.

Most applications exploit the selective reflection of light mentioned above. Such interference effects, which are also exploited in nature (the iridescent colours of beetles is a nice example), were early used for simple applications, like LC thermometers and fever sensors, which base on the change of colour accompanying the change of pitch with temperature.

5.1 Photoaddressable LC reflectors and lasers

Cholesteric liquid crystals find practical applications in colour information technology.⁵⁴ The colour of the reflected light can be tuned by changing p and this can be obtained by using photochromic chiral additives whose switchable isomers have different β values. Molecular switches with high β values allowing direct accessibility to the pitch in the visible region have been developed by Spada and co-workers⁵⁵ and Li and co-workers.⁵⁶ Their structures are based on chiral bis(azo) binaphthyl molecular switches that undergo a trans–cis reversible photo/thermal isomerisation directly affecting the pitch length through a configuration dependent β. Recently White, Bunning and coworkers⁵⁷ using these types of dopants described the development of photoaddressable cholesteric LCs capable of large range colour tuning and, possibly, on-off electrical switching. The reversible full-range colour control of a cholesteric system has been described also by Feringa and co-workers,⁵⁸ Lub and co-workers⁵⁹ and Kurihara and co-workers⁶⁰ using a “molecular motor” (see Fig. 9), a cinnamate/isosorbide derivative and azobenzene/isosorbide (isomannide) compounds, respectively, as high β chiral photocromic dopants.

Fig. 9 Colour change with time of an LC film of E7 doped with molecular motor 1 (see Fig. 11) (6.8 wt%) (a) upon irradiation with 365 nm light and (b) during thermal helix inversion. The depicted colours are photographs of the LC sample taken perpendicular to the surface of the film, recorded at room temperature during both processes. (Reprinted with permission from ref. 58. Copyright 2006 Wiley-VCH Vrlag GmbH & Co. KGaA.)

Recently, chiral LC phases have attracted considerable interest for their ability of spontaneous self-organization into photonic bandgap (PBG) structures, without the need of a complex fabrication procedure.⁶¹PBG materials are characterized by a spatial periodicity of the dielectric tensor on a length-scale that matches optical wavelength. As a consequence, they exhibit special characteristics: classical light propagation in them is forbidden for some range of frequencies and the density of photon states diverges at the photonic band edges. These properties are at the basis of distributed feedback lasing, exhibited by dye doped chiral LCs: under optical pumping, lasing at band edges occurs when excitation exceeds a threshold, with the fluorescent dye and liquid crystal host providing gain and distributed feedback, respectively. While the one-dimensional PBG structure of chiral nematic and chiral smectic C* phases gives rise to emission along the helix axis, the three-dimensional PBG of Blue Phases can result in laser emission in three different directions.⁶² An attracting feature of LC lasers is their high wavelength tunability, from ultraviolet, through the visible range, to infrared: the output laser wavelength can be selected by suitable choice of the chiral dopant and can be modified by control of the operating temperature, as well as by application of electric and magnetic fields or mechanical stresses. Photo-tuning of lasing of induced cholesterics by either reversible⁶³ or irreversible⁶⁴photoisomerisation of chiral dopants (azobenzene/isomannide derivatives and aromatic esters, respectively) have been reported: the helical pitch changes upon photoisomerisation and the lasing emission wavelength changes accordingly. Direct and in situ control of the PBG, along with the small size (from tens to hundreds of micrometres), makes LC lasers especially attractive for new applications including photonic information technology, labs-on-a-chip, spectroscopy and medical treatments.

5.2 Photoaddressable cholesteric LC performing work

A new area, in which the modulation of induced cholesteric properties by external stimuli may have relevant implications, is that of molecular scale motors, that can perform work and collectively induce controlled motion of much larger objects.⁶³ Feringa and co-workers were able to produce rotation of macroscopic (sub-millimetre scale) objects placed on top of a nematic liquid crystal film, doped with a suitably designed chiral molecular motor,⁵⁸ undergoing photo- and thermo-addressable shape changes.⁶⁵ The underlying mechanism could be elucidated by considering the interplay of photoisomerization process, elasticity and anchoring behaviour of the liquid crystal.⁶⁶ Under irradiation the dopant, which has high twisting power, is converted into an isomer with analogously high, but opposite in sign, twisting ability. Thus, photoisomerization brings about unwinding and rewinding in the opposite sense of the cholesteric helix. To understand the origin of the observed texture rotation (Fig. 10), the hybrid anchoring of the film must be taken into account: the director is parallel to the substrate and perpendicular to the interface with air. Under these conditions, the free energy of the film is minimized if an almost unperturbed cholesteric helix, with its axis normal to the substrate, is present in most of the film and strong deformations appear close to the free interface, to comply with the boundary conditions. Such deformations, with features determined by the elastic parameters of the liquid crystal, are responsible for the striped structure, visible by optical microscopy, whose rotation accompanies the reorganization of the film.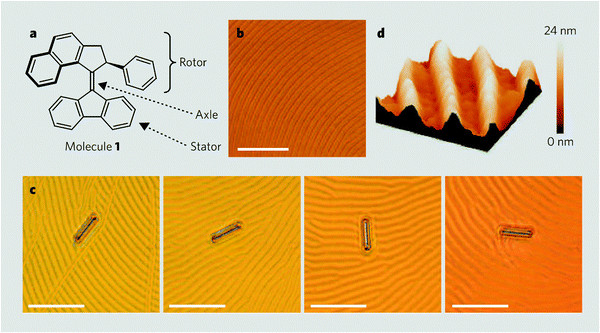

Fig. 10 Features of a light-driven molecular motor: (a) structure of the motor (molecule 1). Bonds in bold point out of the page. (b) Polygonal texture of a liquid-crystal film doped with molecule 1 (1% by weight). (c) Glass rod rotating on the liquid crystal during irradiation with ultraviolet light. Frames 1–4 (from left) were taken at 15 s intervals and show clockwise rotations of 28° (frame 2), 141° (frame 3) and 226° (frame 4) of the rod relative to the position in frame 1 (scale bars, 50 μm). (d) Surface structure of the liquid-crystal film (atomic force microscopy image; 15 μm²). (Reproduced with permission from ref. 65. Copyright 2006 Macmillan Publishers Ltd.)

5.3 Gas detection

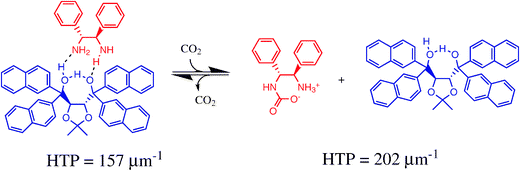
A new approach to optical monitors for gases is introduced using cholesteric liquid crystals doped with reactive chiral compounds.⁶⁷ The approach is based on cholesteric pitch length changes caused by a change in helical twisting power of the chiral dopants upon reaction with the analyte. Sijbesma and co-workers demonstrated this concept for monitoring carbon dioxide (via reversible carbamate formation) and for oxygen (using the irreversible oxidation of a chiral dithiol to a disulfide). In particular, monitoring of CO₂ was achieved by doping a commercial nematic mixture (E7) with 1.6% mol of the 1 : 1 complex of an optically pure diamine with a TADDOL derivative (see chart 6). Upon exposure to carbon dioxide, the reflection band of a thin film of the mixture shifted from 637 to 495 nm as a consequence of dissociation of the complex after carbamate formation of the diamine (Fig. 11).

Fig. 11 Images of a LC film obtained by doping E7 with the TADDOL/diamine 1 : 1 complex before (above) and after (below) exposure of CO₂. (Adapted with permission from ref. 67. Copyright 2010 American Chemical Society.)

These monitoring mechanisms hold promise for application in smart packaging, where carbon dioxide (and oxygen) are of special interest because of their roles in food preservation.

Chart 6

6. Outlook and perspectives

The phenomenon of cholesteric induction is a remarkable example of how changes at the molecular level can be magnified by the phase organization. The relation between chirality at quite different length-scales can be rationalized by a relatively simple model, which however retains the relevant factors coming into play: the molecular shape of the chiral dopant, which controls the chirality of short range intermolecular interactions, and the elastic properties of the nematic environment, which control the restoring torques opposing distortion of the director. Nowadays, induced cholesterics have turned from exotic systems to materials with interesting properties for different applications. These range from the somehow more obvious exploitation of the amplified molecular chirality for stereochemical purposes, e.g. determination of absolute configuration or enantiomeric excess, to new applications in physico–chemical fields. The latter take advantage of the periodicity or of the chiral field, with length-scales ranging from hundreds to thousands of nanometres, which characterise the cholesteric phase.

Valuable properties are the ability to spontaneously self-assemble in periodic structures and the tunability of induced cholesterics, by proper choice of the chiral dopants and their concentration. In the future, new applications are expected, which may entail the design of tailored dopants possessing, in addition to high twisting ability, other ad-hoc properties. Example are provided by switchable dopants, whose chirality can be controlled by external stimuli, or by chiral complexes, which play the twofold role of chiral dopants and catalysts in asymmetric synthesis. Open research fields also include other liquid crystal phases with induced chirality, like Blue Phases and smectic C* phases, as well as chirally doped micelles. In all these systems, the transfer of chirality from dopant to phase has not been thoroughly explored, yet, and more attention should be deserved in the future, both to understand their properties and to apply them.

Acknowledgements

We thank Professor Giovanni Gottarelli (Bologna) for helpful discussion while preparing this tutorial review. We acknowledge the fundamental contribution of Professors Giorgio Moro and Pier Luigi Nordio to the development of the ‘Surface Chirality’ model.

Notes and references

1. P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon, Oxford, 1993.
2. Handbook of Liquid Crystals, ed. D. Demus, J. Goodby, G. W. Gray, H.-W. Spiess and V. Vill, Wiley-VCH, Weinheim, 1998, vol. 1–3.
3. G. Gottarelli, M. A. Osipov and G. P. Spada, J. Phys. Chem., 1991, 95, 3879–3884.
4. Chirality in Liquid Crystals, ed. H. S. Kitzerow and C. Bahr, Springer, New York, 2001.
5. H. J. Coles and M. N. Pivnenko, Nature, 2005, 436, 997–1000 and references therein.
6. H. Kikuchi, M. Yokota, Y. Hisakado, H. Yang and T. Kajiyama, Nat. Mater., 2002, 1, 64–68.
7. A. Yoshizawa, M. Sato and J. Rokunohe, J. Mater. Chem., 2005, 15, 3285–3290.
8. R. P. Lemieux, Chem. Soc. Rev., 2007, 36, 2033–2045.
9. J. W. Goodby, Mol. Cryst. Liq. Cryst., 1997, 292, 245–263.
10. I. Nishiyama, Chem. Rec., 2009, 9, 340–355.
11. J. W. Goodby, R. Blinc, N. A. Clark, S. T. Lagerwall, M. A. Osipov, S. A. Pikun, T. Sakurai, K. Yoshino and B. Seks, Ferroelectric Liquid Crystals: Principles, Properties and Applications, Gordon and Breach, Philadelphia, 1991.
12. G. Friedel, Ann. Phys., 1922, 18, 273–274.
13. G. Solladié and R. Zimmermann, Angew. Chem., Int. Ed. Engl., 1984, 23, 348–362.
14. H. De Vries, Acta Crystallogr., 1951, 4, 219–226.
15. G. Heppke and F. Oestreicher, Z. Naturforsch., 1977, A 32, 899–901.
16. S. Pieraccini, A. Ferrarini and G. P. Spada, Chirality, 2008, 20, 749–759.
17. F. J. Kahn, Phys. Rev. Lett., 1970, 24, 209–212.
18. E. P. Raynes, Liq. Cryst., 2006, 33, 1215–1218.
19. J. W. Goodby, I. M. Saez, S. J. Cowling, V. Görtz, M. Draper, A. W. Hall, S. Sia, G. Cosquer, S.-E. Lee and E. P. Raynes, Angew. Chem., Int. Ed., 2008, 47, 2754–2787.
20. P. Raynes, S. J. Cowling and J. W. Goodby, Anal. Methods, 2009, 1, 88–92.
21. W. J. A. Goossens, Mol. Cryst. Liq. Cryst., 1971, 12, 237–244.
22. B. W. van der Meer and G. Vertogen, Phys. Lett. A, 1979, 74, 242–244.
23. A. V. Emelyanenko, M. A Osipov and D. A. Dunmur, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 2340–2352.
24. K. B. Lipkowitz, Acc. Chem. Res., 2000, 33, 555–562.
25. R. Berardi, H. K. Kuball, R. Memmer and C. Zannoni, J. Chem. Soc., Faraday Trans., 1998, 94, 1229–1234.
26. D. J. Earl and M. R. Wilson, J. Chem. Phys., 2003, 119, 10280–10288.
27. M. A. Osipov, B. T. Pickup and D. A. Dunmur, Mol. Phys., 1995, 84, 1193–1206.
28. H. Kamberaj, M. A. Osipov, R. J. Low and M. P. Neal, Mol. Phys., 2004, 102, 431–446.
29. A. Ferrarini and P. L. Nordio, J. Chem. Soc., Perkin Trans. 2, 1998, 455–460.
30. A. Ferrarini, G. J. Moro and P. L. Nordio, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 681–688.
31. A. Di Matteo, S. M. Todd, G. Gottarelli, G. Solladié, V. E. Williams, R. P. Lemieux, A. Ferrarini and G. P. Spada, J. Am. Chem. Soc., 2001, 123, 7842–7851.
32. A. Ferrarini, G. Gottarelli, P. L. Nordio and G. P. Spada, J. Chem. Soc., Perkin Trans. 2, 1999, 411–417.
33. A. Ferrarini, F. Janssen, G. J. Moro and P. L. Nordio, Liq. Cryst., 1999, 26, 201–210.
34. A. Ferrarini, P. L. Nordio, P. V. Shibaev and V. P. Shibaev, Liq. Cryst., 1998, 24, 219–227.
35. G. Celebre, G. de Luca, M. Maiorino, F. Iemma, A. Ferrrarini, S. Pieraccini and G. P. Spada, J. Am. Chem. Soc., 2005, 127, 11736–11744.
36. See, for example: D. Eisenberg and A. McLachlan, Nature, 1986, 319, 199–203.
37. F. Tombolato and A. Ferrarini, J. Chem. Phys., 2005, 122, 054908–16.
38. G. Proni, G. P. Spada, P. Lustenberger, R. Welti and F. Diederich, J. Org. Chem., 2000, 65, 5522–5527.
39. D. Seebach, A. K. Beck and A. Heckel, Angew. Chem., Int. Ed., 2001, 40, 92–138.
40. R. Eelkema and B. L. Feringa, Org. Biomol. Chem., 2006, 4, 3729–3745.
41. See, for example S. Zahn, G. Proni, G. P. Spada and J. W. Canary, Chem.–Eur. J., 2001, 7, 88–93.
42. R. Eelkema and B. L. Feringa, J. Am. Chem. Soc., 2005, 127, 13480–13481.
43. G. Gottarelli, B. Samorì, S. Marzocchi and C. Stremmenos, Tetrahedron Lett., 1975, 16, 1981–1984.
44. H. J. Krabbe, H. Heggemeier, B. Schrader and E. H. Korte, Angew. Chem., Int. Ed. Engl., 1977, 16, 791–792.
45. P. L. Rinaldi and M. Wilk, J. Org. Chem., 1983, 48, 2141–2146.
46. G. Gottarelli, M. Hibert, B. Samorì, G. Solladié, G. P. Spada and R. Zimmermann, J. Am. Chem. Soc., 1983, 105, 7318–7321.
47. R. Memmer, H.-G. Kuball and A. Schönhofer, Mol. Phys., 1996, 89, 1633–1649.
48. See, for example: R. P. Lemieux, Acc. Chem. Res., 2001, 34, 845–853.
49. C. Rosini, I. Rosati and G. P. Spada, Chirality, 1995, 7, 353–358.
50. G. Gottarelli, G. P. Spada, K. Seno, S. Hagishita and K. Kuriyama, Bull. Chem. Soc. Jpn., 1986, 59, 1607–1608.
51. R. A. Van Delden and B. L. Feringa, Angew. Chem., Int. Ed., 2001, 40, 3198–3200.
52. K. Akagi, Chem. Rev., 2009, 109, 5354–5401; M. Goh, S. Matsushita and K. Akagi, Chem. Soc. Rev., 2010, 39, 2466.
53. H. Goto and K. Akagi, Angew. Chem., Int. Ed., 2005, 44, 4322–4328.
54. N. Tamaoki, Adv. Mater., 2001, 13, 1135–1147.
55. S. Pieraccini, G. Gottarelli, R. Labruto, S. Masiero, O. Pandoli and G. P. Spada, Chem.–Eur. J., 2004, 10, 5632–5639.
56. Q. Li, L. Green, N. Venkataraman, I. Shiyanoskaya, A. Khan, A. Urbas and J. W. Doane, J. Am. Chem. Soc., 2007, 129, 12908–12909.
57. T. J. White, R. L. Bricker, L. V. Natarajan, N. V. Tabiryan, L. Green, Q. Li and T. J. Bunning, Adv. Funct. Mater., 2009, 19, 3484–3488.
58. R. Eelkema and B. L. Feringa, Chem.–Asian J., 2006, 1, 367–369.
59. J. Lub, W. P. M. Nijssen, R. T. Wegh, J. P. A. Vogels and A. Ferrer, Adv. Funct. Mater., 2005, 15, 1961–1972.
60. T. Yoshioka, T. Ogata, T. Nonaka, M. Moritsugo, S.-N. Kim and S. Kurihara, Adv. Mater., 2005, 17, 1226–1229.
61. A. D. Ford, S. M. Morris and H. J. Coles, Mater. Today, 2006, 9, 36–42.
62. W. Y. Cao, A. Munoz, P. Palffy-Muhoray and B. Taheri, Nat. Mater., 2002, 1, 111–113.
63. S. Kurihara, Y. Hatae, T. Yoshioka, M. Moritsugu, T. Ogata and T. Nonaka, Appl. Phys. Lett., 2006, 88, 103121.
64. A. Chanishvili, G. Chilaya, G. Petriashvili, R. Barberi, R. Bartolino, G. Cipparrone, A. Mazzulla and L. Oriol, Adv. Mater., 2004, 16, 791–795.
65. R. Eelkema, M. M. Pollard, J. Vicario, N. Katsonis, B. Serrano Ramon, C. W. M. Bastiaansen, D. J. Broer and B. L. Feringa, Nature, 2006, 440, 163–163.
66. A. Bosco, M. G. M. Jongejan, R. Eelkema, N. Katsonis, E. Lacaze, A. Ferrarini and B. L. Feringa, J. Am. Chem. Soc., 2008, 130, 14615–14624.
67. Y. Han, K. Pacheco, C. W. M. Bastiaansen, D. J. Broer and R. P. Sijbesma, J. Am. Chem. Soc., 2010, 132, 2961–2967.

---

Footnotes

† In memory of Professor Carlo Rosini (1948–2010), a pioneer of chirality aspects of organic stereochemistry. His human and scientific presence will always be with us.

‡ For the model case of an elongated cylindrical solute, the orienting potential obtained in this way takes the simple Maier–Saupe form,¹U ∝ −P₂(cosθ), with θ being the angle between cylinder axis and director: the energy increases with thisangle, with no distinction between parallel and antiparallel orientation.

§ In this context, the P*, M* descriptors do not refer to the configuration of chirality axes, planes or helices according to IUPAC, but simply to the handedness of the twist between the two planes. For example, a biphenyl is designed as P* when the two phenyl rings are arranged in such a way that a clock-wise rotation of the ring closer to the observer is required to obtain the co-planarity of the two aromatic planes. To avoid any confusion with P, M IUPAC notation, the descriptors used here are marked with a star.

---