In situ X-ray probing reveals fingerprints of surface platinum oxide

Abstract

In situ X-ray absorption spectroscopy (XAS) at the Pt L₃ edge is a useful probe for Pt–O interactions at polymer electrolyte membrane fuel cell (PEMFC) cathodes. We show that XAS using the high energy resolution fluorescence detection (HERFD) mode, applied to a well-defined monolayer Pt/Rh(111) sample where the bulk penetrating hard X-rays probe only surface Pt atoms, provides a unique sensitivity to structure and chemical bonding at the Pt-electrolyte interface. Ab initio multiple-scattering calculations using the FEFF code and complementary extended X-ray absorption fine structure (EXAFS) results indicate that the commonly observed large increase of the white-line at high electrochemical potentials on PEMFC cathodes originates from platinum oxide formation, whereas previously proposed chemisorbed oxygen-containing species merely give rise to subtle spectral changes.

---

1. Introduction

One of the greatest challenges in the development of polymer electrolyte membrane fuel cells (PEMFC) is the design of new catalyst materials for the oxygen reduction reaction (ORR), in order to overcome the 25–30% conversion efficiency loss due to the ORR overpotential, and to reduce the Pt content of the ORR catalyst. Theoretical calculations show that the binding energy of chemisorbed atomic oxygen can be used as a descriptor for ORR activity on transition metal surfaces including bimetallic systems, and a volcano-type behavior was shown.^1,2 This computational approach was successful in predicting new catalyst materials such as Pt-Y alloy, which shows a ten-fold increase in activity compared to Pt.² However, it is necessary to determine experimentally which of the possible intermediate or spectator species such as O, OH, OOH, or surface oxides become rate-limiting at different potentials, since their stability can be expected to follow the same trend. Common probes of the chemical state of O or Pt are usually unsuccessful in identifying ORR intermediate or spectator species in situ, since bulk penetration and surface sensitivity are both required but incompatible. Here, we show how this difficulty can be overcome, by applying synchrotron X-ray absorption spectroscopy (XAS) as a probe of unoccupied Pt 5d states to a well-defined model electrocatalyst where Pt is confined to a monolayer on a Rh(111) single-crystal surface, thus only surface Pt atoms and their interaction with oxygen-containing species are probed.

The near-edge region (XANES) of Pt L₃ spectra shows a characteristic “white-line”, i.e. a strong absorption maximum due to a 2p → 5d transition whose intensity can be used as a measure of unoccupied 5d states;^3,4 depletion of occupied 5d states due to Pt–O bond formation thus gives an increased white-line intensity. Previous in situXAS studies^5–14 using nanoparticle samples have consistently shown strong white-line intensity increases at high potentials, but contradictory interpretations were given ranging from chemisorbed OH and atomic O to surface oxide PtO, or even PtO₂. This uncertainty, arising from unknown bulk contributions and the use of very small Pt clusters in multiple-scattering computations that do not represent the much larger particle size in the experiment, motivated us to study a monolayer Pt sample and sufficiently large model structures in the multiple-scattering calculations using the FEFF8 code,¹⁵ for an unambiguous identification of Pt–O species and their spectral features. Moreover, the High Energy Resolution Fluorescence Detection (HERFD) XAS technique,^16,17 applied for the first time to a single-crystal surface in an electrochemical environment, allowed us to significantly reduce the effect of the Pt 2p core-hole lifetime broadening and thus obtain strongly enhanced spectral features.

2. Experimental and computational methods

An 8 mm diameter commercial Rh(111) single-crystal (Surface Preparation Laboratory, Zaandam, The Netherlands) was cleaned under ultrahigh vacuum by repeated sputtering and annealing cycles. A home-built evaporator with resistive heating was used to deposit the Pt film while the sample temperature was held at ∼600 K. The Pt coverage was monitored using the changes in CO thermal desorption spectra from the Pt/Rh(111) surface. It has been previously shown¹⁸ that, during the deposition, Pt atoms are incorporated into the topmost Rh layer to form a surface alloy with increasing Pt content and, eventually, a two-dimensional Pt overlayer.

Subsequent to the Pt deposition, the sample was mounted into our hanging meniscus in situ X-ray electrochemical cell. Similar to a setup recently used for in situ surface X-ray diffraction,^19,20 it consists of a PEEK tube which contains the electrolyte, a counter electrode (Pt wire) and a leak-free Ag/AgCl reference electrode. The contact with the working electrode is established through a free-standing meniscus in the ∼ 2 mm narrow gap between the tube and the sample surface. This design avoids problems caused by beam damage to common X-ray window materials and allows for operation in O₂-saturated solution where very high electrochemical currents can be reached.

The 0.01 M HClO₄ electrolyte was made from 70% HClO₄ (Trace Select Ultra, Sigma-Aldrich) and ultrapure water from a Millipore Gradient system. All potentials were converted to values with respect to the reversible hydrogen electrode (RHE).

All in situ X-ray absorption spectra were measured at the Stanford Synchrotron Radiation Lightsource (SSRL). At Beam Line 11-2, XANES and EXAFS measurements were carried out with conventional fluorescence detection using a large 30-element Ge solid state detector. HERFD-XANES measurements were performed at SSRL Beam Line 6-2 using a Si(111) monochromator in combination with a Rowland circle analyzer spectrometer²¹ consisting of three spherically bent Ge perfect crystals (R = 1 m). The crystals were aligned in a backscattering geometry using the (660) Bragg reflection at 80.0° to select the Pt Lα₁ fluorescence line (9442 eV). The combined resolution of the monochromator and analyzer as determined by measuring the elastic scattering was 1.6 eV. Assuming an intrinsic monochromator resolution of ∼ 1.3 eV the analyzer resolution is estimated to be ∼1 eV.

For all XAS measurements, the incidence angle of the X-ray beam to the Pt/Rh(111) surface was adjusted to the critical angle for total external reflection, thereby enhancing the fluorescence intensity up to fourfold.²² The orientation of the electric field vector of the incident beam was perpendicular to the surface normal.

For the EXAFS data analysis, SIXPack²³ was used for background subtraction, spline fitting and least-square fitting of the Fourier-transformed EXAFS signal. Backscattering phase and amplitude functions required for fitting of spectra were obtained from FEFF 6.²⁴

All HERFD XAS calculations were carried out using the FEFF 8.4 program, which employs a full multiple-scattering formalism.¹⁵ By using the “NOHOLE” card, potentials and phase shifts were calculated assuming complete screening of the core-hole, resulting in better agreement with experimental white-line intensities. This is fully consistent with previously reported FEFF results on transition metal L₂ and L₃ edges.^17,25–28 The line-sharpening effect observed in HERFD was modeled by reducing the theoretical lifetime broadening by 1.75 eV using the “EXCHANGE” card. This value was determined by comparing the computed XANES spectrum of a clean Pt/Rh(111) surface with an experimental spectrum at a potential corresponding to the double-layer region, namely E = +0.4 V. More detailed information about the model structures and input parameters for the FEFF8 calculations are provided in the Supplementary Information.

3. Results and discussion

Fig. 1a shows HERFD XAS for 1 ML Pt/Rh(111) in N₂-saturated 0.01 M HClO₄, recorded in order of increasing potential with respect to the reversible hydrogen electrode (RHE). As the potential exceeds 1.0 V, significant changes occur: the absorption edge is shifted to higher energy, the white-line increases in both width and peak intensity, and the absorption decreases in the post-edge region above 11 573 eV. In comparison with conventional XANES measurements under the same electrochemical conditions (Fig. 2a), the features are strongly enhanced with more spectral details due to the reduction of the Pt 2p core hole lifetime broadening. The strong white-line intensity and the “dip” in the post-edge region at high potentials are characteristic spectral features of platinum oxides.²⁹

Fig. 1 (a) PtL₃ edge HERFD XAS of 1 ML Pt/Rh(111) in 0.01 M HClO₄ as function of increasing potential, (b) potential hysteresis of platinum oxide formation as seen in the integrated white-line intensity, for increasing (red) and decreasing (blue) potentials. Values were obtained by integrating the HERFD XAS from 11 545 eV to 11 573 eV.

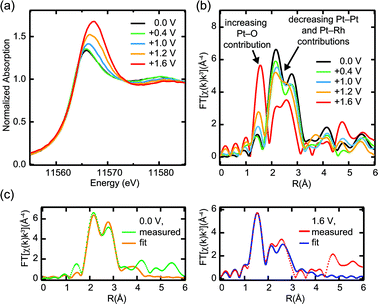Fig. 2 In situ Pt L₃ XAS in conventional fluorescence detection for 1 ML Pt/Rh(111) in 0.01 M HClO₄: (a) near-edge region, (b) Fourier transform of the EXAFS signal, (c) EXAFS fits corresponding to metallic monolayer Pt/Rh(111) at 0.0 V and Pt oxide layer at +1.6 V.

A strong potential hysteresis effect in the white-line intensity as function of the potential is shown in Fig. 1b. After an anodic potential excursion to +1.6 V, metastable platinum oxide remains present at potentials as low as +0.6 V, indicating significant activation barriers for oxide formation and reduction.

Further evidence for the formation of a Pt oxide film was obtained from EXAFS data (Fig. 2b) which were recorded simultaneously with conventional low-resolution XANES. Platinum oxide formation at high potentials is evident from the breaking of metallic Pt–Pt and Pt–Rh bonds (strong decrease of the double peak at ∼2.5 Å) that accompanies the formation of Pt–O bonds (new peak at ∼1.6 Å). EXAFS fitting results for two potentials, 0.0 V and +1.6 V, are shown in Fig. 2c and summarized in Table 1. At 0.0 V, the coordination numbers for Pt and Rh nearest neighbors around the Pt absorber are in good agreement with the expected values of 6 (Pt) and 3 (Rh) for a two-dimensional monolayer Pt on Rh(111). Including an additional contribution from the next-nearest neighbor Rh atoms improved the statistical R factor from 0.0661 to 0.0282, without significantly changing the ratio between the two nearest-neighbor coordination numbers. Note that at +1.6 V, the changes in the Pt–Pt and Pt–Rh contribution at ∼2.5 Å cannot be explained with a mere amplitude reduction of a metallic Pt fraction. Instead, we find a significant expansion of both Pt–Pt and Pt–Rh bond distances. This clearly indicates that the metallic coordination environment is completely displaced by an oxide structure with the corresponding wider distances between metal atoms.

Table 1 In situ EXAFS fitting results for 1 ML Pt/Rh(111) in 0.01 M HClO₄. Data ranges of k = 3.0–9.8 Å⁻¹ and k = 3.0–9.5 Å⁻¹ were used at 0.0 V and +1.6 V, respectively

	Pt–Pt	Pt–Rh	Pt–Rh (2nd shell)	Pt–O	R factor
E = 0.0 V					0.0282
N	6.5 ± 0.8	3.2 ± 0.7	2.6 ± 0.7	—
R (Å)	2.72 ± 0.02	2.72 ± 0.02	3.94 ± 0.02	—
σ ^2 (Å^2)	0.005	0.005	0.005	—
E = +1.6 V					0.0478
N	2.1 ± 0.9	2.6 ± 0.4	—	3.8 ± 0.4
R (Å)	3.23 ± 0.03	2.81 ± 0.01	—	1.95 ± 0.02
σ ^2 (Å^2)	0.005	0.005	—	0.01

---

Platinum oxide formation on Pt(111) has been studied previously with X-ray reflectivity measurements.³⁰ In 0.1 M HClO₄, a place-exchange mechanism for platinum oxide formation was reported at all potentials studied between 1.025 V and 1.425 V, and an irreversible roughening of the surface was found for potentials exceeding 1.25 V. This is fully consistent with our results.

FEFF8 calculations¹⁵ of HERFD XANES for several different structure models allow us to elucidate further the structure of the Pt oxide film formed at high potentials, and to identify the more subtle spectral fingerprints of chemisorbed oxygen-containing species on a metallic Pt surface (Fig. 3). Using large hemispherical Pt/Rh(111) clusters (Fig. 3a) in the FEFF8 input, we calculated spectra for 1 ML Pt/Rh(111) without any adsorbate, with a mixed OH/H₂Oc(3 × 3) layer, as well as chemisorbed oxygenp(2 × 2) and p(2 × 1) layers corresponding to oxygen coverages of 0.25 and 0.5 ML, respectively. The hypothetical adlayer structures of oxygen-containing species were modeled after structures that have been experimentally observed on Pt(111),^31–35 using the same Pt–O bond distances and laterally compressing the unit cells to match with the Pt/Rh(111) lattice (Supplementary Table S1†).

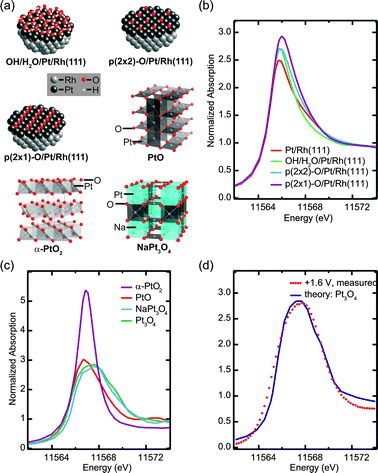Fig. 3 Simulation of HERFD XANES using FEFF8: (a) hemispherical adsorbate-covered Pt/Rh(111) clusters and representative sections of Pt oxide structures, (b) and (c) simulated spectra of (b) Pt/Rh(111) with different chemisorbed oxygen-containing species and (c) of oxides PtO₂, Na_xPt₃O₄ and PtO, (d) comparison of simulated Pt₃O₄ XANES with measured high-potential data.

The calculated XANES for adsorbate-free Pt/Rh(111) is in good agreement with experimental spectra taken at +0.4 V. The addition of adsorbed oxygen-containing species causes a gradual increase of the white-line peak intensity (Fig. 3b). Chemisorbed OH or atomic oxygen could therefore explain the subtle changes measured for increasing potentials from +0.4 V up to +1.0 V. Note, however, that this peak intensity increase is much weaker in the measurement than the predicted changes for addition of 0.25 ML oxygen, indicating a rather low coverage and thus weak oxygen affinity of the Pt/Rh(111) system.

In order to characterize the ultrathin platinum oxide film formed at potentials above 1.0 V, we assume that its short-range structure resembles one of the well-known structures^36–39 of bulk Pt oxides (Fig. 3a, Supplementary Table S2†). Therefore, calculated spectra for these compounds (Fig. 3c) were used as a first approximation to identify important features of the ultrathin film.

The calculated HERFD XANES of α-PtO₂, where Pt in the formal +IVoxidation state is octahedrally coordinated with six O atoms, shows a significant dip in the post-edge region and a sharp white-line with more than twice the intensity compared to metallic Pt. The formation of a PtO₂ layer in the system studied here can be ruled out based on the white-line spectral width and intensity. PtO and Na_xPt₃O₄ — two hypothetical compositions with x = 0 and x = 1 were studied — contain square planar PtO₄ units and have computed peak intensities similar to the measurement at +1.6 V, while the white-line width increases in the order PtO < NaPt₃O₄ < Pt₃O₄. This can be explained with the crystal field splitting of the Pt 5d states into four different energy levels, where the highest, fully unoccupied level alone would give rise to a sharp white-line while additional vacancies in the second highest level cause the broadening. The simulation for Pt₃O₄ gives the best agreement with the measurement at the highest potential in terms of the white-line intensity and width (Fig. 3d). Therefore, we propose that the ultrathin Pt oxide film contains square planar PtO₄ units, with Pt in a slightly higher oxidation state than in PtO.

Similar PtO₄ units have been reported to form one-dimensional chain structures on Pt(110) and Pt(111) surfaces in ultrahigh vacuum under high coverages of atomic oxygen.^34,35,40

We propose that surface platinum oxide formation will take place on all types of Pt/M(111) electrodes, including Pt(111), and on Pt surfaces in general, including those of nanoparticles. The onset potential for oxide formation can be expected to be kinetically influenced by the stability of its precursor state, i.e. chemisorbed oxygen on the metallic Pt surface. Based on DFT calculations, oxygen has been predicted to be ca. 0.6 eV more strongly bound on Pt(111) than on Pt/Rh(111).² This is in good agreement with our observations on Pt/Rh(111) that indicate only low coverages of chemisorbed oxygen-containing species at potentials up to 1.0 V and an oxide formation onset potential of ∼1.0 V.

On such surfaces where atomic oxygen is more weakly adsorbed, the dissociation of molecular oxygen can become the rate-limiting step of the ORR. This appears to be the case in the Pt/Rh(111) system studied here, for which lower ORR activity and increased H₂O₂ formation in comparison to Pt(111) was found.⁴¹L₃-edge spectra of pure Pt nanoparticles^6,8–12 exhibit a strong increase and broadening of the white-line, similar to what we observe on Pt/Rh(111), already at lower onset potentials of around 0.8 V but with less intensity since bulk Pt atoms also contribute significantly to the L-edge peak. The similarities between our data and previously reported spectra of Pt nanoparticles suggest a re-interpretation of the latter, with the generally observed white-line increase being due to oxide formation rather than OH or O chemisorption. Since oxide formation occurs at lower potentials for nanoparticles it can contribute significantly to the ORR overpotential. We conjecture that nanoparticles provide corner and edge sites where oxide can nucleate at lower potentials and then spread over to the low-index facets. This can explain the decrease in ORR activity per surface Pt atom in nanoparticles compared to single-crystals.⁴²

Since the bond strength of the various Pt–O species, including oxides, will scale with the atomic oxygen chemisorption energy, the latter still provides an overall good descriptor for ORR activity. However, oxide formation could additionally be affected by other parameters such as metal cohesion, metal/oxide interface energy and surface diffusion barriers. Selectively inhibiting oxide growth without compromising the stability of chemisorbed oxygen may therefore represent a useful criterion for catalyst design. Such a case could be the modification of Pt nanoparticles with Au clusters,⁷ which was shown to significantly enhance the stability of Pt against oxidation while retaining almost identical ORR half-wave potentials. Improved ORR activities were also found on Pt-alloy and bimetallic core-shell nanoparticles,^5,6,9,43 concomitantly with a suppression of Pt oxidation at high potentials.^5,6,9 HERFD XAS applied to bimetallic systems could, as demonstrated in the present work, elucidate details of the inhibition mechanism for Pt oxide growth, especially when suitable absorption edges of both metal components are studied.

4. Conclusions

The application of EXAFS, HERFD XANES and FEFF8 calculations to a well-defined Pt monolayer system has enabled us to unambiguously differentiate the XANES signatures of chemisorbed oxygen-containing species and several platinum oxides. The theoretically predicted position of Pt/Rh(111) on the low oxygen-affinity slope of the ORR volcano plot² can be confirmed by our observation of only subtle spectral changes indicating low oxygen coverage at potentials up to 1.0 V, and Pt oxide formation at potentials above 1.0 V. The comparison of our data with previous XAS measurements on Pt nanoparticles indicates that the latter can form a surface oxide already at lower potentials. Therefore, destabilization of platinum oxide could be an important ORR catalyst design criterion.

Acknowledgements

This work was supported by the Division of Materials Sciences and Engineering, Office of Basic Energy Sciences, US Department of Energy, under the auspices of the President’s Hydrogen Fuel Initiative, and by the Swedish National Research Council. This research was partly carried out at the Stanford Synchrotron Radiation Lightsource, a National User Facility operated by Stanford University on behalf of the U.S. Department of Energy, Office of Basic Energy Sciences. D. F. is grateful to the Alexander von Humboldt Foundation for a Feodor Lynen fellowship. We acknowledge helpful discussions with A. Sorini, J. J. Rehr, T. Devereaux, T. Schiros and J. F. Weaver.

References

1. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
2. J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556.
3. J. A. Horsley, J. Chem. Phys., 1982, 76, 1451–1458.
4. A. N. Mansour, J. W. Cook and D. E. Sayers, J. Phys. Chem., 1984, 88, 2330–2334.
5. M. B. Vukmirovic, J. Zhang, K. Sasaki, A. U. Nilekar, F. Uribe, M. Mavrikakis and R. R. Adzic, Electrochim. Acta, 2007, 52, 2257–2263.
6. J. Zhang, Y. Mo, M. B. Vukmirovic, R. Klie, K. Sasaki and R. R. Adzic, J. Phys. Chem. B, 2004, 108, 10955–10964.
7. J. Zhang, K. Sasaki, E. Sutter and R. R. Adzic, Science, 2007, 315, 220–222.
8. A. Teliska, W. E. O’Grady and D. E. Ramaker, J. Phys. Chem. B, 2005, 109, 8076–8084.
9. S. Mukerjee, S. Srinivasan, M. P. Soriaga and J. Mcbreen, J. Electrochem. Soc., 1995, 142, 1409–1422.
10. S. Mukerjee and J. McBreen, J. Electroanal. Chem., 1998, 448, 163–171.
11. M. Tada, S. Murata, T. Asakoka, K. Hiroshima, K. Okumura, H. Tanida, T. Uruga, H. Nakanishi, S. Matsumoto, Y. Inada, M. Nomura and Y. Iwasawa, Angew. Chem., Int. Ed., 2007, 46, 4310–4315.
12. H. Imai, K. Izumi, M. Matsumoto, Y. Kubo, K. Kato and Y. Imai, J. Am. Chem. Soc., 2009, 131, 6293–6300.
13. P. G. Allen, S. D. Conradson, M. S. Wilson, S. Gottesfeld, I. D. Raistrick, J. Valerio and M. Lovato, J. Electroanal. Chem., 1995, 384, 99–103.
14. E. Principi, A. Witkowska, S. Dsoke, R. Marassi and A. Di Cicco, Phys. Chem. Chem. Phys., 2009, 11, 9987–9995.
15. A. L. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Phys. Rev. B, 1998, 58, 7565–7576.
16. F. M. F. de Groot, M. H. Krisch and J. Vogel, Phys. Rev. B: Condens. Matter, 2002, 66, 195112.
17. O. V. Safonova, M. Tromp, J. A. van Bokhoven, F. M. F. de Groot, J. Evans and P. Glatzel, J. Phys. Chem. B, 2006, 110, 16162–16164.
18. M. Duisberg, M. Dräger, K. Wandelt, E. Gruber, M. Schmid and P. Varga, Surf. Sci., 1999, 433, 554–558.
19. F. U. Renner, Y. Gründer and J. Zegenhagen, Rev. Sci. Instrum., 2007, 78, 033903.
20. O. M. Magnussen, K. Krug, A. H. Ayyad and J. Stettner, Electrochim. Acta, 2008, 53, 3449–3458.
21. P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65–95.
22. G. A. Waychunas, Reviews in Mineralogy & Geochemistry, Mineralogical Soc America, 2002, vol. 49, pp. 267–315.
23. S. M. Webb, Phys. Scr., 2005, T115, 1011–1014.
24. J. J. Rehr, R. C. Albers and S. I. Zabinsky, Phys. Rev. Lett., 1992, 69, 3397–3400.
25. P. Glatzel, J. Singh, K. O. Kvashnina and J. A. van Bokhoven, J. Am. Chem. Soc., 2010, 132, 2555–2557.
26. A. L. Ankudinov, J. J. Rehr, J. Low and S. R. Bare, Phys. Rev. Lett., 2001, 86, 1642–1645.
27. A. L. Ankudinov, J. J. Rehr, J. J. Low and S. R. Bare, J. Synchrotron Rad., 2001, 8, 578–580.
28. M. Teliska, V. S. Murthi, S. Mukerjee and D. E. Ramaker, J. Electrochem. Soc., 2005, 152, A2159–A2169.
29. A. N. Mansour, D. E. Sayers, J. W. Cook, D. R. Short, R. D. Shannon and J. R. Katzer, J. Phys. Chem., 1984, 88, 1778–1781.
30. H. You, D. J. Zurawski, Z. Nagy and R. M. Yonco, J. Chem. Phys., 1994, 100, 4699–4702.
31. H. Ogasawara, B. Brena, D. Nordlund, M. Nyberg, A. Pelmenschikov, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2002, 89, 276102.
32. T. Schiros, L. Å. Näslund, K. Andersson, J. Gyllenpalm, G. S. Karlberg, M. Odelius, H. Ogasawara, L. G. M. Pettersson and A. Nilsson, J. Phys. Chem. C, 2007, 111, 15003–15012.
33. N. Materer, U. Starke, A. Barbieri, R. Doll, K. Heinz, M. A. Vanhove and G. A. Somorjai, Surf. Sci., 1995, 325, 207–222.
34. S. P. Devarajan, J. A. Hinojosa and J. F. Weaver, Surf. Sci., 2008, 602, 3116–3124.
35. J. M. Hawkins, J. F. Weaver and A. Asthagiri, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125434.
36. H. R. Hoekstra, S. Siegel and F. X. Gallagher, in Advances in Chemistry, ed. U. V. Rao, American Chemical Society, Washington, DC, 1971, ch. 4, vol. 98, pp. 39–53.
37. O. Muller and R. Roy, J. Less Common Met., 1968, 16, 129–146.
38. K. B. Schwartz, C. T. Prewitt, R. D. Shannon, L. M. Corliss, J. M. Hastings and B. L. Chamberland, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 363–368.
39. W. J. Moore and L. Pauling, J. Am. Chem. Soc., 1941, 63, 1392–1394.
40. S. Helveg, H. T. Lorensen, S. Horch, E. Laegsgaard, I. Stensgaard, K. W. Jacobsen, J. K. Nørskov and F. Besenbacher, Surf. Sci., 1999, 430, L533–L539.
41. J. L. Zhang, M. B. Vukmirovic, Y. Xu, M. Mavrikakis and R. R. Adzic, Angew. Chem., Int. Ed., 2005, 44, 2132–2135.
42. V. R. Stamenkovic, B. Fowler, B. S. Mun, G. F. Wang, P. N. Ross, C. A. Lucas and N. M. Markovic, Science, 2007, 315, 493–497.
43. P. Strasser, S. Koh, T. Anniyev, J. Greeley, K. More, C. Yu, Z. Liu, S. Kaya, D. Nordlund, H. Ogasawara, M. F. Toney and A. Nilsson, Nature Chem., 2010, 2, 454–460.

---

Footnote

† Electronic supplementary information (ESI) available: Details of FEFF calculations. See DOI: 10.1039/c0cp01434f

---