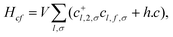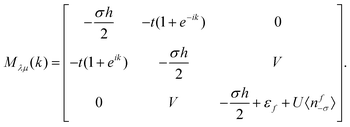Field-controlled magnetic order with insulator–metal transitions in a periodic Anderson-like organic polymer
Received
11th April 2010
, Accepted 15th September 2010
First published on 29th October 2010
Abstract
The zero- and low-temperature behaviors of a quasi-one-dimensional organic polymer proposed as a symmetrical periodic Anderson-like chain model, in which the localized f orbitals hybridize with the conduction orbitals at even sites, are investigated by means of many-body Green's function theory. In the absence of magnetic field, the ground state of the system turns out to be ferrimagnetic. The temperature-induced phase diagrams have been explored, where the competition between the Hubbard repulsion U on the localized f orbital and the hybridization strength V makes an important impact on the transition temperature. In a magnetic field, it is found that a 1/3 magnetization plateau appears and two critical fields indicating the insulator–metal transitions at zero temperature emerge, which are closely related to the energy bands. Furthermore, the single-site entanglement entropy is a good indicator of quantum phase transitions. The temperature-field-induced phase diagram has also been attained, wherein the magnetization plateau state, the gapless phase and the spin polarized state are revealed. The temperature dependence of thermodynamic quantities such as the magnetization, susceptibility and specific heat are calculated to characterize the corresponding phases. It is also found that the up-spin and down-spin hole excitations are responsible for the thermodynamic properties.
1. Introduction
Due to quantum effect and ferromagnetic properties, the low-dimensional organic magnets have attracted considerable attention both by chemists and physicists in recent years.1–13 Besides, the nonlinear optical coefficients and transport properties significant for molecular electronics of low-dimensional quantum systems were also investigated by Pati et al.14–21 As far as we know, several quasi-one-dimensional organic ferromagnets have been synthesized experimentally such as poly-BIPO,1p-NPNN2 and poly(9,10-anthryleneethynylene)6 with pendant radicals. Subsequently, some theoretical models4,5,22 were proposed to describe the quasi-one-dimensional conjugated organic polymer, which was considered as a delocalized π-electron system, where the orbitals of successive carbon atoms overlap, giving rise to charge mobility along the backbone of the polymer chain. However, it is still unclear for many issues concerning these conjugated organic ferromagnets. To obtain organic ferromagnets, one basic idea, first proposed by Ovchinnikov,23 is the synthesis of alternate hydrocarbon with high-spin ground state, as schematically illustrated in Fig. 1, where the π-electrons along the main zigzag chain were considered to be itinerant, while the unpaired electrons on the side radicals were taken into account as two cases: delocalized and totally localized. Thus, the Hubbard model associated with Su–Schrieffer–Heeger (SSH) model Hamiltonians including electron–electron and electron–phonon interactions were employed to investigate the ground state properties and magnon excitation.24,25 Later on, the interchain coupling effect26,27 and spin transport properties28,29 were also investigated. In addition to the carbon-based light weight advantage of the conjugated organic polymer, the π-electron, with spin degrees of freedom, suggests that it has significant potential for novel spintronics applications like organic spin-valves30 whose conductivity depends on the spin state of electrons controlled by an external magnetic field. Furthermore, the quasi-one-dimensional conjugated polymer was theoretically considered to be with only one radical, which can also be regarded as a single magnetic impurity, as shown in Fig. 1 of both ref. 31 and 32. A variety of elementary excitations such as solitons,31 polarons32–34 and bipolarons,35 due to the strong electron–phonon interactions, were uncovered. Indeed, this structure can also be taken as a one-dimensional Anderson model with one single magnetic impurity.
 |
| | Fig. 1 Schematic illustration of a quasi-one-dimensional periodic Anderson-like organic polymer chain model. | |
However, if each unit cell contains a radical (a single magnetic impurity), the conjugated organic polymer (see Fig. 1) is developed as a periodic Anderson-like model (PALM), whose ground state was first studied by Wang36 using the exact diagonalization technique in the absence of magnetic field. The conduction electrons with uncorrelated orbitals which reside in the main zigzag chain form a conduction sea, while a correlated localized f orbital locates at the side radical R. Generally in inorganic materials, the periodic Anderson model (PAM), which is the extension of the single impurity Anderson model first proposed by Anderson37 on the localized magnetic states in metals, is considered as a good candidate to describe heavy-fermion behaviors. Usually, this feature is associated with the large effective masses of quasi-particle owing to the coulomb repulsion on the localized f orbital. In these systems, the f electrons are strongly localized, while the conduction electrons form a conduction sea distribute throughout the system, which presents a Fermi liquid coupling with localized spins, wherein two interactions compete for dominance.38–40 One interaction is the Kondo coupling, which happens as the spin of localized f electron is screened by the conduction sea; the other is the superexchange, i.e., the indirect Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction, which occurs between the neighboring localized spins mediated by the waves of conduction sea, resulting in the magnetic order in the system. For the symmetrical case, the Kondo coupling JK ∼ V2/U41,42 gives rise to the fact that the behavior of the system is controlled by two parameters: the hybridization V between the conduction and localized f orbitals, and the Hubbard repulsion U on the localized f orbital. Thus, the competition between Kondo coupling and magnetic order due to the RKKY interaction is attributed to the consequence of interplay between Coulomb interaction and hybridization. In particular, the Kondo insulator behaviors and insulator-metal transitions were strongly affected by an external magnetic field.43
Likewise, in this periodic Anderson-like organic polymer, for the symmetrical case U + 2εf = 0, there is a competition between Kondo coupling due to the localized f spin screened by the conduction orbital (l,2) and indirect non-concussively ferromagnetic RKKY interaction of the two contiguous localized spins mediated by conduction sea. Although the ground state lies in the gapless ferrimagnetic phase, it is neither metallic nor insulating. However, when an external magnetic field is applied to the system, apart from the 1/3 magnetization plateau indicating typical ferrimagnetism of ground state, the insulator–metal transitions may happen at the critical fields. Meanwhile, the transition from low-spin state to high-spin state induced by magnetic fields is an excellent application in organic spin-valves.30 Accordingly, at finite temperatures, phase crossover behaviors are expected.44–46
Since the PALM takes on many intriguing properties in an external magnetic field, it is quite necessary to take deeper investigations. Herein, we shall explore the ground state and thermodynamic properties of this periodic Anderson-like organic polymer by means of Green's function theory in an external magnetic field. In the forthcoming section, we present the model Hamiltonian and give an outline of the Green's function method. In section 3, the energy bands, magnetization, susceptibility and specific heat will be calculated; the temperature- and magnetic-field-induced phase diagrams will be explored; and the hole excitations, which are closely related to the thermodynamic behaviors, will also be discussed. Finally, conclusions are drawn in section 4.
2. Model Hamiltonian and theoretical method
The Hamiltonian for the quasi-one-dimensional periodic Anderson-like chain model as illustrated in Fig. 1 in an external magnetic field is written as| | | H = Hc + Hf + Hcf + Hh. | (1) |
Here, the term Hc describes the conduction electrons of the main zigzag chain with uncorrelated orbitals,| |  | (2) |
where t is the hopping integral between the nearest-neighboring conduction orbitals, c+l,η,σ, cl,η,σ (η = 1,2) denote the creation and annihilation operators with spin σ = ↑, ↓ for the conduction electrons and nηl,σ = c+l,η,σcl,η,σ is the number operator in the conduction orbital.
The term Hf depicts the localized f orbital with consideration of electron–electron correlated interaction and takes the form
| |  | (3) |
where
c+l,f,σ,
cl,f,σ are the creation and annihilation operators for the localized f electrons in the side radical R,
εf is the bare energy of the localized f orbital, and
U characterizes the Coulomb repulsion of electrons on the localized f orbital. The next term
Hcf describes the hybridization of the localized f electron with the conduction orbital (
l,2),
| | 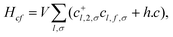 | (4) |
where
V is the hybridization strength.
Finally, the last term Hh in eqn (1) is the Zeeman splitting in an external magnetic field,
| |  | (5) |
Where
h =
gμBB is the reduced magnetic field (Zeeman energy).
Now, we employ the equations of motion method to calculate the retarded Green's function47–50 for the electrons, which is defined as
| | | Gσij(t1 − t2) = 〈〈ci,σ(t1); c+j,σ(t2)〉〉 = −iθ(t1 − t2)〈ci,σc+j,σ+c+j,σci,σ〉, | (6) |
where the subscripts
i and
j number the lattice sites. After the time Fourier transformation, the Green's function is put into the equation of motion,
| | | ω〈〈ci,σ; c+j,σ〉〉 = 〈[ci,σ, c+j,σ]+〉 + 〈〈[ci,σ, H]; c+j,σ〉〉. | (7) |
By performing the equation of motion analogous to
eqn (7) for the high-order Green's function 〈〈[
ci,σ,
H];
c+j,σ〉〉, it will generate higher-order Green's function on the right side, giving rise to an infinite set of coupled equations. In terms of Wick's theorem, we adopt the decoupling scheme for the four-operator Green's functions,
51| | | 〈〈A+BC; D+〉〉 ≈ 〈A+B〉〈〈C; D+〉〉 − 〈A+C〉〈〈B; D+〉〉. | (8) |
Meanwhile, it is important to introduce the Green's functions for each spin channel (up-spin and down-spin) respectively,
i.e., the Green's functions are diagonal in spin space
.
For further Fourier transformation into k-space, the Green's function can be expressed as
| |  | (9) |
The integral of the wavevector
k extends over the first Brillouin zone. So, the momentum space Green's function
gσ(
k,
ω) can be described as a function of wavevector
k and the elementary excitation spectrum
ω =
ω(
k). From the commutating between
cη,σ(
η = 1,2,
f) and the Hamiltonian
H, together with the equations of motion, the linear equations can be obtained
| |  | (10) |
where
Mμλ(
k) is a 3×3 matrix due to the fact that each cell contains three sublattices (
e.g., the sublattice 1, 2 and
f) as follows:
| | 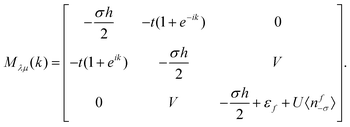 | (11) |
Here, we set
σ = ±1 for up-spin and down-spin, respectively. The corresponding Green's function
matrix in momentum space can be written as
| |  | (12) |
So, each
matrix element of
gσμv can be solved through the linear
eqn (10).
According to the standard spectral theorem, the correlation function of the product of electron operators can be calculated through the corresponding Green's function gσ(k,ω)
| |  | (13) |
where
β = 1/
kBT,
kB is the Boltzman's constant, and
T is the absolute temperature.
The spin density (sublattice magnetization) at one site is defined as
| | | 〈Szi,η〉 = ½(〈nηi,↑〉 − 〈nηi,↓〉), (η = 1,2,f). | (14) |
Then the average magnetization of the unit cell
M and the magnetic susceptibility
χ are expressed as
| |  | (15) |
Likewise, the specific heat can be attained as
| |  | (16) |
Thereby, the above equations can be solved self-consistently.
50 In calculation, an initial state, composed of a set of electron number and spin density of f orbital, is put into the equations to produce resultant values. The iteration continues until convergence is reached.
3. Results and discussion
First, the sublattice magnetization (spin density) and the temperature-induced phase diagrams for the quasi-one-dimensional periodic Anderson-like chain in the absence of magnetic field are discussed. In what follows, all parameters are scaled by the hopping integral t, which is set as a unit. Herein, we only consider the symmetrical case U + 2εf = 0, for which there is no charge fluctuation, and the ground state always lies in ferrimagnetic phase which is clearly manifested in the lower inset of Fig. 2(a) and the inset of Fig. 2(c), where the magnetization per unit cellM = 0.5 = Ms/3 (Ms = 1.5 is the saturation magnetization). For fixed U = 2.0, it is evident that the sublattice magnetization 〈Sz1〉, 〈Szf〉 > 0, and 〈Sz2〉 < 0, indicating that antiferromagnetic correlations occur between conduction orbitals, and also between localized f orbital and conduction orbital (l,2), as shown in the lower inset of Fig. 2(a). Though 〈Sz2〉 < 0, its absolute value is close to zero, indicating the serious double occupation on the conduction orbital (l,2). Nevertheless, the sublattice magnetization 〈Sz1〉 increases monotonously with increasing hybridization V, whereas it is opposite to 〈Szf〉, implying the spin density mainly transfers from the localized f orbital to the conduction orbital (l,1) through the conduction orbital (l,2). Fig. 2(a) manifests the temperature dependence of sublattice magnetization 〈Szα〉 = (α = 1,2,f), where the hybridization V is taken as 0.1, 1.0 and 2.0 with U = 2.0. For weak hybridization, the f orbital is nearly singly occupied and highly localized, which mainly contributes to the ferrimagnetism, while a large double occupation locates on the conduction orbital, implying the paramagnetism-like (disorder) behavior takes place in the main zigzag chain (see the upper inset of Fig. 2(a)). In this case, the indirect RKKY interaction predominates. With increasing V, the transition temperature TC (As T → TC, the magnetization becomes zero) declines because the Kondo coupling becomes more and more dominant and the chain shows ferromagnetic correlation between adjacent conduction orbitals (l,1) and (l + 1,1) gradually, the magnetic moment of which becomes more subtle with respect to temperature. As V is very large, the conduction orbital (l,1) is nearly singly occupied while the f orbital is almost doubly occupied, giving rise to the spin correlation between two f orbitals (indirect RKKY interaction) nearly vanishing. From above discussions, we can obtain the T − V phase diagram as shown in Fig. 2(b), from which it is found that the transition temperature decreases monotonously with increasing V, revealing that the ferrimagnetic state can be stabilized by indirect RKKY interaction while suppressed by Kondo coupling at low temperatures. Likewise, at zero temperature, for intermediate hybridization V = 2.0, |〈Sz2〉| first increases, after reaching maximum it decreases slowly with increasing U (see the inset of Fig. 2(c)). However, 〈Sz1〉 and 〈Szf〉 decreases and increases monotonously with increasing U, respectively, suggesting the spin density mainly transfers from the conduction orbitals to the localized f orbital. Fig. 2(c) manifests the temperature dependence of the sublattice magnetization 〈Szα〉(α = 1,2,f), where the Hubbard repulsion U is taken as 2.0, 5.0 and 8.0 for V = 2.0. With increasing U, the transition temperature ascends and the spin density transfers to the localized f orbital gradually, resulting in a singly occupied f orbital and the enhancement of RKKY interaction favoring ferrimagnetic state. The corresponding T − U phase diagram is illustrated in Fig. 2(d). It is clearly seen that with increasing U, the transition temperature ascends monotonously for U < 5.0 due to the dominant Kondo coupling, while it increases linearly for U > 5.0, owing to that, the indirect RKKY interaction wins over the Kondo coupling. Therefore, even at low temperatures, we can also get ferrimagnetism of the PALM which is stabilized by the large Hubbard repulsion, in accordance with the result of ground state obtained by Zhao et al. using the mean-field theory.24
 |
| | Fig. 2 (a) The sublattice magnetization (spin density) as a function of temperature for different V values with U = 2.0; the upper inset is the magnified part for the weak hybridization; and the lower inset is the sublattice magnetization as a function of V at zero temperature. (b) the T − V phase diagram, where a transition from ferrimagnetic order to paramagnetic phase occurs. (c) the sublattice magnetization as a function of temperature for different U values with V = 2.0; the inset is the sublattice magnetization as a function of U at zero temperature. The corresponding T − U phase diagram is shown in (d). | |
In order to present the nature of ferrimagnetism, the energy bands have been calculated and plotted in Fig. 3, where there are three up-spin and three down-spin bands, respectively. The Fermi level is located at EF = 0. In the ground state, two up-spin bands and one down-spin band below Fermi level are occupied. Therefore, the ground state is ferrimagnetic and possesses the net spin S = 0.5 per unit cell, which is also demonstrated in the insets of Fig. 2. In the weak hybridization, the flat parts of the bands below Fermi level are almost occupied by the f electrons (see Fig. 3(a) for V = 0.1),52 the magnetic moment of which is the main contribution for the ferrimagnetism, reflecting the nearly single occupation on localized f orbital. As V ascends, the flat bands below Fermi level vanishes, implying the double occupation on the f orbital is enhanced, as shown in Fig. 3(b) for V = 2.0. In fact, both the conduction orbitals and localized f orbital are partially doubly occupied in this case. In the large-V limit, the splits of the energy bands with respect to spin becomes much smaller than those for intermediate hybridization and the bandwidth becomes narrower, which are shown in Fig. 3(c) for V = 4.0 clearly. In this case, the conduction orbital (l,1) is almost singly occupied and the nearly double occupation locates on the f orbital. Hence, the conduction orbital (l,1) mainly contributes to the ferrimagnetism. One can also find this tendency in the lower inset of Fig. 2(a). In addition, it is clearly seen from the energy bands that though the system is gapless, it is neither metallic nor insulating.
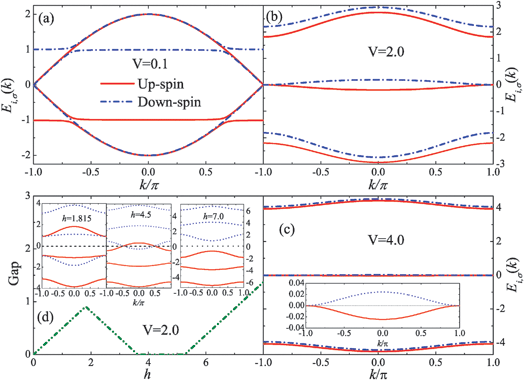 |
| | Fig. 3 The energy bands Ei,σ(k) for V = 0.1 in (a), V = 2.0 in (b) and V = 4.0 in (c) with U = 2.0 in the absence of magnetic field. The inset of (c) is the magnified intermediate bands. (d) the energy gap as a function of magnetic field, the insets are the energy bands under different phases. | |
When an external magnetic field is applied to the system, it may undergo insulator–metal transitions. Recalling Fig. 2, in the intermediate hybridization V = 2.0, though both the conduction orbitals and localized f orbital are partially doubly occupied, most electrons on the localized f orbital are screened by conduction orbital (l,2),53 which would come into being Kondo-singlet-like state, resulting in that the ferrimagnetism mainly comes from the magnetic moment of conduction orbital (l,1). Thus, the Kondo coupling still predominates. However, the strong magnetic field may destroy the Kondo-singlet-like state and make all spins align along the chain. Herein, in a magnetic field, for V = U = 2.0, the temperature-field-induced phase diagram will be explored and the magnetization, the susceptibility and the specific heat will also be calculated to characterize various phases. In Fig. 4(a), we show the magnetization curves for different temperatures. At zero temperature, it clearly demonstrates that we have a 1/3 magnetization plateau and two critical fields hc and hs (labeled in the figure), which suggest that quantum phase transitions (QPTs) may occur. The magnetic order in the plateau state presents a typical feature of quantum ferrimagnetism. Furthermore, the QPTs can also be detected by the divergent peaks of dM/dh,44 which separate the magnetization plateau phase, gapless phase and spin polarized state of the system. According to Gu54 and Larsson,55 the single-site entanglement entropy (local entanglement for the localized f orbital) Ev = −z log2z − u+log2u+ − u− log2u− − wlog2w, where w = 〈nf↑nf↓〉, u+ = 〈nf↑〉 − w, u− = 〈nf↓〉 − w and z = 1 − 〈nf↑〉 − 〈nf↓〉 + w, is a good indicator of QPT, as shown in the upper inset of Fig. 4(a). It is apparent that the entanglement entropy is characterized by a plateau in the same field region where the 1/3 magnetization plateau occurs, and vanishes when h > hs, which corresponds to the fully polarized state (singly occupied state). Indeed, the magnetization plateau phase is realized as the ferrimagnetic insulator, which is demonstrated in Fig. 3(d), where the energy gap behaves linearly against magnetic field. As the field is applied, the down-spin bands are lifted while the up-spin ones are lowered, resulting in an energy gap being opened up. Similarly, the Mott insulating state in a Bose gas corresponds to the magnetization plateau in a quantum antiferromagnet.56 Nevertheless, here, for h < hc, the magnetic field plays dual roles: it can either open up an energy gap for h < hc/2 or close it for h > hc/2 gradually, as shown in the left inset of Fig. 3(d). When h > hc, the energy gap vanishes and the intermediate up-spin and down-spin bands are traversed by the Fermi level (see the intermediate inset of Fig. 3(d)), indicating the system lies in metallic phase. The critical field hc, signaling the end of the 1/3 plateau, denotes the phase transition from ferrimagnetic insulator to metallic phase, and reflects that the Zeeman splitting destroys the Kondo screening of the f-electron local moment. For the field beyond hs, the system shows ferromagnetism and all up-spin bands are below the Fermi level while all down-spin ones are above it (see the right inset of Fig. 3(d)). As a result, the energy gap is opened up again and increases linearly with increasing field. The critical field hs, marking either the fully polarized state or the single occupation by up-spin electrons on both conduction orbitals and localized f orbitals, demonstrates the phase transition from metallic state to ferromagnetic insulator. The changes between the low-spin and high-spin states induced by magnetic fields in this PALM proceed a similar way as in ref. 32, where the spin-flip of polarons induced by a magnetic impurity in conjugated polymer was regarded as logic swap in quantum information processing via changes in the electron spin states.32 Besides, this periodic Anderson-like organic polymer, in which the conductivity relies on the transition of spin states of electrons controlled by magnetic fields, is a good candidate for the spacer of organic spin-valves.30 Furthermore, it shows that the entanglement entropy reaches its maximum at ferrimagnetic (low-spin) state while it vanishes at ferromagnetic (high-spin) state, indicating a switching behaviour.
 |
| | Fig. 4 (a) Magnetization as a function of magnetic field for different temperatures; the upper inset is the entanglement entropy that behaves with the field at zero temperature; the lower inset is dM/dh versus h for different temperatures. (b) h − T phase diagram: the phase boundary between each two of the magnetization plateau state, the gapless regime and the spin polarized state, indicated as values of h and T maximizing dM/dh. | |
At finite temperatures, again, we return to the field dependence of magnetization in Fig. 4(a), where the 1/3 magnetization plateau is smeared out by thermal fluctuations. In addition, the peaks of dM/dh become analytic and can still depict the crossover behaviors of various phases.44,45 As temperature is enhanced, the two peaks of dM/dh at hc,s gradually merge into one single peak at T ≈ 0.2, and then, the single peak vanishes at T ≈ 0.76 (see the lower inset of Fig. 4(a)). Based on the above observation, a temperature-field-induced phase diagram can be constructed from the shifts of the peaks of dM/dh as shown in Fig. 4(b). Strictly speaking, only for T = 0, QPTs happen at hc,s, which are induced solely by quantum fluctuations, whereas at finite temperatures only a crossover takes place. It shows that, with increasing temperature, the gapless regime shrinks gradually and vanishes at T ≈ 0.2 and h ≈ (hc + hs)/2, beyond which hc,s are “forgotten” and the crossover line separates the magnetization plateau state and the spin polarized phase.
Now, let us elaborate on the temperature dependence of magnetization M(T) under different magnetic fields, which is presented in Fig. 5. One can find that M(T) behaves differently in various phases. In the gapless regime, the energy gap is closed by the strong field. Fig. 5(b) shows that at low temperature region, the magnetization has a minimum or maximum as a function of temperature (dM/dT = 0), which also exist in the low-dimensional gapped spin systems.56–58 However, the minimum of M is different from that signaling magnon Bose-Einstein condensation (BEC) in magnetic insulators,56 which reflects the three-dimensional long-range order. The minima here are close to the crossover boundary between the magnetization plateau state and gapless regime, whereas the maxima are close to that between the gapless and spin polarized regimes, which provide another determination of the crossover temperature for the gapless phase. From eqn (14) and (15), it is clearly demonstrated that the magnetization is related to the number of occupied electrons. Recalling the intermediate inset of Fig. 3(d), as the field exceeds hc but is still nearby, the intermediate down-spin and up-spin energy bands cross the Fermi level slightly, making the excitations with minus energies become the hole type. Thus, the magnetization at low temperatures is determined by the competition of the down-spin and up-spin hole excitations near the Fermi level. According to the dispersion relation of the energy bands, the density of states of up-spin holes is larger than that of the down-spin ones near the Fermi level, yielding more up-spin holes excited and thus the decline in M(T) at low temperature regime. After the few up-spin holes are occupied, the down-spin hole excitations predominate, giving rise to the emergence of a minimum of M(T). Likewise, the analogous arguments can also be applied for the appearance of the maximum of M(T) near the critical field hs. Furthermore, it is evident that in the inset of Fig. 5(b), at low temperatures, the magnetization curves are roughly symmetric with respect to M = 1.0, reflecting the particle-hole symmetry in another way. However, when the field exceeds hs, the magnetization declines monotonously with increasing temperature due to that the energy gap opened up by the field is washed out by thermal fluctuations and only the up-spin hole excitations take place at finite temperatures. In the magnetization plateau, Fig. 5(a) shows that M changes slowly at low temperatures in the field hc/2, which is the crossing field of the magnetization curves (see Fig. 4(a)), and also corresponds to the point of the largest gap. For h < hc/2, M decreases sharply to a certain value with temperature ascending, and then, declines smoothly to zero. This declining behavior is also illustrated by dM/dT<0 as shown in the inset of Fig. 5(a), wherein after a dip, dM/dT − T curve appears to become flat when T extends a certain value, which separates the high temperature regime. When h > hc/2, M increases to a maximum, and then declines to zero with increasing temperature. The maximum of M(T) with dM/dT = 0 also measures the variation of magnetic properties from low temperature to high temperature region (also see the inset). Interestingly, as temperature tends to zero, M approaches 0.5, indicating the typical ferrimagneism of ground state. These magnetic behaviors can be explained as follows. For the weak and strong field, the energy gap is rather small, which can be washed out easily by thermal fluctuations even at ultra-low temperature first, after that, the up-spin and down-spin hole excitations predominate, respectively. As the field approaches hc/2, the gap is larger, resulting in the magnetization staying constant M = 0.5 at low temperatures (see Fig. 5(a)).
 |
| | Fig. 5 Magnetization as a function of temperature for (a) h < hc and (b) hc < h < hs. The inset in (a) shows the behavior of dM/dT for the field corresponding to (a), and in (b) shows the minimum and maximum (labeled by the circle) at low temperatures in the gapless regime. | |
The temperature dependence of magnetic susceptibility in various phases is also discussed. In the plateau state, the susceptibility displays a single peak, and goes exponentially to zero as T → 0, which is due to the gap opened up by the field. With h ascending, the peak of the susceptibility shifts towards high temperature region with decreasing maximum as h < hc/2, whereas it moves to low temperature side with increasing maximum when h > hc/2, as shown in Fig. 6(a). These distinct behaviors of susceptibility result from the crossing of the up-spin and down-spin hole excitations near the Fermi level. When h < hc/2, the susceptibility is dominated by the up-spin hole branch whose gap ascends with increasing field, yielding the peak movement towards higher temperatures and decrease in amplitude. After the field exceeds hc/2, the susceptibility is contributed from the down-spin hole branch whose gap declines with h ascending, resulting in the peak movement towards lower temperatures with increase in amplitude. However, for the temperature high enough, the susceptibility coincides under different fields, indicating the paramagnetic behavior, by that the thermal fluctuations predominate. In the gapless regime, with decreasing temperature, the susceptibility increases slowly at high temperatures, and then ascends sharply until reaching a peak at low temperature, after that it goes to a finite value as T → 0 (see Fig. 6(b)), as a consequence of the closure of the energy gap. When the field exceeds hs, the system goes into the fully polarized state, and an energy gap is opened up again by the field, thus, the susceptibility goes exponentially to zero as T → 0 after a round maximum which decreases and shifts towards high temperatures with h ascending, as shown in the inset of Fig. 6(a).
 |
| | Fig. 6 Temperature dependence of the magnetic susceptibility for (a) h < hc; (b) hc < h < hs; and the inset of (a) is of h > hs. | |
Fig. 7 shows the temperature dependence of specific heat under different fields. From the above analysis, we know that the magnetization and susceptibility are determined only by the occupied number of the hole excitations. However, different from the magnetization and susceptibility, the behavior of the specific heat can not be characterized simply by the hole excitations because it is affected by both the numbers and energies of the quasiparticles. In the plateau state, at low fields, the small gap is washed out by thermal fluctuations, resulting in a double-peak structure of the temperature dependence of specific heat (see the inset of Fig. 7(a)), wherein the low-temperature peak shifts towards high temperature region while the high temperature peak moves to lower temperatures with increasing the magnitudes. With further increasing field, the double peaks merge into one, and then it shifts towards lower temperatures with maximum enhanced due to the larger gap opened up by the strong field and the enhancement and decline of energies for the down-spin and up-spin bands, respectively. After h exceeds hc/2, however, the single peak moves to higher temperature region with decreasing the magnitude, as in Fig. 7(a). When the field is close to hc, a shoulder at low temperature side emerges gradually. The emergence of the specific heat peak at low-temperature exhibits a gapless behavior when hc < h < hs, where the local minima are located outside but near the gapless regime. When h is in the vicinity of hs, though the low-temperature peak of specific heat disappears, a shoulder can still be observed (see the inset of Fig. 7(b)), where the specific heat decays exponentially. On the whole, the shoulder can be observed outside the gapless regime but at the vicinity of its boundary. However, in a sufficiently high field, the shoulder vanishes and only one single peak is presented due to the larger gap opened up by the field.
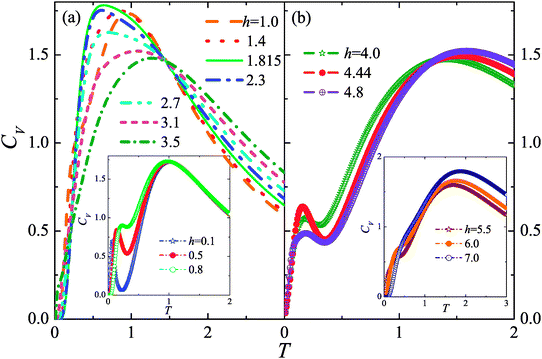 |
| | Fig. 7 Temperature dependence of the specific heat for (a) h = 1.0, 1.4, 1.815, 2.3, 2.7, 3.1, and 3.5; (b) h = 4.0, 4.44 and 4.8; the inset of (a) is at low fields; and the inset of (b) is of h > hs. | |
4. Conclusions
In conclusion, the ground-state and thermodynamic properties of a quasi-one-dimensional periodic Anderson-like organic polymer have been investigated by means of Green's function theory for the symmetrical case. In the absence of magnetic field, the ground-state of the system always lies in a ferrimagnetic phase. The temperature-induced phase diagrams have been explored, where a transition from ferrimagnetic state to paramagnetic phase takes place. The transition temperature can be enhanced by the disorder of conduction electrons and ferromagnetic correlation between the localized spins (also an increase of the local f moment) due to the enhancement of Hubbard U on the localized f orbital, while it can be reduced by the Kondo screening behavior due to the enhancement of hybridization V, reflecting the magnetic properties are dominated by the RKKY interaction.
When the magnetic field is turned on, a striking finding is that the field dependence of magnetization exhibits a 1/3 plateau and two critical fields: hc (indicating the ferrimagnetic insulator transition to metallic phase), and hs (marking the metal transition to ferromagnetic insulator). Furthermore, the single-site entanglement entropy can also be exploited as a useful tool to detect the QPTs. It shows that this periodic Anderson-like organic polymer is a good candidate for the spacer of organic spin-valves and can be regarded as an entanglement switch controlled by magnetic fields. The temperature-field-induced phase diagram has also been explored, in which the magnetization plateau state, gapless phase and spin polarized state are unveiled.
It is also shown that there are three up-spin and three down-spin energy bands, with which the energies below the Fermi level become the hole excitations at low temperatures. For T = 0, the open and closure of the energy gap in magnetic fields can account for the magnetization process and the insulator–metal transitions. In addition, at finite temperatures, it is also found that the thermodynamic properties are determined by the competition between the up-spin and down-spin hole excitations.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 10774051 and 10804034, the National 973 Project under Grant No. 2006CB921605, the Research Fund for the Doctoral Program of Higher Education under Grant No. 20090142110063, and the National Science Foundation of Hubei Province of China under Grant No. 2008CDB003.
References
- Y. V. Korshak, T. V. Medvedeva, A. A. Ovchinnikov and V. N. Spector, Nature, 1987, 326, 370 CrossRef CAS.
- M. Takahashi, P. Turek, Y. Nakazawa, M. Tamura, K. Nozawa, D. Shiomi, M. Ishikawa and M. Kinoshita, Phys. Rev. Lett., 1991, 67, 746 CrossRef CAS.
- A. J. Heeger, J. Phys. Chem. B, 2001, 105, 8475 CrossRef CAS.
- T. Giamarchi, Chem. Rev., 2004, 104, 5037 CrossRef CAS.
- M. A. Hajj and J. P. Malrieu, J. Chem. Phys., 2007, 127, 144902 CrossRef.
- T. Kaneko, T. Makino, H. Miyaji, M. Teraguchi, T. Aoki, M. Miyasaka and H. Nishide, J. Am. Chem. Soc., 2003, 125, 3554 CrossRef CAS.
- S. Patiy, R. Chitraz, D. Senxk, S. Ramaseshayk and H. R. Krishnamurthy, J. Phys.: Condens. Matter, 1997, 9, 219 CrossRef CAS.
- S. Mandal, S. K. Pati, M. A. Green and S. Natarajan, Chem. Mater., 2005, 17, 2912 CrossRef CAS.
- S. Sarkar, A. Datta, A. Mondal, D. Chopra, J. Ribas, K. K. Rajak, S. M. Sairam and S. K. Pati, J. Phys. Chem. B, 2006, 110, 12 CrossRef CAS.
- F. Wu and W. Z. Wang, J. Phys.: Condens. Matter, 2006, 18, 3837 CrossRef CAS.
- S. Mohakud, S. K. Pati and S. Miyashita, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 014435 CrossRef.
- S. Q. Su, Z. B. Huang, R. Fan and H. Q. Lin, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125114 CrossRef.
- S. K. Pati and R. R. P. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 7695 CrossRef CAS.
- S. Ramaseshar, S. K. Patir, H. R. Krishnamurthy, Z. Shuai and J. L. Bredas, Synth. Met., 1997, 85, 1019 CrossRef CAS.
- S. K. Pati, S. Ramasesha, Z. Shuai and J. L. Brédas, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 14827 CrossRef CAS.
- S. Lakshmi and S. K. Pati, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 193410 CrossRef.
- S. Sengupta, S. Lakshmi and S. K. Pati, J. Phys.: Condens. Matter, 2006, 18, 9189 CrossRef CAS.
- S. Dutta, S. Lakshmi and S. K. Pati, J. Phys.: Condens. Matter, 2007, 19, 322201 CrossRef.
- S. Dutta and S. K. Pati, J. Phys.: Condens. Matter, 2008, 20, 075226 CrossRef.
- P. Parida, S. Lakshmi and S. K. Pati, J. Phys.: Condens. Matter, 2009, 21, 095301 CrossRef.
- S. Lakshmi, S. Dutta and S. K. Pati, J. Phys. Chem. C, 2008, 112, 14718 CrossRef CAS.
- A. J. Heeger, S. Kivelson and W. P. Su, Rev. Mod. Phys., 1988, 60, 781 CrossRef CAS.
- A. A. Ovchinnikov, Theor. Chim. Acta, 1978, 47, 297 CrossRef CAS.
- L. Zhao, K. L. Yao and Y. F. Duan, Phys. Chem. Chem. Phys., 2000, 2, 4001 RSC.
- S. J. Xie, J. Q. Zhao, J. H. Wei, S. G. Wang, L. M. Mei and S. H. Han, Europhys. Lett., 2000, 50, 635 CrossRef CAS.
- W. Z. Wang, K. L. Yao and H. Q. Lin, J. Chem. Phys., 2000, 112, 487 CrossRef CAS.
- Y. Meng, B. Di, X. J. Liu, Z. An and C. Q. Wu, J. Chem. Phys., 2008, 128, 184903 CrossRef CAS.
- J. H. Wei, X. J. Liu, S. J. Xie and Y. J. Yan, J. Chem. Phys., 2009, 131, 064906 CrossRef CAS.
- S. J. Sun, Eur. Phys. J. B, 2009, 72, 423 CrossRef CAS.
- Z. H. Xiong, D. Wu, Z. V. Vardeny and J. Shi, Nature, 2004, 427, 821 CrossRef CAS.
- Z. J. Li, H. Q. Lin, Z. An and K. L. Yao, J. Chem. Phys., 1998, 109, 10082 CrossRef CAS.
- H. Zhao, Y. G. Chen, Y. Yao, C. Q. Wu, X. M. Zhang and Z. An, J. Chem. Phys., 2009, 131, 154901 CrossRef.
- Y. Qiu and L. P. Zhu, J. Chem. Phys., 2009, 131, 134903 CrossRef.
- H. B. Ma and U. Schollwöck, J. Phys. Chem. A, 2009, 113, 1360 CrossRef CAS.
- H. Zhao, Y. G. Chen, X. M. Zhang, Z. An and C. Q. Wu, J. Chem. Phys., 2009, 130, 234908 CrossRef.
- W. Z. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 035118 CrossRef.
- P. W. Andeson, Phys. Rev., 1961, 124, 41 CrossRef CAS.
- M. F. Crommie, Science, 2005, 309, 1501 CrossRef CAS.
- C. A. Hooley and A. P. Mackenzie, Science, 2007, 317, 1332 CrossRef CAS.
- P. Gegenwart, Q. M. Si and F. Steglich, Nat. Phys., 2008, 4, 186 CrossRef CAS.
- H. Tsunetsugu, M. Sigrist and K. Ueda, Rev. Mod. Phys., 1997, 69, 809 CrossRef CAS.
- Th. Pruschke, R. Bulla and M. Jarrell, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 12799 CrossRef CAS.
- T. Saso and M. Itoh, Phys. Rev. B: Condens. Matter, 1996, 53, 6877 CrossRef CAS.
- X. Q. Wang and L. Yu, Phys. Rev. Lett., 2000, 84, 5399 CrossRef CAS.
- S. S. Gong, S. Gao and G. Su, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 014413 CrossRef.
- A. W. Rost, R. S. Perry, J. F. Mercure, A. P. Mackenzie and S. A. Grigera, Science, 2009, 325, 1360 CrossRef CAS.
-
D. A. Ryndyk, R. Gutiérrez, B. Song and G. Cuniberti, Energy Transfer Dynamics in Biomaterial Systems, Springer, Berlin, Heidelberg, 2009, vol. 93, pp. 213–335 Search PubMed.
- P. Fröbrich and P. J. Kuntz, Phys. Rep., 2006, 432, 223 CrossRef.
- H. H. Fu, K. L. Yao and Z. L. Liu, J. Chem. Phys., 2008, 128, 114705 CrossRef.
- L. J. Ding, K. L. Yao and H. H. Fu, Phys. Chem. Chem. Phys., 2009, 11, 11415 RSC.
- N. A. Zimbovskaya, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035331 CrossRef.
- H. Q. Lin, H. Y. Shik, Y. Q. Wang, C. D. Batista and J. E. Gubernatis, J. Magn. Magn. Mater., 2004, 281, 240 CrossRef CAS.
- I. Zerec, B. Schmidt and P. Thalmeier, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 245108 CrossRef.
- S. J. Gu, S. S. Deng, Y. Q. Li and H. Q. Lin, Phys. Rev. Lett., 2004, 93, 086402 CrossRef.
- D. Larsson and H. Johannesson, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 042320 CrossRef.
- T. Giamarchi, C. Rüegg and O. Tchernyshyov, Nat. Phys., 2008, 4, 198 CrossRef CAS.
- Y. Maeda, C. Hotta and M. Oshikawa, Phys. Rev. Lett., 2007, 99, 057205 CrossRef.
- S. Wessel, M. Olshanii and S. Haas, Phys. Rev. Lett., 2001, 87, 206407 CrossRef CAS.
|
| This journal is © the Owner Societies 2011 |
Click here to see how this site uses Cookies. View our privacy policy here.