Chemically reactive species remain alive inside carbon nanotubes: a density functional theory study

Abstract

The behavior of alkyl guest radicals inside carbon nanotube hosts with different diameters is analyzed using density functional theory (DFT) calculations. Here the inner alkyl radicals are assumed to be formed by decomposition of their precursors, which had been incorporated into the tubes. DFT calculations show that inner alkyl radicals prefer to exist separately from the nanotube wall (separate form) rather than forming an inner covalent bond with the wall (bound form). Keeping a radical apart from the inner wall is more likely for a more bulky radical inside a smaller diameter tube. A key to the preference for the separate forms over the bound forms is that the bound forms gain a weak attraction due to the formation of a bond with the inner wall. The weak attraction, ascribed to the inertness of the inner surface, is counteracted by destabilization due to deformations of a tube and radical induced by guest–host coupling. The energy balance argument illuminates that the inertness of the inner wall makes an alkyl radical species remain alive inside a tube and retain its reactivity. These findings can help us to understand experimental results where chemical reactions inside a tube proceed after guests are activated.

---

1. Introduction

Carbon nanotubes have inner spaces of the order of nanometres in size,^1,2 and thus they are able to encapsulate guest molecules.^3,4 In fact, various types of guest molecule have been easily encapsulated in uncapped host tubes, according to several experimental studies.⁴ Inside a carbon nanotube host, transformation of a guest molecule and its resultant reaction with an adjacent guest have been reported to occur by heating or electron irradiation.^4–8 During the reactions, a reactive guest species should be formed as a reaction intermediate.^7b,c The inner reactive species only seem to attack adjacent guests to result in guest polymerization.^5–8 The experimental findings are in marked contrast to our common knowledge in chemistry, because a textbook (e.g., ref. 9) says that a reactive species randomly attacks, and thus the reactive guests can bind to not only a neighboring guest but also the inner wall of a tube. The uniqueness of chemical reactions inside a nanotube may originate from the chemical inertness of the inner tube surface. However, our understanding of the character of the inner tube wall is still lacking.

Although there are no experimental reports of stable covalent bonds formed between a guest and the inner tube surface, covalent grafting of the outer surface has been achieved.¹⁰ Knowledge of the outer covalent functionalization provides us with a baseline for understanding the characteristics of the inner surface. With respect to the outer covalent functionalization, only highly reactive species such as carbenes¹¹ and organic radicals are used.^12–17 Note that the highly reactive species are generally produced by the decomposition of their precursors by heating or irradiation with light. For example, the precursors for organic radicals are organic peroxides, azo compounds, alkyl iodides, and diazonium salts.^12–17 The covalent bond formation in a tube by outer radicals has been ascertained by measuring their conductivity, because it reduces the conductance of the tube^18–20 due to sp² to sp³ conversion at the binding site.²¹ Although the functionalization can be utilized to modulate the electronic properties of a tube, the limited number of outer species that can be attached covalently to a tube wall suggests chemical inertness of the outer surface.

Compared with the outer tube surface, the inner tube surface is much less reactive. With respect to the inner covalent functionalization, there is a relevant theoretical study based on density functional theory (DFT) calculations by Chen et al.²² In ref. 22, the H or F atom is bound to both inner and outer surfaces of finite-length tubes. Their DFT calculations show that the binding energies in the inner C–H or C–F bonds are less significant than those in the outer bonds. The findings clearly indicate that the concave surface of a tube exhibits a lower reactivity toward addition reactions than the convex surface. Following this pioneering work, divalent carbene bindings onto the outer^23–27 and inner²⁷ tube surfaces have been also investigated theoretically. In particular, ref. 27 used DFT calculations to compare the inner carbene bindings with the outer bindings. According to ref. 27, the divalent carbon atom is preferentially bound to a CC bond orthogonal to the tube axis, irrespective of the outer and inner additions. In the inner addition, the CC bond at the binding site is retained, whereas in the outer addition the CC bond breaks. Retaining the CC bond in the inner addition comes from rigorous restrictions of surface relaxation toward the tube center. These restrictions are one of the origins of the uniqueness of the inner CC bonds.

Despite obtaining a preliminary insight into the characteristics of the inner tube wall, it is still intriguing to elucidate why an inner reactive species can react with an adjacent guest without making a bond between a guest and a host tube. To answer the essential questions, we employed density functional theory calculations with the PW91 functional²⁸ to study interactions between an alkyl radical (methyl, ethyl, isopropyl, and tert-butyl radicals) and the inner walls of armchair (n,n) tubes with different diameters. Based on the relevant experimental studies,^4,12–17 we assume in the present study that precursors for alkyl radicals (e.g.organic peroxides, azo compounds, and alkyl iodides^12–17) can be incorporated into the inside of a tube, and then they are decomposed by thermolysis or photolysis to generate the organic radicals. The present DFT study will investigate from the viewpoint of energetics whether an inner alkyl radical prefers to exist separately from the tube wall or to make a covalent bond with the wall. In order to clarify factors determining a stable configuration of an alkyl radical inside a tube, we will analyze in detail the characteristics of a covalent bond formed between the radical and the inner wall. For obtaining a baseline for comparison, we have also investigated graphenes bound by an alkyl radical to elucidate whether tube curvature affects the inner covalent bond formation.

2. Calculations

To elucidate the properties of an alkyl radical on the inside of a tube, we carried out DFT calculations using the Perdew–Wang (PW91) functional,²⁸ implemented in the Vienna ab initio Simulation Package (VASP v.4.6).²⁹ For this purpose, we used (8,8), (10,10), and (12,12) armchair nanotubes as hosts, and methyl, ethyl, isopropyl, and tert-butyl radicals as guests. All calculations for the encapsulation of an alkyl radical in a tube were spin-polarized. The kinetic energy cutoff of the plane-wave basis set is 349.5 eV with ultrasoft Vanderbilt-type pseudopotentials.³⁰ In this study, a hexagonal supercell is used, containing 20 × n C atoms from the (n,n) nanotube and one alkyl radical guest to avoid interactions between the guests located on neighboring unit cells. We allowed full geometry relaxation in the axial direction, but we fixed the inter-tube distances at 6 Å, which is large enough to avoid significant inter-tube interactions.²⁷ We used a 1 × 1 × 5 (15 × 15 × 1) k-point mesh for geometry optimizations for the nanotube (graphene) systems. For the graphene optimization, the interlayer spacing is fixed at 12 Å. This value is also large enough that the effects of interlayer interactions on the optimization are negligible.³¹ Convergence was enhanced using fractional occupancy generated by a Gaussian broadening (σ_GB = 0.03 eV) of the one-electron energy levels. Based on PW91 calculations, the CC bond length in graphene was optimized to be 1.421 Å, which is fully consistent with that obtained experimentally.³² In addition, we employed Gaussian 03 program³³ in order to obtain energetics of an isolated alkyl radical by using the same functional with the 6-31G* basis set.³⁴

3. Results and discussion

3.1 Alkyl radical guests inside nanotube hosts

We obtained from PW91 DFT calculations²⁸ optimized geometries for alkyl radicals (methyl, ethyl, isopropyl, and tert-butyl radicals) inside armchair tubes with different diameters. The optimized geometries inside the (10,10) tube are shown in Fig. 1, and those inside the (8,8) and (12,12) tubes are shown in Fig. S1 and S2 of the ESI†. For the encapsulation of a methyl, ethyl, or isopropyl radical into a tube there are two local minima, one has a covalent bond newly formed between an alkyl radical and the inner wall of a tube (bound form), whereas the other does not have such an inner bond (separate form). In contrast, a tert-butyl radical cannot make a covalent bond with the inner wall of a tube, and accordingly is apart from the wall.

Fig. 1 Optimized structures for an alkyl radical inside the (10,10) nanotube. Methyl, ethyl, isopropyl, and tert-butyl radicals are each considered as a guest from left to right. In the upper structures, an alkyl radical binds to a C atom of a tube to make a covalent bond with the inner wall (bound form), whereas in the bottom structures, an alkyl radical exists separately from the tube wall (separate form). The energy difference between the bound and separate forms of an alkyl radical inside a tube, ΔE_total (kcal mol⁻¹), is defined as E_total(bound form) − E_total(separate form). A positive ΔE_total value indicates that a separate form is energetically more stable than a bound form. Bond lengths of the CC bonds formed inside a tube are given in Å.

Here we focus on the addition of an alkyl radical into (10,10) tubes as examples of the bound forms. As shown in Fig. 1 and Table 1, the lengths of the inner CC bonds increase with an increase in the number of methyl groups in the radicals: 1.709 Å (isopropyl radical) > 1.647 Å (ethyl radical) > 1.605 Å (methyl radical). The dependencies of the CC bond lengths indicate that repulsion between the methyl groups and the wall weakens the strength of the inner bonds. Accompanying the inner covalent bond formation, the radical carbon of a guest is pyramidalized to become sp³-hybridized (Fig. 1 and Fig. 2). On the side of the tube the C atom attached by an alkyl radical sags towards the tube axis.

Fig. 2 Magnified view of an inner methyl radical binding to a carbon atom of the (10,10) tube. The bound carbon atom sags towards the tube center, which can be quantitatively analyzed by comparing a dihedral angle (φ) before and after the radical binding. The dihedral angle (φ) is defined by the four carbon atoms labeled as 0, 1, 2, and 3.

Table 1 Key parameters of optimized geometries for alkyl radicals bound to the inner walls of tubes with different diameters

		CH3 radical	CH2(CH3) radical	CH(CH3)2 radical
a B cc in Å is the length of the CC bond formed by the addition of an inner radical into a tube or graphene. b Δϕ in degrees is the difference in a dihedral angle (ϕ, defined in Fig. 2) between before and after the inner radical binding.
(8,8) tube	B CC ^a	1.614	1.654	1.732
	Δϕ^b	30.4	31.7	34.1
(10,10) tube	B CC ^a	1.605	1.646	1.709
	Δϕ^b	33.6	34.9	37.3
(12,12) tube	B CC ^a	1.606	1.640	1.690
	Δϕ^b	36.7	37.3	38.9
Graphene	B CC ^a	1.590	1.615	1.659
	Δϕ^b	49.5	50.2	52.1

---

In contrast to the bound forms, the separate forms retain sp² characteristics in the radical carbon of a guest, as well as the tube carbon atoms. It is interesting to investigate which forms are energetically preferable for an alkyl radical inside a tube. Fig. 1 lists the differences in the total energies of the two forms (ΔE_total = E_total(bound form) − E_total(separate form)). Surprisingly, we obtained positive ΔE_total values for all alkyl radicals inside the (10,10) tube, as shown in Fig. 1. The positive values indicate that a separate form is energetically more stable than a bound form. The ΔE_total values strongly depend on the alkyl radicals considered: with a significant increase in ΔE_total values for more bulky radicals inside the (10,10) tube. From the ΔE_total trends, we can understand that a tert-butyl radical inside the tube only adopts the separate form.

Next let us discuss how the ΔE_total values depend on the diameters of the armchair (n,n) tubes, where n is 8, 10, and 12. The ΔE_total values are plotted as a function of the tube diameters, ranging from 10.8 to 16.2 Å, in Fig. 3. For comparison we also obtained the ΔE_total values for the corresponding graphene cases (Table 2) whose optimized geometries are seen in Fig. S3 of the ESI†. As shown in Fig. 3, the ΔE_total values decrease with an increase in the tube diameter. For example, for isopropyl radical inside a tube the ΔE_total value changes from 27.2 ((8,8) tube) to 15.2 ((12,12) tube) kcal mol⁻¹. The ΔE_total values for an isopropyl radical inside a tube are larger than the graphene value (7.8 kcal mol⁻¹), given by the lateral bold line in Fig. 3. The diameter-dependencies of the ΔE_total values are more significant for a more bulky radical inside a tube. In addition, Fig. 3 shows that the type of the alkyl radical has a strong influence on the ΔE_total values. In fact, we see large ΔE_total values for the isopropyl cases, however negligible ΔE_total values for the methyl radical (1.6 and 2.8 kcal mol⁻¹ for the (12,12) and (10,10) tubes, respectively). Note that the ΔE_total value for the methyl radical in the graphene case has a negative value (−5.5 kcal mol⁻¹) in contrast to the nanotube cases. This difference suggests that the concave surface of a tube has an impact on the strength of the inner bond.

Fig. 3 Energy differences between the separate and bound forms of an alkyl radical inside a tube (ΔE_total = E_total(bound form) − E_total(separate form)) are plotted as a function of the tube diameter. The values for the inner methyl, ethyl, and isopropyl additions are given by circles, squares, and triangles, respectively. For comparison, the corresponding values for graphene bound by methyl, ethyl, and isopropyl radicals are given by lateral dotted, straight, and bold lines, respectively.

Table 2 The energy differences between two optimized structures for an alkyl radical inside a tube, ΔE_total (kcal mol⁻¹), given by E_total(bound form) − E_total(separate form). Here E_total(bound form) is the total energy of an alkyl radical making an inner covalent bond with the tube wall, and E_total(bound form) is that of an alkyl radical separated from the inner tube wall. A positive ΔE_total value indicates that a separate form is energetically preferable relative to a bound form

	CH3 radical	CH2(CH3) radical	CH(CH3)2 radical
(8,8) tube	6.4	13.3	27.2
(10,10) tube	2.8	11.1	21.4
(12,12) tube	1.6	7.4	15.2
Grapehene	−5.5	0.1	7.8

---

To check whether the PW91 results can be reproduced by calculations using other functionals, we used the Perdew–Burke–Ernzerhof (PBE) functional instead.³⁵ In the PBE calculations in the VASP v.4.6 program, the interaction between electrons and ions is described by the projector augmented wave (PAW) method.³⁶ Due to limitation of computational resources, we calculated only the ΔE_total values for methyl radicals inside (8,8), (10,10), and (12,12) tubes as well as for an ethyl radical inside a (12,12) tube. As a result of the PBE calculations, we obtained positive ΔE_total values in the selected cases (6.2, 3.7, 1.8, and 8.6 kcal mol⁻¹ for CH₃˙@(8,8), CH₃˙@(10,10), CH₃˙@(12,12), and C₂H₅˙@(12,12), respectively), being essentially close to the corresponding PW91 values. Within the two different DFT functionals based on general gradient approximation,³⁷ keeping a radical apart from the tube wall is more likely when a radical with a larger number of methyl groups is on the inside of a smaller-diameter tube. The DFT results mark a deviation from a concept based on general chemistry, because the concept suggests that a radical species can randomly attack, and thus it can bind to the inner wall of a tube. In contrast, a reactive (radical) species generated inside a tube does not create a bond with the inner wall to retain its reactivity, and accordingly it can act as an initiator of a chemical reaction inside a nanotube. These findings can help us to understand unusual chemical reactions proceeding easily inside a tube.^5–8

3.2 Factors for determining the stability of an alkyl radical inside a tube

In section 3.2 we will elucidate why an alkyl radical adopts preferentially a separate form rather than a bound form by closely looking at the differences in their geometrical features. As mentioned above, the inner CC bond formation deforms a tube and a guest in the bound form, while such deformations cannot be seen in the separate form. Of course, the bound forms gain attractive interactions due to the covalent bond formation. On the other hand, the deformations of a tube and a guest destabilize their structures. Accordingly, the balance between the stabilization due to the inner bond formation and the destabilization due to the geometrical deformations determines whether an alkyl radial inside a tube takes a separate form or a bound form. We will compare quantitatively the three components E_BE, ΔE_guest, and ΔE_tube into which the ΔE_total values are partitioned in Table 3. The three components are defined as,

E_BE = E_total(bound form) − E_total(deformed tube) − E_total(deformed guest) (1)

ΔE_tube = E_total(deformed tube) − E_total(optimized tube) (2)

and

ΔE_guest = E_total(deformed guest) − E_total(optimized guest), (3)

where E_total(bound form) is the total energy of the optimized geometry for an alkyl radical guest bound to the inner wall of a tube, E_total(deformed tube) (E_total(deformed guest)) is the energy of a deformed tube (guest) taken from the optimized alkyl-bound tube, and E_total(optimized tube) (E_total(optimized guest)) is the energy of the optimized tube (guest).

Table 3 Energy decomposition analyses of the energy differences between the two optimized conformations for an alkyl radical inside a tube, the separate and the bound forms (ΔE_total = E_total(bound form) − E_total(separate form)). The energy differences are partitioned into the three components, E_BE,^a ΔE_tube,^b and ΔE_guest^c

		CH3 radical	CH2(CH3) radical	CH(CH3)2 radical
a E BE in kcal mol^−1 is the energy obtained by the addition of an inner radical into a tube, given in eqn (1). b ΔEtube in kcal mol^−1 is the energy required by the deformation of a tube host induced by the inner radical addition, given in eqn (2). c ΔEguest in kcal mol^−1 is the energy required by the deformation of a guest radical induced by the inner radical addition, given in eqn (3).
(8,8) tube	E BE	−34.9	−29.6	−22.6
	ΔEtube	34.3	34.8	38.9
	ΔEguest	7.1	8.1	10.8
(10,10) tube	E BE	−35.0	−30.5	−25.5
	ΔEtube	30.7	33.8	36.1
	ΔEguest	7.1	8.5	10.8
(12,12) tube	E BE	−36.0	−31.5	−26.8
	ΔEtube	30.7	31.0	32.4
	ΔEguest	7.0	7.9	9.6
Graphene	E BE	−40.7	−36.9	−33.1
	ΔEtube	28.0	28.6	30.5
	ΔEguest	7.1	8.0	9.9

---

3.2.1 Guest deformation. First, we pay attention to the energy required by the deformation of a guest alkyl radical, because the guest deformation is an indispensable event for the inner bond formation. To gain a preliminary insight into the guest deformation, we discuss pyramidalization of an isolated alkyl radical.³⁵ The transformation can be represented by the angle (θ) between one C–H (or C–C) bond and a line perpendicular to its trigonal plane in Fig. 4. In the simplest case, pyramidalization of a methyl radical corresponds to its D_3h → C_3v transformation. Fig. 5(a) shows changes in the total energy of an alkyl radical as a function of the angle θ (90 ≤ θ ≤ 110). We can see in Fig. 5(a) that there is one local minimum at θ = ∼90 for methyl, ethyl, and isopropyl radicals, and at θ = ∼96 for the tert-butyl radical. With increasing θ, their total energies increase in a parabolic manner. The energy changes in the range of 90 < θ < 110 were calculated to be 6.9, 7.3, 8.2, and 9.6 kcal mol⁻¹ for methyl, ethyl, isopropyl, and tert-butyl radicals, respectively.

Fig. 4 Pyramidalization of an isolated alkyl radical.

Fig. 5 Energetics of pyramidalization of an isolated alkyl radical. (a) Energies required by pyramidalization of an alkyl radical. (b) Energy changes of singly occupied molecular orbital of an alky radical upon pyramidalization. These values for isolated methyl, ethyl, isopropyl, and tert-butyl radicals are given by closed circles, closed squares, closed triangles, and open circles, respectively.

The deformation energy for an isolated methyl radical (6.9 kcal mol⁻¹) is almost identical to the ΔE_guest value for a methyl radical bound to the inner wall, listed in Table 3. The consistency is understandable, because the tube-bound methyl radicals have θ values of ∼110 degrees (Table 4). In contrast, there are slight differences in the deformation energy between isolated and tube-bound radicals in the other two cases (0.6–1.2 kcal mol⁻¹ for ethyl radicals and 1.2–2.6 kcal mol⁻¹ for isopropyl radicals). The differences come from deviations in the θ values for a tube-bound ethyl or isopropyl radical from those in the isolated cases (Table 4). The deviations suggest that repulsion between methyl groups and the inner wall of a tube affects the stable conformation of an inner alkyl radial.

Table 4 Pyramidalization of an alkyl radical bound to the inner wall of a tube. The computed θ values, defined in Fig. 4, are given in degrees

	CH3 radical	CH2(CH3) radical	CH(CH3)2 radical
(8,8) tube	109.3, 109.3, 109.9	105.1, 105.1, 118.9	100.4, 114.1, 117.6
(10,10) tube	109.4, 109.4, 109.8	104.6, 104.6, 120.7	100.5, 114.3, 116.9
(12,12) tube	109.4, 109.4, 109.6	105.2, 105.2, 118.2	101.0, 114.3, 114.7
Graphene	109.6, 109.6, 109.6	105.7, 105.7, 117.5	102.2, 114.2, 114.2

---

Upon pyramidalization of an alkyl radical, the shape and energy of the singly occupied molecular orbital (SOMO) changes. In fact, we can see in Fig. 5(b) that the SOMOs are stabilized as shown by an increase in θ of the radicals. The energy changes come from the sp² to sp³ conversion of a radical carbon atom. For example, the SOMO of a pyramidalized methyl radical has sp³ characteristics where the lobes are extended farther into space than those of the sp² orbitals of the planar D_3h case. The orbital changes can be understood by mixing the SOMO and the LUMO in the D_3hmethyl radical, following a second-order perturbation concept.^38,39 See detail discussions in Fig. S4 of the ESI.† The sp³ characteristics play an important role in gaining additional attractive interactions with the inner wall of a tube, compared with an sp² planar radical.

From these simple analyses we can derive two important findings. When a guest radical is located far from the tube wall its planar structure is a local minimum, and it does not need to make a bond with the tube. Conversely a guest radical near a tube tends to be pyramidalized to gain attractive interactions with the inner wall. If the attraction overcomes destabilization due to the guest deformation, the pyramidal structure can be also a local minimum inside a tube. According to these simple analyses, the double minima for the addition of an alkyl radical into a tube in Fig. 1, S1,† and S2† seem to be reasonable except for the tert-butyl addition.

3.2.2 Attractive interactions due to the inner bond formation. In the previous subsection, we found that pyramidalization of an alkyl radical costs energy less than 10 kcal mol⁻¹, but it is necessary for interactions between the inner wall of a tube and the radical. Next, we discuss quantitatively how much attractive energy a pyramidalized alkyl radical gains by the inner covalent bond formation, as shown in Fig. 6. Fig. 6(a) and (b) show how the lengths (B_CC) and binding energies (E_BE) of the inner CC bonds formed between alkyl radicals and tubes depend on the tube diameters, respectively. For comparison, the corresponding values for alkyl-bound graphene are given by lateral lines.

Fig. 6 Tube-diameter dependencies of the lengths (B_CC in (a)) and binding energies (E_BE in (b)) of the inner CC bonds between alkyl radicals and tubes. These values in the inner methyl, ethyl, and isopropyl additions are given by circles, squares, and triangles, respectively. For comparison the corresponding values for graphene bound by methyl, ethyl, and isopropyl radicals are given by lateral dotted, straight, and bold lines, respectively.

Fig. 6(a) shows that the newly formed CC bond lengths (B_CC) range from 1.61 to 1.73 Å, values of which are larger than those for usual single C–C bonds (∼1.5 Å). The B_CC values decrease with an increase in the tube diameter as well as with a decrease in the number of methyl groups in the radicals. In all of the alkyl-bound tubes considered, the B_CC values are also larger than those for the corresponding graphenes. The differences in the CC bond lengths between the tube and graphene cases (ΔB_CC) are significant for a smaller diameter tube. The behaviors of the ΔB_CC values are reasonable, because a smaller-diameter tube has a greater curvature. The results clearly show that the tube curvature is one of the important factors in determining the interactions with an inner alkyl radical.

Given that the CC bonds formed between the inner alkyl radicals and the tubes are longer than those in the graphene cases, their interactions in the alkyl-bound tubes would be weaker. In fact, we can see in Fig. 6(b) that the calculated binding energies are −36.0–−22.6 kcal mol⁻¹, being less significant than those in the graphene cases (−40.7–−33.1 kcal mol⁻¹). The E_BE values are also correlated with the tube curvature as well as the number of methyl groups in an alkyl radical: interactions for a larger-diameter tube with a less bulky radical are more pronounced than those for a smaller-diameter tube with a more bulky radical. More importantly, all the interaction energies obtained from the DFT calculations are less significant than those in usual single CC bonds (E_BE: −80–−88 kcal mol⁻⁹), indicating that the CC bonds formed between an inner radical and a tube are quite weak. The weakness of the inner CC bonds is one of the reasons for the preference of an alkyl radical separated from the tube wall over a tube-bound alkyl radical, as will be discussed.

The formation of the weak inner CC bonds is related to how smoothly the tube C atom attached by an alkyl radical sags towards the center. The sagging can be quantitatively analyzed by the difference in a dihedral angle (φ, defined in Fig. 2) between before and after the radical binding (Δφ). The Δφ values suggest how much a tube carbon atom is required to shift to a position suitable for the interaction with an alkyl radical. Table 1 lists the Δφ values for the alkyl-bound tubes and graphenes. We can see from Table 1 that the Δφ values range 50–53 degrees for the alkyl-bound graphenes. The Δφ values in the graphene cases are a baseline to help us understand how the inner concave surface of a tube affects the interactions with an alkyl radical. Compared with the graphene case, smaller Δφ values were obtained for the alkyl-bound tubes, as shown in Table 1. These results suggest that the shift of the tube carbon atom upon alkyl binding is more restricted than in the graphene cases. Reflecting on the smaller Δφ values for the alkyl-bound tubes, their interaction energies are less significant than those for the alkyl-bound graphenes, as shown in Fig. 6. Furthermore, the Δφ values for the alkyl-bound tubes strongly depend on the tube curvature as well as the type of radical. Considering the Δφ tendencies, we can understand the tube-diameter dependencies of the E_BE values. In other words, the E_BE values link to Δφ values for the addition of an alkyl radical into tubes with different diameters. For example, the absolute E_BE values for the isopropyl additions increase in the order (8,8) < (10,10) < (12,12). The E_BE values increase in the same order that the Δφ values decrease.

3.2.3 Tube deformation. As mentioned above, the tube surface sags toward the tube center when an inner CC bond is formed between an alkyl radical and a tube. Another event in the bindings is that the CC bondings in the sp² surface also are significantly deformed relative to those in the unperturbed case. The sagging as well as the deformation of the sp² bondings destabilize the tube itself, whose required energy is tabulated in Table 3. Significant destabilization can be seen in a narrower tube bound by a more bulky radical. For example, the deformation in the (8,8) tube by the isopropyl addition costs 38.9 kcal mol⁻¹, being larger than the (12,12) case (32.4 kcal mol⁻¹). The tube diameter dependencies of the destabilization by the isopropyl addition are significant relative to those by the methyl and ethyl additions.

To increase our understanding of the destabilization by the tube deformation, we pay attention to some details of the geometrical features of the methyl-bound (10,10) tube. Fig. 7 shows the deformation of the sp² framework of the tube induced by the interaction with a methyl radical. For comparison, the optimized geometry for methyl-bound graphene is also given in Fig. 8. In the deformed sp² surfaces, there are some CC bonds that are lengthened or shortened by at least 0.009 Å, compared with those in the pristine sp² surface. The lengthened and shortened CC bonds are given in Fig. 7 and Fig. 8 by bold and hashed lines, respectively. Significant changes in the CC bonds are only seen in the vicinity of the methyl binding site. Roughly speaking, the methyl-bound graphene has a deformation pattern with one three-fold axis of rotational symmetry. Similar deformation patterns are seen in the methyl-bound tube. However, the high-symmetry cannot be retained in the tube deformation. The tube deformations due to the CH₃ addition are quite different from those due to the CH₂ addition.²⁷ The differences in the tube deformations between the two systems are understandable by considering the number of π electrons that participate in the inner CC bond formations. In the CH₃ interaction, one π electron moves from the surface of the tube into the new σ-bond, while two π electrons move in the CH₂ addition.

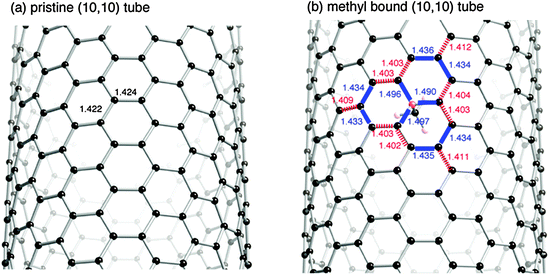Fig. 7 Changes in CC bondings of the (10,10) tube upon the addition of a methyl radical. The methyl radical is bound to a C atom of the tube in the right-hand side geometry. Bold and hashed lines indicate CC bonds in the methyl-bound tube lengthened and shortened by at least 0.009 Å compared with the pristine tube, respectively.

Fig. 8 Changes in CC bondings of graphene upon the addition of a methyl radical. The methyl radical is bound to a C atom of graphene in the right-hand side geometry. Bold and hashed lines indicate CC bonds in the methyl-bound graphene lengthened and shortened by at least 0.009 Å compared with the pristine graphene, respectively.

3.2.4 Factors determining a stable conformation of an alkyl radical species inside a tube. Finally let us discuss which components (E_BE, ΔE_tube, and ΔE_guest) mainly contribute to ΔE_total, as shown in Table 3 and Fig. 9. As shown in Table 3, ΔE_tube values and absolute E_BE values have similar amounts around 30 kcal mol⁻¹, while ΔE_guest values are less than 10 kcal mol⁻¹. Thus the energy decomposition analyses illuminate that major contributions to the ΔE_total values are the binding energies between an alkyl radical and a tube as well as energies required by the tube deformation, while energies required by the guest deformation are a minor but measurable contribution to the ΔE_total values. Despite the significant E_BE and ΔE_tube values, the ΔE_tube values always have a sign opposite to those in the corresponding E_BE values, and therefore the E_BE and ΔE_tube contributions largely compensate for each other. As a result, the absolute ΔE_tube + E_BE values are competing with the ΔE_guest values. In fact, the ΔE_tube+E_BE values have a less significant amount ranging from −5.3 to 10.6, and depend on the tube diameters as well as types of alkyl radical considered. The less significant ΔE_tube + E_BE values are characteristic of the covalent bond formation inside a tube, because the inner CC bond is weaker (E_BE: −22.6–−34.9 kcal mol⁻¹) than usual single CC bonds (E_BE: −80–−88 kcal mol⁻¹),⁹ which comes from the inertness of the inner tube wall.

Fig. 9 Energy decomposition analyses of the energy differences between separate and bound forms of an alky radical inside a tube (ΔE_total = E_total(bound form) − E_total(separate form)). The ΔE_total values can be partitioned into three components, the binding energy (E_BE), the energy required by the deformation of a tube (ΔE_tube), and the energy required by the deformation of a guest (ΔE_guest). A panel shows E_BE, ΔE_tube, E_BE + ΔE_tube, ΔE_guest, and ΔE_total from the left to the right.

Whether a ΔE_tube + E_BE value is negative or positive is a good indicator to categorize the radical additions into two subgroups. Fig. 9 and Table 3 show that most configurations have positive values of ΔE_tube + E_BE. In particular, significant positive ΔE_tube + E_BE values are seen for a more bulky alkyl radical inside a smaller diameter tube. In these configurations, the destabilization by the tube deformation outweighs the attraction due to the inner bond formation. As a result, the configurations with a positive ΔE_tube + E_BE value have a ΔE_total value larger than 10 kcal mol⁻¹, indicating that only a separate form is allowed for an alkyl radical inside the tube. These analyses clearly show that the preference of a separate form over a bound form is an indirect result of the inertness of the inner tube wall.

On the other hand we can see some exceptions for a methyl radical inside the (8,8), (10,10), and (12,12) tubes as well as an ethyl radical inside the (12,12) tube. Negative ΔE_tube + E_BE values were found for these configurations, where the attraction by the inner bond formation overcomes the destabilization by the tube deformation. Accordingly its ΔE_total value is always less than 10 kcal mol⁻¹. In these situations, the separate form is close in energy to the bound form. The energy decomposition analyses show the balance between the attraction by the inner bond formation and the destabilization by the deformation of a tube is a key factor in determining a stable conformation for an alky radical inside a tube.

4. Conclusion

DFT PW91 calculations show that an alkyl radical guest preferentially exists separately from the inner wall of a tube rather than making one inner covalent bond with the inner wall. The existence of an inner alkyl radical apart from the tube wall is more likely when a tube host has a smaller diameter as well as when a radical guest is more bulky. In fact, an inner isopropyl radical separated from the wall of the (8,8) tube (separate form) is 27.2 kcal mol⁻¹ more stable than that covalently binding to the wall (bound form). The energy difference (ΔE_total = E_total(bound form) − E_total(separate form)) is the most significant among the other host–guest materials considered in the present study, where the host is an (8,8), (10,10), or (12,12) tube, and the guest is a methyl, ethyl, or isopropyl radical. On the other hand, a negligible ΔE_total value (1.6 kcal mol⁻¹) was found for a methyl radical inside the (12,12) tube. The preferences of the separate forms over the bound forms are understandable by considering different structural features between the two forms. In the bound forms, the inner bond formation deforms the structures of a tube host and a radical guest, while such deformations cannot be seen in the separate forms. Compared with the separate forms, the bound forms gain attraction by the inner bond formation, however, the accompanying deformations destabilize the systems. Thus, the balance between attraction by the inner bond formation and destabilization by their geometrical deformations determines whether an alkyl radial inside a tube prefers a separate form or a bound form. According to DFT calculations, attraction by the inner bond formation is quite weak compared with that of a usual single CC bond, due to the inertness of the inner concave surface of a tube. The attraction is completely counteracted by the destabilization due to the deformations of a host tube and a radical guest. Accordingly, the existence of a free alkyl radical inside a tube is characteristic of an alkyl group in nano-sized space surrounded by an inert concave surface. We nicely demonstrated from DFT calculations that an alkyl radical species remains alive inside a tube and retains its reactivity, and thus the present study can shed light on some of the mystery about chemical reactions taking place inside tubes.

Acknowledgements

T.Y. thanks Prof. M. Kertesz at Georgetown University (US) for valuable discussions on the origin of the weak bond formed inside a tube.

References

1. S. Iijima, Nature, 1991, 354, 56.
2. S. Iijima and T. Ichihashi, Nature, 1993, 363, 603.
3. B. W. Smith, M. Monthioux and D. E. Luzzi, Nature, 1998, 396, 323.
4. A. N. Khobystov, D. A. Britz and G. A. D. Briggs, Acc. Chem. Res., 2005, 38, 901.
5. (a) S. Bandow, M. Takizawa, K. Hirahara, M. Yudasaka and S. Iijima, Chem. Phys. Lett., 2001, 337, 48; (b) S. Bandow, T. Hiraoka, T. Yumura, K. Hirahara, H. Shinohara and S. Iijima, Chem. Phys. Lett., 2004, 384, 320; (c) T. Yumura, K. Hirahara, S. Bandow, K. Yoshizawa and S. Iijima, Chem. Phys. Lett., 2004, 386, 38; (d) Y. Fujita, S. Bandow and S. Iijima, Chem. Phys. Lett., 2005, 413, 410.
6. D. A. Britz, A. N. Khobystov, K. Porfyrakis, A. Ardavan and G. A. D. Briggs, Chem. Commun., 2005, 37.
7. (a) K. Urita, Y. Sato, K. Suenaga, A. Gloter, A. Hashimoto, M. Ishida, T. Shimada, H. Shinohara and S. Iijima, Nano Lett., 2004, 4, 2451; (b) Y. Sato, T. Yumura, K. Urita, K. Suenaga, H. Kataura, T. Kodama, H. Shinohara and S. Iijima, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 233409; (c) T. Yumura, Y. Sato, K. Suenaga, K. Urita and S. Iijima, Nano Lett., 2006, 6, 1389; (d) L. Guan, K. Suenaga, S. Okubo, T. Okazaki and S. Iijima, J. Am. Chem. Soc., 2008, 130, 2162; (e) M. Koshino, Y. Niimi, E. Nakamura, H. Kataura, T. Okazaki, K. Suenaga and S. Iijima, Nat. Chem., 2010, 2, 117.
8. A. Chuvilin, A. N. Khobystov, D. Obergfell, M. Haluska, S. Yang, S. Roth and U. Kaiser, Angew. Chem., Int. Ed., 2009, 48, 193.
9. T. W. G. Solomons, Organic Chemistry, John Wiley & Sons Inc., New York, 5th edn, 1992.
10. A. Hirsch, Angew. Chem., Int. Ed., 2002, 41, 1853.
11. (a) Y. Chen, R. C. Haddon, S. Fang, A. M. Rao, W. H. Lee, E. C. Dickey, E. A. Grulke, J. C. Pendergrass, A. Chavan, B. E. Haley and R. E. Smalley, J. Mater. Res., 1998, 13, 2423; (b) J. Chen, M. A. Hamon, H. Hu, Y. Chen, A. M. Rao, P. C. Eklund and R. C. Haddon, Science, 1998, 282, 95; (c) H. Hu, B. Zhao, M. A. Hamon, K. Kamaras, M. E. Itkis and R. C. Haddon, J. Am. Chem. Soc., 2003, 125, 14893; (d) K. Kamaras, M. E. Itkis, H. Hu, B. Zhao and R. C. Haddon, Science, 2003, 301, 1501.
12. M. Holzinger, O. Vostrowsky, A. Hirsch, F. Hennrich, M. Kappes, R. Weiss and F. Jellen, Angew. Chem., Int. Ed., 2001, 40, 4002.
13. (a) J. L. Bahr, J. Yang, D. V. Kosynkin, M. J. Bronikowski, R. E. Smalley and J. M. Tour, J. Am. Chem. Soc., 2001, 123, 6536; (b) J. L. Bahr and J. M. Tour, Chem. Mater., 2001, 13, 3823; (c) C. A. Dyke and J. M. Tour, J. Am. Chem. Soc., 2003, 125, 1156.
14. Y. Ying, R. K. Saini, F. Liang, A. K. Sadana and W. E. Billups, Org. Lett., 2003, 5, 1471.
15. P. Umek, J. W. Seo, K. Hernadi, A. Mrzel, P. Pechy, D. D. Mihailovis and L. Forró, Chem. Mater., 2003, 15, 4751.
16. (a) H. Peng, P. Reverdy, V. N. Khabashesku and J. L. Margrave, Chem. Commun., 2003, 362; (b) H. Peng, L. B. Alemany, J. L. Margrave and V. N. Khabashesku, J. Am. Chem. Soc., 2003, 125, 15174.
17. T. Nakamura, M. Ishihara, T. Ohara, A. Tanaka and Y. Koga, Chem. Commun., 2004, 1336.
18. F. Li, Y. Xia, M. Zhao, X. Liu, B. Huang, Z. Tan and Y. Ji, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 165415.
19. A. López-Bezanilla, F. Triozon, S. Latil, X. Blasé and S. Roche, Nano Lett., 2009, 9, 940.
20. S. Kim, E. Cho, S. Han, Y. Cho, S. H. Cho, C. Kim and J. Ihm, Solid State Commun., 2009, 149, 670.
21. B. R. Goldsmith, J. G. Coroneus, V. R. Khalap, A. A. Kane, G. A. Weiss and P. G. Collins, Science, 2007, 315, 77.
22. Z. Chen, W. Thiel and A. Hirsch, ChemPhysChem, 2003, 4, 93.
23. (a) Z. Chen, S. Nagase, A. Hirsch, R. C. Haddon, W. Thiel and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2004, 43, 1552; (b) J. Zhao, Z. Chen, Z. Zhou, H. Park, P. v. R. Schleyer and J. P. Lu, ChemPhysChem, 2005, 6, 598.
24. H. Park, J. Zhao and J. P. Lu, Nano Lett., 2006, 6, 916.
25. (a) H. F. Bettinger, Org. Lett., 2004, 6, 731; (b) H. F. Bettinger, Chem.–Eur. J., 2006, 12, 4372.
26. (a) Y.-S. Lee and N. Marzari, Phys. Rev. Lett., 2006, 97, 116801; (b) Y.-S. Lee and N. Marzari, J. Phys. Chem. C, 2008, 112, 4480.
27. (a) T. Yumura and M. Kertesz, Chem. Mater., 2007, 19, 1028; (b) T. Yumura, M. Kertesz and S. Iijima, Chem. Phys. Lett., 2007, 444, 155; (c) T. Yumura and M. Kertesz, J. Phys. Chem. C, 2009, 113, 14184.
28. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244.
29. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169.
30. D. Vanderbilt, Phys. Rev. B: Condens. Matter, 1990, 41, 7892.
31. K. Yoshizawa, T. Yumura, T. Yamabe and S. Bandow, J. Am. Chem. Soc., 2000, 122, 11871.
32. M. S. Dresselhaus, G. Dresselhaus and R. C. Eklund, Science of Fullerenes and Carbon Nanotubes, Academic Press, New York, 1996.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03 (Revision E.01), Gaussian, Inc., Wallingford, CT, 2004.
34. (a) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257; (b) P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213.
35. (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
36. P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953.
37. General gradient approximations (GGA) such as the PW91 and PBE functionals correct the overbinding tendency inherent in the local density approximation (LDA). Currently the GGA is a popular form and its use is accepted as a reasonable compromise between accuracy and efficiency, although a GGA is not superior to alternatives such as hybrid functionals like B3LYP. See a recent review: J. Hafner, J. Comput. Chem., 2008, 29, 2044.
38. T. A. Albright, J. K. Burdett and M.-H. Whangbo, Orbital Interactions in Chemistry, Wiley, New York, 1985.
39. (a) K. Yoshizawa, T. Kato and T. Yamabe, J. Chem. Phys., 1995, 103, 2126; (b) K. Yoshizawa, T. Kato and T. Yamabe, J. Chem. Phys., 1996, 105, 2099; (c) K. Yoshizawa, T. Yumura and T. Yamabe, J. Chem. Phys., 1999, 110, 11534; (d) T. Yumura, S. Bandow, K. Yoshizawa and S. Iijima, J. Phys. Chem. B, 2004, 108, 11426.

---

Footnote

† Electronic supplementary information (ESI) available: optimized structures for an alkyl radical inside the (8,8) nanotube (Fig. S1); optimized structures for an alkyl radical inside the (12,12) nanotube (Fig. S2); optimized structures for an alkyl radical binding into graphene (Fig. S3); schematic view of changing frontier orbitals during the D_3h to C_3v conversion of methyl radical (Fig. S4); detailed information on two types of methyl radical inside the (10,10) nanotube, and methyl radical bound to graphene (fraction coordinate and total energy); full author list in ref. 33. See DOI: 10.1039/c0cp00796j

---