Self-assembly of alkylcatechols on HOPG investigated by scanning tunneling microscopy and molecular dynamics simulations

Abstract

Two alkylcatechols have been studied by means of STM at the liquid–solid interface. While for catechol 3 no molecular domains on the surface have been observed most likely due to the steric constraints imposed by the tert-butyl group, catechol 2 self-organizes both in nonanoic acid and TCB solvents. Combined molecular dynamics simulations have shown the large tendency of this catechol to remain and organize on surfaces. Moreover, by comparison with the results previously described for catechol 1, valuable information about the energetic and thermodynamics for the adsorption process of catechols can be extracted.

---

Introduction

Catechols have been found to strongly interact with surfaces in different natural systems. One of the most well-known examples is the aminoacid L-3,4-dihydroxyphenylalanine (DOPA), which has been found to play a crucial role in the strong adhesive capacity of mussels.¹ In this case, interfacial adhesion to substrates arises from interactions between the catechol form of DOPA and a variety of substrates (e.g.minerals, metal surfaces, and wood, among others). Catechol derivatives also play an important role in Asian lacquers used as durable coating materials.² All these saps present catechol compounds with alkyl and alkenyl chains of different length, degree of saturation and position in the benzene ring,³ that upon a cross-linked polymerization constitute the protective film.⁴

This ability of catechol derivatives to interact with surfaces has been exploited by many scientists worldwide to prepare new synthetic functional adhesives⁵ and coatings.⁶ However, understanding the basic behaviour and assembly of catechols on surfaces still remains a challenge. For this reason, new basic studies that gain information about the self-assembly and interaction of catechols with surfaces are highly required. Scanning tunneling microscopy (STM) is an excellent technique for such studies.⁷STM can allow the direct observation of the molecular self-assembly processes on surfaces with molecular resolution, and therefore, the study and modelization of molecule–molecule and molecule–surface interactions.^7b–g A wide range of compounds have been studied with STM at the liquid–solid interface, including simple linear alkanes,⁸ long chain alcohols,⁹ aromatic carboxylic acids,¹⁰amides,¹¹ aromatic cores functionalized with alkyl chains,¹²crown¹³ and thiacrown ethers¹⁴ and even more complex structures like fullerenes¹⁵ and macrocyclic coordination compounds.¹⁶ Nevertheless, no examples of catechols at the liquid–solid interface can be found in the literature, and only scarce examples of these compounds on surfaces have been studied by STM under UHV conditions.¹⁷

For this reason we have started new research focused to study the self-assembly of catechols at the liquid–solid interface by STM. Following this approach, very recently we described for the first time the self-assembly of the 4-heptadecylcatechol 1 (Fig. 1) at the nonanoic acid–HOPG interface.¹⁸ Compound 1 was shown to exhibit a large tendency to adsorb on the surface as a result of both energetic (interactions on the surface) and entropic factors (temperature and solvent). Energetic factors arise from the presence of attractive van der Waals (vdW) interactions with the HOPG surface and alkyl chains of other adsorbed molecules as well as from the formation of hydrogen bonds between different catechol moieties. Entropic factors arise from the relatively poor solvation of compound 1 in solvents such as nonanoic acid. This combination of complex factors, resulted in a rich self-assembly behaviour of 1 at the HOPG surface (with and without coadsorption of the solvent) that depends on thermodynamic and kinetic aspects. Moreover, the nontrivial implications of structural factors on the interaction with surfaces are also relevant.

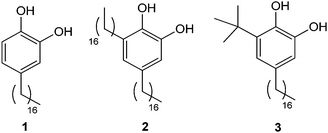Fig. 1 Structure of alkylcatechols 1–3.

These interesting results led us to continue within this research line by studying how modifications on their chemical structure can affect the self-assembly on surfaces. With this aim, in this work we report the synthesis of two new alkylcatechols 2 and 3 (Fig. 1) and the study of their self-assembly on HOPG by STM in two different solvents. The addition of a second alkyl chain in 2 is used to evaluate the contribution of the catechol unit to the energetic interplay of thermodynamic and kinetic aspects that control the self-assembly. Compound 3 has also been synthesized for comparison purposes, bearing a bulky tert-butyl group that is expected to disrupt the assembly processes. The experimental results have been rationalized according to theoretical calculations.

Results and discussion

Synthesis of compounds 2 and 3

The synthesis of the 3,5-dialkyl-1,2-dihydroxybenzene 2 started from the isophthalaldehyde 4 (ref. 19) which was treated with methyl sulfate in basic conditions to afford the methoxy protected derivative 5 (ref. 20) in 67% yield (Scheme 1). The Wittig reaction of the dialdehyde 5 with hexadecyl triphenylphosphonium bromide and potassium tert-butoxide in dry THF afforded in 70% yield a mixture of olefinic isomers 6 wherein the (Z,Z)-6 was the major component. Conventional hydrogenation, using hydrogen and palladium on carbon catalyst, followed by demethylation by treatment with boron tribromide in CH₂Cl₂ gave catechol 2 in 77% yield for the two steps.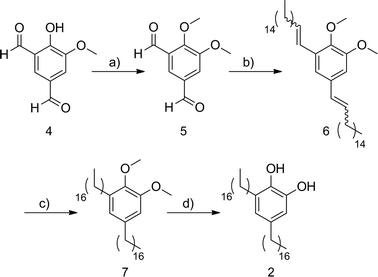

Scheme 1 (a) Me₂SO₄, K₂CO₃, (n-Bu)₄NI, DMF, 67%; (b) 1-(hexadecyl)triphenylphosphonium bromide, tBuOK, THF, 70%; (c) H₂, Pd/C, ethyl acetate, 80%; (d) BBr₃, CH₂Cl₂, 96%.

The synthesis of catechol 3 began from the commercially available phenol 8 which was converted to 9 in a moderate 55% yield by reaction with tBuOH in H₃PO₄ (Scheme 2). Oxidation of 9 and demethylation of the resulting aldehyde 10 (ref. 21) afforded the catechol 11 which was protected as the MOM derivative 12 (ref. 22) by standard conditions in 37% yield for the three steps. Then, the Wittig reaction of aldehyde 12 with hexadecylidene(triphenyl)phosphorane gave the olefin 13 as a 10 : 1 mixture of the (Z)- and (E)-isomers in 58% combined yield.

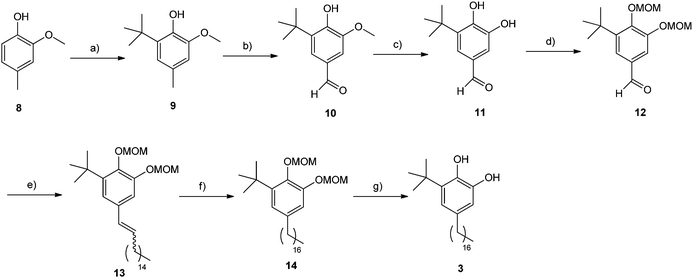Scheme 2 (a) tBuOH, H₃PO₄, 55%; (b) Br₂, tBuOH, 62%; (c) AlCl₃, pyridine, CHCl₃, 85%; (d) methoxymethyl bromide, iPr₂EtN, DMAP, CH₂Cl₂, 70%; (e) 1-(hexadecyl)triphenylphosphonium bromide, tBuOK, THF, 58%; (f) H₂, Pd/C, ethyl acetate, 98%; (g) HCl (cat.), MeOH, 88%.

Hydrogenation of olefins 13 using hydrogen and palladium on carbon catalyst, followed by acid treatment in refluxing methanol to cleave the MOM ethers provided the target compound 3 in 86% yield for the two steps.

Thermodynamics for the adsorption of 2 at the nonanoic acid–HOPG interface

Initially, the Gibbs free energy associated to the transfer of compound 2 from solution to the liquid–solid interface was theoretically evaluated, putting special emphasis on its molecular origin. Technical details of the calculations are described in the Materials and methods section. It should be emphasized here that theoretical predictions of this kind, involving not only enthalpy but also free energy calculations, are rather difficult and very time-consuming for liquid solutions. In fact, the realization of such calculations has become possible thanks to recent new developments in simulation techniques. This is the case for the new MD-ABF technique employed in this work.²³

First, Molecular Dynamics (MD) simulations of a liquid solution composed of 48 molecules of 2 and 400 nonanoic acid molecules at two different temperatures (20 °C and 80 °C) and 1 atm were done. This molecular ratio corresponds to a concentration similar to that used for the STM experiments shown later on. Afterwards, the resulting equilibrated solution was placed in contact with a large graphite surface of 87.81 nm² that was immediately covered by molecules. A second set of MD simulations were then run to allow further equilibration and adsorption/desorption events at the surface. An illustrative snapshot of the simulation is shown in Fig. 2. A first qualitative observation is the strong tendency to adsorb of compound 2, which covers most of the surface after 1 ns together with a small amount of a few nonanoic acid molecules. It is important to mention that this situation takes place in spite of the large excess of the nonanoic acid that has also been shown to organize under these circumstances. However no clear self-assembly patterns were observed on the surface, at least under simulation scales accessible with MD simulations (more details about this issue are given in the next section).

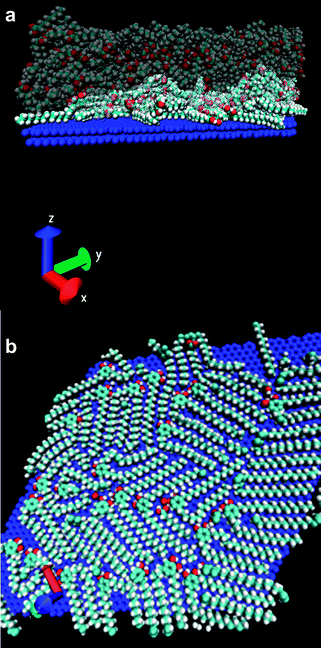Fig. 2 Molecular Dynamics (MD) simulations of a liquid solution composed of 48 molecules of 2 and 400 nonanoic acid molecules at 20 °C. (a) Lateral view of the simulated system, solvent molecules are shown translucent for clarity. (b) Top view showing only the molecules adsorbed at the surface after putting the graphite surface in contact with the pre-equilibrated solution. The rest of the molecules of the system (which correspond to the large majority of the system) are not shown for the sake of clarity. Coadsorption of molecules of 2 with a few nonanoic acid molecules is also observed. The colour code follows standard crystallographical conventions: red for oxygen, cyan for carbon and white for hydrogen (the surface is shown in blue for clarity).

Afterwards, biased MD-ABF simulations were performed on the resulting combined (solution + surface) system to obtain the thermodynamic free energy associated with the transfer of 2 from liquid to the graphite surface as a function of the distance. In these MD-ABF simulations, an adsorbed molecule was selected and pulled out from the surface in a very slow, quasi-static process. We recall that during this pulling process, the selected molecule interacts not only with the surface but also with the other solute molecules and the solvent which are also moving according to Newton motion equations during the simulation. Also, the simulation technique maintains thermal equilibrium during the process by employing a thermostat, as described in the Methods section. The work performed in this process gives the free energy associated with the transfer of compound 2 from the bulk solution to the surface under given thermodynamic conditions (composition, temperature, pressure). The results for the free energy profile at 20 °C and 80 °C are shown in Fig. 3. The insets show representative snapshots of the process, in which the desorption event is highlighted.

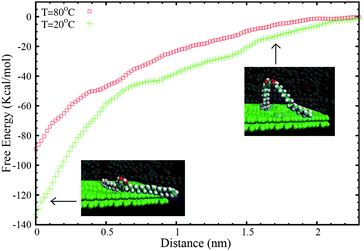Fig. 3 Free energy (ΔG) profile for the transfer of a molecule of 2 from the graphite surface to the bulk solution as a function of the distance of the centre of mass of the molecule (z) to the surface. The MD-ABF calculations were performed at 20 °C and 80 °C. The snapshots are images of a solute molecule in a desorption event. All other molecules of the large simulated system are not shown for clarity.

As can be seen in Fig. 3, the adsorption minimum corresponds to an adsorption free energy of ΔG = −133.5 kcal mol⁻¹ at 20 °C. The first thing to recall is the resulting large value for ΔG, indicating a strong affinity of this compound for the liquid–solid interface, as expected in general for catechols. It is important to emphasize the fact that this value is comparable to the free energy gain previously obtained for the adsorption of compound 1 at the nonanoic acid–HOPG interface (ΔG = −122 kcal mol⁻¹ at 20 °C). Therefore, the addition of a second alkyl chain induces a small increase of the affinity for the surface, smaller than 10%. While the second alkyl chain is expected to enhance the gain in the adsorption free energy by promoting favourable van der Waals interactions, the induction of stronger steric interactions can simultaneously disrupt the formation of hydrogen bonds between catechol units. This fact would indicate that the catechol moiety is responsible for a substantial part of the affinity of these compounds for the surface.

The second remarkable result is the substantial dependence of ΔG on temperature, which confirms that entropic factors also play an important role in the affinity of compound 2 for the surface (recall here the thermodynamic relationship between entropy and T dependence of the free energy at a constant pressure). The adsorption free energy decreases from ΔG = −133.5 kcal mol⁻¹ at 20 °C to ΔG = −89 kcal mol⁻¹ at 80 °C. Such remarkable temperature dependence therefore strongly precludes the use of total energy methods developed to study self-assembly processes under vapour deposition techniques. These simulations can be done only in situations in which temperature (and entropic) factors do not play a significant role, which is not the case.

Experimental self-assembly of 2 and 3 at the nonanoic acid–HOPG interface

The self-assembly of 2 was initially studied at the nonanoic acid-HOPG interface at room temperature. For this, a drop of a nonanoic acid solution of compound 2 (2 mg mL⁻¹) was cast onto a freshly cleaved HOPG surface at room temperature. Considerable experimental difficulties were found when obtaining images of 2 with good resolution, in spite of the numerous experiments attempted. From all the conditions tested, the best large-scale STM images at least over three independent surface areas were obtained with the conditions described in Fig. 4. A representative image of the domains found for 2 is shown in Fig. 4a. The analysis of the images evidences high-contrast bright spots associated to dimers of catechol rings that arrange with a hexagonal centred symmetry. This packing differs from that found for 1 (shown in Fig. 4b for comparison purposes), being an indication of the second chain effect on the 2-D molecular packing.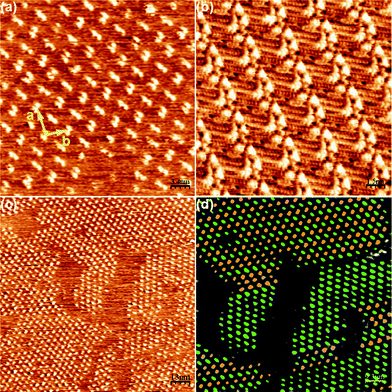

Fig. 4 Self-assembly pattern of 2 at the nonanoic acid–HOPG interface. (a) Zoom of the self-assembly pattern obtained for 2. Unit cell parameters: a = 5.0 ± 0.2 nm, b = 3.4 ± 0.2 nm, γ = 95 ± 2°. Scanning conditions: 34 nm × 34 nm, I_set = 50 pA, V_bias = 540 mV. (b) STM image of the self-assembly pattern of 1. (c) Wide view for the self-assembly of 2 where the different orientations of the dimers can already be seen. Scanning conditions: 130 nm × 130 nm, I_set = 55 pA, V_bias = 540 mV. (d) Code of colours to distinguish the differently oriented dimers shown in (c).

Moreover, two different orientations of these dimers can be observed, with a relative rotation between them of approximately 90°. This leads to the formation of two different domains, as can be seen in Fig. 4c. To facilitate the location and imaging of such orientations, the differently oriented dimers have been coloured in Fig. 4d. As can be observed there, none of them seems to be especially favoured from an energetic point of view, since both spread spontaneously all over the surface with an approximate half occupation. The zones between the bright spots are expected to be occupied by the alkyl chains, though unfortunately the resolution was not good enough to determine the exact number and position of them. Nevertheless, there is room enough in the unit cell (area ≈ 17 nm²) to accommodate all the alkyl chains and 4–6 nonanoic acid molecules.

To gain more insight into the disposition of the alkyl chains, additional experiments were done with trichlorobenzene instead of nonanoic acid. For this, a drop of a TCB solution of compound 2 (2 mg mL⁻¹) was cast onto a freshly cleaved HOPG surface at room temperature using the experimental parameters described in Fig. 5. Immediately after, large-scale STM images under ambient conditions were obtained at least over three independent surface areas. In this case, the resulting molecular packing was obtained with high reproducibility between different casting experiments of freshly prepared samples and its stability assessed by taking different STM images over the same region at different time intervals. As can be seen in Fig. 5, a better molecular resolution is obtained though with a different molecular packing. In this case compound 2 arranges forming rows of bright spots that can be associated to the catechol moieties, from where the alkyl chains can be observed with better resolution lying at both sides of the catechol ring with an angle of 180° between them.

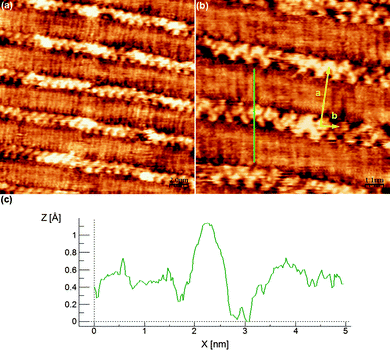Fig. 5 Self-assembly pattern of 2 at the TCB–HOPG interface. (a) Wide view. Scanning conditions: 20 nm × 20 nm, I_set = 63 pA, V_bias = 500 mV. (b) Zoom view. Unit cell parameters: a = 3.4 ± 0.2 nm, b = 1.0 ± 0.2 nm, γ = 95 ± 4°. Scanning conditions: 10 nm × 10 nm, I_set = 64 pA, V_bias = 500 mV. (c) Profile marked as a green line in (b), coincident with the length of 2 molecule in its most extended conformation.

The profile marked as a green line in Fig. 5b is coincident with the length of this molecule in its most extended conformation. The orientation of the catechol moieties can also be resolved from this image, confirming that all of them are pointing in the same direction without establishing hydrogen bonds between them. In fact, taking into account the profile marked in Fig. 5b and the unit cell area (∼3.3 nm²), where only one molecule of 2 per unit cell can be accommodated, it can be concluded that the self-assembly pattern corresponds to an arrangement of monomers of 2 into rows. The neighbouring rows interact between them through van der Waals forces by clearly interdigitating the alkyl chains, resulting in the formation of the mentioned very compact packing.

Finally, the self-assembly of 3 was studied at the liquid–HOPG interface at room temperature in both solvents, nonanoic acid and TCB. For this, a drop of a nonanoic acid solution of compound 3 (2 mg mL⁻¹) was cast onto a freshly cleaved HOPG surface at room temperature. In this case, and even though several different experimental conditions were used including those described in Fig. 3 and 4, no images showing the crystal packing of 3 were obtained. This fact has been attributed to the presence of the bulky tert-butyl group that most likely disrupts the formation of good molecular assemblies on surfaces.

Conclusions

The self-assembly of compounds 2 and 3 at the liquid–solid interface has been studied in two different solvents. While in the case of compound 3 no self-assembly patterns have been experimentally observed most likely due to the presence of the bulky tert-butyl groups, STM images have been obtained in both solvents for compound 2. Experimental results indicate that the molecules arrange on the surface with both alkyl chains extended, forming an angle of 180° for the TCB. Such disposition leads to the observation of a compact packing with interpenetrated chains without coadsorbed solvent molecules. On the contrary, coadsorption phenomena could take place when using nonanoic acid. In this case a hexagonal centred symmetry is observed though the poor image resolution prevents us from observing the positions of the chains.

Theoretical calculations have confirmed the tendency of compound 2 to adsorb on the surfaces with a free energy of ΔG = −133.5 kcal mol⁻¹ at 20 °C. Though this value is high if compared for instance with that obtained for nonanoic acid under the same conditions (ΔG = −45 kcal mol⁻¹ at 20 °C), it is comparable to the free energy gain previously obtained for the adsorption of compound 1 also under the same experimental conditions (ΔG = −122 kcal mol⁻¹ at 20 °C). This is a clear indication of the importance of catechol in front of the alkyl chains to promote their surface organization.

In fact, the gain in the free energy value obtained for 2 can now be used to rationalize some of the experimental results previously described. The argument is as follows. A surface covered only by nonanoic acid considering an effective area of 1.5 nm² per molecule will correspond to a free energy gain of ΔG = 45/1.5 = −30 kcal mol⁻¹ per nm² of the covered surface. A surface covered only by molecules of 2 assuming a unit cell of 17 nm² involving 4 molecules gives an almost identical free energy gain of ΔG = (4 × 133.5)/17 = −31.4 kcal mol⁻¹ per nm² of the covered surface. Finally, a coadsorption pattern with the same hypothetical unit cell but with co-adsorption of 4 nonanoic acid molecules in the remaining free space (6 nm²) gives a free energy gain of ΔG = −(4 × 133.5 + 4 × 45)/17 = −42 kcal mol⁻¹ per nm². These theoretical estimations suggest that the free energy differences between different possible self-assembly patterns are small, which could justify the difficulties observed in obtaining these self-assembly patterns both in the experiments and theoretical calculations. For instance, we tried to obtain clear self-assembly patterns by direct MD simulations, starting from different initial conditions with pre-adsorbed molecules on the surface and putting the system in contact with the liquid solution, without success. Self-assembly patterns cannot be simulated in this case employing popular energy minimization methods to give more insight, due to the importance of thermal and entropic factors in the affinity of compound 2 (neglected in these methodologies).

Materials and methods

Synthesis

NMR experiments were performed at the Servei de Ressonància Magnètica Nuclear of the Universitat Autònoma de Barcelona. ¹H NMR spectra were recorded on Bruker DPX250 (250 MHz) and Bruker DPX360 (360 MHz), spectrometers. Proton chemical shifts are reported in ppm (δ) (CDCl₃, δ 7.26). ¹³C NMR spectra were recorded on Bruker DPX250 (62.5 MHz) and Bruker DPX360 (90 MHz) spectrometers with complete proton decoupling. Carbon chemical shifts are reported in ppm (δ) (CDCl₃, δ 77.2). NMR signals were assigned with the help of COSY and HSQC experiments. Infrared spectra were recorded on a Sapphire-ATR Spectrophotometer; peaks are reported in cm⁻¹. High resolution mass spectra (HRMS) were recorded at Micromass-AutoSpec using (ESI+).

Preparation of 4,5-dimethoxyisophthaldehyde 5. Compound 4 (ref. 11) (250 mg, 1.39 mmol) was dissolved in DMF (8 mL) and K₂CO₃ (576 mg, 4.17 mmol) and (n-Bu)₄NI (22 mg) were added. The mixture was stirred at room temperature for 2 h and then Me₂SO₄ (0.3 mL, 2.78 mmol) was added dropwise. After 24 h, the solvent was evaporated under vacuum, yielding a solid that was redissolved in water and extracted with EtOAc (3 × 3 mL). The combined organic phases were dried over MgSO₄ and the solvent evaporated under reduced pressure yielding 5 (182 mg, 67% yield). The NMR data were consistent with the values reported in the literature.¹²

Preparation of 1,5-di(heptadec-1-enyl)-2,3-dimethoxybenzene 6. Hexadecyl-triphenylphosphonium bromide (1.03 g, 1.82 mmol) was dissolved in anhydrous THF (10 mL) under nitrogen atmosphere and tBuOK (352 mg, 3.14 mmol) was added portionwise. After stirring for 45 min, a solution of 5 (160 mg, 0.83 mmol) in anhydrous THF (4 mL) was added and the mixture was stirred for 2 h. The reaction was quenched with water (10 mL) and the aqueous phase was extracted with EtOAc (3 × 10 mL). The combined organic phases were dried over MgSO₄ and concentrated under vacuum, affording a residue that was purified by column chromatography on silica gel with hexane/EtOAc (6 : 1) to give a mixture of different isomers 6 (318 mg, 63% yield), where the (Z,Z)-isomer is the major component. Spectroscopic data of major isomer: ¹H NMR (250 MHz, CDCl₃) δ 6.80 (s, 1H), 6.68 (s, 1H), 6.50 (d, 1H, J = 12.5 Hz), 6.31 (d, 1H, J = 12.5 Hz), 5.69 (dt, 1H, J = 12.5, 7.5 Hz), 5.59 (dt, 1H, J = 12.5, 7.5 Hz), 3.81 (s, 3H), 3.73 (s, 3H), 2.22 (m, 4H), 1.46–1.08 (m, 52H), 0.84 (t, 6H, J = 6.4 Hz). ¹³C NMR (62.5 MHz, CDCl₃) δ 152.1, 145.5, 133.7, 133.0, 132.5, 131.4, 128.5, 123.9, 122.5, 111.6, 60.5, 55.6, 31.9, 30.1–29.4, 28.7, 22.7, 14.1. IR (ATR) ν 2916, 2849, 1571, 1466, 1326, 1142, 1081, 1008, 721.

Preparation of 1,5-diheptadecyl-2,3-dimethoxybenzene 7. A stirred solution of a mixture of the isomeric olefins 6 (300 mg, 0.49 mmol) in EtOAc (7 mL) was hydrogenated over Pd/C (30 mg) under 1 atm of H₂ for 7 h. Filtration over Celite and evaporation of the solvent yielded 7 as a yellow oil (241 mg, 80% yield). ¹H NMR (250 MHz, CDCl₃) δ 6.57 (s, 2H), 3.84 (s, 3H), 3.78 (s, 3H), 2.58 (t, 2H, J = 7.5 Hz), 2.52 (t, 2H, J = 7.5 Hz), 1.55 (m, 4H), 1.37–1.18 (m, 56H), 0.88 (t, 6H, J = 6.5 Hz). ¹³C NMR (62.5 MHz, CDCl₃) δ 152.3, 144.9, 138.4, 136.2, 121.5, 109.9, 60.6, 55.6, 35.9, 31.9, 31.6, 30.9, 29.9–29.4, 22.7, 14.1. IR (ATR) ν 2915, 2849, 1588, 1491, 1229, 1149, 1014, 720. HRMS (ESI+) calcd for [C₄₂H₇₈O₂ + Na]⁺: 637.5894, found 637.5892.

Preparation of 3,5-diheptadecylcatechol 2. Compound 7 (210 mg, 0.34 mmol) was dissolved in CH₂Cl₂ (4 mL) under nitrogen atmosphere. The mixture was cooled down to −78 °C and BBr₃ (2.1 mL, 2.05 mmol) was added dropwise. After stirring for 1 h, the reaction was allowed to warm up to 0 °C, and then the reaction was quenched with water (4 mL). The organic phase was separated, dried over MgSO₄ and concentrated under reduced pressure affording 2 (191 mg, 96% yield) as a solid. ¹H NMR (250 MHz, CDCl₃) δ 6.54 (d, 1H, J = 2 Hz), 6.50 (d, 1H, J = 2 Hz), 3.72 (broad s, 2H), 2.56 (t, 2H, J = 7.5 Hz), 2.46 (t, 2H, J = 7.5 Hz), 1.60 (m, 4H), 1.35–1.12 (m, 6H), 0.88, 2.56 (t, 6H, J = 6.3 Hz). ¹³C NMR (62.5 MHz, CDCl₃) δ 143.1, 139.6, 135.3, 129.2, 122.0, 113.0, 35.5, 32.1, 30.0, 29.9–29.5, 22.9, 14.2. IR (ATR) ν 3340, 2915, 2849, 1522, 1471, 1199, 815. HRMS (ESI+) calcd for [C₄₀H₇₄O₂ + Na]⁺: 609.5587, found 609.5592.

Preparation of 2-tert-butyl-6-methoxy-4-methylphenol 9. Commercial 2-methoxy-4-methylphenol, 8 (5.00 g, 36.2 mmol), and H₃PO₄ (11 mL) were mixed and heated at 75 °C. Then tert-butanol (5.16 mL, 54.3 mmol) was added and the mixture was heated to reflux for 4 days. The reaction was quenched with water (15 mL). The phases were separated and the aqueous phase was extracted with EtOAc (15 mL) and CH₂Cl₂ (2 × 15 mL). The combined organic layer was dried over MgSO₄ and concentrated under vacuum yielding an oil that was purified by column chromatography on silica gel with hexane/EtOAc (10 : 1) to give 9 as a slightly yellow oil (3.85 g, 55% yield).The NMR data were consistent with the values reported in the literature.¹³

Preparation of 3-tert-butyl-4-hydroxy-5-methoxybenzaldehyde 10. Compound 9 (1.98 g, 10.2 mmol) was dissolved in tBuOH (30 mL) under nitrogen atmosphere and Br₂ (1.32 mL, 25.8 mmol) was added dropwise. The mixture was stirred for 1 h and the reaction was quenched with water (40 mL). The aqueous phase was separated and extracted with EtOAc (3 × 40 mL). The combined organic layers were washed with NaHSO₃ 10% (2 × 50 mL), dried over MgSO₄ and concentrated under vacuum to give a reddish brown oil that was purified by column chromatography on silica gel with hexane/EtOAc (8 : 1), affording 10 (1.33 g, 62% yield). The NMR data were consistent with the values reported in the literature.²¹

Preparation of 3-tert-butyl-4,5-dihydroxybenzaldehyde 11. Compound 10 (2.00 g, 9.61 mmol) was dissolved in CHCl₃ (20 mL) and the solution was cooled down to 0 °C. AlCl₃ (1.79 g, 13.5 mmol) was added and then pyridine (3.4 mL) was added dropwise. The mixture was refluxed for 24 h, cooled down to 0 °C and acidified with HCl 10%. The filtration of the mixture gave a dark brown solid that was washed with little portions of ether (4 × 10 mL) affording 11 (1.59 g, 85% yield). ¹H NMR (250 MHz, acetone-d₆) δ 9.81 (s, 1H), 7.46 (d, 1H, J = 2.0 Hz,), 7.34 (d, 1H, J = 2.0 Hz,), 1.48 (s, 9H). ¹³C NMR (62.5 MHz, acetone-d₆) 192.5, 152,4, 146.8, 138.0, 130.5, 124.6, 113.4, 36.4, 30.4. IR (ATR) ν 3381, 3203, 2959, 2868, 1642, 1591, 1296, 1248, 1167, 864, 670. HRMS (ESI+) calcd for [C₁₁H₁₄O₃ − 1H]⁺: 193.0870, found 193.0865.

Preparation of 3-tert-butyl-4,5-bis(methoxymethoxy) benzaldehyde 12. To a stirred solution of 11 (1.44 g, 7.42 mmol) in CH₂Cl₂ (14 mL) at 0 °C, iPr₂EtN (7.8 mL, 44.5 mmol) and DMAP (0.14 g) were added. Then, methoxymethyl bromide (2.7 mL, 29.7 mmol) was added dropwise, keeping the temperature at 0 °C, for 1 h. Then, the mixture was allowed to reach room temperature and was heated to reflux overnight. The reaction mixture was allowed to cool down to room temperature and washed with brine (15 mL). The phases were separated and the aqueous was extracted with CHCl₃ (3 × 7 mL). The combined organic layers were then dried over MgSO₄ and concentrated under reduced pressure yielding an oil that was purified by column chromatography on silica gel with hexane/EtOAc (20 : 1) to give 12 (1.44 g, 70% yield). The NMR data were consistent with the values reported in the literature.¹⁴

Preparation of 5-(heptadec-1-enyl)-1-tert-butyl-2,3-bis(methoxymethoxy)benzene 13. Hexadecyl-triphenylphosphonium bromide (2.28 g, 4.02 mmol) was dissolved in anhydrous THF (20 mL) under nitrogen atmosphere and tBuOK (0.74 g, 6.59 mmol) was added portionwise. After stirring for 30 min, a solution of 12 (1.03 g, 3.65 mmol) in anhydrous THF (10 mL) was added and the mixture was stirred for 2 h, and then the reaction was quenched with water (20 mL). The aqueous phase was extracted with EtOAc (3 × 15 mL). The combined organic phases were dried over MgSO₄ and concentrated under vacuum, affording a residue that was purified by column chromatography on silica gel with hexane/EtOAc (8 : 1) to give a mixture of (Z)- and (E)-13 (10 : 1) (1.05 g, 58% yield). The NMR spectroscopic data are referred to (Z)-13. ¹H NMR (250 MHz, CDCl₃) δ 7.04 (d, 1H, J = 2.0 Hz), 6.97 (d, 1H, J = 2.0 Hz), 6.35 (d, 1H, J = 11.6 Hz), 5.63 (dt, 1H, J = 11.6, 7.3 Hz), 5.24 (s, 2H), 5.19 (s, 2H), 3.68 (s, 3H), 3.53 (s, 3H), 2.35 (m, 2H), 1.46 (s, 9H), 1.43–1.21 (m, 26H), 0.91 (t, 3H, J = 6.8 Hz,). ¹³C NMR (62.5 MHz, CDCl₃) δ 149.7, 144.5, 142.8, 132.7, 132.4, 128.6, 121.3, 115.1, 98.9, 95.5, 57.5, 56.2, 35.1, 31.9, 30.5, 30.1, 29.7–29.4, 28.9, 22.7, 14.1. IR (ATR) ν 2921, 2852, 1571, 1466, 1391, 1155, 1078, 1037, 1015, 961, 877. HRMS (ESI+) calcd for [C₃₁H₅₄O₄ + Na]⁺: 513.3914, found 513.3920.

Preparation of 1-tert-butyl-5-heptadecyl-2,3-bis(methoxymethoxy)benzene 14. A stirred solution of a mixture of the isomeric olefins 13 (0.92 g, 1.88 mmol) in EtOAc (15 mL) was hydrogenated over Pd/C (92 mg) under 1 atm of H₂ for 24 h. Filtration over Celite and evaporation of the solvent yielded 14 as an oil (0.91 g, 98% yield). ¹H NMR (250 MHz, CDCl₃) δ 6.88 (d, 1H, J = 2.0 Hz,), 6.83 (d, 1H, J = 2.0 Hz,), 5.21 (s, 2H), 5.19 (s, 2H), 3.67 (s, 3H), 3.53 (s, 3H), 2.56 (t, 2H, J = 7.8 Hz), 1.60 (m, 2H), 1.45 (s, 9H), 1.43–1.20 (m, 14H), 0.92 (t, 3H, J = 6.8 Hz,). ¹³C NMR (62.5 MHz, CDCl₃) 149.9, 143.6, 142.9, 137.8, 120.4, 114.5, 98.9, 95.3, 57.4, 56.2, 36.0, 35.0, 31.9, 31.6, 30.6, 29.7–29.3, 22.7, 14.1. IR (ATR) ν 2917, 2849, 1578, 1472, 1434, 1153, 1081, 1035, 1013, 942, 881, 728. HRMS (ESI+) calcd for [C₃₁H₅₆O₄ + Na]⁺: 515.4071, found 515.4065.

Preparation of 3-tert-butyl-5-heptadecylcatechol 3. Compound 14 (0.91 g, 1.85 mmol) was dissolved in MeOH (45 mL) and 10 drops of concentrated HCl were added. The mixture was heated to reflux overnight. Evaporation of the solvent under reduced pressure yielded a solid residue which was dissolved in ether (10 mL), and washed with a NaHCO₃ saturated solution (3 × 4 mL). The organic phase was dried over MgSO₄ and concentrated under vacuum affording 3 (652 mg, 88% yield). ¹H NMR (250 MHz, CDCl₃) δ 6.68 (d, 1H, J = 2.0 Hz), 6.56 (d, 1H, J = 2.0 Hz), 2.48 (t, 2H, J = 7.8 Hz), 1.55 (m, 2H), 1.40 (s, 9H), 1.35–1.20 (m, 14H), 0.90 (t, 3H, J = 6.6 Hz). ¹³C NMR (62.5 MHz, CDCl₃) 142.6, 140.9, 136.2, 133.9, 119.2, 112.9, 35.6, 34.5, 31.9, 31.7, 29.67–29.5, 22.6, 14.1. IR (ATR) ν 3344, 2915, 2848, 1520, 1470, 1443, 1356, 1282, 1183, 1115, 954, 749, 717. HRMS (ESI+) calcd for [C₂₇H₄₈O₂ − 1H]⁺: 403.3582, found 403.3573.

Experimental STM

All experiments were performed at room temperature using a PicoSPM (Agilent) in constant current mode. When the heating of the sample was needed, a LakeShore 331 Temperature Controller was used. Pt/Ir STM tips were prepared by mechanical cutting of the Pt/Ir wire (80 : 20, diameter 0.25 mm, Advent Research Materials, Ltd). The molecules were dissolved in each solvent with a concentration of approximately 2 mg mL⁻¹. A hot drop of the solution was applied to a freshly cleaved graphite substrate (HOPG, grade ZYB, Momentive Performance Materials Quartz GMBH) and the tip was immersed in it. The STM images were then obtained at the liquid–solid interface. It was possible to scan the underlying graphite substrate after scanning the molecules self-assembled monolayer. This enabled us to correct for the drift effects using the Scanning Probe Image Processor (SPIP) software (Image Metrology ApS).

Methodology for the computer simulations. We performed theoretical calculations of the thermodynamic free energy involved in the transfer of compound 2 from liquid solution to the graphite surface. The calculations were made employing the Molecular Dynamics (MD) technique, which is the technique of choice in liquid phase simulations (instead of much simpler total energy molecular mechanics calculations). MD is based on the numerical solution of the Newton equations of motion for all atoms of a molecular system constrained to the thermodynamic conditions (T, p, …). In our simulations, the equations of motion were solved with a 2 fs time step. All MD simulations were performed using the NAMD2 software,²⁴ version 2.7 running in parallel at the Finisterrae Supercomputer (CESGA Supercomputing Center). In our simulations, the temperature was maintained constant (at 20 °C or 80 °C) using the Langevin thermostat with a relaxation constant of 1 ps⁻¹. In simulations at constant pressure and temperature (NPT), we employed the Nosé–Hoover–Langevin piston as implemented in NAMD2 with an oscillation period of 100 fs and a decay time of 50 fs to adjust the solution pressure at 1 atm.

The model for the molecules was based on the CHARMM22/CMAP force field,²⁵ designed for biomolecular simulations. The modular structure of this force field (constructed from quantum chemical calculations of the interactions between model compounds and water) allows one to easily construct the model parameters for a given organic compound from the basic building blocks of the force field. Within this force field, intramolecular interactions contained bonding, torsion and dihedral potentials and intermolecular interactions were described by electrostatic interactions (modelled with partial charges) plus a Lennard-Jones interaction potential. The values of all partial charges and other relevant details of the force field are the same as employed in our previous work.¹⁸ We should note that in this force field, hydrogen bonds appear in a natural way as a result of the interaction between partial charges. Previous work (see for example ref. 26) has shown the validity of this kind of force field for describing the role of hydrogen bonding in self-assembly at interfaces.

The procedure employed in the simulations is the following. First, we conducted a NPT simulation of a system containing 400 nonanoic acid molecules inside a cubic box with periodic boundary conditions in all directions. The barostat was adjusted at 1 atm and the thermostat at 20 °C or 80 °C. After a 2 ns simulation run, the solution was considered equilibrated, since all magnitudes of interest (size of simulation box, pressure, temperature) were clearly stabilized. Then, we added 48 compound 2 molecules and the resulting solution was placed in contact with a large graphite slab. The graphite solid has an area of 87.81 nm² and was made by placing 6724 carbon atoms. In order to speed up our highly time-consuming MD simulations, all atoms of the graphite substrate were maintained fixed in their equilibrium positions, an approximation which is innocuous since we do not expect any reconstruction or chemical alteration of the graphite surface. Then, a second set of MD simulations at constant temperature (NVT conditions) were run to allow equilibration of the solution with the surface and adsorption/desorption events. Periodic boundary conditions were also employed in all directions, employing a simulation cell (in Å) with vectors (50.348,87.207,0), (50.348,−87.207,0) and (0,0,80). This cell follows the geometry of graphite in the x and y directions and allows for a large space above the solution in the z direction to avoid spurious image interactions. The configuration obtained after 10 ns of simulation at the two different temperatures was employed as the starting point for our MD-ABF production runs. Each ns of the NVT simulations has required around 0.2 days running in 32 Itanium Montvale processors.

In our production runs, we have computed the equilibrium free energy profiles (potentials of mean force) characterizing the thermodynamic process of transfer of compound 2 molecules from solution to the interface and vice versa (for an illustration, see snapshots in Fig. 5). These free energy profiles were computed using a new²⁷ fast and efficient Adaptive Biasing Force (ABF) methodology, implemented in version 2.7 of NAMD2. The reaction coordinate for the ABF calculation was the z coordinate of the centre of mass of the molecule being transferred. We have performed two different simulation runs, corresponding to the determination of the free energy profile at 20 °C and 80 °C with 0.2 Å resolution for the reaction coordinate. The force constant employed in the calculations was the default value of 10 kcal mol⁻¹ Å⁻² and the simulations were typically run for 10 ns. All other parameters of the simulation were the same as employed in the previous NVT simulation. Each ns of the MD-ABF simulations has required around 1.57 days running in 32 Itanium Montvale processors.

Acknowledgements

This work was partly funded by grants MAT 2009-13977-C03, CTQ2007-60613/BQU, CTQ2010-15380/BQU, CONSOLIDERNANOSELECT-CSD2007-00041 and FIS2009-13370-C02-02. J.S.-P. thanks the Generalitat de Catalunya for a FI predoctoral Grant and the Institut Català de Nanotecnologia for their support. We also acknowledge the CESGA Supercomputing Center for computational time at the Finisterrae Supercomputer and technical assistance.

Notes and references

1. H. Lee, N. F. Scherer and P. B. Messersmith, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12999–13003.
2. (a) Y. Kuraku, in Lacquer, ed. N. S. Brommelle and P. Smith, Getty Conservation Institute, California, USA, 1988; (b) E. J. Kidder, Ancient People and Places, Thames and Hudson, Japan, 1959.
3. J. Kumanotani, Prog. Org. Coat., 1999, 26, 163–195.
4. R. Lu, Y. Kamiya and T. Miyakoshi, Talanta, 2006, 70, 370–376.
5. (a) Y. Lee, H. J. Cheng, S. Yeo, C.-H. Ahn, H. Lee, P. B. Messersmith and T. G. Park, Soft Matter, 2010, 6, 977–983; (b) S. A. Burke1, M. Ritter-Jones, B. P. Lee and P. B. Messersmith, Biomed. Mater., 2007, 2, 203–210; (c) H. Lee, B. P. Lee and P. B. Messersmith, Nature, 2007, 448, 338–341; (d) B. P. Lee, C.-Y. Chao, F. N. Nunalee, E. Motan, K. R. Shull and P. B. Messersmith, Macromolecules, 2006, 39, 1740–1748; (e) M. Yu and T. J. Deming, Macromolecules, 1998, 3(1), 4739–4745.
6. (a) J. Xia, Y. Xu and J. Lin, Prog. Org. Coat., 2010, 6(7), 365–369; (b) H. S. Kim, J. H. Yeum, S. W. Choi, J. Y. Lee and I. W. Cheong, Prog. Org. Coat., 2009, 65, 341–347; (c) J. Xia, Y. Xu, B. Hu and J. Lin, Prog. Org. Coat., 2009, 65, 510–513; (d) H. Lee, S. M. Dellatore, W. M. Miller and P. B. Messersmith, Science, 2007, 318, 426–430.
7. (a) W. Essolaani, F. Picaud, C. Ramseyer, P. Gambardella, M. Saïd, D. Spanjaard and M.-C. Desjonquères, Surf. Sci., 2011, 605, 917–922; (b) A. Mugarza, N. Lorente, P. Ordejón, C. Krull, S. Stepanow, M.-L. Bocquet, J. Fraxedas, G. Ceballos and P. Gambardella, Phys. Rev. Lett., 2010, 105, 115702; (c) U. Schlickum, F. Klappenberger, R. Decker, G. Zoppellaro, S. Klyatskaya, M. Ruben, K. Kern, H. Brune and J. V. Barth, J. Phys. Chem. C, 2010, 114, 15602–15606; (d) T. Suzuki, T. Lutz, D. Payer, N. Lin, S. L. Tait, G. Costantini and K. Kernae, Phys. Chem. Chem. Phys., 2009, 11, 6498–6504; (e) U. Schlickum, R. Decker, F. Klappenberger, G. Zoppellaro, S. Klyatskaya, W. Auwärter, S. Neppl, K. Kern, H. Brune, M. Ruben and J. V. Barth, J. Am. Chem. Soc., 2008, 130, 11778–11782; (f) M. Ruben, D. Payer, A. Landa, A. Comisso, C. Gattinoni, N. Lin, J.-P. Collin, J.-P. Sauvage, A. de Vita and K. Kern, J. Am. Chem. Soc., 2006, 128, 15644–15651; (g) E. Barrena, E. Palacios-Lidón, C. Munuera, X. Torrelles, S. Ferrer, U. Jonas, M. Salmeron and C. Ocal, J. Am. Chem. Soc., 2004, 126, 385–395.
8. O. Marchenko, J. Cousty and L. P. Van, Langmuir, 2002, 18, 1171–1175.
9. G. Wang, S. Lei and S. De Feyter, Langmuir, 2008, 24, 2501–2508.
10. (a) C. N. Morrison, S. Ahn, J. K. Schnobrich and A. J. Matzger, Langmuir, 2011, 27, 936–942; (b) Z. Ma, Y.-Y. Wang, P. Wang, W. Huang, Y.-B. Li, S.-B. Lei, Y.-L. Yang, X.-L. Fan and C. Wang, ACS Nano, 2007, 1, 160–167; (c) M. Lackinger, S. Griessl, W. M. Heckl, M. Hietschold and M. G. W. Flynn, Langmuir, 2005, 21, 4984–4988.
11. (a) S. Ahn and A. J. Matzger, J. Am. Chem. Soc., 2010, 132, 11364–11371; (b) A. Ciesielski, G. Schaeffer, A. Petitjean, J.-M. Lehn and P. Samorì, Angew. Chem., Int. Ed., 2009, 48, 2039–2043.
12. (a) S. Lei, K. Tahara, F. C. de Schryver, M. Van der Auweraer, Y. Tobe and S. de Feyter, Angew. Chem., Int. Ed., 2008, 47, 2964–2968; (b) G. Schull, L. Douillard, C. Fiorini-Debuisschert and F. Charra, Nano Lett., 2006, 6, 1360–1363; (c) N. Katsonis, A. Marchenko and D. Fichou, J. Am. Chem. Soc., 2003, 125, 13682–13683.
13. S. Yoshimoto, K. Suto, A. Tada, N. Kobayashi and K. Itaya, J. Am. Chem. Soc., 2004, 126, 8020–8027.
14. A. Nion, P. Jiang, A. Popoff and D. Fichou, J. Am. Chem. Soc., 2007, 129, 2450–2451.
15. N. Katsonis, A. Marchenko and D. Fichou, J. Photochem. Photobiol., A, 2003, 158, 101–104.
16. (a) J.-R. Gong, L.-J. Wan, Q.-H. Yuan, C.-L. Bai, H. Jude and P. J. Stang, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 971–974; (b) Q.-H. Yuan, L.-J. Wan, H. Jude and P. J. Stang, J. Am. Chem. Soc., 2005, 127, 16279–16286; (c) U. Ziener, J.-M. Lehn, A. Mourran and M. Möller, Chem.–Eur. J., 2002, 8, 951–957.
17. (a) S.-C. Li, L.-N. Chu, X.-Q. Gong and U. Diebold, Science, 2010, 328, 882–884; (b) S.-C. Li, J.-G. Wang, P. Jacobson, X.-Q. Gong, A. Selloni and U. Diebold, J. Am. Chem. Soc., 2009, 131, 980–984; (c) M. Weinhold, S. Soubatch, R. Temirov, M. Rohlfing, B. Jastorff, F. S. Tautz and C. Doose, J. Phys. Chem. B, 2006, 110, 23756–23769; (d) G.-X. Wei, G.-B. Pan, L.-J. Wan, J.-C. Zhao and C.-L. Bai, Surf. Sci., 2002, 520, L625–L632.
18. J. Saiz-Poseu, J. Faraudo, A. Figueras, R. Alibés, F. Busqué and D. Ruiz-Molina, Chem.–Eur. J., in press.
19. H. Giesecke and J. Hocker, Liebigs Ann. Chem., 1978, 2, 345–361.
20. E. Logemann, K. Rissler, G. Schill and H. Fritz, Chem. Ber., 1981, 114, 2245–2260.
21. Q. Wang, Y. Yang, Y. Li, W. Yu and Z. J. Hou, Tetrahedron, 2006, 62, 6107–6112.
22. D. A. Shultz, S. H. Bodnar, K. E. Vostrikova and J. W. Kampf, Inorg. Chem., 2000, 39, 6091–6093.
23. J. Hénin, J. Fiorin, C. Chipot and M. L. Klein, J. Chem. Theory Comput., 2010, 6, 35–47.
24. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
25. A. D. MacKerell, Jr, M. Feig and C. L. Brooks, III, J. Comput. Chem., 2004, 25, 1400–1415.
26. C. D. Lorenz, J. Faraudo and A. Travesset, Langmuir, 2008, 24, 1654–1658.
27. J. Hénin, J. Fiorin, C. Chipot and M. L. Klein, J. Chem. Theory Comput., 2010, 6, 35–47.

---