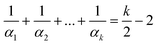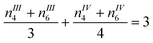On water nets L4(x)6(y)

Abstract

On the basis of the Infantes–Motherwell classification of water clusters in organic hydrates and graph theory, topologies of 2-homeohedral 2-isogonal nets with tetra- and hexagonal cycles were derived. The implication on the structure of water layers in a crystal is discussed.

---

Introduction

In the early 2000's the attention of some researchers specialized in the field of crystal engineering was attracted to crystalline hydrates. By means of statistical analysis of their structures deposited to CSD¹ it was shown² that water molecules frequently form planar (i.e. capable of being projected onto a plane surface without intersecting edges) nets. Such nets are denoted² by the symbol Lm₁(n₁)m₂(n₂)…m_k(n_k), where m_i is the size of disjoint cycles, n_i is the number of cycles, which share water molecules with the i-th one. The most widespread water layers are L4(6)5(7)²6(8) and L5(7) (Fig. 1(a) and (b)) having average size of cycles m = 5. Subsequently it was found³ that this fact is not occasional. The protic excess p of a layer defined as the number of protons not binding the vertices of a net (excess protons) is generally divisible by 1/n (Table 1), where n is the number of water molecules per formula unit M·nH₂O.

Fig. 1 Water layers in hydrates retrieved from CSD:¹ (a) L4(6)5(7)²6(8) (AMHPYR), (b) L5(7) (PINOLH01), (c) L4(6)6(8) (HEKXAW).

Table 1 The protic excess (p) of a layer, CSD¹ refcode, total protic excess of a hydrate (p_∑), hydrate composition, space group and intrinsic layer symmetry (a symbol reflects the orientation of a layer and its crystallographic symmetry elements in accord with the space group)

p	Layer	CSD refcode	p ∑	Composition	Space group	Layer symmetry group
a There are branches of water molecules on the layer. b The are water molecules isolated from the layer.
1/3	L5(7)	BIVMUO	1/3	C7H12N2O2S·3H2O	P212121	P l (YZ)21
		CEYVEH	1/3	C10H18N2·6H2O	P21/c	P l (XY)21
		PINOLH01	1/3	C6H14O2·6H2O	Pnnm	P l (XY)21212
		PIPERH	1/3	C4H10N2·6H2O	P21/n	P l (XY)21
	L4(6)6(8)	HEKXAW	1/3	C5H7N3OS·3H2O	P1̄	P l (XY)1̄
		RABCEY	1/2^a	C2HFClO2·4H2O	P1̄	P l (XY)1̄
	L4(6)5(7)^26(8)	AMHPYR	1/3	C4H8N2O2·3H2O	P21/c	P l (YZ)21/c
		PYRTHA10	1/3	C5H5N·3H2O	Pbca	P l (XZ)21/a
		XIHSEM	1/3	C8H8N4O·3H2O	P21/c	P l (YZ)21/c
		YINFAC	1/3	C6H7N·3H2O	P21/c	P l (YZ)21/c
		YINDUU	1/3	C6H15N·3H2O	P21/c	P l (YZ)21/c
		PUHPOX	1/3	C12H24N4·6H2O	P1̄	P l (XY)1̄
		HOMPRO10	3/4^b	C6H4NO2·4H2O	P21/c	P l (YZ)21/c
2/5	L4(6)5(6)7(8)	GIXDUM	2/5	C4H12N2·5H2O	C2/c	P l(YZ)2/c
3/8	L4(6)5(6)^26(8)^2	HASPIA	3/8	C10H13N5O2·4H2O	P1̄	P l (XY)1̄
1/2	L6(6)	BEWYAE	1/2	C6H8B2O4·4H2O	P1̄	P l (XZ)1̄
		HOSHIG	1/2	C8H12N2O2·4H2O	Pbcn	P l(YZ) bc21
		SAJXEG	2/3^a	C16H25NO2·3H2O	Pna21	P l(YZ) n
		IMIPID	1^b	C4H6N2O2·3H2O	P21ab	P l (XY)21ab
	L4(4)8(8)	GIKZOP	1/2	C16H30N2O2·8H2O	C2/m	C l (XY)2/m
3/5	L4(6)8(6)8(8)^2	GIXDOG	2/3^a	C7H18N2·3H2O	P1̄	P l (XY)1̄
	L4(2)4(4)4(6)16(12)	EBUNIZ	2/3^a	C16H18N2O2·6H2O	P1̄	P l (011)1̄
2/3	L4(4)12(8)	SIFFAO	2/3	C14H13NO·3H2O	P21/c	P l (YZ)21/c
	L6(4)10(8)	REGREA	3/4^a	C12H24O6·8H2O	I2/a	P l(XY)2/a
3/4	L4(4)16(8)	DUDPIB	3/4	C20H38N4O6P2·8H2O	P1	P l(YZ)1
	L8(8)12(8)	JAMNER	3/4	C22H20N2O6·8H2O	P1̄	P l (XY)1̄
4/5	L12(6)	ITEWOT	4/5	C12H10N2O2·5H2O	Pbcn	P l(XY) b2n
5/6	L14(6)	CPMIAL10	6/7^a	C21H20N6O3·7H2O	P21/c	P l(XZ) c
7/8	L18(6)	CATXIE	7/8	C17H19N3O3·4H2O	P21/c	C l (XY)2
		EHULAU	7/8	C12H24N3O6·4H2O	P63	P l(XY)3

---

Water layers in crystalline hydrates are usually formed when n ≥ 3. At the same time the amount of structural data in CSD dramatically decreases with increase of n. Therefore the most widespread layered hydrates are trihydrates.³ If a net contains merely 3- and 4-coordinated vertices (O atoms), then 0 ≤ p ≤ 1/2, specifically, in trihydrates p = 1/3 corresponding to m = 5.

The third most popular water layer with p = 1/3 is L4(6)6(8). In contrast to homeohedral tilings L5(7) of a plane, for which merely two combinatorially distinct types are known,⁴ the number of respective 2-homeohedral tilings (with two transitivity classes of faces with respect to automorphism group of a net) is apparently much greater, however, in concrete hydrates the only variant occurred to date (Fig. 1(c)). In order to understand the causes of this, one should investigate all theoretically feasible nets formed by equivalent tetra- and hexagons. This work is aimed on derivation of such nets in the most ordinary case, when a tiling is 2-isogonal, i.e. each vertex (of degree 3 or 4) generates the sole transitivity class.

Remark that even cycles tend to occupy inversion centres causing centrosymmetric layer as well as the crystal (Table 1). A few exceptions correspond to L6(6) (HOSHIG, SAJXEG, IMIPID) and layers with large 12–18-membered rings (DUDPIB, ITEWOT, CPMIAL10, CATXIE, EHULAU).

Euler’s formula for 2-periodic nets

Homeohedral 2-periodic nets made of k-gons satisfy the following modification of Euler’s formula:⁴
where α_i is the degree of i-th vertex. Let modify this formula for a 2-homeohedral tiling L4(x)6(y) (k = 10) with vertices of degrees 3 and 4:
(n = number of vertices, lower index = number of polygon sides, upper index = vertex degree, n^III₄ + n^IV₄ = 4, n^III₆ + n^IV₆ = 6). Several cases arise (Table 2). Remark the net L4(8)6(6) is impossible since tetra- and hexagon have no vertex shared in this case. Let consider the other cases.

Table 2 Vertex degrees of tilings L4(x)6(y)

n ^III4	n ^IV4	n ^III6	n ^IV6	L4(x)6(y)
4	0	2	4	L4(4)6(10)
3	1	3	3	L4(5)6(9)
2	2	4	2	L4(6)6(8)
1	3	5	1	L4(7)6(7)
0	4	6	0	L4(8)6(6)

---

2-Isogonal nets L4(x)6(y)

L4(4)6(10) . There is the only fashion of arranging 3-coordinated vertices in a hexagon, which fits the latter's adjacency to a tetragon (Scheme 1). However, in this case the tetragon gets imperatively surrounded by four hexagons, at that each hexagons is adjoined to the sole tetragon contradicting their integral ratio 1 : 1. Therefore, no L4(4)6(10) exists.

Scheme 1 Requisite environment of monohedron 4(4). Numbers denote vertex degrees.

L4(5)6(9) . There are three fashions of arranging 3- and 4-coordinated vertices in a hexagon (Scheme 2). In case (a) a priori there are five distinct 3-coordinated vertices, which thus can not be retracted into one node simultaneously for a 2-isogonal net since this implies the only transitivity class for 3-coordinated vertices. In case (b) there are four distinct 3-coordinated vertices. Prima facie a 2-isogonal net is feasible in case (c) (three types of 3-coordinated vertices). However, retracting three vertices into a node, one reveals a contradiction: one of 4-coordinated vertices of hexagon and a 3-coordinated vertex of tetragon are to coincide.

Scheme 2 Monohedra 4(5) and 6(9).

L4(6)6(8) . Since there are three ways of arrangement of 4-coordinated vertices in a hexagon and four ways – in a tetragon, one should consider six cases. However, cases with metha- arrangement of 4-coordinated vertices in a hexagon are eliminated due to reasons discussed above (2-isogonal tiling is impossible here). Vicinal arramgement of 4-coordinated vertices in tetragon combined with para- arrangement in hexagon generate a contradictory domain, which implies adjacency to a polygon with three 3-coordinated vertices located one after another (Scheme 3(a)).

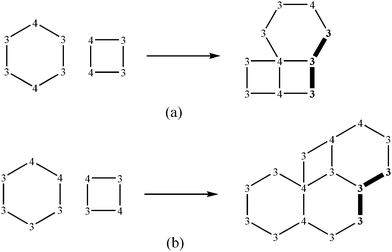Scheme 3 Contradictory environments of 4(6) and 6(8).

From ortho-arrangement of 4-coordinated vertices in a hexagon the tape follows, its margin being formed by 4-coordinated vertices, and interior—by 3-coordinated (Scheme 4(a)). Such tapes can be imposed in two ways generating two layers. At para- arrangement of 4-coordinated vertices in both polygons a tape from hexagons is made, which tetragons univocally adjoin to. Such tapes can be imposed in the only fashion (Scheme 4(b)). In final case (Scheme 3(b)) one finds the same contradiction as for (a).

Scheme 4 Requisite generation of L4(6)6(8).

L4(7)6(7) . Hexagons have to be aggregated by 3-coordinated vertices forming the corresponding tape (Scheme 5) and resulting in the only net.

Scheme 5 Requisite generation of L4(7)6(7).

Conclusion

There are four 2-homeohedral 2-isogonal tilings of a plane surface formed by tetra- and hexagonal tiles (m̄ = 5). Why are not all of these variants realized in crystalline hydrates? The answer can prove to be the following. Since water cycles tend to be localized in inversion centers of a crystal, they are to have even number of adjacent cycles that fits L4(6)6(8), the latter existing of the only type, as shown above.

Remark there can exist (and do exist⁵) 3-isogonal nets L4(5)6(9) and L4(6)6(8). For exhaustive derivation one may utilize the method discussed in current work (instead of “truncating” and “splitting” 1-isohedral tilings of a plane which are less comprehensive). On the other hand, 2-isogonal nets look the most feasible in crystals since water net, in general, tends to be produced at least number of non-equal intermolecular contacts⁶H₂O⋯OH₂.

References

1. F. H. Allen and W. D. S. Motherwell, Acta Cryst., 2002, B 58, 407.
2. L. Infantes and S. Motherwell, CrystEngComm, 2002, 4(75), 454.
3. A. Banaru and Yu. L. Slovokhotov, CrystEngComm, 2010, 12, 1054,  10.1039/b918793f.
4. B. N. Delone, Izv. Akad. Nauk SSSR Ser. Mat., 1959, 23, 365.
5. B. Grünbaum, H.-D. Löckenhoff, G. C. Shepard and Á. H. Temesvári, Geom. Dedicata, 1985, 19, 109.
6. A. M. Banaru, Moscow University Chemistry Bulletin, 2009, 64, 80.

---