Non-linear response of dipolar colloidal gels to external fields

Abstract

Dipolar colloids can be made to gel by forming a reversible but persistent network of chain-like aggregates at very low volume fractions. Using the model of charged soft dumbbells in molecular dynamics simulations, we find that, under the effect of an external electric field, this gel displays a highly non-linear dielectrical susceptibility. We show that the latter is caused by a switch from a network to a structure of bundling chains when the field is strong enough. Such dramatic structural transformation upon applying external fields could allow to control the mechanical and dielectric response of these complex fluids, pointing to new applications of dipolar colloids as smart materials.

---

I. Introduction

Suspensions of dipolar colloidal particles show extremely interesting potentialities as field-responsive soft matter systems,^1–4 thanks to the non-trivial interplay of the external fields with the complex micro-structures induced by dipolar interactions. In fact, the anisotropy of dipolar interactions favours chain-formation in dilute suspensions. The corresponding, early theoretical predictions^5,6 have been experimentally confirmed recently⁷ with magnetic colloidal particles. Besides chain-like structures, body-centered tetragonal ordering has been observed in recent experiments and reproduced in simulations of strongly interacting dipolar hard and soft spheres in the dilute regime.^2,8 In addition, hexagonal columnar ordering has been observed in certain ferrofluids^9,10 which might be due to the presence of depletion attraction.¹¹ Therefore, the structure of dilute, dipolar colloids is in general more complex than a gas of chain-like aggregates.¹² Computer simulations of colloids with extended dipoles have shown that a percolating network of cross-linked chains appears at low temperatures.^13–15 The formation of such a reversible, physical gel has been discussed within the theory of entropic phase separation.^16,17 Experimental realizations¹⁸ and possible applications¹⁹ of these fascinating systems are currently being explored.

A persistent network of cross-linked chains would also explain the occurrence of a yield stress observed in ferrofluids.²⁰ Such a network is reminiscent of colloidal gels which are characterized by long-lived physical bonds between particles,^21,22 forming a sample-spanning network that is able to sustain weak stresses even at low volume fractions.²³ In colloidal gels, particles are typically bonded by short-range attractive potentials, that lead to a low coordination number of each particle.^24,25 The long-range, anisotropic interactions in dipolar colloids are instead not obviously related to those potentials, at first glance.

Starting from the model system of charged soft dumbbells introduced in ref. 13,14 we here analyze the properties of the network structure in different state points and investigate the response of the system to an external electric field. We find that at relatively high temperatures the system behaves like a gas of chain-like structures and its dielectric susceptibility increases smoothly with the intensity of the applied external field. When the gel network is formed, instead, the system displays a highly non-linear response to the applied field. By analyzing the structure and dynamics on different length scales, we show that an external field induces switching of the system from the network back to chain-structure, characterized by strong bundling. Interestingly the onset of the non-linear response due to the formation of the gel is also characterized by a significant hysteresis, upon decreasing the field intensity. Our structural analysis shows that this is associated to a field-driven irreversible change of the micro-structure.

The paper is organized as follows. In Sect. II we describe the model system and its numerical simulation on which the subsequent analysis is based. We first present the static and dynamic properties of the model in absence of the electric field in Sect. III. In the presence of an applied field, the changes in structure and dynamics are described in Sect. IV. Finally, Sect. V contains conclusions and possible developments of this work.

II. Model description

The system introduced in ref. 13 consists of N interacting, charged soft dumbbells, where each dumbbell carries two opposite point charges ±q at a fixed distance d, forming a finite dipole p = qd. Due to the charges, particles i and j interact via (unscreened) Coulomb potential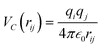 , where r_ij denotes the distance between the particles and ε₀ is the permittivity of vacuum. In addition, particles experience a short range repulsion V_s(r) which prevents permanent aggregation. The particular form of this repulsion is chosen as a soft sphere potential V_s(r) = ε(σ/r)¹², which for computational convenience is cut-off at a distance r_c = 3.5σ. For dipole separation d smaller than the particle diameter σ, the dumbbells are therefore modeled as two interpenetrating soft spheres. Whereas the far-field of the present model is identical to that of a point dipole, deviations due to higher multipoles are noticeable at short distances. We note that the effective finite dipole p modeled here can also be interpreted as a magnetic dipole. The importance of extended dipoles for explaining structure formation in magnetic nanoparticles has been pointed out recently.²⁶

We study three-dimensional systems of N = 1000 dumbbells at very low number densities ρ = N/V, ρσ³ = 0.047, 0.07, and 0.095. Equilibrated configurations are carefully prepared by constrained molecular dynamics simulations in order to keep the dipole separation d fixed. Starting from random initial conditions, the systems are slowly cooled via a Nosé–Hoover thermostat with a linearly decreasing temperature protocol. Coulomb interactions were calculated by the fast PPPM (particle–particle particle-mesh) method and the simulations were done using the molecular dynamics package LAMMPS.²⁷

We introduce the reference length σ and energy E_ref = p²/[4πε₀σ³] in order to define dimensionless quantities, r^*≡r/σ, d^*≡d/σ, T^* = k_BT/E_ref, V^*_C≡V_C/E_ref = (q_iq_j/q²)d^*−2r^*−1, V^*_s≡V_s/E_ref = ε^*r^*−12. The reference time scale is t_ref = (mσ²/E_ref)^1/2. Same as in,¹³ we choose ε^* = 0.0208 and d^* = 0.217. The volume of one dumbbell composed of two spheres with diameter σ separated by a distance d (d ≤ σ) is given by 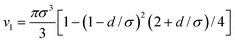. For d = 0, both spheres fully overlap and v₁(d = 0) = πσ³/6, while the two spheres are completely separated at d = σ, v₁(d = σ) = 2v₁(d = 0). Therefore, we estimate the volume fraction corresponding to the density ρ as ϕ = ρv₁. For the values chosen here we find ϕ≈0.0328, 0.0484 and 0.065. We believe that this definition of the volume fraction is closer to experimental values than the definition used in ref. 13, where v₁ is replaced by πσ³/6. In the following, all symbols refer to dimensionless quantities, if not stated explicitly otherwise. For simplicity of notation, we also omit the asterisk.

III. Structure and dynamics in the absence of an external field

A. Structure

In the absence of an external field, the structuring of the system upon lowering the temperature is signalled by the sharp increase of the first and second neighbor peaks in the pair correlation function g(r). For ϕ = 0.065, our findings are fully consistent with the earlier results of ref. 13 at a very close state point. Information on the large scale structure are more easily extracted from the static structure factor defined by . The plot in the main frame of Fig. 1 shows S(q) for ϕ = 0.0484. Upon decreasing temperature, a peak of S(q) at q ≈ 2π/σ is growing, in agreement with the growing first-neighbour peak in g(r).^13,28 More interestingly, large scale spatial correlations, of intensity larger than at the first neighbour peak, appear at low q, indicating the formation of large scale structures in the system. The inset of Fig. 1 shows that, at low q, S(q)follows a 1/q dependence, i.e. the large scale structure is dominated by chain-like aggregates.^29,30 Moreover, at the lowest accessible wave-vectors we note a stronger dependence on the volume fraction ϕ, suggesting the presence of more complicated structures on these length scales.¹⁴ In fact, this kind of behavior closely resembles the one typically found in colloidal gels formed from attractive colloidal suspensions.²²

Fig. 1 Main frame: Static structure factor for volume fraction ϕ = 0.0484 at different temperatures, from T = 0.6 to T = 0.04. The dashed line indicate the dependence 1/q. Inset: S(q)atT = 0.1 for different concentrations.

B. Cluster size distribution

From direct analysis of particle positions, we evaluate the cluster size distribution (not shown). Upon lowering the temperature, the distribution significantly widens, indicating the formation of rather large aggregates. For temperatures T ≳ 0.15, an exponential cluster size distribution is observed³¹ as predicted theoretically (see e.g.ref. 32 and references therein) and seen in recent experiments⁷ for chain-like aggregates. For temperatures T ≲ 0.15, the cluster size distribution is no longer exponential but shows a tail that decays only with a power-law, n(s)∝s^−αwith α ≈ 2.2 a typical value for random percolation.³³ This result indicates a transition from an ensemble of individual chains to a connected, at least instantaneously, percolating network, very similar to the findings of ref. 13,14 at a close state point. For ϕ ≃ 0.10, the percolation transition was located in ref. 14 from percolation probability to be around T^* ≈ 0.177, consistently with our findings. Similar observations are made also in other models for colloidal gelation,³⁴ where a short range attraction replaces the dipolar interaction. It is interesting to note that the liquid–vapour critical temperature for (point-)dipolar hard spheres has been estimated around the same temperature T^* ≈ 0.15–0.16 in a similar range of densities.³⁵ For the closely related model of charged hard dumbbells, the liquid–vapour transition was found around T^* ≈ 0.12–0.13 by extensive Monte-Carlo simulations for the present concentration range and charge separation,³⁶ whereas T^* ≈ 0.2 for ϕ = 0.1 with a truncated and discretized Coulomb potential.¹⁵ These reduced temperatures are significantly lower than what is predicted for the condensation phase transition of point dipolar particles.³⁷ Another interesting feature is that, immediately after the percolation regime a large gap in the cluster size distribution appears, indicating that rapidly the large majority of the particles aggregate into a unique structure.²²

C. Connectivity

In order to quantify the local connectivity, we study the coordination number c(n), defined as the fraction of particles with n neighbors, where two particles are neighbors if they are separated by a distance less than r_cl = 1.5σ. We verified that results change only mildly when varying r_cl in the region of this value. In Fig. 2, we plot the coordination number c(n) as a function of temperature at ϕ = 0.065: most particles have two neighbors in the regime T ≳ 0.15, indicating the predominance of chain-like structures. For lower temperatures T ≲ 0.15, the probability of having three and four neighbors (“junctions”) strongly increases, supporting therefore the network scenario. We also observe that the fraction of junctions increases with volume fraction, i.e. junction formation is favoured by steric hindrances. In the figure we have plotted the values of c(n) averaged over the simulation runs and over the different samples. We have in fact also studied their time dependence, which does not show any significant aging over the simulation time window, even at the low temperatures.

Fig. 2 The fraction of particles c(n) with n neighbors as a function of temperature at ϕ = 0.065. Symbols denote the numerical values for different n, while the two solid lines are fits of n = 1 and n = 3 to the theoretical prediction c(n)∝e^−ε_n/T from ref. 16.

The gas-liquid transition in dipolar fluids upon lowering the temperature was predicted theoretically by Tlusty and Safran¹⁶ as a phase separation between end-defects (n = 1) and junctions (n ≥ 3). Tlusty and Safran argue that “Y-defects” (three-fold junctions) are the most probable junctions. They locate the critical point as a connectivity transition where the concentration of end-defects equals that of Y-defects, ρ₁ = ρ₃. Within a mean-field model, they predict that the concentration of ends and Y's scale as ρ₁ = c(1)ρ∝ϕ^1/2e^−ε₁/T and ρ₃ = c(3)ρ∝ϕ^3/2e^−ε₃/T, respectively, where ε_n are the corresponding defect energies.¹⁶ From Fig. 2 we observe that this scenario might hold in a rather narrow temperature interval 0.1 ≲ T ≲ 0.2 around the percolation transition. For higher temperatures, the chain-like structures are not well developed, whereas at lower temperatures c(1) and c(3) seem to reach a temperature-independent value. Within the interval T ∈ [0.1,0.2], we extract the defect energies ε₁ = 0.57(5) and ε₃ = 0.14(2) from a least-square fit of the theoretical predictions to our numerical values, where the numbers in brackets give the confidence interval of the last digit. Interestingly, these values are quite close to those estimated by Tlusty and Safran from the critical point found in ref. 38, ε₁ ≈ 0.67,ε₃ ≈ 0.12, which, however, are about a factor of two larger than those estimated in ref. 31. We conclude therefore that our numerical results can at least qualitatively be interpreted within the theory of Tlusty and Safran¹⁶ in the vicinity of the connectivity transition.

D. Persistence of structure

The persistence of the chain- and network structures is important for mechanical and dielectric properties of the system. To better elucidate this point, we assign a bond variable n_ij(t) to be 1 or 0 for the pair of particles i and j if they are neighbors according to the criterion introduced above. From n_ij(t), we calculate a bond time correlation function C_b(t). The results are shown in Fig. 3 where we plot C_b(t) at ϕ = 0.065. The data indicate that the temperature regime in which a percolating structure is signaled by the cluster size distribution and by the presence of junctions corresponds to very persistent bonds: the data show that the bond lifetime in the network regime is so long that only very small structural rearrangements are possible thanks to bond breaking. We also study the persistence of the network by calculating time correlations of the network nodes: we assign a node variable n_3i(t) to a particle i to be 1 or 0 if the particle has 3 neighbors according to the criterion used for bonding; from n_3i(t), we calculate the node time correlation function C_3b(t), which is plotted as a function of time at ϕ = 0.065 for different temperatures in Fig. 4. Same as in Fig. 3, the numerical uncertainties are of the order of the symbol sizes. Although noisy due to the limited statistics, the curves clearly show a significantly slower decay with time upon lowering the temperature: the onset of percolation corresponds to significant time correlations between network nodes²² with a decay that is significantly slower than exponential, although most of them are not persistent over the whole simulation time window. Upon further lowering the temperature, also network rearrangements due to nodes become very limited within the time scale investigated. These findings suggest that the structuring just reported will have a strong effect on the dynamics of the system.

Fig. 3 Bond correlation functions C_b(t) defined in the text for volume fraction ϕ = 0.065 and different temperatures.

Fig. 4 Nodes correlation functions C_3b(t) defined in the text for volume fraction ϕ = 0.065 and different temperatures.

E. Particle dynamics

The structural changes at low temperatures just described are in fact accompanied by a slowing down of the dynamics, as also found in ref. 13,14. Whereas for high temperatures the mean square displacement of the particles (Δr⃑_i(t))² shows the well-known crossover from ballistic to diffusive behavior on a time-scale of t_ref, for temperatures below the percolation transition, a plateau in (Δr⃑_i)² develops, indicating a slowing down of particle mobility, as observed in ref. 14. Eventually, diffusive behavior will set in at much longer times, beyond the simulation time window. Such subdiffusive behavior is typical not only of dense, glass-forming systems but also of gels, where such localization process is instead induced by the formation of a persistent network.²² We have also investigated the correlations in particle motions over different length scales, by means of the intermediate scattering functionwhere the values of the wave vector q⃑ considered are the ones compatible with the periodic boundary conditions. In Fig. 5, F_s(q⃑,t)is plotted as a function of time t for the lowest accessible wave vector q = 0.29 and different temperatures at volume fraction ϕ = 0.065. Again, the numerical uncertainties are of the order of the symbol size. For high temperatures, we observe an exponential decay of F_s(q⃑,t) where the relaxation time increases as the temperature is lowered. At sufficiently low temperatures, deviations from the exponential form appear, due to the slowing down of the system's global dynamics. A similar behavior of F_s(q⃑,t) was found in ref. 13 for a larger q -value, i.e. on a more local scale. In particular, close to the onset of the percolating network, i.e. T ≃ 0.1, the data display the onset of a stretched exponential decay ∝e^{−(t/τ(q))β}, with β < 1.0 and decreasing with T. This indicates that the presence of the persistent spanning network structure significantly slows down the relaxation dynamics and introduces cooperative processes as typically observed in gelation phenomena.

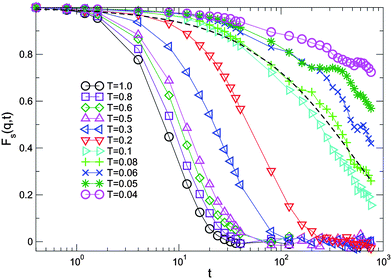Fig. 5 Incoherent scattering function at wave vector q = 2π/L as a function of time at ϕ = 0.065, for temperatures decreasing from left to right; the dashed line is a stretched exponential decay with β ≃ 0.6.

The slow, glassy dynamics just described may be associated to an aging of the structure: as a consequence correlation functions will strongly depend on the time at which the measurement has started (t_w). However, in recent simulations of colloidal gels^22,39 it has been observed that, when the structure is formed upon slow cooling, the aging does not start before the network is sufficiently persistent and, once this happens, it is sufficiently slow not to give a significant signal over the typical simulation time windows. This must be related to the fact that the characteristic time for bond-breaking is in these cases far longer the simulation time window in the temperature regime where the network is persistent enough to produce gelation. The scenario is very similar here, also in agreement with ref. 13,14: we have measured two-time correlations, upon restarting the simulations after t_w = 10⁶ and 2 × 10⁶ MD-timesteps. The data do not show any significant dependence on t_w that can be detected. The overall picture we obtain is consistent with the study of the structure and of its persistence reported above.

IV. Static and dynamics in the presence of a field

We now apply an external field E⃑ = Ee⃑_z to the system, which leads to the additional force q_iE⃑ on charge i. For clarity, we distinguish dimensionless quantities by an asterisk in the beginning of this paragraph until all quantities have been introduced. The polarization P⃑ is defined as the average total dipole moment per unit volume, , and P_z = P⃑·e⃑_z. The value P_sat = ρp is the saturation polarization when all dipoles are aligned parallel to each other. The dimensionless field strength is defined by E^* = (ε₀/P_sat)E. An important role plays the dimensionless Langevin parameter α = pE/k_BT, which is the ratio of the dipole energy in the field E over the thermal energy. The Langevin parameter can also be expressed as α = 3χ_LE^*, with χ_L = 4πρ^*/(3T^*) the dielectric susceptibility. In the following, we use only dimensionless quantities and omit the asterisk.

A. Induced polarisation

Fig. 6 shows the resulting, normalized polarization P_z/P_sat as a function of the dimensionless applied field E^* for ϕ = 0.0484. For temperatures T ≳ 0.15 we observe a field-induced polarization, with a typical (nonlinear) dielectric behavior, i.e. a linear increase for small fields and an approach towards the saturation value P_sat for large E. This behavior is well-known also in paramagnets.^40,41 The functional form of P_z(E) is rather well described by the second order perturbation approximation P_z/P_sat = L₁(α_eff), where L₁(x) = coth(x) − 1/x is the Langevin function and the modified effective mean-field acting on each dipole.⁴¹ At low temperatures, where the gel network is present, we observe a markedly different behavior. For small field strengths E, we find that the polarization is almost unchanged and increases sharply after reaching a threshold field strength E_c. The threshold value increases with decreasing temperature.

Fig. 6 Normalized polarization P_z/P_sat as a function of applied field at volume fraction ϕ = 0.0484 for different temperatures. Full and empty symbols refer to simulation results upon increasing measured and reducing the applied field, respectively. Solid lines are the corresponding predictions of the modified mean-field approximation, see main text.

We have checked the dependence of our results upon changing the protocol for applying the external field: the same induced polarization (within the errors) is found when the measurement is performed instantaneously after applying the field or upon waiting 2 × 10⁶ steps) before measurement, for all the temperatures investigated. The same values are also found upon instantaneous or slow step-wise increase of the field intensity.

This strongly non-linear response of the gel to the external electric field is an extremely interesting feature from a theoretical point of view as well as for technological applications and is here reported for the first time. Such possibility would be even more interesting if one could connect it to a significant structural change in the system: This would indicate that the mechanical or rheological properties of this gel can be significantly tuned upon applying an electric field or that one could use instead the gelation to obtain a material with very different dielectric response. In order to elucidate this point, we have investigated the changes in the structure induced by the external electric field.

B. Structure

Fig. 7 shows a snapshot of particle positions for ϕ = 0.0484, T = 0.06 in the absence of an external field and in the presence of a strong field. The difference between the two snapshots is striking. A direct analysis of anisotropic structures can be done by expanding the angular part of the pair correlation function g(r⃑) in Legendre polynomials P_k(x), , where are unit vectors. The numerical coefficients are chosen as c_k = [4π(2k + 1)]⁻¹ such that .^28,42 This expansion is valid for uniaxial symmetry around the field direction E⃑ and for symmetry reasons, only even terms appear in the sum. For isotropic liquids only g₀(r) is non-zero and corresponds to the usual pair correlation function, whereas functions g_k(r) with k ≥ 2 characterize the anisotropy of the system. At a fixed temperature, g₀ hardly changes with increasing E. For low fields we observe only mildly anisotropic structures, but upon increasing E (E ≥ 0.7), a drastic increase of g_k with k ≥ 2 is observed. Fig. 8 shows g_k(r) with k = 0,6 for ϕ = 0.0484 at T = 0.06 for E = 0.0 and E = 1.0: g₀ has a relatively small change with increasing E, whereas g₆ changes significantly. At these low temperatures, pronounced peaks in g_k located at multiples of the particle diameter signal the presence of oriented chains. Similar observations have been made also in other dipolar fluids.^28,42 However, we here observe that peaks in g_k with k ≥ 2 are comparable to those in g₀ and are thus much stronger than what found in ref. 28, 42. We like to mention that finite-size effects are more pronounced under strong field condition, as particle chains start to span the simulation cell for low temperatures. Unfortunately, a systematic investigation of this effect is beyond the scope of the present work.

Fig. 7 Snapshot of particle coordinates at ϕ = 0.0484, T = 0.06 without field (top) and in the presence of a strong field E = 0.75 (bottom) in the vertical direction.

Fig. 8 Pair correlation functions g_k(r) for ϕ = 0.0484, T = 0.06 without field (solid line) and in the presence of a strong external field of strength E = 1.0 (broken line).

C. Connectivity

In Fig. 9 we plot the coordination number c(n) in the gel (ϕ = 0.0484, T = 0.06) as a function of the applied field strength E. A weak field (E ≤ 0.3) favours the formation of larger clusters (chains), and this could push the percolation threshold towards higher temperatures. Nevertheless, as soon as the branching becomes relevant, it is disfavoured by the presence of the field. Therefore the net effect on the percolation threshold is very weak at the volume fraction investigated here. In the ranges of value where the response of the system is strongly non-linear, i.e. E ≈ 0.6, c(n) indicates instead a significant change in the topology of the structure: the fraction of particles with a higher connectivity (n ≥ 4) grows significantly, whereas the fraction of particles with only one or two neighbors drops consistently, i.e. the strong field breaks the gel structure.

Fig. 9 Coordination number c(n) as a function of applied field for ϕ = 0.0484, T = 0.06 in the gel regime.

The information contained in Fig. 9 and 8 together with the snapshot shown in Fig. 7, indicates that a sufficiently strong field makes the system switch from an interconnected gel network to a system of oriented, bundled chains. For higher temperatures, instead, the external field just orients individual particle chains. The bundling of the chains can be made plausible by the following argument. Two parallel, perfectly rigid particle chains of lengths ≳10 particles show a small overall attraction of ∼0.05E_ref when shifted half a diameter with respect to each other. At high temperatures, very few particle chains of this length are present and the energy well is negligible compared to the thermal energy. The situation changes however at low temperatures, where many long chains are present and the thermal energy becomes comparable to the attractive well.

We have monitored the coordination number c(n) under the action of the field as a function of time: at low temperature after an initial reduction of particle connectivity, due to the breaking of network junctions, for example, we observe an increase in particles with higher connectivity (n ≥ 3) as some of the network junctions were recreated. This finding can be explained in terms of the chains finding the optimal relative configuration which is required for the bundling to happen, as suggested by the argument above.

D. Persistence of structure

This dramatic change in the structure will of course significantly affect the dynamics of the system. In Fig. 10 we plot the bond correlation function C_b(t) at ϕ = 0.0484 and T = 0.06 as a function of time for different values of the applied field. The data clearly show that for E ≲ 0.5, the field is not strong enough to cause an appreciable modification of bonds in addition to the one being present without field, see Fig. 3. For strong fields E ≥ 0.7, however, a consistent fraction of bonds is broken as compared to the starting gel network. This rather abrupt response to the external field happens at the same field strength where the polarization and the number of highly (n > 4) coordinated particles strongly increases. C_3b(t)is plotted as a function of time in the inset of Fig.10 and displays a similar abrupt change for E ≥ 0.7 but in the opposite direction: interestingly the presence of a strong external field enhances time correlations of multiply connected particles, as effect of the bundling. Moreover, we also notice a non-monotonic dependence of C_3b(t) on time, which hints to correlations under the action of strong fields (E ≥ 0.5), that are probably caused by the dynamics of the bundled chains. In particular, due to the lateral diffusion of chains perpendicular to the field direction, particle coordination can increase (n ≥ 4) and decrease (n = 2) due to presence or absence of nearby chains.

Fig. 10 Main frame: Bond correlation function C_b(t) for ϕ = 0.0484, T = 0.06 under the effect of the field. Inset: Nodes correlation function C_3b(t).

These results overall confirm our interpretation of a complex and rather dramatic structural transition underlying the highly non-linear dielectric response. They also suggest that the non-linear dielectric response of the gel network should correspond to an abrupt transition in the viscoelastic response of the material due to the transition from the connected network to bundled chains. The latter are characterized by strongly anisotropic magnetoviscous behavior,^11,40,43 while the former behave as soft solids with a field-dependent yield stress.⁴⁴ In the network phase, we also expect field-induced hardening as recently reported for a copolymer gel.⁴⁵

E. Particle dynamics

We have also studied the effect of the field on the particle mean square displacements. At high temperature, the anisotropy in the particle motion smoothly increases with increasing field strength, similar to previous studies and theoretical expectations.⁴⁶ In Fig. 11 we show the particle mean square displacement under the action of a strong field (E = 0.75) as a function of time in the gel. The same conditions as in Fig. 10 are chosen. In particular we distinguish the different contributions along the directions parallel (ẑ) and perpendicular to the external field. For these low temperatures, we find that the mean square displacement is isotropic not only in the absence of a field (solid line) but also for field amplitudes E ≲ 0.5 (not shown). Even the values of the mean square displacements are very similar in these two cases. It is clear from the figure that a strong anisotropy is instead induced beyond a critical field strength. Particle motion slows down significantly in the presence of such a strong field, especially at intermediate times 10⁰ < t < 10² where the mean square displacement develops a plateau. The motion parallel to the field direction is hindered even more, probably due to the presence of chain-like structures. In fact, we notice that the localization time associated with the plateau in the mean square displacement in a strong field is roughly the time where C_3b(t) displays the minimum mentioned above (see Sect. IV.D). This suggest that the strong localization of the particle motion along the chains due to strong fields also affects the change toward higher or lower connectivity typical of different relative configurations of chains in the bundles. Only for very long times does the mean square displacement become isotropic again and diffusive behavior might set in at even later times, beyond the simulated time window. Similar conclusions can be drawn from the anisotropy in the intermediate scattering function F_s(q⃑,t), when orienting the wave vector q⃑ parallel and perpendicular to the field direction.

Fig. 11 Dumbbell mean square displacement under the effect of a field E = 0.75 (symbols) at ϕ = 0.0484 and T = 0.06. The solid line is the result in the absence of a field.

F. Hysteresis effects

In order to further investigate the dramatic structural transition just described, starting from the configurations at E = 1.0 we have then reduced the intensity of the field to E = 0.0, with steps of ΔE = 0.05. The system is subjected to the reduced field for 2 × 10⁶ MD steps, before the analysis starts. In Fig. 6, also the normalized polarization P/P_sat obtained upon decreasing the field is shown. In contrast to what is observed at higher temperatures where the field induced changes are totally reversible, the gel displays a strong hysteresis in the response to the external field. This feature becomes evident as soon as the system enters the gelation regime. The coordination number c(n), measured upon reducing the external field, clearly confirms that the field-induced structural transition taking place in the gel is strongly hysteretic and the original structure can be by no means recovered upon reducing the external field.

V. Conclusions

We have studied the equilibrium and field-induced structural properties of soft dumbbells, carrying a finite dipole moment. For moderate temperatures 0.2 ≲ T ≲ 0.5, where dipolar and thermal energies are comparable, the system is characterized by chain-like structures with an exponential distribution of chain lengths. An external magnetic field orients not only the particle's dipole moments but also the chain-like structures as a whole. These features are typical for many dipolar systems. For even lower temperatures instead, where the dipolar interactions are more dominant, the system undergoes a percolation transition to an interconnected network of particle chains showing a power-law distribution of cluster sizes. Below the percolation transition, almost all particles belong to the same sample-spanning network. In the network regime, we find a much longer bond life time together with a much slower relaxational dynamics compared to the chain regime. Thus, the network is rather persistent and therefore has a big influence on the system's mechanical properties. These properties are typically observed in colloidal gels.

Here we have shown that gelation dramatically, and rather irreversibly, changes the response of the material to an external electric field. In fact, since particles are strongly bound in the network, they can not easily reorient according to the field. Hence the polarizability of the gel network is initially relatively weak, as compared to the initial dipolar fluid. When the external field strength reaches a critical value, however, the particle's dipole moments orient rather abruptly along the field direction, with a strongly non linear increase of the polarization. This reorientation breaks the network structure and particles rearrange into oriented, bundled chains. Such significant structural reorganizations beyond a critical field strength allows to change the mechanics and the dielectric properties at the same time, and could offer new applications for dipolar colloidal suspensions as field-responsive, smart materials. Because of this field-induced structural transition, the gel dielectric response displays a significant hysteresis, which is stronger for the more persistent network structures. A similar ferromagnetic hysteresis is known for ferrogels, where superparamagnetic particles are incorporated into a chemical gel.^47,48 Since there is no underlying chemical gel here, the present system is much more susceptible to external fields and therefore might have an even greater potential for several applications. An experimental realisation of this model system would therefore be highly promising.

References

1. A. Goyal, C. K. Hall and O. D. Velev, Bicontinuous gels formed by self-assembly of dipolar colloid particles, Soft Matter, 2010, 6, 480–484.
2. A. Yethiraj and A. van Blaaderen, A colloidal model system with an interaction tunable from hard sphere to soft and dipolar, Nature, 2003, 421, 513–517.
3. L. Cohen-Tannoudji, E. Bertrand, J. Baudry, C. Robic, C. Goubault, M. Pellissier, A. Johner, F. Thalmann, N. K. Lee, C. M. Marques and J. Bibette, Measuring the kinetics of biomolecular recognition with magnetic colloids, Phys. Rev. Lett., 2008, 100, 108301.
4. C. Alexiou, R. Jurgons, C. Seliger, O. Brunke, H. Iro and S. Odenbach, Delivery of superparamagnetic nanoparticles for local chemotherapy after intraarterial infusion and magnetic drug targeting, Anticancer Research, 2007, 27(4A), 2019–2022.
5. P. G. de Gennes and P. A. Pincus, Pair correlations in a ferromagnetic colloid, Eur. Phys. J. B, 1970, 11, 189–198.
6. P. C. Jordan, Association phenomena in a ferromagnetic colloid, Mol. Phys., 1973, 25(4), 961–973.
7. M. Klokkenburg, R. P. A. Dullens, W. K. Kegel, B. H. Erné and A. P. Philipse, Quantitative real-space analysis of self-assembled structures of magnetic dipolar colloids, Phys. Rev. Lett., 2006, 96, 037203.
8. A.-P. Hynninen and M. Dijkstra, Phase diagram of dipolar hard and soft spheres: Manipulation of colloidal crystal structures by an external field, Phys. Rev. Lett., 2005, 94, 138303.
9. A. Wiedenmann, A. Hoell, M. Kammel and P. Boesecke, Field-induced pseudocrystalline ordering in concentrated ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 031203.
10. M. Klokkenburg, B. H. Erné, Johannes D. Meeldijk, A. Wiedenmann, A. V. Petukhov, R. P. A. Dullens and A. P. Philipse, In situ imaging of field-induced hexagonal columns in magnetite ferrofluids, Phys. Rev. Lett., 2006, 97, 185702.
11. P. Ilg, Importance of depletion interactions for structure and dynamics of ferrofluids, Eur. Phys. J. E, 2008, 26, 169–176.
12. C. Holm and J. J. Weis, The structure of ferrofluids: A status report, Curr. Opin. Colloid Interface Sci., 2005, 10, 133–140.
13. R. Blaak, M. A. Miller and J.-P. Hansen, Reversible gelation and dynamical arrest of dipolar colloids, Europhys. Lett., 2007, 78, 26002.
14. M. A. Miller, R. Blaak, C. N. Lumb and J.-P. Hansen, Dynamical arrest in low density dipolar colloidal gels, J. Chem. Phys., 2009, 130, 114507.
15. A. Goyal, C. K. Hall and O. D. Velev, Phase diagram for stimulus-responsive materials containing dipolar colloidal particles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 77, 031401.
16. T. Tlusty and S. A. Safran, Defect-induced phase separation in dipolar fluids, Science, 2000, 290, 1328–1331.
17. A. Zilman, T. Tlusty and S. A. Safran, Entropic networks in colloidal, polymeric, and amphiphilic systems, J. Phys.: Condens. Matter, 2003, 15, S57–S64.
18. E. Sanz, M. E. Leunissen, A. Fortini, A. van Blaaderen and M. Dijkstra, Gel formation in suspensions of oppositely charged colloids: Mechanism and relation to the equilibrium phase diagram, J. Phys. Chem. B, 2008, 112(35), 10861–10872.
19. M. Babincová, D. Leszczynska, P. Sourivong, P. C̆ic̆manec and P. Babinec, Superparamagnetic gel as a novel material for electromagnetically induced hyperthermia, J. Magn. Magn. Mater., 2001, 225(1–2), 109–112.
20. H. Shahnazian and S. Odenbach, Rheological investigations of ferrofluids with a shear stress controlled rheometer, J. Phys.: Condens. Matter, 2008, 20, 204137.
21. A. Fierro, E. Del Gado, A. de Candia and A. Coniglio, Dynamical heterogeneities in attractive colloids, J. Stat. Mech.: Theory Exp., 2008, L04002.
22. E. Del Gado and W. Kob, A microscopic model for colloidal gels with directional effective interactions: network induced glassy dynamics, Soft Matter, 2010, 6(7), 1547–1558.
23. H. Löwe, P. Müller and A. Zippelius, Dynamics of gelling liquids: a short survey, J. Phys.: Condens. Matter, 2005, 17, S1659–S1680.
24. A. Fortini, E. Sanz and M. Dijkstra, Crystallization and gelation in colloidal systems with short-ranged attractive interactions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78(4), 041402.
25. E. Del Gado and W. Kob, Length-scale-dependent relaxation in colloidal gels, Phys. Rev. Lett., 2007, 98, 028303.
26. D. V. Talapin, E. V. Shevchenko, C. B. Murray, A. V. Titov and P. Král, Dipole–dipole interactions in nanoparticle superlattices, Nano Lett., 2007, 7(5), 1213–1219.
27. S. J. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 URL: http://lammps.sandia.gov/index.html.
28. P. Ilg, E. Coquelle and S. Hess, Structure and rheology of ferrofluids: simulation results and kinetic models, J. Phys.: Condens. Matter, 2006, 18, S2757–S2770.
29. P. J. Camp and G. N. Patey, Structure and scattering in colloidal ferrofluids, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62(4), 5403–5408.
30. J. P. Huang, Z. W. Wang and C. Holm, Computer simulations of the structure of colloidal ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061203.
31. H. Braun and R. Hentschke, Tracking gas-liquid coexistence in fluids of charged soft dumbbells, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 041401.
32. A. Yu. Zubarev. Statistical physics of non-dilute ferrofluids. In S. Odenbach, editor, Ferrofluids. Magnetically Controllable Fluids and Their Applications, volume 594 of Lecture Notes in Physics, pages 143–161. Springer, Berlin, 2002.
33. A. Aharony and D. Stauffer. Introduction to percolation theory. Taylor and Francis, London, 1994.
34. E. Del Gado and W. Kob, Structure and relaxation dynamics of a colloidal gel, Europhys. Lett., 2005, 72(6), 1032.
35. P. I. C. Teixeira, J. M. Tavares and M. M. Telo da Gama, The effect of dipolar forces on the structure and thermodynamics of classical fluids, J. Phys.: Condens. Matter, 2000, 12, R411–R434.
36. G. Ganzenmüller and P. J. Camp, Vapor-liquid coexistence in fluids of charged hard dumbbells, J. Chem. Phys., 2007, 126, 191104.
37. L. Yu. Iskakova, G. A. Smelchakova and A. Yu. Zubarev, Condensation phase transitions in ferrofluids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011401.
38. P. J. Camp, J. C. Shelley and G. N. Patey, Isotropic fluid phases of dipolar hard spheres, Phys. Rev. Lett., 2000, 84(1), 115–118.
39. E. Del Gado, Aggregation of model gels with directional interactions, J. Phys.: Condens. Matter, 2010, 22(10), 104117.
40. P. Ilg and S. Odenbach. Ferrofluid structure and rheology. In S. Odenbach, editor, Colloidal Magnetic Fluids: Basics, Development and Applications of Ferrofluids, volume 763 of Lecture Notes in Phys. Springer, Berlin, 2008.
41. A. O. Ivanov and O. B. Kuznetsova, Magnetic properties of dense ferrofluids: an influence of interparticle correlations, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 041405.
42. S. Hess, J. B. Hayter and R. Pynn, A comparison of molecular dynamics and analytic calculations of correlations in an aligned ferrofluid, Molec. Phys., 1985, 43, 1527.
43. P. Ilg, M. Kröger and S. Hess, Magnetoviscosity of semi-dilute ferrofluids and the role of dipolar interactions: Comparison of molecular simulations and dynamical mean-field theory, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 031205.
44. B. D. Chin and H. H. Winter, Field-induced gelation, yield stress, and fragility of an electro-rheological suspension, Rheol. Acta, 2002, 41(3), 265–275.
45. H. An, S. J. Picken and E. Mendes, Enhanced hardening of soft self-assembled copolymer gels under homogeneous magnetic fields, Soft Matter, 2010, 6, 4497.
46. P. Ilg and M. Kröger, Anisotropic self-diffusion in ferrofluids studied via Brownian dynamics simulations, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 031504.
47. M. Zrínyi, Intelligent polymer gels controlled by magnetic fields, Colloid Polym. Sci., 2000, 278(2), 98–103.
48. S. Monz, A. Tschöpe and R. Birringer, Magnetic properties of isotropic and anisotropic CoFe O2-based ferrogels and their application as torsional and rotational actuators, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021404.

---