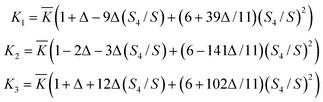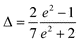Elastic constants of hard thick platelets by Monte Carlo simulation and virial expansion†
Paul A. C.
O'Brien
a,
Michael P.
Allen
a,
David L.
Cheung
b,
Matthew
Dennison‡
c and
Andrew
Masters
c
aDepartment of Physics and Centre for Scientific Computing, University of Warwick, Coventry, CV4 7AL, UK
bDepartment of Chemistry and Centre for Scientific Computing, University of Warwick, Coventry, CV4 7AL, UK
cSchool of Chemical Engineering and Analytical Science, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
First published on 21st October 2010
Abstract
In this paper we present an investigation into the calculation of the Frank elastic constants of hard plate-like particles via molecular simulation and virial expansion beyond second order. We adopt the cut-sphere model, in which each particle consists of a hard sphere from which the top and bottom have been removed by cuts parallel to, and equidistant from, the equatorial plane. Monte Carlo simulations were carried out and director fluctuations measured as a function of wavevector k, giving the elastic constants through a fit in the low-k limit. Additionally, the virial expansion coefficients of the elastic constants up to sixth order were calculated, and the validity of the theory determined by comparison with the simulation results. The simulation results are also compared with experimental measurements on colloidal suspensions of plate-like particles.
I. Introduction
The liquid crystalline nematic phase, characterized by long-range orientational order and translational disorder of the molecules, is typically found in systems of rod-like and plate-like molecules.1 It has long been recognised, going back to the theoretical work of Onsager,2 that the existence of liquid crystalline phases, phases possessing orientational and no or partial translational order, may be explained purely by anisotropy in molecular shape. Sufficiently anisotropic particles, both prolate and oblate, often exhibit the nematic phase, while in some cases (e.g. spherocylinders or cut-spheres) positionally ordered phases, such as smectic and columnar phases, are obtained. The liquid crystalline behaviour of hard, anisotropic particles has been further investigated using molecular simulations, dating back to the work of Frenkel and co-workers.3–6 As well as comprehensively mapping out the phase diagram of these systems, simulations have been used to study many of their properties including, as in this paper, the Frank elastic constants.7,8While hard core interactions are a gross simplification of low-molecular mass liquid crystals, they constitute an accurate approximation to suspensions of anisotropic colloidal particles, in much the same way as hard spheres closely approximate the behaviour of spherical colloidal particles. A number of colloidal systems exhibiting liquid crystalline behaviour, such as tobacco mosaic virus9 or colloidal gibbsite platelets10–13 have been studied. For some platelet systems, such as clays, the hard-core model is supplemented by a charge distribution, which may have dramatic effects on the thermodynamics and structure.14
In hard particle systems, both prolate and oblate, the isotropic-nematic transition is entropic in origin. Onsager's theory2 of elongated molecules amounts to a virial expansion in density ρ, truncated at the ρ2 term. (For an introductory review, see ref. 15). This provides an excellent description of the NI-transition in the limit of infinitely long, thin rods as the reduced higher virial coefficients Bn/Bn−12 tend towards zero as the elongation tends to infinity.16 For shorter rods, Onsager theory may be empirically modified17,18 to give good agreement with simulation down to very modest elongations.7,19,20 For oblate particles the situation is quite different. Even for thin, zero-thickness, disks, the higher-order virial coefficients are significant, and Onsager theory gives a poor description of the phase behaviour.3,4 Approximate resummations of the virial series17,18 fail in the zero-thickness limit, although this approach has been applied to plates of non-zero thickness.21 More sophisticated density-functional theories22–24 and interaction-site theories25 may be applied to the thermodynamics and structure of platelet suspensions; in some cases a restricted-orientation model is adopted for simplicity.26
The failure of a simple theoretical description of plate-like particle thermodynamics also extends to other properties. The Frank elastic constants are characteristic properties of nematic liquid crystals. They describe the free energy cost of (long-wavelength) deformations of the nematic director, and are the key quantities in Frank–Oseen elastic theory.27,28 Experimentally, together with a few other parameters (such as surface anchoring strength) they are sufficient to describe many of the interesting large-scale structures formed in liquid crystals. The theoretical calculation of the elastic constants provides an exacting test for theory. As for the phase behaviour, theoretical predictions for the elastic constants are reasonably accurate in the high elongation limit.16 For oblate particles, however, less is known. Recently we have measured the elastic constants of zero-thickness platelets using Monte Carlo simulations and have shown that a sufficiently high order virial expansion predicts these with surprising accuracy (of approximately 10%).8 However, the convergence of the virial theory to simulation results is not monotonic, but oscillates due to the appearance of negative virial coefficients. Both theory and simulation show that the bend elastic constant is at least an order of magnitude lower than the twist or splay constants. Good agreement was obtained with experimental measurements of splay and bend elastic constants for a colloidal suspensions of platelike particles.12,13
For oblate particles of non-zero thickness, which should be more closely related to the experimental systems, simulation results are rather limited.29 This paper presents Monte Carlo calculations of the Frank elastic constants for systems composed of hard tablet shapes (cut spheres) over their full nematic range, and compares with the previous results for thin platelets, and with theoretical estimates based on a virial expansion. The paper is arranged as follows. Section II reviews the orientational elastic theory of Frank and Oseen, and describes the fitting procedures used to extract the elastic constants from simulation. Section III summarizes the virial theory for calculating the elastic constants. Section IV gives the simulation details. The results are presented in section V and conclusions in section VI.
II. Elastic theory
For bulk systems in the nematic phase, slowly-varying spatial inhomogeneities in the director field n give rise to the following free energy penalty:28 | (1) |
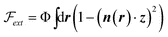 | (2) |
It is convenient to work in reciprocal space with the Fourier components ñ(k):
| ñ(k) = ∫ n(r)exp(ik·r)dr | (3) |
For small variations of n away from the 3-direction, the distortion free energy can be written in terms of the Fourier transforms ñ1(k), ñ2(k):
 | (4) |
Equipartition of energy then gives, at low k
 | (5) |
The use of eqn (5) to calculate elastic constants from molecular simulations is well established,7,30–32 and so only a brief description will be given here. For molecular orientations represented by unit vectors ui = (uix,uiy,uiz), define the Fourier-transformed second-rank order tensor
 | (6) |
![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) μν at zero k. At low k, fluctuations of
μν at zero k. At low k, fluctuations of ![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) μν(k) are predominantly due to director variations:33
μν(k) are predominantly due to director variations:33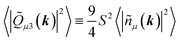 | (7) |
The elastic constants can be obtained by fitting the functions
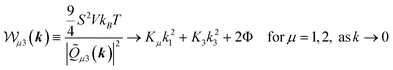 | (8) |
III. Virial theory
The Helmholtz energy, F, of a system with number density ρ = N/V, and temperature T is given by | (9) |
 | (10) |
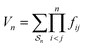 | (11) |
The summation here is over all star integrals Sn with n points, and fij is the Mayer f-bond between particles i and j. As we are dealing with hard particles, this is equal to −1 when the particles are overlapping, and 0 when they are not. φ(u) is determined as the function that minimizes F subject to the normalization condition
| ∫ φ(u)du = 1 | (12) |
At low density, the only solution is φ(u) = 1/4π (for axially symmetric particles), corresponding to the isotropic phase. At higher densities a nematic solution also appears. The isotropic-nematic coexistence densities are determined by equating the chemical potentials and pressures of the two phases. The calculation of the nematic virial coefficients is done by making use of Onsager's trial function for φ(u)2
 | (13) |
| S = P2(cosθ)〉 = 1 + 3α−2−3α−1coth α | (14) |
Using this trial function gives F as a function of α, akin to a Landau Helmholtz energy expression. α can then be determined for a given density by requiring ∂F/∂α = 0, to give the α value for which F is minimized. The virial coefficients are calculated using a modified version of the Ree–Hoover method34,35 as described elsewhere.8
The Frank elastic constants of a nematic liquid crystal are calculated in a related manner to the calculation of the equation of state. K1, K2 and K3 are given by36,37
 | (15) |
| c(1,2) = f12 + ρ∫f12f23f13φ(u3)dr3du3 + … | (16) |
The expansion takes into account the Mayer function between each pair of particles at each virial level. Again, further details are given elsewhere.8
IV. Simulation details
The simulated systems consist of a fluid of identical hard cut-spheres (interaction potential between a pair of molecules Vij = ∞ if the molecules overlap, and zero otherwise), with diameter D, varying thickness (distance between the circular end faces) H, and H/D taking the value 1/20, 1/15 or 1/10. The overlap criterion is described elsewhere.38 For this system, due to the absence of any finite interaction potentials, the temperature is irrelevant, except as a scaling factor for energies and free energies. Reduced units of energy in these simulations are obtained by taking kBT = 1 and reduced units of distance by setting the platelet diameter D = 1.The orienting field of eqn (2) is applied in the simulation as the following potential energy term:
 | (17) |
Monte Carlo simulations were performed for systems of 8000 particles with cubic periodic boundary conditions in the canonical ensemble. Equilibration runs consisted of at least 105 sweeps, and simulation averages were taken during production runs of 3 × 106 sweeps (1 sweep = 1 attempted MC move, combined translation and rotation, per particle). Displacement parameters were chosen to give a move acceptance rate in the range 30–40%.
The calculation of director fluctuation spectra was performed every 102MC sweeps, with configurations for the structure factor recorded every 103 sweeps.
The close-packed density of a system of cut-spheres is given by
 | (18) |
While the complete phase behaviour of cut-spheres at thicknesses H/D < 1/10 has not been thoroughly categorised in the published literature, the isotropic–nematic transition has been found to begin at ρD3 ≈ 3.9 and end at 4.139 for cut-spheres with H/D = 1/20 and 1/15. This corresponds to ρ/ρcp = 0.22–0.23 for H/D = 1/15 and ρ/ρcp = 0.17–0.18 for H/D = 1/20 respectively. The phase behaviour of cut-spheres with H/D = 1/10 has been well studied.40–42 According to,42 for H/D = 1/10, the isotropic-nematic transition occurs in the range ρ/ρcp ≈ 0.351–0.371, or ρD3 ≈ 4.1– 4.3; the nematic–columnar transition begins at ρ/ρcp ≈ 0.44 or ρD3 ≈ 5.1.
Our interest here is in the nematic phase, and our main concern is to ensure that all state points lie below the nematic-columnar transition region. We achieved this by examining the structure factor in the transverse, x,y-plane, S(kx,ky), and by inspecting snapshots. In the nematic phase, S(kx,ky)should possess a cylindrically symmetrical ring-shaped main peak of finite height due to liquid-like positional order. As density increases, regions exhibiting columnar order arise, breaking the cylindrical symmetry of the ring into more intense individual peaks of greater height. Well defined columnar order on a single lattice will produce peaks of height O(N).43 Representative examples for H/D = 1/15 are shown in Fig. 1.The lower density shows the expected structure for a nematic phase, while the higher density shows a roughly hexagonal pattern characteristic of columnar order. The first-order main peaks are close to k1D/2π = 1, indicating a correlation distance ≈D, which seems a reasonable first approximation for the intercolumnar distance. Corresponding configuration snapshots are given in Fig. 2. When viewed as cut-spheres, it is difficult to distinguish between the nematic and columnar phases, as while the orientational order is immediately apparent in both cases, the extent of positional order in certain regions cannot be deduced as it may appear to contain columns with molecules widely dispersed normal to the directional vector. When viewed as a system of thin rods with length H, however, the positional order at the higher density becomes noticable along a portion of the simulation box, with the remainder of the fluid in the nematic phase. This indicates that this state point is likely to have entered the nematic–columnar coexistence region. The lattice vectors for the columnar region are present in the structure factor as the locations of the first-order peaks, with higher-order peaks corresponding to shorter-range order. Of course, if the main focus of this study were the columnar phase itself, attention would have to be paid to adjusting the periodic box size and shape, to accommodate the long-range order.
 | ||
| Fig. 1 The transverse structure factor S(kx, ky) of cut-spheres, H/D = 1/15, for ρD3 = 7.5 (left) and 8.0 (right). | ||
 | ||
| Fig. 2 Instantaneous configurations of a system of hard cut-spheres, H/D = 1/15, for ρD3 = 7. (left) and ρD3 = 8 (right), colour coded according to their angle relative to the vertical axis. The molecules are plotted conventionally (upper image) and as thin rods of length H (lower). | ||
Pre-transitional columnar fluctuations affect the fitting process for the elastic constants. Structure develops along the 1-direction (normal to the director) in the region of k1D/2π = 1, with the diameter of a molecule D being a reasonable first approximation for an intercolumn spacing. Hence, in the fitting of Wα3, only data points for k1 up to some maximum value below 2π/D are included in each fitting procedure. The three different limiting values in the fitting process for 2π/k1D were 1.5, 1.65 and 1.8. With the onset of crystalline order, a correlation distance in the 3-direction of the order of H will induce structure in the Wα3. This, however, is not approached whilst still in the nematic phase, meaning that it was sufficient to set the bounds in the fitting for 2π/k3D to 0.6, 0.52 and 0.45.
V. Results
Average values of order parameter for each density are reported in Table 1–3. All of the state points appearing in the tables are in the nematic phase.| ρD 3 | S | K 1 D/kBT | K 2 D/kBT | K 3 D/kBT |
|---|---|---|---|---|
| 4.00 | 0.626(1) | 1.96(4) | 3.03(4) | 0.611(8) |
| 4.10 | 0.6713(8) | 2.53(4) | 3.80(4) | 0.706(7) |
| 4.20 | 0.7096(7) | 3.2(2) | 4.88(6) | 0.78(5) |
| 4.30 | 0.7375(5) | 3.83(4) | 5.66(8) | 0.85(1) |
| 4.40 | 0.7605(6) | 4.53(5) | 6.7(1) | 0.95(2) |
| 4.50 | 0.7812(4) | 5.2(2) | 7.70(7) | 0.97(1) |
| 4.60 | 0.7991(4) | 5.95(6) | 8.88(6) | 1.074(9) |
| 4.70 | 0.8139(3) | 6.7(1) | 9.89(7) | 1.14(1) |
| 4.80 | 0.8269(3) | 7.83(8) | 11.3(1) | 1.24(1) |
| 4.90 | 0.8379(4) | 8.7(2) | 12.60(8) | 1.33(3) |
| 5.00 | 0.8485(3) | 9.57(9) | 13.8(1) | 1.30(1) |
| 5.20 | 0.8661(3) | 11.8(2) | 16.7(2) | 1.49(3) |
| 5.50 | 0.8883(3) | 15.4(3) | 21.2(5) | 1.63(3) |
| 6.00 | 0.9145(3) | 23.1(3) | 32.5(6) | 2.22(5) |
| 6.50 | 0.9335(2) | 34.1(6) | 45.9(6) | 2.71(7) |
| 7.00 | 0.9463(2) | 46.(1) | 61.(1) | 3.11(8) |
| 7.50 | 0.9574(2) | 60.2(6) | 83.(1) | 4.03(7) |
| 8.00 | 0.9660(2) | 83.(1) | 115.(2) | 4.9(2) |
| ρD 3 | S | K 1 D/kBT | K 2 D/kBT | K 3 D/kBT |
|---|---|---|---|---|
| 4.00 | 0.668(1) | 2.49(3) | 3.82(5) | 0.748(9) |
| 4.10 | 0.7152(6) | 3.32(5) | 4.83(4) | 0.86(2) |
| 4.20 | 0.7470(8) | 4.06(9) | 5.95(8) | 0.94(2) |
| 4.30 | 0.7753(6) | 4.99(4) | 7.08(7) | 1.083(9) |
| 4.40 | 0.7962(5) | 5.81(9) | 8.5(1) | 1.17(1) |
| 4.50 | 0.8146(4) | 6.70(8) | 9.5(2) | 1.25(2) |
| 4.60 | 0.8303(3) | 7.69(7) | 11.1(1) | 1.37(3) |
| 4.70 | 0.8431(5) | 8.68(8) | 12.36(9) | 1.44(2) |
| 4.80 | 0.8562(3) | 10.32(6) | 14.4(2) | 1.60(1) |
| 4.90 | 0.8665(3) | 11.1(2) | 15.7(3) | 1.66(3) |
| 5.00 | 0.8770(3) | 12.4(2) | 17.9(4) | 1.79(3) |
| 5.20 | 0.8932(2) | 15.3(2) | 21.4(4) | 2.03(2) |
| 5.50 | 0.9121(4) | 20.3(4) | 27.5(5) | 2.41(3) |
| 6.00 | 0.9362(2) | 30.2(3) | 43.(1) | 3.29(9) |
| 6.50 | 0.9521(2) | 43.9(8) | 65.(1) | 4.75(6) |
| 7.00 | 0.9646(2) | 59.7(7) | 91.(1) | 6.7(1) |
| 7.50 | 0.9737(1) | 76.(1) | 122.(5) | 9.4(2) |
| ρD 3 | S | K 1 D/kBT | K 2 D/kBT | K 3 D/kBT |
|---|---|---|---|---|
| 4.00 | 0.717(2) | 3.60(4) | 5.35(6) | 1.21(1) |
| 4.10 | 0.775(1) | 4.86(8) | 7.2(1) | 1.53(2) |
| 4.20 | 0.8121(8) | 6.20(8) | 9.1(2) | 1.83(2) |
| 4.30 | 0.8416(6) | 7.8(1) | 12.1(2) | 2.18(6) |
| 4.40 | 0.8599(6) | 9.1(1) | 13.7(2) | 2.46(4) |
| 4.50 | 0.8784(4) | 10.9(4) | 16.7(3) | 2.85(7) |
| 4.60 | 0.8918(3) | 12.1(2) | 17.9(3) | 3.24(4) |
| 4.70 | 0.9028(3) | 14.4(4) | 21.0(5) | 3.60(4) |
| 4.80 | 0.9144(2) | 15.8(5) | 24.0(4) | 4.09(6) |
| 4.90 | 0.9224(3) | 17.7(5) | 26.6(6) | 4.86(6) |
| 5.00 | 0.9302(3) | 19.7(6) | 29.9(6) | 5.31(6) |
| 5.20 | 0.9425(2) | 23.5(5) | 37.(2) | 6.7(1) |
The elastic constants obtained from the fitting procedure are summarized in Table 1–3, with Fig. 3 showing the elastic constants as a function of order parameter.
 | ||
| Fig. 3 The splay, twist and bend elastic constants, on a logarithmic scale, as a function of order parameter S, for cut-spheres with indicated values of H/D. Splay, K1, circles (red); twist, K2, squares (green); bend, K3, diamonds (blue). In all cases the errors are smaller than the plotting symbols. The solid lines are the predictions of B6 virial theory using the simulation values of S; for H/D = 1/10, the B5 theory value of K3 is indicated by a dashed line. | ||
The qualitative features of the results are as expected for disk-like particles:44 director twist induces the largest free energy penalty, bend is the least expensive and splay lies between the others. As for the thin platelets, the bend elastic constant K3 is significantly smaller than the others, however the discrepancy with the other elastic constants becomes less extreme with increasing H/D, highlighting the reducing anisotropy of the cut-spheres. The large K1 and K2 values generally decrease, and K3 generally increases, with increasing thickness.
These results are also in reasonable agreement with experimental results for nematic tactoids in colloidal suspensions of gibbsite particles:12,13K1 = 9.0–26.0 × 10−14 N and K3 = 6.0–8.0 × 10−14 N for an order parameter in the range S ≈ 0.80–0.85. If one inserts estimates for D ≈ 237 nm and kBT ≈ 4 × 10−21 J, these correspond to reduced values of K1D/kBT ≈ 5–15 and K3D/kBT ≈ 3.5–5. The corresponding simulation results are K1D/kBT ≈ 10 for zero-thickness platelets, decreasing by about 10% as the thickness increases to H/D = 1/10, and K3D/kBT ≈ 1.3 for zero thickness, increasing to ≈2.4 for H/D = 1/10. For comparison, the estimated thickness of the gibbsite particles is H ≈ 18 nm12 making H/D = 0.076 ≈ 1/13. So the main effects of increasing the platelet thickness are to bring the value of K3 closer to the experimentally measured range, and improve the agreement of the ratio K1/K3 with experiment. In making these comparisons, of course, we must bear in mind the likely effects of polydispersity on the experimental measurements, and the likelihood that a hard repulsive potential is not a perfect representation of the experimental situation.
Finally, we note that the splay and twist elastic constants K1 and K2 are predicted to diverge on the approach to the nematic–columnar transition,45 which can be understood on geometrical grounds as the correlation length for columnar order grows. Fig. 3 is certainly consistent with this, although the relative value of K3 also increases quite quickly with increasing nematic order; larger system sizes would be required to study this divergence properly.
The more detailed structure of the (inverse) fluctuation spectra W13(k1,k3) and W23(k1,k3), defined by eqn (8), is of interest, both as a description of the behaviour on the approach to the nematic-columnar transition, and in the effect on the quality of fit which yields the elastic constants. In the ESI‡ we show these functions for all three shapes studied here, at the highest densities studied within the nematic phase (i.e. close to the columnar transition). The common feature is that the surfaces are relatively featureless in the k3 direction, but show much more structure along k1 reflecting pretransitional columnar fluctuations of periodicity λ/D≈1.0–1.1, i.e. close to the molecular diameter. W13 follows the structure over a maximum as k1 and k3 increase together and W23 describes the smoothing out of a sharply peaked profile in k1 as k3 increases. This behaviour is also illustrated in Fig. 4–6, showing various slices of the data sets. The structure for varying k1 is quite evident here. It is apparent that the lower bend elastic constant, causing only gradually increasing fluctuations, couples with a lack of structure developing parallel to the director (compared to normal fluctuations) to allow more points to be included in the low-k treatment along to n. Precursors to columnar order are increasingly visible in the Wα3 for the thicker cut-spheres, in the form of more abrupt structure around the correlation distance, as well as statistical noise for higher-k1.
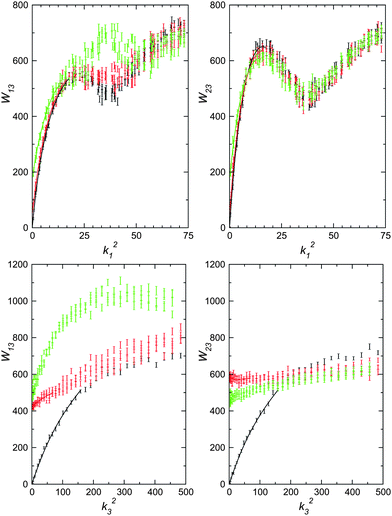 | ||
| Fig. 4 Slices through the W13 (left) and W23 (right) surfaces from simulations of cut spheres with H/D = 1/20, ρD3 = 8.0. Top row: as functions of k21, for fixed k3L/2π = 0 (black), 15 (red), 30 (green), where L is the simulation box length, showing respectively splay and twist fluctuations. Bottom row: as functions of k23 for fixed k1L/2π = 0 (black), 5 (red), 10 (green), showing bend fluctuations. The error bars give the data points with statistical error and the lines correspond to the fitting function for the entire surface in each case. | ||
 | ||
| Fig. 5 Slices through the W13 (left) and W23 (right) surfaces from simulations of cut spheres with H/D = 1/15, ρD3 = 7.5. Notation as for Fig. 4. | ||
 | ||
| Fig. 6 Slices through the W13 (left) and W23 (right) surfaces from simulations of cut spheres with H/D = 1/10, ρD3 = 5.2. Notation as for Fig. 4. | ||
Although the estimates for the elastic constants are sensitive to the range of wavevector spectrum and number of fitting parameters included, there is negligible visible effect on the low-k regions of each graph. Hence, we have plotted the fitting function as fitted up to the highest cutoff values of k chosen with the largest number of parameters used, in order to guide the eye over as much of the observed data as possible.
Finally we come to the comparison of the simulation results with theoretical predictions using the virial expansion of section III. Fig. 3 shows good agreement with the B6 theory, for all the elastic constants, for the two thinner shapes. The agreement is somewhat worse for H/D = 1/10, especially for the bend elastic constant K3, and there is a strong indication that the expansion has not converged in this particular case; a discussion of convergence follows. The curves plotted in Fig. 3 use the simulation-determined order parameter S as input to the theory; it is also possible to calculate S theoretically, making the theory completely independent of the simulations, and in the following discussion we use an 8th-order virial theory for this purpose. The comparison of theoretical and simulation order parameters is shown in Fig. 7.
 | ||
| Fig. 7 Nematic order parameter S measured in simulation (symbols) and predicted by 8th-order virial theory (lines) vs. density for three different platelet shapes. | ||
In Fig. 8 we show results for thickness H/D = 1/20. For this system, slightly more accurate results are obtained by using the simulation-determined value of the order parameter S in the calculation, rather than one derived from the theory, particularly for K1 and K2. Good convergence of the theoretical results towards the simulation values can be seen with increasing order of the virials, as was the case for zero-thickness platelets.8 Results for H/D = 1/15. are shown in Fig. 9. Here, a similar story holds, with good convergence as the order of the theory increases, although the bend elastic constant K3 is significantly underestimated. For the thickest case studied, H/D = 1/10, the theory is less accurate, as shown in Fig. 10. For K1, the B5-level theory is quite accurate, but B6 overestimates the simulation values at the higher densities. For K2, both B5- and B6-level theories are underestimates. For the much smaller bend elastic constant K3, the theory does not seem to be converging well, and the correspondence with simulation is only approximate.
 | ||
| Fig. 8 Elastic constants for platelets of thickness H/D = 1/20 (symbols with error bars) compared with predictions of virial theory (lines). For clarity we show only the B2 (red), B4 (green) and B6 (blue) predictions. Calculations using the simulation values of the order parameter are shown as solid line, while those using a theoretical value predicted by 8th-order virial theory are shown as dashed lines. | ||
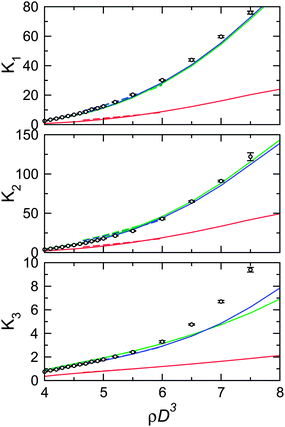 | ||
| Fig. 9 Elastic constants for platelets of thickness H/D = 1/15 (symbols with error bars) compared with predictions of virial theory (lines). Notation as for Fig. 8. | ||
 | ||
| Fig. 10 Elastic constants for platelets of thickness H/D = 1/10 (symbols with error bars) compared with predictions of virial theory (lines). We show the B2 (red), B3 (yellow), B4 (green), B5 (cyan) and B6 (blue) predictions. Otherwise, notation as for Fig. 8. | ||
In addition to the convergence, it is also important to consider the approximation made in adopting a single-parameter Onsager-like trial function of eqn (13). This is known to give good results for the thermodynamic properties of the isotropic and nematic phases,42 but the elastic constants may be more sensitive to the precise functional form. In Fig. 11 we show one measure of accuracy, namely the fourth-rank order parameter S4 = 〈P4(cosθ)〉, as a function of S. For the trial function used here, this is given by
| S4 = 1 + 45α−2 + 105α−4 − (10 + 105α−2)α−1cothα | (19) |
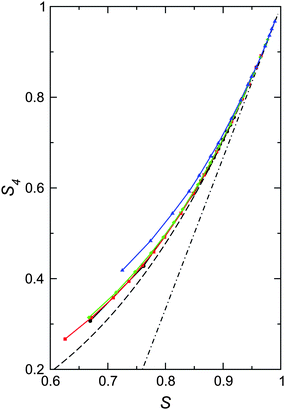 | ||
| Fig. 11 Fourth-rank order parameter S4 as a function of nematic order S for different thicknesses H/D = 0 (circles, black), 1/20 (squares, red), 1/15 (diamonds, green) and 1/10 (triangles, blue). Horizontal and vertical error bars are smaller than the symbol size. The prediction of the Onsager trial function eqn (13) is shown by a dashed line, and the asymptotic gradient in the Odijk limit46 is a dot-dashed line. | ||
It is of some interest to compare our results with the predictions of rather simple theories which assume that the liquid crystal structure may be approximated by that of a perfectly-aligned fluid, and hence by affine transformation to that of a simple liquid of spherical particles.47 The theory should really only be applied to hard ellipsoids of revolution of axial ratio e, which become hard spheres for e = 1 and infinitesimally thin platelets in the limit e → 0; for our cut sphere model there is no affine transformation to a hard-sphere fluid even in the perfectly ordered case. Nonetheless, we may hope that the theory gives comparable results, setting e ≈ H/D in our case. The specific predictions for the elastic constants are:47
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) depends on e, S, and the properties of the reference sphere fluid at the same density as the liquid crystal, and
depends on e, S, and the properties of the reference sphere fluid at the same density as the liquid crystal, anddepends only on the axial ratio, being negative for oblate particles, e < 1. Therefore, the theory predicts that elastic constant ratios such as K2/K1 and K3/K1 depend in a known way on the ratio S4/S, determined by a single parameter Δ which characterizes the molecular shape. To test this, we plot these ratios, for H/D = 1/20,1/15,1/10, in Fig. 12, together with the theoretical predictions for two values of e which should conservatively bracket our range, namely e = 0 and e = 0.2. It can be seen that, although the orders of magnitude are comparable, the agreement between theory and simulation is not especially good. Especially, the decreasing trend of K3/K1 as the ratio S4/S approaches unity is not reproduced. However, it is possible that this feature is quite sensitive to the molecular shape, particularly at high density, and it would be of interest to repeat this comparison for hard ellipsoids.
 | ||
| Fig. 12 Elastic constant ratios K2/K1 (upper) and K3/K1 (lower) as functions of the ratio of fourth-rank to second-rank order parameters S4/S for different thicknesses H/D = 1/20 (squares, red), 1/15 (diamonds, green) and 1/10 (triangles, blue). Horizontal and vertical error bars are smaller than the symbol size. The predictions of a simple affine transformation theory47 are shown for ellipsoids of axial ratio e = 0 (solid line) and e = 0.2 (dashed line). | ||
VI. Conclusions
We have computed the Frank elastic constants for hard platelets of three different thicknesses, by Monte Carlo simulation of the cut-sphere model. The results have been compared with theoretical calculations based on a virial expansion up to 6th order. Both simulation and theoretical results are qualitatively as expected, with the bend elastic constant K3 being the smallest, and all elastic constants increasing quite rapidly with increasing density and nematic order parameter S. While using values of S from simulation in the virial calculation appears to give more accurate results than a purely theoretical approach, the results using a complete self-contained virial theory are still very good, especially for the thinner shapes. For thicker platelets, results for K1 and K2 are reasonably well predicted, but there are indications of incomplete convergence in the theory, and these are particularly noticeable for K3. Increasing the thickness of the platelets improves the agreement of K3, and the ratio K1/K3, with experimental results on gibbsite particles.12,13There are two main issues associated with using the virial series to calculate elastic constants. The first is whether the virial series has converged. This can be judged by looking at how the predicted results vary with level of truncation and it would appear that although the predictions for the thin platelets have essentially converged, this is not the case for the 1/10 cut-spheres. Indeed, the rate of convergence appears to vary for each elastic constant, with B6 overestimating K1 and underestimating K2 and K3. The reason for this is not clear, although it may well be that each elastic constant requires truncation at differing levels to give good convergence. The second issue concerns the use of a one-parameter trial function for the orientational distribution function, as given in eqn (13). While this function has been shown to give good results for the thermodynamic properties of the isotropic and nematic phases,42 and appears to be quite accurate especially at high order parameter, it is not clear how sensitive the elastic constant predictions will be to this approximation. We plan to examine this, and the implications associated with truncation of the virial series, further in future work.
Unfortunately, statistical errors in the calculation of the contributions at each virial level are much more prominent in the calculation of the elastic constants than for the calculation of the equation of states, preventing the calculation of these at orders above B6. This is likely due to the presence of the φ′(u) term in eqn (15), where we are calculating the elastic constant virial coefficients. For high nematic ordering, φ(u)has extreme peaks for values of u aligned along the nematic director, and hence it is extremely difficult to integrate eqn (15) with a high degree of accuracy.
Future work will focus on the prediction of elastic constants by other means, and a more detailed examination of the approach to the nematic–columnar phase transition.
Acknowledgements
Computational resources were provided by the Centre for Scientific Computing, University of Warwick, and Manchester Computing, University of Manchester. EPSRC funded the postgraduate studentships for PAO and MD. The suggestions of the referees are gratefully acknowledged.References
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, Oxford, 1995, second, paperback edn Search PubMed.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627 CrossRef CAS.
- D. Frenkel and R. Eppenga, Phys. Rev. Lett., 1982, 49, 1089 CrossRef CAS.
- R. Eppenga and D. Frenkel, Mol. Phys., 1984, 52, 1303 CAS.
- D. Frenkel, B. M. Mulder and J. P. McTague, Phys. Rev. Lett., 1984, 52, 287 CrossRef CAS.
- D. Frenkel and B. M. Mulder, Mol. Phys., 1985, 55, 1171 CAS.
- B. Tjipto-Margo, G. T. Evans, M. P. Allen and D. Frenkel, J. Phys. Chem., 1992, 96, 3942 CrossRef CAS.
- P. A. O'Brien, M. P. Allen, D. L. Cheung, M. Dennison and A. J. Masters, Phys. Rev. E, 2008, 78, 051705 CrossRef.
- S. Fraden, in Observation, prediction and simulation of phase transitions in complex fluids, edited by M. Baus, L. F. Rull, and J.-P. Ryckaert (Kluwer Academic Publishers, Dordrecht, 1995), vol. 460 of NATO ASI Series C, pp. 113–164, proceedings of the NATO Advanced Study Institute on `Observation, prediction and simulation of phase transitions in complex fluids', Varenna, Italy, July 25–August 5, 1994 Search PubMed.
- F. M. van der Kooij, D. van der Beek and H. N. W. Lekkerkerker, J. Phys. Chem. B, 2001, 105, 1696 CrossRef CAS.
- D. van der Beek, H. Reich, P. van der Schoot, M. Dijkstra, T. Schilling, R. Vink, M. Schmidt, R. van Roij and H. N. W. Lekkerkerker, Phys. Rev. Lett., 2006, 97, 087801 CrossRef CAS.
- D. van der Beek, P. Davidson, H. H. Wensink, G. J. Vroege and H. N. W. Lekkerkerker, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031708 CrossRef CAS.
- A. A. Verhoeff, R. H. J. Otten, P. van der Schoot and H. N. W. Lekkerkerker, J. Phys. Chem. B, 2009, 113, 3704 CrossRef CAS.
- M. Dijkstra, J. P. Hansen and P. A. Madden, Phys. Rev. Lett., 1995, 75, 2236 CrossRef CAS.
- G. J. Vroege and H. N. W. Lekkerkerker, Rep. Prog. Phys., 1992, 55, 1241 CrossRef CAS.
- G. T. Evans and E. B. Smith, Mol. Phys., 1991, 74, 79 CrossRef CAS.
- J. D. Parsons, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 19, 1225 CrossRef.
- S.-D. Lee, J. Chem. Phys., 1987, 87, 4972 CrossRef CAS.
- B. Tjipto-Margo and G. T. Evans, J. Chem. Phys., 1990, 93, 4254 CrossRef CAS.
- P. J. Camp, C. P. Mason, M. P. Allen, A. A. Khare and D. A. Kofke, J. Chem. Phys., 1996, 105, 2837 CrossRef CAS.
- H. H. Wensink and H. N. W. Lekkerkerker, Mol. Phys., 2009, 107, 2111 CrossRef CAS.
- L. Harnau and S. Dietrich, in Soft Matter, edited by G. Gompper and M. Schick, Wiley-VCH, Weinheim, 2007, vol. 3, pp. 159–317, ISBN 978-3-527-31370-9 Search PubMed.
- L. Harnau, Mol. Phys., 2008, 106, 1975 CrossRef CAS.
- D. L. Cheung, L. Anton, M. P. Allen, A. J. Masters, J. Phillips and M. Schmidt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041201 CrossRef.
- D. Costa, J. P. Hansen and L. Harnau, Mol. Phys., 2005, 103, 1917 CrossRef CAS.
- M. Bier, L. Harnau and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021506 CrossRef CAS.
- C. Oseen, Trans. Faraday Soc., 1933, 29, 883 RSC.
- F. C. Frank, Discuss. Faraday Soc., 1958, 25, 19 RSC.
- J. Stelzer, M. A. Bates, L. Longa and G. R. Luckhurst, J. Chem. Phys., 1997, 107, 7483 CrossRef CAS.
- M. P. Allen and D. Frenkel, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 37, 1813 CrossRef.
- M. P. Allen and D. Frenkel, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 3641 CrossRef erratum..
- M. P. Allen, M. A. Warren, M. R. Wilson, A. Sauron and W. Smith, J. Chem. Phys., 1996, 105, 2850 CrossRef CAS.
- D. Forster, Hydrodynamic Fluctuations, Broken Symmetry and Correlation Functions, vol. 47 of Frontiers in Physics, Benjamin, Reading, 1975 Search PubMed.
- F. H. Ree and W. G. Hoover, J. Chem. Phys., 1964, 40, 939 CrossRef.
- F. H. Ree and W. G. Hoover, J. Chem. Phys., 1967, 46, 4181 CrossRef CAS.
- A. Poniewierski and J. Stecki, Mol. Phys., 1979, 38, 1931 CAS.
- A. Poniewierski and J. Stecki, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 25, 2368 CrossRef CAS.
- M. P. Allen, G. T. Evans, D. Frenkel and B. Mulder, Adv. Chem. Phys., 1993, 86, 1 CAS.
- R. P. S. Fartaria and M. B. Sweatman, Chem. Phys. Lett., 2009, 478, 150 CrossRef CAS.
- D. Frenkel, Liq. Cryst., 1989, 5, 929 CrossRef.
- J. A. C. Veerman and D. Frenkel, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 5632 CrossRef.
- P. D. Duncan, M. Dennison, A. J. Masters and M. R. Wilson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 031702 CrossRef.
- H. Azzouz, J. M. Caillol, D. Levesque and J. J. Weis, J. Chem. Phys., 1992, 96, 4551 CrossRef.
- M. Kroger and P. Ilg, J. Chem. Phys., 2007, 127, 034903 CrossRef.
- J. Swift and B. Andereck, J. Phys., Lett., 1982, 43, 437 CrossRef CAS.
- T. Odijk, Macromolecules, 1986, 19, 2313 CrossRef CAS.
- M. A. Osipov and S. Hess, Mol. Phys., 1993, 78, 1191 CrossRef CAS ISSN 0026–8976.
Footnotes |
| † Electronic supplementary information (ESI) available: Inverse fluctuation spectra. See DOI: 10.1039/c0sm00541j |
| ‡ Current address: Soft Condensed Matter, Debye Institute for Nanomaterials Science, Utrecht University, Princetonplein 5, 3584 CC Utrecht, The Netherlands |
| This journal is © The Royal Society of Chemistry 2011 |