Interactions between planar polyelectrolyte brushes: effects of stiffness and salt
Aaron
Wynveen
* and
Christos N.
Likos
*
Institute of Theoretical Physics, Heinrich-Heine-University of Düsseldorf, Universitätsstraße 1, D-40225 Düsseldorf, Germany. E-mail: a.wynveen@googlemail.com; likos@thphy.uni-duesseldorf.de
First published on 17th November 2009
Abstract
We perform molecular dynamics simulations and develop a theoretical approach based on the two-dimensional cylindrical cell model to investigate the salt-dependent interactions between two sparsely-grafted, rigid polyelectrolyte brushes. Extending our previous study, (A. Wynveen and C. N. Likos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 010801), we find that the repulsive force between the brushes arises in equal parts from the compression of osmotically-active counterions trapped within the brushes, and from the necessary distortion of the rigid polyelectrolytes as the brushes approach each other. This latter, bending-force contribution also depends on the ionic environment within the brush as ionic screening reduces the effective persistence length of the polyelectrolyte chains. Our investigations yield results that are consistent with those of experimental studies of the salt-dependent forces between DNA-grafted colloids.
I. Introduction
Polyelectrolyte (PE) brushes are solid surfaces on which macromolecular ionic chains are grafted at their ends. PE-brushes have recently garnered a great deal of attention by means of theoretical investigations, experiments, as well as simulation studies, for recent reviews, see Refs 1 and 2. Most of this attention has been paid to single brushes and takes the form of studies of the conformational transitions of a brush from the “osmotic” regime,3,4 in which the osmotic stress of trapped counterions within a brush extends the brush chains to a collapsed state with added salt.5–7 Additionally, considerable work has also been initiated to explore interactions between brushes,8–11 with applications ranging from lubrication between PE grafted surfaces to stabilization of colloidal brush dispersions.Recently, there has been keener interest in studies of sparse brushes, grafted with shorter, rigid polyelectrolyte chains, such that the distance between the grafted chains is of the order of the chain lengths: here, the chains on a single brush interdigitate and interact with one another indirectly, via the rearrangements of the counterionic clouds, whilst the chains can be additionally compressed against the colloidal surface of the opposite-lying brush. For example, Kegler et al.12 carried out experiments on the interactions between brushes sparsely grafted with double-stranded DNA, using DNA strands with lengths close to that of the intrinsic bending persistence length of the molecules. For these brushes, unlike their densely grafted counterparts, interdigitation of chains on opposite brushes may occur. In this way, chains of one brush may interact with the grafted surface of the other, providing a different distance-dependent force than that for densely grafted brushes in the osmotic regime, as analyzed theoretically in Ref. 13. In the experimental investigations,12 the dependence of the interactions between the brushes on length of the DNA chains, grafting density, and salt concentration, has been investigated as well, finding that increased salt concentrations reduce the range of the force and/or the magnitude of the repulsive force at a given brush separation.
In a previous study,14 we provided a combination of simulation and theoretical approaches to understand the force vs. distance curves of salt-free, stiff PE-brushes. To this end, we carried out simulations and developed a theory for the interactions between planar brushes sparsely grafted with rigid polyelectrolyte chains.14 We found the pressure between the brushes arose from two different, but equally important, sources. The first was the increased pressure of osmotically-active brush counterions trapped between the brushes as the brushes were brought closer together. For this contribution to the pressure, we found good agreement between the simulations and a theory, which we developed, based on an implementation of the cylindrical cell model and solving the corresponding Poisson–Boltzmann equation. The second component derived from the work required to bend the rigid polyelectrolyte chains. In Ref. 14, we employed a ground state theory of the buckling of rigid rods to describe the results of the simulations. In this work, we extend both the simulations and the theory to account for the addition of salt in the interacting brush systems, an issue that has not been hitherto addressed. As before, predictions of the theory yield good agreement with the simulation results. We find that, upon including salt, there is a reduction in the absolute pressure between the brushes, as compared to the salt-free case, due to (i) an expulsion of the salt ions between the brushes as they are pushed together and (ii) a decrease in the rigidity of the polyelectrolyte chains with the increased screening of the chains by the salt ions. Moreover, both the results of the simulations, although limited to a much smaller scale, and those of the theory, are found to be compatible with the observed salt-dependent interactions between DNA brushes in the experiments.12
The rest of the paper is organized as follows: In section II we describe the simulation and the theory and in section III we present a detailed comparison between the two. A critical discussion of the results and a comparison with experimental data are presented in section IV, and in section V we summarize and draw our conclusions.
II. Methods
A. Molecular dynamics simulation
We adopt a particle-based model for the DNA-chains and the counter- and co-ions in the problem, while the aqueous solvent is treated as a continuum; for the sparse brushes considered here, the chain–chain separations are large enough for the standard dielectric screening approach to be valid. In particular, molecular dynamics (MD) simulations were performed for flat brushes consisting of polyelectrolyte chains of N = 50 monomers (M−) of unit charge, enough monovalent counterions (C+) to neutralize the brushes, and, in some simulations, monovalent salt co-ions (S−) and counterions (S+). The short-ranged excluded volume interactions of the chain monomers, their counterions, and the salt ions, are described by shifted Lennard-Jones potentials, assuming good solvent conditions: | (1) |
The interactions of the various species with the planar wall are described by a potential similar to that of eqn (1), viz:
 | (2) |
The connectivity of chains was modeled using a bead-spring model with adjacent beads bonded with a harmonic potential
 | (3) |
The stiffness in the chains was modeled via a harmonic valence angle potential:
 | (4) |
Each flat brush was composed of a triangular grid of 42 chains, each of which was grafted at one end to a wall in the simulation cell. Grafted chains roughly covered a 104 nm area of each wall, which corresponded to a grafting density, σ, with an average nearest neighbor distance equal to an N = 50-monomer chain length, L = 170 Å. The brushes faced each other with the gridded grafting points on one brush staggered by half the lattice spacing relative to the opposing brush, a situation that evidently minimizes electrostatic interactions. The total cross-sectional area, Lx × Ly (with the brush extending normally to the wall, along the z-direction) of the simulation box was greater, by a factor of 4 or more, than the grafting area. This allowed for a fraction of the counterions to be free of the brushes. This brush-free volume of the simulation cell thus effectively acted as an ion source or sink, mimicking the brush-free regions of brush experiments. Furthermore, the total accessible volume V of the system, V = Lx × Ly × D, with  , was kept constant as the distance D between the brush walls was varied, hence guaranteeing that the average counterion and salt density in the accessible volume remained constant across simulations.
, was kept constant as the distance D between the brush walls was varied, hence guaranteeing that the average counterion and salt density in the accessible volume remained constant across simulations.
Coulombic interactions in the simulations were computed using the three dimensional version of the Ewald summation method with conducting boundary conditions. The parameters for the Ewald sum were chosen to give a relative error in the computation of the Coulombic interactions of the order of 10−6. Since the brushes constitute an effectively two-dimensional system, the size Lz of the full simulation box was chosen to be much larger (>3 ×) than D, and a correction term for this slab geometry was included25 to eliminate the effect of interactions between periodic replicants in the z-direction. Simulations were carried out within the canonical (NVT) ensemble using the Nosé–Hoover thermostat at a temperature T = 298 K. Initial configurations were chosen with the chains being fully extended when the inter-wall separation, D, was greater than their length, or bent along a cosine curve with the ends perpendicular to both surfaces when the length of the chains, L, exceeded D. The distance between adjacent monomers was initially set at their equilibrium bond length, b, and the counterions were distributed randomly within a distance of 100 Å of a chain. For those simulations containing salt, the salt ions were distributed randomly within the accessible volume of the simulation cell at the beginning of the simulations. A typical simulation consisted of >105 equilibration time steps (2 fs/step) and ∼106 production steps. Two trials were carried out, one without salt and one with monovalent salt at a concentration of ∼5 mM, with the same accessible system volume, V = 12 × 105 nm, for each.
In the simulations, the calculated force on each brush was divided between a part arising from the chain deformation and that due to the momentum transfer of the free, osmotically-active chain- and salt-ions to the brush wall. The former consisted of the force on the grafting points of the brush, as well as the force imparted by the monomers of the chains of the opposing brush, whereas the latter only included those free ions within the brush. Therefore, the total force divided by the cross-sectional area of the brush or, equivalently, the pressure, Π(D), on each brush, is simply given by the sum of these individual contributions,
| Π(D) = Πosm(D) + Πchain(D) | (5) |
B. Theory
In the case of salt-free brushes, the theoretical assumption has been made that nearly all counterions are confined within the brush to fully neutralize the brushes in the osmotic brush regime;2,3,26 this is fully supported by our simulations for sparsely grafted brushes.14 The introduction of salt to the system complicates matters. Here, the assumption of neutralization of the brush provides no information concerning the concentration of salt ions, as long as the number of salt coions is offset by the same number of salt counterions, within the brush. Furthermore, the inclusion of salt complicates studies of counterion condensation along finite, strong (having a Manning parameter ξ > 127), polyelectrolyte chains,28–32 and therefore predictions that rely on condensation arguments become problematic. A model that offers a way to deal with these issues, and can be used as an alternative means to determine the osmotic pressure between the brushes, has been proposed in our previous study.14 This model provided predictions for the osmotic pressure contribution, consistent with those of an elementary model in which the pressure was simply assumed to be proportional to the average concentration of the counterions, the total number of which remained constant as the brushes were brought together, within each brush.This theory for the osmotic pressure contribution entails mapping the sparse brush problem onto a two-dimensional cell model for infinite line charges.33,34 In Ref. 14, the assumption is made that the pressure at the cylindrical cell boundary of the polyelectrolyte chain is equivalent to the pressure at the brush walls, invoking the argument by Antypov and Holm32 for a similar system (isotropically distributed charged rods). Antypov and Holm have established that, for the finite cylindrical cell surrounding a rod, which provides the lowest free energy in the system, the average counterion density and, hence, the osmotic pressure at the lateral cell wall, is the same as the osmotic pressure at the ends of the cell. This mapping of the problem onto the 2-D cylindrical cell model not only affords simple inclusion of salt to determine the osmotic pressure between the brushes but it also provides the counterion and salt ion distributions about the brush chains, which may be compared to those found in the simulations.
Accordingly, we have extended our theoretical model presented in Ref. 14 through the inclusion of salt ions and assuming that the sum of the brush and salt coions are fully neutralized by their counterions within each individual cell, i.e., invoking local charge neutrality at the length scales set by the cylindrical cells. The theory amounts to solving the non-linear Poisson–Boltzmann equation
 | (6) |
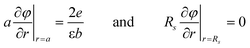 | (7) |
 . The pressure at the cell boundary and, thus, between the brushes is determined from the ion density at the cell boundary, viz:
. The pressure at the cell boundary and, thus, between the brushes is determined from the ion density at the cell boundary, viz: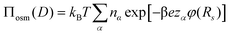 | (8) |
Additional to this osmotic pressure term arising from the counterion and salt ion interactions with the brush wall, the polyelectrolytes contribute an additional repulsive force between the brushes in the form of work that must be done to bend the chains upon increasing confinement. Being that sparse brushes of stiff chains are completely interpenetrating,10 as opposed to brushes with flexible polyelectrolytes and/or with large grafting densities, this force is realized when chains make contact with the wall of the opposing brush, i.e., when D < L.
The chain-deformation component of the total force is determined by calculating the bending energy of a buckled inextensible chain,35,36 given by
 | (9) |
 | (10) |
It is convenient to recast the problem in terms of ϕ(s), the angle subtended by the tangent vector and the line perpendicular to the brush wall, and ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a3.gif) (s), the rate of change of this angle along the contour. Eqn (9) then takes the form:
(s), the rate of change of this angle along the contour. Eqn (9) then takes the form:
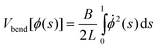 | (11) |
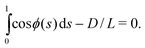 | (12) |
 | (13) |
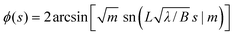 | (14) |
In contrast with the systems studied in Refs 36 and 37, in which solutions are found for a chain conformation when it is clamped at each end, such that it lies perpendicular to the surface at both ends, here we have only one local boundary condition, i.e., that the chain lies perpendicular to the wall at its grafting end, ϕ(s = 0) = 0; the other boundary condition is global and is given by eqn (12). The minimum energy solution of the Euler–Lagrange equation with these boundary conditions yields a chain conformation for which the chain's curvature, ![[greek phi with two dots above]](https://www.rsc.org/images/entities/char_e19d.gif) (s), vanishes at its free end, s = L. The mathematical form of the solutions splits into two classes, determined by the inter-wall separation, D. There exists a crossover value at D = D*, such that when D > D*, the curvature of the chain is finite throughout its contour length, becoming zero only at its free end, whereas when D < D* a whole section of the chain lies flat on the opposing wall and supports no curvature.
(s), vanishes at its free end, s = L. The mathematical form of the solutions splits into two classes, determined by the inter-wall separation, D. There exists a crossover value at D = D*, such that when D > D*, the curvature of the chain is finite throughout its contour length, becoming zero only at its free end, whereas when D < D* a whole section of the chain lies flat on the opposing wall and supports no curvature.
More precisely, in the range D* < D ≤ L, the solution takes the following form:
 | (15) |
 | ||
| Fig. 1 The equilibrium shape of a rod of length, L, for various wall separations, D, as determined by minimization of the bending energy, eqn (9), under the constraint of eqn (10) and the condition that the chain emerges perpendicularly from the wall, located at z = 0, on which it is grafted. Note the change in the conformation when the threshold value D = D* is crossed. | ||
In the range 0 < D ≤ D*, the solution crosses over to a different form, namely:
 | (16) |
According to eqn (16), the equilibrium conformation of the confined chain in the regime 0 < D ≤ D* features two segments: one that is bent and one that has the form of a straight line in contact with the opposing wall and running parallel to it. Comparing the form of the solution for the bent part with that from eqn (15), we see the shape of the chain up to the point where this section goes over to the straight one has the same form as the chain conformation when D = D*, with the contour location, s, rescaled by D/D*. The shape is also shown in Fig. 1. The critical distance at which the solution of the minimum energy contour takes a new form is given by D*/L = 2E[1/2]/K[1/2] − 1 = 0.456946…, where E[m] is the complete elliptic integral of the second kind.
Knowing the form of the chain conformation, we may calculate the bending energy as a function of D using eqn (11) and the known solutions for the contour shape:
 | (17) |
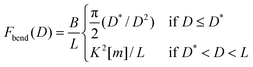 | (18) |
Eqn (18) gives the force acting on each end of a single, bent chain confined between two parallel walls. Considering now two interdigitating, stiff and sparse PE-brushes, the total force per chain is given by twice the value of eqn (18), since each wall experiences a force by the chain grafted to it and an equal one from the chain of the opposing wall. For PE-brushes with grafting density σ, the chain contribution to the pressure of eqn (5) is thus given by the expression:
| Πchain(D) = 2σFbend(D). | (19) |
As a test of this theory for the chain-bending force at finite temperatures, we performed Monte Carlo (MC) simulations on neutral chains, incorporating a bending rigidity as prescribed in section IIA. A Monte Carlo step consisted of rotating each pivot point of the chain by a finite angle and accepting those rotations for which: (i) the projection of the chain on a line perpendicular to the grafting surface was less than D, mimicking a chain compressed between two walls; and (ii) the Boltzmann weight of the change in energy of the chain upon the rotation of this pivot point was greater than a randomly generated number between zero and one (the usual Metropolis algorithm). At a temperature of 300 K, the bending force found from the MC simulations differed very little from the ground state calculation, eqn (18), for chains with the length and rigidity used in the MD simulations. Thus, temperature effects (thermal fluctuations of the chains) may be neglected upon fitting the chain-bending forces found in the MD simulations, as shown in the following section.
III. Comparison of theory with MD simulations
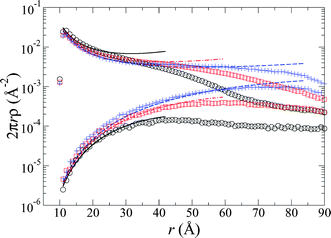
For the osmotic pressure contribution to the total force between the brushes, we solved the non-linear Poisson–Boltzmann equation, eqn (6), upon mapping the system onto a 2D cell model, where, again, the radius of the cell decreases with decreasing separation of the brushes, . Solutions for the theoretical ion distributions, determined from the electrostatic potential, are compared with simulations in which salt is excluded, so that the only free ions are the chain counterions with a concentration nC+ = 5.8 mM, and for simulations with a bulk monovalent salt concentration of nS+ = nS− = 5.0 mM. The distributions of both counterions and coions are shown in Fig. 2 and 3. A comparison with the salt-free system at one brush separation is shown in the inset of Fig. 2.
. Solutions for the theoretical ion distributions, determined from the electrostatic potential, are compared with simulations in which salt is excluded, so that the only free ions are the chain counterions with a concentration nC+ = 5.8 mM, and for simulations with a bulk monovalent salt concentration of nS+ = nS− = 5.0 mM. The distributions of both counterions and coions are shown in Fig. 2 and 3. A comparison with the salt-free system at one brush separation is shown in the inset of Fig. 2.
 | ||
Fig. 2 The distribution of the counterions' (chain monomer and salt) shortest distance to a (bent) brush chain, averaged over the entire length of the chain at brush separations of D/L = 0.44 (○), 0.88 (□), and 1.76 (+). Lines illustrate the cell model calculations at the corresponding separations where  . Inset: comparisons between systems with salt (○: simulation; . Inset: comparisons between systems with salt (○: simulation; ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) : theory) and without salt (□: simulation; : theory) and without salt (□: simulation; ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) : theory) for the counterion (top curves) and salt co-ion (lower curve) distributions. Both in the main plot and in the inset, the results for the salted brushes correspond to 5.0 mM monovalent salt concentration. : theory) for the counterion (top curves) and salt co-ion (lower curve) distributions. Both in the main plot and in the inset, the results for the salted brushes correspond to 5.0 mM monovalent salt concentration. | ||
 | ||
| Fig. 3 The same as the main plot of Fig. 2, but with the corresponding co-ion distributions (lower curves) shown as well. As in the previous plot, the points represent simulation results and the lines the predictions of the cell model theory. | ||
As illustrated in these figures, the 2D cell model formulation yields distributions that fit the simulation data rather admirably, with the same trends as seen in Ref. 14. With the addition of salt, we find that in both the simulations and the theory the number of salt counter- and co-ions decreases with decreasing distance between the brushes. Again, because the brush is neutralized (as assumed for the theory and observed in the simulations), any additional coions of the salt within the brush must be matched by the same number of salt counterions.
The pressure between the brushes, both from MD and from theory, is shown in Fig. 4. Here, the contribution solely due to the chains in the simulations, Πchain(D) is also provided for the salt-free and salt simulations, demonstrating that this concentration of salt has little effect on this contribution to the total pressure. This chain contribution follows the analytical solution, eqn (18) and (19), for the work required to bend a chain with a bending rigidity of B = 3.0 × 10−28 J m, which corresponds to a persistence length of 725 Å. The agreement between the analytical theory for chain bending and the results from the simulation is also manifest in the conformations of the chains in the MD simulations, which are similar to those predicted by the chain-bending theory (Fig. 1). The total pressure in the simulations also includes the force of the free ions (counterions and salt) on the brush walls. Again, the total pressures are shown for the cases in which there was no added salt and in which salt was included. The cell model predictions for the osmotic pressure, with no free parameters, shows the same trends as the simulation. The results shown in Fig. 5 illustrate that salt increases the pressure at large brush separations, in both the simulation and the theory, as compared to that of unsalted brushes. However, as the brushes near each other, the pressure for the salt case approaches that of the system with no added salt as salt ions leak into the bulk. Essentially, as the brushes approach each other, the salt ions are “squeezed out” of the brush. Note that the difference in the pressure between the salt-free and salt cases at the point just before the brush chains begin to interdigitate (D = 2L) is approximately that of the osmotic pressure for the salt at its bulk concentration, i.e., (ns+ + ns−)kBT = 0.025 pN nm−2.
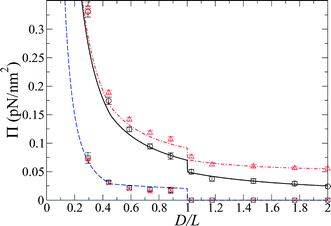 | ||
Fig. 4 The osmotic pressures from simulations and the theoretical calculations for systems with and without added salt. The squares (without salt) and crosses (with salt) show the contribution to the total pressure from bending of the chains and the theoretical prediction, eqn (18) and (19), with B = 3.0 × 10−28 J m (![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ). The total pressure as a function of brush separation for the system without salt (with salt) is given by the circles (triangles) for the simulation with the respective theoretical prediction of the cell model given by ). The total pressure as a function of brush separation for the system without salt (with salt) is given by the circles (triangles) for the simulation with the respective theoretical prediction of the cell model given by ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) ( (![[dash dot, graph caption]](https://www.rsc.org/images/entities/char_e090.gif) ). The pressures for the systems with and without salt begin to converge at small separations as the salt is “squeezed out” of the brush. ). The pressures for the systems with and without salt begin to converge at small separations as the salt is “squeezed out” of the brush. | ||
 | ||
Fig. 5 The total absolute pressures, i.e. the pressures subtracting off the value when the brushes first interdigitate, using the theoretical calculations for systems with and without added salt. The solid line shows the absolute pressure for a system without salt and the dash-dotted line the absolute pressures with 5.0 mM monovalent salt concentrations, the same used for the simulations. Here, however, the dependence of the persistence length on the ionic environment, eqn (20), is used to determine the contribution to the pressure of the chain-bending force for the salt-free (![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ) and salt (○) systems. For this set of parameters (chain length, grafting density, etc.), the same used for our simulations, the effect of the salt on the bending force is negligible. ) and salt (○) systems. For this set of parameters (chain length, grafting density, etc.), the same used for our simulations, the effect of the salt on the bending force is negligible. | ||
IV. Discussion
Although our analysis has been restricted to planar brushes, a comparison with recent experimental results for the force vs. distance curves of spherical DNA brushes 12,13 is possible. The forces were measured by Kegler et al.12,13 employing a very accurate laser-tweezer apparatus. Our results from theory and simulation are consistent with the experimental ones, although there are qualitative differences mainly arising from the different (flat) geometry we have employed, as elaborated below.In the experiments, increasing the salt concentration resulted in the forces between the brushes becoming shorter-ranged and/or the force curves being shifted downward to lower values at the same brush separation. Despite the deceiving appearance of the curves in Fig. 4, which seem to show the opposite effect, our results share this trend if proper account of the possibility of escape of the salt ions is taken into account. For the case of planar brushes, we assume that all ions are trapped in between the two planar walls, ignoring the possibility that, when being emerged in a solution, there will also be salt ions on the “outside” part of the two walls. In the case of spherical brushes, this happens automatically, since the curved surfaces do not provide a restricted region of space in which the ions can be trapped.
If we take into consideration the fact that the bulk salt ions exert an osmotic pressure on the reverse side of the brushes (not included in the simulations), providing a force opposite to that of those ions in between the brushes, the effective pressure upon including salt becomes less than that of the salt-free case. This difference in the total pressures, between the salt-free case and that with salt, including the forces due to osmotically-active ions on the other side of the brushes, grows larger at closer brush separations as salt is expelled from the brush. In other words, as the brushes approach each other, the absolute pressure of systems with salt would grow even smaller than that for systems without added salt. This can easily be seen from Fig. 4 by assuming that the osmotic pressure on the reverse side of the brush is given by the ideal gas law (dilute salt solution). This contribution, as argued at the end of the preceding section, will cancel the offset of the dark and lighter curves in Fig. 4 at D = 2L, thus bringing the pressure for the salted case to lower values than its counterpart for the salt-free case.
There is, however, an additional effect that salt will have on the pressure curves, which is related with the renormalization of the bending rigidity, B, of the chains, so that salt will also affect the Πchain(D)-contribution to the osmotic pressure. This has been hitherto neglected in our analysis of the simulation results because the different ion concentrations employed there barely change the bending rigidity of the chains with the addition of salt, as we will demonstrate shortly. Experiments, on the other hand, employ salinities well within the regimes in which such effects are important.12,13
The increased screening of the bare charge of the chains by added salts reduces the effective persistence length of the chains.23,24 Therefore the pressure contribution from the chain-bending force becomes weaker, as compared to the salt-free case, since it becomes easier to bend chains whose persistence lengths are reduced by the increase in the electrostatic screening of the bare charges along the polyelectrolyte chain by the salt ions. This reduction in the chain-bending force further enhances the difference between the pressures of the two cases. Accordingly, we consider below how the contribution of the bending force of the polyelectrolyte chains changes with the different ionic environment when salt is added.
The effect of salt on the chain rigidity can be incorporated into our model for the chain-bending force by employing a rigidity modulus or, equivalently, a chain persistence length that is modified to account for the changing ionic environment in the brush with different salt concentrations, as well as brush separation. Yet there is no single recipe for altering the persistence length of the chain according to its ionic environment. Disparate theories exist for explaining how electrostatic screening by salt ions affects the persistence length of polyelectrolyte chains, see, e.g., Refs 23, 24, 38 and 39. However, for all theories, as most experiments demonstrate (see, e.g., Refs. 40 and 41), increasing the salt concentration tends to reduce the persistence lengths. Here we employ the approaches of Odijk23 and Skolnick and Fixman,24 which have been shown to provide an adequate description for the monovalent salt concentration dependence of the DNA persistence length40,41 as a prescription for modifying the rigidity modulus of the polyelectrolyte chain to reflect changes upon adding salts and/or changes in the ion concentrations at varying brush separations. In this theory, the total persistence length lp = B/(kBT) is given by the sum of an intrinsic persistence length in the absence of electrostatic forces, l0, and an electrostatic contribution, expressed as:
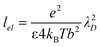 | (20) |
Using this equation for the ion concentration-dependent persistence length, with the intrinsic DNA persistence length of l0 = 500 Å38,40 for solutions of DNA in monovalent salts, and including the forces due to the osmotically-active ions on the other side of the brushes, we may determine how salt alters the absolute pressure between the brushes. In Fig. 5, we show this comparison for systems with the parameters (chain length, chain grafting density, etc.) used in our simulations. As previously stated, the system with added salt has a lower absolute pressure than for the salt case. However, the difference in the chain-bending contribution to the pressure arising from changes in the persistence length because of added salt is barely distinguishable for the parameters used in the simulation. Therefore, our assumption that the rigidity modulus (or persistence length) for the chains remains unchanged between the salt and salt-free simulations, and that it also is constant with the changing conditions in the ionic environment with brush separation, is indeed valid for the choice of parameters in the simulation.
The situation is different for the typical values involved in experimental brush systems,12,13 which lie outside the range of the simulations. There, the change in the rigidity modulus and, hence, chain-bending force, yield a much more pronounced change in the pressure between the brushes when salt is included, due to the influence of salt on a chain's persistence length. The much smaller grafting density (∼10−4 nm−2) of the experiments, leaving an extremely dilute concentration of the chains' own counterions, intimates that the brush interaction is more heavily influenced by the concentration of added salt and its influence on the chain-bending force, as shown in Fig. 6. Here, the large difference between the absolute pressures for the salt-free and salt cases is dominated by the change in the chain-bending force rather than due to the pressure induced by the concentration of osmotically-active ions within the brushes. Translating the bending force for the planar system onto that of spherical brushes by employing the Derjaguin approximation, we are able to reproduce the effects of added salt in the spherical DNA brush force experiments.12,13 We note that the Derjaguin approximation places an upper limit on the chain-bending force between spherical brushes. For spherical brushes, where the chains extend radially from the surface of these brushes and impinge on the curved surface of the opposite brush at an angle offset from the normal, the distortion of the chains, at the same surface–surface distance, is necessarily smaller than that for flat brushes, where the chains initially meet the opposite wall perpendicularly. Testing this approximation, MD simulations of spherical brushes, with radii of the order of the brushes used in experiments, of uncharged rigid chains were performed. These simulations shared the same force–distance dependent behavior as that predicted upon applying the Derjaguin approximation to the theory of the interaction between flat brushes, and yielded forces between the brushes that were ∼10–20% less than that of these predictions at all brush separations. And so, despite the limitations of employing the Derjaguin approximation for this system, we find excellent quantitative agreement of the shapes and magnitudes of the resulting curves between theory and experiment.
 | ||
Fig. 6 The contribution to the total pressure of the chain-bending force for a system with a grafting density 50 times smaller than that used in the previous calculations and for chains 5 times as long, (L = 850 Å), mirroring the conditions used in spherical DNA brush experiments.12,13 The ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) curve corresponds to a system with a 0.5 mM monovalent salt concentration, whereas the curve corresponds to a system with a 0.5 mM monovalent salt concentration, whereas the ![[dash dot, graph caption]](https://www.rsc.org/images/entities/char_e090.gif) curve to a 5.0 mM salt concentration, thereby showing the strong effect that varying salt concentration has on the chain-bending force for these systems. Inset: the force due to chain bending between two identical spherical brushes derived using the Derjaguin approximation, F(D) = πRcW(D) where Rc = 1100 nm, the radius of the colloids used in the experiments of Refs 12 and 13 and W(D) is the potential of the mean force of the bending contribution per unit area of the planar brush. Again, the curve to a 5.0 mM salt concentration, thereby showing the strong effect that varying salt concentration has on the chain-bending force for these systems. Inset: the force due to chain bending between two identical spherical brushes derived using the Derjaguin approximation, F(D) = πRcW(D) where Rc = 1100 nm, the radius of the colloids used in the experiments of Refs 12 and 13 and W(D) is the potential of the mean force of the bending contribution per unit area of the planar brush. Again, the ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) curve corresponds to a system with a salt concentration 0.5 mM and the curve corresponds to a system with a salt concentration 0.5 mM and the ![[dash dot, graph caption]](https://www.rsc.org/images/entities/char_e090.gif) curve to a 5.0 mM salt concentration, for brushes with chain lengths of L = 850 Å, the contour length of a 250 base-pair DNA helix. curve to a 5.0 mM salt concentration, for brushes with chain lengths of L = 850 Å, the contour length of a 250 base-pair DNA helix. | ||
V. Conclusions
In agreement with our previous study of rigid polyelectrolyte brushes,14 we found that the interactions between simulated brushes can be accurately described by theories that take into account both the osmotic forces due to ions trapped within the brushes, as well as forces arising from the bending of the rigid polyelectrolyte chains as the brushes are compressed against each other. The former contribution could be described via a mapping of a two-dimensional cylindrical cell model onto the brush system and the validity of the theory formulated for salt-free systems14 carries over to the salted brushes. This formulation not only furnishes the force between the brushes but could accurately predict the distribution of the chains' counterions and the salt ions. As the brushes are brought together, the salt ions are gradually squeezed out of the brush, with the same number of coions and counterions of the chain being expelled so that the interior of the brush remained net neutral. Hence, systems with added salt are characterized by a smaller repulsive force between the brushes at a given brush separation, compared to systems without salt upon taking into account the osmotic pressure of salt ions on the other side of the brushes.The chain-bending force contribution to the pressure between the brushes for the parameters used in the simulation, however, remained unchanged in the simulation with added salt. Using a simple form for the dependence of a polyelectrolyte's persistence length on its ionic environment,23,24 coupled with the cell model theory for the ion distributions about the brush chains, we found that the amount of added salt in the simulations has little influence on the persistence length of the chains. Hence, as evident from the simulation, the chain-bending force for systems with and without added salt were roughly the same. However, we also determined that, for systems with the chain-grafting densities and salt concentrations of brush experiments,12,13 the persistence lengths would be dramatically different upon adding salt, yielding a very different force–distance dependence between the brushes. At very low salt concentrations, the persistence length of the chains can be quite large, providing a strong repulsive force between the brushes when the length of the chains is smaller than the surface-to-surface separation of the brushes' grafting surfaces. Upon adding larger concentrations of salt, however, the salt ions screen the naked charge of the polyelectrolyte chains, reducing their persistence length. This reduces the contribution of the chain-bending force to the total pressure between the brushes. Therefore adding salt diminishes both the osmotic and chain-bending contributions to the total pressure.
The results obtained here are consistent with those of interacting DNA brush experiments.13 Here, increased concentrations of salts of different valencies were found to drastically reduce the forces between the brushes, with a force–distance dependence that scales approximately as D−2 at small brush separations, which is the same scaling law found here for the chain-bending contribution to the pressure between the brushes. Note that this power law dependence, derived for chains with lengths smaller than their persistence length, will necessarily break down for more flexible or longer chains in which entropic effects, such as thermal undulations of the chains, must be taken into account.35,36 Furthermore, multivalent salts may condense the polyelectrolyte chains and/or further reduce the electrostatic component of their persistence length,40 thus leading to an additional decrease in the range of the repulsive forces between the brushes as compared to the forces measured between brushes with added monovalent salts at the same ionic strength. The simple theory and simulations presented here display trends similar to those of the brush experiments.
We finally remark that the particular characteristics of the force vs. distance curves for the systems at hand, in terms of its range and separation-dependence, open up new possibilities for manipulating effective interactions between colloidal particles. Since both the bending contributions and the osmotic term from the ions result from local rearrangements, the validity of the pair potential approximation seems to be guaranteed for these systems, in contrast to charge-stabilized colloids.42,43 Superimposing dispersion or polymer-induced depletion attractions on these colloids would lead to novel ways to tune, e.g., the succession of short-range attractions and longer-range repulsions in colloidal suspensions.
Acknowledgements
A.W. wishes to thank the Alexander von Humboldt Foundation for financial support.References
- J. Rühe, M. Ballauff, M. Biesalski, P. Dziezok, F. Gröhn, D. Johannsmann, N. Houbenov, N. Hugenberg, R. Konradi, S. Minko, M. Motornov, R. R. Netz, M. Schmidt, C. Seidel, M. Stamm, T. Stephan, D. Usov and H. N. Zhang, Adv. Polym. Sci, 2004, 165, 79–150.
- A. Naji, C. Seidel and R. R. Netz, Adv. Polym. Sci., 2006, 198, 149–183 CAS.
- P. Pincus, Macromolecules, 1991, 24, 2912–2919 CrossRef CAS.
- O. V. Borisov, T. M. Birshtein and E. B. Zhulina, J. Phys. II, 1991, 1, 521–526 CrossRef CAS.
- N. A. Kumar and C. Seidel, Macromolecules, 2005, 38, 9341–9350 CrossRef CAS.
- Y. Mei, K. Lauterbach, M. Hoffmann, O. V. Borisov, M. Ballauff and A. Jusufi, Phys. Rev. Lett., 2006, 97, 158301 CrossRef.
- Y. Mei, M. Hoffmann, M. Ballauff and A. Jusufi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031805 CrossRef.
- M. Balastre, F. Li, P. Schorr, J. Yang, J. W. Mays and M. V. Tirrell, Macromolecules, 2002, 35, 9480–9486 CrossRef CAS.
- U. Raviv, S. Giasson, N. Kampf, J.-F. Gohy, R. Jérôme and J. Klein, Nature, 2003, 425, 163–165 CrossRef CAS.
- O. J. Hehmeyer and M. J. Stevens, J. Chem. Phys., 2005, 122, 134909 CrossRef.
- N. A. Kumar and C. Seidel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 020801 CrossRef.
- K. Kegler, M. Salomo and F. Kremer, Phys. Rev. Lett., 2007, 98, 058304 CrossRef CAS.
- K. Kegler, M. Konieczny, G. Dominguez-Espinosa, C. Gutsche, M. Salomo, F. Kremer and C. N. Likos, Phys. Rev. Lett., 2008, 100, 118302 CrossRef.
- A. Wynveen and C. N. Likos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 010801 CrossRef.
- P. L. Hansen, R. Podgornik and V. A. Parsegian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 021907 CrossRef CAS.
- A. A. Kornyshev, D. J. Lee, S. Leikin and A. Wynveen, Rev. Mod. Phys., 2007, 79, 943–996 CrossRef CAS.
- W. Saenger, Principles of Nucleic Acid Structure, Springer-Verlag, New York, 1984 Search PubMed.
- H. M. Berman, W. K. Olson, D. L. Beveridge, J. Westbrook, A. Gelbin, T. Demeny, S. H. Hsieh, A. R. Srinivasan and B. Schneider, Biophys. J., 1992, 63, 751–759 CrossRef CAS.
- A. Wynveen, D. J. Lee, A. A. Kornyshev and S. Leikin, Nucleic Acids Res., 2008, 36, 5540–5551 CrossRef CAS.
- P. S. Crozier and M. J. Stevens, J. Chem. Phys., 2003, 118, 3855–3860 CrossRef CAS.
- C. N. Likos, R. Blaak and A. Wynveen, J. Phys.: Condens. Matter, 2008, 20, 494221 CrossRef.
- J. F. Marko and E. D. Siggia, Macromolecules, 1995, 28, 8759–8770 CrossRef CAS.
- T. Odijk, J. Polym. Sci., Polym. Phys. Ed., 1977, 15, 477–483 CrossRef CAS.
- J. Skolnick and M. Fixman, Macromolecules, 1977, 10, 944–948 CrossRef CAS.
- I.-C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162 CrossRef CAS.
- A. Naji, R. R. Netz and C. Seidel, Eur. Phys. J. E, 2003, 12, 223–237 CrossRef CAS.
- G. S. Manning, J. Chem. Phys., 1969, 51, 924–933 CrossRef CAS.
- G. V. Ramanathan and J. C. P. Woodbury, J. Chem. Phys., 1982, 77, 4133–4140 CrossRef CAS.
- T. Odijk, Phys. A, 1991, 176, 201–205 CrossRef CAS.
- P. González-Mozuelos and M. Olvera de la Cruz, J. Chem. Phys., 1995, 103, 3145–3157 CrossRef CAS.
- A. Deshkovski, S. Obukhov and M. Rubinstein, Phys. Rev. Lett., 2001, 86, 2341–2344 CrossRef CAS.
- D. Antypov and C. Holm, Phys. Rev. Lett., 2006, 96, 088302 CrossRef.
- T. Alfrey, P. W. Berg and H. Morawetz, J. Polym. Sci., 1951, 7, 543–547 CrossRef.
- R. M. Fuoss, A. Katchalsky and S. Lifson, Proc. Natl. Acad. Sci. U. S. A., 1951, 37, 579–589 CAS.
- T. Odijk, J. Chem. Phys., 1998, 108, 6923–6928 CrossRef CAS.
- M. Emanuel, H. Mohrbach, M. Sayar, H. Schiessel and I.M. Kulić, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 061907 CrossRef.
- A. E. H. Love, A Treatise on the Mathematical Theory of Elasticity, Cambridge University Press Warehouse, London, 2nd edn, 1906 Search PubMed.
- R. Podgornik, P. L. Hansen and V. A. Parsegian, J. Chem. Phys., 2000, 113, 9343–9350 CrossRef CAS.
- G. S. Manning, Biophys. J., 2006, 91, 3607–3616 CrossRef CAS.
- C. G. Baumann, S. B. Smith, V. A. Bloomfield and C. Bustamante, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 6185–6190 CrossRef CAS.
- J. R. Wenner, M. C. Williams, I. Rouzina and V. A. Bloomfield, Biophys. J., 2002, 82, 3160–3169 CrossRef CAS.
- M. Brunner, J. Dobnikar, H. H. von Grünberg and C. Bechinger, Phys. Rev. Lett., 2004, 92, 078301 CrossRef.
- J. Dobnikar, M. Brunner, H. H. von Grünberg and C. Bechinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031402 CrossRef.
| This journal is © The Royal Society of Chemistry 2010 |
