Reverse micelles with spines: L2 phases of surfactant ion—polyion complex salts, n-alcohols and water investigated by rheology, NMR diffusion and SAXS measurements†
Juliana Silva
Bernardes
a,
Marcelo Alves
da Silva
a,
Lennart
Piculell
*b and
Watson
Loh
*a
aInstitute of Chemistry, Universidade Estadual de Campinas (UNICAMP), Caixa Postal, 6154, Campinas, SP, Brazil. E-mail: wloh@iqm.unicamp.br; Fax: +55 19 3521 3023; Tel: +55 19 3521 3148
bPhysical Chemistry 1, Center for Chemistry and Chemical Engineering, Lund University, P.O. Box 124, S-221 00, Lund, Sweden. E-mail: lennart.piculell@fkeml.lu.se
First published on 11th November 2009
Abstract
Homogeneous alcoholic isotropic solutions (L2 phases) of “complex salts” of hexadecyltrimethylammonium neutralized by polyacrylate CTAPAn (n = 30 or 6000), in the presence of water were examined at 25 °C by means of small-angle X-ray scattering (SAXS), rheology and NMR self-diffusion measurements for different n-alcohols (octanol, hexanol and butanol) and at varying water contents. The greater water solubility and the slower water self-diffusion coefficients in these L2 phases, when compared to results with surfactant-free alcohols, suggested that these phases are composed of reverse aggregates with water in their cores. A comparatively rapid self-diffusion of the surfactant ion in butanol suggested a significant fraction of “free” surfactant ions, dissociated from the reverse aggregates. Rheological data confirmed that the obtained viscoelastic properties were consistent with a system containing entangled elongated micelles, whose properties were controlled by the polyion chain length. NMR diffusion measurements for complex salt solutions with the shorter counter-polyion (CTAPA30) produced estimates of the aggregate lengths that were close to the extended length of one PA30 chain. In summary, these results support the formation of aggregates composed by surfactant decorated polyion chains with a water core, whose properties are determined by the polyion chain length, behaving like reverse micelles with spines.
1. Introduction
In recent years, a series of reports have been published using the new approach to oppositely charged polymer-surfactant mixtures developed by Piculell and coworkers which involves the direct preparation of “complex salts” composed of charged surfactants with polyions as counterions.1–7 Based on this approach, phase equilibria in truly binary mixtures containing complex salts and solvent (so far, water) or in ternary mixtures with the addition of surfactant, polymer or organic solvents, have been investigated, and the obtained results could be directly compared with the phase equilibria for similar surfactant systems containing monomeric counterions. In general, these results indicate that polymeric counterions change the phase equilibria in the direction of an increasing attraction between surfactant ion aggregates in water, which has been ascribed to contributions from polyion bridging and increased ion correlation forces. As a result of this attraction, most complex salts are virtually insoluble in water, except for some systems with smaller surfactant chain lengths or smaller, oligometric, counterions, where micellar solutions can be found.6Ternary phase diagrams in systems also containing oils showed that the structure of the liquid crystalline phases can be changed in different ways due to the nature of the organic solvent added.4,5 Solvents with low polarity, such as cyclohexane or xylene, favor the formation of normal hexagonal mesophases, while lamellar phases predominate when solvents such as long-chain alcohols are used. These previous investigations of our group4,5 on hexadecyltrimethyl ammonium polyacrylate or polymethacrylate complex salts showed that they are almost insoluble in hydrocarbon solvents such as cyclohexane and xylene, and only slightly soluble in decanol.
However, other studies on solution properties of surfactant ion-polyion complex salts soluble in organic solvents have been reported. Antonietti and coworkers8 prepared complexes of poly(styrenesulfonate) with various cationic surfactants which could be dissolved in polar solvents such as short-chain alcohols or THF. Their most hydrophobic complex salt, with the trioctylmethylammonium cation, was also soluble in more apolar solvents such as acetone or chloroform. In these systems, viscosity and light scattering investigations confirmed that the complex salts exhibit polyelectrolyte behavior, due to dissociation of the surfactant ions, with a transition to standard polymer behavior depending on the chemical nature of the solvent. Bakeev et al9 have also studied various complex salts in different organic solvents. In stoichiometric mixtures these complex salts were molecularly dissolved in low-polarity organic solvents, but displayed ionomer type behavior, such as aggregation, when the surfactant ion was substituted by smaller ions in non-stoichiometric mixtures. In another report by the same group,10 the studies were extended to a variety of polyelectrolytes and surfactants, which were found to produce interesting colloidal structures depending on the solvent properties or the chemical structures of the components, featuring properties such as solubilization of smaller molecules, stabilization of oil-in-water microemulsions and viscosity control in organic solvents. Two reports by Shioi et al11,12 describe studies where a polycation could be dissolved in the L2 phase of the anionic surfactant Aerosol OT mixed with n-hexane and water, and where polyacrylate similarly could be dissolved in an L2 phase of the double-chained (didodecyl)dimethylammonium (DDA) cationic surfactant in cyclohexane and water, in both cases resulting in significant changes of the solution properties. In summary, all these previous studies reveal that complex salts dissolved in oils may display polymer-like or polyelectrolyte-like solution properties that depend on the solvent polarity and the chemical properties of the surfactant.
In a study to be published separately, we report13 ternary phase diagrams for mixtures of the complex salt hexadecyltrimethylammonium polyacrylate (CTAPA) with water and different n-alcohols. The liquid crystalline phases formed by this complex salt were strongly affected by the content and the nature of the n-alcohol. The n-alcohol acts as a co-surfactant independent of its carbon chain length, leading to phase transition from hexagonal to lamellar phases with small amounts of added n-alcohol. Shorter alcohols, most notably ethanol, are an exception, acting more as a co-solvent and, hence, favoring formation of disordered phases. In systems containing octanol, a reverse hexagonal phase was detected next to the L2 phase region. Differences were also observed when comparing the phase behavior of complex salts containing polyacrylates of 30 and 6000 units, PA30 and PA6000, respectively. A reverse hexagonal phase was observed in systems containing hexanol and PA6000, and a particularly small L2 region was found for systems containing octanol and PA6000. At high n-alcohol concentrations an alcoholic isotropic L2 solution was detected for all of the systems analyzed, and the size of the L2 region—which is the focus of the present investigation—increased for n-alcohols with shorter carbon chain lengths, as can be seen in Figure 1. Earlier studies on the equilibrium phase diagrams of ternary mixtures of the common surfactant hexadecyltrimethylammonium bromide (CTAB) with water and various n-alcohols14 similarly indicated the presence of large L2 regions that tended to increase in size with a decrease in the alcohol chain length.
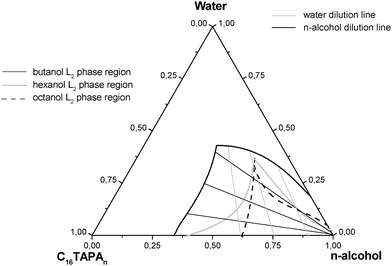 | ||
| Fig. 1 Extensions of the L2 phases in phase diagrams of various CTAPA30/water/n-alcohol (butanol, hexanol or octanol) mixtures. Based on data from Ref. 13. | ||
In the present investigation, the nature of the alcoholic isotropic solution in mixtures of CTAPA with n-alcohols and water is investigated in more detail by means of small-angle X-ray scattering (SAXS), rheology and NMR self-diffusion measurements, providing information concerning the nature of the aggregates present in these L2 phases. This investigation fills the gap between previous reports on the behavior of complex salts in water-rich environments, and the reports cited above that investigate the polymeric solution behavior of dry complex salts in organic solvents. Compared to the studies of solutions of dry complex salts in organic solvents, the present study investigates the effect of adding water to these systems, with the possible formation of reverse aggregates with aqueous cores. From another perspective, this study investigates the effect of replacing simple surfactant counterions in the reverse aggregates, as in the previously studied mixtures containing CTAB,14 with polymeric counterions. In the latter type of mixture, the minimum aggregation number should be dictated by the number of charges of the poly-counterion—a restriction that is absent for conventional reverse micelles.
By using the approach involving the direct preparation of polyion-surfactant ion complex salts, our study involves a minimum number of components, thus reducing the complexity considerably compared with previous studies where polyelectrolytes have been dissolved in L2 phases of surfactant, oil and water.11,12
2. Materials and methods
Materials
Hexadecyltrimethylammonium bromide (CTAB) 99% was purchased from Sigma and used without further treatment. Poly (acrylic acid) samples, PAA, with molar masses of 2000 and 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 (30 and 6000 AA units, respectively), from Sigma, were used as received. Octanol from Merck and hexanol and butanol from Acros, all of the highest purity available, were also used without further treatment. Millipore® water with a resistivity of 18 MΩ.cm−1 was used throughout the study.
000 g mol−1 (30 and 6000 AA units, respectively), from Sigma, were used as received. Octanol from Merck and hexanol and butanol from Acros, all of the highest purity available, were also used without further treatment. Millipore® water with a resistivity of 18 MΩ.cm−1 was used throughout the study.
Synthesis of complex salts
Complex salts of CTA+ with polyacrylate counterions were prepared by titration of the hydroxide form of the surfactant (CTAOH) with the acid forms of the polymers (PAA), according to the procedure developed by Svensson et al.1–3 Throughout this text, the complex salts will be named CTAPA30 and CTAPA6000, where 30 and 6000 refer to the degrees of polymerization of the two polyions used.Sample preparation and characterization
Desired amounts of complex salt, water and n-alcohol were added to test tubes, which were then flame sealed. After, the samples were mixed in a Vortex agitator (MS2 mini-shaker IKA) for at least one minute; the tubes were then centrifuged alternatively upright and upside-down for a few days. The samples were left at 25 °C to equilibrate for some days.Samples were visually inspected to determine the presence of the L2 phase. In addition, they were also examined between crossed polarizers to detect birefringence at rest or under shear. Selected samples were analyzed by Small Angle X-Ray Scattering (SAXS), rheology and NMR diffusion measurements.
Small Angle X-Ray Scattering (SAXS)
Scattering curves were obtained in the SAXS beamline (D02A) of the Brazilian Synchrotron Laboratory (LNLS), in Campinas, Brazil. The experimental set-up involved the use of X-rays at the wavelength of 1.488 Å and a sample-to-detector distance of 591.2 mm. Typical acquisition times were around 5 min. For these experiments, a sample cell with mica windows was used which allowed temperature control (all measurements were made at 25 °C). The collected data were treated using the software Fit2D, which allows the integration of CCD images.15 The correlation distance between the scattering centers was determined from the following equation: | (Eq. 1) |
Rheology
Steady and dynamic rheological experiments were performed using a HAAKE RheoStress 1, at 25.0 °C. Samples were run on a plate-and-plate geometry (20 mm diameter). Dynamic frequency sweep measurements were conducted in the linear viscoelastic regime of the samples and the frequency range used was 0.01 to 40 Hz with a maximum stress of 3 Pa depending on the characteristics of the sample.NMR self-diffusion measurements
The NMR experiments where performed on a Bruker DMX-200 operating at 200 MHz proton resonance frequency equipped with a Bruker diffusion probe having a maximum gradient strength of 9.6 Tm−1. Pulsed field gradients (PFGs) where generated in a Bruker DIFF-25 gradient probe driven by a BAFPA-40unit. These measurements were performed using a maximum gradient strength of 4.52 Tm−1, with a pulse gradient time of 1.0 ms and the time between the start of two gradient pulses was 20 ms. The NMR method used to determine the self- diffusion of the water and surfactant ion consists of the application of two pulsed gradients in the dephasing and rephasing periods of spin echo. The method used in this work is the stimulated echo (PFG-SE) with a pulse sequence of 90°-τ1–90°-τ2–90°-τ1–echo.16,173. Results
The strategy adopted to study the alcoholic isotropic phase was to focus on a matrix of samples located along both water and n-alcohol dilution lines within the L2 phase areas of ternary mixtures of water, n-alcohol (butanol, hexanol or octanol) and complex salt (CTAPA30 or CTAPA6000), as shown in Figure 1. Along a water dilution line, the complex salt/alcohol ratio is kept constant, whereas the complex salt/water ratio is constant along an alcohol dilution line. The phase boundaries in Figure 1 are taken from an investigation of the full phase diagrams, which will be published separately.13 Samples belonging to the L2 phase were isotropic at rest, but displayed birefringence under shear for the CTAPA6000 system.Small angle X-ray scattering (SAXS)
SAXS spectra from the studied L2 phases display a well-defined correlation peak that changes position and shape along the different dilution lines, as shown in Figures 2–4. On diluting the system by either water or n-alcohol, the distance between the scattering centers increases, as would be expected, for all analyzed systems as shown in Figures 2 and 4. Note that the curves in each figure correspond to different dilution lines for the different alcohols, hence, a direct comparison of different systems is not straightforward. The system CTAPA6000/octanol/water was not systematically studied because the L2 phase area of this system was too small for the construction of meaningful dilution lines. | ||
| Fig. 2 Correlation distances derived from SAXS spectra as function of the water content in indicated n-alcohol systems at constant n-alcohol:complex salt mass ratios of (a) 2.0, (b) 2.0, (c) 2.3, (d) 3.7 and (e) 3.0. | ||
 | ||
| Fig. 3 SAXS spectra for a series of samples along a water dilution line for the system butanol/water/CTAPA30. Butanol: complex salt mass ratio = 1.4. | ||
 | ||
| Fig. 4 Correlation distances derived from SAXS spectra as function of the n-alcohol content in indicated n-alcohol systems at constant complex salt:water mass ratios of (a) 3.1, (b) 3.0, (c) 2.3, (d) 3.0 and (e) 2.7. | ||
As regards the shapes of the correlation peaks, different trends were found on dilution with water or alcohol, respectively. The correlation peaks became broader with an increase in the n-alcohol content as shown in Figure 5. The continuous medium in the disordered L2 phase is n-alcohol and on increasing its content, it may be expected that the distance between the scattering centers becomes less well-defined. By contrast, the correlation peak along the water dilution lines became sharper with an increase in the water content, as can be seen in Figure 3. This indicates that the increasing distances between the scattering centers became more well-defined on addition of water.
 | ||
| Fig. 5 SAXS spectra along a butanol dilution line for the system butanol/water/CTAPA30. Complex salt:water mass ratio = 3.1. | ||
Rheology
A rheological study of the L2 phase was performed along different dilution lines. It was immediately observed that samples of the complex salt CTAPA30 presented low viscosity throughout all the L2 phase for octanol, hexanol and butanol. However, with the longer polyacrylate, the isotropic phase with butanol and hexanol presented high viscosities and visible elasticities at higher CTAPA6000 contents. With octanol, the latter behavior was not observed, probably because the L2 phase was not capable of incorporating high enough amounts of CTAPA6000.Flow curves for L2 samples containing butanol showed different patterns for CTAPA30 and CTPA6000 (data not shown). For CTAPA6000, the L2 phase viscosity decreased with an increase in shear rate, a typical behavior observed for systems composed by structures that align under shear (shear thinning fluid). The flow curve of the CTAPA30 system showed Newtonian fluid behavior, and the L2 phase viscosity assumed an almost constant value (c.a. 13 mPas, for a system containing 72 wt. % butanol, 7% water and 21% complex salt) along the entire range of shear rates analyzed.
Dynamic experiments along n-alcohol and water dilution lines were performed for both types of complex salts (long and short polyions). During these measurements, the L2 phase was subjected to a fixed amplitude of stress, σ0, well within the linear viscoelastic region as determined by amplitude sweep experiments (data not shown) at different angular frequencies, ω. The results obtained for CTAPA30 were close to the sensitivity limit of the rheometer and since no clear patterns were obtained, these results are not presented. For the complex salt CTAPA6000, a systematic dynamic study was performed in the butanolic system and the results are shown in Figures 6 and 7.
 | ||
| Fig. 6 Elastic (G′) and viscous (G″) modulii as a function of angular frequency along a water dilution line for the system butanol/water/CTAPA6000. Butanol:complex salt mass ratio = 1.9. | ||
 | ||
| Fig. 7 Elastic G′ and G″ viscous moduli as a function of angular frequency along an n-alcohol dilution line of the system butanol/water/CTAPA6000. Complex salt:water mass ratio = 3.0. | ||
Figure 6 shows dynamic frequency sweep curves of the CTAPA6000 L2 phase in butanol along a water dilution line. All samples analyzed showed a characteristic viscoelastic response, featuring a crossover of the storage modulus G′ and the loss modulus G″ at a characteristic angular frequency ωc. The sample response could be divided in two limiting regimes, separated by an intermediate transition. On shorter time scales, the L2 phase behaved more like an elastic solid, and on longer time scales it behaved more like a viscous liquid.18 Furthermore, the storage and loss moduli values did not change very much along the dilution line, suggesting that the L2 rheological behavior was only weakly affected by addition of water. An effective relaxation time tR of these viscoelastic samples can be estimated as tR = 1/ωc.
Experiments along butanol dilution lines (Figure 7) revealed that at low butanol concentrations, the elastic modulus (G′) assumed higher values through most of the frequency range analyzed. Nevertheless, at low frequencies, it crossed over the viscous modulus (G″). On the other hand, at high butanol concentration, the viscous modulus (G″) assumed higher values in almost all of the investigated frequency range with the crossover point occurring at higher frequency values. The effective relaxation time varied from 0.1 s to 3 s with a decreasing butanol content along the butanol dilution line.
NMR self-diffusion
Water, alcohol and surfactant ion (CTA+) self-diffusion coefficients were measured for the L2 phases. The surfactant ion self-diffusion was analyzed directly from the methyl proton signal of the trimethylammonium headgroup, located at δ = 3.27 ppm. The alcohol diffusion coefficient was obtained from the signal of the protons on carbon 1 next to OH group, located at δ = 3.10 ppm. The water self-diffusion was obtained from the signal at δ = 4.80 ppm, which had contributions from both water and the hydroxyl protons of n-alcohol molecules, which exchange rapidly, on the NMR diffusion time scale, with water. Thus, to obtain the self-diffusion coefficient for water alone, the following equation was used:| Dobs = faDa + 2fwDw | (Eq. 2) |
Figures 8A and 8B show the variation of the self-diffusion coefficient of CTA+ for CTAPA30 and CTAPA6000 along different water dilution lines in mixtures with butanol. For both complex salts, the surfactant ion diffusion coefficient increased strongly with increasing water content and with increasing butanol content. The surfactant ion diffusion was faster, at comparable compositions, for complex salts with the shorter polyanion (PA30) compared to those with the longer polyanion (PA6000). However, anticipating the discussion below, we may immediately note that the difference is not as large as would have been expected if the surfactant ion diffusion coefficient were to directly reflect the self-diffusion of entire dissolved polyion-surfactant ion complexes differing by a factor of 200 in their degree of polymerization.
 | ||
| Fig. 8 Surfactant ion self-diffusion coefficients along different water dilution lines for the systems (A) butanol/water/CTAPA30 and (B) butanol/water/CTAPA6000. | ||
Figure 9 compares measured diffusion coefficients along water dilution lines in mixtures of CTAPA30 with three different alcohols: octanol, hexanol and butanol. Figure 9A gives results for the surfactant ion and Figure 9B for water. Both diffusion coefficients increased with decreasing hydrocarbon chain length of the alcohol, and both diffusion coefficients increased markedly on addition of water to the butanol system. By contrast, small or no variations were seen when adding water to the hexanol or octanol systems in the studied composition range. The water self-diffusion coefficients in the various L2 phases (Figure 9B) were much smaller than those obtained in the binary solutions of water in the respective n-alcohols (Table 1). By contrast, the alcohol diffusion coefficients (not shown) were not significantly different from those obtained in the binary mixtures.
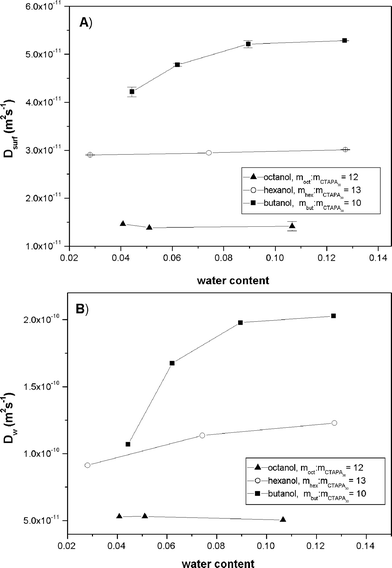 | ||
| Fig. 9 Surfactant ion (A) and water (B) self-diffusion coefficients along different water dilution lines for systems containing octanol, hexanol or butanol. | ||
4. Discussion
The nature of the reverse aggregates
Based on previous studies of similar systems (cf. the Introduction), as well as on a priori considerations, we expect that the studied L2 solutions contain some sort of reverse aggregates containing polyions surrounded by surfactant ions. We will now attempt to deduce, from our various measurements, more precise information on the nature of these aggregates.We first note that the phase diagrams in Figure 1 show that the maximum amount of dissolved water in the L2 phases is much greater than the water solubility in the corresponding surfactant-free alcohols. Furthermore, the water self-diffusion coefficients determined in the L2 region (Fig 9B) are strongly reduced in comparison with the diffusion of water molecules in binary mixtures with alcohols (see Table 1). Both observations support the notion that the reverse polyion-surfactant ion aggregates can incorporate significant amounts of water molecules, in addition to the water dissolved in the alcohol surrounding the aggregates, in this region of the phase diagrams. Colloidal obstruction effects can be ruled out as the major cause for the observed slower diffusion of water molecules. If such effects were important, we would have obtained reduced self-diffusion coefficients also for the alcohols, compared to the diffusion in the neat alcohols, contrary to our observations. As a further control, the obstruction effects may be estimated using the approach of Jonströmer et al.19 For the systems studied in Figure 9B, assuming short prolate aggregates at a concentration of 10 wt.%, the reduction of the diffusion coefficients, due to obstruction effects, of the water and alcohol molecules surrounding the aggregates is not greater than 20–30% compared to the infinite dilution diffusion coefficients.
A second important observation is the comparatively rapid diffusion of the surfactant ion, particularly in the L2 phases of the complex salt with the longer polyion, CTAPA6000. The surfactant ion diffusion coefficient is much too large to reflect the diffusion of a discrete polyion-surfactant ion aggregate. Even if we assume the most compact aggregate conceivable, that is, a dry spherical aggregate of one polyacrylate ion and 6000 surfactant ions, we obtain an estimated diffusion coefficient of 9 × 10−12 m2s−1 at infinite dilution for such an aggregate, using the Stokes-Einstein equation, a density of 1gcm−1 for the aggregate and a viscosity of 2.5 mPas for butanol. This represents the largest possible aggregate diffusion coefficient, since incorporation of water, or a deviation from spherical geometry, or a finite aggregate concentration would all give a slower aggregate diffusion. Nevertheless, most recorded surfactant ion diffusion coefficients in Figure 8B are much larger. We see two possible, fundamentally different, origins of the fast diffusion coefficient of the surfactant ion for CTAPA6000 in the butanolic system. One is a partial dissociation of the surfactant ions from the aggregate, so that the observed diffusion coefficient is an average between the diffusion of free surfactant ions and the aggregates. The other possibility is that the system is composed of infinite, branched networks, so that the measured diffusion coefficient reflects the three-dimensional diffusion of surfactant ions along such aggregates.
We will start by considering alternative possibilities of discrete aggregates, possibly containing more than one polyion, versus branched networks. As a point of departure for this discussion, we recall that systems containing so-called worm-like micelles can be structured in two different ways, as summarized by Cates and Candau,20,21 leading to different structures called living polymers and living networks, respectively. Living polymer systems contain elongated linear micelles whose lengths are determined not chemically, but thermodynamically. This type of system reaches a dynamic equilibrium, where the self-assembly aggregates have a finite lifetime and can break and reconnect on a specific time scale, hence the expression living. In the semi-dilute regime the worm-like micelles entangle, similar to the situation in semi-dilute polymer solutions. A living network system contains a persistent network composed by elongated micelles that are actually fused and not only entangled.
The identification of living polymers or living networks should be possible from the analysis of rheology data. In a living network system, the viscosity does not change so significantly with the increase in surfactant content, due the different mechanisms of relaxation that this system can exhibit, for example, by a change in position of the bifurcations of the aggregates. If, on the other hand, the system is organized as living polymers, the viscosity is expected to increase significantly with the surfactant content, due to the difficulty of the system to relax caused by the higher degree of micellar entanglements.
Results with CTAPA6000 in butanol showed that both elastic (G′) and viscous moduli (G″) are significantly affected by the complex salt concentration (Figure 7), indicating that this system is formed by reverse elongated micelles with entanglements. In addition to these rheological features, along the n-alcohol dilution lines, a phase separation on dilution would be expected for a system formed by a living network due to a finite maximum swelling of the network.20–22 The predicted phase sequence on dilution would be a viscoelastic L2 phase followed by a phase separation with an excess of n-alcohol. Since neither the rheology nor the phase sequence behave as expected for a living network, we reject this structure as a possibility for our L2 systems.
For living polymer systems at high surfactant concentrations, the elongated micelles entangle, giving rise to a characteristic viscoelastic behavior with a single relaxation time (the chain reptation time), similar to that found in flexible polymer transient networks.20,22 In this way, the rheological response of living polymer solutions should be close to that expected for a Maxwell fluid.20,21 However, the extended rheological “mechanical spectra” recorded in our systems (Figure 7) do not show a single relaxation time, but a wide distribution of relaxation times, as is well established for polydisperse polymer solutions. In light of this result, the assumption that the reverse micelles contain several polyanion chains with a length determined by thermodynamics, such as in living polymer systems, does not seem reasonable for the systems analyzed in this work.
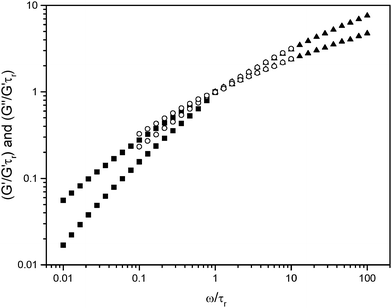
A remaining possibility is that the alcoholic isotropic phase is composed by entangled reverse aggregates, but where each aggregate contains a single polyion chain and thus, the micelles assume lengths determined by the polyion chain. This situation is entirely compatible with our rheology results, with a low viscosity for aggregates with the short polyion and, for the long polyion, a viscoelastic behavior giving evidence of a polydisperse set of entangled micelles. To further explore this possibility, we adjusted the L2 phase dynamic rheological data obtained along a butanol dilution line (Figure 7) in a master curve (Figure 10). To obtain the overlap, all frequencies were divided by the frequency of the cross point ωc, and all elastic and viscous moduli were divided by the values of the modulus at ωc. As observed in Figure 10 all curves nearly overlap, which suggests that the observed concentration dependence along the butanol dilution line is mainly due to dilution effects, rather than to a change of the size or shape of the complex salt aggregates. For further comparison, we also made dynamic rheological measurements for solutions of pure PAA6000 in water. The obtained data (not shown) were very similar to those observed for the L2 phase with the CTAPA6000 complex salt in Figure 7 and agreed with the same master curve.
Based on all the above considerations, we tentatively conclude that the alcoholic isotropic phase is composed of finite reverse micelles, each containing one polyion chain, and that these aggregates can be viewed as polydisperse polyions dressed with surfactant ions. An aggregate can also take up water molecules in its core. However, finite fractions of both water molecules and surfactant ions are dissociated from the aggregates and exist as free molecules in the alcoholic solvent surrounding the aggregates. A dissociation of surfactant ions from the reverse complex salt aggregates has previously been reported for other complex salts.8 We will now continue to examine this model in more detail.
Free surfactant ions and water molecules
The fraction of free water molecules and surfactant ions should increase with an increasing polarity, that is, a decreasing chain length of the alcohol. A coupling is also expected, since an increasing concentration of water molecules in the alcoholic solvent should increase the dissociation of surfactant ions. These effects provide qualitative explanations for the trends seen in Figures 8 and 9, where there is a marked increase in both surfactant ion and water diffusion on addition of water to the butanolic systems. By contrast, for the longer alcohols, octanol and hexanol, the surfactant ion diffusion coefficients do not vary significantly as the water content is raised from 4 to 13% (Figure 9A), and a similar trend is observed for the water diffusion coefficients (Figure 9B).For the surfactant ion specifically, the observed diffusion coefficient should vary with the degree of dissociation, α, of the surfactant ions according to the following equation:
| Dsurf, obs = α Dsurf, free + (1 − α) Dsurf,aggr | (Eq. 3) |
From Eq (3) we may immediately conclude that the observed surfactant ion diffusion should be most strongly influenced by surfactant ion dissociation for large aggregates, where Dsurf,aggr is small, and for large degrees of surfactant ion dissociation. In our systems, the extremes of these conditions occur to the right in Figure 8B, for CTAPA6000 in butanol at high water contents. At the other extreme we have small CTAPA30 aggregates dissolved in octanol at low water contents, see Figure 9A. We can apply Eq (3) to the data in Figure 9A to obtain a rough estimate of the fraction of free surfactant ions at high water contents in butanol. We first assume that we may neglect the dissociation of surfactant ions at the lowest water content, so that Dsurf, obs = Dsurf, aggr at 4% water for CTAPA30 in butanol. The diffusion coefficient for free CTA+ can be estimated from values reported in the literature for CTA+ diffusion in D2O, correcting for the solvent viscosities (viscosity for water-butanol mixtures was taken from ref. 23). This calculation, which should be regarded as an order-of-magnitude estimate, yields that 8% of the surfactant ions dissociate from the reverse micelles of CTAPA30 in butanol at the highest water contents (13 wt%).
The analysis above implies that the surfactant ion diffusion data reported in Figure 9A at the lowest water content, hence disregarding CTA+ dissociation, reflects the diffusion of CTAPA30 aggregates. We may test this conclusion by calculating the theoretically predicted diffusion coefficient for a short rod-like aggregate containing a stretched PA30 polyion surrounded by surfactant ions, using the following equation:24,25
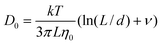 | (Eq. 4) |
Here L and d are the length and diameter of the rod, respectively, ν = 0.312 + 0.565/(L/d) − 0.1/(L/d)2 in a regime where 5 < L/d < 30, and η0 is the solvent viscosity. Assuming a cross-sectional diameter of 18 Å,13 considering that the length of a fully stretched molecule of PA30 is 75 Å, and using the viscosities 7.2, 4.5 and 2.5 mPas for octanol, hexanol and butanol, respectively,26 we obtain aggregate self-diffusion coefficients of 4.3 × 10−11 m2s−1, 2.4 × 10−11 m2s−1 and 1.7 × 10−11 m2s−1 for butanol, hexanol and octanol, respectively, values that are only slightly lower than the experimental results. In view of the uncertainties in both L and d, we conclude that the experimental self-diffusion coefficients agree well with the formation of elongated reverse micelles each consisting of one polyion associated with surfactant ions.
As a further consistency check, we will use the estimated aggregate self-diffusion coefficient for the butanol system to interpret the measured diffusion coefficient of the NMR signal at δ = 4.80 ppm, which has contributions from both water and butanol molecules. The water contribution can also be divided in two parts, from molecules inside and outside the aggregates, producing the following equation:
| Dobs = faDa + 2(ffwDfw + faggwDaggw) | (Eq. 5) |
Here Dobs is the measured self-diffusion coefficient for the pool of exchanging hydroxyl protons and water protons, fa is the mole fraction of butanol, Da is the measured butanol self-diffusion coefficient, fwf is the mole fraction of “free” water; Dwf is the “free” water molecule self- diffusion coefficient; fwagg (=1 − fwf) is the mole fraction of water inside the aggregates (bound water) and Dwagg is the self-diffusion coefficient for bound water, that is, the aggregate self-diffusion coefficient. By using the above estimated value of 4.3 × 10−11 m2s−1 for the aggregate diffusion coefficient, we obtain the only unknown, that is, the fraction of water dissolved in butanol (free water molecules). This amounts to 15 wt%, which is consistent with the water solubility in butanol (20 wt%), supporting the assumptions taken. The free water concentration in the L2 phase should generally be less than 20 wt% except in two- or three-phase samples where the L2 phase is in equilibrium with a dilute water phase.
Structural information from SAXS
SAXS data provide information on the variation of the structure of the L2 phases along the water and alcohol dilution lines. The SAXS patterns for most of the systems investigated display a broad peak that we ascribe to a correlation distance among the reverse aggregates. As seen in Figures 2–5, this distance generally increases on dilution with either alcohol or water, as expected. Figure 11 displays correlation data from SAXS for the investigated systems, plotted against the concentration of the complex salt as a single variable. Clearly, no universal behavior is seen in this plot, but, in general, it seems that these correlation distances decay more pronouncedly along the water dilution lines than the ones observed for the butanol dilution lines, as indicated in Figure 11. To make an attempt at a quantitative interpretation of the data in Figure 11, we will use an idealized structural model of our systems as a starting point. For this purpose, we choose a hexagonal array of cylindrical, rod-like micelles of infinite length. A more-or-less stretched polyion is at the center of each rod. From simple geometrical considerations (see Supplementary Material†) one obtains the following expression for the variation of the correlation distance, d, with the concentration of complex salt in such a structure| d2 = (2/√3)vs/(lrepϕs) | (Eq. 6) |
 | ||
| Fig. 11 Correlation distances derived from SAXS spectra for the complex salts CTAPA30 and CTAPA6000 in ternary mixtures with butanol and water, plotted against the mass fraction of complex salt. A line describing the behavior predicted by a structural model is also plotted (see text for details). | ||
Here vs is the partial specific volume of a repeating unit of the complex salt, lrep is the incremental increase in length of the reverse micelle on adding one repeating unit of the complex salt to the micelle, and ϕs is the volume fraction of complex salt in the system. We see that the correlation distance d in the idealized structure only depends on two variables (vs can be assumed to be constant): the concentration of complex salt ϕs and the degree of stretching of the polyion inside the (infinitely long) micelle, expressed by lrep. Thus, the correlation distance does not explicitly depend on the distribution of the various molecular species (surfactant ion, alcohol and water) radially away from a polyion.
For explicit numerical calculations, we will chose lrep = 0.25 nm, which is the length per repeating unit of a fully stretched polyacrylate polyion. Previous studies have shown that the partial specific volume of the complex salt in water is very close to 1 ml/g. Since the molar mass of a repeating unit of the complex salt is 355 g/mol, we thus obtain vs = 0.589 nm3. We may further approximate the volume fraction of complex with the weight fraction, that is, ϕs ≈ ws. Inserting these approximations and numerical values gives
| d/nm = √(2.722/ws) | (Eq. 7) |
We have plotted Equation 7 in Figure 11 along with the experimental data. While the calculations yield distances of the correct order of magnitude, we see that the experimental distances represent both positive and negative deviations from the idealized model predictions. We can immediately identify two reasons for such discrepancies.
(1) The polyions are not fully stretched. The configurational entropy of the polyion should lead to some coiling inside the micelle. This effect leads to a lower value of lrep and, hence, a larger value of d than predicted. Moreover, there will be a driving force to contract of the micelle in the axial direction in order to decrease the surface between the aqueous interior and the predominantly hydrocarbon exterior of the reverse micelle. On the other hand, the partial dissociation of surfactant ions, discussed earlier, gives rise to a long-range repulsion that should act to stretch the micelle.
(2) The true structure deviates significantly from the assumed hexagonal packing. Neglecting that the number of neighbouring chains may be different from six, a particularly unrealistic assumption in the idealized structure is that of infinite cylinders. The real micelles are finite in length, and even if the hexagonal arrangement should be a good approximation, two consecutive micelles along the rod axis will surely be separated by a finite gap, which also increases on dilution (the swelling is not strictly two-dimensional). In the model, such a gap will lead to a higher (average) lrep.
Based on the above considerations, we may attempt to discuss the different concentration dependencies along the water and alcohol dilution lines observed in Figure 11. Dilution along the alcohol dilution line gives a very weak concentration dependence in the real systems, compared to the ws−1/2 dependence predicted by the model. This could be due to a partial cancellation of the decrease in ws by an increase in lrep on dilution. Both the dilution per se (effect 2 above) and a stretching of the polyion chain, due to an increasing dissociation of surfactant ions, should contribute to such an increase in lrep on dilution.
Dilution along the water dilution line, on the other hand, gives an experimental concentration dependence that is close to the model prediction. Here the pure dilution effect—which still must operate—may be partially cancelled by a contraction of the micelle. Added water predominantly enters into the micellar interior, and an increase in the volume of the aqueous interior should lead to a contraction of the micelle in the axial direction, in order to decrease the unfavourable increase in surface area of the aqueous interior. We note in this context that a value of the area per surfactant ion headgroup at the water/hydrocarbon boundary is difficult to estimate, since an unknown fraction of alcohol may act as a cosurfactant at this boundary.
Comparisons with previous studies on related systems
In a study of L2 phases formed in mixtures of a long poly(acrylic acid) (n = 6000) and a double-chained (didodecyl) cationic surfactant in the presence of water and cyclohexane, Shioi et al.11 proposed the formation of reverse cylindrical surfactant aggregates which were interconnected via the polymer chain dissolved in the water pool of the aggregates. Although this model has similarities with the one we propose, an essential difference is that we believe that each aggregate is one micelle containing one polyion: an elongate micelle with a spine. On a priori grounds, we reject a necklace-type model where a long polyion connects many smaller micelles. This type of structure would imply the existence, in each extended aggregate, of many micellar ends, as well as short stretches of polyion exposed to the alcoholic solvent as it connects one micelle to the next. Such an arrangement would only increase the free energy of the aggregate compared to a structure where a single rodlike micelle encloses the entire polyion.Systems containing a complex salt of DNA with the dodecyltrimethylammonium counterion (DTA-DNA)27 mixed with water and different n-alcohols also presents an L2 phase region in the n-alcohol-rich corner, which also occupies an increasingly larger area of the phase diagram with a decrease in the n-alcohol chain length. In the cited study, the nature of the alcoholic isotropic phase was not extensively analyzed. However, it was proposed that the L2 phase was composed of dissolved complex salts. Interestingly, Leal et al27 also observed that the alcoholic isotropic phases with butanol and hexanol were highly viscous for high contents of the DTA-DNA complex salt and displayed rubber-like mechanical behavior, which suggests that reverse aggregates similar to the ones formed by CTAPA complex salts were formed in those systems.
5. Conclusions
In this work we have studied the alcoholic isotropic L2 phase present in systems composed of complex salts CTAPAn (n = 30 or 6000), n-alcohol (octanol, hexanol or butanol) and water by a range of methods. By using mixtures containing a minimum number of components (complex salt, alcohol and water) we could approach these systems in a systematic way and study trends that occur along well-defined dilution lines. We have arrived at the following picture of the aggregates formed, which is consistent with all our experimental data.The L2 phase contains discrete reverse micelles, where each micelle contains one polyion chain (reverse micelles with spines). These micelles can take up added water in their cores, but there is a partitioning of the water molecules between the micellar core and the surrounding alcoholic solvent. A finite fraction of surfactant ions dissociate from the reverse micelles, leading to polyelectrolyte behavior, increased aggregate-aggregate repulsion and a comparatively rapid surfactant ion diffusion, especially when the short-chain butanol is the continuous medium. On addition of water to the system, the increasing concentration of water in the continuous alcohol solvent domain leads to increasing dissociation of the surfactant ions from the reverse micelles. This effect was again most notable for butanol, where the water solubility is comparatively high.
This study illustrates that one can tune the size of reverse micelles in alcoholic L2 solutions by using polymeric, rather than monomeric, counterions, leading to strong variations in the rheological properties of the solutions. Still, these reverse aggregates can take up a significant amount of water in their cores. Hence, they represent interesting systems in which one can couple attractive macroscopic (rheological) properties, with interesting microstructures (the presence of an aqueous core).
6.Acknowledgements
The authors thank the Brazilian Agencies FAPESP, for financial support on this work, and for a PhD scholarship to J.S.B., and CNPq, for support and for a senior researcher grant to W.L. The Brazilian Synchrotron Laboratory (LNLS) is also acknowledged for the use of the SAXS beamline and for the support of line staff. We thank Ingrid Åslund for her help with the NMR diffusion measurements. LP is grateful to the Swedish Research Council for funding.7.References
- A. Svensson, L. Piculell, B. Cabane and P. Ilekti, J. Phys. Chem. B, 2002, 106, 1013 CrossRef CAS.
- A. Svensson, D. Topgaard, L. Piculell and O. Söderman, J. Phys. Chem. B, 2003, 107, 13241 CrossRef CAS.
- A. Svensson, J. Norrman and L. Piculell, J. Phys. Chem. B, 2006, 110, 10332 CrossRef CAS.
- J. S. Bernardes, J. Norrman, L. Piculell and W. Loh, J. Phys. Chem. B, 2006, 110, 23433 CrossRef CAS.
- J. S. Bernardes and W. Loh, J. Colloid Interface Sci., 2008, 318, 411 CrossRef CAS.
- J. Norrman, I. Lynch and L. Piculell, J. Phys. Chem. B, 2007, 111, 8402 CrossRef CAS.
- L. Piculell, J. Norrman, A. Svensson, I. Lynch, J. S. Bernardes and W. Loh, Adv. Colloid Interface Sci., 2009, 147–148, 228 CrossRef CAS.
- M. Antonietti, S. Förster, M. Zisenis and J. Conrad, Macromolecules, 1995, 28, 2270 CrossRef CAS.
- K. N. Bakeev, Y. M. Shu, A. B. Zezin, V. A. Kabanov, A. V. Lezov, A. B. Mel'nikov, I. P. Kolomiets, E. I. Rjumtsev and W. J. MacKnight, Macromolecules, 1996, 29, 1320 CrossRef CAS.
- K. N. Bakeev, E. A. Lysenko, W. J. MacKnight, A. B. Zezin and V. A. Kabanov, Colloids Surf., A, 1999, 147, 263 CrossRef CAS.
- A. Shioi, M. Harada, M. Obika and M. Adachi, Langmuir, 1998, 14, 5790 CrossRef CAS.
- A. Shioi, M. Harada, M. Obika and M. Adachi, Langmuir, 1998, 14, 4737 CrossRef CAS.
- J. S. Bernardes, W. Loh and L. Piculell, unpublished results Search PubMed.
- K. Fontell, A. Khan, B. Lindström, D. Maciejewska and S. Puang-Ngern, Colloid Polym. Sci., 1991, 269, 727 CrossRef CAS.
- A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Häusermann, Int. J. High Pressure Res., 1996, 14, 235 Search PubMed.
- C. Cabaleiro- Lago, M. Nilsson and O. Söderman, Langmuir, 2005, 21, 11637 CrossRef CAS.
- G. Lafitte, K. Thuresson and O. Söderman, Langmuir, 2005, 21, 7097 CrossRef CAS.
- J. W. Goodwin and R. W. Hughes, Rheology for Chemists: an Introduction, The Royal Society of Chemistry, Tyne and Wear, UK 2000 Search PubMed.
- M. Jonströmer, B. Jönsson and B. Lindman, J. Phys. Chem., 1991, 95, 3293 CrossRef.
- J. Appell, G. Porte, A. Khatory, F. Kern and S. J. Candau, J. Phys. II, 1992, 2, 1045 CrossRef CAS.
- T. J. Drye and M. E. Cates, J. Chem. Phys., 1992, 96, 1367 CrossRef CAS.
- L. Ambrosone, R. Angélico, A. Ceglie, U. Olsson and G. Palazzo, Langmuir, 2001, 17, 6822 CrossRef CAS.
- A. D'Aprano, I. D. Donato, E. Caponetti and V. Agrigento, J. Solution Chem., 1979, 8, 793 CAS.
- M. Tirado and J. Garcia de la Torre, J. Chem. Phys., 1979, 71, 2581 CrossRef CAS.
- M. Tirado and J. Garcia de la Torre, J. Chem. Phys., 1980, 73, 1986 CrossRef CAS.
- D. R. Lide, Handbook of Chemistry and Physics, CRC Press, Washington D.C., 2000 Search PubMed.
- C. Leal, A. Bilalov and B. Lindman, J. Phys. Chem. B, 2006, 110, 17221 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Structural model to describe the L2-phase of complex salt. See DOI: 10.1039/b917187h |
| This journal is © The Royal Society of Chemistry 2010 |