Detection limits in photothermal microscopy†
Alexander
Gaiduk
,
Paul V.
Ruijgrok
,
Mustafa
Yorulmaz
and
Michel
Orrit
*
Institute of Physics, Leiden University, P.O. Box 9504, 2300 RA, Leiden, The Netherlands. E-mail: orrit@molphys.leidenuniv.nl; Fax: +31 71 520 5910
First published on 18th June 2010
Abstract
We show how to push the detection limits in photothermal microscopy towards weaker single absorbers, by a systematic optimization of signal and noise sources. In particular, we (i) maximize the power of the probe laser beam, (ii) select optimal optical and thermal properties for the medium embedding the absorber, and (iii) thermally isolate the absorber from the glass substrate. These different experimental conditions are optimized in turn with single immobilized gold nanoparticles. We demonstrate the detection of a dissipated power of 3 nW with a signal-to-noise ratio of 8, and an integration time of 10 ms. This corresponds to a less than 0.1 K surface temperature rise for a 20 nm-diameter gold nanosphere (0.4 K for 5 nm). As an example of the achieved detection sensitivity, we show simultaneous photothermal and fluorescence detection of individual 20 nm fluorescent beads, each containing about 20 Nile red dye molecules.
Introduction
Photothermal, photoacoustic and photo-optical (photorefractive and photochromic) effects are widely used in physics, analytical chemistry and medicine.1 Photothermal spectroscopy is a two-color nonlinear optical technique, in which a heating (pump) beam is absorbed by the species to be detected, causing heat release and a local change of refractive index. The propagation of a second beam at a different wavelength, the probe, will thus be modified by the produced heat. These changes produce the observed signal.2 Photothermal spectroscopy provides a number of ultrasensitive methods to measure optical absorbance and estimate concentrations of nanometre-sized particles and non-fluorescent molecules in solvents.3,4 Photothermal detection has two main advantages. First, the signal is free from background and not sensitive to weak scattering, because the signal only arises from absorbing centers that dissipate heat. Second, because the probe only reacts to refractive index changes, the probe wavelength can be chosen outside of the absorption range of the centers. Therefore, the probe power can be increased to very high values, for which photon noise in the probe detection may become extremely small. The maximum probe power applicable is ultimately limited by sample damage.Recent developments based on the combination of photothermal effects and interferometric detection have opened up absorption properties of individual labels to optical detection with a high signal-to-noise ratio. Such absorbing labels do not need to fluoresce and have been small (<40 nm diameter) noble metal nanoparticles, quantum dots, or single-walled carbon nanotubes.5–13 In contrast to the organic molecules used in fluorescence detection, these labels generally show neither photobleaching nor photoblinking, which makes them attractive for many applications, such as DNA microarrays,14 gold-labeled protein detection in cells,15 optical tracking in live cells16 and high-throughput screening.17 Recently, the dynamic range of photothermal microscopy experiments has expanded and new applications have been suggested. Photothermal correlation spectroscopy has been proposed to study the diffusion of single gold nanoparticles in fluid media, and was demonstrated with protein–gold complexes and gold-labeled bacteriophage viruses.18–20 The selectivity and sensitivity of photothermal detection was demonstrated for direct imaging of mitochondria in live cells, without need for any labeling.21 The origin of the photothermal contrast of mitochondria is still not well understood, for the abundant inter-membrane protein cytochrome c was excluded as the source of the photothermal signal. The anisotropic absorption properties of small (25 × 75 nm) gold nanorods have been probed with polarization-sensitive photothermal microscopy.22 The authors of that work propose to use plasmon resonances of rods to probe orientation and dynamics of macromolecules in highly scattering environments. A photothermal excitation combined with digital heterodyne holography23 provides wide-field (up to 100 μm2 area) photothermal detection of 50 nm and smaller gold particles. The method involves a trade-off between large observation areas, video rate acquisition speed, and a large radius of heat diffusion.24 Compared to single-point detection, the signal-to-noise of wide-field detection is about an order of magnitude lower.
To further expand the performance and applications of single-point photothermal detection, it is important to look for its detection limits. To our knowledge, the best signal-to-noise ratio measured in single-point photothermal detection8 was about 10 for a 5 nm gold nanoparticle (NP) heated with a power of 500 μW (514 nm), with unspecified probe power, and with an integration time of 10 ms.9 We estimate the absorbed power in these experiments to 20 nW. It is important to know how far this result is from the theoretical limit.12,18 In the several publications following this early work, little attention has been paid to the various factors which may influence the signal-to-noise ratio in photothermal detection. In this work, we examine how the probe power, the thermal properties of the medium, and thermal isolation of the absorber from the glass substrate influence the signal-to-noise ratio. To demonstrate how important the control of these parameters is, we report the simultaneous detection of photothermal and fluorescence signals from single, weakly absorbing, 20 nm-diameter fluorescent polystyrene beads.
The paper is organized as follows. We first discuss the photothermal method to identify the origin of the signal and the possible noise sources. The Experimental section describes the experimental setup and sample preparations. We then report and discuss results in the Results and discussion section before concluding.
Method
Photothermal detection is sensitive to the amount of energy absorbed by a nanoobject and dissipated as heat into its local environment. We define as the dissipated power Pdiss the power provided by a heating beam (with power Pheat), which is dissipated as heat by the absorber. Because the heating beam intensity is modulated at an angular frequency Ω, we call Pdiss the maximum instantaneous value of this power during the modulation period. The time-averaged dissipated power is therefore Pdiss/2. For a spherical gold particle of radius R placed in a homogeneous medium with thermal conductivity κ, the maximum temperature increase ΔT(r,t) = ΔTsurf scales as R2, because the cross-section σabs scales as R3.25–27 The thermal radius is the characteristic length of heat diffusion in the medium. Dissipation of the absorbed energy into the medium results in a temperature profile ΔT(r,t), which in steady conditions with sinusoidal modulation is given by:5
is the characteristic length of heat diffusion in the medium. Dissipation of the absorbed energy into the medium results in a temperature profile ΔT(r,t), which in steady conditions with sinusoidal modulation is given by:5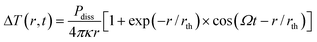 | (1) |
Assuming the response to be instantaneous, this temperature profile in turn causes a refractive index profile Δn(r,t) = ΔT(r,t) × ∂n/∂T in the medium, acting as a modulated thermal nanolens.2 A probe beam is used to detect that nanolens. In the usual photothermal geometry2,4,7 the scattered probe field Esc(t) interferes with a reference probe field Eref (usually the transmitted beam or a reflection), and the resulting intensity Idet ∝ |![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ref +
ref + ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) sc|2 is detected. In this discussion, we neglect the difference in spatial modes of the two fields, which are supposed to be similar. The lock-in amplifier filters out the weak contribution to the interference signal 2Re[E*refEsc(t)] modulated at the same frequency as the heating beam. The contribution of the modulated scattered intensity |
sc|2 is detected. In this discussion, we neglect the difference in spatial modes of the two fields, which are supposed to be similar. The lock-in amplifier filters out the weak contribution to the interference signal 2Re[E*refEsc(t)] modulated at the same frequency as the heating beam. The contribution of the modulated scattered intensity |![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) sc|2 is neglected for small particles (typically <60 nm).27 For larger particles, a non-negligible static scattered field acts as an additional in-phase reference field. Its contribution to the interference intensity Idet is reported in photothermal correlation spectroscopy experiments for 80 nm gold particles.18
sc|2 is neglected for small particles (typically <60 nm).27 For larger particles, a non-negligible static scattered field acts as an additional in-phase reference field. Its contribution to the interference intensity Idet is reported in photothermal correlation spectroscopy experiments for 80 nm gold particles.18
The photothermal signal S is proportional to the field scattered by an effective volume V where the refractive index is modulated. The refractive index change Δn depends on the absorption cross-section σabs of the nanoobject and the heating beam with intensity Iheat focused into a diffraction-limited spot with area A. Δn is proportional to the power dissipated by the nanoobject Pdiss = Iheatσabs = σabsPheat/A. The field scattered by the thermal lens can be approximated by that of an equivalent dipole |![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) |≈2nΔn·V·|
|≈2nΔn·V·|![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) probe|, where Δn·V stands for the volume integral of the position-dependent refractive index change of the lens. The scattered field is radiated by this dipole:
probe|, where Δn·V stands for the volume integral of the position-dependent refractive index change of the lens. The scattered field is radiated by this dipole:  , and the photothermal signal can then be written as an optical power:
, and the photothermal signal can then be written as an optical power:
 | (2) |
The noise in actual experiments arises from the detector, from fluctuations of the probe laser power, and from photon noise of the detected optical power. In practice, the experimental noise is always larger than the photon noise, but can be close to it for an optimized setup. Here, assuming an ideal detector and a shot-noise limited detection, the noise on the photothermal signal N would be:
 | (3) |
Combining the expressions for the signal and the noise, we see that the signal-to-noise ratio SNR for the shot-noise-limited photothermal detection is given by:
 | (4) |
We now discuss how the SNR can be optimized by tuning all factors in expression (4), and the practical limits to optimization.
1. Increase the dissipated power up to the allowed maximum, usually fixed by saturation. For gold nanoparticles, the applicable powers are very high (the bulk melting temperature of gold is about 1300 K, and the temperature rise to reshape gold nanorods, although significantly lower28,29 is still some hundreds of K). The allowed temperatures in biological samples, however, will be much lower. The melting intensity for a spherical particle with diameter 20 nm in water is around 20 MW cm−2 at 514 nm (about 20 mW focused on a spot), and scales with R−2. For a non-fluorescent molecule, the saturation intensity is determined mostly by the excited state lifetime τ, typically 0.1 ns, which leads to a dissipated power of a few nW.
2. Increase Pprobe as much as possible. Practical limits are set by the maximum available laser power and by residual absorption of the probe beam by the sample. For example, the probe power can be increased until the probe-induced and pump-induced heating are comparable. For small gold NPs in glycerol, for example, we can use up to 170 times more probe power at 800 nm than heating power at 532 nm, as given by the ratio of the absorption cross-sections (see ESI B†).
3. Match the heat diffusion length rth with the spot size, by choosing the right modulation frequency Ω.5,12 A lower modulation frequency generally leads to a higher photothermal signal, until the thermal lens exceeds the size of the focused probe beam (see ESI C†). The optimal value of the modulation frequency also depends on the experimental noise spectrum.
4. Optimize the optical and thermal properties of the photothermal medium, including refractive index, its derivative with respect to temperature, heat capacity and conductivity (see Section 3 and ESI A†).
5. Increase the integration time of the lock-in amplifier. This parameter can be increased arbitrarily, provided the mechanical stability of the experimental setup and the photostability of a sample allow it.
Experimental
Sample preparation
Samples of gold colloids with diameters of 5 nm and 20 nm (British Biocell International, EM.GC5 and EM.GC20) were prepared by dilution in ultra-pure water at the ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and 1
40 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8, respectively. Approximately 50 μL of the suspension were deposited on the surface immediately after the filtration through a 450 nm porous membrane and spin coated at 2000 rpm for 5 s, followed by drying at 4000 rpm for 90 s. Fluorescent Nile red beads with a diameter of 20 nm were purchased from Sigma-Aldrich and deposited on the surface after dilution in ultra-pure water (1
8, respectively. Approximately 50 μL of the suspension were deposited on the surface immediately after the filtration through a 450 nm porous membrane and spin coated at 2000 rpm for 5 s, followed by drying at 4000 rpm for 90 s. Fluorescent Nile red beads with a diameter of 20 nm were purchased from Sigma-Aldrich and deposited on the surface after dilution in ultra-pure water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000) without filtration.
1000) without filtration.
Glass coverslides (Menzel, Germany) were cleaned by sonication for 20 min in the following solvents: 2% Hellmanex (Hellma) solution in water, acetone (96% purity), ethanol (96% purity). Additional sonication in water was performed prior to each cleaning step. The glass coverslides were then dried and treated in a UV-ozone cleaner for at least 30 min prior to following sample preparation steps.
PMMA, poly(methyl methacrylate), with Mw = 96.7 kDa (Sigma-Aldrich) was used to prepare a thermal isolation layer on top of clean substrates. About 50 μL of PMMA solution in toluene at 30 g L−1 concentration was spin coated. The thickness of the resulting PMMA layer was measured by AFM and found to be 100–120 nm.
For the preparation of nanoparticles (NP) on PMMA, a 2% PVA solution (polyvinyl alcohol, Mw = 130 kDa, Fluka) in water was mixed with NPs to provide the desired concentrations of gold colloids and 1% concentration of PVA. The sample was prepared via spin coating, resulting in a PVA layer thickness of approximately 20 nm. The thin PVA film was found to be dissolved after several hours in glycerol. NPs remain adsorbed on the PMMA surface.
The measurements were performed in a fluid cell with ∼50 μL photothermal medium. The cell was assembled from two glass coverslips with a rubber o-ring attached to the bottom one. Clean glycerol (>99.5%, spectrophotometric grade), ethanol (spectroscopy grade), chloroform (spectroscopy grade), dichloromethane, pentane, and hexane (all AR grade) were used as photothermal media.
Experimental setup
The experimental setup is based on a home-built microscope equipped with an Olympus 60× oil immersion objective (NA = 1.4 or NA = 1.45) and is sketched in Fig. 1.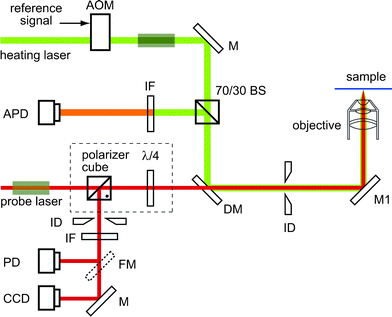 | ||
| Fig. 1 Scheme of the experimental setup for simultaneous photothermal and fluorescence detection. The heating light for photothermal microscopy also excites fluorescence at the same time. AOM – acousto-optical modulator, M – mirror, FM – flip mirror, BS – beam splitter, DM – dichroic mirror, ID – iris diaphragm, λ/4 – quarterwaveplate, IF – interference filters, APD – avalanche photodetector, PD – photodiode, CCD – video camera. Polarizer, spatial filters are not shown in this scheme. Grey boxes schematically indicate the positions of the telescopes and beam expander. A dashed line indicates the position of the “cat's eye” parts (a polarizer beam splitter and a waveplate) that are replaced by a beamsplitter in the “50/50 BS” configuration (see experimental section for details). | ||
Photothermal detection
The heating beam is provided by either a laser diode at 532 nm (Shanghai Lasers, power 150 mW) or by an Ar-ion laser at 514 nm (Coherent, max. output 10 W). The heating light passes an acousto-optical modulator (AOM) which is operated typically at Ω = 740 kHz. The beam is expanded in a spatial filter (60 mm and 100 mm lenses, with a 30 μm pinhole) and a telescope (100 mm and 200 mm) to about 20 mm, and overfills the entrance pupil of the microscope objective (approximately 10 mm). The expanded beam is sent towards the microscope objective by a dichroic mirror (BS 669, AHF) on which heating and probe beams are combined. The probe beam at 790 nm or 800 nm is provided by a Ti:sapphire laser (either Mira, Coherent, pumped with Coherent Verdi V10; or Spectra Physics, 3900S, pumped by 90% of the power of the Ar-ion laser). The near-infrared light (NIR) passes a polarizer and a spatial filter (two 75 mm lenses with a 30 μm pinhole). A variable beam expander 2–5× provides the continuous adjustment of the diameter of the probe light to ensure the optimal overfilling of the objective lens with the desired probe power.We have used two further modifications of the setup:
(i) “50/50 BS” reflector. A 50/50 beam splitter (Halle) is used to reflect half the power of the probe laser to the microscope and transmit half the back-scattered probe light towards the detector. Unless specified otherwise, all our experimental data were obtained in this “50/50 BS” configuration.
(ii) “Cat's eye” reflector (see Fig. 1). The linearly polarized probe light passes a polarizing beam splitter cube (Halle) and a λ/4 waveplate (Halle) without loss. The emerging circularly polarized light is sent to the objective after a silver mirror. The back-scattered probe light travels back towards the detector. Passing the λ/4 waveplate, it becomes linearly polarized perpendicular to the incoming probe light. The polarizing beamsplitter reflects the back scattered light towards an iris diaphragm, a notch filter for 532 nm and a long-pass filter (LP 750) to block any residual heating light. For paraxial rays, the “cat's eye” reflector allows one to minimize probe power losses, thus providing better signal-to-noise ratio. However, additional polarization changes are caused by the silver mirror and by depolarization for the off-axis back-scattered rays by the objective. This may explain why the theoretical signal-to-noise gain of the cat's eye configuration (see ESI E†) is not realized in practice.
The spectrally filtered probe light is focused with a 100 mm lens onto a photodiode (Femto DHPCA-100-F, Germany) or optionally monitored by a CCD camera (Ganz, Germany).
A wave generator (33250A, Agilent) provides the modulation signal for the AOM and the reference of the lock-in amplifier (SR844, Stanford Research Systems) analyzing the photodiode output. All data acquisition and processing is performed by an acquisition card (ADWin Gold, Germany) linked to a computer. The sample is scanned with a 3-axis piezostage (NanoCube, Physik Instrumente).
Fluorescence detection
The fluorescence is collected in the back-scattered direction, picked up by a 70/30 beamsplitter, spectrally filtered from residual heating light by a band-pass filter (Omega 590/100) and a short-pass filter (SWP 650), and detected by the single-photon counting module (APD, SPCM-AQR-16, Perkin Elmer).Results and discussion
Photothermal imaging of gold nanoparticles
We first demonstrate the performance of our setup with photothermal microscopy on 5 nm and 20 nm diameter gold nanoparticles. A photothermal microscopy image (Fig. 2a) shows about 30 particles with 20 nm diameter (density < 1 NP μm−2) and 3 particles with 5 nm diameter (density < 0.1 NP μm−2). Cross-sections of the spots of some 20 nm NPs and of the 5 nm NPs indicate an intensity ratio of 35, not too far from the expected ratio (20/5)3 = 64 (Fig. 2b). The difference is explained by deviations from the nominal average NP diameter provided by the manufacturer. Indeed, we found by AFM and SEM that the diameters of the nominal 20 nm NPs varied between 14 nm and 18 nm. Moreover, some particles, for example triangles, were found to deviate significantly from the spherical shape (ESI F†). The results of the photothermal imaging and SNR analysis of 73 particles of 20 nm and 119 particles of 5 nm are presented in Fig. 2c and summarized in Table 1. We detect 20 nm NPs with a SNR of 420 and an integration time of 1 ms with 260 μW of heating power and 20 mW of probing power at the sample's position. These values correspond to 810 nW of dissipated heating power and to 170 nW of dissipated probe power. The total power absorbed corresponds to a temperature rise of about 28 K at the surface of a 20 nm NP. A SNR of 12 is achieved with the same integration time, heating, and probe powers for 5 nm NPs. For the 5 nm particles, the dissipated powers are 12.6 nW for the heating beam and 2.6 nW for the probing beam, and the respective surface temperature rise about 0.5 K.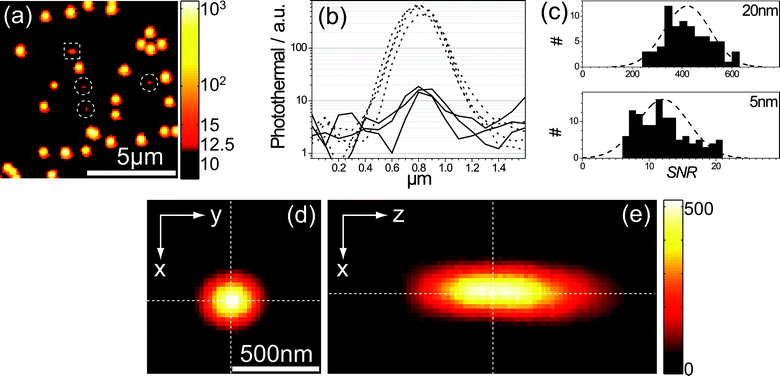 | ||
| Fig. 2 (a) Photothermal microscopy image of a sample with gold nanoparticles of 20 nm and 5 nm diameter immobilized on a glass slide in glycerol. The photothermal signal is color-coded on a logarithmic scale. Circles mark the positions of 5 nm NPs. The NP in the square box may be an aggregate. Pheat = 0.26 mW, Pprobe = 20 mW, Δt = 1 ms, ΔTsurf ∼ 28 K. (b) Several cross-sections of 20 nm (dashed lines) and 5 nm (solid lines) NPs along the slow scan axis (horizontal in the image) present relative signals for particles of different sizes. (c) Histograms of the photothermal SNRs for gold NPs of 20 nm (top, 73 NP) and 5 nm (bottom, 119 NP). The population of 5 nm particles has SNR = 12 ± 4, while the population of 20 nm particles has SNR = 421 ± 92. Experimental data are presented in histograms. (d) Photothermal image of a single 20 nm gold colloid. (e) Photothermal image of a single 20 nm gold NP taken along the vertical z-axis, perpendicular to the glass surface. Gaussian fits of the shape of the signal along the z-, y- and x-axes give FWHM values of 730 nm, 250 nm, and 220 nm, respectively. Vertical dashed lines indicate the position of the glass–glycerol interface (glass on the right-hand side). | ||
| I heat/kW cm−2 | I probe/MW cm−2 | P diss/nW | P diss(probe)/nW | ΔTsurf/K | ΔTsurf(probe)/K | Δt/ms | SNR | |
|---|---|---|---|---|---|---|---|---|
| 20 nm | 130 | 4.5 | 810 | 170 | 23 | 4.8 | 1 | 421 |
| 5 nm | 130 | 4.5 | 12.6 | 2.6 | 0.4 | 0.08 | 1 | 12 |
The spatial overlap of heat and probe beam in photothermal microscopy provides optical sectioning and defines the spatial resolution. The photothermal detection volume is defined by the product of the point spread functions of heating and probe beams. By focusing both beams into overlapped diffraction-limited spots, we achieve a lateral spatial resolution of about 240 nm, and an axial resolution of 730 nm (Fig. 2d, c).
Improvements of SNR in photothermal detection of gold NPs
Hereafter, we discuss several possible ways to increase the photothermal SNR, and verify them experimentally with 20 nm gold NPs.Probe power
As follows from eqn (4), the SNR in ideal photothermal experiments should be proportional to the square root of the probe power. The measurements of SNR are presented in Fig. 3a. The good agreement with the expected power law (eqn (4)) indicates that the noise in our photothermal detection is mainly determined by photon noise (see ESI D†). In particular, for the range of probe powers detected in our experiments, laser noise is negligible. At low probe powers, the SNR deviates from the square-root dependence because of detector noise, which is independent of power. | ||
| Fig. 3 (a) Photothermal signal-to-noise ratio as a function of the incident probe power (λ = 790 nm) measured for 20 nm gold NPs in water on glass. The fit shows the square root dependency of the SNR. (b) Photothermal SNR measured for 20 nm NPs in different fluids as a function of calculated photothermal strength for these fluids ΣPT, scaled with respect to glycerol. Measurements were done on a few NPs in water, 116 NPs in glycerol, 92 NPs in ethanol, 60 NPs in dichloromethane, 41 NPs in hexane, 63 NPs in chloroform and 30 NPs in pentane. The error bars give the standard deviation of the distribution. (c) Normalized histograms of SNR for 20 nm gold NPs in glycerol: (dark grey) deposited on glass, SNR = 272 ± 110 over 38 particles; (light grey) deposited on a 100 nm thick thermal isolation layer of PMMA, SNR = 502 ± 128 over 211 particles. Among them, 6 particles show SNR values twice the mean distribution value (>1000) indicating a few aggregates (<3%) in the area of 1000 μm2. Experimental parameters: heating with 0.27 mW incident power at 514 nm, probe at 800 nm with 23 mW incident power, corresponding to a total ΔTsurf ∼ 28 K (due to heat and probe), integration time 3 ms. | ||
To achieve maximum sensitivity in the photothermal detection, we want to keep the photodetector gain maximal. This gain is limited by the total power reaching the detector. Apart from its weak time-dependent component encoding the photothermal signal, the detected probe power has a strong static contribution, which arises from reflection by the glass–liquid interface. The reflected power, determined by the refractive index mismatch between the BK7 glass (n = 1.52) and the medium (see ESI A†), varies from 4.4 × 10−3 for the glass–water (n = 1.33) to 2.5 × 10−4 for the glass–glycerol (n = 1.473) interfaces, as given by Fresnel's equations for normal incidence. We chose a maximum detected probe power of 18 μW, corresponding to a gain of 105 A V−1, which is a trade-off between high probe power and low photodetector noise (see ESI D†). Then, the maximal incident probe power varies from 4 mW for water to 72 mW for glycerol. Note that achieving photon-noise limited detection in the forward direction is more difficult than in the backward direction for two reasons. First, it is difficult to find fast and sensitive detectors for powers larger than 20 mW. Second, photon-noise limited detection of higher powers requires a lower laser noise.
Solvent
As has been known for many years, the thermal properties of the solvent are crucial for photothermal spectroscopy and its applications to analytical chemistry.2 An obvious step to enhance the photothermal signal is to select a solvent with a high sensitivity of its refractive index to a temperature change, (∂n/∂T). Note, however, that this (usually negative) quantity is only a crude figure for characterization of the heating-induced change of refraction for small enough temperature rises. To account for the full space- and time-dependent changes of refractive index around the heated object, the full function n(r,T) should be considered. In addition to its optical properties, the thermal properties of a medium determine the magnitude of the photothermal signal. We selected several organic fluids based on their expected value for a parameter we call ‘photothermal strength’ (see ESI A†):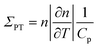 | (5) |
This parameter characterizes the refractive index change that is produced by a given energy density (heat/unit volume) stored in the photothermal medium. However, because the thermal radius rth must be fixed in relation to the probe wavelength, it may be more relevant to define an alternative figure of merit for photothermal media, FOM (see ESI C†):
 | (6) |
Thermal isolation
The thermal conductivity of glass (1.05 W m−1 K−1) is more than 3 times larger than that of most organic liquids (0.28 W m−1 K−1 for glycerol). Therefore, a large part of the generated heat will be lost to glass, where the associated refractive index change is very small. The thermal conductivity of the glass support, which acts as a heat sink, thus reduces the photothermal effect. A thermal isolation layer introduced between the absorber and its solid substrate will reduce the ‘leak’ of heat into the glass. We chose to prepare a thin PMMA film (heat conductivity 0.2 W m−1 K−1) on top of the glass substrate prior to gold NP deposition. The film deposited via spin coating was found to have a homogeneous thickness of 100–120 nm (see ESI G†). An alternative way to achieve thermal isolation is to use a PMMA substrate; however, available substrates have poor optical quality and are too thick compared to the working distance of high NA microscope objectives.A comparison of photothermal SNRs for 20 nm gold particles on glass and on PMMA on glass, both in glycerol, is shown in Fig. 3c. We demonstrate a signal increase by 1.8 times in the presence of the thermal isolation layer, as measured on 38 NPs on glass and 211 NPs on PMMA on glass. This number is smaller than 4, the expected ratio of heat leaks based on the assumption of perfect isolation. Heat diffusion simulations in this complex geometry would be needed for a more quantitative comparison.
Smallest detectable Pdiss in photothermal detection
To compare the efficiencies of photothermal detection of different point-like objects in different conditions, it is sufficient to compare the powers Pdiss they dissipate in their environment. In the following, we probe the limits of photothermal detection in experiments with 20 nm gold NPs in glycerol, which serve as test objects with a well-defined absorption cross-section. We experimentally estimate the smallest Pdiss and temperature rise ΔTsurf which we can detect with a reasonable SNR. Typical results for the photothermal detection of dissipated powers down to 2.6 nW on glass and in glycerol are demonstrated in Fig. 4. Here, heating powers of 9 μW (a) and 1 μW (b) at 514 nm were used. The dissipated powers were 24 nW (a) and 2.6 nW (b) corresponding to temperature rises of 0.7 K (a) and 80 mK (b). These are detected with an average SNR = 20, with a 3 ms integration time (a), and SNR = 8, with a 10 ms integration time (b). | ||
| Fig. 4 Photothermal images of 20 nm gold NPs in glycerol with (a) Pheat = 9 μW, Pprobe = 23 mW, Δt = 3 ms, and with (b) Pheat = 1 μW, Pprobe = 68 mW, Δt = 10 ms. Dissipated powers (Pdiss) and temperature rises (ΔTsurf) are 24 nW and 2.6 nW, and 0.7 K and 80 mK, with average SNRs of 20 and 8, respectively. Heating and probing wavelengths 514 nm and 800 nm. | ||
According to our previous discussion, there are several ways to increase the SNR compared to Fig. 4. We can win a factor of 2 by increasing Pprobe from 68 mW to 280 mW. Another factor of 10 can be gained by increasing the integration time of the lock-in amplifier (Δt) from 10 ms to 1 s. A further enhancement factor of 5 can be gained with a better photothermal medium (pentane instead of glycerol), and one of about 2 with thermal isolation of the particle from the substrate (with PMMA layer). Overall, the SNR can be increased by a factor of 200. Thus, with the achieved sensitivity and proposed experimental conditions we would be able to detect dissipated powers lower than 15 pW within 1 s, with a SNR of 8.
Simultaneous photothermal and fluorescence detection of fluorescent beads
The detection of low dissipated powers with an acceptable SNR opens up the detection and study of other weak absorbers like molecular assemblies. Here, we demonstrate the photothermal detection of individual 20 nm fluorescent beads doped with Nile red dye. The advantage of this sample is that the number of molecules per bead is well-defined and can be estimated from an absorption measurement. The disadvantage is that the dissipation cross-section is much smaller than the absorption cross-section, because most of the absorbed energy is re-emitted as fluorescence. Absorption spectra of 100× diluted stock solution of these beads indicate that there are 25 to 40 Nile red dye molecules per 20 nm bead on average, neglecting the free dye concentration. Fluorescence bleaching experiments with immobilized beads on glass in glycerol indicate that this number is only 5 to 10 dye molecules per bead. We note that, for fluorescein-doped beads of the same size, the manufacturer specifies 180 molecules per bead. This number is not compatible with our absorption and fluorescence measurements of Nile red doped beads (more details can be found in ESI H†).A confocal raster-scan fluorescence image of 20 nm Nile red beads on a glass surface is presented in Fig. 5a. Several beads show signs of bleaching (dark pixel in the lower right corner of the image of a bead) supporting the results of fluorescence bleaching (see ESI H†). A simultaneous photothermal image with the integration time per pixel of 10 ms reveals no detectable photothermal signal originating from the beads (data not shown). We achieve simultaneous fluorescence and photothermal detection in a z-scan (scan in the axial direction, perpendicular to the sample plane) on a single bead (Fig. 5c). An overlap in the fluorescence and photothermal signals illustrates high contrast in fluorescence detection and a corresponding photothermal SNR ∼ 1. Assuming there are 10–40 dye molecules in a bead, the photothermal signal-to-noise ratio for a single dye molecule would be 0.1–0.03 in these conditions.
 | ||
| Fig. 5 (a) Fluorescence microscopy image of immobilized Nile red 20 nm fluorospheres in glycerol. Scanning starts from the top left of the image, with the slow scan axis along the vertical. (b) A cross section along the dashed line indicated in the fluorescence image. Three fluorescent beads show comparable fluorescence intensities. (c) Simultaneous fluorescence and photothermal detection performed on a 20 nm Nile red fluorosphere. The scan is made perpendicular to the surface of the glass, revealing the same positions for the maxima of photothermal (black line) and fluorescence (red line) signals. The photothermal SNR is about 1. Heating with Pheat = 210 μW, probe with Pprobe = 40 mW, and Δt = 10 ms. | ||
Conclusions and outlook
We have proposed several ways to increase the signal-to-noise in photothermal detection. We demonstrate that (i) our SNR is very close to limited by photon noise, in particular laser noise is negligible, (ii) the choice of photothermal medium is very important to achieve a high sensitivity (e.g., pentane gives a 5 times higher signal than glycerol), (iii) a significant signal increase can be achieved by introducing a thin layer of polymer between the glass substrate and the photothermal medium (here, 100 nm of PMMA led to an improvement of the signal by a factor of about 2). The sensitivity of photothermal detection can further be improved by (i) better focusing of the heating and probe beams (for example using radially polarized light30 or immersion in higher indices31); (ii) using a photothermal medium with even larger refractive index changes with temperature, for example fluids close to phase transitions.Furthermore, we have demonstrated the photothermal detection of 3 nW of dissipated power with a SNR ∼ 8 in 10 ms. We also presented the simultaneous photothermal and fluorescence detection of 20 nm fluorescent beads. In these experiments we demonstrate the detection of less than 20 fluorescent molecules with a SNR of about 1. However, the simultaneous fluorescence and photothermal detection of these beads is difficult due to their fast photobleaching at high excitation power, in view of the long integration times required.
Acknowledgements
We thank Anna Pezzarossa and Prof. Thomas Schmidt for help with the wide-field fluorescence microscope, BioAFM lab for providing access to the AFM, and Peter Zijlstra for SEM images of gold NPs. We acknowledge financial support from “Technologiestichting” STW, and the ERC (Advanced Grant SiMoSoMa). This work is part of the research program of the “Stichting voor Fundamenteel Onderzoek der Materie”, which is financially supported by the Netherlands Organization for Scientific Research.References
- M. Terazima, N. Hirota, S. E. Braslavsky, A. Mandelis, S. E. Bialkowski, G. J. Diebold, R. J. D. Miller, D. Fournier, A. R. Palmer and A. Tam, Quantities, terminology, and symbols in photothermal and related spectroscopies, Pure Appl. Chem., 2004, 76, 1083–1118 CrossRef CAS.
- S. E. Bialkowski, Photothermal Spectroscopy Methods for Chemical Analysis, Wiley, 1996 Search PubMed.
- K. Mawatari, T. Kitamori and T. Sawada, Individual detection of single-nanometer-sized particles in liquid by photothermal microscope, Anal. Chem., 1998, 70, 5037–5041 CrossRef CAS.
- M. Tokeshi, M. Uchida, A. Hibara, T. Sawada and T. Kitamori, Determination of subyoctomole amount of nonfluorescent molecules using a thermal lens microscope: subsingle-molecule determination, Anal. Chem., 2001, 73, 2112–2116 CrossRef CAS.
- D. Boyer, P. Tamarat, A. Maali, B. Lounis and M. Orrit, Photothermal imaging of nanometer-sized metal particles among scatterers, Science, 2002, 297, 1160–1163 CrossRef CAS.
- D. Boyer, P. Tamarat, A. Maali, M. Orrit and B. Lounis, Imaging single metal nanoparticles in scattering media by photothermal interference contrast, Phys. E., 2003, 17, 537–540 CrossRef CAS.
- S. Berciaud, L. Cognet, G. A. Blab and B. Lounis, Photothermal heterodyne imaging of individual nonfluorescent nanoclusters and nanocrystals, Phys. Rev. Lett., 2004, 93, 257402 CrossRef.
- S. Berciaud, L. Cognet, P. Tamarat and B. Lounis, Observation of intrinsic size effects in the optical response of individual gold nanoparticles, Nano Lett., 2005, 5, 515–518 CrossRef CAS.
- The same group reported detection of gold NPs as small as 1.4 nm (∼67 atoms) with a signal-to-noise ratio of about 10, achieved with integration of 10 ms and a temperature rise of ∼2 K.7 However, some of the parameters of the experiment are unspecified. Our calculation of the dissipated power for these particles in these conditions is 4 nW.
- S. Berciaud, L. Cognet and B. Lounis, Photothermal absorption spectroscopy of individual semiconductor nanocrystals, Nano Lett., 2005, 5, 2160–2163 CrossRef CAS.
- S. Berciaud, L. Cognet, Ph. Poulin, R. B. Weisman and B. Lounis, Absorption spectroscopy of individual single-walled carbon nanotubes, Nano Lett., 2007, 7, 1203–1207 CrossRef CAS.
- S. Berciaud, D. Lasne, G. A. Blab, L. Cognet and B. Lounis, Photothermal heterodyne imaging of individual metallic nanoparticles: theory versus experiment, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045424 CrossRef.
- L. Cognet, S. Berciaud, D. Lasne and B. Lounis, Photothermal methods for single nonluminescent nano-objects, Anal. Chem., 2008, 80, 2288–2294 CrossRef CAS.
- G. A. Blab, L. Cognet, S. Berciaud, I. Alexandre, D. Husar, J. Remacle and B. Lounis, Optical readout of gold nanoparticle-based dna microarrays without silver enhancement, Biophys. J., 2006, 90, L13–L15 CAS.
- L. Cognet, C. Tardin, D. Boyer, D. Choquet, P. Tamarat and B. Lounis, Single metallic nanoparticle imaging for protein detection in cells, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 11350–11355 CrossRef CAS.
- D. Lasne, G. A. Blab, S. Berciaud, M. Heine, L. Groc, D. Choquet, L. Cognet and B. Lounis, Single nanoparticle photothermal tracking (SNaPT) of 5-nm gold beads in live cells, Biophys. J., 2006, 91, 4598–4604 CrossRef CAS.
- F. Kulzer, N. Laurens, J. Besser, T. Schmidt, M. Orrit and H. P. Spaink, Photothermal detection of individual gold nanoparticles: perspectives for high-throughput screening, ChemPhysChem, 2008, 9, 1761–1766 CrossRef CAS.
- P. M. R. Paulo, A. Gaiduk, F. Kulzer, S. F. G. Krens, H. P. Spaink, Th. Schmidt and M. Orrit, Photothermal correlation spectroscopy of gold nanoparticles in solution, J. Phys. Chem. C, 2009, 113, 11451 CrossRef CAS.
- R. Radunz, D. Rings, K. Kroy and F. Cichos, Hot Brownian particles and photothermal correlation spectroscopy, J. Phys. Chem. A, 2009, 113, 1674–1677 CrossRef CAS.
- V. Octeau, L. Cognet, L. Duchesne, D. Lasne, N. Schaeffer, D. G. Fernig and B. Lounis, Photothermal absorption correlation spectroscopy, ACS Nano, 2009, 3, 345–350 CrossRef CAS.
- D. Lasne, A. Maali, Y. Amarouchene, L. Cognet, B. Lounis and H. Kellay, Label-free optical imaging of mitochondria in live cells, Opt. Express, 2007, 15, 14184–14193 CrossRef CAS.
- W.-S. Chang, J. W. Ha, L. S. Slaughter and S. Link, Plasmonic nanorod absorbers as orientation sensors, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2781–2786 CrossRef CAS.
- M. Atlan, M. Gross, P. Desbiolles, É. Absil, G. Tessier and M. Coppey-Moisan, Heterodyne holographic microscopy of gold particles, Opt. Lett., 2008, 33, 500–502 Search PubMed.
- E. Absil, G. Tessier, M. Gross, M. Atlan, N. Warnasooriya, S. Suck, M. Coppey-Moisan and D. Fournier, Photothermal heterodyne holography of gold nanoparticles, Opt. Express, 2010, 18, 780–786 CrossRef CAS.
- C. F. Bohren, D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, 1998 Search PubMed.
- P. B. Johnson and R. W. Christy, Optical constants of noble metals, Phys. Rev. B: Solid State, 1972, 6, 4370–4379 CrossRef CAS.
- M. A. van Dijk, A. L. Tchebotareva, M. Orrit, M. Lippitz, S. Berciaud, D. Lasne, L. Cognet and B. Lounis, Absorption and scattering microscopy of single metal nanoparticles, Phys. Chem. Chem. Phys., 2006, 8, 3486–3495 RSC.
- S. Link and M. A. El-Sayed, Spectroscopic determination of the melting energy of a gold nanorod, J. Chem. Phys., 2001, 114, 2362–2368 CrossRef CAS.
- P. Zijlstra, J. W. M. Chon and M. Gu, White light scattering spectroscopy and electron microscopy of laser induced melting in single gold nanorods, Phys. Chem. Chem. Phys., 2009, 11, 5915–5921 RSC.
- R. Dorn, S. Quabis and S. Leuchs, Sharper focus for a radially polarized light beam, Phys. Rev. Lett., 2003, 91, 233901 CrossRef CAS.
- S. Moehl, H. Zhao, B. Dal Don, S. Wachter and H. Kalt, Solid immersion lens-enhanced nano-photoluminescence: principle and applications, J. Appl. Phys., 2003, 93, 6265–6272 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Thermal and optical constants; absorption cross-sections for gold nanoparticles; analysis of the variations of SNR; noise of the photothermal detection; comparison of the “Cat’s eye” and “50/50 BS” configurations; AFM measurements; analysis of PMMA thickness; and analysis of the number of dye molecules in fluorospheres. See DOI: 10.1039/c0sc00210k |
| This journal is © The Royal Society of Chemistry 2010 |
