Macrocyclization of enzyme-based supramolecular polymers†
Maartje M. C.
Bastings
ab,
Tom F. A.
de Greef
ac,
Joost L. J.
van Dongen
c,
Maarten
Merkx
b and
E. W.
Meijer
*abc
aInstitute for Complex Molecular Systems, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: e.w.meijer@tue.nl
bLaboratory of Chemical Biology, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
cLaboratory of Macromolecular and Organic Chemistry, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
First published on 18th March 2010
Abstract
AB type monomers for supramolecular polymers have been developed based on the strong and reversible noncovalent interaction between ribonuclease S-peptide (A) and S-protein (B), resulting in an active enzyme complex as the linking unit. Two AB-type protein constructs are synthesized differing in the length of the flexible oligo(ethylene glycol) spacer separating the two end groups. Using an experimental setup where size exclusion chromatography is directly coupled to Q-TOF mass spectrometry, we have analyzed the self-assembled architectures as a function of concentration. The theory of macrocyclization under thermodynamic control is used to quantitatively analyze the experimental data. Using this theory, we show that AB-type monomers linked by flexible linkers grow reversibly via ring–chain competition. Inherently the formation of linear polymeric assemblies is beyond the capability of these types of building blocks due to concentration limits of proteins. The results therefore contribute to the general understanding of supramolecular polymerization with biological building blocks and demonstrate design requirements for monomers if linear polymerization is desired.
Introduction
Supramolecular polymer chemistry has emerged from the combination of supramolecular chemistry and polymer science, and focuses on the development of individual monomeric units, held together by strong, directional and reversible noncovalent interactions.1 The reversibility and temperature dependence of noncovalent interactions allows the development of novel polymeric materials that combine excellent mechanical properties and good processability at low temperatures.2 Based on the current understanding1p there are three main growth mechanisms for supramolecular polymerizations: isodesmic,3 cooperative4 and ring–chain competition,5 in which the linear polymers are in equilibrium with their cyclic counterparts. In the last two cases there exists a critical concentration above which high-molecular weight supramolecular polymers are formed. In Nature, many examples of supramolecular architectures assembled from monomeric protein building blocks exist, which follow identical growth mechanisms as synthetic supramolecular polymers. Well-known examples hereof include the cooperative growth of actin monomers into filaments,6 the isodesmic assembly of FtsZ proteins into the Z-ring during cell-division7 and serpin polymerization,8 in which cyclic intermediates play a prominent role. For biomedical applications such as drug delivery and tissue engineering, biomolecular complexes have great potential as structural units in supramolecular polymers because of their biocompatibility, biodegradability and inherent stability in water. Furthermore, because the noncovalent interaction between the associating end groups can be tuned using methods developed in protein engineering, the macroscopic properties of the resulting supramolecular materials can be tailored for specific applications.The combination of biological macromolecules with synthetic components to yield semi-synthetic or hybrid molecules, offers the possibility to combine the strengths of biology and chemical synthesis.9 Biological architectures are constructed with high fidelity but the variety of building blocks is limited. Synthetic chemistry on the other hand provides an infinite variation in topology but is less efficient in error-free synthesis. Merging both fields yields a challenging approach to assemble and study semi-synthetic protein architectures. Linking protein and substrate through a flexible linker enables the synthesis of interesting supramolecular building blocks and provides opportunity in the rapidly emerging field of supramolecular protein engineering. Recently, several groups have reported on synthetic supramolecular polymers based on protein–ligand interactions.1j,10,11 For example, Hayashi and co-workers1j,10 reported the formation of linear supramolecular polymers based on heme proteins to which an external cofactor moiety was appended via a flexible spacer. This one-dimensional concept was further expanded to two dimensions by mixing in a heme-triad to enable network formation. Recently Wagner et al.11 presented an in-depth study on the assembly of discrete protein nano-rings by combining a dimeric protein construct with a flexible spacer and a divalent synthetic ligand.
These two examples demonstrate that both linear as well as discrete cyclic assemblies can be obtained using flexible spacers. Indeed, it is well known that the use of flexible linkers inherently brings along the formation of cycles. In the early 1930s Kuhn12 introduced the concept of effective concentration (Ceff) to provide a relation between the mean squared end-to-end length of a linker and the cyclization probability of the end groups when the two ends of the linker are an infinitesimal distance apart. The effective concentration can be thought of as the local concentration of one chain end in the vicinity of the other chain end when these two ends are connected by a linker. As such, the Ceff theoretically quantifies the advantage for an intra- vs. an intermolecular interaction. Because the Ceff depends on the length and conformational flexibility of the linker, changes in these values will have a pronounced effect on the supramolecular polymerization of monomeric building blocks and should therefore be taken into consideration in the design process. Besides the effective concentration, other factors such as the presence of linker strain or specific noncovalent interactions within oligomeric assemblies can also play a crucial role in the supramolecular polymerization process as will be shown in this paper.
The objective of this work is to quantitatively analyze and study the mechanism of the supramolecular polymerization of biological building blocks in which the reversibly associating A and B end groups are separated by a flexible spacer. To this end, an AB monomer was developed based on the strong, noncovalent interaction between the ribonuclease (RNase) S-protein and S-peptide (Scheme 1, Ka ∼ 7 × 106 M−1 in NaOAc at 25 °C),13 thereby constructing supramolecular architectures entirely consisting of enzymatically active proteins as linking units. This RNase S system has previously been successfully used in the noncovalent synthesis of protein dendrimers by our group.14 Both S-protein and S-peptide were connected via a flexible oligo(ethylene glycol) (EG) linker. EG linkers are commonly used to construct multivalent ligands and are known to be resistant to nonspecific protein adsorption.15 This minimizes the influence of the protein fragments on the flexibility and thus the Ceff of the linker. Upon successive addition of monomers to the growing chain, the AB building block can undergo cyclic as well as linear polymerization, the distribution of which is determined by the effective molarity of each oligomer and the overall monomer concentration. The influence of the length of the EG linker on the supramolecular polymerization will be experimentally demonstrated using concentration dependent size exclusion chromatography and the results obtained will be quantitatively analyzed using the theory of macrocyclization under thermodynamic control. Finally, a comparison is made between the experimentally determined product compositions and a reversible isodesmic polymerization model in which no cyclization occurs.
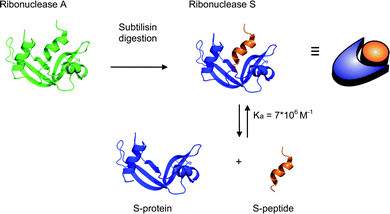 | ||
| Scheme 1 The formation of ribonuclease S upon cleavage of ribonuclease A by the protease subtilisin. Ribonuclease S can be separated into the S-peptide and S-protein that form a tightly bound supramolecular complex. | ||
Results and discussion
AB monomer synthesis and characterization
AB monomers were synthesized using aniline catalyzed oxime chemistry16 which requires the introduction of either an aldehyde/ketone function or aminooxy functionality on the peptide and protein. The S-protein is formed after subtilisin digestion of RNase A (Scheme 1) and consists of residues 21–124. Because serine is the natural N-terminal residue on the RNase S protein an aldehyde can be easily obtained via oxidation using NaIO4.17 Heterogeneous digestion of RNase A by subtilisin yields a minor cleavage product that corresponds to residues 22–124;18 however, the N-terminal residue here is again a serine. Since no difference in affinity for the S-peptide has been described, and both products can be oxidized and used for oxime ligation, no separation between the two forms was necessary. The aldehyde function on the S-peptide was introduced via solid phase peptide synthesis by addition of an N-terminal serine and subsequent NaIO4 oxidation. An aminooxy terminated oligo(ethylene glycol) linker with two different lengths was synthesized and ligated to the S-protein and S-peptide using a tandem synthetic strategy (Scheme 2). By using 2 equivalents of linker relative to S-protein and the steric hindrance resulting from the protein ligation, the mono-ligated protein product was obtained exclusively. Addition of an excess of S-peptide resulted in ligation to the remainder of the aminooxy functionalities, yielding the AB S-peptide S-protein hetero product as well as the di-S-peptide side-product. These products were purified using preparative RP-HPLC and fully characterized using LC-MS and activity assays (see ESI†). The AB1 monomeric building block contains a flexible linker of 19 ethylene glycol repeats while the AB2 monomer contains a flexible linker of 6 ethylene glycol repeats.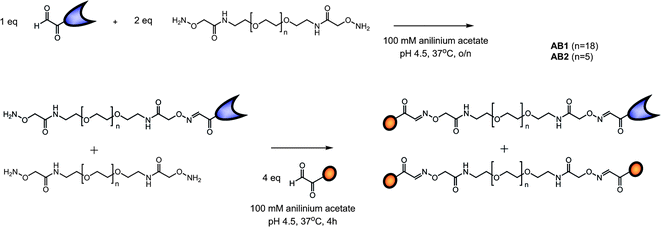 | ||
| Scheme 2 Synthetic outline of the AB1 (n = 18) and AB2 (n = 5) S-peptide S-protein monomeric building blocks, formed via aniline catalyzed oxime chemistry between the oxidized serine residues on the S-peptide and S-protein and aminooxy end groups on the EG linkers. | ||
As only a correctly folded and associated RNase S complex is enzymatically active, measurements of the enzymatic activity of the tethered RNase S constructs AB1 and AB2 can reveal whether the protein still contains its native structure after synthesis and that the enzyme can be used to direct self-assembly. The fluorescent 6-FAM-dArUdAdA-6-TAMRA substrate, specifically developed to quantify RNase activity, was used to monitor enzymatic activity.19 At 1–10 nM concentrations, we obtained enzymatic activities of ∼60 and ∼80% of that of commercially available RNase A and S for AB1 and AB2, respectively (see ESI†). Since MS analysis showed no evidence that other parts of the S-protein besides the N-terminus are oxidized during synthesis, this diminished activity could be due to substrate hindrance by the flexible EG linker.15 From the retained enzymatic activity of both AB1 and AB2 we conclude that both ends of the monomer are still able to form a native RNase S complex and can therefore be used as a linking unit for supramolecular assemblies.
Size exclusion chromatography and Q-TOF mass analysis
Self-assembled architectures increase in weight and size with every additional monomer; therefore, size exclusion chromatography (SEC) was used to study the self-assembled structures in solution. A SEC column (Superdex 75) was coupled to a quadrupole time-of-flight (Q-TOF) mass spectrometer to enable direct and sensitive analysis of the supramolecular complexes in their self-assembled state. Different AB-monomer sample concentrations were prepared and injected after equilibration onto the SEC column and analyzed during a 30 min run at 0.1 ml min−1 flow rate. As the buffer system 0.1 M ammonium acetate pH 4.5 was chosen to enable good ionization for MS analysis while strong S-peptide/S-protein complexation is preserved.AB1 was injected after equilibration in a concentration series of 100 μM, 1 mM and 10 mM. Measurements at higher concentrations could not be included due to practical limitations. At the lowest concentration analyzed (Fig. 1a, dotted line) the TIC trace shows the presence of one main peak and a second smaller peak. Q-TOF MS measurements attributed the first peak to the AB1-monomer (Fig. 1b, c), whereas for the second peak no conclusive MS spectrum was obtained and it was therefore attributed to low molecular weight buffer compounds that are present in relatively large quantities compared to the protein monomer at this concentration. Injection of a 1 mM AB1 solution yielded not only monomeric, but also dimeric architectures (Fig. 1a, dashed line, d + e) and upon further increment of the concentration, the sample of 10 mM showed, besides monomeric and dimeric, also trimeric species (Fig. 1a, solid line, f + g). DLS analysis confirmed that no larger aggregates were present (see ESI†).
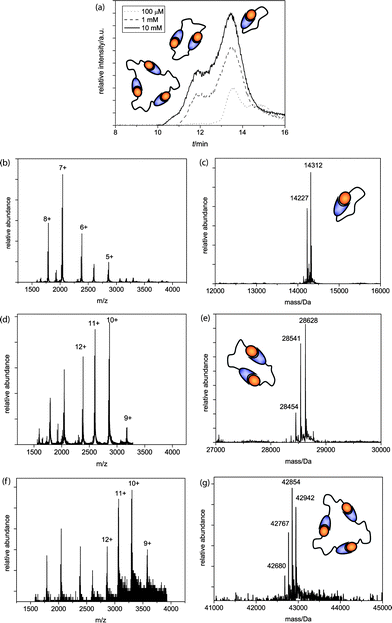 | ||
| Fig. 1 (a) Q-TOF analysis chromatograms of the AB1 SEC runs, with schematic representations of ring sizes at the corresponding peaks; (b)m/z and (c) deconvoluted spectra of the cyclic monomer (MWcalc = 14314 Da, MWcalc - ser = 14227 Da); (d)m/z and (e) deconvoluted spectra of the dimer (MWcalc = 28628 Da, MWcalc - ser = 28541 Da, MWcalc – 2 ser = 28454 Da) and (f)m/z and (g) deconvoluted spectra of the trimer (MWcalc = 42942 Da, MWcalc – ser = 42855 Da, MWcalc – 2 ser = 42768 Da, MWcalc – 3 ser = 42681 Da). | ||
AB2 was injected in a concentration series of 10 μM, 100 μM, 1 mM and 10 mM after equilibration of the mixtures. For this building block the linker is significantly shorter than for AB1 and therefore the equilibrium between rings and chains is expected to shift. Injection at a concentration of 10 μM yielded only monomeric species (Fig. 2a, dash-dotted line, b + c). Injection at a higher concentration of 100 μM resulted in the appearance of dimeric species (Fig. 2a, dotted line, d + e) while injection of a 1 mM solution resulted in the formation of trimeric species (Fig. 2a, dashed lines, f + g). At a concentration of 1 mM AB2 we observe an increased amount of dimeric species compared to AB1, indicating that the short linker length in AB2 enforces preferential formation of these species when the overall monomer concentration is sufficient. Successive concentration increments up to a final concentration of 10 mM showed, besides monomers, dimers and trimers, also tetrameric species (Fig. 2a, solid line, h + i) and the dimer has become the predominant species. The difference in the distribution of species for the two different AB monomers as a function of concentration clearly demonstrates the influence of linker length on the supramolecular polymerization of the two AB monomers.
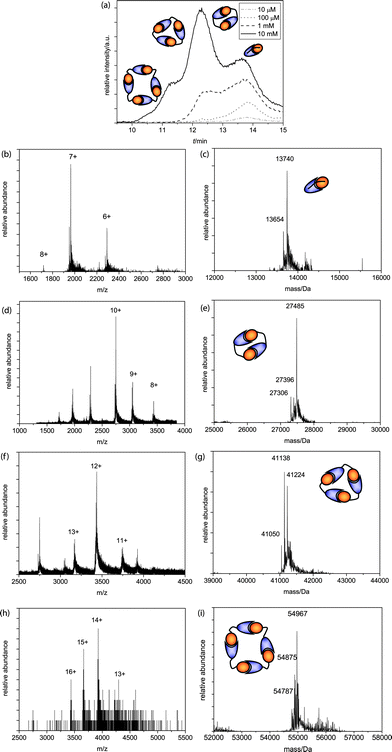 | ||
| Fig. 2 (a) Q-TOF analysis chromatograms of the 10 mM, 1 mM, 100 μM and 10μM AB2 SEC runs, with schematic representations of ring sizes at different peaks; (b)m/z and (c) deconvoluted spectra of the monomer (MWcalc = 13740 Da, MWcalc - ser = 13653 Da); (d)m/z and (e) deconvoluted spectra of the dimer (MWcalc = 27480 Da, MWcalc - ser = 27393 Da, MWcalc – 2 ser = 27306 Da); (f)m/z and (g) deconvoluted spectra of the trimer (MWcalc = 41220 Da, MWcalc – ser = 41133 Da, MWcalc – 2 ser = 41046 Da); (h)m/z and (i) deconvoluted spectra of the tetramer (MWcalc = 54960 Da, MWcalc – ser = 54873 Da, MWcalc – 2 ser = 54786 Da). | ||
The kinetic stability of the aggregates during the course of the 15 min time interval (flow rate = 0.1 ml min−1) required for SEC-MS was probed by performing SEC at different flow rates. We slowed down the flow rate to 0.075 ml min−1, resulting in an increase in the length of time the complex spent on the column by a factor of 1.33. Integration of the peak areas of the UV chromatogram at this lower flow rate resulted in the same distribution of species observed for the higher flow rate (see ESI†), indicating the kinetic stability of the aggregates is high enough not to be affected by any dilution effects that occur upon injection of the self-assembled architectures to the SEC.
Calculation of the Ceff of the monomers
In order to corroborate the influence of ring–chain competition from our experimental data the effective concentration (Ceff) of both AB monomers was calculated. Theoretical methods from polymer physics can calculate the Ceff as a function of chain length either by assuming that the linker can be modeled as a random-coil20–22 or as a worm-like chain.23,24 The theoretical concept of effective concentration is often replaced by the identical, but empirical concept of effective molarity (EM).15 Whereas effective concentration is based on concentrations calculated from the physical properties of the chain connecting the two end groups, EM denotes the ratio of the experimentally determined intra- and intermolecular equilibrium constant. For example, Zhou24 and Whitesides et al.25 demonstrated that calculations of the Ceff using respectively a worm-like chain model and a Gaussian chain model were in agreement with experimentally determined EM values and thereby showed that this approach can provide valuable insight into complex thermodynamic phenomena such as protein–ligand binding.We have calculated the effective concentration of the two different AB monomers by assuming that the end-to-end displacement vector for the ethylene glycol linker separating the two end groups has a Gaussian probability density:26
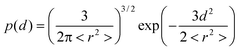 | (1) |
| Ceff(d) = p(d)/NAV | (2) |
Assuming that the buffers used conform to θ conditions, the root-mean-square distance <r2> can be estimated assuming a three dimensional random flight model:28
| <r2> = Cnnl2 | (3) |
Combining eqn (2) with eqn (3), relates the effective concentration to the amount of PEG repeats in a linker, for different values of the distances, d. The distance d between the end of the S-peptide and S-protein is approximately 25 Å31 and the number of PEG units in the linker is 19 and 6 for AB1 and AB2, respectively. Using these values and a characteristic ratio of 4.1, the calculated effective concentrations then become 8 mM for AB1 and 0.7 mM for AB2.32
Calculation of the product distribution of a ring–chain supramolecular polymerization
Theoretical distributions of cyclic and linear products in thermodynamically controlled (i.e. supramolecular) polymerizations were first described by Jacobson and Stockmayer (JS),21 who pointed out the existence of a critical concentration, below which the system is composed of cyclic products only and above which the concentration of cyclic species remains constant and excess monomer produces linear species only. They also related the equilibrium constant for cyclization to the cyclization probability of the chain, thereby providing a direct link between the effective molarity and the effective concentration. Ercolani et al.33 extended the treatment of JS to describe the distribution of cyclic oligomers under dilute conditions and a wide range of association constants. They pointed out that the phenomenon of a critical concentration is only manifested when the intermolecular association constant is sufficiently high (>105 M−1). Recently, Ercolani and Di Stefano34 summarized the assumptions of the JS theory: (i) the thermodynamic reactivity of the end groups is independent of the chain length; (ii) all of the rings are strainless; (iii) the end-to-end distribution function of a chain in solution is Gaussian; (iv) the mean square end-to-end distance is proportional to the number of skeletal bonds (i.e.θ conditions are assumed) and (v) the cyclization probability depends on the fraction of configurations for which the ends coincide without taking into account the torsional states of the polymer chain (i.e. no angle corrections are considered). For short linkers, however, the Gaussian assumption is no longer adequate and deviations from theory and experimental data are expected (vide infra).As most supramolecular polymerizations occur in relatively dilute solutions, the model proposed by Ercolani et al.,33 is eminently suited to describe the equilibrium between cyclic and linear species in these equilibrium polymerizations. The ring–chain model developed by Ercolani et al. is characterized by two distinct thermodynamic constants (Fig. 3) i.e. an intermolecular binding constant (Kinter) and the intramolecular binding constant for i-th ring closure (Kintra(i)).
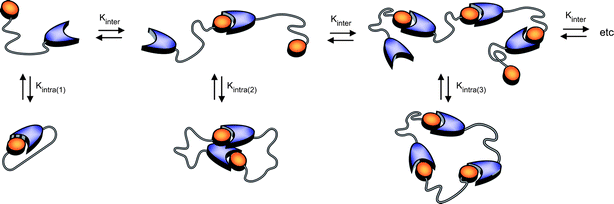 | ||
| Fig. 3 Schematic representation of the ring–chain supramolecular polymerization of RNase S building blocks in which Kinter (M−1) represents the intermolecular binding constant for bimolecular association and Kintra(i) represents the dimensionless intramolecular equilibrium constant for i-th ring closure. | ||
Under the fulfilment of conditions (i)–(v), the EMi values for i > 1 can be conveniently written as a function of EM1 (the effective molarity of the bifunctional AB monomer):
 | (4) |
In such a case, the mass-balance equation takes the following form:33
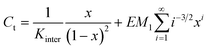 | (5) |
| [Ci] = EM1i−5/2xi | (6) |
The percentage of cyclic oligomers is then calculated as:
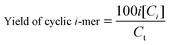 | (7) |
Under the conditions that eqn (4) applies (vide supra), the yield of cyclic monomer is always higher than any other cyclic oligomer (Fig. S9†).
Quantitative experimental analysis
Gaussian peak deconvolution of the TIC trace of AB1 at an injection concentration of 10 mM was performed using the function “fit multipeaks” available in the analysis software Origin. This procedure revealed the presence of four distinct peaks at a concentration of 10 mM (Fig. 4a). Peak areas of the chromatogram were integrated to determine the mole fraction of each oligomer. Since all cyclic structures are assembled from the same AB-monomers, ionization can be assumed equal and therefore a direct relation between TIC-trace intensity and relative concentration of the sample is justified. With the fourth peak being tailing of monomers, a distribution of 71 ± 2.5% monomeric, 28 ± 1% dimeric and 1 ± 0.2% trimeric cycles was obtained. Deconvolution of the AB2 TIC-trace at 10 mM shows a different composition, as is expected from the decreased value of Ceff for this monomer. Six peaks were necessary to reconstruct the TIC-trace accurately, from which two peaks were necessary to account for monomer tailing and successive low molecular weight buffer compounds (Fig. 4b).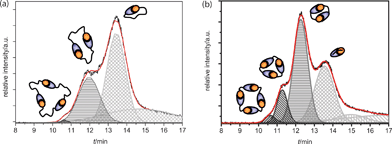 | ||
| Fig. 4 (a) Gaussian peak deconvolution of the Q-TOF TIC trace of AB1 at 10 mM. Trimeric rings are represented by the dark grey peak (diagonal filling), dimeric rings by the medium grey peak (horizontal filling) and monomeric rings by the light grey peak (checker filling). With these four distinct graphs, the original curve is accurately reproduced (red line). (b) Gaussian peak fits to the Q-TOF TIC trace of AB2 at 10 mM. Tetrameric rings are represented by the black peak (diagonal filling). Trimeric rings are represented by the dark grey peak (diagonal filling), dimeric rings by the medium grey peak (horizontal filling) and monomeric rings by the light grey peak (checker filling). With these distinct graphs, the original curve is accurately reproduced (red line). | ||
We have compared the experimentally determined product distribution with the calculated product distribution obtained using the previously discussed ring–chain competition model and a standard isodesmic polymerization model in which no cycle formation occurs.35 For both AB monomers an intermolecular equilibrium constant of 7 × 106 M−1 was used and EM1 values were based on the calculated Ceff using the Gaussian chain model, thus for AB1EM1 = 8 mM and for AB2EM1 = 0.7 mM. Comparison of the experimentally determined product distribution with the calculated product distribution determined using the ring–chain model (eqn (5)–(7)) at various total concentrations of AB1 (10, 1 and 0.1 mM) shows good correspondence (Table 1). The small deviation between theory and experiment for the AB1 monomer is most likely due to the excluded volume effects between the protein and ligand which have been neglected in the calculation of the Ceff but have been shown to be important in other studies on reversible cyclizations.24,26 Comparison of the experimentally determined mole fractions to the calculated mole fractions obtained using an isodesmic polymerization model, in which only linear association with equilibrium constant 7 × 106 M−1 occurs, clearly shows that this model is unable to describe the supramolecular polymerization of monomer AB1. Hence, for this monomer, the experimental data closely obey the Jacobson–Stockmayer theory. As a consequence, the mole fraction of cyclic monomer is always higher than the mole fraction of any other cyclic oligomer below the critical concentration while for concentrations higher than the critical concentration, which are beyond experimental boundaries here, rapid polymerization into linear chains occurs.
| 10 mM | AB1 | Ring–chain | Isodesmic | AB2 | Ring–chain | Isodesmic |
|---|---|---|---|---|---|---|

|
71 ± 2.5 | 64 | ≪1 | 39 ± 1 | 7 | ≪1 |

|
28 ± 1 | 18 | ≪1 | 43 ± 0.5 | 2.5 | ≪1 |

|
1 ± 0.2 | 8 | ≪1 | 9 ± 1 | 1.5 | ≪1 |

|
0 | 4 | ≪1 | 4 ± 1 | <1 | ≪1 |
| Linear | 0 | 0 | 100 | 0 | 84 | 100 |
| DPn | — | — | 265 | — | 10 | 265 |
| 1 mM | AB1 | Ring–chain | Isodesmic | AB2 | Ring–chain | Isodesmic |
|---|---|---|---|---|---|---|

|
80 ± 4 | 95 | <1 | 80 ± 2 | 60 | <1 |

|
20 ± 0.6 | 4 | <1 | 18 ± 5 | 18 | <1 |

|
0 | <1 | <1 | 1.5 ± 6 | 8 | <1 |

|
0 | ≪1 | <1 | 0 | 4.5 | <1 |
| Linear | 0 | 0 | 100 | 0 | 0.5 | 100 |
| DPn | — | — | 84 | — | 1.4 | 84 |
| 0.1 mM | AB1 | Ring–chain | Isodesmic | AB2 | Ring–chain | Isodesmic |
|---|---|---|---|---|---|---|

|
100 | >99 | 1 | 89 ± 1 | 95 | 1 |

|
0 | ≪1 | 1 | 11 ± 1 | 5 | 1 |

|
0 | ≪1 | 1 | 0 | 0.5 | 1 |

|
0 | ≪1 | 1 | 0 | <1 | 1 |
| Linear | 0 | 0 | 96 | 0 | 0 | 96 |
| DPn | — | — | 27 | — | — | 27 |
Comparison of the experimentally determined product distribution of the AB2 monomer at various monomer concentrations with the Jacobson–Stockmayer theory, shows a good correspondence for the lower concentrations (0.1 mM and 1 mM). However, large deviations between the experimentally determined product composition and calculated values are observed at a concentration of 10 mM. Where the experimental data indicate the formation of oligomeric assemblies with the dimer as most abundant species, the ring–chain competition model, in which all cycles are assumed to be strainless, suggests the initiation of linear polymers with a DPn of 10. Comparison between the experimental data and values obtained using an isodesmic polymerization model show that this model cannot describe the experimental data as it predicts a number averaged degree of polymerization of 265 at this concentration. A possible explanation for the failure of the Jacobson–Stockmayer theory to describe the experimental data at higher concentrations can be found in the shorter EG linker of AB2. Discrepancy between the Jacobson–Stockmayer theory and experimental data has been observed in other studies in which short linkers have been used, for example during ring formation in covalent polymers,36–38 cyclization of short DNA fragments39 and cyclization of synthetic supramolecular polymers.40 It has been suggested that the origin of this discrepancy is due to the fact that short chains are inherently strained in their cyclic conformation and therefore do not obey Gaussian statistics, an important assumption in the derivation of eqn (4). As a result, the effective molarity of the cyclic AB2 monomer is close to, or lower than the effective molarity of the cyclic dimer and the mole fraction of cyclic dimer can surpass the mole fraction of cyclic monomer33 as is also observed experimentally. This effect is most notable at concentrations slightly above EM1, in our case at concentrations around 10 mM.
The experimental data on the AB2 monomer elegantly show that linker composition and concentration can be used to tune the yield of a specific cyclic supramolecular biological assembly. Whereas in the AB1 monomer the linker connecting the protein and ligand is large enough for the formation of a cyclic monomer, in the AB2 monomer the formation of the cyclic monomer is hindered, resulting in high yields of the cyclic dimer at concentrations close to the critical concentration. Alternatively, the higher effective molarity of cyclic AB2 dimer formation compared to AB2 cyclic monomer formation can also be caused by additional noncovalent interactions between the two protein–ligand complexes in the cyclic dimer of AB2.
Conclusions
The linking together of molecular fragments is a common approach in chemical biology. However, the effect of linker length, structure and rigidity on the binding affinities of the construct is seldom studied. This study describes the quantitative analysis of the self-assembly of peptide and protein fragments linked via a flexible oligo(ethylene glycol) linker that, upon complexation, form an active enzyme complex. Because of the tethering of the peptide and protein fragment, the system is able to reversibly polymerize into linear oligomers which are in equilibrium with their corresponding cyclic counterparts. To study the effect of linker length and the resulting changes in effective concentration, two systems were synthesized that varied in the number of ethylene oxide units in the linker, resulting in different effective concentrations, i.e. 8 mM for AB1, and 0.7 mM for AB2. Using an experimental setup where size separation was directly coupled to accurate mass spectrometry, the concentration dependent product distribution of the supramolecular polymerization could be studied in great detail.By combining experimental data with theoretical modeling, valuable insights were obtained into the supramolecular polymerization mechanisms and design criteria for protein based supramolecular polymeric architectures. The experimentally obtained product distribution could be quantitatively described using the theory of reversible macrocyclization and shows the relation between linker length, the effective molarity of the monomer and the concentration of higher molecular weight cyclic oligomers and as such confirms that the supramolecular polymerization occurs via ring–chain competition. Consequently, the mole fraction of cyclic monomer is always higher than other cyclic oligomers below and close to the critical concentration.
The shorter linker in AB2 results in a decreased effective concentration for this monomer. With this decreased Ceff the presence of various sized cyclic species as well as linearly polymerized architectures was predicted by the ring–chain competition model at the highest concentration. In sharp contrast, the experimental data clearly show the presence of oligomeric species instead of larger linear supramolecular polymers. The higher yield of the dimeric cycle compared to the monomeric cycle at concentrations close to the critical concentration indicates that the linker in the monomeric cycle of AB2 is either strained, resulting in an enthalpic contribution to the cyclization constant, or cannot be described as a random Gaussian coil. Hence, the effective molarity of cyclic AB2 dimer formation must be close to or even higher than the effective molarity of cyclic monomer formation, resulting in the preferred formation of the cyclic dimer at concentrations close to the critical concentration.
The described system is characterized by synthetic ease and can be analyzed in great detail. It therefore is promising in the further study of self-assembly directed by protein and peptide interactions to form active biological objects. Besides the here described AB homo-polymerization, the system is very suitable to study AA–BB hetero-polymerization in a comparable fashion as well as to analyze multivalency when used in combination with more branched linker structures.
When dealing with AB type protein monomers in which the A and B end groups are separated by a flexible tether, formation of linear polymers is excluded by solubility limitations and inherently only cyclic assemblies can be obtained. As implied by the ring–chain mechanism, only with an effective concentration close to 0, where cyclization is excluded, combined with a high association constant between the A and B units that is in the order of 1011 M−1, is linear polymerization reachable in biologically workable concentrations (<10−3 M). This is the case in several examples of supramolecular polymers found in Nature like actin filaments and microtubuli, but is hard to design for synthetic protein based AB building blocks. Finally, longer linear polymers can be obtained when the growth of the linear chains is coupled to growth in the lateral direction resulting in fiber like aggregates as in such a case a first order nucleated transition can occur.41 Lateral association due to the presence of a hydrophobic linker has been suggested to occur in the growth of serpin polymers in which competition between rings and chains also takes place.8
When aiming for linear polymers, cycle formation needs to be considered for all systems with flexible linkers. The ring–chain competition mechanism therefore sets out clear guidelines for the design criteria of monomeric building blocks to be used in supramolecular polymerization, either cyclic or linear.
Experimental procedures
Unless stated otherwise, all reagents and chemicals were obtained from commercial sources and used without further purification. Diamino-PEG(18) and amino-azido-PEG(5) were obtained from Polypure, 6-FAM-dArUdAdA-6-TAMRA from Integrated DNA Technologies, DIPEA and TFA from Aldrich, DCM was distilled prior to use. ESI-MS spectra were recorded on an Applied Biosystems single quadrupole electrospray ionization mass spectrometer API-150EX in positive mode. MALDI-TOF MS spectra were measured on a Perspective DE Voyager spectrometer using an α-cyano-4-hydroxycinnamic acid matrix. Reversed phase HPLC was performed on a Shimadzu LC-8A HPLC system by using a VYDAC protein and peptide semi-prep C4 column. A gradient of water in acetonitrile, both containing 0.1% TFA was used to elute the different ligation products. Detection was performed by a Shimadzu SPD-10AV UV-detector (λ = 214 nm). Fluorescence spectroscopy was performed on a Varian Cary Eclipse spectrometer at 10 °C. All activity assays were performed in a 0.1 M Tris, 0.1 M NaCl, pH 8.0 buffer, with a substrate concentration of 400 nM. Size exclusion chromatography was performed on a Superdex 75 column equilibrated with 0.1 M ammonium acetate pH 4.5 buffer, with a flow rate of 0.1 ml min−1. UV-vis was measured on a Varian Cary UV-vis spectrometer at room temperature, and a Shimadzu LC-20AD + SPD-M20A. ESI mass analyses were performed on a Q-TOF Ultima GLOBAL mass spectrometer (Micromass, Manchester, UK).Computational procedure
A computer script was written using Matlab R2007B. The input consists of a vector of initial concentrations, KAB and the effective molarity of the first cyclization (EM1). Using a combination of bisection, secant, and inverse quadratic interpolation methods present in the Matlab script fzero, eqn (8) was solved for x at each initial concentration C. Instead of evaluating the sum in eqn (8) from 1 to infinity it was evaluated to ring sizes up to 100.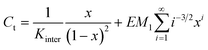 | (8) |
RNase S purification
RNase S was separated into the S-peptide and S-protein using RP-HPLC with a C4 semi-prep column. RNase S (21.63 mg) was dissolved in deionized water and eluted using a linear gradient of 0–50% acetonitrile in water over 25 min. The S-protein was obtained in 80% yield. Mass spectrometry clearly showed the heterogeneous RNase A digestion by the protease subtilisin. Hydrolysis between amide bonds 20 and 21 as well as between 21 and 22 is observed. LC-MS: S-protein MWcalc = 11534 Da, MWobs = 11533.4 and MWcalc -ser = 11446.9 Da, MWobs = 11445.8; S-peptide MWcalc = 2095 Da, MWobs = 2094.8 and MWcalc + ser = 2166 Da, MWobs = 2165.7Diaminooxy linker
PEG(18)-diamine (100 mg) was reacted with NHS-activated tBoc-protected aminooxy (69 mg) and DIPEA (120 μL) in dry CH2Cl2 (2 mL) overnight. The solution was stirred for 30 minutes with diethyl ether (5 mL) and, after removal of the solvent, for another 15 minutes with 3 mL diethyl ether. After solvent evaporation, NHS was removed by application of the product on a weak basic ion exchanger (ira 95, 6 × 1 cm) eluted with MeOH. Deprotection of the tBoc groups was achieved upon dilution in DCM/TFA (3/3 mL) at 0 °C for 2 hours. Cold solvent evaporation and co-evaporation with toluene removed the residual TFA. After water/ether extractions, the product was lyophilized.Azido-PEG(5)-amine was reduced with Pd/C and H2 gas to obtain the diamine prior to use. PEG(5)-diamine (195 mg) was reacted with NHS-activated tBoc-protected aminooxy (381 mg) and DIPEA (500 μL) in dry CH2Cl2 (4 mL) overnight. After solvent evaporation, the product was dissolved in 40 mL CHCl3 and washed 2× with 40 mL NaHCO3 and once with 40 mL brine. After drying with MgSO4 and filtration, the product was purified on a silica column with DCM/MeOH (20/3 mL). Deprotection of the tBoc groups was achieved upon dilution in TFA/H2O (5/0.25 mL) at 0 °C for 1 hour. After cold solvent evaporation the product was dissolved in 20 mL water and washed with 2 × 10 mL diethyl ether. After removal of the diethyl ether the product was lyophilized.
1H NMR (CDCl3-d1, 400 MHz): tBoc-protected PEG18 linker δ = 8.2 (s, 2H, CH2–NH–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), δ = 7.8 (bs, 2H, O–NH–C
O), δ = 7.8 (bs, 2H, O–NH–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), δ = 4.6 (s, 4H, O–CH2–C
O), δ = 4.6 (s, 4H, O–CH2–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), δ = 3.6–3.7 (80H, O–CH2–CH2–O), δ =1.5 (18H, C–(CH3)3); 1H NMR (CDCl3-d1, 400 MHz): unprotected PEG18 linker δ = 8.1 (bs, 2H, CH2–NH–C
O), δ = 3.6–3.7 (80H, O–CH2–CH2–O), δ =1.5 (18H, C–(CH3)3); 1H NMR (CDCl3-d1, 400 MHz): unprotected PEG18 linker δ = 8.1 (bs, 2H, CH2–NH–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), δ = 4.7 (bs, 4H, O–CH2–C
O), δ = 4.7 (bs, 4H, O–CH2–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), δ = 3.6–3.8 (80H, O–CH2–CH2–O); 13C NMR (CDCl3-d1, 400 MHz): tBoc-protected PEG18 linker δ = 169.01, 157.39, 82.42, 75.85, 70.57, 69.60, 38.92, 28.20; 13C NMR (CDCl3-d1, 400 MHz): unprotected PEG18 linker δ = 168.70, 71.64, 69.49, 69.29, 68.52, 38.62; MALDI-TOF MS protected PEG18 linker MWcalc = 1243.43 Da, MWobs = 1265.70 Da (Na+); MALDI-TOF MS unprotected PEG18 linker MWcalc = 1043.20 Da, MWobs = 1043.62 Da.
O), δ = 3.6–3.8 (80H, O–CH2–CH2–O); 13C NMR (CDCl3-d1, 400 MHz): tBoc-protected PEG18 linker δ = 169.01, 157.39, 82.42, 75.85, 70.57, 69.60, 38.92, 28.20; 13C NMR (CDCl3-d1, 400 MHz): unprotected PEG18 linker δ = 168.70, 71.64, 69.49, 69.29, 68.52, 38.62; MALDI-TOF MS protected PEG18 linker MWcalc = 1243.43 Da, MWobs = 1265.70 Da (Na+); MALDI-TOF MS unprotected PEG18 linker MWcalc = 1043.20 Da, MWobs = 1043.62 Da.
1H NMR (CDCl3-d1, 400 MHz): tBoc-protected PEG5 linker δ = 8.2 (s, 2H, CH2–NH–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), δ = 7.8 (bs, 2H, O–NH–C
O), δ = 7.8 (bs, 2H, O–NH–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), δ = 4.4 (s, 4H, O–CH2–C
O), δ = 4.4 (s, 4H, O–CH2–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), δ = 3.6–3.7 (m, 24H, O–CH2–CH2–O), δ = 3.5 (q, 4H, NH–CH2–CH2–O), δ = 1.5 (18H, C–(CH3)3); 1H NMR (CDCl3-d1, 400 MHz): unprotected PEG5 linker δ = 8.0 (bs, 2H, CH2–NH–C
O), δ = 3.6–3.7 (m, 24H, O–CH2–CH2–O), δ = 3.5 (q, 4H, NH–CH2–CH2–O), δ = 1.5 (18H, C–(CH3)3); 1H NMR (CDCl3-d1, 400 MHz): unprotected PEG5 linker δ = 8.0 (bs, 2H, CH2–NH–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), δ = 4.5 (4H, O–CH2–C
O), δ = 4.5 (4H, O–CH2–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), δ = 3.6–3.7 (24H, O–CH2–CH2–O), δ = 3.5 (m, 4H, NH–CH2–CH2–O), δ = 1.9 (4H, O–NH2); 13C NMR (CDCl3-d1, 400 MHz): tBoc-protected PEG5 linker δ = 169.06, 157.37, 82.42, 75.79, 70.53, 69.56, 38.93, 28.20.
O), δ = 3.6–3.7 (24H, O–CH2–CH2–O), δ = 3.5 (m, 4H, NH–CH2–CH2–O), δ = 1.9 (4H, O–NH2); 13C NMR (CDCl3-d1, 400 MHz): tBoc-protected PEG5 linker δ = 169.06, 157.37, 82.42, 75.79, 70.53, 69.56, 38.93, 28.20.
Ser-S-peptide
The ser-S-peptide was a kind gift from Edith Lempens.42N-terminal serine oxidation
1 equiv. of S-protein or ser-S-peptide was reacted with 1.2 equiv. of NaIO4 during 5 min in pH 7.4 PBS buffer at a concentration of ∼1 mg protein ml−1 at 4 °C. Direct RP-HPLC purification of the reaction mixture was carried out with a semi-prep C4 column using a linear gradient of 10–35% acetonitrile in water over 25 min. The oxidized S-protein was obtained in 70% yield. ESI-Q-TOF S-protein MWcalc = 11503 Da, MWobs + OH = 11519 Da, MWobs = 11501 Da, MWcalc-ser = 11416 Da, MWobs-ser + OH = 11433 Da, MWobs-ser = 11414 Da; LC-MS S-peptide MWcalc = 1805 Da, MWobs + OH = 1821 Da, MWobs = 1805 Da.AB-monomer synthesis
1 equiv. of oxidized S-protein was reacted with 2 equiv. of aminooxy-linker in 0.1 M anilinium acetate pH 4.5 buffer at 37 °C overnight. 4 equiv. of oxidated ser-S-peptide was added to the reaction mixture and ligated in 4 h at 37 °C to yield the AB-monomer as well as the AA-peptide-monomer. Separation and purification of the products was achieved with RP-HPLC using a Vydac C4 semi-prep column with a linear gradient of 10–50% over 40 min. The AB-monomer was obtained in 40% yield relative to the S-protein. ESI-Q-TOF AB1 MWcalc = 14314 Da, MWobs = 14313.9 Da, MWcalc-ser = 14227 Da, MWobs-ser = 14227.1 Da. ESI-Q-TOF AB2 MWcalc = 13740 Da, MWobs = 13740 Da, MWcalc-ser = 13653 Da, MWobs-ser = 13654 Da.Activity assay
RNase A was dissolved in assay buffer (0.1 M Tris, 0.1 M NaCl, pH 8.0) to a 40 μM stock. Upon addition of substrate (400 nM), fluorescence emission was monitored in time at 515 nm with excitation at 490 nm. The initial reaction rate V0 was calculated from a linear fit of the emission intensity in time over the first 30 s. A concentration range of RNase A was prepared and measured to obtain a calibration curve (1–10 nM; dilutions were freshly made before each measurement).Size exclusion chromatography and ESI-QTOF mass spectrometry
Size exclusion chromatography was performed using a Superdex 75 column (GE Biosciences) equilibrated with 0.1 M ammonium acetate pH 4.5. The AB-monomer was dissolved in the same buffer to concentrations of 10 mM, 1 mM and 100 μM and incubated for one hour. Samples were injected onto the equilibrated column using a 30 min run at a flow rate of 0.1 ml min−1. ESI-QTOF mass spectrometry was performed on a Micromass QTOF Ultima Global mass spectrometer in positive mode. The flow outlet of the Superdex 75 size exclusion column was connected to the inlet of the mass spectrometer. Micromass MaxEnt 1 software was used for deconvolution.Flow speed analysis was performed on a Superdex 75 column coupled to UV-vis (Shimadzu LC-20AD liquid chromatography, Shimadzu SPD-M20A prominence diode detector, 230 nm). Flow speed was varied from 0.1 ml min−1 to 0.075 ml min−1. Manual injections were performed with 4 μL samples in 0.1 M ammonium acetate, pH 4.5.
Acknowledgements
The authors would like to thank Bas de Waal for synthetic help, Edith Lempens for providing the S-peptide, Holger Grüll and Sander Langereis for assistance with DLS, and the Council for Chemical Sciences of the Netherlands Organization of Scientific Research (CW-NWO) for financial support.Notes and references
- Supramolecular polymers general: (a) L. Brunsveld, B. J. B. Folmer, E. W. Meijer and R. P. Sijbesma, Chem. Rev., 2001, 101, 4071 CrossRef CAS; (b) P. S. Corbin and S. C. Zimmerman, in Supramolecular Polymers, ed. A. Ciferri, Marcel Dekker, New York, 2000, p. 147 Search PubMed; (c) A. Ciferri, J. Macromol. Sci., Polym. Rev., 2003, 43, 271; (d) J.-M. Lehn, Polym. Int., 2002, 51, 825 CrossRef CAS; (e) A. J. Wilson, Soft Matter, 2007, 3, 409 RSC; (f) L. Bouteiller, Adv. Polym. Sci., 2007, 207, 79 CAS; M. J. Serpe and S. L. Craig, Langmuir, 2007, 23, 1626 CrossRef CAS; (g) A. Harada, A. Hashidzume and Y. Takashima, Adv. Polym. Sci., 2006, 201, 1 CAS; (h) F. Huang, D. S. Nagvekar, X. Zhou and H. W. Gibson, Macromolecules, 2007, 40, 356; (i) C. A. Hunter and S. Tomas, J. Am. Chem. Soc., 2006, 128, 8975 CrossRef CAS; (j) H. Kitagishi, K. Oohora, H. Yamaguchi, H. Sato, T. Matsuo, A. Harada and T. Hayashi, J. Am. Chem. Soc., 2007, 129, 10326 CrossRef CAS; (k) V. H. Soto Tellini, A. Jover, J. C. Garcia, L. Galantini, F. Meijide and J. V. Tato, J. Am. Chem. Soc., 2006, 128, 5728 CrossRef CAS; (l) R. K. Castellano, R. Clark, S. L. Craig, C. Nuckolls and J. Rebek Jr., Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 12418 CrossRef CAS; (m) V. Berl, M. Schmutz, M. J. Krische, R. G. Khoury and J. M. Lehn, Chem.–Eur. J., 2002, 8, 1227 CrossRef CAS; (n) W. H. Binder, C. Bernstoff, L. Kluger, L. Petraru and M. J. Kunz, Adv. Mater., 2005, 17, 2824 CrossRef CAS; (o) T. F. A. de Greef and E. W. Meijer, Nature, 2008, 453, 171 CrossRef CAS; (p) T. F. A. de Greef, M. M. J. Smulders, M. Wolffs, A. P. H. J. Schenning, R. P. Sijbesma and E. W. Meijer, Chem. Rev., 2009, 109, 5687 CrossRef CAS.
- (a) R. P. Sijbesma, F. H. Beijer, L. Brunsveld, B. J. B. Folmer, J. H. K. K. Hirschberg, R. F. M. Lange, J. K. L. Lowe and E. W. Meijer, Science, 1997, 278, 1601 CrossRef CAS; (b) P. Y. W. Dankers, E. N. M. van Leeuwen, G. M. L. van Gemert, A. J. H. Spiering, M. C. Harmsen, L. A. Brouwer, H. M. Janssen, A. W. Bosman, M. J. A. van Luyn and E. W. Meijer, Biomaterials, 2006, 27(32), 5490 CrossRef CAS; (c) Patricia Y. W. Dankers, Martin C. Harmsen, Linda A. Brouwer, Marja J. A. Van Luyn and E. W. Meijer, Nat. Mater., 2005, 4(7), 568 CrossRef CAS.
- Isodesmic supramolecular polymerizations: (a) S. Lahiri, J. L. Thompson and J. S. Moore, J. Am. Chem. Soc., 2000, 122, 11315 CrossRef CAS; (b) D. Zhao and J. S. Moore, J. Org. Chem., 2002, 67, 3548 CrossRef CAS; (c) M. Kastler; W. Pisula; D. Wasserfallen; T. Pakula.; K. Müllen; (d) F. Würthner, C. Thalacker, S. Diele and C. Tschierske, Chem.–Eur. J., 2001, 7, 2245 CrossRef CAS.
- Cooperative supramolecular polymerizations: (a) M. M. J. Smulders, A. P. H. J. Schenning and E. W. Meijer, J. Am. Chem. Soc., 2008, 130, 606 CrossRef CAS; (b) P. Jonkheijm, P. P. A. M. van der Schoot, A. P. H. J. Schenning and E. W. Meijer, Science, 2006, 313, 80 CrossRef CAS; (c) V. Simic, L. Bouteiller and M. Jalabert, J. Am. Chem. Soc., 2003, 125, 13148 CrossRef CAS; (d) F. Lortie, S. Boileau and L. Bouteiller, Chem.–Eur. J., 2003, 9, 3008 CrossRef CAS; (e) A. Arnaud, J. Belleney, F. Boué, L. Bouteiller, G. Carrot and V. Wintgens, Angew. Chem., Int. Ed., 2004, 43, 1718 CrossRef CAS; (f) P. P. A. M. van der Schoot, M. A. J. Michels, L. Brunsveld, R. P. Sijbesma and A. Ramzi, Langmuir, 2000, 16, 10076 CrossRef CAS.
- Ring-chain mediated supramolecular polymerizations: (a) A. T. ten Cate, H. Kooijman, A. L. Spek, R. P. Sijbesma and E. W. Meijer, J. Am. Chem. Soc., 2004, 126, 3801 CrossRef; (b) T. F. A. de Greef, G. Ercolani, G. B. W. L. Ligthart, E. W. Meijer and R. P. Sijbesma, J. Am. Chem. Soc., 2008, 130, 13755 CrossRef CAS; (c) H. W. Gibson, N. Yamaguchi and J. W. Jones, J. Am. Chem. Soc., 2003, 125, 3522 CrossRef CAS; (d) K. Ohga, H. Takahashi, Y. Kawaguchi, H. Yamaguchi and A. Harada, Macromolecules, 2005, 38, 5897 CrossRef CAS; (e) C. Schmuck, T. Rehm, L. Geiger and M. Schäfer, J. Org. Chem., 2007, 72, 6162 CrossRef CAS; (f) V. G. H. Lafitte, A. E. Aliev, P. N. Horton, M. B. Hursthouse and H. C. Hailes, Chem. Commun., 2006, 2173 RSC; (g) S. J. Cantrill, G. J. Youn and J. F. Stoddart, J. Org. Chem., 2001, 66, 6857 CrossRef CAS; (h) J. Xu, E. A. Fogleman and S. L. Craig, Macromolecules, 2004, 37, 1863 CrossRef CAS; (i) F. Wang, C. Han, C. He, Q. Zhou, J. Zhang, C. Wang, N. Li and F. Huang, J. Am. Chem. Soc., 2008, 130, 11254 CrossRef CAS.
- F. Oosawa and M. Kasai, J. Mol. Biol., 1962, 4, 10 CrossRef CAS.
- G. Rivas, A. Lopez, J. Mingorance, M. J. Ferrandiz, S. Zorrilla, A. P. Minton, M. Vicente and J. M. Andreu, J. Biol. Chem., 2000, 275, 11740–11749 CrossRef CAS.
- M. Yamasaki, W. Li, D. J. D. Johnson and J. A. Huntington, Nature, 2008, 455, 1255–1259 CrossRef CAS.
- (a) H. Yamaguchi and A. Harada, Biomacromolecules, 2002, 3, 1163–1169 CrossRef CAS; (b) H. Yamaguchi and A. Harada, Top. Curr. Chem., 2003, 228, 237–258 CAS.
- H. Kitagishi, Y. Kakikura, H. Yamaguchi, K. Oohora, A. Harada and T. Hayashi, Angew. Chem., Int. Ed., 2009, 48(7), 1271–1274 CrossRef CAS.
- (a) J. C. T. Carlson, S. S. Jena, M. Flenikken, T. Chou, R. A. Siegel and C. R. Wagner, J. Am. Chem. Soc., 2006, 128, 7630–7638 CrossRef CAS; (b) T. F. Chou, C. So, J. T. C. Carlson, B. R. White, M. Sarikaya and C. Wagner, ACS Nano, 2008, 2, 2519–2525 CrossRef CAS.
- W. Kuhn, Kolloid Z., 1934, 68, 2 CrossRef CAS.
- (a) R. T. Raines, Chem. Rev., 1998, 98, 1045–1065 CrossRef CAS; (b) P. R. Connelly, R. Varadarajan, J. M. Sturtevant and F. M. Richards, Biochemistry, 1990, 29, 6108–6114 CrossRef CAS; (c) confirmed by ITC measurements (not published).
- E. H. M. Lempens, I. van Baal, J. L. J. van Dongen, T. M. Hackeng, M. Merkx and E. W. Meijer, Chem.–Eur. J., 2009, 15, 8760–8767 CrossRef CAS.
- S. Kubetzko, C. A. Sarkar and A. Pluckthun, Mol. Pharmacol., 2005, 68, 1439 CrossRef CAS.
- (a) A. Dirksen, S. Dirksen, T. M. Hackeng and P. E. Dawson, J. Am. Chem. Soc., 2006, 128, 15602 CrossRef CAS; (b) A. Dirksen, T. M. Hackeng and P. E. Dawson, Angew. Chem., Int. Ed., 2006, 45, 7581 CrossRef CAS.
- K. F. Geoghegan and J. G. Stroh, Bioconjugate Chem., 1992, 3, 138–146 CrossRef CAS.
- (a) M. S. Doscher and C. H. W. Hirs, Biochemistry, 1967, 6, 304–312 CrossRef CAS; (b) T. J. Mendez, J. V. Johnson and D. E. Richardson, Anal. Biochem., 2000, 279, 114–118 CrossRef CAS.
- (a) B. R. Kelemen, T. A. Klink, M. A. Behlke, S. R. Eubanks, P. A. Leland and R. T. Raines, Nucleic Acids Res., 1999, 27, 3696–3701 CrossRef CAS; (b) C. Park, B. R. Kelemen, T. A. Klink, R. Y. Sweeney, M. A. Behlke, S. R. Eubanks and R. T. Raines, Methods Enzymol., 2001, 341, 81–94 CAS.
- L. Mandolini, Adv. Phys. Org. Chem., 1987, 22, 1–111.
- H. Jacobson and W. H. Stockmayer, J. Chem. Phys., 1950, 18, 1600–1606 CrossRef CAS.
- (a) A. Mulder, T. Auletta, A. Sartori, S. Del Ciotto, A. Casnati, R. Ungaro, J. Huskens and D. N. Reinhoudt, J. Am. Chem. Soc., 2004, 126, 6627–6636 CrossRef CAS; (b) R. H. Kramer and J. W. Karpen, Nature, 1998, 395, 710–713 CrossRef CAS.
- T. H. Evers, E. M. W. M. van Dongen, A. C. Faesen, E. W. Meijer and M. Merkx, Biochemistry, 2006, 45(44), 13183–13192 CrossRef CAS.
- (a) H. X. Zhou, J. Phys. Chem. B, 2001, 105(29), 6763–6766 CrossRef CAS; (b) H. X. Zhou, J. Am. Chem. Soc., 2001, 123, 6730–6731 CrossRef CAS; (c) H. X. Zhou, J. Mol. Biol., 2003, 329, 1–8 CrossRef CAS.
- V. M. Krishnamurthy, V. Semetey, P. J. Bracher, N. Shen and G. M. Whitesides, J. Am. Chem. Soc., 2007, 129(5), 1312–1320 CrossRef CAS.
- H. X. Zhou, Biochemistry, 2004, 43, 2141 CrossRef CAS.
- J. M. Gargano, T. Ngo, J. Y. Kim, D. W. K. Acheson and W. J. Lees, J. Am. Chem. Soc., 2001, 123, 12909–12910 CrossRef CAS.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, NY, 1953 Search PubMed.
- S. P. Powers, I. Foo, D. Pinon, U. G. Klueppelberg, J. F. Hedstrom and L. J. Miller, Biochemistry, 1991, 30, 676–682 CrossRef CAS.
- P. J. Flory, Statistical Mechanics of Chain Molecules, Wiley-Interscience, New York, 1969 Search PubMed.
- Determined via PyMol, PDB 1FS3.
- For long PEG chains the characteristic ratio is found to be 4.1, for shorter PEG chains this number decreases as given by Flory, to ∼3.9 for a 6-repeat EG spacer. However, contributions of the flexible ends of the S-protein and S-peptide justify the use of 4.1 for our AB2 system.
- G. Ercolani, L. Mandolini, P. Mencarelli and S. Roelens, J. Am. Chem. Soc., 1993, 115, 3901–3908 CrossRef CAS.
- G. Ercolani and S. Di Stefano, J. Phys. Chem. B, 2008, 112, 4662–4665 CrossRef CAS.
- R. B. Martin, Chem. Rev., 1996, 96, 3043–3064 CrossRef CAS.
- J. A. Semlyen, Adv. Polym. Sci., 1976, 21, 41 CAS.
- H. Morawetz and N. Goodman, Macromolecules, 1970, 3, 699 CrossRef CAS.
- Y. Yamashita, J. Mayumi, Y. Kawakami and K. Ito, Macromolecules, 1980, 13, 1075 CrossRef CAS.
- D. Shore and R. L. Baldwin, J. Mol. Biol., 1983, 170, 957 CrossRef CAS.
- S. Abed, S. Boileau and L. Bouteiller, Macromolecules, 2000, 33, 8479–8487 CrossRef CAS.
- B. A. H. Huisman, P. G. Bolhuis and A. Fasolino, Phys. Rev. Lett., 2008, 100, 188301 CrossRef CAS.
- E. H. M. Lempens, B. A. Helms, M. Merkx and E. W. Meijer, ChemBioChem, 2009, 10, 658–662 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed experimental procedures. Analytical characterization data of all compounds. DLS. Extended simulations on ring–chain equilibria. Detailed SEC flow-speed analysis. See DOI: 10.1039/c0sc00108b |
| This journal is © The Royal Society of Chemistry 2010 |
