The structure of randomly branched polymers synthesized by living radical methods†
Dominik
Konkolewicz
a,
Angus
Gray-Weale
b and
Sébastien
Perrier
*a
aKey Centre for Polymers and Colloids, School of Chemistry, The University of Sydney, Building F11, University of Sydney NSW, 2006, Australia. E-mail: s.perrier@chem.usyd.edu.au
bSchool of Chemistry, Monash University, Victoria, 3800, Australia
First published on 27th May 2010
Abstract
We present a new versatile model for the description of randomly branched polymers. Hyperbranched and highly branched polymers have many potential applications including viscosity modification, drug-delivery vehicles or supports for catalysts. Because of their complex architectures, it is difficult to visualize and describe the structure of randomly branched polymers. This work aims to introduce a new tool that will address this issue, by developing a model called kinetic random branching theory (KRBT). This new theory is based on random branching theory, optimized so that it is applicable to a wider range of polymers. In order to test the robustness of our model, we have considered three classes of branched polymers synthesized by radical polymerisation using the well-established ‘Strathclyde approach’, which is known to produce polymers of very complex structure. The three classes of polymer studied are methyl methacrylate, alternating styrene-maleic anhydride and divinyl benzene-only polymers, and in each case reversible addition-fragmentation chain transfer (RAFT) was used. We find that the majority of the polymer structures studied agree well with the predictions of our model, thus implying that they are indeed randomly hyperbranched polymers. The only case where the model failed to predict the structure of the polymer for a highly branched methyl methacrylate, synthesized to high conversions, in presence of an excess of brancher. This suggests that the sample is not a hyperbranched polymer, instead the polymers structure may be dominated by loops and cross-links such as in a nano-gel. By demonstrating the robustness of our model against these typical examples, we have established a new tool for characterising the structure of complex branched structures.
I. Introduction
Highly branched polymers such as dendrimers and hyperbranched polymers have many applications, e.g. drug-delivery, gene-delivery, viscosity modification, and since these polymers have many end-groups they can be used as supports for catalysts and scaffolds for further synthesis.1–12 Dendrimers are highly branched polymers with a regular structure, arranged into layers extending from the center of the polymer. Each new layer of the dendrimer is a new ‘generation’, and each potential branch-point in the dendrimer is fully occupied up to the final generation number. Due to this ordered structure, dendrimers are monodisperse and have a known number of end-groups. This makes dendrimers attractive candidates for applications such as drug-delivery or supports for catalysts. However, dendrimer synthesis involves multiple reaction-purification steps,13–15 and it is difficult to obtain a large amount of the polymer. This restricts the viability of dendrimers for large-scale applications.Hyperbranched polymers are also highly branched polymers, with many end-groups and they have been proposed as alternatives to dendrimers.9 Hyperbranched polymers can be synthesized in a one-pot reaction, and do not require multiple reaction-purification steps in their synthesis.10,16–19 Unlike the regular structure of the dendrimer, the branches in a hyperbranched polymer are distributed randomly throughout the polymer.20,21 The random distribution of branches makes the structure of a hyperbranched polymer more difficult to describe than the structure of a dendrimer. These structural irregularities and the broad molecular weight distributions have significantly limited the use of hyperbranched polymers, and an understanding of a hyperbranched polymer's structure will be beneficial for applications such as drug-delivery or supports for catalysis. This is because the polymer's structure affects its ability to encapsulate or release a drug molecule, and affects the number of end-groups that can be catalytically functionalized.
In recent years, a revolutionary synthetic route has been developed for the synthesis of highly branched and hyperbranched polymers. The so-called Strathclyde route, introduced by Sherrington and coworkers in 2000, is a method for synthesizing hyperbranched polymers that is applicable to large scale syntheses, due to its simplicity. In the Strathclyde approach a hyperbranched polymer is synthesized using a combination of linear monomer, difunctional monomer and chain transfer agent.18,23–25 The chain transfer agent can be both a conventional transfer agent such a thiol,18 or a controlling group that also imparts pseudo-livingness to the polymerisation system.10,25 Reversible addition–fragmentation chain transfer (RAFT) polymerization is one of the most versatile of the living radical polymerisation methods that impart pseudo-livingness to a radical polymerisation system, as it can be adapted to the widest range of monomers.22,26,27 RAFT mediated polymerization gives excellent control over the molecular weight of linear polymers and can be used to make architectures such as blocks or stars.27–30 In addition RAFT has been used to synthesize highly branched polymers, using strategies that resemble self condensing vinyl polymerization31–34 and by the Strathclyde approach.10,25,35–38 Despite the growing use of the Strathclyde approach and living radical techniques such as RAFT to synthesize hyperbranched polymers, the structure of the polymer is not well understood. The kinetics of these Strathclyde reactions has been modeled by Wang et al.,39 Poly et al.40 and Bannister et al.41 There have also been many kinetic models for cross-linked networks.42–46 These simulations of cross-linked networks are a limiting case of our model, where many loops are formed, although in some cases these models have been adapted to more branched systems.47,48 These kinetic models are very useful, since they allow the researcher to determine the rate at which various branched species are formed. However, it is also important to study the structure of the final polymer after polymerization. This structural information is complementary to the kinetic data, and determines the applicability and usefulness of a given polymer in a specific application. In this paper, we develop a model for the structure of polymers synthesized using the Strathclyde approach, and other related syntheses.
In the literature, there have been many studies on the structure of dendrimers, starting with the work of De Gennes and Hervet,49 and these studies have been reviewed by Ballauff and Likos.50 In contrast to dendrimers, there have been far fewer studies on the structure and properties of hyperbranched polymers. Of these studies of hyperbranched polymers there have been simulation studies of relatively low molecular-weight polymers.51–58 In those studies the polymer's structure is relatively close to dendritic, with a high degree of branching. In addition, Mulder et al. developed a model for hyperbranched polymers that can be described in terms of partially filled generations and thought of as an incomplete dendrimer.59 However, these simulations and models do not capture randomly branched polymers where the structure of the polymer is sufficiently complex that it cannot be described in terms of a generational structure. Watts et al.60 addressed these limitations by simulating hyperbranched polymers made by random attachment of linear chains. The simulations were run to very high degrees of polymerization and later improved by forbidding overlap between the monomers.61 The simulations described above laid the foundation for random branching theory,20,21 the first flexible and general model for the structure of highly branched polymers.
Random branching theory20,21 was developed to describe the solution structure of randomly branched polymers without restricting the polymer to follow a generation-like structure. In random branching theory, the central variable is the density profile, which is proportional to the polymer mass at various distances form the center of the polymer. The density profile is an important description of the solution structure of the polymer, and can be used to determine quantities such as the radius of gyration. In random branching theory the density profile is evolved by the sequential addition of ‘simple units’. These simple units are entities whose structure is simpler than the structure of the resulting hyperbranched polymer. These simple units can range from monomers whose size is only a few angstroms to the β particles in glycogen (β particles are spherical polysaccharides with diameters up to 50 nm).20,21,62 In earlier work, random branching theory was shown to agree well with both simulated and experimental hyperbranched polymers.20,21 In these comparisons, random branching theory predicted the experimentally observed size-mass scaling law rg ∼ log M and simulated density profiles.20,21 Random branching theory has also been used to analyze the location of the end-groups in hyperbranched polymers made under different conditions.63 In addition, Gilbert and co-workers have used random branching theory to gain information about the hyperbranched biopolymers glycogen and amylopectin.64,65
In this paper we outline a model that gives structural information about a variety of highly branched polymers. We call this model kinetic random branching theory (KRBT), and it is built on random branching theory.20,21 In this paper, we study methacrylic, alternating styrene-maleic anhydride and brancher only polymers, fitting our model to the experiments and drawing conclusions from the comparison. KRBT will determine which polymers are consistent with a randomly branched polymer, and which polymers are not consistent with the assumptions of random branching. When an experiment agrees with the model, we argue that these polymers are well described as randomly branched, and we obtain information about the structure of the polymer from the fitted parameters. If a polymer does not fit the model, the polymer has a different structure such as a nano-gel, or perhaps it is close to a linear chain. Although we have tested our model on polymers synthesized by the Strathclyde approach under RAFT control, our model is not limited to these polymers. Our model is general enough that it may be applied to any randomly branched polymer, such as any other polymer synthesized using the Strathclyde approach18 or self condensing vinyl polymerization. In all cases our model can give information about the structure and properties of the hyperbranched polymer, that can then be utilized in applications.
II. Theory
A. Random branching theory and kinetic random branching theory
We develop a theory called ‘kinetic random branching theory’ (KRBT) which is based on ‘random branching theory’.20,21 Random branching theory is a model that describes the solution structure of branched polymers. Random branching theory is a thermodynamic theory, and assumes that the system is at thermodynamic equilibrium at all points in time. In random branching theory the branched polymer is built up by random assembly of smaller particles or polymers called ‘simple units’. These simple units can be small oligomeric chains, clusters of linear chains, or even β particles in the polysaccharide glycogen which are 20–50 nm in diameter.20,21 Random branching theory allows the simple units to have a well defined size or mass distribution, but the theory does not model systems where the properties of the simple units are rapidly evolving. In this way, random branching theory is a model that gives the structure of randomly assembled units. Random branching theory does not assume anything about the synthesis of the simple units, or the kinetic process that joins these units to each-other.Some of the assumptions of random branching theory are not valid for RAFT mediated synthesis of highly branched polymers, and other related syntheses. The molecular weight vs. conversion curve for RAFT mediated highly branched polymers shows an initial period where the molecular weight follows a linear evolution of number average molecular weight with conversion.10 This suggests that the majority of the polymers are well controlled linear chains. When the conversion reaches ∼50–60%, the molecular weight begins to grow very rapidly. This rapid growth in the molecular weight suggests that the polymerization does not only proceed by the addition of linear chains to branched polymers. Instead the rapid growth of the molecular weight suggests that there are many reactions between two branched polymers. For instance if a polymer with 7 linear chains reacts with a polymer of 5 linear chains, the resulting polymer will have 12 linear chains. The polymer with 12 chains can then react even further.
This rapid growth of the molecular weight over time suggests that at high conversion the dominant reaction is between polymers, such as the reaction between a polymer with 5 linear chains and one with 7 linear chains. In this reaction the first simple unit would be the polymer with 5 chains, and the second simple unit would be the polymer with 7 chains. Once the polymer with 12 linear chains is formed, it can itself be a simple unit for further reactions. Therefore, if we analyze a sample of hyperbranched polymers, we argue that the average simple unit is quite similar to the average polymer only a short time before. In other words the majority of polymers observed at a given sample were most likely to be formed a relatively short time before. Furthermore, if the reaction is allowed to proceed, the polymers in this sample will act as simple units and form larger hyperbranched polymers.
The reaction scheme outlined above implies that the properties of the simple units change over time. Until about 50% conversion the average simple unit is well approximated as a single linear chain, whereas at high conversion the average simple unit will have tens or possibly hundreds of linear chains. Although at low conversion there is a small probability of branching, the concentration of linear monomer is high compared to the concentration of pendant double bonds, which implies that linear propagation is the dominant mechanism. In this early phase of the reaction, the free brancher must also be incorporated into the chain, to give a polymer chain with a pendant double bond. At higher conversions branching is more likely, due to the larger number of pendant double bonds, and the lower concentration of linear monomer. Typically experimental data, such as the data of Armes et al.,36 show that the molecular weight begins to grow very rapidly at approximately 50% conversion. This rapid growth in molecular weight is due to the branching reactions. Since most of these Strathclyde systems show that the molecular weight follows the linear theoretical prediction up until about 50% conversion, we argue that branching is minimal during the early phases of the reaction, and dominates after some minimal conversion is reached. This allows us to assume that the average simple unit is a linear chain at low conversion, however, at high conversion the average simple unit will typically have many linear chains.
Since the properties of the simple unit change from being approximately one linear chain at low conversion, to the simple unit itself being a branched cluster of linear polymers, there are significant kinetic influences on the properties of the hyperbranched polymers observed at any point in time. This suggests that random branching theory, which only assumes random attachment of units, is not the best model to use in describing these structures. We should include some of these kinetic effects in a model that describes these polymers. KRBT is developed to address these concerns, since it relaxes some of the assumptions in random branching theory and can describe new kinds of polymers.
In this work, we are not simply linking simple units together to form a hyperbranched structure, as is done in random branching theory. We will now use kinetic information to describe our simple units, and form hyperbranched polymers from these ‘evolving’ simple units. Although all the assumptions of the thermodynamic random branching theory are not satisfied in the studied highly branched polymers, we can use and extend the ideas in random branching theory to explain the structure of these polymers. We use KRBT to determine the structure of complex polymers using kinetic information about the size or mass distribution of the simple units.
In KRBT, we assume that at each point in time there is a well-defined molecular weight or size distribution of simple units. Although this distribution is well-defined at each time point, we expect the distribution to evolve rapidly over time. From earlier arguments, we expect these simple units to be the branched polymers a short time before the sample was taken. If instead the simple units were the polymers at some earlier point in time, for instance if the simple units were primarily linear chains, we would not find the accelerating growth in molecular weight with conversion. Since we assume that the polymers formed in a given sample were formed from the polymers a short time earlier, we propose that the molecular weight distribution a short time before the sample is taken is a good approximation to the distribution of simple units that make up the polymer in the analyzed sample. Since the simple units are similar to the polymers a short time before the sample was taken, we argue that the distribution of the simple units that make up the sample should be similar to the molecular weight distribution of the sample. A corollary of this proposition is a similarity between the average molecular weight in the analyzed sample and the average molecular weight of the simple units. However, when fitting experimental data, we only input the shape of the distribution, and fit the average molecular weight and sizes of the simple units. We will then compare the fitted average molecular weight to the actual average molecular weight of the sample. In most cases, we will show that the fitted simple unit molecular weight and actual molecular weights agree well with each other, showing that our assumptions are valid.
KRBT uses the distribution of simple units at each point in time to generate the structure of more complex polymers at the point in time soon after. That is we start with one simple unit, and randomly attach another simple unit which gives the average structure of a polymer with double the average molecular weight, then add a third simple unit to generate the structure of a polymer with on average triple the molecular weight of the average simple unit. For instance, if the average simple unit at some point in time has 5 linear chains, we use KRBT to determine the average structure of a polymer with 10 or 15 linear chains. In this way KRBT can be used to couple random branching theory to a kinetic scheme or system of kinetic equations. However, in this paper we do not couple the random branching theory equations to kinetic equations, instead we use experimentally determined molecular weights and kinetic data throughout. This is sufficient to demonstrate the applicability of the KRBT concepts to experimental systems. In the future, the KRBT equations could be directly connected with kinetic equations, which could be used to predict monomer conversion, degree of branching over time, and potentially predict the onset of gelation in many system.
B. Evolution of the density profile
KRBT, gives the density profile of simple units, or monomers, from the center of mass, which we denote by ρ. ρ describes the solution structure of the polymer and the Fourier transform of ρ is related to the X-ray or neutron scattering profile. Our model can describe the evolution of ρ as the number of simple units N is increased. The density profile of the new simple unit is assumed to be distributed as a Gaussian function about the center of mass. ζ denotes the density profile of the simple unit. The density profile of the simple unit with n monomers is given by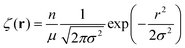 | (1) |
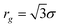 .
.
KRBT describes the structure of the branched polymer by randomly attaching the simple units from the instantaneous simple unit distribution. There are several physical effects that are included in our model to describe the probability of adding a new simple unit at a given location. The first effect is the random branching of the units. In our model each simple unit already in the polymer is a potential branch point for additional simple units. Since each simple unit is a potential branch point, the probability of adding a new chain is proportional to the density of simple units at the point of interest. In addition to the random branching term, there is also a term which describes the repulsion between segments of the polymer. This term prevents a new simple unit adding to a region of very high polymer density, as this would cause significant segmental repulsion. The final term we consider is the solvent swelling or compression term. In good solvents the polymer is swollen from its unperturbed size, and in a poor solvent the polymer is compressed. In this model we use the Flory-Huggins χ parameter to describe the solvent interactions.66 With the effects mentioned above, the probability of adding a new simple unit at the position R is given by21
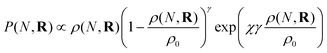 | (2) |
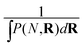 .21
.21
We assume that the evolution of the density profile ρ can be described by considering the probability of adding the new simple unit at a give location, P, and the physical properties of the new simple unit ζ.21 The evolution in the density profile is written as
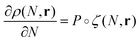 | (3) |
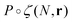 is the convolution given by ∫P(N,R)ζ(r−R)dR.21
is the convolution given by ∫P(N,R)ζ(r−R)dR.21
C. Distribution of simple units
In general simple units are not uniform in size, but instead they have some distribution in their size and molecular weight. Earlier work showed how an exponential or Gaussian distribution of simple unit sizes can be incorporated into random branching theory.21 These distributions can be incorporated into KRBT the same way as they are included in random branching theory. In living radical polymerizations, such as RAFT polymerizations, the resulting molecular weight distribution is generally narrowly distributed.67,68 These narrow distributions that result from living radical polymerizations have often been approximated by a Gaussian function,69–72 therefore the Gaussian distribution is a good approximation of the chain-length distribution of linear chains made by living radical methods. Exponential distributions are common in free radical polymerizations, and based on the kinetic studies of Wang et al.39 we argue that it is also an acceptable approximation for the distribution of the number of monomers per polymer in a RAFT polymerization of mono and di-functional monomer. If the average simple unit has μ monomers then an exponential distribution in the number of monomers per simple can be obtained by the following differential equation:21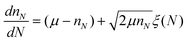 | (4) |
This differential equation gives nN the number of monomers of the Nth simple unit given that the overall distribution is exponential.
In this work, we assume that the squared size σN2 of the simple unit is proportional to nN, the number of monomers in the unit. Ideally, we would use a logarithmic scaling such as σ ∼ log n to determine the size of the simple unit from the number of monomers. This is because random branching theory tends to predict this logarithmic scaling law, and the simple units in this work are themselves branched polymers. However, this would require the estimation of two parameters, for each fit, the intercept and slope of this scaling law. An additional complication is that for some parameter choices the branched polymer theories predict the logarithmic law σ2 ∼ log n. If instead we use the power law we only need to estimate the average size, or pre-factor of the power law, and we do not need to decide whether the size or the squared size grows logarithmically with the number of monomers in the unit.
In the ESI† we compare the law σ ∼ log N, to the power law σ2 ∼ N for several data series. These data series span the sets of parameters used in this paper, and represent many ‘typical’ parameters in our branched polymer theories. The logarithmic laws are the ones that best fit through several experimental data series. Typically we find excellent agreement up to N ≈ 5, and good agreement up to N ≈ 10. Although many samples show deviations at high N, the exponential distribution of monomers per simple unit suggests that the likelihood of selecting one of these large units is very small. Therefore, to minimize the number of fitted parameters, we use the power law to convert between the physical size of the unit, σ, and the number monomers in the unit, n. We have also used this assumption when analyzing other synthetic branched polymers, and found good agreement between theory and experiment.20
D. Parameters in the model
KRBT has several parameters that govern the structure of the polymer. The first parameter is![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) which describes the mean size of the simple unit.
which describes the mean size of the simple unit. ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) is related to the average radius of gyration of the simple unit by the following expression
is related to the average radius of gyration of the simple unit by the following expression 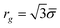 . γ is the average number of random steps in the simple unit. γ is related to n the number of monomers in a linear chain by the following expression
. γ is the average number of random steps in the simple unit. γ is related to n the number of monomers in a linear chain by the following expression 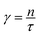 , where τ is the persistence number.21 Over short distances there are correlations in the orientation of one monomer with respect to the previous monomer. The persistence number τ is the number of monomers after which the chain's conformation reorients and takes a random direction. The parameter χ is the Flory-Huggins solvent interaction parameter,66 and it describes the interaction between the polymer and the solvent. The parameter ρ0 is the maximal density of simple units, analogous to a packing density. It is often simpler to express ρ0 in terms of the size of the simple unit
, where τ is the persistence number.21 Over short distances there are correlations in the orientation of one monomer with respect to the previous monomer. The persistence number τ is the number of monomers after which the chain's conformation reorients and takes a random direction. The parameter χ is the Flory-Huggins solvent interaction parameter,66 and it describes the interaction between the polymer and the solvent. The parameter ρ0 is the maximal density of simple units, analogous to a packing density. It is often simpler to express ρ0 in terms of the size of the simple unit ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) and a dimensionless number κ. Therefore we write
and a dimensionless number κ. Therefore we write 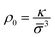 .21
.21
III. Results
In this section KRBT is used to describe the structure of various highly branched polymers. KRBT is used to distinguish between polymers that follow the assumptions of random branching of simple units, and polymers that do not follow this assumption. All the calculations reported in this paper were done with the branched polymer structure theory programs on a G5 PowerPC using an ibmxl Fortran compiler.73 These programs are freely available.73A. Poly(methyl methacrylate)
We analyzed several samples of highly branched poly(methyl methacrylate), studying polymers with linear segments of 20 monomer units and 200 monomer units. We also varied the amount and kind of branching monomer, using both divinyl benzene (DVB) and ethylene glycol dimethacrylate (EGDMA) as branching monomers. KRBT is compared to the experimental size-mass scaling data. If the theory is consistent with the experiments then it suggests that the model predicts the polymer's structure and that the polymers can be thought of as randomly branched simple units. If the theory does not agree with the experiments, then the polymers have a structure not consistent with the model, such as a nano-gel.We use the notation MMADVB20 to denote polymers where the brancher is DVB, the linear monomer is MMA and it has 20 MMA units per RAFT agent. In this way MMAEGDMA200 is a polymer with EGDMA as the brancher, and 200 MMA units per RAFT agent. Fig. 1 shows the fit of our model to two samples of MMA polymer, namely MMAEGDMA200 and MMADVB20. In both of these polymers there is good agreement between the KRBT and the experimental data. In both cases we used the Flory-Huggins interaction parameter of 0.44, taken as the literature value for MMA and tetrahydrofuran.74 We used an average γ = 7 for the MMA 20 sample and γ = 70 for the MMA 200 sample. This corresponds to γ being the linear chain length divided by a persistence number, τ of 3. In both cases we used an exponential distribution in the number of monomers per simple unit, and γ was proportional to the number of monomers in that simple unit. We allow γ to be proportional to the number of monomers per simple unit, since this describes that fact that it is easier to fit in small unit into a given region than a larger unit. The exponential distribution is a reasonable approximation to the distribution of the number of chains per polymer once branching is significant.39 The parameters used to fit the data are given in Table 1.
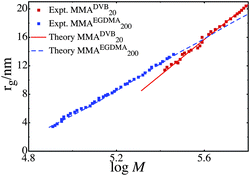 | ||
| Fig. 1 The experimental and theoretical size-mass scaling for the samples MMADVB20 and MMAEGDMA200. | ||
| Parameter | MMADVB20 | MMAEGDMA200 |
|---|---|---|
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (nm) (nm) |
4.8 | 1.9 |
| κ | 0.03 | 0.03 |
| γ | 7 | 70 |
| χ | 0.44 | 0.44 |
| μ | 2060 | 780 |
| M0 | 100 | 100 |
In both of these cases the KRBT agrees well with the experimental size-mass scaling relationship in the polymer, suggesting that MMADVB20 and MMAEGDMA200 are consistent with the polymer being made of randomly branched simple units. Furthermore the parameters used to fit the data are consistent with the expected size of the clusters of simple units and the experimentally measured molecular weight data. In particular μ the mean number of linear chains per simple unit agrees very well with the μ obtained from the molecular weight data. The experimentally determined number-averaged molecular weights are approximately Mn = 127000 g mol−1 and Mn = 50000 g mol−1 (μ = 1270 and μ = 500) for MMADVB20 and MMAEGDMA200 respectively. These values agree well with the fitted values of μ = 2060 and μ = 780 for the series MMADVB20 and MMAEGDMA200. In both the sample MMADVB20 and MMAEGDMA200 we used κ = 0.03, which as shown earlier corresponds approximately to random packing of spheres of radius rg. This suggests that both the structures MMADVB20 and MMAEGDMA200 are very dense, with little free volume available.
We also analyze the structure of the series MMAEGDMA20, as shown in Fig. 2. In contrast to the earlier graphs, the size-mass scaling in the series MMAEGDMA20 does not agree with KRBT, or random branching theory. In both models there is a regime at low number of simple units where the size grows with the logarithm of the molecular weight.20,21 Examples of these scaling laws are seen in Fig. 1, however, there is also a regime at a large number of simple units where rg ∼ M1/3. The data clearly do not fit the logarithmic scaling laws (e.g. rg ∼ log M). However, due to the high conversion and large number of chains per polymer we compared the experiments to the scaling law rg ∼ N1/3, as shown in Fig. 2
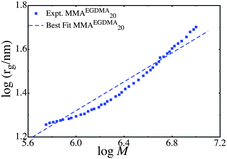 | ||
| Fig. 2 Comparison of the scaling law rg ∼ N1/3 and the data series MMAEGDMA20. | ||
Since the model does not fit the MMAEGDMA20 very well, and fails to predict many of the details of the size-mass scaling, this suggests that the polymers in MMAEGDMA20 have grown beyond the regime where KRBT holds and instead the polymer may resemble a nano-gel. This is a plausible explanation, as this polymer was synthesized with a 20% excess of brancher, relative to RAFT agent, and this reaction reached high monomer conversion when this sample was taken. The excess of brancher relative to RAFT agent implies that there must be some degree of cross-linking at high conversion. The formation of a partially cross-linked product is likely to explain the disagreement between the series MMAEGDMA20 and KRBT.
B. Alternating maleic anhydride and styrene
We analyze alternating highly branched polymers of maleic anhydride and styrene. We consider samples of the polymer where the RAFT to styrene to maleic anhydride ratio is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25. The ratio of the branching monomer, DVB, to RAFT was varied between 0.8
25. The ratio of the branching monomer, DVB, to RAFT was varied between 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, with these series denoted as Sty-MANDVB = 0.8 and Sty-MANDVB = 1. In both series we use the exponential distribution as the distribution of simple unit sizes, and a Flory-Huggins interaction parameter of 0. Although no accurate data for Flory-Huggins interaction parameters could be found for styrene-maleic anhydride at the appropriate temperatures, extrapolation of high temperature data75 gave a χ value of approximately 0. We also used an average γ = 8, with the value of γ for a given simple unit being proportional to the number of monomer in that unit. The value γ = 8 was determined by treating the each styrene-maleic anhydride unit as a single entity, therefore a linear chain will have 25 Sty-MAN units in it, and assuming this the polymer has a persistence number of 3. This is the same value of the persistence as in the MMA polymers. The fit of KRBT to the experiments is shown in Fig. 3 and the parameters used are shown in Table 2.
1, with these series denoted as Sty-MANDVB = 0.8 and Sty-MANDVB = 1. In both series we use the exponential distribution as the distribution of simple unit sizes, and a Flory-Huggins interaction parameter of 0. Although no accurate data for Flory-Huggins interaction parameters could be found for styrene-maleic anhydride at the appropriate temperatures, extrapolation of high temperature data75 gave a χ value of approximately 0. We also used an average γ = 8, with the value of γ for a given simple unit being proportional to the number of monomer in that unit. The value γ = 8 was determined by treating the each styrene-maleic anhydride unit as a single entity, therefore a linear chain will have 25 Sty-MAN units in it, and assuming this the polymer has a persistence number of 3. This is the same value of the persistence as in the MMA polymers. The fit of KRBT to the experiments is shown in Fig. 3 and the parameters used are shown in Table 2.
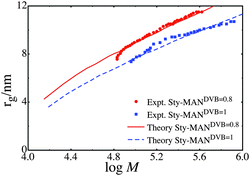 | ||
| Fig. 3 Comparison between experimental data series Sty-MANDVB = 0.8 and Sty-MANDVB = 1 and theoretical fit. | ||
| Parameter | Sty-MANDVB = 0.8 | Sty-MANDVB = 1 |
|---|---|---|
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (nm) (nm) |
2.4 | 2.1 |
| κ | 10 | 10 |
| γ | 8 | 8 |
| χ | 0 | 0 |
| μ | 70 | 76.5 |
| M0 | 202 | 202 |
As in the pure MMA polymers, the structure of the alternating polymer is well predicted by KRBT. It is interesting to note that the value of μ obtained from the fits corresponds well to the measured number average molecular weight with experimental values of Mn = 24000g mol−1 corresponding to μ = 119 for Sty-MANDVB = 1 and Mn = 18000 g mol−1 corresponding to μ = 89 for Sty-MANDVB = 0.8. Unlike the pure MMA polymers, the value of κ is large in the alternating polymer. The reason for the large value of κ is not clear, but the theory suggests that the alternating polymers are more compressible than the pure MMA polymer. This could be due to the presence of the maleic anhydride monomer. Alternatively, the large value of κ could be because the alternating polymers tend to be closer to linear chains than the pure MMA polymer, which suggests greater compressibility.
C. Brancher only experiments
In these systems, there is only RAFT agent and branching monomer, with the possible addition of maleic anhydride as a spacer monomer. We consider three different polymers: DVB1; DVB – MAN1 and DVB20 which are polymers where the divinyl benzene to RAFT ratio is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, divinyl benzene to maleic anhydride to RAFT ratio is 1
1, divinyl benzene to maleic anhydride to RAFT ratio is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and where the divinyl benzene to RAFT ratio is 20
1 and where the divinyl benzene to RAFT ratio is 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The polymers DVB1 and DVB – MAN1 scale approximately as rg2 ∼ log M. This scaling law has been theoretically predicted for polymers that have very weak repulsive forces between the units, and therefore they have a large κ.21 In all cases an exponential distributions of simple unit masses is used, and for the series DVB1 and DVB – MAN1 a large κ is used. For the divinyl benzene only polymers we use the Flory-Huggins interaction parameter for styrene, specifically χ = 0.47,74 and for the alternating divinyl benzene maleic anhydride polymer we use χ = 0. When fitting the DVB1, DVB20 and DVB – MAN1 polymers a constant value of γ = 1 is used, which corresponds to the addition of a single unit at random. Since DVB1 and DVB – MAN1 are polymers with 1 brancher per RAFT agent this is a natural choice. For the analyzed sample of DVB20 the reaction reached approximately 30% conversion, which corresponds to a chain length of approximately 6 units per RAFT agent. If a persistence number is 3 is assumed, as in the MMA and Sty-MAN samples an average γ = 2 is found, which is very close to γ = 1. Therefore for simplicity and minimizing the number of fitting parameters, γ = 1 is used in the series DVB20. The fits are shown in Fig. 4 and the parameters in Table 3
1. The polymers DVB1 and DVB – MAN1 scale approximately as rg2 ∼ log M. This scaling law has been theoretically predicted for polymers that have very weak repulsive forces between the units, and therefore they have a large κ.21 In all cases an exponential distributions of simple unit masses is used, and for the series DVB1 and DVB – MAN1 a large κ is used. For the divinyl benzene only polymers we use the Flory-Huggins interaction parameter for styrene, specifically χ = 0.47,74 and for the alternating divinyl benzene maleic anhydride polymer we use χ = 0. When fitting the DVB1, DVB20 and DVB – MAN1 polymers a constant value of γ = 1 is used, which corresponds to the addition of a single unit at random. Since DVB1 and DVB – MAN1 are polymers with 1 brancher per RAFT agent this is a natural choice. For the analyzed sample of DVB20 the reaction reached approximately 30% conversion, which corresponds to a chain length of approximately 6 units per RAFT agent. If a persistence number is 3 is assumed, as in the MMA and Sty-MAN samples an average γ = 2 is found, which is very close to γ = 1. Therefore for simplicity and minimizing the number of fitting parameters, γ = 1 is used in the series DVB20. The fits are shown in Fig. 4 and the parameters in Table 3
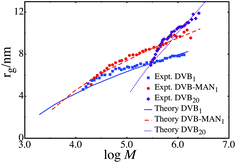 | ||
| Fig. 4 Comparison between experimental data series DVB1, DVB – MAN1 and DVB20 and theoretical fit. | ||
| Parameter | DVB1 | DVB – MAN1 | DVB20 |
|---|---|---|---|
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (nm) (nm) |
1.28 | 1.6 | 2.45 |
| κ | 10 | 10 | 0.1 |
| γ | 1 | 1 | 1 |
| χ | 0.47 | 0 | 0.47 |
| μ | 15 | 15 | 900 |
| M0 | 130 | 228 | 130 |
The value of μ = 900 we obtain for the DVB20 series is consistent with the experimental average molecular weight Mn = 200000 g mol−1 which corresponds to μ ≈ 1500. The series DVB1 and DVB – MAN1 do not follow this trend. For those series we predict a μ ≈ 15. This suggests that the average molecular weight of the simple unit is an order of magnitude lower than the average molecular weight of the sample (Mn = 65000 g mol−1 for DVB1 and Mn = 90000 g mol−1 for DVB – MAN1). The molecular weight distribution measured by either MALLS or DRI in the sample DVB1 shows a distinct peak at low molecular weight, which is likely to correspond to the average simple unit added to the polymer. Such low molecular weight peaks are not present in other samples such as MMADVB20. Although the kinetics of these reactions are not well understood, the results of these analyses are consistent with the low molecular weight peak observed in the distribution.
In the case of DVB1 and DVB – MAN1, these data showed the scaling rg2 ∼ log M and could only be fitted with very large κ (κ = 10). A large value of κ suggests very weak repulsive interactions between the units. This is somewhat counterintuitive, given that these polymers are only made up of RAFT agents and branching monomers. Based on a priori expectations, these polymers should be very dense and have strong repulsive interactions between the units. Typically, a dense polymer's size would grow very rapidly with mass. This is not consistent with the experiments that show the polymer's size increasing only minimally over two orders of magnitude in mass.
We may explain these results by postulating that these polymers do not have simple structures but that there is some ordering such as π–π stacking or the linking of many branchers together to give a fairly rigid unit. If a simple unit has significant π–π stacking or is quite long and rigid it could have reasonably large units. However these units would be largely only in one direction, implying that many units could be added in a given region simply by rotating the units with respect to each-other. This is our hypothesis for the scaling observed in the data, namely small increases in the size over two decades in molecular weight.
D. Analysis of scaling behavior
The earlier results suggest that our model can describe a variety of branched polymer structures, agrees well with the kinetic mechanism and the experimental size-mass scaling. Both the experiments and our model show a variety of scaling laws such as rg ∼ log M, and rg2 ∼ log M, as well as experimental scaling laws that are not predicted by our model when the polymer approaches a gel. In this section we analyze the regimes where our model follows the two most commonly observed scaling laws. These are the scaling laws rg ∼ log M and rg2 ∼ log M. This is important for applications of our model as it allows the researcher to determine properties of their polymer such as density or compressibility from the size-mass scaling. This section studies the effect of variations in the input parameters on the size mass scaling, assuming an athermal solvent, that is χ = 0. In this way a phase diagram is created for the different scaling laws. An exponential distribution of the number of monomers per simple unit is assumed. We vary the parameter κ, the parameter that describes the compressibility of the simple units and γ the number of steps in the new unit's random walk. γ is not treated as a random variable in this analysis, unlike some of the earlier cases. This restriction simplifies the calculation and allows direct comparison between the cases of γ = 1 and γ > 1. Fig. 5 shows the parameters that give the scaling laws rg ∼ log M and rg2 ∼ log M when the simple unit's distribution is exponential.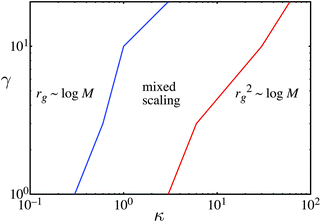 | ||
| Fig. 5 Phase diagram showing the parameters that give the scaling laws rg ∼ log M and rg2 ∼ log M. This is for exponentially distributed simple units. | ||
The scaling behavior is categorized into various cases. The first case is where the scaling is rg ∼ log M, the second case is where the scaling is rg2 ∼ log M, and the final case is where the scaling is in between these two laws. A least squares line is fitted to both the rg ∼ log M and rg2 ∼ log M scaling from N = 1 to N = 20 for each combination of κ and γ. In all cases the value of the R2 was high, typically greater than 0.97, However, to discriminate between these scaling laws, if the value of the R2 for the scaling rg ∼ log M was greater than 0.997, we state that the scaling behavior is rg ∼ log M. Similarly, if the value of the R2 for the scaling rg2 ∼ log M was greater than 0.997, we state that the scaling behavior is rg2 ∼ log M. If neither of these conditions is satisfied we state that there is mixed scaling.
In all cases we find that increasing κ changes the behavior from rg ∼ log M to rg2 ∼ log M. Large κ is consistent with weak repulsive interactions between units, eventually causing the simple units to have essentially no repulsive interactions. Earlier work showed that a randomly branched polymer with no repulsive interactions between the units follows the scaling law rg2 ∼ log M.20,21 From the exponential case we observe that increasing γ changes the scaling away from rg2 ∼ log M towards rg ∼ log M. This is because a larger value of γ increases the strength of the repulsive forces, causing a shift away from the scaling rg2 ∼ log M.
E. Evolution of scaling with time
This section analyzes the evolution of the size-mass scaling over time. We observe that the average molecular weight grows very rapidly at high conversion, which is because the reaction at high conversion progresses by linking high molecular weight polymers. In this section we use the high conversion MMADVB20 series, and the experimental molecular weight data at different points in time to predict the size-mass scaling of samples taken at different points in time. We analyze 3 high conversion samples, with the number and weight averaged molecular weights determined experimentally. We assume that the average size of the simple unit scales as![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ∼ M1/2n, which is the working assumption throughout this paper. However, we obtain similar results if we assume
∼ M1/2n, which is the working assumption throughout this paper. However, we obtain similar results if we assume ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ∼ M1/3n, or
∼ M1/3n, or ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ∼ M1/2n. As mentioned earlier, and shown in the supplementary information, this power law approximation is generally an acceptable approximation to the logarithmic scaling laws of RBT and KRBT, and for the MMADVB20 series it agrees well over a large range of molecular weights.
∼ M1/2n. As mentioned earlier, and shown in the supplementary information, this power law approximation is generally an acceptable approximation to the logarithmic scaling laws of RBT and KRBT, and for the MMADVB20 series it agrees well over a large range of molecular weights.
Although we do not have the time dependent size-mass scaling data, the approximation ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ∼ M1/2n serves to illustrate the qualitative evolution of the size-mass scaling data over time. In Table 4 we show the experimentally determined number and weight-average molecular weights, estimates of the average size of the simple unit
∼ M1/2n serves to illustrate the qualitative evolution of the size-mass scaling data over time. In Table 4 we show the experimentally determined number and weight-average molecular weights, estimates of the average size of the simple unit ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) , number of chains per simple unit and the predicted radius of gyration at the weight-average molecular weight.
, number of chains per simple unit and the predicted radius of gyration at the weight-average molecular weight.
| Time/min | M n | M w |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (nm) (nm) |
μ | r g |Mw/nm |
|---|---|---|---|---|---|
| 1790 | 26200 | 60300 | 2.17 | 422 | 5.85 |
| 2930 | 83300 | 441000 | 3.87 | 1340 | 16.5 |
| 4320 | 128000 | 986000 | 4.8 | 2060 | 24.7 |
The parameters ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) and μ from Table 4 are used to predict the size-mass scaling for the times shown. The values of κ, γ and χ at each time point are taken to be the same as those used in the series MMADVB20. However, the value of
and μ from Table 4 are used to predict the size-mass scaling for the times shown. The values of κ, γ and χ at each time point are taken to be the same as those used in the series MMADVB20. However, the value of ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) and μ is taken from Table 4 at the relevant point in time. This evolution of size-mass scaling is shown in Fig. 6
and μ is taken from Table 4 at the relevant point in time. This evolution of size-mass scaling is shown in Fig. 6
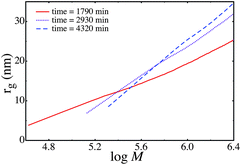 | ||
| Fig. 6 Predicted size-mass scaling for different points in time. | ||
The predicted size-mass scaling can also be used to determine the radius of gyration at the weight-average molecular weight (Mw). This is shown in the last column of Table 4. The radius of gyration at the Mw is plotted as a function of Mw in Fig. 7. That is in Fig. 7 for each time sample we plot the experimental Mw and the radius of gyration at the Mw (from the predicted size-mass scaling data at that time slice).
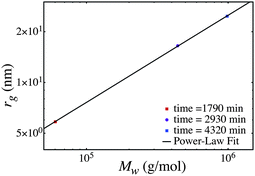 | ||
| Fig. 7 Evolution of the radius of weight average molecular weight and the radius of gyration at the weight average molecular weight. | ||
The time evolved scaling of radius of gyration vs. molecular weight follows a power law of 0.52. If instead we assume ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ∼ M1/3n, we obtain a power-law of 0.42. It is important to distinguish the difference between the analysis in earlier section and this analysis. Our model predicts scaling laws such as rg ∼ log M (or rg2 ∼ log M) at a given point in time. This means that if we take a sample of a branched polymer at a given point in time and determine the size and molecular weight of various size fractions, these fractions follow rg ∼ log M (or rg2 ∼ log M). In the last analysis case we take several samples at different times and determine the weight average molecular weight of all polymers in the sample, and estimate the radius of gyration at the Mw. If we plot the time evolved rg at Mw and the sample Mw we observe a power-law.
∼ M1/3n, we obtain a power-law of 0.42. It is important to distinguish the difference between the analysis in earlier section and this analysis. Our model predicts scaling laws such as rg ∼ log M (or rg2 ∼ log M) at a given point in time. This means that if we take a sample of a branched polymer at a given point in time and determine the size and molecular weight of various size fractions, these fractions follow rg ∼ log M (or rg2 ∼ log M). In the last analysis case we take several samples at different times and determine the weight average molecular weight of all polymers in the sample, and estimate the radius of gyration at the Mw. If we plot the time evolved rg at Mw and the sample Mw we observe a power-law.
IV. Discussion
We have studied a variety of highly branched polymers synthesized using the Strathclyde approach, from methyl methacrylate to the alternating styrene-maleic anhydride and brancher only samples. We used KRBT to analyze these polymers and to obtain information about the branching structure. The theory was able to discriminate between different types of polymer structures, and give information about the properties of the units that are added to make the polymer.Our model may be fitted and compared to experiments and give information about the likely structure of the polymer. Our model predicts the scaling-law rg ∼ log M when the polymer is randomly branched with moderate to strong repulsive forces between the units that make up the polymer. This is the scaling observed for the MMADVB20 and MMAEGDMA200. This scaling is also a reasonable approximation to the scaling of the series Sty-MANDVB = 0.8 and Sty-MANDVB = 1. In addition, our model predicts a scaling law of rg2 ∼ log M when the polymer is randomly branched with weak repulsive interactions between the units. This scaling is seen in many of the brancher only experiments.
The series MMAEGDMA20 does not match any scaling patterns predicted by our model. However, an approximate agreement is reached with our model's scaling-law of rg ∼ M1/3, which is predicted by our model for a polymer with a very large number of units. The fit of our model to the data series MMAEGDMA20 is not good, and only captures the crude scaling and misses all the features in the data. The poor fit of our model suggests that these polymers do not follow the assumptions in KRBT, and since these polymers are incredibly highly branched and reached high conversion, it is likely that they resemble a nano-gel, rather than a randomly branched polymer. This result highlights the usefulness of our model, as it can distinguish between a well-behaved randomly branched polymer, and a polymer that is so highly branched that it approaches a nano-gel like structure.
An additional possibility is that the majority of the polymers in a given sample are linear chains. This is expected to be the case early on in a Strathclyde reaction, when the reaction time is too short for branching to be significant. Although in its current form the model cannot predict the exact amount of linear material, the model can be used to qualitatively determine if a sample is dominated by linear chains. This is because a linear chain's size-mass scaling is typically the power-law rg ∼ Ma, where a is between 0.5 and 0.6.76 This is significantly different from the scaling laws like rg ∼ log M typically predicted by KRBT. Therefore, by performing a size-mass scaling analysis a sample that is dominated by linear polymers may be distinguished from a sample dominated by branched polymers.
In the polymers with relatively long linear chains and one brancher per chain, our model suggests that the polymer grows initially by the sequential addition of linear units to give a branched polymer. After this initial phase, the polymer grows by linking branched polymers, which themselves have many linear chains. In this way the molecular weight distribution evolves quite rapidly, as seen by the rapid growth of the average molecular weight with conversion. When we model polymers such as MMADVB20 or Sty-MANDVB = 1 we find that the average molecular weight of the simple unit agrees well with the number average molecular weight of the polymer sample, typically to within a factor of 2. This suggests that the polymers at a given point in time are formed by linking polymers that were formed quite soon before, and the molecular weight distribution is a very good approximation for the distribution of simple units. This trend is replicated in the series DVB20. Two series that do not fit this trend are DVB1 and DVB – MAN1. In these polymers the simple units have much lower molecular weight than the sample's Mn. Close inspection of the molecular weight distribution reveals a low molecular weight peak which is likely to correspond to the low molecular weight simple unit.
Our model was also used to predict the changes in the size-mass scaling over time. Suppose a polymer sample is taken at fixed point in time, and that sample is fractionated by size. In this case we expect the size-mass scaling to follow rg ∼ log M or possibly rg2 ∼ log M. However, if this is repeated for a sample taken later in time, an increase in the gradient and origin of these size-mass scaling laws is expected. In other words as the polymers grows by branching units together, the mass of the simple unit increases, and the average size of the simple unit increases. Therefore, if we analyze fractionated samples from an early and late time, the gradient of the rg ∼ log M (or rg2 ∼ log M) scaling law becomes steeper with time, and the curve shifts to higher molecular weight as later time slices are analyzed. If instead we analyze the time evolution of the average molecular weight and size at the weight average molecular weight we find a power-law relationship.
Our model can also predict which polymers are dense with only a few units able to be packed into a region, and those that are not dense and can fit many units in to a given region. Information about the relative density of polymers is important for applications of hyperbranched polymer, especially targeted-delivery. For such applications the density of the polymer should be sufficiently high to encapsulate the drug molecule and minimize leaching out, but not so dense that nothing can enter the polymer. Our model predicts the density of the hyperbranched polymer, and in the future it could be used to determine the suitability of a given polymer for a drug-delivery application.
V. Conclusion
A model called kinetic random branching theory, or KRBT, was used to study the structure of a variety of highly branched polymers synthesized by the Strathclyde approach. KRBT is an extension of random branching theory, and in KRBT the branched polymer is built up by randomly branching units whose structure is simpler than the resulting polymer's structure. The simple units studied in this paper are typically branched polymers themselves. In this work, we analyzed the size-mass scaling of methacrylic, and alternating styrene-maleic anhydride polymers. KRBT was used to describe the structure of these polymers by testing which polymers agree with the model. If the model agreed with the experiments the predicted molecular weight of a simple unit was similar to the experimentally determined number-averaged molecular weight and molecular weight distribution. This suggests that the polymers grow by randomly branching large polymer units to other large polymer units, which is consistent with kinetic studies on the polymerization.39In some cases our model did not agree with the experimental size-mass scaling, such as the MMAEGDMA20 series that reached high conversion with an excess of brancher. This system is better described as a nano-gel rather than a randomly branched polymer, since it disagrees with our model for randomly branched polymers. This series is expected to be a nano-gel since it was made with an excess of branchers, and reached high conversion, and these factors imply that loops must be present in the polymer.
In addition to polymers which have a relatively long linear chain with approximately 1 brancher per chain, we also studied polymers which have only branchers and RAFT agents. Our model also agreed with the experimental size-mass scaling data of polymers with just one brancher and 20 branchers per chain. These results highlight the versatility and usefulness of our model, as it can describe hyperbranched polymers made by a wide variety of syntheses and experimental conditions. Although this study focuses on hyperbranched polymers synthesized under RAFT control, our model is not limited to RAFT-mediated polymerzations. Since our model doesn't assume any particular chemical composition, but instead focuses on the structure of the resulting polymer, our model will apply to hyperbranched polymers synthesized with other controlled radical methods, such as ATRP or NMP, or even uncontrolled radical reactions such as those of O'Brien et al.18
We have shown that a simple model can give information about the structure of a variety of randomly branched polymers. The model may be used for hypothesis testing, to determine whether a given polymer agrees with the assumptions of random hyperbranching. When the model agrees with the experiments, the details of the fit data give information about the relative density of the polymer. Structural insights, gained from the model are important for applications of highly branched polymers in fields such as drug-delivery. Therefore, we envisage that our model will be important and useful to the development of hyperbranched polymers for a variety of applications.
Acknowledgements
DK would like to thank the Australian Government for an Australian Postgraduate Award. Dr Philip Mounteney is gratefully acknowledged for the provision of polymer samples.References
- F. Aulenta, W. Hayes and S. Rannard, Eur. Polym. J., 2003, 39, 1741 CrossRef CAS.
- U. Gupta, H. B. Agashe, A. Asthana and N. K. Jain, Nanomed.: Nanotechnol., Biol. Med., 2006, 2, 66 CrossRef CAS.
- X. Hao, E. Malmstrom, T. P. Davis, M. H. Stenzel and C. Barner-Kowollik, Aust. J. Chem., 2005, 58, 483 CrossRef CAS.
- J. B. Wolinsky and M. W. Grinstaff, Adv. Drug Delivery Rev., 2008, 60, 1037 CrossRef CAS.
- L. Y. Qiu and Y. H. Bae, Pharm. Res., 2006, 23, 1 CrossRef CAS.
- M. Marcos, R. Martin-Rapun, A. Omenat and J. L. Serrano, Chem. Soc. Rev., 2007, 36, 1889 RSC.
- K. Uhrich, Trends. Polym. Sci., 1997, 5, 388 CAS.
- C. Gao, Y. Xu, D. Yan and W. Chen, Biomacromolecules, 2003, 4, 704 CrossRef CAS.
- R. K. Kainthan and D. E. Brooks, Biomaterials, 2007, 28, 4779 CrossRef CAS.
- B. Liu, A. Kazlauciunas, J. T. Guthrie and S. Perrier, Macromolecules, 2005, 38, 2131 CrossRef.
- S. Suttiruengwong, J. Rolker, I. Smirnova, W. Arlt, M. Seiler, L. Luederitz, Y. Perez de Diego and P. J. Jansens, Pharm. Dev. Technol., 2006, 11, 55 CrossRef CAS.
- T. Satoh, Soft Matter, 2009, 5, 1972 RSC.
- D. A. Tomalia, H. Baker, J. Dewald, M. Hall, G. Kallos, S. Martin, J. Roeck, J. Ryder and P. Smith, Polym. J., 1985, 17, 117 CrossRef CAS.
- G. R. Newkome, Z. Yao, G. R. Baker and V. K. Gupta, J. Org. Chem., 1985, 50, 2003 CrossRef CAS.
- C. J. Hawker and J. M. J. Frechet, J. Am. Chem. Soc., 1990, 112, 7638 CrossRef CAS.
- R. K. Kainthan, E. B. Muliawan, S. G. Hatzikiriakos and D. E. Brooks, Macromolecules, 2006, 39, 7708 CrossRef CAS.
- S. G. Gaynor, S. Edelman and K. Matyjaszewski, Macromolecules, 1996, 29, 1079 CrossRef CAS.
- N. O'Brien, A. McKee, D. C. Sherrington, A. T. Slark and A. Titterton, Polymer, 2000, 41, 6027 CrossRef CAS.
- D. Konkolewicz, A. Gray-Weale and S. Perrier, J. Am. Chem. Soc., 2009, 131, 18075 CrossRef CAS.
- D. Konkolewicz, R. G. Gilbert and A. Gray-Weale, Phys. Rev. Lett., 2007, 98, 238301 CrossRef.
- D. Konkolewicz, O. Thorn-Seshold and A. Gray-Weale, J. Chem. Phys., 2008, 129, 054901 CrossRef.
- J. Chiefari, Y. K. Chong, F. Ercole, J. Krstina, J. Jeffery, T. P. T. Le, R. T. A. Mayadunne, G. F. Meijs, C. L. Moad, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 1998, 31, 5559 CrossRef CAS.
- P. A. Costello, I. K. Martin, A. T. Slark, D. C. Sherrington and A. Titterton, Polymer, 2002, 43, 245–254 CrossRef CAS.
- S. Durie, K. Jerabek, C. Mason and D. C. Sherrington, Macromolecules, 2002, 35, 9665–9672 CrossRef CAS.
- F. Isaure, P. A. G. Cormack, S. Graham, D. C. Sherrington, S. P. Armes and V. Buetuen, Chem. Commun., 2004, 1138–1139 RSC.
- G. Moad, Aust. J. Chem., 2006, 59, 661 CrossRef CAS.
- S. Perrier and P. Takolpuckdee, J. Polym. Sci., Part A: Polym. Chem., 2005, 43, 5347 CrossRef CAS.
- C. Barner-Kowollik, T. P. Davis and M. H. Stenzel, Aust. J. Chem., 2006, 59, 719 CrossRef CAS.
- L. Barner, C. Barner-Kowollik, T. P. Davis and M. H. Stenzel, Aust. J. Chem., 2004, 57, 19 CrossRef CAS.
- P. Takolpuckdee, J. Westwood, D. M. Lewis and S. Perrier, Macromol. Symp., 2004, 216, 23 CrossRef CAS.
- Z. Wang, J. He, Y. Tao, L. Yang, H. Jiang and Y. Yang, Macromolecules, 2003, 36, 7446 CrossRef CAS.
- S. Carter, B. Hunt and S. Rimmer, Macromolecules, 2005, 38, 4595 CrossRef CAS.
- A. P. Vogt, S. R. Gondi and B. S. Sumerlin, Aust. J. Chem., 2007, 60, 396 CrossRef CAS.
- A. P. Vogt and B. S. Sumerlin, Macromolecules, 2008, 41, 7368 CrossRef CAS.
- B. Liu, A. Kazlauciunas, J. T. Guthrie and S. Perrier, Polymer, 2005, 46, 6293 CrossRef CAS.
- C.-D. Vo, J. Rosselgong, S. P. Armes and N. C. Billingham, Macromolecules, 2007, 40, 7119 CrossRef CAS.
- J. Rosselgong, S. P. Armes, W. Barton and D. Price, Macromolecules, 2009, 42, 5919 CrossRef CAS.
- J. Poly, D. J. Wilson, M. Destarac and D. Taton, Macromol. Rapid Commun., 2008, 29, 1965 CrossRef CAS.
- R. Wang, Y. Luo, B.-G. Li and S. Zhu, Macromolecules, 2009, 42, 85 CrossRef CAS.
- J. Poly, D. J. Wilson, M. Destarac and D. Taton, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 5313 CrossRef CAS.
- I. Bannister, N. C. Billingham and S. P. Armes, Soft Matter, 2009, 5, 3495 RSC.
- H. Tobita and A. E. Hamielec, Macromolecules, 1989, 22, 3098 CrossRef CAS.
- H. Tobita and K. Ito, Polym. Gels Networks, 1994, 2, 191 CrossRef CAS.
- H. Tobita, Macromolecules, 1994, 27, 5413 CrossRef CAS.
- D. L. Kurdikar, J. Somvarsky, K. Dusek and N. A. Peppas, Macromolecules, 1995, 28, 5910 CrossRef CAS.
- M. Wen, L. E. Scriven and A. V. McCormick, Macromolecules, 2003, 36, 4140 CrossRef CAS.
- H. Tobita, J. Polym. Sci., Part B: Polym. Phys., 1993, 31, 1363 CrossRef CAS.
- H. Tobita and N. Hamashima, J. Polym. Sci., Part B: Polym. Phys., 2000, 38, 2009 CrossRef CAS.
- P. G. De Gennes and H. Hervet, J. Phys., Lett., 1983, 44, 351 CrossRef CAS.
- M. Ballauff and C. N. Likos, Angew. Chem., Int. Ed., 2004, 43, 2998 CrossRef CAS.
- A. V. Lyulin, D. B. Adolf and G. R. Davies, Macromolecules, 2001, 34, 3783 CrossRef CAS.
- P. F. Sheridan, D. B. Adolf, A. V. Lyulin, I. Neelov and G. R. Davies, J. Chem. Phys., 2002, 117, 7802 CrossRef CAS.
- I. M. Neelov and D. B. Adolf, J. Phys. Chem. B, 2004, 108, 7627 CrossRef CAS.
- G. K. Dalakoglou, K. Karatasos, S. V. Lyulin and A. V. Lyulin, J. Chem. Phys., 2007, 127, 214903 CrossRef CAS.
- J. Aerts, Comput. Theor. Polym. Sci., 1998, 8, 49 CrossRef CAS.
- T. C. Le, B. D. Todd, P. J. Daivis and A. Uhlherr, J. Chem. Phys., 2009, 130, 074901 CrossRef.
- T. C. Le, B. D. Todd, P. J. Daivis and A. Uhlherr, J. Chem. Phys., 2009, 131, 044902 CrossRef CAS.
- T. C. Le, B. D. Todd, P. J. Daivis and A. Uhlherr, J. Chem. Phys., 2009, 131, 164901 CrossRef.
- T. Mulder, A. V. Lyulin, P. Van der Schoot and M. A. J. Michels, Macromolecules, 2005, 38, 996 CrossRef CAS.
- C. J. C. Watts, A. Gray-Weale and R. G. Gilbert, Biomacromolecules, 2007, 8, 455 CrossRef CAS.
- D. Konkolewicz, A. A. Gray-Weale and R. G. Gilbert, J. Polym. Sci., Part A: Polym. Chem., 2007, 45, 3112 CrossRef CAS.
- J.-L. Putaux, A. Buleon, R. Borsali and H. Chanzy, Int. J. Biol. Macromol., 1999, 26, 145 CrossRef CAS.
- D. Konkolewicz, Aust. J. Chem., 2009, 62, 823 CrossRef CAS.
- A. A. Gray-Weale, R. A. Cave and R. G. Gilbert, Biomacromolecules, 2009, 10, 2708 CrossRef CAS.
- M. A. Sullivan, F. Vilaplana, R. A. Cave, D. Stapleton, A. A. Gray-Weale and R. G. Gilbert, Biomacromolecules, 2010, 11, 1094 CrossRef CAS.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, 1953 Search PubMed.
- D. Konkolewicz, B. S. Hawkett, A. Gray-Weale and S. Perrier, Macromolecules, 2008, 41, 6400 CrossRef CAS.
- D. Konkolewicz, M. Siauw, A. Gray-Weale, B. S. Hawkett and S. Perrier, J. Phys. Chem. B, 2009, 113, 7086 CrossRef CAS.
- S. C. Hong and K. Matyjaszewski, Macromolecules, 2002, 35, 7592 CrossRef CAS.
- J. Listak, W. Jakubowski, L. Mueller, A. Plichta, K. Matyjaszewski and M. R. Bockstaller, Macromolecules, 2008, 41, 5919 CrossRef CAS.
- D. Boschmann and P. Vana, Macromolecules, 2007, 40, 2683 CrossRef CAS.
- A. J. Inglis, S. Sinnwell, T. P. Davis, C. Barner-Kowollik and M. H. Stenzel, Macromolecules, 2008, 41, 4120 CrossRef CAS.
- D. Konkolewicz and A. Gray-Weale, http://confluence-vre.its.monash.edu.au/display/bpt/(2009.
- T. Shiomi, K. Kuroki, A. Kobayashi, H. Nikaido, M. Yokoyama, Y. Tezuka and K. Imai, Polymer, 1995, 36, 2443 CrossRef CAS.
- A. Polese, C. Mio and A. Bertucco, J. Chem. Eng. Data, 1999, 44, 839 CrossRef CAS.
- P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University, Ithaca NY, 1979 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details and a comparison between logarithmic and power law size versus mass scalings. See DOI: 10.1039/c0py00064g |
| This journal is © The Royal Society of Chemistry 2010 |
