Prediction of the main macrocyclic conjugation pathway for porphyrinoids from the ring current distribution†
Jun-ichi Aihara*ab and Masakazu Makinob
aDepartment of Chemistry, Faculty of Science, Shizuoka University, Oya, Shizuoka 422-8529, Japan. E-mail: scjaiha@yahoo.co.jp
bInstitute for Environmental Sciences, University of Shizuoka, Yada, Shizuoka 422-8526, Japan
First published on 15th October 2009
Abstract
For some porphyrinoids, such as orangarin and amethyrin, the main route of macrocyclic π-circulation is different from the main macrocyclic conjugation pathway predicted by porphyrin chemists. Our analytical theory of ring-current diamagnetism allows us to predict the main macrocyclic conjugation pathway from the ring current distribution. We can now interpret macrocyclic aromaticity and macrocyclic circulation consistently within the same theoretical framework.
1. Introduction
During the last two decades, many expanded, contracted, confused, and fused porphyrins have been synthesized.1–6 Porphyrin chemists used to account for the electronic, magnetic, and chemical properties of porphyrins by a formal analogy between the main conjugation pathway in the macrocycle and the corresponding monocyclic annulene.1–6 For example, natural porphyrins are described as bridged diaza[18]annulenes, and the same convention has been applied to many expanded porphyrins and porphyrinoids.1–5 Porphyrinoids have often been named systematically after the annulene model.2 In fact, not only macrocyclic conjugation but also pyrrole rings are major sources of global aromaticity.5–7 However, it is generally true that macrocyclic conjugation is responsible primarily for the chemical shifts of protons attached to the porphyrinoid macrocycles.1-6 To emphasize this fact, porphyrin chemists refer to macrocyclic aromaticity simply as aromaticity.Macrocyclic aromaticity and macrocyclic circulation are two different manifestations of macrocyclic conjugation in porphyrinoids.1-6 A ring current distribution in a polycyclic π-system, however, is strongly dependent on molecular geometry, so that information on global and macrocyclic aromaticity cannot be extracted directly from it. For some expanded porphyrins, such as orangarin and amethyrin, the main stream of π-circulation8,9 deviates from the so-called main macrocyclic conjugation pathway5,10 even if the direction of the macrocyclic ring current might be predicted from the annulene picture. In this paper, we propose a general theoretical method for extracting information on the main macrocyclic conjugation pathway from the ring current distribution, and interpret macrocyclic conjugation and macrocyclic circulation within the same theoretical framework.
2. Terminology
Certain terms in porphyrin chemistry have sometimes been used to mean different things;1-12 however, in this paper, the following meanings are applied. Circuits stand for all possible cyclic or closed paths that can be chosen from a cyclic π-system.13 As shown in Fig. 1, 11 non-identical circuits and 20 circuits in all can be chosen from the π-system of porphine (1).7 As in classical chemistry,14 the term aromatic describes molecules that benefit energetically from the delocalization of π-electrons in closed circuits. Topological resonance energy (TRE), a kind of aromatic stabilization energy (ASE), is employed as a primary criterion of aromaticity,11,12 which arises from a collection of circuits.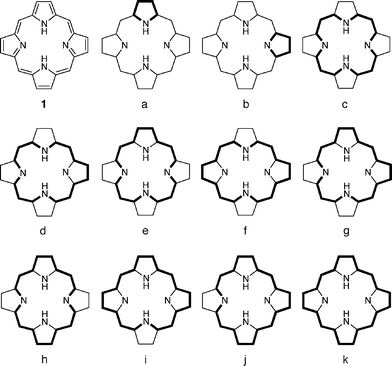 | ||
| Fig. 1 Non-identical circuits in porphine (1). | ||
The term macrocycle is used to represent a planar or quasi-planar polycyclic π-system with a large inner cavity. Porphyrins and kekulene are such macrocyclic compounds. A macrocyclic circuit is any large circuit that surrounds the inner cavity (e.g., circuits c–k in Fig. 1), also being referred to as a conjugation pathway in the macrocycle. This is distinguished from a local circuit located in each five-membered ring (e.g., circuits a and b in Fig. 1). All macrocyclic circuits constitute macrocyclic conjugation.5-7Macrocyclic aromaticity and macrocyclic circulation are the aromaticity and π-circulation associated with macrocyclic circuits, respectively. Superaromatic stabilization energy (SSE) represents an extra ASE due to macrocyclic conjugation.5-7,15,16 Thus, the term superaromaticity is a synonym of macrocyclic aromaticity.
3. Theoretical background
The concept of bond resonance energy (BRE) is useful for justifying the idea of macrocyclic aromaticity in porphyrin chemistry.5-7 BRE is defined as follows.17-19 A hypothetical π-system, in which a given π-bond (e.g., a π-bond formed between the pth and qth atoms) interrupts the cyclic conjugation at that point, is constructed by multiplying βpq by i and βqp by −i, where βpq is the resonance integral between the two conjugated atoms and i is the square root of −1. In this π-system, no circulation of π-electrons is expected along the circuits that share the p–qπ-bond in common. BRE for the p–qπ-bond is given as a destabilization energy of this hypothetical π-system. That is, BRE for a given π-bond represents the contribution of all circuits that share the bond to TRE. This quantity was originally defined to justify the isolated pentagon rule for fullerenes.17 For porphyrinoids, SSE is equal to the BRE for any of the C–C bonds that link any pair of adjacent pyrrole rings.5–7Our theory of ring-current diamagnetism19–22 is nothing other than an exact or analytical reformulation of Hückel–London theory.23,24 It allows a decomposition of the ring current induced in a polycyclic π-system, G, exactly into individual circuit contributions. A current induced in each circuit may be termed a circuit current, the intensity of which is given in the form:20–22
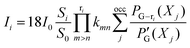 | (1) |
Hückel heteroatom parameters proposed by Van-Catledge30 were employed. In addition, all nitrogen atoms coordinated to a metal ion were dealt with as imine (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) nitrogens. This assumption is fully consistent with the geometry of magnesium porphine (2) and with the ring current distribution in it. Fig. 2 shows the molecular geometry of magnesium porphine calculated by Cyrański et al.31 at the B3LYP/6-31G* level of theory,32–34 where all outer C–C bonds in pyrrole rings behave as formal double bonds.35 As will be seen later, the ring current distribution we calculated for magnesium porphine is very similar to the current density map reported by Steiner and Fowler,36,37 in which the current flowing along the inner cross is slightly stronger than the one flowing along the 20-membered outer periphery. Hückel parameters we employed for the nitrogen atoms reasonably reproduce these aspects of metalloporphyrins. There are two extra π-electrons in the inner ring, formally making a 16-membered aromatic dianion.
N–) nitrogens. This assumption is fully consistent with the geometry of magnesium porphine (2) and with the ring current distribution in it. Fig. 2 shows the molecular geometry of magnesium porphine calculated by Cyrański et al.31 at the B3LYP/6-31G* level of theory,32–34 where all outer C–C bonds in pyrrole rings behave as formal double bonds.35 As will be seen later, the ring current distribution we calculated for magnesium porphine is very similar to the current density map reported by Steiner and Fowler,36,37 in which the current flowing along the inner cross is slightly stronger than the one flowing along the 20-membered outer periphery. Hückel parameters we employed for the nitrogen atoms reasonably reproduce these aspects of metalloporphyrins. There are two extra π-electrons in the inner ring, formally making a 16-membered aromatic dianion.
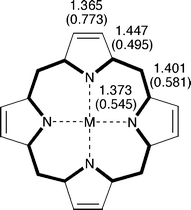 | ||
| Fig. 2 Bond lengths (in Å) in magnesium porphine (2, M = Mg). Values in parentheses are Hückel π-bond orders. | ||
Realistic molecular geometries are necessary to evaluate the intensities of ring and circuit currents. Geometries used for 1–6 are those obtained by Jusélius and Sundholm38,39 at the resolution-of-the-identity density-functional theory (RI-DFT) level40 using the Becke–Perdew (B–P) parametrization41-43 as implemented in TURBOMOLE.44 We optimized molecular geometries of 7–9 at the B3LYP/6-31G** level of theory33,34 using a GAUSSIAN 03 program.32 For the optimized geometries of 7–9, see the ESI†. These geometries were used to calculate the areas enclosed by the circuits.
3. Results and discussion
We first explored macrocyclic aromaticity in the cores of natural porphyrinoids (1–6) and three expanded porphyrins (7–9), structural formulae of which are given in Fig. 2. Sapphyrin (8) is noted as the first expanded porphyrin.45,46 Orangarin (7) and amethyrin (9) were prepared in 1995 by Sessler's group.10 TREs and SSEs for these species are listed in Table 1, where β is the standard value for the resonance integral between two adjacent carbon 2pz orbitals. All these species are moderately aromatic with positive TREs. All species but 7 and 9 are slightly superaromatic with small positive SSEs, whereas 7 and 9 are slightly anti-superaromatic with small negative SSEs. It is obvious from these TREs and SSEs that macrocyclic conjugation never contributes significantly to the global aromaticity of a porphyrinoid π-system.5-7 Macrocyclic annulene pathways proposed by previously1–6 are shown in bold in Fig. 3. These annulene pathways are consistent with the signs of SSEs, in that aromatic and antiaromatic annulene pathways correspond to positive and negative SSEs, respectively.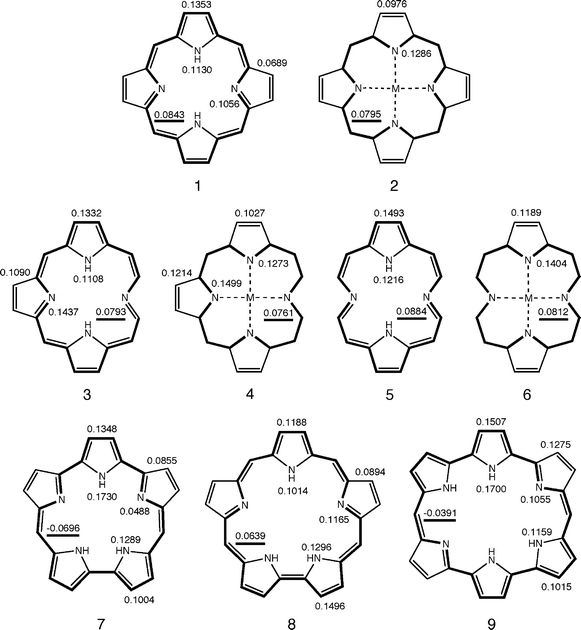 | ||
| Fig. 3 Main macrocyclic conjugation pathways and BREs in nine porphyrinoids. | ||
BREs for all non-identical π-bonds in 1–9 are graphically summarized in Fig. 3. For porphyrinoids with positive SSEs (1–6, 8), the main macrocyclic conjugation pathway can be traced by choosing a π-bond with a larger BRE at every bifurcation of the π-network.5,6 Those in free-base porphyrins 1, 3, 5, and 8 are aromatic [4n+2]annulene pathways, which are all conjugated circuits in Randić's termonology.47 For metal complexes 2, 4, and 6, π-bonds with larger BREs constitute the innermost, shortest possible, [16]annulene pathway along which 18 π-electrons formally reside. All π-bonds located along these conjugation pathways are intensified, with larger positive BREs than those located along the bypasses.
There are no such aromatic annulene pathways in orangarin (7) and amethyrin (9), because they have negative SSEs. Another type of macrocyclic pathways can instead be traced by choosing a π-bond with a smaller BRE at every bifurcation of the π-network.5,6 Main macrocyclic pathways thus determined for 7 and 9 are antiaromatic [4n]annulene pathways, which are also conjugated circuits in Randić's sense.47 These pathways will also be referred to as main macrocyclic conjugation pathways, because they are closely associated with macrocyclic antiaromaticity. All π-bonds located along these antiaromatic pathways are weakened, with smaller BREs than those located along the bypasses. Macrocyclic annulene pathways proposed by porphyrin chemists can thus be justified in terms of BREs.1-7
Next, let us examine the geometric patterns of macrocyclic circulation in porphyrinoids. Steiner and Fowler8,9,36,37 carried out ring-current calculations on 1–3 and 7–9 with the 6-31G** basis by means of coupled Hartree–Fock theory within the ipsocentric48,49 CTOCD-DZ (continuous transformation of origin of current density diamagnetic zero) formulation.50,51 They noted that all these porphyrinoids give clearly dominant macrocyclic currents; intense diamagnetic currents are induced along the macrocycles of 1–3 and 8, whereas the macrocycles of 7 and 9 sustain intense paramagnetic currents.8,9 The occurrence of paramagnetic ring currents in 7 and 9 may be due partly to the absence of substituents. Sessler et al. reported that polysubstituted forms of 7 and 9 are 20π- and 24π-electron nonaromatic macrocycles, respectively.10
Main streams of Steiner–Fowler macrocyclic currents in porphine (1)36 and sapphyrin (8)8 follow the main macrocyclic conjugation pathways shown in Fig. 3. In metalloporphine (2) and chlorin (3), however, no distinct main stream is observable in the Steiner–Fowler current density maps;36,37π-currents of comparable intensity flow along the outer C–C and inner C–N bonds of one or more pyrrole rings. On the other hand, orangarin (7) and amethyrin (9) are predicted to sustain intense paramagnetic currents along the inner periphery, but not along the conventional annulene pathways.8,9 The main streams of these paramagnetic currents necessarily pass through all nitrogen atoms including all amine nitrogens.
Global ring current patterns we calculated for 1–9 are shown as 1a–9a in Fig. 4. Here, counterclockwise and clockwise circulations represent diatropic and paratropic ring currents, respectively. As far as 1–3 and 7–9 are concerned, our Hückel-London calculations reproduce well the global ring current patterns obtained by Steiner and Fowler.8,9,36,37 Main streams of macrocyclic circulation in free bases 1, 5, and 8 follow the main conjugation pathways, whereas those in the other species do not always follow the main conjugation pathways. In 2–4 and 6, π-currents of comparable intensity flow along the outer CC and inner CN bonds of one or more pyrrole rings. Therefore, no distinct main streams are observable in these species. As noted by Steiner and Fowler,8,9 the main streams of macrocyclic ring currents in 7 and 9 runs along the inner periphery. These aspects of macrocyclic circulation do not conform to the annulene picture of porphyrinoids.
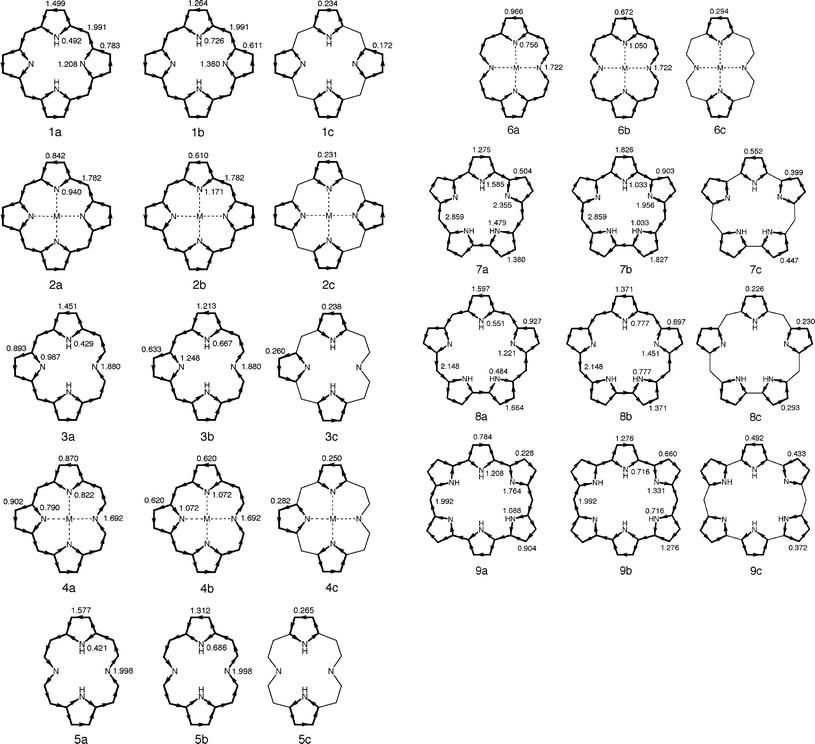 | ||
| Fig. 4 Decomposition of ring currents induced in 1–9 (1a–9a) into macrocyclic (1b–9b) and local (1c–9c) circuit contributions. All current intensities are given in units of the benzene value. | ||
Although our ring current distributions for 7 and 9 indeed are similar to Steiner and Fowler's current density maps,8,9 it seems that our simpler calculations somewhat overestimate the intensities of macrocyclic paramagnetic currents. This kind of drawback is possibly due to the neglect of bond-length alternation and/or deformation that might occur along the antiaromatic annulene pathways. Note that many porphyrinoid macrocycles with [4n]annulene pathways do not exhibit antiaromatic ring current effects and have been regarded as nonaromatic ones.2–6 This experimental fact implies that macrocyclic antiaromaticity tends to be suppressed significantly by structural modifications. Steiner–Fowler current density maps for 7 and 98,9 can be reproduced formally by assigning a resonance integral of ca. 0.8β to all π-bonds that link adjacent pyrrolic rings. However, such a modification of the π-system does not affect the discussion below.
As has been seen above, at least for 7 and 9, the main macrocyclic conjugation pathway is never the same as the main stream of macrocyclic circulation.6,8,9 We then describe how to extract information on the main macrocyclic conjugation pathway from the ring current distribution. Note that local circulations within individual pyrrolic rings are superposed on macrocyclic circulation, both constituting the global current distribution.7 Local circulations in the pyrrolic rings of 1–9 are always diamagnetic in nature. In the case of porphyrinoids with positive SSEs, a diamagnetic current is induced along the macrocycle; it is bifurcated when it runs across every pyrrole ring. Both diamagnetic macrocyclic and diamagnetic local currents flow in the same direction on the outer C–C bonds of the pyrrole rings. However, both currents totally or partially cancel each other out on the inner C–N bonds, because both currents flow in opposite directions there. Thus, local circulations may obscure the location of the main macrocyclic circulation pathway.
On the other hand, porphyrinoids with negative SSEs sustain a paramagnetic current along the macrocycle. The current is bifurcated when it runs across every pyrrole ring. Apart from this, a strong diamagnetic current is induced in every five-site circuit. In this case, both paramagnetic macrocyclic and diamagnetic local currents flow in opposite directions on the outer C–C bonds of the pyrrole rings and so totally or partially cancel each other out there. However, both currents flow in the same direction on the inner C–N bonds. As a result, the intensified current is observed on all inner C–N bonds. This must be the main reason why 7 and 9 appear to sustain strong paramagnetic circulations along the inner peripheries.
Therefore, if one wants to trace macrocyclic circulation only, the motion of π-electrons along the macrocycle only must be extracted from the global current distribution. Fortunately, our analytical theory of ring-current diamagnetism20-22 allows us to decompose the ring current distribution exactly into individual circuit contributions. As shown in Fig. 4, the entire ring current in each porphyrinoid species can then be decomposed exactly into the contributions of macrocyclic and local five-site circuits. For example, the entire ring current induced in porphine (1a) can be partitioned into the contributions of macrocyclic (1b) and local five-site (1c) circuits; 1b and 1c consist of currents induced in 16 macrocyclic circuits (circuits c–k in Fig. 1) and 4 five-site ones (circuits a and b in Fig. 1), respectively. It is 1b that represents the net macrocyclic circulation induced in 1. Comparison of 1a with 1b reveals that the main stream of macrocyclic circulation in 1a remains unchanged in 1b, which indicates that the main macrocyclic circulation pathway is the same as the main stream of circulation in the entire π-system. Both agree with the main macrocyclic conjugation pathway exactly. The same is true for two other free-base porphyrinoids 5 and 8. Here, we tacitly assumed that the areas of all macrocyclic circuits are roughly of comparable magnitude, being much larger than those of local five-site circuits. This possibly is a fairly reasonable assumption for all porphyrinoids studied.
The entire ring current in orangarin (7a) can be decomposed into the contributions of macrocyclic (7b) and local five-site (7c) circuits; 7b and 7c consist of currents induced in 32 macrocyclic and 5 five-site circuits, respectively. Likewise, the entire ring current in amethyrin (9a) can be decomposed into the contributions of 64 macrocyclic (9b) and 6 five-site (9c) circuits. That is, 7b and 9b represent net macrocyclic circulations induced in 7 and 9, respectively. One sees that the main circulation pathways in 7b and 9b are different from the main streams of global circulation in 7a and 9a, respectively, but are identical with the main macrocyclic conjugation pathways in Fig. 1. As differences between the intensities of currents that flow on the outer C–C and inner C–N bonds are sizeable in 7b and 9b, there is no doubt that strong macrocyclic currents are induced along the conventional annulene pathways.
As stated above, 2–4 and 6 exhibit a current distribution pattern in which the π-currents of similar intensity flow along the outer C–C and inner C–N bonds in one or more pyrrole rings. These ring current patterns can be analyzed in the same manner. If we exclude local circulations in pyrrole rings from the ring current distribution as in 2b–4b and 6b, we can discern the same annulene pathways as predicted from the BREs. Thus, for all of 1–9, authentic main macrocyclic conjugation pathways are clearly discernible in the macrocyclic current distributions (1b–9b) in which local circulations are missing. We can now safely say that, as far as porphyrinoid macrocycles are concerned, the main macrocyclic circulation pathway is identical with the main macrocyclic conjugation pathway. All main macrocyclic conjugation pathways pass through imine (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) nitrogens but avoid amine (–NH–) nitrogens.
N–) nitrogens but avoid amine (–NH–) nitrogens.
Finally, one might have noted that some five-site or pyrrole circuits, such as those in 7c and 9c, sustain much larger diamagnetic currents than those in other porphyrinoids. It may be interesting to see that highly antiaromatic and aromatic circuits coexist in 7 and 9. In such polycyclic π-systems, both the aromaticity of aromatic circuits and the antiaromaticity of antiaromatic circuits are often enhanced appreciably; paramagnetic and diamagnetic circuit currents induced in these circuits are necessarily intensified simultaneously. This is why all five-site circuits in 7 and 9 sustain large diamagnetic currents. Similar intensification of circuit currents was observed in many charged polycyclic benzenoid hydrocarbons.52
4. Concluding remarks
In 1989, Katritzky et al. pointed out that ‘geometric-energetic aromaticity’ is orthogonal to ‘magnetic aromaticity’.53,54 In fact, aromatic stabilization is determined primarily by the connectivity of conjugated atoms, whereas π-circulation is a complicated function of the connectivity and geometry of conjugated atoms. It follows that, for porphyrinoids, a main route of macrocyclic circulation is not always the same as the main macrocyclic conjugation pathway. This is particularly true for antiaromatic macrocycles, such as orangarin (7) and amethyrin (9). The main streams of macrocyclic circulation in 7 and 9 pass through amine nitrogens,8,9 although a main macrocyclic conjugation pathway in any free-base porphyrinoid species never passes through these atoms.5,6 Such an apparent dichotomy was solved successfully by removing local circulations in the pyrrole rings from the global ring current distribution. As in other porphyrinoids, the main macrocyclic circulation pathways in 7 and 9 proved to follow their respective macrocyclic annulene pathways. At present, our theory of ring-current diamagnetism is the only tool for distinguishing macrocyclic currents from the local ones.20-22 The theoretical approach proposed in this paper must be applicable to elucidating many other electronic and magnetic properties of macrocyclic π-systems consistently.Acknowledgements
This work was supported by a Grant-in-Aid for Scientific Research (No. 16550016) from the Japan Society for the Promotion of Science. Computations were carried out at the Information Processing Center, Shizuoka University, and the Research Center for Computational Science, Okazaki National Research Institutes.References
- E. Vogel, Pure Appl. Chem., 1993, 65, 143 CAS.
- B. Franck and A. Nonn, Angew. Chem., Int. Ed. Engl., 1995, 34, 1795 CrossRef CAS.
- T. D. Lash, Synlett, 2000, 279 CAS.
- J. L. Sessler and D. Seidel, Angew. Chem., Int. Ed., 2003, 42, 5134 CrossRef CAS.
- J. Aihara, J. Phys. Chem. A, 2008, 112, 5305 CrossRef CAS.
- J. Aihara and H. Horibe, Org. Biomol. Chem., 2009, 7, 1939 RSC.
- J. Aihara, E. Kimura and T. M. Krygowski, Bull. Chem. Soc. Jpn., 2008, 81, 826 CrossRef CAS.
- E. Steiner and P. W. Fowler, Org. Biomol. Chem., 2004, 2, 34 RSC.
- E. Steiner and P. W. Fowler, Org. Biomol. Chem., 2006, 4, 2473 RSC.
- J. L. Sessler, S. J. Weghorn, Y. Hiseada and V. Lynch, Chem. Eur. J., 1995, 1, 56 CrossRef CAS.
- J. Aihara, J. Am. Chem. Soc., 1976, 98, 2750 CrossRef CAS.
- I. Gutman, M. Milun and N. Trinajstić, J. Am. Chem. Soc., 1977, 99, 1692 CrossRef CAS.
- A. Graovac, I. Gutman, N. Trinajstić and T. Zivković, Theor. Chim. Acta, 1972, 26, 67 CAS.
- V. I. Minkin, M. N. Glukhovtsev and B. Ya. Simkin, Aromaticity and Antiaromaticity: Electronic and Structural Aspects, Wiley-Interscience, New York, 1994, Ch. 3 Search PubMed.
- J. Aihara, J. Am. Chem. Soc., 1992, 114, 865 CrossRef CAS.
- J. Aihara, J. Chem. Soc., Faraday Trans., 1995, 91, 237 RSC.
- J. Aihara, J. Am. Chem. Soc., 1995, 117, 4130 CrossRef CAS.
- J. Aihara, J. Chem. Soc., Perkin Trans. 2, 1996, 2185 RSC.
- M. Makino and J. Aihara, Phys. Chem. Chem. Phys., 2008, 10, 591 RSC (Electronic Supplementary Information).
- J. Aihara, J. Am. Chem. Soc., 1985, 107, 298 CrossRef CAS.
- J. Aihara, Bull. Chem. Soc. Jpn., 2004, 77, 651 CrossRef CAS.
- J. Aihara, J. Am. Chem. Soc., 2006, 128, 2873 CrossRef CAS.
- F. London, J. Phys., 1937, 8, 397 CAS.
- B. Pullman and A. Pullman, Les Théories Electroniques de la Chimie Organique, Masson et Cie, Paris, 1952, Ch. IX Search PubMed.
- J. Aihara, J. Am. Chem. Soc., 1979, 101, 5913 CrossRef CAS.
- J. Aihara and T. Horikawa, Chem. Phys. Lett., 1983, 95, 561 CrossRef CAS.
- J. A. Pople, Mol. Phys., 1958, 1, 175 CAS.
- R. McWeeny, Mol. Phys., 1958, 1, 311 CAS.
- E. Steiner and P. W. Fowler, Org. Biomol. Chem., 2003, 1, 1785 RSC.
- F. A. Van-Catledge, J. Org. Chem., 1980, 45, 4801 CrossRef.
- M. C. Cyrański, T. M. Krygowski, M. Wisiorowski, M. N. J. R. van Eikema Hommes and P. v. R. Schleyer, Angew. Chem., Int. Ed., 1998, 37, 177 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. J. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople, Gaussian 03, Revision B.02, Gaussian, Inc., Pittsburgh, PA, 2003 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- E. B. Fleischer, Acc. Chem. Res., 1970, 3, 105 CrossRef CAS.
- E. Steiner and P. W. Fowler, ChemPhysChem, 2002, 3, 114 CrossRef CAS.
- E. Steiner, A. Soncini and P. W. Fowler, Org. Biomol. Chem., 2005, 3, 4053 RSC.
- J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 2000, 2, 2145 RSC.
- J. Jusélius and D. Sundholm, J. Org. Chem., 2000, 65, 5233 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B, 1986, 33, 8822 CrossRef.
- A. D. Becke, Phys. Rev. B, 1988, 38, 3098 CrossRef CAS.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165 CrossRef CAS.
- M. J. Broadhurst, R. Grigg and A. W. Johnson, J. Chem. Soc., Perkin Trans. 1, 1972, 2111 RSC.
- V. J. Bauer, D. L. J. Clive, D. Dolphin, J. B. Paine, F. L. Harris, M. M. King, J. Loder, S.-W. C. Wang and R. B. Woodward, J. Am. Chem. Soc., 1983, 105, 6429 CrossRef CAS.
- M. Randić, J. Am. Chem. Soc., 1977, 99, 444 CrossRef CAS.
- E. Steiner and P. W. Fowler, Chem. Commun., 2001, 2220 RSC.
- E. Steiner and P. W. Fowler, J. Phys. Chem., 2001, 105, 9553 Search PubMed.
- T. A. Keith and R. F. W. Bader, Chem. Phys. Lett., 1993, 210, 223 CrossRef CAS.
- S. Coriani, P. Lazzeretti, R. Malagoli and R. Zanasi, Theor. Chim. Acta, 1994, 89, 181 CAS.
- T. Ishida, H. Kanno and J. Aihara, Pol. J. Chem., 2007, 81, 699 CAS.
- A. R. Katritzky, P. Barczynski, G. Musumarra, D. Pisano and M. Szafran, J. Am. Chem. Soc., 1989, 111, 7 CrossRef.
- J. Aihara, Bull. Chem. Soc. Jpn., 2008, 81, 241 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: B3LYL/6-31G**-optimized geometries of orangarin (7), sapphyrin (8), and amethyrin (9). See DOI: 10.1039/b910521b |
| This journal is © The Royal Society of Chemistry 2010 |
