The two-step mechanism of nucleation of crystals in solution
Peter G.
Vekilov
Department of Chemical and Biomolecular Engineering and Department of Chemistry, University of Houston, Houston, Texas 77204-4004, USA
First published on 8th October 2010
Abstract
The formation of crystalline nanoparticles starts with nucleation and control of nucleation is crucial for the control of the number, size, perfection, polymorph modification and other characteristics of particles. Recently, there have been significant advances in the understanding of the mechanism of nucleation of crystals in solution. The most significant of these is the two-step mechanism of nucleation, according to which the crystalline nucleus appears inside pre-existing metastable clusters of size several hundred nanometers, which consist of dense liquid and are suspended in the solution. While initially proposed for protein crystals, the applicability of this mechanism has been demonstrated for small-molecule organic and inorganic materials, colloids, and biominerals. This mechanism helps to explain several long-standing puzzles of crystal nucleation in solution: nucleation rates which are many orders of magnitude lower than theoretical predictions, nucleation kinetic dependencies with steady or receding parts at increasing supersaturation, the role of heterogeneous substrates for polymorph selection, the significance of the dense protein liquid, and others. More importantly, this mechanism provides powerful tools for control of the nucleation process by varying the solution thermodynamic parameters so that the volume occupied by the dense liquid shrinks or expands.
 Peter G. Vekilov | Peter Vekilov received his PhD in 1991 from the Russian Academy of Sciences. He is now Professor of Chemical and Biomolecular Engineering and of Chemistry at the University of Houston. His main research interests are in the area of protein phase transitions and aggregation. Nucleation kinetics have been a major focus of study. The existence of mesoscopic metastable phases in protein solutions, which appear to be a universal precursor for many types of aggregates, was discovered. The microscopic mechanisms of crystallization from solution have been elucidated with unique molecular-resolution real-time in situ methods, revealing how stochastic events couple to macroscopic fluxes. A novel mechanism of kink generation was discovered. The studies of sickle cell hemoglobin polymerization revealed the role of free heme as a crucial co-factor for the polymerization process. |
Introduction
Nanoparticles are often synthesized in solution through crystallization. Thus, the nucleation of crystals determines many properties of the emerging nanocrystal population. Since nucleation selects the polymorphic form, if a different polymorph is desired, conditions at which its nucleation is faster than that of the other possible polymorphs should be sought. If nucleation is fast, many crystals form nearly simultaneously. Their growth depletes the solution of solute and may lead to cessation of nucleation at the later stages of crystallization. Thus, the majority of crystals grow to approximately identical sizes. In contrast, if nucleation is slow and fewer crystals nucleate at a time, the supersaturation in the solution drops slowly, the nucleation of new crystals continues and a population of crystals of various sizes forms. Ultimately, if nucleation is hindered everywhere in the growth container but at a few selected spots, crystals only nucleate at these spots and grow large before the solution is depleted of nutrient. Hence, control of nucleation is a means to control size, size distribution, polymorphism and other properties of the crystals.Here, we review recent advances in the understanding of nucleation of crystals from solution. Besides nanoparticles synthesis, solution crystallization underlies a broad range of industrial, laboratory, and physiological processes. Single solution-grown crystals of inorganic salts or mixed organic-inorganic materials are used in non-linear optics elements1 and for other electronic and optical-electronic applications; chemical products and production intermediates are precipitated as crystals in thousands-of-tons amounts. Another area which relies on solution-grown crystals is pharmacy: the slow crystal dissolution rate is used to achieve sustained release of medications: small-molecules organic,2 or protein such as insulin, interferon-α, or the human growth hormone.2–6 If the administered dose consists of a few equidimensional crystallites, steady medication release rates can be maintained for longer periods than for doses comprised of many smaller crystallites. The formation of protein crystals and crystal-like ordered aggregates underlies several human pathological conditions. An example is the crystallization of hemoglobin C and the polymerization of hemoglobin S that cause, respectively, the CC and sickle cell diseases.7–10 The formation of a crystals in the eye lens underlies the pathology of several forms of cataract.11,12 A unique example of benign protein crystallization in humans and other mammals is the formation of rhombohedral crystals of insulin in the islets of Langerhans in the pancreas.13 Traditionally, protein crystals have been used for the determination of the atomic structure of protein molecules by X-ray crystallography;14 this method contributes ∼87% of all protein structures solved, with the majority of the other determinations carried out by nuclear magnetic resonance (NMR) spectroscopy.15 Nanoparticle synthesis can benefit from the advances in these and other research areas.
Below, we first discuss the thermodynamic and kinetic aspects of the classical nucleation theory, which still represents the main framework for the understanding of nucleation phenomena. Then we consider recent data on the rates of nucleation of protein crystals and show that several of the features of the experimentally determined kinetic dependencies do not comply with the predictions of the classical theory. We introduce the two-step mechanism of nucleation, according to which the crystalline nuclei appear inside metastable clusters of size several hundred nanometers, which consist of dense liquid and are suspended in the solution. Finally, we review recent evidence suggesting that while this mechanism was first proposed for the nucleation of protein crystals, it applies to the nucleation of small-molecule organic and inorganic, as well as colloid and biomineral crystals.
The classical nucleation theory
The crystallization driving force
In correspondence to the typical physiological, laboratory, and industrial conditions, nucleation is typically considered under constant temperature and pressure. With such constraints, the transfer of solute molecules from solution to the crystal is driven by the change of Gibbs free energy.16 The change in Gibbs free energy of crystallization, ΔG°cryst, at constant temperature T, is the sum of the contributions of the enthalpy ΔH°cryst and entropy ΔS°cryst: ΔG°cryst = ΔH°cryst − TΔS°cryst. The associated crystallization equilibrium constantKcryst ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) exp exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (−ΔG°cryst/RT), Kcryst = C−1e (−ΔG°cryst/RT), Kcryst = C−1e | (1) |
Crystal formation occurs in supersaturated solution, in which the concentration C is higher than the solubility Ce. Accordingly, the chemical potential of the solute μ in the solution is greater than the one at equilibrium μe, which in turn is equal to the chemical potential of the crystallizing material in the crystal, μe = μcrystal.. The chemical potential μ = μo + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γC and μe = μ0 + RT
γC and μe = μ0 + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γeCe, where γ and γe are, respectively, the activity coefficients of the solute in the crystallizing solution and in a solution with equilibrium concentration Ce, and μo is the chemical potential in a standard solution. Then the nucleation driving force Δμ = μ − μe = RT
γeCe, where γ and γe are, respectively, the activity coefficients of the solute in the crystallizing solution and in a solution with equilibrium concentration Ce, and μo is the chemical potential in a standard solution. Then the nucleation driving force Δμ = μ − μe = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γC/γeCe). Often, it is assumed that γ = γe so that Δμ = RT
ln(γC/γeCe). Often, it is assumed that γ = γe so that Δμ = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(C/Ce).
ln(C/Ce).
Since γ is a function of concentration, if C ≫ Ce, the assumption γ = γe is unjustified. In protein and colloid solutions, the activity coefficients are evaluated form the relation ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ ≅ 2B2C, where B2 is the second osmotic virial coefficient. B2 depends on the intermolecular interactions between the solute molecules and can be independently determined from the dependence of the osmotic compressibility (dΠ/dC) = RT(KC/Rθ) on the concentration C, where Π is the osmotic pressure, K is an instrument constant and Rθ is the Raleigh ratio of intensity scattered at angle θ to the incident light intensity; the dependence KC/Rθ(C) is measured by static light scattering.17,18
γ ≅ 2B2C, where B2 is the second osmotic virial coefficient. B2 depends on the intermolecular interactions between the solute molecules and can be independently determined from the dependence of the osmotic compressibility (dΠ/dC) = RT(KC/Rθ) on the concentration C, where Π is the osmotic pressure, K is an instrument constant and Rθ is the Raleigh ratio of intensity scattered at angle θ to the incident light intensity; the dependence KC/Rθ(C) is measured by static light scattering.17,18
In solutions of biominerals and other complex salts the supersaturation is defined as 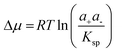 , Where the solubility product Ksp = ae+ae− takes the role of Kcryst. The activities of the cations a+ and anions a− in the growth solution and at equilibrium, denoted with superscript e, are calculated from the concentrations of the respective species, accounting for the other solution components.19 For compounds more complex than the binary salts assumed in the above expressions for Δμ and Ksp, they become correspondingly more complex.
, Where the solubility product Ksp = ae+ae− takes the role of Kcryst. The activities of the cations a+ and anions a− in the growth solution and at equilibrium, denoted with superscript e, are calculated from the concentrations of the respective species, accounting for the other solution components.19 For compounds more complex than the binary salts assumed in the above expressions for Δμ and Ksp, they become correspondingly more complex.
This definition of Δμ = μ − μe = μ − μcrystal, accepted in the fields of phase transformations, nucleation and crystal growth, contradicts the standard definition of the change of a thermodynamic variable in a physical or chemical process. In the standard definition, Δ signifies the difference between the final and initial states, while in the above definition, the crystal is the final state and the solution is in the initial state. Hence the two definitions of Δμ differ in sign.
The thermodynamic theory of J. W. Gibbs
The formation of crystals is a first-order phase transition. Accordingly, it is characterized with non-zero latent heat, the crystallization enthalpy ΔH°cryst discussed above. More significant for the kinetics of nucleation is the second feature of first order phase transitions: the discontinuity of the concentration at the phase boundary. As a result of this discontinuity, the solution-crystal boundary possesses non-zero surface free energy. If a small piece of a condensed phase forms in a supersaturated solution, the surface free energy of the emerging phase boundary makes this process unfavorable. Thus, a very limited number of embryos of the condensed phase appear as a result of the few fluctuations which overcome the free energy barrier. The first step in the formation of a new phase, in which the kinetics of the phase transformation is determined by this barrier, is called nucleation.The thermodynamic part of the classical nucleation theory was developed by J. W. Gibbs in two papers.20,21 We present it here with a slight modification: we consider the free energy balance of creating a cluster consisting of n molecules of size a, instead of a cluster of radius r, as in the Gibbs's papers. In a supersaturated solution, i.e., one in which the solute chemical potential is higher than that of molecules in the crystal so that Δμ > 0, the formation of such a cluster leads to a free energy loss of –nΔμ. On the other hand, the creation of the phase boundary with area S and surface free energy α between the cluster and the solution leads to a free energy gain Sα. Assuming that the crystal cluster is a cube, S = 6a2n2/3; other shapes will lead to coefficients different than 6a2 in this relation, but the 2/3 scaling with n will be preserved for all three dimensional nuclei. Thus,
| ΔG(n) = −nΔμ + 6a2n2/3α. | (2) |
This dependence is plotted in Fig. 1.
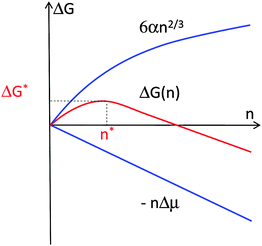 | ||
| Fig. 1 Illustration of the thermodynamic effects of formation of a crystal. n—number of molecules in crystal; Δμ—solution supersaturation; α—surface free energy; ΔG—free energy; * denotes critical cluster. | ||
Differentiating ΔG(n), we find the cluster size n* for which ΔG passes through a maximum ΔG*
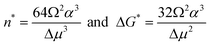 | (3) |
ΔG* from eqn (3) is the barrier that must be overcome to form a crystal from solute molecules. The growth of clusters smaller than n* is associated with an increase of free energy and is unfavorable. Clusters may still grow to such sizes as a result of a fluctuation, but since a driving force exists for the decay of these clusters, such events are rare. On the other hand, if as a result of a fluctuation a cluster reaches as size greater than n*, its growth is accompanied by a decrease of free energy and occurs spontaneously. A cluster of size n* has equal probabilities of growth and decay and, hence, such clusters are called critical and they represent the nuclei of the new phase. Note that by this definition all nuclei are critical and the term “critical nuclei” is redundant.22
The rate of crystal nucleation
To model the nucleation rate J, i.e., the number of nuclei which appear is a unit solution volume per unit time, M. Volmer postulated—in analogy to the Arrhenius equation—that J = J0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔG*/kBT), where kB is the Boltzmann constant.23 The external parameters, such as temperature, concentration and pressure, as well the solution supersaturation, affect the nucleation rate through ΔG* according to eqn (3). There are numerous statistical-mechanical derivations of the of the nucleation rate law within the assumption of the classical nucleation theory, for an example, see Ref. 24. The final expression of these derivations can be represented as25
exp(−ΔG*/kBT), where kB is the Boltzmann constant.23 The external parameters, such as temperature, concentration and pressure, as well the solution supersaturation, affect the nucleation rate through ΔG* according to eqn (3). There are numerous statistical-mechanical derivations of the of the nucleation rate law within the assumption of the classical nucleation theory, for an example, see Ref. 24. The final expression of these derivations can be represented as25J = ν*Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−G*/kBT). exp(−G*/kBT). | (4) |
A major assumption in the derivation of eqn (4) is that the solution molecules exchange directly with an ordered cluster. To understand the meaning of this assumption and why it might not apply to nucleation of crystals in solution, we need to step back and consider the distinction between a solution and a crystal.
Let us consider the phase diagram of a solution or any other two-component system in coordinates concentration and temperature at constant pressure. This phase diagram typically contains three phases: a dilute solution, a dense liquid, and crystal; a higher number of phases are possible if more than one crystalline polymorph may form. While with some solutions of small-molecule compounds the dense liquid might not be observable because it would occur at temperatures higher than the solvent boiling point, the dense liquid is readily seen in protein, colloid, and some organic solutions.27–30 To distinguish between the three phases present in the phase diagram, at least two parameters, called order parameters, are needed. Thus, the dilute solution and the dense liquid differ by the solute concentration, the dense liquid and the crystal differ by structure (there may be a slight difference in concentration), and the dilute solution and the crystal differ by both concentration and structure.
From this point of view, the formation of crystals in solution should be viewed as a transition along two order parameters: concentration and structure.18 While a fluctuation along the concentration axis is easy to imagine, structure transitions appear less trivial. Pure structure transitions are only possible in melts, whose concentration is similar to that of the emerging crystalline phase. Crystalline nuclei form as a result of a fluctuation along the structure axis. The smallest structure fluctuation can be viewed as a pair of molecules from the melt that has an orientation identical to the orientation of a pair of molecules in the crystal, for informative examples, see Ref. 62,63. This crystals-like orientation in the pair is preserved over times significantly longer than the lifetime of a “bond” in the melt. A nucleus arises as a result of accumulation of such ordered pairs into an ordered piece of new phase. In a sense, structure fluctuations can be viewed as fluctuations of the density of ordered pairs.
If a crystal nucleates not from its melt, but from a dilute solution or gas, both a concentration and a structure fluctuation are needed so that a crystalline nucleus may form, Fig. 2a. Thus, the above assumption that an ordered nucleus forms directly in the dilute solution corresponds to the assumption that the solution to crystal transformation occurs as a transition along both order parameters, density and crystallinity, simultaneously; in Fig. 2a this pathway is represented by the arrow along the diagonal of the (Concentrations, Structure) plane. It could be argued that a more logical pathway is for the transition is to proceed along the two order parameters in sequence. Such a sequential pathway would correspond to the formation of droplet of a dense liquid followed by the formation of a crystalline nucleus inside this droplet, as illustrated in Fig. 2b.
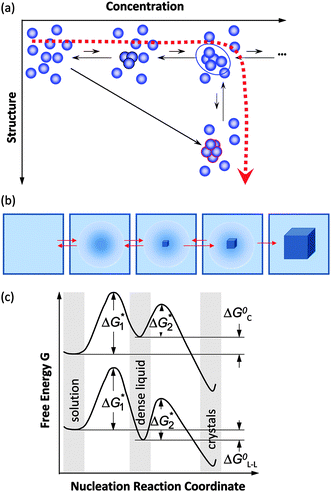 | ||
| Fig. 2 Schematic illustration of the two-step mechanism of nucleation of crystals. A dense liquid cluster forms. A crystal nucleus may form inside the cluster. (a) Microscopic viewpoint in the (Concentration, Structure) plane; (b) Macroscopic viewpoint of events along dashed line in (a). (c) The free-energy ΔG along two possible pathways for nucleation of crystals from solution. If dense liquid is unstable and ΔG0L–L > 0 (ΔG0L–L is the standard free energy of formation of dense liquid phase), dense liquid exists as mesoscopic clusters, ΔG0L–L transforms to ΔG0C, and upper curve applies; if dense liquid is stable, ΔG0L–L < 0, reflected by lower curve. ΔG*1 is the barrier for formation of a cluster of dense liquid, ΔG*2 the barrier for a structure fluctuation leading to an ordered cluster. | ||
This mechanism was first suggested by simulations and analytical theory.31–33 These theoretical efforts predicted that the density and structure fluctuations are only separated near the critical point for liquid–liquid (L–L) separation occurring in model protein solution systems,31,34,35 while for off-critical compositions, the fluctuations of the density and structure order parameters occur synchronously,31 similarly to the classical viewpoint.
The experiments discussed below demonstrate that nucleation of crystals of the protein lysozyme, under a broad range of conditions, proceeds in two steps: the formation of a droplet of a dense liquid, followed by nucleating a periodic crystal within the droplet,36–39 as schematically illustrated in Fig. 2. If the dense liquid is stable with respect to the dilute solution, the nucleation of crystals occurs inside macroscopic droplets of this phase. A far more common case is when the dense liquid is not stable but has a higher free energy than the dilute solution.28,29 In these cases, the dense liquid is contained in metastable clusters, intriguing objects in their own right, and crystal nucleation occurs within the clusters.
After and concurrently with the evidence for the operability of the two-step mechanism in the case of lysozyme crystallization, additional experimental results demonstrated that this mechanism applies to many other proteins, to small molecule organic and inorganic compounds, including biominerals, and colloids. Below, we discuss these and other issues related to the two-step nucleation mechanism
Experimental data on the rate of nucleation of crystals
To understand the mechanism of nucleation of crystals in solution we turn to data on the dependence of the nucleation rate on supersaturation for crystals of the protein lysozyme, a convenient and often used model system. The dependencies of the homogeneous nucleation rate of lysozyme crystals on the thermodynamic supersaturation σ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Δμ/kBT at three different concentrations of the precipitant, NaCl, are presented in Fig. 3. The data in Fig. 3 were obtained using the technique for direct determination of the nucleation rates of proteins discussed in Ref. 40,41, which allows distinction between homogenously and heterogeneously nucleated crystals so that the data points in Fig. 3 are homogenous nucleation rates. In support of the conclusion that the rates plotted in Fig. 3 characterize homogeneous nucleation is the fact that they are lower by several orders of magnitude than the those stemming from less careful measurements which may have been contaminated by heterogeneous nucleation events41–44
Δμ/kBT at three different concentrations of the precipitant, NaCl, are presented in Fig. 3. The data in Fig. 3 were obtained using the technique for direct determination of the nucleation rates of proteins discussed in Ref. 40,41, which allows distinction between homogenously and heterogeneously nucleated crystals so that the data points in Fig. 3 are homogenous nucleation rates. In support of the conclusion that the rates plotted in Fig. 3 characterize homogeneous nucleation is the fact that they are lower by several orders of magnitude than the those stemming from less careful measurements which may have been contaminated by heterogeneous nucleation events41–44
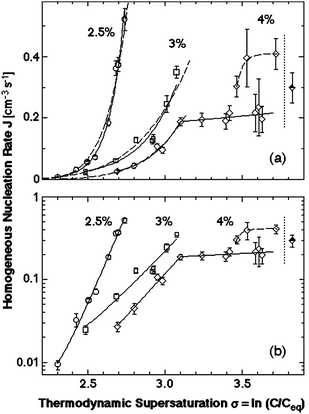 | ||
Fig. 3 The dependence of the rate of homogeneous nucleation J of lysozyme crystals of supersaturation σ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Δμ/kBT at T = 12.6 °C and at the three concentrations of the precipitant NaCl indicated on the plots. Solid lines—fits with exponential functions; dashed lines fits with the classical nucleation theory expression, eqn (4). Vertical dotted lines at σ = 3.9 indicate the liquid–liquid coexistence boundary at this T and CNaCl = 4%; this supersaturation corresponds to lysozyme concentration 67 mg ml−1. (a) Linear coordinates; (b) semi-logarithmic coordinates. With permission from Ref. 61. Δμ/kBT at T = 12.6 °C and at the three concentrations of the precipitant NaCl indicated on the plots. Solid lines—fits with exponential functions; dashed lines fits with the classical nucleation theory expression, eqn (4). Vertical dotted lines at σ = 3.9 indicate the liquid–liquid coexistence boundary at this T and CNaCl = 4%; this supersaturation corresponds to lysozyme concentration 67 mg ml−1. (a) Linear coordinates; (b) semi-logarithmic coordinates. With permission from Ref. 61. | ||
Each data series in Fig. 3 corresponds to nucleation experiments carried out at a fixed precipitant concentration and at fixed temperature. In agreement with general expectations, the nucleation rate increases exponentially with supersaturation at each of the three precipitant concentrations, and, overall, is higher at higher precipitant concentrations. However, the dependencies contain four peculiarities.
(i) The J(C) dependence at the highest precipitant concentration, CNaCl = 4%, breaks at 33.5 mg/ml, and, in dramatic contrast to prediction of eqn (3) and (4), the section above this concentration is practically steady as supersaturation increases.
(ii) At C > 48 mg/ml the same dependence bifurcates so that the data points belong to either of two branches.
(iii) All measured nucleation rates are of order 0.1–1 cm−3s−1, which is about ten orders of magnitude less than the prediction of the classical nucleation theory; the estimate of J stemming from the classical nucleation theory is discussed below.
(iv) The dependence of the nucleation rate on temperature, shown in Fig. 4 presents another puzzling complexity: as supersaturation is increased upon lowering of temperature, the nucleation rate first increases exponentially, as expected from the classical theory, but then passes through as sharp maximum and recedes following a weaker dependence.
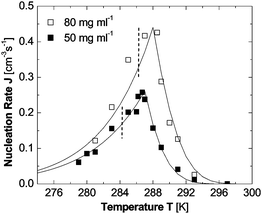 | ||
| Fig. 4 The dependence of the rate of homogeneous nucleation J of lysozyme crystals on temperature T at two fixed lysozyme concentrations indicated in the plot. The temperatures of equilibrium between crystals and solution are 315 K at Clys = 50 mg ml−1 and 319 K at Clys = 80 mg ml−1. The temperatures of L–L separation are 285 K at Clys = 50 mg ml−1 and 287 K at Clys = 80 mg ml−129 and are marked with vertical dashed lines. Symbols represent experimental results from.38 Lines are results of eqn (6)–(8). With permission from Ref. 54. | ||
In the following subsections, we discuss these four peculiarities.
The nucleus size and solution-to-crystal spinodal
To understand the breaking J(C) dependency, feature (i) above, we use the nucleation theorem to determine the size of the critical nucleus for crystallization. According to eqn (3), the number of molecules in the nucleus n* largely determines the height of the free energy barrier for nucleation ΔG*, and hence the nucleation rate J. The nucleation theorem,45–48 a universal, model-independent nucleation law, provides an estimate for n* from the nucleation rate J,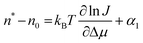 | (5) |
Fig. 3b indicates that at CNaCl = 2.5 and 3%, n* does not change throughout the respective supersaturation ranges, while at CNaCl = 4% the nucleus size changes abruptly at σ = 3.1, corresponding to C = 33.5 mg/ml. The value of the parameter n0, which roughly corresponds to the number of solution protein molecules displaced by the nucleus, can be roughly estimated as less than 1. Then the nucleus sizes n* − n0, extracted from the four linear segments in Fig. 3b are 10, 4, 5 and 1 molecules, respectively. From here we see that the breaking in the J(C) dependence at CNaCl = 4% is due to the transition of the nucleus size from five to one molecules.
Nucleus size n* − n0 = 1 means that every molecule in the solution can be an embryo of the crystalline phase, and the growth to dimer and larger clusters occurs with a free energy gain. Thus, the free-energy barrier for the formation of the crystalline phase ΔG* is below the thermal energy of the molecules. In analogy to the nucleation of a fluid within another fluid, we call spinodal the phase line at which the nucleation barrier vanishes and the rate of generation of the new phase is only limited by the kinetics of growth of its clusters. The spinodal is defined as the boundary between metastability and instability of an “old” phase, supersaturated with respect to a “new” phase.20,21,49
The case discussed here, the solution-to-solid phase transition, is one for which a mean-field free energy expression encompassing both phases cannot be formulated because of different standard states. Since the inflection point in the dependence of ΔG on the order parameter along which the phase transition occurs is typically used to define the spinodal,50–52 a thermodynamic definition of the solution-to-crystal spinodal is impossible.50 The definition proposed here is a kinetic one, based on the transition to nucleus size of one molecule, i.e., to where no thermodynamic barriers for the formation of the crystalline phase exist.
In Fig. 5, we have depicted the solution-to-crystal spinodal line in the (C,T) plane, determined as the concentration C at the transition to n* − n0 = 1 from Ref. 53. Since at concentrations and temperature below this spinodal line ΔG* ≈ 0, the nucleation rate J does not increase as supersaturation is increased by increasing C or lowering T. This explains puzzle (i) above. The existence of a solution-to-crystal spinodal also helps to explains the maxima in the dependencies of the nucleation rate J on temperature in Fig. 4, puzzle (iv) above; for a further details and a theoretical model of these factors, see below.
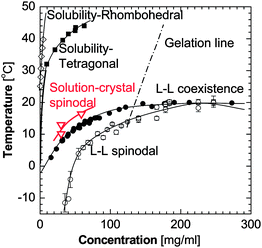 | ||
| Fig. 5 The phase diagram of a lysozyme solution determined experimentally in 0.05 M Na acetate buffer at pH = 4.5 and 4.0% NaCl. Liquidus, or solubility lines—from Ref. 106,107, liquid–liquid (L–L) coexistence and respective spinodal—from Ref. 29, gelation line—from Ref. 28,29. Solution-to-crystal spinodal is highlighted in red and is from Ref. 81. | ||
The transition to a spinodal regime of crystal formation also explains the bifurcation of J(C) at σ > 3.35, puzzle (ii) above. As seen in Fig. 4 and Ref. 38,54 and discussed below, at the point of transition from nucleation to spinodal decomposition the nucleation rate undergoes a sharp maximum: on the one side is an ascending branch due to the decrease of the size of the nucleus, and on the other side is a descending branch due to the temperature decrease and associated kinetic factors. Near this maximum, the nucleation rate is very sensitive to variations of the experimental conditions: temperature, protein and precipitant concentrations, and others. Hence, minor inconsistencies of these parameters may lead to the nearly two-fold variations in J seen in Fig. 3.37
The classical theory overestimates the crystal nucleation rate by 10 orders of magnitude.
To understand puzzle (iii) above, we use eqn (4) for an estimate of the crystal nucleation rate based on the classical nucleation theory. The rate ν* can be evaluated form the rate of attachment of molecules to lysozyme crystals at similar protein concentrations. As discussed is Ref. 55, the surfaces of crystal growing in solution are smooth and molecules only attach to growth steps which occupy about 10−3–10−2 of the crystal surface. Hence, the rate of attachment of molecules to crystals should be estimated from the velocity of step propagation rather than form the rate of growth of the crystal faces.There are numerous determinations of the step velocities of lysozyme crystals.56–58 At temperatures and concentrations similar to those during the determination of the nucleation rate in Fig. 3 the step velocities are ∼1 μm s−1. This yields, with molecular size of lysozyme of 3.5 nm, attachment rate to the steps ∼300 s−1. In contrast to that of large crystals, the nucleus surface is likely rough (because of the small size of the nucleus) and molecules can attach anywhere. Hence, we assume that ν* ≈ 300 s−1.
The Zeldovich factor Z accounts for the width of the free energy profile along the nucleation reaction coordinate around the location of the maximum.22,24,59,60 It is expected to be of order 0.1–0.01 for nucleation of any protein condensed phase.22,60,61 The protein number density in a solution of concentration ∼50 mg ml−1 as the one used for the experiments in Fig. 362 is n = 2 × 1018 cm−3. With these values for ν*, Z and n, the pre-exponential factor in eqn (4) is of order 1019–1020 cm−3 s−1.
The nucleation barrier ΔG*, determined from the slope of the dependencies in Fig. 3b, ΔG* ≈ 10−19 J. We can use eqn (3) to evaluate the surface free energy α of the interface between the dense liquid and the solution from the value of ΔG*. From the crystal structure, Ω ≅ 3 × 10−20 cm3 (Ref. 63) we get α = 0.5–0.6 erg cm−2 (Ref. 61), which is close to determinations for number of other protein crystals64,65 and this correspondence supports the estimate of ΔG* from the data in Fig. 3.
Combining the estimate for the pre-exponential factor with this estimate for ΔG* from eqn (4) we get a prediction for J ≈ 108–109 cm−3 s−1. This value is about 10 orders of magnitude higher than the one in Fig. 3. It is important to note that since we estimate ΔG* from experimental data, the difference between the experimentally determined J and the prediction of the classical nucleation theory is due to a lower pre-exponential factor.
The two-step mechanism of nucleation of crystal in solution
To understand puzzles (iii) and (iv) above, that the nucleation rate is lower by many orders of magnitude than the prediction of the classical theory and the non-monotonic dependence of the nucleation rate on temperature, we show below that the nucleation of crystals occurs inside metastable mesoscopic clusters of dense protein liquid, as illustrated in Fig. 2.Direct observations of ordered nuclei forming within the dense liquid exist, but only for the case of stable dense protein liquid, Fig. 6 and 7.66,67 Such direct imaging would be difficult or impossible for the more common case in which the dense liquid is unstable. The action of the two-step mechanism in this case is inferred from two pieces of evidence: First, we demonstrate the existence metastable mesoscopic dense liquid clusters in solutions. Then, we analyze of the complex kinetic curves in Fig. 3 and 4, propose a kinetic law for the two-step mechanism and show that its predictions qualitatively and quantitatively agree with the experimental data.
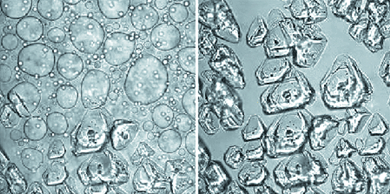 | ||
Fig. 6 Bright field imaging of nucleation of crystals of glucose isomerase within dense liquid droplets. Polyethylene glycol with molecules mass 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 (PEG 10000) used to induce crystallization. The time interval between the left and right images is 380 s. Cprotein = 55 mg ml−1, CPEG = 9.5%, 0.5 M NaCl, 10 mM Tris pH = 7; dimensions of each image: 326 μm × 326 μm. With permission from Ref. 66. 000 g mol−1 (PEG 10000) used to induce crystallization. The time interval between the left and right images is 380 s. Cprotein = 55 mg ml−1, CPEG = 9.5%, 0.5 M NaCl, 10 mM Tris pH = 7; dimensions of each image: 326 μm × 326 μm. With permission from Ref. 66. | ||
 | ||
| Fig. 7 The nucleation of polymers of deoxy sickle cell hemoglobin (HbS) in dense liquid droplets existing in solution of this protein. Concentration of HbS is 220 mg ml−1. (a)–(d) temperature is lowered from 42 to 35 °C, the smaller of the dense liquid droplets disappear, while the larger ones serve as nucleation centers for HbS spherulites. Spherulites also appear at the locations where smaller droplets have been, apparently because of the undissipated locally higher concentration. Time elapsed between (a) and (d) is 27 s, as indicated in the panels. With permission from Ref. 67. | ||
Dense liquid clusters in the homogenous region of the phase diagram
If crystallization is carried out at a point in the phase diagram where the dense liquid is unstable, all density fluctuations are expected to decay with a characteristic time of order of the diffusion time of the protein molecules, 10 μs, see below.68–70 Since the molecules in the region of high concentration within the fluctuation move with the same characteristic time, it would be impossible for them to probe various structures and find the right one for the crystalline nucleus. Thus the crucial question for the understating of nucleation from dilute media is: How does the transition along the order parameter concentration occur? The answer lies in the recently discovered metastable mesoscopic clusters of dense liquid.The evidence for metastable dense liquid clusters comes from monitoring solutions of three hemoglobin variants, oxy-HbA, oxy-HbS, and deoxy-HbS, and the proteins lumazine synthase and lysozyme, by dynamic light scattering (DLS). Fig. 8a shows a typical intensity correlation function of a lysozyme solution in the homogeneous regions of the phase diagram. The correlation function reveals two processes: the faster process, with characteristic time of ∼10–100 μs, is the Brownian motion of single lysozyme molecules; it is present at all solution concentrations. The corresponding hydrodynamic radius, determined via the Stokes–Einstein equation, is about 1.5 nm and matches well the diameter of a lysozyme molecule of 3.2 nm. The slower process takes milliseconds; its amplitude increases with higher lysozyme concentrations. This longer time could come from either compact lysozyme clusters suspended in the lysozyme solution, or from single lysozyme molecules embedded in a loose network structure constraining their free diffusion. Since the measured low-shear viscosity of lysozyme solutions is equal to those determined using high shear rates,71 no loose networks in lysozyme molecules exist in these solutions and we conclude that long times in Fig. 8a indeed correspond to lysozyme clusters.68 The time-dependence of their radius is shown in Fig. 8c. The clusters appear immediately after solution preparation; their radius is relatively steady, Fig. 8. We therefore conclude that these are clusters of dense liquid.
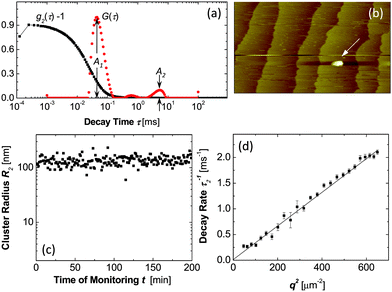 | ||
| Fig. 8 Characterization of dense liquid clusters. (a) Examples of correlation function of the scattered intensity g2(τ) and the respective intensity distribution function G(τ) of a lysozyme solution with C = 148 mg ml−1 in 20 mM HEPES buffer; data collected at angle 145°. (b) Atomic force microscopy imaging of liquid cluster landing on the surface of a crystal in a lumazine synthase solution. Tapping mode AFM imaging, scan width 20 μm. Apparent lateral cluster dimensions are misleading, cluster height is 120 nm, with permission from Ref. 72. (c) Time dependence of the radius of dense liquid clusters in the same lysozyme solution as in a. (d) The dependence of the decay rate Γ2 = τ2−1 of the cluster peak in the correlation function on the squared wave vector q2 for a lysozyme solution as in (a). | ||
The number density n2 of the dense liquid clusters and the fraction of the total solution volume φ2 they occupy are evaluated from the amplitudes A1 and A2 of the respective peaks in the distribution function.68 Further results on the behavior of clusters of dense liquid in solutions of hemoglobin and lumazine synthase are presented in Ref. 68,70,72. It was found that with all studied proteins, the clusters exist in broad temperature and protein concentration ranges. The clusters occupy φ = 10−6–10−3 of the solution volume.68
To evaluate the lifetime of the lysozyme clusters, we note that cluster decay processes contribute a q-independent component to the overall rate sensed by DLS Ref. 73, Γ2 = Γ0 + D2q2, and can be distinguished from cluster diffusion. (Γ0 is the rate of cluster decay, D2 is the cluster diffusion coefficient, and q is the wave-vector.) The q-dependent, diffusion component indeed dominates the DLS signal, Fig. 8d. Using Γ0 ≪ D2q2 with q2 = 3.5 × 1010 cm−2 and D2 = 2 × 10−9 cm2s−1, Γ0 ≪ 70 s−1, we obtain a lower bound 1/Γ0 ≈ 15 ms for cluster lifetimes.
The determination of the lifetime of the clusters of lumazine synthase was more straightforward and yielded an estimated of ∼10 s.70,72 In addition to detection by dynamic light scattering, clusters of lumazine synthase were directly imaged by atomic force microscopy, Fig. 8b,70,72 which confirmed their macroscopic lifetimes.
The lifetimes of the clusters (>15 ms for Hb and lysozyme and ∼10 s for lumazine synthase) significantly exceed the equilibration times of the protein concentration at sub-micrometer length scales, i.e. ∼10−5 s. Thus the compact clusters represent a metastable phase separated from the bulk, dilute solution by a free energy barrier.
Attempts to rationalize the finite size of clusters have focused on a balance of short-range attraction, due to van der Walls, hydrophobic or other forces, and screened Coulombic repulsion between like-charged species.74,75 While small clusters, tens of particles or so, naturally appear in such approaches, large clusters are expected only if the constituent particles are highly charged, with hundreds or so elementary charges. Such high charges are feasible for micron-size colloidal particles, however proteins in solution are known to carry less than 10 elementary changes per molecule. While these theories have been successfully applied to aggregation in colloidal suspensions,76–78 a distinct mechanism is at work in protein systems, where clusters contain as many as 106 molecules.69 A recent study concluded that the clusters consist of a non-equilibrium mixture of single protein molecules and long-lived but ultimately unstable complexes of proteins.69 The puzzling mesoscopic size of the clusters is determined by the lifetime and diffusivity of these complexes. Several possible mechanisms of complex formation: domain swapping, hydration forces, dispersive interactions, and other, system-specific interactions were highlighted.
The rate law for the two-step mechanism of crystal nucleation
A phenomenological theory was developed that takes into account intermediate high-density metastable states in the nucleation process.54 The rate law for the dependence of the nucleation rate on protein concentration and temperature emerging from this theory is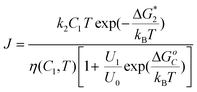 | (6) |
Following Ref. 79, the nucleation barrier ΔG* in the vicinity of the solution-to-crystal spinodal was modeled as
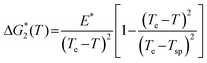 | (7) |
The viscosity inside the dense liquid clusters was modeled as
η = η0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) {1 + [η]C1exp(kη[η]C1)}exp(−Eη/kBT) {1 + [η]C1exp(kη[η]C1)}exp(−Eη/kBT) | (8) |
A crucial assumption is eqn (8) is that the concentration inside the dense liquid clusters C1 increases as temperature is lowered, in agreement with the phase diagram in Fig. 5 and the likely similarity between the dense liquid in the clusters and the stable sense liquid depicted in the phase diagram.54 As a result of this C1(T) dependence, the viscosity η increases much more strongly in response to decreasing temperature T then suggested by the quasi-Arrhenius member of eqn (8) with Eη about 10–20 kJ mol−1.80
The nominator of eqn (6) offers another pathway by which decreasing temperature affects the nucleation rate J, besides the temperature dependence of the viscosity. Since (U0/U1)exp(- ΔGoC/kBT) is the non-equilibrium volume fraction occupied by the clusters, the term in the square brackets in the denominator of eqn (6) is approximately the reciprocal non-equilibrium volume fraction occupied by the clusters, ϕ2−1. Since ΔGoC > 0, see above, lower T leads to a greater value of the denominator, which corresponds to a lower volume of the dense liquid clusters and accordingly to lower J. This contributes about factor of five in the decrease in J as temperature is lowered from Tsp to the lowest values probed in Fig. 4.
Using eqn (6)–(8) nucleation rate data at varying temperature and protein concentrations in Fig. 3 and Ref. 81, as well as non-monotonic dependencies of the nucleation rate on temperature in Fig. 4 were reproduced with high fidelity using literature values or independently determined parameters of the thermodynamic and kinetic parameters of the system.54 The good correspondence between the model results and the experimental data supports the validity of the two-step nucleation mechanism. According to eqn (6), the increasing part of the J(T) as temperature is lowered below Te is due to the increase of the supersaturation Δμ which shrinks ΔG* according to eqn (3); this leads to exponential increase in the nucleation rate J. The maximum in J(T) is reached exactly at T = Tsp, where ΔG*2 vanishes; note that Tsp is independently determined from plots similar to the one at 4% in Fig. 3c.81 The steep decrease in the nucleation rate as T is lowered beyond the maximum at Tsp is a a crucial part in the proof of the validity of the two-step mechanism: within the two-step mechanism this steep decrease is explained by the smaller volume of the dense liquid clusters at lower temperature, and by the higher concentration inside them, leading to higher viscosity. Both the lower volume of the clusters and the higher viscosity lead to lower nucleation rate.
No pathway of steep decrease of nucleation rate beyond the spinodal temperature exists if one assumes one step nucleation: nuclei forming within the dilute solution would be exposed to its viscosity, which is a weak function of temperature. Thus, the nucleation rate would decrease almost imperceptibly, by ∼16%, assuming Eη = 20 kJ mol−1, within the 5–6 K range probed. Note that the decrease in nucleation rate in glass forming melts in response to temperature decrease, interpreted as a result of viscosity increase in the melt, occurs over 40–50 K;82 furthermore, this response is significantly enhanced by the stronger temperature dependence of viscosity of melts as compared to the viscosity of solutions.
To understand puzzle (iii) above, that the nucleation rate is lower by 10 orders of magnitude than the prediction of the classical theory, we compare the nucleation kinetic law in eqn (6) to that in eqn (4). We see that ϕ2k2C1T/η takes the place of the product νZn. In solutions of concentration C in the range 20 to 60 mg ml−1 as the ones in which the nucleation rates in Fig. 3 were measured, the cluster volume fraction ϕ2, represented by the denominator in eqn (6), is of order 10−7–10−6. With the concentration C1 in the clusters around 300 mg ml−1, eqn (8) shows that the viscosity η of the dense liquid in the clusters is around 100 centiPoise, or ∼100 × higher than in the normal solution. We get that the nucleation rate should be ∼109× lower than the prediction of the classical theory, which assumes nucleation in the solution bulk. Thus, the two-step mechanism explains the third peculiarity of the nucleation rate data in Fig. 3: the significantly lower pre-exponential factor in the nucleation rate law.
The rate determining step in the two-step nucleation mechanism
The derivation of eqn (6) is based on the assumption that the first step in the two-step mechanism, the formation of the dense liquid clusters is fast and that the second step, the formation of the crystal nuclei within the dense liquid clusters, is rate determining. While the excellent agreement between the experimental data and the prediction of eqn (6) in Fig. 4 can be viewed as a support of this assumption, it should and can be tested independently.As first evidence in favor of the fast rate of generation of the dense liquid clusters, we view data on the time dependence of three characteristics of the cluster population: average radius, number density, and volume fraction, illustrated for the case of average cluster radius in Fig. 8c. All of these dependencies, monitored for the proteins lumazine synthase,70,72 lysozyme,69 and three hemoglobin variants68 reveal that the clusters appear within several seconds of solution preparation. After that, the cluster populations are stable for several hours.
For an additional test, we use the similarity between the clusters and stable droplets of dense liquid which exist below the liquid–liquid coexistence line in the phase diagram in Fig. 5. The rate of nucleation of the dense droplets was determined by monitoring the increase in time of the number of droplets appearing in an isothermal solution supersaturated with respect to the formation of dense liquid.62 These data yield droplet nucleation rates, which are of order 108 cm−3 s−1. These rates are about ten orders of magnitude faster than the rates of crystal nucleation and support the conclusion that the nucleation of the dense liquid precursors, stable or unstable, is much faster than the rate of crystal nucleation within these precursors.
The conclusion that the rate of nucleation of crystals within the dense liquid clusters is the rate determining step in the two-step nucleation mechanism supports the applicability of eqn (6) as the rate law for this process. Another important consequence of this conclusion is related to the applicability of the nucleation theorem to the two-step nucleation mechanism. Since cluster formation is fast, the clusters can be considered in equilibrium with the solution. Then the chemical potential of the protein in the clusters is equal to the chemical potential of the protein in the solution, and Δμ = μsolute − μcrystal is the supersaturation to which the crystal nuclei are exposed within the clusters. Since the cluster number is steady, J is the rate of nucleation of crystals inside the clusters. From the latter two conclusions, it follows that applying the nucleation theorem, eqn (5) with the macroscopically observed nucleation rate and the external supersaturation, is equivalent to applying the nucleation theorem to the nucleation of crystlline the dense liquid. Hence, the size of the nuclei determined using the nucleation theorem refers to the crystalline nuclei within the clusters. Furthermore, the transition to spinodal regime occurs when the crystalline nuclei reach size one molecule and this transition corresponds to ΔG*2 = 0.
Finally, we can resolve an apparent controversy. From the above estimate of the lowering of the nucleation rate due to the low volume fraction and the high viscosity of the dense liquid, it may appear that the selection of the two-step mechanism violates the principle of fastest increase of entropy, e.g.ref. 83,84. This principle governs the selection of kinetic pathways towards, in most cases, the mechanism leading to the fastest rate: faster consumption of supersaturation corresponds to faster increase of the total entropy of the universe. This is an incorrectly posed problem: the estimate of the nucleation rate above used the value of the nucleation barrier ΔG* extracted from the experimental data. As just demonstrated, this barrier is in fact ΔG*2 from Fig. 2c and eqn (6), i.e., the barrier for nucleation of crystals inside the clusters. Since the surface free energy at the interface between the crystal and the solution is likely significantly higher than at the interface between the crystal and the dense liquid, the barrier for nucleation of crystals from the solution would be much higher. This would lead to much slower nucleation of crystals directly from the solution than inside the clusters. Thus, the protein crystal nucleation follows the two-step nucleation mechanism because it provides for faster rate of the solution to crystal phase transition and in this way for faster decrease of the free energy of the system, which corresponds to faster increase of the entropy of the universe.
The role of heterogeneous nucleation substrates
Knowing that the nucleation of crystal within the dense liquid clusters is the rate limiting step in the two-step mechanism, we can address a broader related question: Since from a general point of view, the rate of nucleation via the two-step mechanism depends on two pre-exponential factors, J01 and J02, and two barriers, ΔG*1 and ΔG*2, which of these four parameters is the most significant. Clearly, the answer should be sought between J02 and ΔG*2. Since nucleation occurs in the vicinity of the solution-to-crystal spinodal, ΔG*2 is very small, and hence, the most important parameter is J02. This is a surprising conclusion, and it sheds light on the role of heterogeneous substrates in nucleation.Nucleation is often facilitated by heterogeneous centers.50,85 The generally accepted mechanism of heterogeneous nucleation is that it follows the kinetic law for homogeneous nucleation but is faster due to lowering of the nucleation free energy barrier.50 Since we now know that ΔG*2 is insignificant, we conclude that in contrast to the generally accepted viewpoint heterogeneous nucleation centers assist nucleation not by lowering ΔG*2, but by assisting the growth of the ordered clusters through the factor accounted for in the pre-exponential factor J02.
There may be many mechanisms by which a surface may facilitate the growth of the ordered clusters. The most obvious one is that the “right” crystal structure, i.e., the one that minimizes the free energy of the system, is similar to the structure of the surface. Alternatively, the surface structure may stabilize a necessary intermediary en route to the “right” crystal structure, similar to the way enzymes stabilize the transition state, and not the final product of the catalyzed reaction.86 Another possibility is that the surface may catalyze the formation of the intermolecular bonds in the crystal. If the structure of a substrate is similar to the structure of the growing crystal, this is referred to as templating.87,88 Examples were found for crystallization of proteins on mineral substrates and on ordered lipid layers.89,90 One may view the acceleration of nucleation of γ-glycine crystals in the bulk of a supersaturated solution by elliptically polarized light, and α-glycine crystals by linearly polarized light as examples of assisted structuring of the dense liquid by appropriately structured electric field.91
Other systems for which the two-step nucleation mechanism applies
Above, we analyzed in detail data on the kinetics of nucleation of crystals of the protein lysozyme, which allow a rather confident conclusion about the applicability of the two-step mechanism. The evidence for the applicability of this mechanism to the nucleation of crystals of other proteins is less direct. In Ref. 92, crystals of several intact immunoglobins were found to coexist for extended lengths of time with dense liquid droplets without the droplets generating additional crystal nuclei. The crystals that were nucleated on the droplet boundaries grew into the dilute solution, rather than into the dense liquid. This was interpreted in favor of nucleation of the crystals within dense liquid clusters suspended in the solution.Besides the nucleation of protein crystals, the action of the two-step mechanism has recently been demonstrated for the homogeneous nucleation of HbS polymers, with metastable dense liquid clusters serving as precursor to ordered nuclei of the HbS polymer.68,93,94 Other studies have shown that the nucleation of amyloid fibrils of several proteins and peptide fragments, such as Alzheimer-causing A-β-peptide or the yeast prion protein follows a variant of the two-step mechanism in which the role of the intermediate liquid state is played by a molten globule of consisting of unfolded protein chains.95,96
The applicability of the two-step mechanism to the nucleation of crystals of urea and glycine was deduced in a series of experiments, in which high power laser pulses were shone on supersaturated solutions.91,97 It was fond that the nucleation rate increases as a result of the illumination by eight-nine orders of magnitude and that by using elliptically or linearly polarized light, α− or γ− glycine crystals could be preferentially nucleated. Since glycine does not absorb the illumination wavelength, and the electric field intensity was insufficient to orient single glycine molecules, it was concluded that the elliptically or linearly polarized pulses stabilize the structure fluctuations within the dense liquid, which lead to the respective solid phases.36,97
Colloid systems are the ones for which the evidence in favor of the applicability of the two-step mechanism is the strongest. By tracking the motions of individual particles of size a few microns by scanning confocal microscopy, the nucleation of crystals in colloidal solutions was directly observed.98–100 These experiments revealed that the formation of crystalline nuclei occurs within dense disordered and fluid regions of the solution.
The role of an amorphous precursor in the nucleation of crystal of biominerals has been speculated for a long time, for a historic overview, see.101 However, it was envisioned that the precursor does not facilitate that formation of the crystalline nuclei, but only serves as a source of material for re-precipitation into a crystalline phase. Only recently it was shown that amorphous or liquid clusters of calcium and carbonate ions are present in calcium carbonate solutions and facilitate the nucleation of calcite crystals, in a manner similar to the role of the mesoscopic clusters in lysozyme crystallization discussed above.102,103 The free energy landscape along the nucleation reaction pathway in Fig. 2c was used to characterize kinetics of the process of calcite crystallization.103
Stable dense liquid was found to exist in solutions of organic materials and serve as location where crystals nucleate and grow.30 The existence of the dense liquid in these solutions has been attributed to the same fundamental physical mechanism as the one acting in protein solutions: the size of the solute molecules is larger than the characteristic lengthscale of the intermolecular interactions in the solution.35 On the other hand, unpublished evidence from the pharmaceutical industry suggests that in many other cases the stable dense liquid, referred to as “oil” by the practitioners in the field, is so viscous that no crystals can form in it. This is in contrast to the observations in Fig. 6 and 7, in which crystals and sickle cell hemoglobin polymers form in the relatively non-viscous dense protein liquid. While this has not been tested, it is possible that the two-step mechanism operates in these organic systems by utilizing dense liquid clusters, similar to those seen in protein, colloid, and calcium carbonate solutions.
In general, the two possible intermediate states for the two-step mechanism, the stable dense liquid and the metastable clusters, have distinct mechanisms: the discrepancy of the lengthscale of the intermolecular interactions in the solution and the size of the crystallizing molecules for the stable dense liquid, and the existence of limited lifetime complexes for the clusters. Thus, for a given system the availability of any of these two intermediate states is independent of the other; both of them depend on the exact physicochemical characteristics of the system.
The broad variety of systems in which the two-step mechanism operates suggests that its selection by the crystallizing systems in preference to the nucleation of ordered phases directly from the low-concentration solution may be based on general physical principles. This idea is supported by two examples of general physical theory: by Sear104 and by Lutsko and Nicolis.105 Of particular interest is the latter work. It treated a range of points in the phase diagram of two different model systems which likely encompass a broad variety of real solutions and demonstrated that the two-step formation of crystalline nuclei, via a dense liquid intermediate, encounters a significantly lower barrier than the direct formation of an ordered nucleus and should be faster. Interestingly, the intermediate state resulting from the theory was not stabilized and represents a just a well developed density fluctuation.
Summary and conclusions
In this review of the recent advances in the understanding of nucleation of crystals in solutions, we show that the classical nucleation theory fails to provide understanding of several features of measured kinetic curves: nucleation rates, which are orders of magnitude lower than the classical prediction; nucleation kinetics curves which exhibit saturation, or, even more puzzling, maxima and decreasing branches, with increasing supersaturation, as well as the role of the other, stable and unstable, phases possible in solution.We show that these features of the nucleation kinetics reflect the action of two factors, which are unaccounted by the classical nucleation theory: the existence of a spinodal for the solution to crystal phase transition, and the action of a two-step nucleation mechanism. As the spinodal is reached upon supersaturation increase, the barrier for nucleation of crystals vanishes and further increases in supersaturation do not yield faster nucleation rate. According to the two-step mechanism, the nucleation of crystal, step two, occurs within mesoscopic clusters of dense liquid, step one. While the initial thought provoking results on the nucleation kinetics were obtained for the nucleation of protein crystals, and, correspondingly, the two-step mechanism was first proposed for these types of crystals only, further investigations have shown the validity of this mechanism to organic, inorganic and colloid materials, including the important class of biominerals.
Since the main body of experimental data supporting the concepts of the solution to crystal spinodal and the two-step mechanism were obtained with protein solutions, a crucial question is the general applicability of these concepts to other crystallizing systems.
The issue of the spinodal appears more straightforward: the nucleation of numerous crystals in industrial and laboratory practice is carried out at such high supersaturations that the nucleation occurs either in the spinodal regime or in the immediate vicinity of this regime, where the nucleus consist of just a few molecules.
The action of the two-step mechanism relies of the availability of disordered liquid or amorphous metastable clusters in the homogeneous solutions prior to nucleation. While such clusters have been demonstrated for several protein systems and for calcium carbonate solutions it is likely that not all solutions would support the existence of such clusters with properties allowing the nucleation of crystals in them. In such systems the action of the direct nucleation mechanism might be the only option. On the other hand, an intriguing hypothesis is presented by one of the theories discussed above: that a stabilized intermediate state, as a stable dense liquid, as seen in Fig. 6 and 7, or as a metastable mesoscopic cluster, as in Fig. 8, is not needed and the two-step mechanism will act even if the intermediate step is just a density fluctuation. Thus, the two-step mechanism may in fact operate in systems where no intermediate is independently found.
Acknowledgements
I thank NSF (Grant MCB 0843726) and the Normal Heckerman Advanced Research Program (Grant 003652-0078-2009) for financial support.References
- J. J. De Yoreo, A. K. Burnham and P. K. Whitman, Int. Mater. Rev., 2002, 47, 113–152 Search PubMed.
- US Patent Pat., 5,441,734., 1995.
- J. Brange, Galenics of Insulin, Springer, Berlin, 1987 Search PubMed.
- M. L. Long, J. B. Bishop, T. L. Nagabhushan, P. Reichert, G. D. Smith and L. J. DeLucas, J. Cryst. Growth, 1996, 168, 233–243 CrossRef CAS.
- S. Matsuda, T. Senda, S. Itoh, G. Kawano, H. Mizuno and Y. Mitsui, J. Biol. Chem, 1989, 264, 13381–13382 CAS.
- S. Peseta, J. A. Langer, K. C. Zoon and C. E. Samuel, in Annual Review of Biochemistry, ed. C. C. Richardson, P. D. Boyer, I. B. Dawid and A. Meister, Annual Reviews, Palo Alto, 1989, vol. 56, pp. 727–778 Search PubMed.
- S. Charache, C. L. Conley, D. F. Waugh, R. J. Ugoretz and J. R. Spurrell, J. Clin. Invest., 1967, 46, 1795–1811 CAS.
- R. E. Hirsch, C. Raventos-Suarez, J. A. Olson and R. L. Nagel, Blood, 1985, 66, 775–777 CAS.
- W. A. Eaton and J. Hofrichter, in Advances in protein chemistry, ed. C. B. Anfinsen, J. T. Edsal, F. M. Richards and D. S. Eisenberg, Academic Press, San Diego, 1990, vol. 40, pp. 63–279 Search PubMed.
- P. Vekilov, Br. J. Haematol., 2007, 139, 173–184 CrossRef CAS.
- C. R. Berland, G. M. Thurston, M. Kondo, M. L. Broide, J. Pande, O. Ogun and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 1214–1218 CAS.
- N. Asherie, J. Pande, A. Pande, J. A. Zarutskie, J. Lomakin, A. Lomakin, O. Ogun, L. J. Stern, J. King and G. B. Benedek, J. Mol. Biol., 2001, 314, 663–669 CrossRef CAS.
- G. Dodson and D. Steiner, Curr. Opin. Struct. Biol., 1998, 8, 189–194 CrossRef CAS.
- A. McPherson, Introduction to Macromolecular CrystallographyJohn Wiley, Hoboken, New Jersey, 2009 Search PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS.
- J. Prausnitz and L. Foose, Pure Appl. Chem., 2007, 79, 1435–1444 CrossRef CAS.
- K. S. Schmitz, Dynamic Light Scattering by Macromolecules, Academic Press, New York, 1990 Search PubMed.
- D. N. Petsev, B. R. Thomas, S.-T. Yau, D. Tsekova, C. Nanev, W. W. Wilson and P. G. Vekilov, J. Cryst. Growth, 2001, 232, 21–29 CrossRef CAS.
- N. Takeno, Open File Report of GSJ, 1988, 49, 26–143 Search PubMed.
- J. W. Gibbs, Trans. Connect. Acad. Sci., 1876, 3, 108–248 Search PubMed.
- J. W. Gibbs, Trans. Connect. Acad. Sci., 1878, 16, 343–524 Search PubMed.
- D. Kashchiev, Nucleation. Basic theory with applications, Butterworth, Heinemann, Oxford, 2000 Search PubMed.
- M. Volmer, Kinetik der Phasenbildung, Steinkopff, Dresden, 1939 Search PubMed.
- B. Mutaftschiev, in Handbook of crystal growth, ed. D. T. J. Hurle, Elsevier, Amsterdam, 1993, vol. I, pp. 189–247 Search PubMed.
- P. G. Vekilov, L. A. Monaco, B. R. Thomas, V. Stojanoff and F. Rosenberger, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1996, 52, 785–798 CrossRef CAS.
- J. Lothe and G. M. Pound, J. Chem. Phys., 1966, 45, 630–634 CrossRef CAS.
- M. L. Broide, C. R. Berland, J. Pande, O. O. Ogun and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 5660–5664 CAS.
- M. Muschol and F. Rosenberger, J. Chem. Phys., 1997, 107, 1953–1962 CrossRef CAS.
- D. N. Petsev, X. Wu, O. Galkin and P. G. Vekilov, J. Phys. Chem. B, 2003, 107, 3921–3926 CrossRef CAS.
- P. E. Bonnett, K. J. Carpenter, S. Dawson and R. J. Davey, Chem. Commun., 2003, 698–699 RSC.
- P. R. ten Wolde and D. Frenkel, Science, 1997, 277, 1975–1978 CrossRef.
- V. Talanquer and D. W. Oxtoby, J. Chem. Phys., 1998, 109, 223–227 CrossRef CAS.
- K. G. Soga, J. M. Melrose and R. C. Ball, J. Chem. Phys., 1999, 110, 2280–2288 CrossRef CAS.
- J. A. Thomson, P. Schurtenberger, G. M. Thurston and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 7079–7083 CrossRef CAS.
- N. Asherie, A. Lomakin and G. B. Benedek, Phys. Rev. Lett., 1996, 77, 4832–4835 CrossRef CAS.
- D. W. Oxtoby, Nature, 2002, 420, 277–278 CrossRef CAS.
- P. G. Vekilov, Cryst. Growth Des., 2004, 4, 671–685 CrossRef CAS.
- O. Galkin and P. G. Vekilov, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 6277–6281 CrossRef CAS.
- V. J. Anderson and H. N. W. Lekkerkerker, Nature, 2002, 416, 811–815 CrossRef CAS.
- O. Galkin and P. G. Vekilov, J. Phys. Chem., 1999, 103, 10965–10971 Search PubMed.
- P. G. Vekilov and O. Galkin, Colloids Surf., A, 2003, 215, 125–130 CrossRef CAS.
- V. Bhamidi, S. Varanasi and C. A. Schall, Cryst. Growth Des., 2002, 2, 395–400 CrossRef CAS.
- N. M. Dixit, A. M. Kulkarni and C. F. Zukoski, Colloids Surf., A, 2001, 190, 47–60 CrossRef CAS.
- N. M. Dixit and C. F. Zukoski, J. Colloid Interface Sci., 2000, 228, 359–371 CrossRef CAS.
- D. Kashchiev, J. Chem. Phys., 1982, 76, 5098–5102 CrossRef CAS.
- D. W. Oxtoby and D. Kashchiev, J. Chem. Phys., 1994, 100, 7665–7671 CrossRef CAS.
- I. J. Ford, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 5615–5629 CrossRef CAS.
- J. W. P. Schmelzer, J. Colloid Interface Sci., 2001, 242, 354–372 CrossRef CAS.
- J. D. van der Waals, in Nobel Lectures, Physics 1901-1921, Elsevier Publishing Company, Amsterdam, 1910 Search PubMed.
- P. G. Debenedetti, Metastable Liquids, Princeton Univ Pr, Princeton, 1996 Search PubMed.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- J. S. Langer, in Fluctuations and Instabilities in Phase Transitions, ed. T. Riske, Plenum, New York, 1975, pp. 19–42 Search PubMed.
- L. Filobelo, PhD, University of Houston, 2005.
- W. Pan, A. B. Kolomeisky and P. G. Vekilov, J. Chem. Phys., 2005, 122, 174905 CrossRef.
- P. G. Vekilov, in Perspectives on Inorganic, Organic and Biological Crystal Growth: From Fundamentals to Applications: AIP Conference Proceedings, ed. M. Skowronski, J. J. DeYoreo and C. A. Wang, AIP, Melville, NY, 2007, vol. 916, pp. 235–267 Search PubMed.
- A. E. S. Van Driessche, F.n. Otálora, G. Sazaki, M. Sleutel, K. Tsukamoto and J. A. Gavira, Cryst. Growth Des., 2008, 8, 4316–4323 CrossRef CAS.
- A. J. Malkin, Y. G. Kuznetsov and A. McPherson, J. Cryst. Growth, 1999, 196, 471–488 CrossRef CAS.
- P. G. Vekilov, B. R. Thomas and F. Rosenberger, J. Phys. Chem. B, 1998, 102, 5208–5216 CrossRef CAS.
- Y. B. Zel'dovich, Acta Physicochimica URSS, 1943, 18, 1–22 Search PubMed.
- D. Kashchiev, in Science and technology of crystal growth, ed. J. P. v. d. Eerden and O. S. L. Bruinsma, Kluwer Academic Publishers, 1995, pp. 53–56 Search PubMed.
- O. Galkin and P. G. Vekilov, J. Am. Chem. Soc., 2000, 122, 156–163 CrossRef CAS.
- M. Shah, O. Galkin and P. G. Vekilov, J. Chem. Phys., 2004, 121, 7505–7512 CrossRef CAS.
- L. K. Steinrauf, Acta Crystallogr., 1959, 12, 77–78 CrossRef CAS.
- A. J. Malkin and A. McPherson, J. Cryst. Growth, 1993, 128, 1232–1235 CrossRef CAS.
- A. J. Malkin and A. McPherson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1994, 50, 385–395 CrossRef CAS.
- D. Vivares, E. Kaler and A. Lenhoff, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2005, 61, 819–825 CrossRef.
- O. Galkin, K. Chen, R. L. Nagel, R. E. Hirsch and P. G. Vekilov, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 8479–8483 CrossRef CAS.
- W. Pan, O. Galkin, L. Filobelo, R. L. Nagel and P. G. Vekilov, Biophys. J., 2007, 92, 267–277 CrossRef CAS.
- W. Pan, P. G. Vekilov and V. Lubchenko, J. Phys. Chem. B, 2010, 114, 7620–7630 CrossRef CAS.
- O. Gliko, W. Pan, P. Katsonis, N. Neumaier, O. Galkin, S. Weinkauf and P. G. Vekilov, J. Phys. Chem. B, 2007, 111, 3106–3114 CrossRef CAS.
- W. Pan, L. Filobelo, N. D. Q. Pham, O. Galkin, V. V. Uzunova and P. G. Vekilov, Phys. Rev. Lett., 2009, 102, 058101 CrossRef.
- O. Gliko, N. Neumaier, W. Pan, I. Haase, M. Fischer, A. Bacher, S. Weinkauf and P. G. Vekilov, J. Am. Chem. Soc., 2005, 127, 3433–3438 CrossRef CAS.
- E. E. Uzgiris and D. C. Golibersuch, Phys. Rev. Lett., 1974, 32, 37–40 CrossRef CAS.
- F. Sciortino, S. Mossa, E. Zaccarelli and P. Tartaglia, Phys. Rev. Lett., 2004, 93, 055701 CrossRef.
- J. Groenewold and W. K. Kegel, J. Phys. Chem. B, 2001, 105, 11702–11709 CrossRef CAS.
- Y. Liu, W.-R. Chen and S.-H. Chen, J. Chem. Phys., 2005, 122, 044507 CrossRef.
- S. Mossa, F. Sciortino, P. Tartaglia and E. Zaccarelli, Langmuir, 2004, 20, 10756–10763 CrossRef CAS.
- A. Stradner, H. Sedgwick, F. Cardinaux, W. C. K. Poon, S. U. Egelhaaf and P. Schurtenberger, Nature, 2004, 432, 492–495 CrossRef CAS.
- D. Kashchiev, J. Chem. Phys., 2003, 118, 1837–1851 CrossRef CAS.
- W. J. Fredericks, M. C. Hammonds, S. B. Howard and F. Rosenberger, J. Cryst. Growth, 1994, 141, 183–192 CrossRef CAS.
- L. F. Filobelo, O. Galkin and P. G. Vekilov, J. Chem. Phys., 2005, 123, 014904 CrossRef.
- A. A. Chernov, Modern Crystallography III, Crystal Growth,, Springer, Berlin, 1984 Search PubMed.
- M. A. Lauffer, Mol. Biol. Biophys., 1975, 20, 1–264 Search PubMed.
- A. Hill, Nature, 1990, 348, 426–428 CrossRef.
- A. G. Walton, in Nucleation, ed. A. C. Zettlemoyer, Marcel Dekker, New York, 1969, pp. 225–307 Search PubMed.
- A. Fersht, Structure and mechanism in protein science, W.H. Freeman, New York, 1999 Search PubMed.
- M. D. Hollingsworth, Science, 2002, 295, 2410–2413 CAS.
- J. S. Lee, Y.-J. Lee, E. L. Tae, Y. S. Park and K. B. Yoon, Science, 2003, 301, 818–821 CrossRef CAS.
- A. McPherson and P. Shlichta, J. Cryst. Growth, 1988, 90, 47–50 CrossRef CAS.
- S. A. Hemming, A. Bochkarev, S. A. Darst, R. D. Kornberg, P. Ala, D. S. Yang and A. M. Edwards, J. Mol. Biol., 1995, 246, 308–316 CrossRef CAS.
- B. Garetz, J. Matic and A. Myerson, Phys. Rev. Lett., 2002, 89, 175501 CrossRef.
- Y. G. Kuznetsov, A. J. Malkin and A. McPherson, J. Cryst. Growth, 2001, 232, 30–39 CrossRef CAS.
- O. Galkin, R. L. Nagel and P. G. Vekilov, J. Mol. Biol., 2007, 365, 425–439 CrossRef CAS.
- O. Galkin, W. Pan, L. Filobelo, R. E. Hirsch, R. L. Nagel and P. G. Vekilov, Biophys. J., 2007, 93, 902–913 CrossRef CAS.
- A. Lomakin, D. S. Chung, G. B. Benedek, D. A. Kirschner and D. B. Teplow, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 1125–1129 CrossRef CAS.
- R. Krishnan and S. L. Lindquist, Nature, 2005, 435, 765–772 CrossRef CAS.
- J. E. Aber, S. Arnold and B. A. Garetz, Phys. Rev. Lett., 2005, 94, 145503 CrossRef.
- M. E. Leunissen, C. G. Christova, A.-P. Hynninen, C. P. Royall, A. I. Campbell, A. Imhof, M. Dijkstra, R. van Roij and A. van Blaaderen, Nature, 2005, 437, 235–240 CrossRef CAS.
- J. R. Savage and A. D. Dinsmore, Phys. Rev. Lett., 2009, 102, 198302 CrossRef CAS.
- T. H. Zhang and X. Y. Liu, J. Phys. Chem. B, 2007, 111, 14001–14005 CrossRef CAS.
- L. B. Gower, Chem. Rev., 2008, 108, 4551–4627 CrossRef CAS.
- E. M. Pouget, P. H. H. Bomans, J. Goos, P. M. Frederik, G. de With and N. Sommerdijk, Science, 2009, 323, 1455–1458 CrossRef CAS.
- D. Gebauer, A. Volkel and H. Colfen, Science, 2008, 322, 1819–1822 CrossRef CAS.
- R. P. Sear, J. Chem. Phys., 2009, 131, 074702 CrossRef.
- J. F. Lutsko and G. Nicolis, Phys. Rev. Lett., 2006, 96, 046102 CrossRef.
- E. Cacioppo and M. L. Pusey, J. Cryst. Growth, 1991, 114, 286–292 CrossRef CAS.
- S. B. Howard, P. J. Twigg, J. K. Baird and E. J. Meehan, J. Cryst. Growth, 1988, 90, 94–104 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2010 |
