The nucleation kinetics of ZnO nanoparticles from ZnCl2 in ethanol solutions†
A. G.
Vega-Poot
a,
G.
Rodríguez-Gattorno
*ab,
O. E.
Soberanis-Domínguez
a,
R. T.
Patiño-Díaz
a,
M.
Espinosa-Pesqueira
c and
G.
Oskam
*a
aDepartamento de Física Aplicada, CINVESTAV-IPN, Merida, Yucatán 97310, Mexico
bCentro de Investigación en Ciencia Aplicada y Tecnología Avanzada, Instituto Politécnico Nacional, Irrigación, Mexico, D.F., 11500, Mexico
cDepartamento de Tecnología de Materiales, Instituto Nacional de Investigaciones Nucleares (ININ), Ocoyoacac, Mexico, D.F., 52750, Mexico
First published on 28th September 2010
Abstract
The first stages of the synthesis of ZnO nanoparticles by forced hydrolysis of ZnCl2 with NaOH and water in ethanol have been investigated using UV-Vis spectrophotometry. At sufficiently low water concentrations, focusing of the nanoparticle size distribution was observed during the nucleation and growth phase, followed by a defocusing phase when coarsening becomes significant. During nucleation and growth, only the smaller particles grow while the larger particles have an essentially zero growth rate, indicating that the growth rate decreases rapidly with particle size. As the average particle size remains nearly constant in this regime, the absorbance increase with time can be used to determine the nucleation rate. The nucleation rate was found to depend on both the water concentration and the reactant concentrations. The results are discussed in terms of a mechanism where water determines the precursor formation kinetics thus controlling the nucleation rate.
1. Introduction
Several solution-phase routes to the synthesis of zinc oxide nanoparticles and nano-architectures have been reported, based on either hydrolysis of a zinc salt in an organic solvent1–13 or non-hydrolytic methods.14–17 The main steps during a precipitation synthesis can be summarized as follows: (i) precursor formation (e.g. neutralization reactions), (ii) nucleation, (iii) growth, and (iv) aging processes such as aggregation and coarsening.9,18,19 The degree of overlap of these processes is an essential reaction parameter that determines the ability to control the particle shape, morphology, and size distribution. In order to tailor the properties of the nanomaterial to specific applications, it is essential to develop a fundamental understanding of the different processes that lead to particle formation and their kinetics. UV-Vis spectrophotometry has provided a fast and reliable tool to determine the ZnO nanoparticle growth kinetics, due to the dependence of the optical band gap on the nanoparticle size up to relatively large dimensions. However, because of the nature of reactions involved (e.g. acid–base reactions), the kinetics of the processes during the first three stages of colloidal synthesis are usually fast, and it has been difficult to observe the nucleation and growth processes. The aging processes have been studied in detail, and in previous work the effects of the anion of the zinc salt, the solvent, and the hydroxide-providing reagent on the coarsening kinetics have been reported.2–8 In addition, it was shown that oriented attachment processes can affect the aging kinetics.16,20,21The mechanism of nanoparticle formation and the associated kinetics can be envisaged to involve the formation of zero-charge precursor molecules Znn(OH)m(H2O)lLk, where L is a ligand, and subsequent homogeneous nucleation. For the system of zinc acetate in ethanol using LiOH, the complex nature of the precursor chemistry has been convincingly shown, and the simultaneous presence of ZnO nanoparticles, a zinc double hydroxide salt (Zn-HDS), as well as precursor molecules as mentioned above was illustrated.22–24
In classical nucleation theory, the nucleation rate, J, is determined by an Arrhenius-type rate constant containing the Gibbs free energy needed to form a nucleus of critical size, ΔG*:
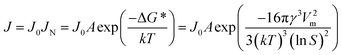 | (1) |
The chemical reaction for the colloidal synthesis of ZnO from ZnCl2 and NaOH in ethanol with a low concentration of water can be represented as follows:
| nZnCl2 + 2nNaOH + lH2O → Zn2+n(OH−)m(H2O)lCl−k + (2n − k) Cl− + (2n − m) OH− + 2nNa+ → nZnO + (l + n) H2O + 2nNaCl | (2) |
Note that the intermediate steps in the reaction are not conveyed by eqn (2). The zinc–ligands molecule can be seen as the precursor for nucleation, and in the case of a zero-charge precursor for homogeneous nucleation, 2n = m + k.
If the precursor formation kinetics are fast, the supersaturation increases strongly with time and, at a certain nucleation threshold, a burst of nucleation takes place. Depending on the relative velocities of precursor formation and nucleation, as well as the total amount of materials present in the system, the supersaturation decreases, thus slowing down and eventually halting nucleation. For a system where the precursor formation kinetics are slow, nucleation may take place at an essentially constant supersaturation for a prolonged period of time. In this paper, we show experimental evidence that the nucleation kinetics of ZnO nanoparticles from ZnCl2, NaOH, and water in ethanol solution are determined by the precursor formation kinetics. Experimental results show that it is possible to effectively decouple the nucleation and growth processes by tuning the water concentration.
2. Experimental details
The synthesis pathway used is based on classical forced hydrolysis starting from ZnCl2 and NaOH in the presence of a controlled amount of water, using ethanol as solvent. Stock solutions of 0.4 M ZnCl2 (Aldrich, 99.9%) and 0.2 M NaOH (Aldrich 99.9%) are prepared in ethanol (J. T. Baker, anhydrous absolute ethanol, 99.9%) by ultrasonic dispersion of the solids for 5 min followed by heating at 60 °C for 20 min. The required volumes of the reactants are separately transferred to similar quantities of the solvent (25 mL) to obtain the desired concentrations of ZnCl2 and NaOH in separate recipients. The solutions are mixed under controlled, vigorous stirring at room temperature (22.5 °C). In a series of experiments under the same conditions, this procedure guarantees reproducibility with a typical standard deviation of ±0.025 absorbance units at the absorbance maximum in the UV-Vis spectra. The time evolution of the UV-Vis absorbance spectra was followed with an Agilent 8453 UV-Vis diode array spectrophotometer. In order to verify that the synthesis results in a colloid of nanoparticles, high-resolution TEM (HRTEM) was performed. The images were obtained on a JEM 2010 microscope by allowing evaporation of a drop of a dilute colloid on HC-coated Cu grids.3. Results and discussion
The particle size and particle size distribution of a colloidal dispersion of ZnO nanoparticles can be obtained from UV-Vis absorbance spectra due to the dependence of the optical transition energy on the particle size. The relation between particle radius, r, and optical transition energy, ΔEg, can be estimated using the effective mass model developed by Brus:31,32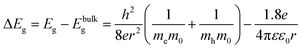 | (3) |
The absorbance, A, of a colloidal system is related to the extinction coefficient, which for the case of colloids has an implicit dependence on the nature of the material (optical constants), the mean particle size and size distribution.33,34 The extinction coefficient results mainly from the sum of two contributions, the absorption coefficient and the scattering coefficient. The scattering coefficient can usually be neglected when the particles are much smaller than the measurement wavelength, and the absorption coefficient of each particle can be described as proportional to the volume of the particle. In this case, the absorbance of a colloidal solution is proportional to the total volume of the ZnO nanomaterial formed, i.e., the sum of the volumes of all particles. For a colloidal dispersion with a single size of metal oxide semiconducting nanoparticles, the absorbance edge, λg, of the absorbance spectrum is generally used to estimate the particle size from eqn (3). When there is a distribution of particle sizes, the wavelength at the half of the absorbance maximum, λ1/2, is a better criterion as it represents the mean particle size; in this case, the absorbance spectrum is a result of the combined contributions from each particle size in a specific particle size distribution.34–36 Taking these considerations into account and assuming that particles are spherical, a given particle size distribution N(r) modulates an absorbance spectrum of a colloidal dispersion according to:35,37
 | (4) |
In Fig. 1a, a TEM image is shown illustrating that the average ZnO nanoparticle size is on the order of 5–6 nm, and a comparison between TEM results and the nanoparticle size distribution obtained using the effective mass model shows a decent match as illustrated in Fig. 1b, using eqn (3) with me = 0.26, mh = 0.59, Egbulk = 3.2 eV and ε = 8.5; the relation between wavelength and radius depends strongly on the values used for these parameters, however, and the model is mainly used here as a guideline to report trends. No evidence of a significant contribution of oriented attachment was found in the analyzed micrographs.
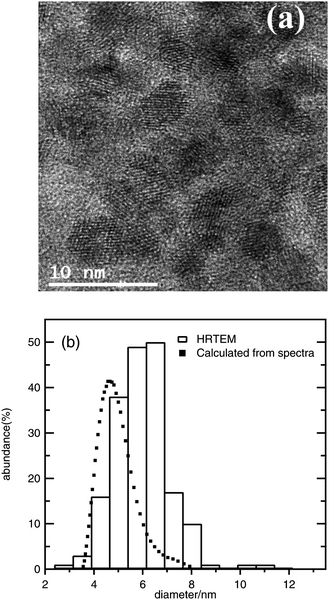 | ||
| Fig. 1 (a) Typical HRTEM micrograph of ZnO nanoparticles obtained from 1 mM ZnCl2, 1.6 mM NaOH, and 100 mM H2O in ethanol (after 48 h); (b) comparison between the particle size distribution obtained from HRTEM observations and the distribution calculated from UV-Vis spectra for the same sample. | ||
Fig. 2 shows a representative series of absorbance spectra as function of time during ZnO nanoparticle synthesis using as starting reagents 1 mM ZnCl2, 1.6 mM NaOH, and 50 mM H2O. It can be observed from Fig. 2a and b that the absorbance maximum increases with time, which is related to the increase of the amount of ZnO formed, until it reaches a maximum after about 80 minutes; at this point, the reaction is complete. Since the total amount of ZnO formed depends on both the number of nanoparticles and the nanoparticle size, from these results alone it is not possible to determine if the reaction proceeds by formation of more nanoparticles or growth of already nucleated particles.38 In order to distinguish between nucleation and growth, the average particle size can be simultaneously determined from the absorbance spectrum from the wavelength at half of the maximum absorbance, λ1/2. It can be observed in Fig. 2a and c that there is a period of time of about 50 min in which λ1/2 is essentially independent of time.
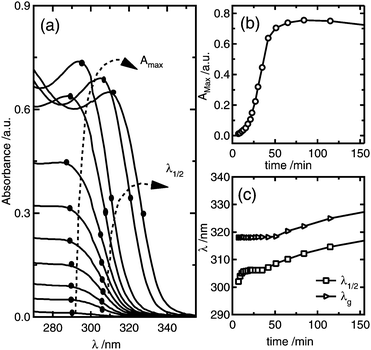 | ||
| Fig. 2 (a) Time dependence of the absorbance spectra for the colloidal synthesis of ZnO nanoparticles from 1 mM ZnCl2, 1.6 mM NaOH, and 50 mM H2O; the dots and dashed arrows indicate the evolution of the absorbance maximum and wavelength values at half of the absorbance maximum, λ1/2. (b) shows the absorbance maximum versus reaction time, while (c) shows the time evolution of λ1/2 and the absorption edge λg. | ||
These results indicate that during this period, the average particle size remains constant and, hence, that the increase in the absorbance maximum is mainly due to the nucleation of more nanoparticles. As a consequence, a unique situation is found where the nucleation reaction is essentially decoupled from growth during a certain period of time, where the slope of the absorbance maximum vs. time curve is directly proportional to nucleation rate. Hence, the time dependence of the absorbance maximum can be used as a chronomal variable having the information of the advance of the nucleation reaction by taking the derivate of the time dependence of the absorbance at λ1/2 constant.39 The nucleation rate with dimensions of number of particles per unit time per unit volume in the time range where λ1/2 is constant can be calculated as follows:
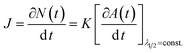 | (5) |
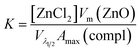 | (6) |
The results from Fig. 2 were analyzed in more detail using eqn (4)–(6), in order to relate the particle size distribution evolution to the nucleation and growth kinetics. Fig. 3a shows the particle size distribution as a function of the reaction time. Initially, the total number of particles in the size distribution increases while maintaining the same average particle size, which corresponds to the period where mainly nucleation occurs. At a certain time, the average particle size starts increasing, and the size distribution starts to widen. This is shown in more detail in Fig. 3b, where the average particle size, as well as the particle sizes at half of the maximum of the size distribution on both sides of the distribution (see the inset in Fig. 3a) are shown versus time. From this figure, it can be concluded that when mainly nucleation occurs, the size distribution focuses with time, as the smaller particles grow up to a certain size, while the larger particles do not grow noticeably. This focusing mechanism results in a narrowing of the size distribution to a relative width, defined by the fwhm divided by the average particle size, from 21% at the onset of the focusing process down to 16% at the end of the nucleation period, corresponding to a 25% decrease of the distribution width. After this period, the size distribution widens as the average particle size increases with time, although the relative distribution width increases only weakly, in accordance with predictions for the coarsening process.29,40 These observations are similar to results reported for III–V and II–VI semiconductor nanoparticles, where the focusing–defocusing processes were explained by a slowing down of the growth kinetics with increasing particle size.19,25 This explanation is also in accordance with the apparent decoupling of nucleation and growth, and the observation of a certain unique particle size, as the growth kinetics for particles close to that size have slowed down significantly compared to the nucleation kinetics. From these results, it appears that the competition for precursor molecules between the nucleation and growth processes is affected by an inhibition of growth at a certain particle size, thus allowing nucleation to proceed with imperceptible growth of the larger particles. Note that this focusing model has generally been reported for systems where the particle density is essentially constant during growth. The results presented here illustrate that focusing can also be observed when nucleation is the main process and growth is very slow for the larger particles.
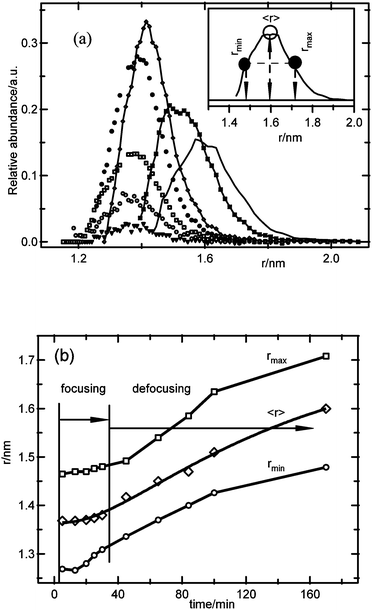 | ||
| Fig. 3 (a) Calculated particle size distributions for ZnO obtained from 1 mM ZnCl2, 1.6 mM NaOH, and 50 mM H2O; the inset illustrates the definitions of rmax, rmin and 〈r〉. (b) Average particle size and the particle size values at half-width of the size distributions versus time, illustrating the focusing–defocusing phenomena during the nucleation and growth stage, and after the onset of coarsening processes, respectively. | ||
The nucleation rate was found to depend strongly on the water concentration used in the synthesis; without any added water, ZnO was not formed even after several days. A series of experiments were performed at fixed [ZnCl2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NaOH] ratio (1
[NaOH] ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6) and changing the water concentration from 25 mM to 200 mM. Fig. 4a shows the reaction time dependence of the absorbance maximum, illustrating that with increasing water concentration, the absorbance maximum reaches a saturation value at shorter times, corresponding to an increase in the rate of formation of ZnO nanomaterial.
1.6) and changing the water concentration from 25 mM to 200 mM. Fig. 4a shows the reaction time dependence of the absorbance maximum, illustrating that with increasing water concentration, the absorbance maximum reaches a saturation value at shorter times, corresponding to an increase in the rate of formation of ZnO nanomaterial.
![Time dependence of (a) absorbance maximum and (b) λ1/2, for different water concentrations during ZnO nanoparticle formation using a constant [ZnCl2] : [NaOH] ratio of 1 : 1.6; (c) dependence of the nucleation rate on water concentration for the time period where λ1/2 is constant, determined from the slope of the Amaxvs. time curve.](/image/article/2010/NR/c0nr00439a/c0nr00439a-f4.gif) | ||
Fig. 4 Time dependence of (a) absorbance maximum and (b) λ1/2, for different water concentrations during ZnO nanoparticle formation using a constant [ZnCl2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NaOH] ratio of 1 [NaOH] ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6; (c) dependence of the nucleation rate on water concentration for the time period where λ1/2 is constant, determined from the slope of the Amaxvs. time curve. 1.6; (c) dependence of the nucleation rate on water concentration for the time period where λ1/2 is constant, determined from the slope of the Amaxvs. time curve. | ||
Fig. 4b illustrates that λ1/2 shows a plateau at a wavelength of about 306 nm, where the average particle size remains constant with reaction time, however, the width of the plateau depends on the water concentration used in the synthesis. At water concentrations higher than 50 mM, there is essentially no plateau (within the resolution of the measurements which is on the order of 10 s, related to taking the sample, adjustment of the concentration, and measurement), while a 3 hours wide plateau is observed for the synthesis employing 25 mM water. Comparing with Fig. 4a, the time period of the plateau coincides with the observation of a steady increase of the absorbance with time, indicating that the slope of the absorbance versus time curve describes the nucleation kinetics. It can be concluded that the nucleation rate increases with increasing water concentration. The plateau value of 306–308 nm implies that the mean particle diameter of ZnO nuclei during this period is around 2.6 nm according to eqn (3), which agrees with a particle model formed by 306 ZnO4 tetrahedrons condensed in a ZnO wurtzite structure (assuming equal dimensions along the three axis). Interestingly, this particle size is independent of the water concentration, while the nucleation kinetics are strongly dependent on water concentration. The existence of a unique particle size generally implies a higher stability of the cluster compared to the stability of clusters with a couple of monomers more or less incorporated. In some cases, the existence of a unique particle size may be associated to the critical nucleus size, as given by the Gibbs–Kelvin equation. However, in these experiments, the unique size is defined as the average particle size, and is more likely related to a relative inhibition of growth of the larger particles in a water deficient environment, or aging processes that depend on particle size, for example, the onset of faceting or renucleation.
Fig. 4c shows the calculated values of the nucleation rate versus water concentration for the time period where λ1/2 is constant. The nucleation rate, J, is found to be linear with water concentration:
| Jλ1/2=const. = 5.3 × 1016 [H2O] − 1.2 × 1015 | (7) |
After the nucleation and growth processes have completed, aging processes such as aggregation and coarsening modify the average particle size and particle size distribution. In previous work, diffusion limited coarsening was shown to adequately describe the evolution of the average particle size with time, resulting in the average particle volume being proportional with time.2–8 However, it has been shown that a partial kinetics limitation cannot be excluded in many of these cases and that the incorporation of monomers for larger particles can be slow.10,11
Fig. 5 shows the particle size, r3, obtained versus time for the results shown in Fig. 4, using eqn (3).4–9 After an initial period, approximately linear behavior is observed, and the inset shows that the rate constant given by the slope of the indicated lines is essentially independent of the water concentration. It can be concluded that the water concentration strongly affects the nucleation kinetics, while the coarsening kinetics are insensitive to the water content.
![Time dependence of radius as r3vs. time for different water contents at a fixed [ZnCl2] : [NaOH] ratio of 1 : 1.6. The inset shows the calculated coarsening rate constants.](/image/article/2010/NR/c0nr00439a/c0nr00439a-f5.gif) | ||
Fig. 5 Time dependence of radius as r3vs. time for different water contents at a fixed [ZnCl2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NaOH] ratio of 1 [NaOH] ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6. The inset shows the calculated coarsening rate constants. 1.6. The inset shows the calculated coarsening rate constants. | ||
With the purpose of establishing how the [ZnCl2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NaOH] ratio influences the kinetics of the various processes, a series of experiments were carried out at a constant water concentration of 100 mM, while the [ZnCl2]
[NaOH] ratio influences the kinetics of the various processes, a series of experiments were carried out at a constant water concentration of 100 mM, while the [ZnCl2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NaOH] ratio was varied from 0.5 to 2. The time-dependence of the absorbance maximum and λ1/2 are shown in the ESI†, and the results can be summarized as follows: (i) the completeness of reaction is determined only by the NaOH concentration, i.e., the excess of ZnCl2 is not converted to ZnO by reaction with water; (ii) the time dependence of the λ1/2 values is essentially independent of the NaOH concentration, hence, nucleation, growth and/or coarsening do not seem to be affected by under-stoichiometric conditions. It should be noted that ratios of [ZnCl2]
[NaOH] ratio was varied from 0.5 to 2. The time-dependence of the absorbance maximum and λ1/2 are shown in the ESI†, and the results can be summarized as follows: (i) the completeness of reaction is determined only by the NaOH concentration, i.e., the excess of ZnCl2 is not converted to ZnO by reaction with water; (ii) the time dependence of the λ1/2 values is essentially independent of the NaOH concentration, hence, nucleation, growth and/or coarsening do not seem to be affected by under-stoichiometric conditions. It should be noted that ratios of [ZnCl2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NaOH] < 0.5 were not explored, because the existence of soluble species of zinc complexes with OH− at these ratios considerably modifies the solubility of ZnO.42
[NaOH] < 0.5 were not explored, because the existence of soluble species of zinc complexes with OH− at these ratios considerably modifies the solubility of ZnO.42
According to classical nucleation theory, the nucleation rate is expected to increase with increasing supersaturation, which can be achieved by increasing the precursor concentration or decreasing the solubility. From Fig. 4c it was concluded that the increase of the nucleation rate with increasing water concentration suggests that water affects the precursor formation kinetics. In order to study the influence of the precursor concentration on the nucleation kinetics, a series of experiments were carried out changing the reactant concentrations at a fixed ratio for [ZnCl2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NaOH]
[NaOH]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [H2O] of 1
[H2O] of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6
1.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50. It should be noted that without the knowledge of the chemical structure of the precursor, it is not possible to design an experiment where the precursor concentration is varied while maintaining the precursor chemistry the same. Fig. 6 shows the absorbance maximum and λ1/2 values versus time for four different reactant concentrations.
50. It should be noted that without the knowledge of the chemical structure of the precursor, it is not possible to design an experiment where the precursor concentration is varied while maintaining the precursor chemistry the same. Fig. 6 shows the absorbance maximum and λ1/2 values versus time for four different reactant concentrations.
 | ||
| Fig. 6 Time dependence of (a) the absorbance maximum, (b) λ1/2 for four different reactant concentrations. In (c), the dependence of the nucleation rate on the reactant concentrations for the time period where λ1/2 is constant is shown. | ||
Also in this case, related to the relatively low water concentration, a plateau is observed in the λ1/2versus time plot, indicating the existence of a unique size, which in addition to being independent of the water concentration (see Fig. 4) is also found to be independent of the reactant concentration. During the period where the average particle size is independent of time, the apparent nucleation rate can be obtained. Interestingly, in this case the plateau width is independent of the reactant concentration, and for the lowest concentrations, the plateau width is much smaller than the time needed to reach the maximum absorbance value, indicating pure nucleation is only observed for a limited period of time, at the onset of nucleation. Fig. 6c shows the nucleation rate versus the reactant concentration, illustrating an approximate proportionality with the reactant concentrations (J ≥ 0):
| Jλ1/2=const. = 7.7 × 1017 [ZnCl2] − 5.3 × 1014 | (8) |
| Jλ1/2=const. = 1.5 × 1016 [H2O] − 5.3 × 1014 | (9) |
| Jλ1/2=const. = 4.8 × 1017 [NaOH] − 5.3 × 1014 | (10) |
As observed for the results in Fig. 4c, the nucleation rate is zero for a certain critical reactant concentration. Fig. 7 shows the dependence of the nucleation rate on the water concentration from the two experiments that were performed: (A) changing the water concentration, while keeping the ZnCl2 and NaOH concentrations constant, and (B) changing the water concentration, and also changing the ZnCl2 and NaOH concentrations by the same factor. Analyzing the dependence of the nucleation rate on the water concentration from experiment B (eqn (9)), it is found that the slope is a factor 3.3 smaller than for the results of experiment A (eqn (7)). In addition, the water concentration where the nucleation rate is zero is at a somewhat higher water concentration of 35 mM for experiment B. These results indicate that the nucleation kinetics do not only depend on the water concentration, but also have an additional dependence on the reactant concentrations.
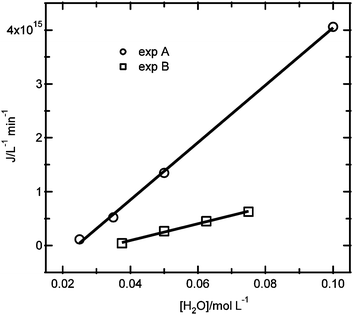 | ||
| Fig. 7 Comparison between the nucleation rate as a function of the water concentration for the experiments with constant ZnCl2 and NaOH concentrations (exp A) and for the experiments with varying ZnCl2, NaOH and H2O concentrations at a fixed ratio (exp B). | ||
Although it is not clear whether the precursor chemistry changes in these experiments, it is interesting to note that the nucleation rate is a much stronger function of the water concentration than of the combined reactant concentrations, illustrating it is likely that the precursor formation kinetics may strongly affect the nucleation kinetics. The unknown chemical composition of the precursor complicates the experimental design to adequately obtain reaction orders: a combinatorial approach would be needed to resolve these ambiguities.
In summary, a comparative study was performed of the formation kinetics of ZnO nanoparticles by controlling the reactant concentrations and the amount of water in the system. At sufficiently low water concentration, the nucleation rate of ZnO nanoparticles was obtained in a regime where the average particle size was independent of time, related to the observation that the growth rate of larger particles was essentially zero, and only the smallest particles were growing, thus focusing the size distribution by about 25%. When coarsening becomes important, the size distribution defocuses somewhat, in agreement with previous reports in the literature. The nucleation rate was found to be proportional to the water concentration in this regime, independently of whether the reactant concentrations were constant or modified, however, the nucleation rate was strongly affected by the reactant concentrations. In all experiments, the coarsening rate was found to be essentially independent of the water concentration and the [ZnCl2]/[NaOH] ratio. Overall, the results indicate that the nucleation kinetics are likely determined by the chemical mechanisms and kinetics for precursor formation rather than the supersaturation.
Acknowledgements
This work was supported by the Consejo Nacional de Ciencia y Tecnología (CONACYT, Mexico) under Grant No. 80002. GRG thanks CINVESTAV and CONACYT for a post-doctoral scholarship.References
- X. Y. Kong and Z. L. Wang, Spontaneous polarization-induced nanohelices, nanosprings, and nanorings of piezoelectric nanobelts, Nano Lett., 2003, 3, 1625–1631 CrossRef CAS.
- G. Oskam, Z. S. Hu, R. L. Penn, N. Pesika and P. C. Searson, Coarsening of metal nanoparticles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011403 CrossRef.
- Z. S. Hu, G. Oskam, R. L. Penn, N. Pesika and P. C. Searson, The influence of anion on the coarsening kinetics of ZnO nanoparticles, J. Phys. Chem. B, 2003, 107, 3124–3130 CrossRef CAS.
- Z. S. Hu, G. Oskam and P. C. Searson, Influence of solvent on the growth of ZnO nanoparticles, J. Colloid Interface Sci., 2003, 263, 454–460 CrossRef CAS.
- Z. S. Hu, D. J. Escamilla-Ramirez, B. E. Heredia-Cervera, G. Oskam and P. C. Searson, Synthesis of ZnO nanoparticles in 2-propanol by reaction with water, J. Phys. Chem. B, 2005, 109, 11209–11214 CrossRef CAS.
- Z. S. Hu, J. F. Herrera-Santos, G. Oskam and P. C. Searson, Influence of the reactant concentrations on the synthesis of ZnO nanoparticles, J. Colloid Interface Sci., 2005, 288, 313–316 CrossRef CAS.
- G. Oskam and F. D. P. Poot, Synthesis of ZnO and TiO2 nanoparticles, J. Am. Chem. Soc., 2006, 37, 157–160 CAS.
- G. Rodríguez-Gattorno, P. Santiago-Jacinto, L. Rendon-Vázquez, J. Németh, I. Dékany and D. Díaz, Novel synthesis pathway of ZnO nanoparticles from the spontaneous hydrolysis of zinc carboxylate salts, J. Phys. Chem. B, 2003, 107, 12597–12604 CrossRef CAS.
- L. Spanhel, Colloidal ZnO nanostructures and functional coating: a survey, J. Sol-Gel Sci. Technol., 2006, 39, 7–24 CrossRef CAS.
- R. Viswanatha, H. Amenitsch and D. Sarma, Growth kinetics of ZnO nanocrystals: a few surprises, J. Am. Chem. Soc., 2007, 129, 4470–4475 CrossRef CAS.
- R. Viswanatha, P. K. Santra, C. Dasgupta and D. D. Sarma, Growth mechanism of nanocrystals in solution: ZnO, a case study, Phys. Rev. Lett., 2007, 98, 255501 CrossRef.
- A. S. Ratkovich and R. L. Penn, Controlling nanosized ZnO growth kinetics using various Zn:OH concentration ratios, J. Phys. Chem. C, 2007, 111, 14098–14104 CrossRef CAS.
- A. Ratkovich and R. L. Penn, Zinc oxide nanoparticle growth from homogenous solution: influence of Zn:OH, water concentration, and surfactant additives, Mater. Res. Bull., 2009, 44, 993–998 CrossRef CAS.
- T. Andelman, Y. Gong, M. Polking, M. Yin, I. Kuskovsky, G. Neumark and S. O'Brien, Morphological control and photoluminescence of zinc oxide nanocrystals, J. Phys. Chem. B, 2005, 109, 14314–14318 CrossRef CAS.
- S. Choi, E. Kim, J. Park, K. An, N. Lee, S. C. Kim and T. Hyeon, Large-scale synthesis of hexagonal pyramid-shaped ZnO nanocrystals from thermolysis of zinc–oleate complex, J. Phys. Chem. B, 2005, 109, 14792–14794 CrossRef CAS.
- P. D. Cozzoli, M. L. Curri and A. Agostiano, ZnO nanocrystals by a non-hydrolytic route: synthesis and characterization, J. Phys. Chem. B, 2003, 107, 4756–4752 CrossRef CAS.
- Y. Chen, M. Kim, G. Lian, M. B. Johnson and X. Peng, Side reactions in controlling the quality, yield, and stability of high quality colloidal nanocrystals, J. Am. Chem. Soc., 2005, 127, 13331–13337 CrossRef CAS.
- J.-P. Jolivet, Metal Oxide Chemistry and Synthesis—from Solution to Solid State, Wiley, New York, 2003 Search PubMed.
- T. Sugimoto, Preparation of monodispersed colloidal particles, Adv. Colloid Interface Sci., 1987, 28, 65–108 CAS.
- C. Pacholski, A. Kornowski and H. Weller, Self-assembly of ZnO: from nanodots to nanorods, Angew. Chem., Int. Ed., 2002, 41, 1188–1191 CrossRef CAS.
- R. L. Penn, Kinetics of oriented aggregation, J. Phys. Chem. B, 2004, 108, 12707–12712 CrossRef CAS.
- V. Briois, Ch. Giorgetti, F. Baudelet, S. Blanchandin, M. S. Tokumoto, S. H. Pulcinelli and C. V. Santilli, Dynamical study of ZnO nanocrystal and Zn-HDS layered basic zinc acetate formation from sol–gel route, J. Phys. Chem. C, 2007, 111, 3253–3258 CrossRef CAS.
- M. S. Tokumoto, V. Briois, C. V. Santilli and S. H. Pulcinelli, Preparation of ZnO nanoparticles: structural study of the molecular precursor, J. Sol-Gel Sci. Technol., 2003, 26, 547–551 CrossRef CAS.
- M. S. Tokumoto, S. H. Pulcinelli, C. V. Santilli and V. Briois, Catalysis and temperature dependence on the formation of ZnO nanoparticles and of zinc acetate derivatives prepared by sol–gel route, J. Phys. Chem. B, 2003, 107, 568–574 CrossRef CAS.
- J. Y. Rempel, M. G. Bawendi and K. F. Jensen, Insight into the kinetics of semiconductor nanocrystal nucleation and growth, J. Am. Chem. Soc., 2009, 131, 4479–4489 CrossRef CAS.
- X. Peng, An essay on synthetic chemistry of colloidal nanocrystals, Nano Res., 2009, 2, 425–447 Search PubMed.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Nucleation of crystals from solution: classical and two-step models, Acc. Chem. Res., 2009, 42, 621–629 CrossRef CAS.
- J. Y. Rempel, M. G. Bawendi and K. F. Jensen, Kinetics of II–VI and III–V colloidal semiconductor nanocrystal growth: focusing of size distribution, J. Am. Chem. Soc., 1998, 120, 5343–5344 CrossRef CAS.
- D. V. Talapin, A. L. Rogach, M. Haase and H. Weller, Evolution of an ensemble of nanoparticles in a colloidal solution: theoretical study, J. Phys. Chem. B, 2001, 105, 12278–12285 CrossRef CAS.
- D. Gebauer, A. Völkel and H. Cölfen, Stable prenucleation calcium carbonate clusters, Science, 2008, 322, 1819–1822 CrossRef CAS.
- L. E. Brus, Electron–electron and electron–hole interactions in small semiconductor crystallites: the size dependence of the lowest excited electronic state, J. Chem. Phys., 1984, 80, 4403–4409 CrossRef CAS.
- L. E. Brus, Electronic wave functions in semiconductor clusters: experiment and theory, J. Phys. Chem., 1986, 90, 2555–2560 CrossRef CAS.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, New York, 1983 Search PubMed.
- H. C. Van de Hulst, Light Scattering by Small Particles, Dover Publications, Inc., New York, 1981 Search PubMed.
- N. S. Pesika, K. J. Stebe and P. C. Searson, Relationship between absorbance spectra and particle size distributions for quantum-sized nanocrystals, J. Phys. Chem. B, 2003, 107, 10412–10415 CrossRef CAS.
- E. A. Meulenkamp, Synthesis and growth of ZnO nanoparticles, J. Phys. Chem. B, 1998, 102, 5566–5572 CrossRef CAS.
- N. S. Pesika, K. J. Stebe and P. C. Searson, Determination of the particle size distribution of quantum nanocrystals from absorbance spectra, Adv. Mater., 2003, 15, 1289–1291 CrossRef CAS.
- L. Qu, W. W. Yu and X. Peng, In situ observation of the nucleation and growth of CdSe nanocrystals, Nano Lett., 2004, 4, 465–469 CrossRef CAS.
- A. E. Nielsen, Kinetics of Precipitation, Mc Millan Co & Pergamon Press Ltd., Oxford, UK, 1964, pp. 53–65 Search PubMed.
- E. M. Wong, J. E. Bonevich and P. C. Searson, Growth kinetics of nanocrystalline ZnO particles from colloidal suspensions, J. Phys. Chem. B, 1998, 102, 7770–7775 CrossRef CAS.
- M. Haase, H. Weller and A. Henglein, Photochemistry and radiation chemistry of colloidal semiconductors. 23. electron storage on ZnO particles and size quantization, J. Phys. Chem., 1988, 92, 482–487 CrossRef CAS.
- P. Bénézeth, D. A. Palmer, D. J. Wesolowski and C. Xiao, New measurements of the solubility of zinc oxide from 150 to 350 °C, J. Solution Chem., 2002, 31, 947–973 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Figures illustrating the time dependence of (a) the absorbance maximum and (b) λ1/2 for different [NaOH]/[ZnCl2] ratios at a fixed water concentration of 100 mM and 1 mM ZnCl. See DOI: 10.1039/c0nr00439a |
| This journal is © The Royal Society of Chemistry 2010 |
