Analytical ultracentrifugation of colloids†
Karel L.
Planken
*a and
Helmut
Cölfen
*b
aMax-Planck-Institute of Colloids and Interfaces, Colloid Chemistry, Research Campus Golm, Am Mühlenberg, D-14424, Potsdam, Germany. E-mail: karel.planken@mpikg.mpg.de; Fax: ++49-331-567-9502
bMax-Planck-Institute of Colloids and Interfaces, Colloid Chemistry, Research Campus Golm, Am Mühlenberg, D-14424, Potsdam, Germany. E-mail: Coelfen@mpikg.mpg.de; Fax: ++49-331-567-9502
First published on 6th September 2010
Abstract
In this contribution the use of Analytical Ultracentrifugation (AUC) for the modern analysis of colloids is reviewed. Since AUC is a fractionation technique, distributions of the sedimentation coefficient, particle size and shape, molar mass and density can be obtained for particle sizes spanning the entire colloidal range. The Ångström resolution and the reliable statistics with which particle size distributions can be obtained from analytical ultracentrifugation makes this a high resolution analysis technique for the characterization of nanoparticles in solution or suspension. Several examples showing successful applications of AUC to complex problems in colloid science are given to illustrate the broad range and versatility of questions that can be answered by AUC experiments.
 Karel L. Planken | Karel L. Planken conducted his PhD research at the Van't Hoff Laboratory at the Utrecht University and graduated in 2008. His PhD thesis on analytical ultracentrifugation of interacting and non-interacting inorganic colloids brought him into the field of AUC. After a post-doc position at the Utrecht University he expanded his research employing a AUC equipped with a multi-wavelength detection system on quantum dots, gold dispersions and proteins at the Max Planck Institute for Colloids and Interfaces in Potsdam. In 2010 he joined Helmut Cölfen's group (Physical Chemistry) at the Konstanz University. |
 Helmut Cölfen | Helmut Cölfen completed his PhD on Analytical Ultracentrifugation of gels in 1993. After postdoctoral work on solution characterization of complex biopolymers at the National Centre for Macromolecular Hydrodynamics, he joined the Max Planck Institute of Colloids and Interfaces in Potsdam where he was leading the projects “Biomimetic Mineralization” and “Fractionating Colloid Analytics” in the colloid chemistry department. In 2010 he changed to the University of Konstanz as a professor of physical chemistry. His current research focuses on non-classical crystallization, pre-nucleation clusters and additive controlled crystallization as well as Analytical Ultracentrifugation. |
Introduction to AUC
Analytical ultracentrifugation (AUC) has been widely applied in biochemistry,1 biophysics and pharmacy.2 In these fields proteins, DNA and RNA as well as polysaccharides and their interactions are studied via sedimentation velocity (SV) and sedimentation–diffusion equilibrium (SE) ultracentrifugation.3,4 In physical and colloid chemistry AUC has been less extensively employed compared to the field of biophysics even though AUC was initially developed by Svedberg and co-workers5–7 in the nineteen twenties to study gold particle size distributions (psd).8 Svedberg was awarded the Nobel Prize for chemistry in 1926 for his work on disperse systems, employing among other techniques analytical ultracentrifugation.AUC experimental data provide a wealth of information on solution and dispersion composition.8 AUC allows the hydrodynamic and thermodynamic characterization of macromolecules or colloids in situ. Quantities obtained via AUC are, among others, sedimentation and diffusion coefficients, which are interdependent via the friction factor or, equivalently, via the frictional ratio f/f0. Molecular weights can be computed combining sedimentation and diffusion coefficients obtained from globally fitted multi-speed SV AUC experiments, provided the particle density is known. From sedimentation and diffusion coefficient pairs, parameters as particle shapes, hydrodynamic radii, molecular weights and shapes of particle size distributions for homogeneous and heterogeneous solutes or colloids (mono-, pauci- and polydisperse particles) can be obtained. Furthermore, SV and SE experiments are excellent tools for studying reversible association (equilibrium constants) or aggregation of particles. Experimental SV and SE data for interacting systems can be modeled to determine equilibrium constants. SV experimental data may, in contrast to SE experimental data, even yield information about reaction rate constants.
In this contribution the progress of soft- and hard-ware developments improving AUC are briefly discussed, followed by a description of suitable analysis methods applicable to different scenarios encountered in AUC of colloids, extending previous summaries on this topic.8–17
Since SV and density-gradient analytical ultracentrifugation experimental data contain and therefore offer the most information concerning colloidal dispersions, we will focus on these two methods, i.e. two fundamental AUC experiments.
Before proceeding to the progress in AUC we spend a few words on the working principle of an AUC. A common feature in AUC is the synchronization of events such as positioning the cell, computed from the angular rotor velocity and the timing for the right moment at which the optical signal is detected during data acquisition. Every event during analytical ultracentrifugation is synchronized with the revolution and position of the rotor. The rotor contains one or more samples for which the concentration distributions are to be measured as a function of the radial position and time. The synchronization is achieved by the detection of a small magnet implemented in the rotor. The location of rotor holes, containing AUC cell assemblies with reference and sample sectors, relative to the position of the magnet is achieved via a single delay-time calibration procedure. This delay-time calibration is performed when the rotor is accelerated to the intended angular velocity. Each rotor-hole position is then calculated from the magnet's position via delay-times. The radial calibration is obtained from the counterbalance that has two holes for which the absolute radial position is known.
Progress in AUC
In the last two decades substantial progress has been made regarding AUC. The progress made concerns data analysis software, triggered by the introduction of a new commercial AUC with digital data output18 as well as hardware improvements, predominantly the development of new and existing optical detection systems. In what follows, the progress in AUC is subdivided into soft- and hardware developments.We focus on the high-end analytical ultracentrifuges manufactured by Beckman Coulter. These ultracentrifuges have the largest range of rotational speeds and the digitized acquired data can be analyzed using third-party data analysis software including whole-boundary fitting routines. Besides the Beckman Coulter analytical ultracentrifuges, there are three other types of commercially available centrifuges, which are all bench-top instruments. These centrifuges are (i) the Brookhaven Instruments X-ray Disc Centrifuge (BI XDC), (ii) CPS Instruments Disc Centrifuge (CPS DC24000 UHR) and (iii) L.U.M. GmbH LUMiFuge/LUMiSizer analytical centrifuges. The latter centrifuge is not capable of performing sedimentation-diffusion equilibrium experiments. These three centrifuges offer similar particle characterization methods regarding the assessment of particle size distributions via sedimentation velocity experiments (see for example ref. 19). However, their rotor speeds are much more limited and the detection systems operate at a single fixed wavelength and therefore do not allow one to vary the wavelength with which the particles are detected. All three centrifuges comply to the ISO13318 (2001–2007) norm. Additionally, they are cheaper compared to the Beckman Coulter analytical ultracentrifuges.
Software developments
The software development is aided by the progresses of mathematical analysis20–30 and data-analysis software.27,31–38 With the latter references we restricted ourselves to SV AUC. See for example http://rasmb.bbri.org/software/(RASMB) for a list of available software as well as a discussion group for investigators in the field of AUC. Further development of data-analysis led to the implementation of relational data bases,27 laboratory information management systems (LIMS) and high throughput super computing40 using clusters that are connected via networks and the internet.The new type of analyses comprises the time derivative method,32 which is nowadays even available for the analysis of multi-speed experiments,34 analysis of continuous sedimentation coefficient distributions c(s),31 the 2-dimensional spectrum analysis40–42 and the genetic algorithm optimization routine for the analysis of SV AUC. The latter algorithm29 can also be used to globally fit multi-speed SV data to obtain via the determination of the sedimentation and diffusion coefficients accurate molecular weights (mono and paucidisperse systems only). Most of the commonly applied methods and software packages for the analysis of SV experiments proved to be well applicable for the characterization of nanoparticles.43
Hardware developments
In the early 1990s the Beckman Model E AUC available from 1947 was followed up by the Beckman Optima XL-A AUC (Beckman Coulter, Palo Alto CA USA).18 The introduction of the XL-A equipped with a precision absorption optical system (UV-Vis), enabling a analog-to-digital conversion data acquisition, was a crucial step forward. The Optima XL, however, is originally designed for preparative ultracentrifugation, something wich impedes the implementation of advanced optical detection systems. Later on, the XL-A was complemented by a Rayleigh interference optical system (XL-I), which provides great accuracy but cannot selectively discriminate between solution components as is possible with an absorption optics. Advantages of the interference optics are a much higher data density due to fast data acquisition and radial resolution, and everything that causes a refractive index difference is detected. This allows the determination of very precise particle size distributions, with an especially high resolution for small particles as is often necessary in the field of colloid science. In addition, to the interference optics, the Schlieren optics of the Model E AUC was transferred to an XL ultracentrifuge.16,44–46 Of special importance for the analysis of colloids—especially latex systems—turbidity optics was introduced into a preparative XL-ultracentrifuge.9,10,47,48 Using a speed profile, up to 8 dispersions can be investigated in the same experiment with sizes ranging from a few tens of nanometres to several micrometres.Furthermore there have been numerous attempts to improve and complement the existing XL-A/I AUC regarding the optical detection systems. For example larger photoelectric charged coupled device arrays for the absorption and interference optics as well as light scattering optics were introduced.49,50 Also the AUC sample holder components, e.g. centerpieces and additional masks for measuring with the interference optics, are subjected to improvements by other labs or companies.
Another exciting addition to the Optima XL ultracentrifuge is the development of a multi-wavelength optical detection system (MDS).50–52 This detection system is based on absorption optics but it allows radially scanning using many wavelengths within a range simultaneously, instead of a single wavelength as for the XL-A. Each scan can then be represented as a surface (see for example Fig. 1). Solutes contained in a mixture of solutes each having their characteristic absorbance maxima can be studied individually, provided that they are fractioned and often, already the raw data contain important information about the system.39 This is exemplified by Fig. 1 showing the raw SV data acquired with the multi-wavelength optics by Karabudak et al.39 Information on particle composition can already be obtained from visual inspection of the raw data of this single band sedimentation velocity experiment on colloidal particles of crystalline and amorphous β-carotene that are sterically stabilized with gelatin. The sedimentation of gelatin, β-carotene and their corresponding composite particles can be followed separately since gelatin and β-carotene absorba at different wavelengths. From Fig. 1 it can be seen that the dispersion contains probably aggregated β-carotene particles that sediment fast. In addition to the largest fraction of gelatin coated β-carotene colloids (the two largest peaks in the lower left panel of Fig. 1 that sediment together), the dispersion contains some free gelatin that lags behind since it sediments relatively slowly.
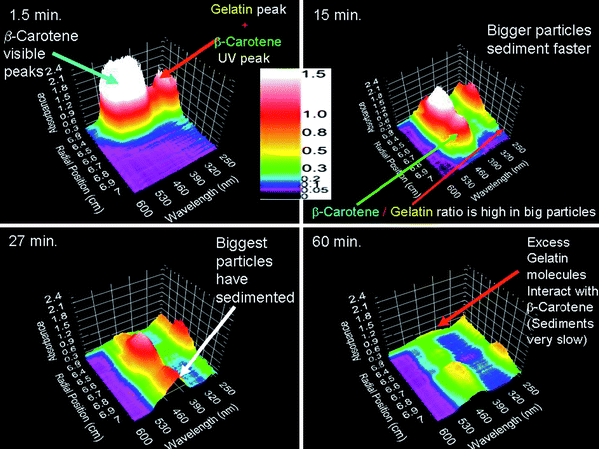 | ||
| Fig. 1 4 of 40 consecutive sedimentation velocity scans (recording time is indicated) acquired with the multi-wavelength optics. The 3-dimensional plots of absorbance (z-axis), radial distance to the center of rotation (x-axis) and wavelength (y-axis) show raw data from a band sedimentation experiment with β-carotene. Image reproduced from ref. 39 with permission of Springer Verlag. | ||
The multi-wavelength detection and its development is open source and part of the recently launched “Open AUC Project”.53 Moreover, it is designed such that it can be implemented into the preparative Optima XL ultracentrifuge to lower purchase costs. Attempts have been made to improve intensity and reduce errors due to alignment and chromatic abberation for the MDS by substituting the optical lenses with mirrors, accordingly moving on to the 2nd generation MDS. The 3rd generation of optical lens based MDS (for the 2nd generation see ref. 52) with improved intensity in the Vis region as well as the UV region should soon become available. The first experimental studies reported employing the MDS are on BSA and polystyrene latex mixtures,49 and β-carotene-gelatin composite particles.39
Besides the MDS a prototype fluorescence detector54 has been developed, which became commercially available in early 2006 as the Aviv Biomedical AU-FDS fluorescence detection retrofit system55 for the Beckman XL-I AUC. The radial distribution of fluorophores is detected via confocal optics. Picomolar concentrations can be detected with the AU-FDS but this requires the macromolecules or colloids to be fluorescent, offering high selectivity. Additionally, the FDS allows to study solutes in impure mixtures or even in a “crowded” fluid as a cell lysate. The AU-FDS was designed with its own data acquisition system that allows light intensity readings from three detectors simultaneously. This advanced operating software (AOS, see RASMB) is also compatible with the next generation of AUC, namely the Centrifugal Fluid Analyzer (CFA).
The developments and emerging new ideas from the 1990s56 eventually led to designing a new AUC. The future outlook given by Laue, “New Horizons for Analytical Ultracentrifugation: What Will the Next Generation of Instrument Look Like?”, presented on the 14th international symposium on AUC in Lausanne 2005 has now become within reach.
The CFA, being developed by Spin Analytical Inc. (Durham, NH), is designed from the ground up for analytical ultracentrifugation specifically for the “Open AUC Project”.53 The “Open AUC Project” includes the CFA instrument, modular software components, and a standardized database, all of which are open source, encouraging further development and user customizations. This new instrument should allow the user to plug and play detection systems at will.
AUC of Colloids
Colloids have a number of characteristics which distinguish them from commonly investigated biomacromolecules such as proteins and DNA. These characteristics are:1. In addition to shape, density and hydration polydispersity, colloidal dispersions may exhibit very broad particle size distributions and, consequently, extremely broad sedimentation coefficient distributions. A common problem is that a small concentration of big aggregates or small impurities is not detected.
2. Colloids can aggregate or grow during centrifugation (concentration dependent aggregation).
3. Generally, the density of hybrid colloids is unknown, impeding sedimentation coefficient to particle size conversions.
4. Charge stabilization often leads to non-ideal sedimentation behavior, which complicates SV AUC data analysis. Electrostatic repulsion can not be compensated by application of buffers since this frequently affects the dispersion stability.
5. High particle density often makes density gradients or density variation methods impossible.
6. Colloidal dispersions are often multi-component mixtures.
Fig. 2 shows the example of a sedimentation coefficient distribution of aggregating BaSO4 colloids.12 The particle size distribution is very broad and spans 2 orders of magnitude in the very high sedimentation coefficient range. In comparison, typical sedimentation coefficients for macromolecules are in the range of 1–10 S (1 S = 1 × 10−13 s) and in rare cases up to 100 S at the most. This shows already that for colloids, often a single centrifugation speed is not sufficient for the characterization of the sample and speed profiles have to be applied.
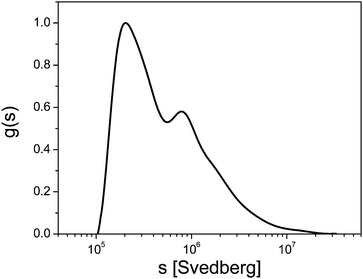 | ||
| Fig. 2 Sedimentation coefficient distribution of aggregated BaSO4 (1 S = 1 × 10−13 s). Image reproduced from ref. 12 with permission of Springer Verlag. | ||
A further complication arises from MIE scattering of colloids if their concentration is detected via light absorption and/or turbidity. Due to their larger size as compared to macromolecules, colloids can exhibit significant particle size dependent light scattering, which needs to be corrected.57 However, the MIE correction has the potential problem that it amplifies artifacts or uncertainties in the small particle size range.
Fig. 3 shows that MIE scattering significantly enhances the detected signal of larger nanoparticles, leading to overstimating their concentrations, in turbidity and absorption optics. However, the refractive index detection remains unaffected by the scattering and shows the “true” distribution with which the MIE corrected signal corresponds well. Therefore, a refractive index optics can be desirable for experiments with colloids. Due to the broad particle size distributions, multi-speed evaluation methods are often preferable and available.34,58
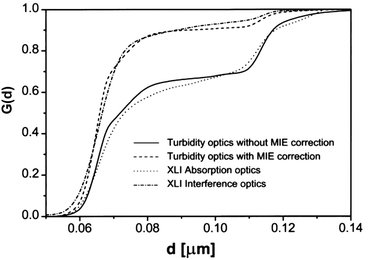 | ||
| Fig. 3 Illustration of the MIE scattering effect and its impact on quantitative detection for a binary 9 : 1 by wt. polystyrene latex mixture (66 nm & 119 nm). Integral distributions were obtained from single speed runs (10 krpm) using the absorption (360 nm) and Rayleigh interference optics, whereas gravity sweep was applied (0–40 krpm) for the turbidity optics run. The MIE corrected distribution from the turbidity optics agrees well with result from Rayleigh interference optics, showing that MIE correction is significant. Image reproduced from ref. 8 with permission of the Royal Society of Chemistry. | ||
A couple of different scenarios can be distinguished for SV and SE AUC experiments on colloids and macromolecules. These scenarios include: case (1) highly monodisperse colloids,59 and case (2), polydisperse particles with AUC. The sedimentation velocity analysis for monodisperse particles or solutes, case (1), is relatively straightforward; However, the characterization of polydisperse particles with AUC, case (2), is much more challenging.60,61 For colloids and macromolecules, average size, “individual” particle shapes and shapes of particle size distributions can be obtained from sedimentation velocity experiments.58,62,63
There are several case studies comparing SV AUC experimental results on (shapes of) particle size distribution and average particle size with results obtained from for example transmission electron microscopy images (TEM), hydrodynamic chromatography and hydrodynamic radii from dynamic light scattering experiments.60,61,64,65
Another case (3) is the investigation of colloids that attract each other. This attraction is significant if the interaction energy is on the order of several times the thermal energy at room temperature. Such interactions can result in the self-assembly of monomers into supra-colloidal complexes which may be studied via SV AUC.66 Spontaneous structure formation is, for example, also observed for magnetic colloids that were studied via SV AUC by Planken et al.67 where the concentration dependent sedimentation is modeled in terms of dimerization thermodynamics.
Case (4), which is encountered frequently in colloid chemistry, is a salt-concentration dependent sedimentation velocity of colloids which repel each other due to charge stabilization.68,69 The dominating interaction remains repulsive (stabilization), resulting in a decrease of the sedimentation rate with concentration. For SE AUC, evidence for the existence of a macroscopic electrical field is found for like-charged colloids.70–72 The observations on like-charged colloids are in marked contrast to the behavior studied via AUC for colloids that tend to associate.
Apart from the 4 cases discussed above, hydrodynamic interactions are always present in SV AUC resulting in a decrease of the sedimentation velocity with concentration, even for hard-sphere colloids.73–75 For highly diluted systems this concentration dependence almost vanishes. Concentration effects may impair the analysis of sedimentation data, they can however, offer a wealth of information as well.66 Here the reader is specifically referred to the book section of Philipse for further reading on sedimentation of colloids.76
In the following section we give a brief overview of suitable analysis methods which can be used to analyze sedimentation velocity data for the 4 different cases.
Basic AUC experiments
The basic equation for ultracentrifugation experiments is the Lamm equation,77eqn (1), which describes the local concentration, c, variations of the sample in the ultracentrifugal field with time, t, due to diffusion and sedimentation (D and s respectively):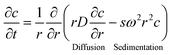 | (1) |
There are four fundamental types of AUC experiments, all based on eqn (1), from which complementary physicochemical information can be obtained, Table 1 and Fig. 4. The Lamm equation, however, can also be used to model more exotic experiments but this may require introducing additional parameters. Examples for this are the swelling pressure equilibrium experiments78,79—a special case of sedimentation–diffusion equilibrium experiments for gels—or synthetic boundary crystallization experiments, which are a special case of band centrifugation experiments for the in situ formation of crystals.80,81
| Experiment | Operative term in the Lamm eqn (1) | Characteristics of experiment | Accessible parameter |
|---|---|---|---|
| Sedimentation velocity | Sedimentation term may prevail diffusion term | High rotational speed | Sedimentation coefficient |
| Zone/Band sedimentation | Both terms | High rotational speed | Sedimentation and diffusion coefficient |
| Synthetic boundary experiment | Only diffusion term operative | Low rotational speed | |
| Synthetic boundary cell | Diffusion coefficient | ||
| Sedimentation–diffusion equilibrium | Both terms, equilibrium between sedimentation and diffusion | Low to moderate rotational speed | Molar mass, equilibrium constants and stoichiometries of interacting systems |
| Density gradient | Both terms, equilibrium between sedimentation and diffusion | Moderate to high rotational speed, establishment of a radial solvent density gradient | Density |
Sedimentation velocity experiment
A sedimentation velocity run, generally carried out at high centrifugal fields, is the most important AUC experiment (Fig. 4, graph A) for nanoparticle characterization, since particle size distributions can be obtained from sedimentation coefficient distributions. It is also a classical experiment for polymer characterization.82,83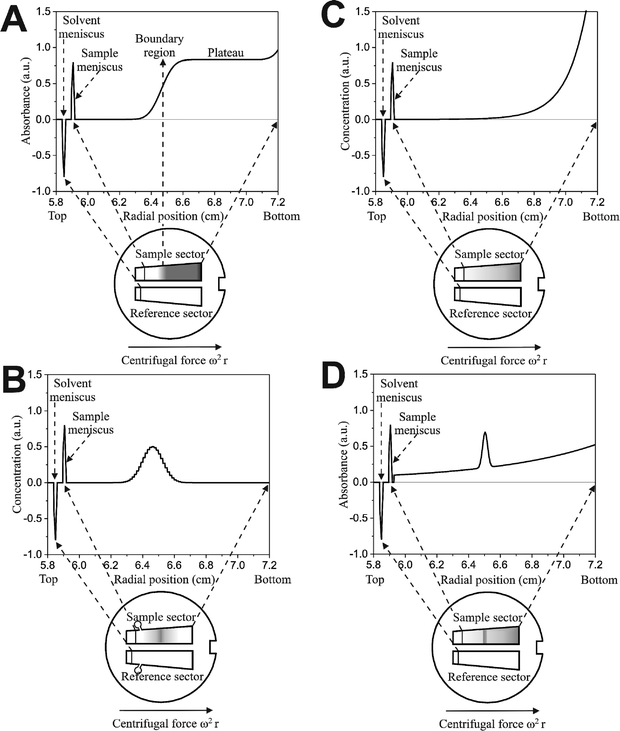 | ||
| Fig. 4 Four basic analytical ultracentrifugation experiments: sedimentation velocity and zone or band sedimentation (A and B respectively, each showing one out of many scans), sedimentation–diffusion equilibrium without (C) and with a density gradient (isopycnic banding). | ||
Colloids or macromolecules sediment according to their mass/size, density and shape. Sufficiently large and dense colloids do not significantly diffuse resulting in a steep concentration gradient. Under such conditions, a sample mixture is separated and a step-like concentration profile in the ultracentrifuge cell, usually exhibiting an upper and a lower plateau (Fig. 4, graph A) may be detected. Each step corresponds to one species. However, colloids are often so polydisperse, that no plateaus are formed. If the radial concentration gradient is detected in certain time intervals, the sedimentation of the molecules/particles can be monitored and sedimentation coefficients and their distributions can be calculated.
Evaluation methods for sedimentation velocity data analysis can be divided in techniques that yield apparent sedimentation coefficients and diffusion corrected sedimentation coefficients. The latter evaluation techniques can be subdivided into three groups according to the method to correct for diffusion. These groups are:
1. Run time extrapolation procedures. Running time extrapolation procedures make use of the fact that the sedimentation of a particle is proportional to the run time (see eqn (3)), whereas the diffusion is proportional to the square root of the time, t1/2. That means extrapolation to infinite t yields diffusion-corrected or “true” sedimentation. All extrapolation procedures give true sedimentation coefficient values as well as their integral or differential distributions. For example, the particle diameter or radius distribution may be calculated from these distributions.
2. Application of the Lamm equation, eqn (1). Since the Lamm equation cannot be solved analytically, approximate numerical solutions of the Lamm equation are used to describe AUC experimental data.24,28,42
3. Correction procedure. This means correction of the apparent sedimentation coefficient distribution with respect to an average diffusion coefficient.22
In the following, the main evaluation methods for sedimentation velocity experiments with colloids are briefly introduced.
Second moment method
For colloids, the classical calculation of a single weight-average sedimentation coefficient is, as other analyses, useful to a limited extent. Such a single s-value is for example calculated from the second moment (SM) position of the sedimenting boundary84: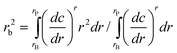 | (2) |
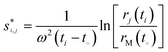 | (3) |
Eqn (3) follows from the definition of the sedimentation coefficient1 and is widely used for the determination of apparent, i.e. not corrected for diffusion, sedimentation coefficients. For example when measuring sedimentation in time-mode, that is measuring the concentration at a fixed radius as in the turbidity detection system,9 apparent sedimentation coefficient distributions are obtained viaeqn (3).
By observing the second moment sedimentation coefficient over the course of the run, important diagnostics can be obtained:
1. Aggregation;
2. Degradation;
3. Concentration dependency.
For an ideal non-interacting system the second moment s-values should not change over the course of the run. Changes of sedimentation coefficient values during a run or with increasing the total concentration, one of the conditions (1–3) may apply. In the case of concentration dependent (nonideality) settling of colloids, the s-value increases with concentration for colloids that exhibit (self)-association or decreases due to hydrodynamic interactions, the latter especially for repulsive particles. However, fine details in particle size distributions can remarkably alter the colloid properties so that an average quantity as a second moment sedimentation coefficient usually does not provide sufficient information
van Holde–Weischet method
A problem arising from the diffusion broadening of boundaries is that individual solution components cannot be resolved such that an overall smooth boundary appears to be that of a single component. An approach to deconvolute diffusion and sedimentation and thus enabling to determine the diffusion corrected s-distribution G(s) was introduced by van Holde and Weischet85 (vHW).The vHW analysis is based on the principle that transport due to sedimentation is proportional to time, whereas diffusional displacement is proportional to the square-root of time. Briefly, for a vHW analysis, the sedimentation velocity boundaries are each discretized in equally sized fractions (divisions) between the lower (baseline) and upper stable plateaus (horizontal regions). For each boundary division a corresponding apparent sedimentation coefficient is calculated via the eqn (3). The apparent sedimentation coefficients are then plotted versus the inverse square-root of the corresponding scan time. Diffusion-corrected sedimentation coefficients are obtained by extrapolating each linear fit of apparent sedimentation coefficients for the boundary fractions to infinite time. The linear extrapolation to t = ∞ in the vHW analysis method is achieved via a formula based on a Faxén-type approximate solution of the Lamm eqn (1), e.g. infinite solution column length, which introduces restrictions to the scans for analysis.
For multi-component dispersions, the corresponding number of intersects is obtained whereas the intersection point is shifted to times less than infinity in case of non-ideality. Therefore, the van Holde–Weischet analysis is a rigorous test for sample homogeneity or non-ideality85–90 and does not require any assumptions about the sample. Thus it is potentially well suited for the analysis of colloids but suffers from the requirement of an upper and lower plateau as well as the consideration of only a single speed experiment. So in fact, the van Holde–Weischet method is a useful diagnostic tool for colloids and for monodisperse colloids, also a tool for the determination of true diffusion corrected particle size distributions.60
The modified and so-called enhanced vHW analysis circumvents the majority of the drawbacks associated with the classic vHW method.91 For example, the enhanced vHW analysis allows inclusion of scans that have not cleared the meniscus and that lack stable lower and upper horizontal regions, in contrast to the classical vHW (see ref. 91 for a detailed derivation and discussion of the enhanced vHW analysis). However, the restriction of a constant speed for the evaluation still applies so that very polydisperse colloids with sedimentation coefficients spanning orders of magnitude, which require speed profiles, cannot be evaluated. However, it must be mentioned that for speed profiles, diffusion correction is so far not possible so that all these sedimentation coefficient distributions have an apparent character with respect to diffusion spreading. Nevertheless, for the usually investigated particle sizes > 50 nm, the boundary spreading effect is quite small.
In contrast to a continuous distribution c(s) analysis, where the sedimentation velocity boundaries for the species under consideration are fitted with a single frictional ratio, i.e. all particles have the same shape,31 the vHW analysis can be used for any kind of colloids, regardless of their shape. The deconvolution of diffusion and sedimentation via the enhanced vHW analysis is of special importance for spherical particles, because the assessment of size polydispersity with this analysis is then straightforward. For other particle shapes or for particles that exhibit shape heterogeneity, an equivalent sphere radius may be introduced to assess an apparent size polydispersity.
The psd can be obtained by converting the differential vHW sedimentation coefficient distribution, which is corrected for diffusion, viaeqn (9). For spherical particles, for which the bare particle radius equals the hydrodynamic radius, the size distribution can be obtained from the sedimentation coefficient distribution viaeqn (8).60 Both conversions require the input of particle density, solvent viscosity, and solvent density. The particle density, however, can be determined via several techniques, e.g. in a density oscillation tube, density gradient centrifugation or refractive index measurements.
Time-derivative method
In many cases, colloidal particles are polydisperse (almost continuous size distribution) or the dispersion particles show a multimodal distribution. In such cases, it is of interest to determine the integral G(s) or its differential g(s) sedimentation coefficient distribution. Although this is in principle possible by the vHW-method, another method for the determination of g(s) suited for colloids is the time derivative method32,92 (dc/dt). The time derivative differential s-distribution reads: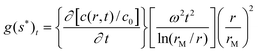 | (4) |
Via the time derivative (dc/dt) method the g(s*) differential sedimentation coefficient distribution is calculated by subtraction of consecutive scan pairs and mapping the resulting difference curves to the s domain to obtain dc/dt curves.
The advantage of this method is the subtraction of time invariant noise, such as window scratches and dirt, as well as refractive index hetereogeneities in the windows. The latter is particularly important for low-concentration interference data. Unlike the vHW method, the dc/dt method does not correct for diffusion. In order to obtain accurate results with this method, it is important that only a small scan range over which diffusion has not changed significantly is included. In case of sufficiently large and dense colloids sedimented at high rotor speeds, g(s*) equals the true distribution g(s), since diffusional boundary broadening is negligible.
This approach specifically excels by the rapid data acquisition of modern analytical ultracentrifuges (Rayleigh interference optics) where 100 or more scans per velocity experiment are no experimental problem any more. Hence, even scans for highly diluted solutions where the sedimenting boundary can hardly be seen anymore in the raw scans can be evaluated with the time derivative method. By that means, concentrations as low as 10 μg mL−1 can be analyzed such that interacting macromolecules and particles can be addressed in a concentration range previously not accessible with the analytical ultracentrifuge. However, a drawback of the time-derivative method is that only scans from a relatively narrow time interval can be used for a single evaluation so that in fact, no full advantage is taken of the possibility to record several hundreds of experimental scans throughout an experiment.
If diffusion is significant, extrapolation of g(s*) curves calculated for different times to infinite time yield the true distribution. The diffusion coefficient can also be derived from the g(s*) distribution using the maximum of the g(s*) curve:32
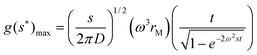 | (5) |
A plot of g(s*)maxvs. t/[1 − exp(−2ω2st)]0.5 yields a line with a slope χ that is proportional to the square root of s/D so that the Svedberg equation, see eqn (7), can be applied to derive the molar mass:
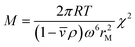 | (6) |
However, for heterogeneous systems, the molar mass can be underestimated up to 10–20%. For very polydisperse colloids this error is certainly much larger. Nevertheless, a former limitation that g(s*) could only be evaluated for a single speed experiment limiting the application of the method to reasonably narrow particle size distributions could be overcome by application of speed profiles for polydisperse systems.34 The dc/dt method can even be applied to a mixture of colloids spanning a range of sedimentation coefficients over several orders of magnitude.
The determination of g(s*) can already yield a lot of important information beside the sample homogeneity and number of components. In case of slowly interacting systems, i.e. slow on the time scale of a typical SV AUC experiment (2–3 h), interaction constants and stoichiometries can be derived.32,33 If multiple Gauss curves with a maximum at fixed s are fitted to g(s), each of them corresponds to one component.93 By that means, the aggregation state as well as the corresponding concentration of the different aggregates can be determined for systems so that the equilibrium constant and thus the Gibbs free energy of the association is accessible. An example of the advantageous application of this technique was reported for the precrystallization aggregation of lysozyme which yielded the smallest oligomer being able to form a crystal.94
Fitting approximate or finite element solutions of the lamm equation
One new and recently much investigated approach has proved useful for the determination of s and D and thus the molecular weight (M) as well as the concentrations of individual components from sedimentation velocity data.As the Lamm eqn (1) is the fundamental equation in analytical ultracentrifugation capable to describe all types of ultracentrifuge experiments, fitting of this equation to experimental data is a potentially very powerful approach. However, a drawback is that this method is clearly model-dependent. Nevertheless, it is widely applicable and sedimentation and diffusion coefficients can be determined quite accurately, even in mixtures up to eight components.29
In case of unknown samples, results obtained from a vHW or dc/dt analysis can be used to determine the type of system under investigation and the appropriate model for fitting the Lamm equation. For mixtures of more than 3 components, at least the range of sedimentation coefficients should be known and restricted (as obtained from a vHW or dc/dt analysis) to get reliable fitting results.
Fitting of (sums of) Lamm equation solutions to experimental data has its special merits for small macromolecules or nanoparticles which sediment rather slowly (s < 1 S) such that there is no meniscus depletion.95 Furthermore, these approaches offer a rapid determination of molar masses with an accuracy of 10% within 15–30 min. after the start of a sedimentation equilibrium experiment using a modified Archibald approach.96 This is especially important for unstable samples which have to be characterized rapidly. However, for the majority of colloids, this approach is not useful, as the requirement of a very limited degree of polydispersity is usually not fulfilled.
Recently, the restriction to monodisperse samples for fitting Lamm equation solutions was overcome so that now even sedimentation coefficient and molar mass distributions of polydisperse samples can be investigated.31 However, the particle density should be known. If the frictional ratio is not known, it can also be fitted which in turn allows one to relate the actual particle shape to one of the four basic shapes (sphere, prolate or oblate ellipsoid or rigid rod).
The most significant merit of this approach for nanoparticle analysis is the possibility to correct for the effects of diffusion on the broadening of the sedimenting boundary so that diffusion-corrected sedimentation coefficient distributions can be obtained reflecting the true sample polydispersity. The method was shown to yield reliable results for different model systems.97 It was recently extended to account for solvent compressibility effects, which are significant for organic solvents. Solvent compressibility is even non-negligible for water at very high speeds, which have to be applied in case of small colloids.98 In addition the sedimentation in a dynamic density gradient formed by the sedimentation of co-solutes was treated, which is a relevant case for the AUC analysis of colloids.99 Therefore, fitting to approximate solutions of the Lamm equation with constrained algorithms for the determination of diffusion coefficients associated to a given sedimentation coefficient distribution is a very appropriate method for the analysis of the sedimentation coefficient distribution of colloids. In addition, radial and time invariant noise can be removed from the experimental data which allows for the evaluation of quite diluted samples in similarity to the time derivative method.
It should be noted that increasing the angular velocity of the AUC rotor containing a sample with a sufficiently long solution column, suppresses sedimentation boundary broadening due to diffusion and therefore enhances the sedimentation coefficient resolution. The maximum angular velocity, however, is restricted by the speed with which the scans are recorded, the degree of polydispersity (s-range), and the minimum amount of scans that need to be included in the analysis. Also, excluding early scans (scans recorded at the beginning of the sedimentation velocity run/experiment) where the fractionation of differently sized particles is minimal and the diffusion due to the initially steep concentration gradient is maximal, improves the sedimentation coefficient resolution.
The diffusion on the other hand, can provide important shape information. For such an experiment, the angular velocity should be relatively low to obtain as much information on particle shapes as possible. Regarding the assessment of particle shape, an analysis method is available (implemented in UltraScan27 and similar but different in SEDFIT,31 the latter is without the parallel computation and high performance computing) that allows one to simultaneously determine the sedimentation coefficients and frictional ratios via a sedimentation velocity whole boundary fitting routine. This 2-dimensional spectrum analysis (2DSA40,42) was initially intended for the parameter initialization to confine the search space for the genetic algorithm optimization29 for sedimentation velocity data fitting.
The 2DSA decomposes the experimental sedimentation velocity data into a sum of finite element solutions to the Lamm equation, describing the noninteracting settling particles present in solution. Because the computational effort to decompose sedimentation and diffusion can quickly become very large (typically several gigabytes of RAM are required), the implementation of parallel computing using supercomputers (clusters) facilitates this analysis method. The solution obtained, thus provides information on the distribution of sedimentation coefficients and shapes (frictional ratios), as shown in Fig. 5.
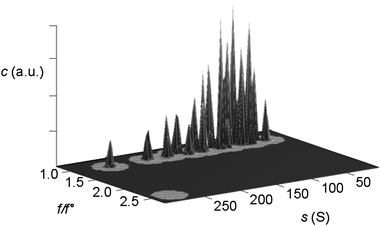 | ||
| Fig. 5 Three-dimensional plot of particle concentration (c in arbitrary units) vs. the frictional ratio (f/f0) and sedimentation coefficient (s) as obtained from a 2-dimensional spectrum analysis (UltraScan) on SV AUC interference experimental data. All particles are spherical, i.e. the frictional ratio for all silica nanoparticles within this large sedimentation coefficient range (radius ∼ 2–14 nm) is equal or close to f/f0 = 1.0. This s distribution can thus be converted to a particle size distribution viaeqn (8), provided that the bare particle radius equals the hydrodynamic radius. Figure reproduced from ref. 60 with permission of the American Chemical Society. | ||
Clearly, a genetic algorithm (GA) optimization of 2DSA s- and f/f0 distributions works best if the Lamm equation solutions are globally fitted to multi-speed (fast and slow speed) sedimentation velocity experiments. It should be noted that the GA optimization is suited for mono- or paucidisperse solutes only, therefore this routine does not work for typical (polydisperse) colloidal dispersions. In principle, if accurate sedimentation and diffusion coefficients are obtained, these methods (2DSA and GA) allow the determination of molecular weights via the so-called Svedberg equation:
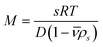 | (7) |
This approach to determine the molecular weights holds for noninteracting macromolecules or colloids. Interparticle attractions and repulsions may have pronounced effects on the sedimentation behavior, resulting in a nonrepresentative psd.
Meanwhile, equilibrium constants can also be obtained from sedimentation velocity data combining multiple runs and concentrations and mixing ratios of the interacting compounds by fitting time difference data and applying finite element solutions of the Lamm equation.99 Models describing reversible association reactions that can be fitted to SV data have been implemented in the majority of currently available data analysis software. One of these uses the genetic algorithm optimization to optimize the model describing the appropriate reversible association to obtain solution properties of all components present in the system and was recently applied to synthetic and experimental data.100 Demeler et al.100 also suggest limits for the accessible kinetic range. They conclude that equilibrium constants obtained from SV and SE analysis are equivalent. SV AUC experiments, however, provide better confidence for the dissociation equilibrium constant (Kd), can better account for the presence of contaminants and provide additional information as rate constants and shape parameters. SV AUC data analysis programs as SEDFIT31 and SedAnal35 also offer models describing association reactions that can be fitted to experimental data for associating systems; however, they lack a genetic algorithm optimization.
Comparison of sedimentation velocity evaluation methods
The above-presented methods have their special merits and are thus briefly compared to allow an assessment of the methods in view of colloid analysis. For a detailed comparison of analysis methods to obtain particle size distributions the reader is referred to the work of Mittal et al.43 In their contribution the sedimentation analysis of spherical SiO2 and ZrO2 and non-spherical ZrO2 of different particle sizes in various solvents as nanoparticle model systems was conducted employing the interference optics. Size distributions for these particles were obtained employing the dc/dt (SedAnal32), ls-g*(c), c(s) (the latter two in SEDFIT31), the Gosting Fujita Lechner (GFL) principle,22,24,101,102 van Holde-Weischet and 2DSA with Monte Carlo statistical analysis (UltraScan27) to assess the pros and cons of these analysis methods for colloid characterization.43The second moment method and all other methods that return only average sedimentation coefficients are of limited use for the characterization of colloids since their physical properties are determined by their size and therefore by the fine details of their size distribution. The vHW-method is a rigorous test for sample homogeneity and non-ideality. It corrects for sedimentation boundary broadening due to diffusion. However, the vHW analysis is limited to only a single sedimentation velocity run at a single speed and therefore puts restrictions on the range of sedimentation coefficient values that can be monitored with a single SV run, despite that the accessible range was extended to evaluate broader distributions.91
The time derivative (dc/dt) method is valuable if distributions of a good quality are desired but it does not correct for diffusion resulting in too broad s- or size distributions. Another drawback is that only scans of a limited time interval can be analyzed so that this method does not make full use of the possibility of modern ultracentrifuges to acquire hundreds of experimental scans in a single experiment. However, scans covering several time intervals can be evaluated separately. In the latter case, the calculation of the diffusion coefficient is possible. Very recently, a step speed profile became applicable for evaluation of experimental data by the dc/dt method so that colloids with sedimentation coefficients spanning over orders of magnitude can now be evaluated by this method.34
Fitting to approximate solutions of the Lamm equation can make full use of the possibility of including all acquired scans even for large experimental data sets. This can even yield the particle shape distributions via the f/f0 distribution if it is determined simultaneously to the s-distribution by approaches like 2DSA. Inlcuding all information contained in the acquired data for fitting with Lamm equation solution can yield very accurate results but can get computationally very demanding if shape information is sought as well, like in a 2DSA evaluation. Additionally, time and radially invariant noise can be removed and it is possible to obtain diffusion corrected sedimentation coefficient distributions—even for polydisperse particles. However, in case of polydispersity, artificial peaks can be generated by the diffusion correction. Therefore it is a good practice to compare the diffusion-corrected with the diffusion-uncorrected distribution.
Particle size distributions
The potential of analytical ultracentrifugation to assess high-resolution particle sizes and particle size distributions was already realized by the pioneers of this technique. The power of SV AUC experiments lies in the fractionation of solutes on the basis of particle sizes/molar masses and shapes.7,103–106 Nevertheless, it appears that the potential of this application is still not yet commonly recognized. It is relatively straightforward to convert a sedimentation coefficient distribution into a particle size distribution. Each sedimentation coefficient can be calculated from the corresponding radius viaeqn (3) for every data point rj if a radial scan has been acquired at a specified time ti or for every ti if the concentration is detected in time at a fixed radial position.Assuming the validity of Stokes' law (e.g. the colloids are all perfect spheres and the bare particle radius equals the hydrodynamic radius), the following equation:
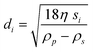 | (8) |
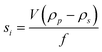 | (9) |
In eqn (7) and (8)di is the particle diameter corresponding to si and ρp and ρs are the density of the sedimenting particle and solvent respectively, η the solvent viscosity, V the particle volume and f the friction factor. If the particles are not spherical, only the equivalent sphere diameter is obtained unless form factors are applied, provided the axial ratio of the particles is known from other sources, as for example electron microscopy.
The conversion of sedimentation coefficient distributions to a particle size distribution highly relies on the knowledge of the density of the sedimenting particle. For hybrid (composite/core–shell) particles or very small nanoparticles < 5 nm, this issue could cause the conversion of s to d to become unfeasible, especially in case of mixtures, as the density of the particles is usually not known. Measurements of the average particle density in the mixture can lead to erroneous results, so that in such cases the correlation of the sedimentation coefficient distribution with a distribution obtained from a density insensitive method like flow–field–flow fractionation or dynamic light scattering is indispensable. This can in turn yield the particle density which can yield information about the relative amount of the materials constituting the composite colloids.107,108 The problem of density determination and possible solutions are discussed in more detail below. But even an apparent particle size distribution which is calculated within the limits of reasonable particle densities can already yield very valuable information.109 The issue of particle density for colloidal dispersions is discussed in the section entitled “Density of core–shell and hybrid colloids”.
However, in the case of industrially important latices as well as for all colloids > 20 nm, the particle density is usually exactly known from the chemistry of particle formation/polymerization. Thus, the determination of particle size distributions with the analytical ultracentrifuge is a rapid technique providing parameter values with reliable statistics, in contrast to electron microscopy65 which may yield information on particle shapes but often suffers from drying artifacts (particle shrinkage etc.)60 and limited particle numbers which can be counted.110 A determination of a particle size distribution from microscopy images requires counting of at least a thousand particles to obtain reliable statistics.76 This problem has only partly been diminished by the advent of commercially available picture evaluation algorithms. A test of the worldwide operating Bayer group in 17 laboratories dedicated to particle size analysis confirmed the view that TEM and/or analytical ultracentrifugation are the best techniques for the determination of particle size distributions65 as previously addressed. A combination of TEM, AUC and X-ray diffraction techniques can provide most complete insight into a colloidal system.111
Analytical ultracentrifugation in combination with electron microscopy in its various forms can be considered the most powerful characterization technique for determining particle size distributions and particle morphologies to date. The following example illustrates the fractionation power of the analytical ultracentrifuge.
The particle size distribution in Fig. 6, obtained via SV AUC and published by Müller,58 shows the resolving power of this technique. The dispersion is a mixture of nine different calibration latices. Clearly, the partial concentrations of the nine different components as well as their sizes from SV AUC experimental data agree well with the target values (inset Fig. 6).
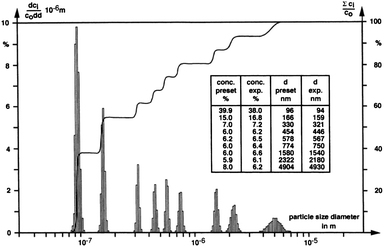 | ||
| Fig. 6 A particle size distribution for a dispersion mixture of nine different calibration latices showing the resolving power of SV AUC. Figure reproduced from ref. 58 with permission of Springer Verlag. | ||
High-resolution particle size distributions
It is interesting to note that already in the very first reported AUC experiments on colloidal systems, particles of only a few nanometres size could be successfully analyzed. The classical paper of Svedberg and Rinde from 19247 reporting the characterization of gold colloids of only 1.5 nm, illustrates that AUC is quite a precise technique to determine particle size distributions.112,113 Taking into account that the optical detection systems in these days were by far not as sophisticated as today, their results are notable. Nevertheless, it is not astonishing that modern detection systems combined with modern sedimentation velocity evaluation methods can reveal details which were hidden in previous studies.One example is the Au55 cluster, which is of interest as it is considered to be at the transition between a particle and a molecule. The initial investigation by analytical ultracentrifugation revealed a monodisperse population.114 In the method used, the sedimentation of the clusters was followed by a Schlieren optical system (gray/black transition on a photographic record due to the deeply coloured sample) and a homogeneous sample was stated from the boundary movement. Concentration profiles, which represent the integral particle size distribution, were not given even though the authors noted that there was a pronounced transition area. The determination of a precise sedimentation coefficient distribution is nowadays feasible, as concentration values can be determined precisely along the radial direction using the UV-Vis absorption or Rayleigh interference optical system of modern analytical ultracentrifuges. Consequently, it can now be precisely detected if an Au55 cluster preparation is monodisperse or a mixture of different species.111 The resolution between the observed species is in the Ångström range and it has to be noted that the modern optics of an XL-I AUC has such a high resolving power (i.e. high resolution), even in routine experiments.
For very small particles, diffusion becomes significant and must therefore be corrected. Therefore, it has to be maintained that either the particle diffusion can be suppressed by application of high speeds,115 or that the diffusion boundary broadening can be deconvoluted from sedimentation by for example extrapolation to infinite time as in the vHW.91 Another method based on the calculation of the diffusion coefficient from the particle size was suggested by Lechner et al.22 This method calculates the diffusion broadening of the sedimenting boundary and subtracts it from the measured concentration distribution yielding the diffusion corrected particle size distribution. This procedure works best for monomodal and relatively narrow distributions (small polydispersity), whereas it loses accuracy for broad and/or multimodal distributions.
Considering the hard- and software progress made in the last decades in AUC, addressed previously, it is not surprising that to date high resolution particle size distributions can be routinely obtained. One of the early examples for such a high resolution particle size distribution is certainly the one reported in ref. 115. Here, Pt colloids were quenched during their growth and analyzed at the highest possible speed (60000 rpm for the XL-A/I) where sedimentation dominates over diffusion (Fig. 7). The obtained particle size distribution shows an extremely high baseline resolution (i.e. the different species are well resolved) of 1 Ångström between the different species, which corresponds to differences of only 21 Pt atoms.115 Such highly resolved particle size distributions provide information on the growth mechanism. For Pt colloids as deduced from the constant increments of atoms between the detected species (although not explicitly stated in ref. 115) this mechanism involves particle coalescence and restructuring to a spherical particle. Very recently, this growth mechanism of Pt nanoparticles was independently confirmed in an electron microscopy study by Zheng et al.116
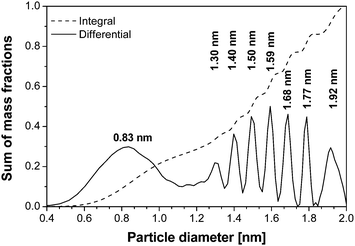 | ||
| Fig. 7 Integral and differential particle size distributions of a Pt colloid.115 Reproduced with permission of Springer Verlag. | ||
The second example of a high resolution particle size distribution shows in an impressive manner how much experiments with very small nanoparticles can profit from the capabilities of diffusion correction. In the following example, CdS was generated by the so-called “band or zone analytical (crystallization) ultracentrifugation”.81,82 In this technique, the CdS nanoparticles were in situ generated in the ultracentrifuge cell by layering Na2S onto a CdCl2/thioglycerin solution leading to a sharp reaction boundary where CdS is formed. After formation, the various CdS species are fractionated and characterized by analyzing the sedimentation velocity data. The advantage of the in situ nanoparticle generation followed by a quenched growth process is that all growth species are formed and can be characterized.80,81 The initially determined particle size distribution of thioglycerine stabilized CdS based on the evaluation of a single experimental scan was monomodal due to interdiffusion of the different species. The analysis of a single scan does not provide information on all sedimenting species in the dispersion (Fig. 8, dashed line).80,81 In addition, due to the analysis method available at that time, the resulting distribution does not show all species present in the sample. Re-evaluation of the data set by least-squares fitting a s-distribution for zone centrifugation experiments using the program SEDFIT31 and including all acquired experimental scans yields an Ångström resolved particle size distribution starting with a 3 Ångström sized single thioglycerin complexed Cd2+ ion. The detected growth species include and agree well with all literature reported discrete CdS species. Moreover, the distribution includes two additional species which were not yet characterized in structure.
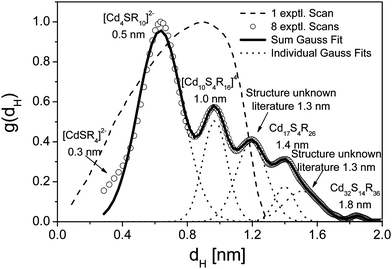 | ||
| Fig. 8 Particle size distribution of thioglycerine stabilized CdS as obtained from band or zone analytical (crystallization) ultracentrifugation. The dashed line with one scan shows data from ref. 80 and 81. Re-evaluation of these data with SEDFIT31 including all acquired sedimentation velocity scans reveals the different CdS growth species. | ||
The CdS experiment exemplifies the information content contained in a SV AUC experiment from a single run that can be performed in about 1–2 h. Such highly resolved particle size distributions including various growth species are indispensable to investigate particle nucleation and growth phenomena, which are the basis for every tailored colloid synthesis.
Concentration non-ideality
The sedimentation velocity for colloidal particles in a sufficiently concentrated dispersion is sensitive to the nature and strength of any interaction between the colloids.76 For example, long-range electrical double-layer repulsions may produce a pronounced retardation of the sedimentation rate, even at fairly low colloid concentrations.68,70 In that case, the average sedimentation velocity of the charged colloids may even be an exponential function of the colloid volume fraction,68,69 with an exponent between 0 and 1.When sufficient salt is added to compress the electric double-layer and, consequently, screen the inter-particle repulsions, the concentration dependence weakens and eventually becomes linear in volume fraction.68 If there is a significant concentration effect on the sedimentation rate, due to hydrodynamic and colloid–colloid interactions, then the sedimentation coefficient can be approximated by an empirical s versus c relation:23
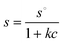 | (10) |
The validity of this equation is limited to fairly low concentrations. For sufficiently dilute dispersions, this equation can be replaced by the first term of its Taylor expansion:
| s = s∘(1−kcc) | (11) |
In eqn (10) and (11), s is the apparent sedimentation coefficient for which c > 0, k and kc are proportionality constants. Clearly this approach requires the input of the limiting sedimentation coefficient, s° that is generally obtained by extrapolation of s versus c obtained from a dilution series to c = 0. The sedimentation coefficient at any concentration should be obtained from a model independent analysis method as the SM, dc/dt or vHW. In case of size polydispersity, which should be limited at all times for studying concentration dependent sedimentation, the weight average sedimentation coefficient from model independent analysis methods may be used.
For repulsive interactions kc is positive and the first order correction to the sedimentation coefficient at infinite dilution results in a decreased sedimentation rate for relatively concentrated solutions or dispersions. On the other hand, for sufficiently strong attractions kc changes sign, enhancing the sedimentation velocity with concentration. The enhancement of the sedimentation rate is discussed in detail in ref. 67 employing oleic acid coated magnetite particles that exhibit dipolar attractions. In the latter contribution the s values were obtained from vHW and SM analyses, correcting solvent density and viscosity variations due to a fluctuating free oleic acid concentration. Magnetic particle volume fractions were determined from mass concentrations and calculated particle densities. Particle densities were calculated according to eqn (15) using particle radii from Transmission Electron Microscopy images and assuming a oleic acid layer of 2 nm (see next section for a brief discussion on the density of composite colloids).
Eqn (11) is usually expressed in terms of volume fractions ϕ. The concentration dependence of the sedimentation coefficient s of Brownian particles can be written as:
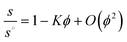 | (12) |
Batchelor73 has shown (for spheres) that K is completely determined by the isotropic equilibrium pair correlation function (pcf). For the hard sphere pcf one obtains for eqn (12) the well-known value of K = 6.55.73 This value corresponds to a modest hindered settling in a dilute dispersion of hard spheres, mainly caused by the retarding effect of solvent backflow. Batchelor73 already pointed out that any attractions will weaken the hindrance of sphere sedimentation. Qualitatively, this weakening is due to the enhanced probability for attractive spheres to shield each other against the backflow. Jansen et al.117 in their ultracentrifugal study of silica spheres, interacting via an isotropic attraction, indeed measured Batchelor coefficients that were significantly below the hard-sphere value of K = 6.55. Nevertheless, K remained positive, implying that in the silica dispersions the isotropic attractions were not strong enough to achieve accelerated settling. In contrast, sufficiently strong particle attractions enhance the sedimentation rate with concentration, resulting in large negative K values down to −242.67
In general, the sedimentation coefficient for pure non-associating solutes decreases with increasing concentration, i.e.K > 0. The magnitude of K strongly depends on the particle geometry and increases from its minimum for spheres (K = 6.55) to a maximum for highly expanded particle shapes e.g. rigid rods that are long and thin. Dogic et al.118 reported a calculation of the leading-order concentration dependence. Employing hydrodynamic interaction tensors for rigid rods, treated as strings of spherical beads within a mean-field approximation, valid for dilute dispersions of hard rigid rods, the result of Dogic et al.118 for K as a function of the aspect ratio or axial ratio p reads:
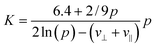 | (13) |
Unfortunately, to date it is not possible to extract an average particle charge from SV AUC experimental data. Regarding AUC however, recently developed theories121,122 may be applied to determine a particle charge from the inflated sedimentation-diffusion equilibrium distribution70–72 for charged colloids provided, of course, the effective molecular weight is known. In ref. 72 the authors obtained sedimentation–diffusion equilibria via analytical ultracentrifugation for well-characterized charged silica spheres in ethanol. The sedimentation–diffusion equilibrium distribution for these particles deviates strongly from a barometric profile and demonstrate the existence and substantial effects of a recently predicted internal macroscopic electric field.123 Experimental SE-profiles yield the gradient of the electrostatic potential energy of the colloids, which clearly manifests an almost homogeneous macroscopic electric field. Electrochemical Donnan potential measurements confirm a difference in electrical potential between the top and bottom of the profiles. Raça et al.71,72 conclude that “a ‘non-barometric' limiting law derived from electroneutrality explains the trends in the SE-profiles quite well”.
Density of core–shell and hybrid colloids
Obtaining particle size distributions, average particle sizes or information on colloids by studying the concentration dependent sedimentation velocity from experimental sedimentation data requires the input of particle densities, see eqn (8). This is generally not a problem in case of nanoparticles larger than 20 nm consisting of a single material.In the case of core–shell and hybrid nanoparticles the actual particle density may be unknown, impeding sedimentation coefficient to radius or mass concentration to volume fraction conversions. Here, analytical ultracentrifugation shows all its merits for the investigation of transformations, aggregation processes etc. In the following, a possible workaround for particle densities in case of core-shell and hybrid nanoparticle is shortly discussed.
For smaller nanoparticles, the influence of the stabilizing shell or surface attached solvent becomes important and usually decreases the average particle density significantly. If this is not taken into account, the determined particle size will be underestimated. For reasonably monodisperse particles, another density independent hydrodynamic method like dynamic light scattering (DLS) can be used to determine the average particle size. Compared to the weight average sedimentation coefficient, this gives the average particle density and allows to calculate the particle size distribution.80 In addition, if the density of the particle core and the shell material are known, the thickness of the stabilizer shell can be determined via:80
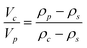 | (14) |
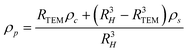 | (15) |
Here, the difference of RH − RTEM is the shell thickness. This procedure works well for rather monodisperse colloids but if the particle size distribution is broader, the range of average particle densities also gets broader. Therefore, a particle size distribution is folded with a particle density distribution which makes standard interpretation of sedimentation data erroneous and actually impossible.
A solution to this problem was recently suggested by Jamison et al.124 who make the reasonable assumption of a constant shell thickness. Jamison et al. derived an “anticipated” density of a nanocrystal consisting of a spherical inorganic core and a thin organic shell. The net density of this nanocrystal-coating assembly can be found via:
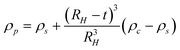 | (16) |
Across a range of sizes and materials, the core–shell model captures the absolute values of the experimental data as well as the steep size-dependent sedimentation coefficient measured in both nanocrystal systems.124 The model could be improved by a more accurate accounting of the non-uniformity of surface coatings, immobilized solvent molecules at the surface or within the coating, and shape effects. Further studies will evaluate these effects in more detail. Note that, for the small particles of interest in their work, dynamic light scattering is not suitable for measuring RH. Therefore RH is estimated by adding the shell thickness to the measured TEM core. Eqn (8) and (16) suggest that nanoparticle density, and ultimately sedimentation properties, can also be manipulated through changes in surface coatings. Fig. 9 shows the effects of varying the thickness of a surface coating on the sedimentation of gold nanocrystals. In this case, very small gold nanocrystals (core diameter = 2.2 ± 0.2 nm) were coated with polystyrene chains via a thiol end group. Using eqn (8) and a modified density as predicted by eqn (16), the sedimentation coefficient of gold coated with a short polymer chain (Mw = 1100 g mol−1) is 45 S, whereas the measured value is 37 S. A major challenge in analyzing these data is the estimate of the polymer coating thickness; if the polymers are more extended, for example, they find a sedimentation coefficient of 39 S. A thicker organic coating (grafting with higher molecular weight polymers) reduces the average sedimentation coefficient since it lowers the total particle density and increases the friction. These data illustrate that the sedimentation coefficients of nanocrystals are exquisitely sensitive to the thickness of their surface coatings. Evaluating these surface features directly in solution is challenging yet often critical in understanding nanocrystal properties in biological and environmental settings.
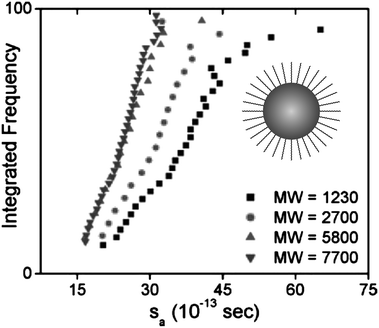 | ||
| Fig. 9 Sedimentation of polystyrene-coated gold nanocrystals in toluene. The longer the polymer chain, the smaller the density of the particles and the smaller the sedimentation coefficient. Average sedimentation coefficients, from left to right, are 23.0, 23.8, 29.2, and 36.6 S, respectively, for polymers of decreasing molecular weight. A schematic representation of a hypothetical gold particle stabilized with a polymer is shown in the graph. Figure reproduced from ref. 124 with permission of the American Chemical Society. | ||
Since the particle densities or partial specific volumes, influenced by their composition and hydration, it is very important to determine the density for converting sedimentation coefficients to radii. An advantage of using the interference optics when measuring a dilution series is that the (partial) specific particle volume can be obtained from the total fringe displacement Y with initial loading concentration c combined with the refractive indices (np and ns) of particle and solvent. The specific index of refraction can be obtained from the same SV AUC interference data, namely from total fringe displacement, Y, via:125
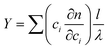 | (17) |
Here, ci is the concentration of component i, l is the SV AUC cell path length and λ is the optical wavelength (675 nm). Y for the total initial loading concentration can be determined for a sedimentation velocity run by extrapolating the fitted plateau concentrations (fringe displacement) of each sedimentation velocity scan included in the analysis with a polynomial to the time at which the rotor started to accelerate.
If the dispersion contains one species only, dn/dc in eqn (17) can be taken out of the summation and the specific refractive index can be calculated by substitution of Y, ∑ci = ctot, is the total concentration, l and λ into eqn (17). Subsequently, the specific particle volume can be calculated from dn/dc by substitution of the particle (np) and solvent (ns) refractive indices in:
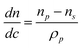 | (18) |
For core-shell particles with density ρp, the refractive index, required to determine the specific particle volume viaeqn (18) can be calculated from a volume weighted particle refractive index:
| np = ncΦc + noΦo | (19) |
This method has been applied to silica-coated boehmite rods by Planken.66 There, a specific particle volume of 0.40 mL g−1 was obtained from sedimentation velocity interference optical data via the above discussed method. This value is comparable to the specific particle volume of 0.41 mL g−1 calculated from TEM particle dimensions and bulk densities. In this case, if the results of these two methods agree well, the conversion of particle weight concentration into volume fraction is much more reliable. The small difference between the two experimentally obtained specific particle volumes may be explained on account of the limited accuracy and precision of the calculated refractive index of the core–shell rods and the shape and size polydispersity of the rods.
The same method has been applied to small silica colloids, radius ∼ 7.5 nm, reported in ref. 60. The resulting density of 1.75 g mL−1 obtained is lower than the literature reported bulk value of 2.2 g mL−1126 for amorphous silica, indicating that using bulk values for very small colloids may not be appropriate.
The importance of particle density is strongly confirmed by results on polymer coated gold particle sizes obtained by a recent contribution by Köth et al.127 Using a gold bulk density only Köth et al. found the particle core diameter of 0.8 nm from SV data. In contrast, they also used the independently determined shell thickness from Small Angle Neutron Scattering (SANS) data, yielding a particle diameter of 4.5 nm, which agrees well with the SANS hybrid diameter of 4.2 nm. This again shows the huge effect of the particle density onto the particle size from SV and underlines the importance of the correct calculation or estimation of the particle density.
An example of determining particle composition from SV comes from paper production, were the paper machines are fed with a slurry of mashed cellulose fibers, thickening agents, inorganic fillers and polymer binders.17 The binder is a latex with low Tg that helps to stick the components together, and strong adsorption to the filler, typically CaCO3, is desirable. AUC can easily determine the degree of adsorption with high statistical relevance due to the ensemble integration over 1012 particles in a single run. The turbidity optics is combined with a rotational ramp from 600 rpm to 40 000 rpm in order to capture both the micron sized filler of high density and the polymer latex (Fig. 10).
 | ||
| Fig. 10 Interaction of a polymeric binder (latex) and the inorganic filler (CaCO3) in paper production slurries. The time-dependent turbidity for the pure binder as reference which sediments after 45 min, a pigment-binder mixture with weak interaction shows the filler and binder (∼15 min.) and another mixture with strong adsorption shows that the hybrid sediments before the other components namely at ∼10 min. A TEM image (inset) of a particle contained in the latex mixture confirms the adsorption of binder (dark) on the CaCO3 (bright). Figure reproduced from ref. 17 with permission of Research Signpost. | ||
The amount of free (non-adsorbed) polymer binder cpoly can be retrieved from the transmission Tpoly at the characteristic sedimentation signal around 45 min. This concentration and transmission, cref and Tref, then serve as reference to determine the amount of free polymer binder after addition of CaCO3.17 With the signals of the turbidity raw data in Fig. 10 it is found that in case of weak adsorption the free binder amount is 95 wt% free binder (6 wt% adsorbed onto the CaCO3) in contrast to 6 wt% free binder (94% adsorbed to the CaCO3) when the binder is strongly adsorbed.17
Another example is a polymer-encapsulated UV pigment, which is thus compatibilized for optimal dispersion in a polymer matrix. The proof of successful encapsulation is the essential quality control for this product, because any fraction of pigment without a polymer coating would significantly deteriorate. Density gradient AUC can be chosen such that both the densities of the pure pigment at 1.112 g cm−3 and of the polymer at 1.18 g cm−3 are covered. Any signal at these values is a proof of non-hybrid material. Any signal in between these values is a proof of successful hybridization. The experimental finding (Fig. 11) is quite different from the usual narrow lines of latexes such as shown in Fig. 6. A broad turbid zone with a sharp edge at 1.18 g cm−3 and gradually decreasing turbidity towards lower densities is observed. This represents a fraction of pure polymer (the edge at 1.18 g cm−3) and a continuous distribution of chemical composition with a pigment loading up to 60 wt% pigment (corresponding to 1.13 g cm−3).
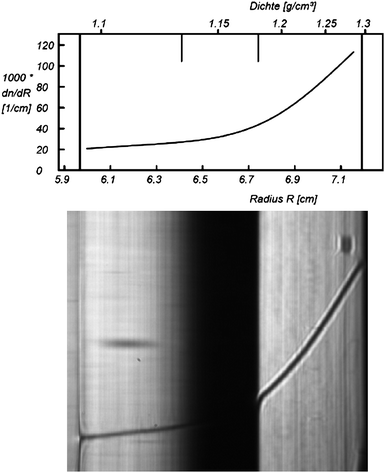 | ||
| Fig. 11 Nanocomposite latex with a pigment encapsulated. Bottom: Schlieren image from the gradient after 22 h at 40 000 rpm, 25 °C, 20 wt% Nycodenz in water. The density gradient spans the densities of the pure substances (1.112 g cm−3 for the pigment, and 1.18 g cm−3 for the polymer). It is immediately evident that the encapsulation is complete, because no pure pigment is detectable. On the high-density side, there is strong signal from pure polymer, and a range of turbid components in between. The particles hence consist of polymer with pigment loading from 0 up to 60 wt% pigment. Reproduced from ref. 17 with permission of Research Signpost. | ||
However, often the simple information on the various species in hybrid colloid mixtures via the sedimentation coefficient distribution is not sufficient to characterize a hybrid colloid system. For complex hybrid colloid mixtures, a combined analysis of AUC data with those from a different independent technique is clearly advantageous. As discussed above, the density of hybrid colloids is often unknown so that their particle size cannot be accessed. In such cases, combinations of AUC data with electron microscopy, dynamic light scattering (DLS) or flow–field–flow fractionation (FFFF) is advantageous.108 While the density independent particle size from DLS or FFFF can be very advantageously combined with the density dependent sedimentation coefficient distribution from AUC for rather monodisperse particles, this does not work well for samples that exhibit strong heterogeneity in size and density. For these cases, size distributions from FFFF can be applied but so far, there exists no available algorithm to quantitatively correlate the particle size and sedimentation coefficient distributions which would yield the density distributions. On the other hand, a global analysis approach was developed for macromolecules combining sedimentation velocity and equilibrium data with DLS to use the experimentally determined parameters from the different techniques to constrain each other and yield a multi-parameter analysis of the sample. This approach is realized in the program SEDPHAT.128–130 These approaches are clearly advantageous for the analysis of complex hybrid particles.
The ill-conditioning of the sedimentation coefficient to size conversion due to unknown particle size and density is also manifested in studies on micelles. In this case detergent/surfactant molecules self-assemble into aggregates for which the size and aggregated density may be unknown. A powerful workaround is to combine sedimentation velocity measurements with independent diffusion measurements as light scattering experiments. An early example for such a determination is reported by Morr et al.,131 reporting the determination of the molecular weights of fractionated bovine milk casein micelles from sedimentation velocity (SV AUC) and diffusion measurements.
Combined particle size and density analysis
A combined particle size and density gradient analysis is a powerful tool for the analysis of complex mixtures where the particle size as well as the density of the components varies. This is illustrated in Fig. 12. Here, a mixture of 4 different polybutylacrylate latexes (PBA) was grafted with a styrene/acrylonitrile copolymer (SAN) which has a higher density than PBA. In the density gradient, the four grafted particles are clearly resolved which indicates that the degree of grafting is different for every particle size. From the particle size distributions of the ungrafted and grafted PBA particles, it becomes obvious that the mass fraction of the smaller particles increases after grafting. This allows the conclusion that the amount of grafting is proportional to the particle surface.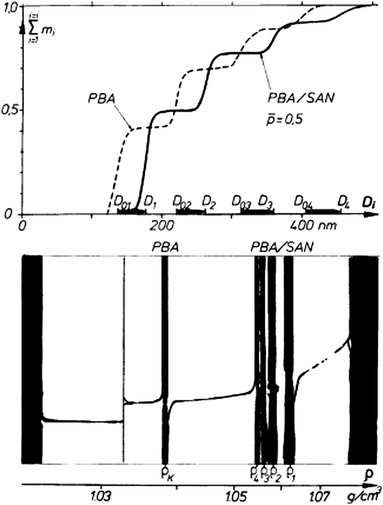 | ||
Fig. 12 Particle size distribution and density gradient of a four-modal ungrafted and a SAN-grafted PBA dispersion (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 wt.−% mixture). In the upper figure D refers to the particle diameter, the index 0i to ungrafted and i to the grafted latex. Reproduced from ref. 9 with permission of the Royal Society of Chemistry. 10 wt.−% mixture). In the upper figure D refers to the particle diameter, the index 0i to ungrafted and i to the grafted latex. Reproduced from ref. 9 with permission of the Royal Society of Chemistry. | ||
Another possibility for obtaining the density of unknown particles is to run two velocity experiments in chemically similar solvents with different densities (e.g. H2O/D2O).63,64 This allows one to simultaneously determine particle size and density distributions (Fig. 13) according to:
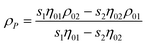 | (20) |
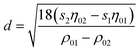 | (21) |
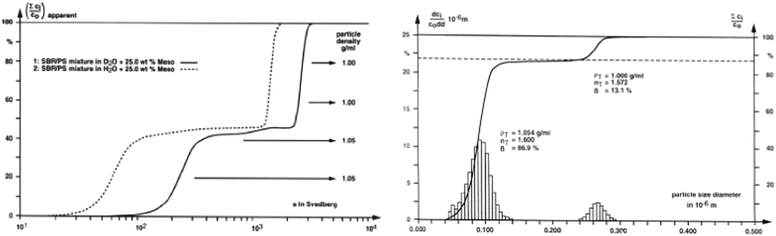 | ||
| Fig. 13 Left: sedimentation coefficient distribution of a polystyrene (PS) and polystyrene/butadiene copolymer (SBR) latex mixture in H2O and D2O63 Right: integral and differential particle size distribution evaluated from the sedimentation coefficient distributions in the left figure by application of the MIE scattering theory. Although PS and SBR float in D2O, the sedimentation coefficients are shown as positive numbers. Reprinted from ref. 63 with permission of Springer Verlag. | ||
The method works best for particles with densities < 1.5 g mL−1 but requires a rather good data quality. A diffusion correction has been implemented into this method which is especially important for small particles or molecules so that even complex mixtures become accessible via this method.132
In Fig. 13 this methodology is demonstrated for a mixture of two latices with densities of 1.000 g cm−3 and 1.054 g cm−3. They are clearly separated by particle size and particle density giving the particle size distribution with the respective particle concentrations and densities. However eqn (20) shows that the entire density distribution is available in case of broad chemical heterogeneity of the latexes.
A different class of colloidal material for which analytical ultracentrifugation has proven to be useful are carbon nanotubes. Via (preparative) density gradient ultracentrifugation (DGU) of single-walled carbon nanotubes (SWNT) Hersam et al. addressed the SWNT polydispersity problem, thus enabling the production of transparent conductors consisting predominantly of metallic SWNTs with small diameter distributions. In the DGU process, SWNTs individually encapsulated in amphiphilic surfactant molecules are ultracentrifuged at high rotational frequency within a density gradient. Under these conditions, the SWNTs are driven to their isopycnic point in the gradient (i.e., the point where the SWNT density matches the density of the surrounding medium). Following ultracentrifugation, colored bands of sorted SWNTs can be recovered and incorporated directly into transparent conductive films. Arnold et al.133 reported an analytical ultracentrifugation study on similar SWNTs. They reported the characterization of hydrodynamic properties of surfactant encapsulated single-walled carbon nanotubes (SWNTs) by optically measuring their spatial and temporal redistribution in situ, via analytical ultracentrifugation. Lamm equation solutions were fitted to experimental sedimentation velocity scans to determine the sedimentation, diffusion, and hydrodynamic frictional coefficients of the surfactant encapsulated SWNTs. For sodium cholate encapsulated SWNTs, they demonstrated that AUC is suited to determine the linear packing density of surfactant molecules along the length of the SWNTs and the anhydrous molar volume of the surfactant molecules on the SWNT surfaces. Additionally, AUC is used to measure and compare the sedimentation rates of bundled and isolated carbon nanotubes. This study serves as a guide for designing centrifuge-based processing procedures for preparing samples of SWNTs for a wide variety of applications and studies. Their results aid in understanding the hydrodynamic properties of SWNTs and the interactions between SWNTs and surfactants in aqueous solution. Arnold et al., among others, show the effect of sorting carbon nanotubes via DGU as shown in Fig. 14. As can be seen from Fig. 14, the sedimentation coefficients for SWNTs are rather small compared to conventional inorganic colloids. From Fig. 14 Arnold et al. conclude that the high-end tail in the α(s) distribution (frequency versus sedimentation coefficient) for sodium cholate encapsulated SWNTs not sorted by DGU (Fig. 14) is due to the existence of bundles that are otherwise removed by DGU. Specifically, they observed that the long tail in the α(s) distribution for bundled SWNTs overlaps the peak in the α(s) distribution near 11 S that is attributed to isolated SWNTs (Fig. 14). As a result of the overlap, the complete separation of isolated and bundled SWNTs by sedimentation-based centrifugation is unlikely.
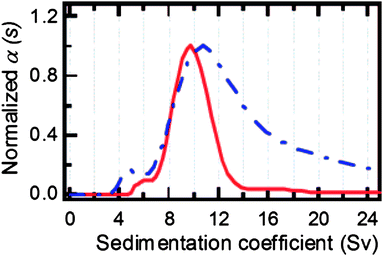 | ||
| Fig. 14 The α(s) (frequency versus sedimentation coefficient) distributions for sodium cholate encapsulated SWNTs sorted via DGU (red, solid) and not sorted by DGU (blue, dashed). Reproduced from ref. 133 with permission of the American Chemical Society. | ||
Characterization of microgels
AUC has proven to be very useful for the characterization of thermodynamic and elastic properties of gels and microgels as reviewed in ref. 134 and 135, revealing information such as whole swelling pressure–concentration curves in case of gels. Even for multiphase systems consisting of solution, lyotropic phase and a gel phase, the osmotic pressures as well as the phase boundaries can be accurately determined.136In the case of microgels in a thermodynamically good solvent, the degree of swelling Q can be directly determined from sedimentation velocity experiments. If the microgel contains uncrosslinked polymer, two components are resolved in the sedimentation coefficient distribution. From G(s) (Fig. 15), the amount of each component can be derived. The swelling degree Q can then be calculated using:
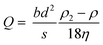 | (22) |
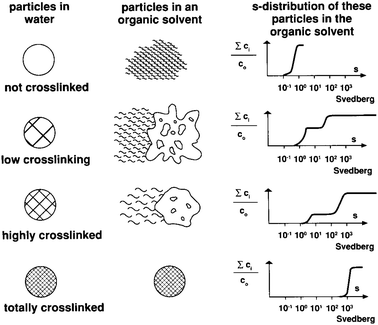 | ||
| Fig. 15 Sedimentation coefficient distributions for latexes with different degrees of cross linking. Reproduced from ref. 138 with kind permission of Springer Verlag. | ||
The particle diameter of the unswollen sample has to be determined in a non-solvent in a separate experiment (a non-solvent means that the particles do not get solvated). This can be a problem if no solvent can be found, where the microgel completely deswells or the stabilization in the non-solvent is insufficient so that aggregation occurs. The swelling degree can be related to the molar mass of the elastically effective network chains and thus to elastic properties of the microgel applying the Flory–Rehner theory.137
Such experiments allow not only the characterization of microgels but can furthermore be used to investigate the efficiency of cross linking reactions by specifying the amount and physicochemical properties of the uncrosslinked polymer.138Fig. 15 shows the sedimentation coefficient distributions, which are derived for different cross linking degrees of latexes. In this way, samples from different cross linking reactions can be easily compared.
Using the latter procedure, it is possible to not only determine average swelling degrees but whole swelling degree distributions by combining the whole sedimentation coefficient distributions for the swollen and deswollen particles in such a way that each data point in the sedimentation coefficient distributions is measured for the swollen and deswollen sample (Fig. 16). This is analogous to the algorithm for the simultaneous determination of particle size and density distributions from the combination of two sedimentation velocity experiments in two solvents of different density (eqn (17) and (18)). This new methodology enables a much more detailed view into the efficiency of cross linking reactions as shown in Fig. 16 for differently crosslinked microgels. For the microgel with low crosslinking degree, a tailing towards lower swelling degrees indicative of higher crosslinking degrees is clearly visible with ca. 5%. For the microgel with high crosslinking degree on the other hand, a broad tailing of ca. 5% of the microgel particles towards higher swelling degrees and therefore lower crosslinking degrees is clearly visible.139
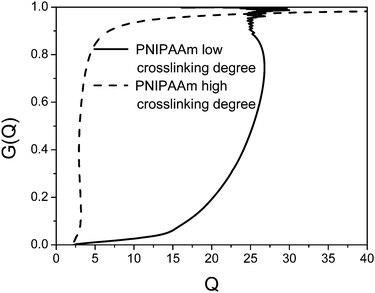 | ||
| Fig. 16 Integral distribution of the volume swelling degree Q for two fully cross linked poly(N-isopropylacrylamide) (PNIPAAm) microgels with a different cross linking density. The non monotonic increase of the distribution for the higher cross linked gel is an artifact from noise in the sedimentation coefficient distributions. Deswelling of the sample was achieved by temperature variation. Reprinted from ref. 139 with permission of the American Chemical Society. | ||
The example in Fig. 16 shows a new dimension in AUC analysis, which could excel the analysis of microgels since up to date only single values of swelling degree or swelling pressure are used to calculate the crosslinking degree. Distributions of the kind shown in Fig. 16 would in principle be transferrable to a distribution of crosslinking degree and thus distribution of network chain lengths between two crosslinks. This would for the first time allow a structural view into microgel samples, which was not possible so far.
Concluding remarks
Analytical ultracentrifugation is a very versatile technique especially suited for the analysis of all kinds of colloidal systems. Since the sample gets fractionated in the centrifugal field, even most complex samples can be separated into the individual components which can then be detected by various optical detection systems. Since no stationary phase is needed for the separation like in chromatographic techniques, sample interactions with the stationary phase can be excluded, which is especially of importance for charged samples. The whole range of colloidal systems consisting of a solvent and a dispersed phase is accessible with AUC ranging from polymers and their complexes via emulsions or nanoparticles and microgels to lyotropic phases and even bulk gels. For all of them, usually distributions of physicochemical quantities like sedimentation and diffusion coefficient, size, shape, molar mass, density, swelling degree, osmotic and swelling pressure and more are available due to the fractionation of the sample into its components.The resolution of AUC experiments is extremely high and in the Ångström range for particle size. This allows important conclusions about nanoparticle growth mechanisms. But even without any evaluation, the AUC raw data can often already yield important information about sample homogeneity, number of components, aggregation and more. The information content of AUC experiments is further increased by the introduction of new detectors like the multi-wavelength detection system, which now yields UV/Vis spectral information for all separated components, see Fig. 1. In addition, methodological improvements like global analyses greatly enhance the availability of the information content of the experiments by combining AUC experiments with other techniques like light scattering or calorimetry. It can certainly be stated that AUC is a very powerful method for colloid analysis. Even 80 years after its introduction by Svedberg, there are still a number of new methods introduced and explored for colloid analysis often yielding information on the colloidal system that cannot be obtained with such reliable statistics by any other technique. Together with new hard- and soft-ware as well as many methodological developments, we are certain that AUC will play an important role not only in its traditional role in biophysics but also in modern nanoscience and nanotechnology in applications for which it was originally developed. Provided of course that researchers become aware of the many possibilities this technique has to offer.
Notes and References
- H. K. Schachman, Ultracentrifugation in Biochemistry, Academic Press, New York and London, 1959, p xii. 272 Search PubMed.
- J. Liu and S. J. Shire, J. Pharm. Sci., 1999, 88(12), 1237–1241 CrossRef CAS.
- S. E. Harding, A. J. Rowe and J. C. Horton, Analytical Ultracentrifugation in Biochemistry and Polymer Science, Royal Society of Chemistry, Cambridge, 1992, p xiii, 629 Search PubMed.
- D. J. Scott, S. E. Harding and A. J. Rowe, Analytical Ultracentrifugation: Techniques and Methods, Royal Society of Chemistry, Cambridge, 2005, p xxiii, 587 Search PubMed.
- T. Svedberg and J. B. Nichols, J. Am. Chem. Soc., 1923, 45(12), 2910–2917 CrossRef.
- T. Svedberg and K. O. Pedersen, The Ultracentrifuge, Clarendon Press, Oxford, 1940, p x, 478 Search PubMed.
- T. Svedberg and H. Rinde, J. Am. Chem. Soc., 1924, 46(12), 2677–2693 CrossRef.
- H. Cölfen, in Analytical Ultracentrifugation: Techniques and Methods, ed. D. J. Scott, S. E. Harding and A. J. Rowe, Royal Society of Chemistry, Cambridge, 2005, pp 501–583 Search PubMed.
- W. Mächtle, in Analytical Ultracentrifugation in Biochemistry and Polymer Science, ed. S. E. Harding, A. J. Rowe and J. C. Horton, Royal Society of Chemistry, Cambridge, 1992, pp 156–162 Search PubMed.
- W. Mächtle, Biophys. J., 1999, 76(2), 1080–1091 CrossRef CAS.
- H. Cölfen, Anal. Bioanal. Chem., 2006, 385(5), 795–796 CrossRef.
- H. Cölfen and A. Völkel, Progress in Colloid Polym. Sci., 2004, 127, 31–47 Search PubMed.
- H. Cölfen, in Particle Sizing and Characterization, ed. T. Provder and J. Texter, ACS, Washington DC, 2004, Vol. 881, pp 119–137 Search PubMed.
- H. Cölfen, in Encyclopedia of Nanoscience and Nanotechnology, ed. H. S. Nalwa, American Scientific Publishers, Los Angeles, 2004, Vol. 1, pp 67–88 Search PubMed.
- H. Cölfen, Polym. News, 2004, 29(4), 101–116 Search PubMed.
- W. Mächtle and L. Börger, Analytical Ultracentrifugation of Polymers and Nanoparticles, Springer-Verlag, Berlin Heidelberg, 2006, p 237 Search PubMed.
- H. Cölfen and W. Wohlleben, in Measurement of Particle Size Distribution of Polymer Latexes, ed. L. M. Gugliotta and J. R. Vega, Research Signpost, 2010 Search PubMed.
- R. Giebeler, in Analytical Ultracentrifugation in Biochemistry and Polymer Science, ed. S. E. Harding, A. J. Rowe and J. C. Horton, Royal Society of Chemistry, Cambridge, 1992, pp 16–25 Search PubMed.
- K. Leschonski, B. Benker and H. Powitz, Part. Part. Syst. Charact., 2000, 17(3), 105–112 CrossRef CAS.
- L. A. Holladay, Biophys. Chem., 1979, 10(2), 187–190 CrossRef CAS.
- L. A. Holladay, Biophys. Chem., 1980, 11(2), 303–308 CrossRef CAS.
- M. Lechner and W. Mächtle, Prog. Colloid Polym. Sci., 1999, 113, 37–43 CAS.
- H. Fujita, Mathematical Theory of Sedimentation Analysis, Academic Press, New York and London, 1962, Vol. 11, p 327 Search PubMed.
- H. Fujita, Foundations of Ultracentrifugal Analysis, Wiley-Interscience, New York, London, Sydney and Toronto, 1975, Vol. 42, p xix, 459 Search PubMed.
- P. Schuck and B. Demeler, Biophys. J., 1999, 76(4), 2288–2296 CrossRef CAS.
- B. Demeler and H. Saber, Biophys. J., 1998, 74(1), 444–454 CrossRef CAS.
- B. Demeler, in Analytical Ultracentrifugation: Techniques and Methods, ed. D. J. Scott, S. E. Harding and A. J. Rowe, Royal Society of Chemistry, Cambridge, 2005, pp 210–230 Search PubMed.
- W. Cao and B. Demeler, Biophys. J., 2005, 89(3), 1589–1602 CrossRef CAS.
- E. Brookes and B. Demeler, Prog. Colloid Polym. Sci., 2006, 131, 33–40 CAS.
- B. Demeler and E. Brookes, Colloid Polym. Sci., 2008, 286(2), 129–137 CrossRef CAS.
- P. Schuck, Biophys. J., 2000, 78(3), 1606–1619 CrossRef CAS.
- W. F. Stafford, Anal. Biochem., 1992, 203(2), 295–301 CAS.
- W. F. Stafford, Methods Enzymol., 2000, 323, 302–325 CAS.
- W. F. Stafford and E. H. Braswell, Biophys. Chem., 2004, 108(1–3), 273–279 CrossRef CAS.
- W. F. Stafford and P. J. Sherwood, Biophys. Chem., 2004, 108(1–3), 231–243 CrossRef CAS.
- J. Philo, in Modern Analytical Ultracentrifugation: Acquisition and Interpretation of Data for Biological and Synthetic Polymer Systems, ed. T. M. Schuster and T. M. Laue, Birkhäuser, Boston, MA, 1994, pp 156–170 Search PubMed.
- J. S. Philo, Biophys. J., 1997, 72(1), 435–444 CrossRef CAS.
- J. Behlke and O. Ristau, in Analytical Ultracentrifugation: Techniques and Methods, ed. D. J. Scott, S. E. Harding and A. J. Rowe, Royal Society of Chemistry, Cambridge, 2005, pp 122–132 Search PubMed.
- E. Karabudak, W. Wohlleben and H. Cölfen, Eur. Biophys. J., 2010, 39, 397–403 CrossRef CAS.
- E. Brookes and B. Demeler, Colloid Polym. Sci., 2008, 286(2), 139–148 CrossRef CAS.
- P. H. Brown and P. Schuck, Biophys. J., 2006, 90(12), 4651–4661 CrossRef CAS.
- E. Brookes, W. Cao and B. Demeler, Eur. Biophys. J., 2010, 39(3), 405–414 CrossRef.
- V. Mittal, A. Völkel and H. Cölfen, Macromol. Biosci., 2010, 10, 754–762 CrossRef CAS.
- W. Mächtle, in Analytical Ultracentrifugation V, ed. H. Colfen, 1999, Vol. 113, pp 1–9 Search PubMed.
- L. Börger, M. D. Lechner and M. Stadler, Progress in Colloid Polym. Sci., 2004, 127, 19–25 Search PubMed.
- P. Rossmanith and W. Mächtle, Prog. Colloid Polym. Sci., 1997, 107, 159–165 CAS.
- H. G. Müller, Colloid Polym. Sci., 1989, 267(12), 1113–1116 CrossRef.
- H. G. Müller, Prog. Colloid Polym. Sci., 1997, 107, 180.
- S. K. Battacharyya, PhD Thesis, Universität Potsdam, 2006.
- E. Karabudak, PhD thesis, Universität Potsdam, 2009.
- S. K. Bhattacharyya, P. Maciejewska, L. Börger, M. Stadler, A. M. Gülsün, H. B. Cicek and H. Cölfen, Prog. Colloid Polym. Sci., 2006, 131, 9–22 CAS.
- H. Strauss, E. Karabudak, S. Bhattacharyya, A. Kretzschmar, W. Wohlleben and H. Cölfen, Colloid Polym. Sci., 2008, 286(2), 121–128 CrossRef CAS.
- H. Cölfen, T. Laue, W. Wohlleben, K. Schilling, E. Karabudak, B. Langhorst, E. Brookes, B. Dubbs, D. Zollars, M. Rocco and B. Demeler, Eur. Biophys. J., 2010, 39(3), 347–359 CrossRef.
- T. M. Laue, A. L. Anderson and B. J. Weber, in Prototype Fluorimeter for the XLA/XLI Analytical Ultracentrifuge, Proc. SPIE-Int. Soc. Opt. Eng., 1997, 1997, pp 196–204 Search PubMed.
- T. M. Laue, J. B. Austin and D. A. Rau, Prog. Colloid Polym. Sci., 2006, 131, 1–8 CAS.
- W. Mächtle, Prog. Colloid Polym. Sci., 1991, 86, 111–118.
- M. D. Lechner, J. Serb. Chem. Soc., 2005, 70(3), 361–369 CrossRef CAS.
- H. G. Müller, Prog. Colloid Polym. Sci., 2004, 127, 9–13.
- S. Roy, K. L. Planken, R. Kim, D.v. d. Mandele and W. K. Kegel, Inorg. Chem., 2007, 46(21), 8469–8471 CrossRef CAS.
- K. L. Planken, B. W. M. Kuipers and A. P. Philipse, Anal. Chem., 2008, 80(23), 8871–8879 CrossRef CAS.
- Y. Dieckmann, H. Cölfen, H. Hofmann and A. Petri-Fink, Anal. Chem., 2009, 81(10), 3889–3895 CrossRef CAS.
- W. Mächtle, Makromol. Chem., 1984, 185(5), 1025–1039 CrossRef.
- H. G. Müller and F. Herrmann, Prog. Colloid Polym. Sci., 1995, 99, 114–119.
- W. Wohlleben and M. Lechner, Colloid Polym. Sci., 2008, 286(2), 149–157 CrossRef CAS.
- H. Lange, Part. Part. Syst. Charact., 1995, 12(3), 148–157 CrossRef CAS.
- K. L. Planken, PhD thesis, Utrecht University, 2008.
- K. L. Planken, M. Klokkenburg, J. Groenewold and A. P. Philipse, J. Phys. Chem. B, 2009, 113(12), 3932–3940 CrossRef CAS.
- D. M. E. Thies-Weesie, A. P. Philipse, G. Nägele, B. Mandl and R. Klein, J. Colloid Interface Sci., 1995, 176(1), 43–54 CrossRef CAS.
- J. K. G. Dhont, An Introduction to Dynamics of Colloids, Elsevier, Amsterdam and Oxford, 1996, Vol. 2p xvii, 642p Search PubMed.
- A. P. Philipse and G. H. Koenderink, Adv. Colloid Interface Sci., 2003, 100–102, 613–639 CrossRef CAS.
- M. Raça and A. P. Philipse, Nature, 2004, 429(6994), 857–860 CrossRef CAS.
- M. Raça, B. H. Erné, B. Zoetekouw, R. van Roij and A. P. Philipse, J. Phys.: Condens. Matter, 2005, 17(15), 2293–2314 CrossRef CAS.
- G. K. Batchelor, J. Fluid Mech., 1972, 52(2), 245–268.
- G. K. Batchelor, J. Fluid Mech., 1982, 119, 379–408.
- G. K. Batchelor and C. S. Wen, J. Fluid Mech., 1982, 124, 495–528 CrossRef CAS.
- A. P. Philipse, Curr. Opin. Colloid Interface Sci., 1997, 2(2), 200–206 CrossRef CAS.
- O. Lamm, Ark. Mat. Astron. Fysik., 1929, 21B(2), 1–4 Search PubMed.
- W. Borchard, Prog. Colloid Polym. Sci., 1991, 86, 84–91 CAS.
- G. Holtus, H. Cölfen and W. Borchard, Prog. Colloid Polym. Sci., 1991, 86, 92–101 CAS.
- L. Börger and H. Cölfen, Prog. Colloid Polym. Sci., 1999, 113, 23–28 CAS.
- L. Börger, H. Cölfen and M. Antonietti, Colloids Surf., A, 2000, 163(1), 29–38 CrossRef CAS.
- P. O. Kinell, Acta Chem. Scand., 1947, 1(3), 335–350 CrossRef CAS.
- R. Signer and H. Gross, Helv. Chim. Acta, 1934, 17, 726–735 CrossRef CAS.
- R. J. Goldberg, J. Phys. Chem., 1953, 57(2), 194–202 CrossRef CAS.
- K. E. van Holde and W. O. Weischet, Biopolymers, 1978, 17(6), 1387–1403 CrossRef CAS.
- B. Demeler, H. Saber and J. C. Hansen, Biophys. J., 1997, 72(1), 397–407 CrossRef CAS.
- J. Geiselmann, T. D. Yager, S. C. Gill, P. Calmettes and P. H. Von Hippel, Biochemistry, 1992, 31(1), 111–121 CrossRef CAS.
- S. C. Gill, T. D. Yager and P. H. Von Hippel, J. Mol. Biol., 1991, 220(2), 325–333 CrossRef CAS.
- J. C. Hansen and D. Lohr, J. Biol. Chem., 1993, 268(8), 5840–5848 CAS.
- J. C. Hansen, J. Ausio, V. H. Stanik and K. E. Van Holde, Biochemistry, 1989, 28(23), 9129–9136 CrossRef CAS.
- B. Demeler and K. E. van Holde, Anal. Biochem., 2004, 335(2), 279–288 CrossRef CAS.
- D. A. Yphantis, Biophys. J., 1984, 45(2), A324–A324.
- J. Behlke and O. Ristau, Eur. Biophys. J., 1997, 25(5–6), 325–332 CrossRef CAS.
- J. Behlke and A. Knespel, J. Cryst. Growth, 1996, 158(3), 388–391 CrossRef CAS.
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322(5909), 1819–1822 CrossRef CAS.
- P. Schuck and D. B. Millar, Anal. Biochem., 1998, 259(1), 48–53 CrossRef CAS.
- P. Schuck, M. A. Perugini, N. R. Gonzales, G. J. Hewlett and D. Schubert, Biophys. J., 2002, 82(2), 1096–1111 CrossRef CAS.
- P. Schuck, Biophys. Chem., 2004, 108(1–3), 201–214 CrossRef CAS.
- P. Schuck, Biophys. Chem., 2004, 108(1–3), 187–200 CrossRef CAS.
- B. Demeler, E. Brookes, R. Wang, V. Schirf and C. A. Kim, Macromol. Biosci., 2010, 10, 1616–5187.
- L. J. Gosting, J. Am. Chem. Soc., 1952, 74(6), 1548–1552 CrossRef CAS.
- J. H. Kehrhahn, M. D. Lechner and W. Mächtle, Polymer, 1993, 34(11), 2447–2452 CrossRef CAS.
- H. Rinde, PhD thesis, Upsala University, 1928.
- J. B. Nichols, J. Appl. Phys., 1931, 1(4), 254–267 CAS.
- J. B. Nichols, E. O. Kraemer and E. D. Bailey, J. Phys. Chem., 1932, 36(1), 326–339 CrossRef CAS.
- J. B. Nichols, E. O. Kraemer and E. D. Bailey, J. Phys. Chem., 1932, 36(2), 505–514 CrossRef CAS.
- H. Cölfen, Habilitation thesis, Potsdam University, 2000.
- H. Cölfen and A. Völkel, Eur. Biophys. J., 2003, 32(5), 432–436 CrossRef.
- H. Cölfen, H. Schnablegger, A. Fischer, F. C. Jentoft, G. Weinberg and R. Schlogl, Langmuir, 2002, 18(9), 3500–3509 CrossRef.
- H. Cölfen, A. Völkel, S. Eda, U. Kobold, J. Kaufmann, A. Puhlmann, C. Göltner and H. Wachernig, Langmuir, 2002, 18(20), 7623–7628 CrossRef.
- D. H. Rapoport, W. Vogel, H. Cölfen and R. Schlögl, J. Phys. Chem. B, 1997, 101(21), 4175–4183 CAS.
- E. A. Hauser and H. K. Schachman, J. Phys. Chem., 1940, 44(5), 584–591 CrossRef CAS.
- E. G. Pickels, in Colloid Chemistry, Theoretical and Applied, ed. J. Alexander, Reinhold Publishing Corporation, New York, 1944, Vol. 5, p 411 Search PubMed.
- G. Schmid, R. Pfeil, R. Boese, F. Bandermann, S. Meyer, G. H. M. Calis and W. A. van der Velden, Chem. Ber., 1981, 114(11), 3634–3642 CrossRef CAS.
- H. Cölfen and T. Pauck, Colloid Polym. Sci., 1997, 275(2), 175–180 CrossRef CAS.
- H. M. Zheng, R. K. Smith, Y. W. Jun, C. Kisielowski, U. Dahmen and A. P. Alivisatos, Science, 2009, 324(5932), 1309–1312 CrossRef CAS.
- J. W. Jansen, C. G. de Kruif and A. Vrij, J. Colloid Interface Sci., 1986, 114(2), 501–504 CrossRef CAS.
- Z. Dogic, A. P. Philipse, S. Fraden and J. K. G. Dhont, J. Chem. Phys., 2000, 113(18), 8368–8380 CrossRef CAS.
- J. G. Garcia de la Torre and V. A. Bloomfield, Q. Rev. Biophys., 1981, 14(1), 81–139 CAS.
- D. M. E. Thies-Weesie, PhD thesis, Utrecht University, 1995.
- A. Torres, A. Cuetos, M. Dijkstra and R. van Roij, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75(4), 041405 CrossRef.
- J. Zwanikken and R. van Roij, Europhys. Lett., 2005, 71(3), 480–486 CrossRef CAS.
- R. van Roij, J. Phys.: Condens. Matter, 2003, 15(48), S3569–S3580 CrossRef CAS.
- J. A. Jamison, K. M. Krüger, C. T. Yavuz, J. T. Mayo, D. LeCrone, J. J. Redden and V. L. Colvin, ACS Nano, 2008, 2(2), 311–319 CrossRef CAS.
- T. M. Laue Choosing Which Optical System of the Optima™ XL-I Analytical Ultracentrifuge to Use, A-1821A, Beckman Instruments, Inc., Fullerton, California, 1996 Search PubMed.
- D. R. Lide, CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data, CRC, Boca Raton, Fla.; London, 81st edn, 2000 Search PubMed.
- A. Köth, B. Tiersch, D. Appelhans, M. Gradzielski, H. Cölfen and J. Kötz, Langmuir Search PubMed , submitted.
- J. C. D. Houtman, P. H. Brown, B. Bowden, H. Yamaguchi, E. Appella, L. E. Samelson and P. Schuck, Protein Sci., 2007, 16(1), 30–42 CrossRef CAS.
- J. Vistica, J. Dam, A. Balbo, E. Yikilmaz, R. A. Mariuzza, T. A. Rouault and P. Schuck, Anal. Biochem., 2004, 326(2), 234–256 CrossRef CAS.
- P. Schuck, Anal. Biochem., 2003, 320(1), 104–124 CrossRef CAS.
- C. V. Morr, S. H. C. Lin, R. K. Dewan and V. A. Bloomfield, J. Dairy Sci., 1973, 56(4), 415–418 CrossRef CAS.
- K. Schilling, PhD thesis, Universität Potsdam, 1999.
- M. S. Arnold, J. Suntivich, S. I. Stupp and M. C. Hersam, ACS Nano, 2008, 2(11), 2291–2300 CrossRef CAS.
- H. Cölfen, Colloid Polym. Sci., 1995, 273(12), 1101–1137 CrossRef.
- H. Cölfen, in Biotechnology & Genetic Engineering Reviews, ed. S. E. Harding and M. P. Tombs, Intercept, Andover, 1999, Vol. 16, pp 87–140 Search PubMed.
- G. P. Miles, Z. Thomas, D. Monique and C. Helmut, ChemPhysChem, 2008, 9(6), 882–890 CrossRef CAS.
- P. J. Flory and J. Rehner, J. Chem. Phys., 1943, 11(11), 521–526 CrossRef CAS.
- H. G. Müller, A. Schmidt and D. Kranz, Prog. Colloid Polym. Sci., 1991, 86, 70–75.
- D. Kuckling, C. D. Vo, H. J. P. Adler, A. Völkel and H. Cölfen, Macromolecules, 2006, 39(4), 1585–1591 CrossRef CAS.
Footnote |
| † The software mentioned in this contribution can be downloaded free of charge from http://www.rasmb.bbri.org/which which also hosts a discussion forum for AUC users. |
| This journal is © The Royal Society of Chemistry 2010 |
