Ab initio modeling of TiO2 nanotubes
Dénes
Szieberth
*a,
Anna Maria
Ferrari
a,
Yves
Noel
b and
Matteo
Ferrabone
a
aDipartimento di Chimica IFM, Università di Torino, NIS -Nanostructured Interfaces and Surfaces - Centre of Excellence, Via P. Giuria 7, 10125 Torino, Italy Web: http://www.nis.unito.it
bInstitut des Sciences de la Terre de Paris (UMR 7193 UPMC-CNRS), UPMC-Paris Universitas, France
First published on 11th November 2009
Abstract
TiO2 nanotubes constructed from a lepidocrocite-like TiO2 layer were investigated with ab initio methods employing the periodic CRYSTAL code. The dependence of strain energies, structural and electronic properties on the tube diameter was investigated in the 18–57 Å range. Nanotubes constructed by a (0,n) rollup proved to be the most stable at all diameters. All three types of rollup undergo significant reconstruction at diameters <25 Å. All investigated structures possess a high (∼5.4 eV) band gap compared to bulk TiO2 phases (3.96 and 4.63 eV for rutile and anatase calculated with the same functional and basis set).
Introduction
TiO2 nanotubes received widespread attention in the last decade owing to their unique chemical properties.1 One of the most common methods of preparation is hydrothermal treatment of titania2 in basic solutions. Despite the large number of investigations, atomic level information on the structure of nanotubes prepared in this way is still ambiguous.1 Based on SAED and HRTEM studies Wang3 found that nanotubes prepared by the hydrothermal method from anatase powder have the anatase layer structure. Saponjic4 also assumed a quasi-anatase structure based on the similarity of the XANES spectra to that of small-diameter titaniananoparticles. A later electron diffraction study by Akita5 gave the conclusion that the crystalline structure of a similarly prepared sample differs from that of anatase, and a lepidocrocite-like structure was proposed. The lepidocrocite-like structure is also supported by the fact that ab initio calculations on thin anatase-derived TiO2 nanolayers found that some of these layers rearrange spontaneously to lepidocrocite.6,7 The trititanate structure H2Ti3O7 as found by XRD and SAED investigations8,9 was also invoked as building motif for nanotubes made by similar methods, and other titanate structures were also proposed10–12Although theoretical calculations can play a major role in providing information on the atomic scale, because of the size of the systems involved, only a handful of computational studies of TiO2 nanotubes appear in the literature. Enyashin13 investigated the structures of several anatase- and lepidocrocite-type nanotubes with varying diameter using a density functional theory—tight binding method (DFT-TB) and found that the topology of the nanotubes did not change significantly from the geometry of the flat layers even in the case of small diameters. The band gap of the (0,n) lepidocrocitenanotubes was found to increase with the diameter of the tube from the value of 3.85 eV at the diameter of 12 Å to the value of 4.50 eV at the diameter of 27 Å, above this diameter there was no change observed in the band gap. The (n,0) lepidocrocite tubes showed a band gap close to the 4.5 eV value already at 11 Å, and this value did not change significantly with the increasing diameter.
Hydroxylated lepidocrocitenanoribbons were also investigated with the help of ab initio methods and were shown to adopt curved structures, enabling them to act as models for nanotubes.14 Zhao15 calculated the structures, strain energies and band gaps of small-radius anatase zigzag and armchair nanotubes using full ab initio methods, finding significantly smaller band gap values than the DFT-TB study.13
The aim of this study is to provide ab initio structural and electronic data for some lepidocrocite-based nanotubes. The electronic properties of TiO2 nanotubes are of great interest due to the possible use of these structures in photocatalytic and optoelectronic applications.1 (n,0) and (0,n) lepidocrocitenanotubes have only been investigated with the DFT-TB method before, and only in a limited diameter range (up to 16 Å).13 In this work the periodic CRYSTAL16 code has been employed for all calculations within a DFT approach. (n,0), (0,n) and (n,n) nanotubes have been considered with a tube diameter D up to 57 Å, which approaches better the experimentally observed size, D ∼ 100 Å.5 The relationships between the steric hindrance and electronic structure of these nanotubes are also addressed.
Methods
Calculations were performed with a development version (containing the ability to exploit helical symmetry) of the periodic ab initio CRYSTAL0616 code, using the hybrid PBE017 DFT functional. This functional was reported to give accurate structural and electronic properties for TiO2 crystals.18 All calculations were performed using an all-electron 8-411G (d) Gaussian-type basis set19 for O, and a Hay–Wadt small core ECP20 with a 411-31 [3sp2d] basis set for valence electrons19 for Ti atoms. These basis sets were proven to give results of acceptable accuracy with moderate computational cost.21 The level of accuracy in evaluating the Coulomb and the exchange series is controlled by five parameters16 for which an 8 8 8 8 16 setting was used. The convergence threshold for SCF energy was set to 10−7 Ha. The reciprocal space was sampled according to a regular sublattice determined by the shrinking factor16 10 (6 independent k-points in the irreducible part of the Brillouin zone).The DFT exchange–correlation energy was evaluated by numerical integration over the unit cell volume. In CRYSTAL, a Gauss–Legendre radial and a Lebedev angular grid of points was used. In the present calculations a (75,974) pruned grid was applied.
Structure optimizations were performed by the use of analytical derivatives of the energy with respect to atomic coordinates and unit cell parameters within a quasi-Newton scheme. For the updating of the Hessian, the BFGS scheme is used. Convergence of the geometry was checked on both gradient components and nuclear displacements for which the default values were chosen.16 These methods do not guarantee the finding of the most stable lepidocrocite-like arrangement, however trial optimizations from slightly modified starting geometries resulted in the same minima.
The computation of nanotubes having large unit cells (432 atoms in case of the (36,36) nanotube) was made possible by the exploitation of the helix roto-translational symmetry of these structures. This symmetry is used for the automatic generation of the structures, for the calculation of one and two-electron integrals (only the irreducible part of the Fock matrix is calculated then rotated by the symmetry operators of the point group to generate the full Fock matrix), and for the diagonalization of the Fock matrix where each irreducible representation is treated separately.22
Results and discussion
The model of the lepidocrocite-like TiO2 structure was built from the unit cell of lepidocrocite FeO(OH) by exchanging the Fe atoms to Ti, omitting the hydrogen atoms and cutting a slab in the (010) direction in the plane between the formerly hydrogen-bonded sheets. The slab was subsequently optimized without constraints on the unit cell geometry. The structure of the resulting TiO2 sheet can be seen on Fig. 1. The calculated unit cell parameters (a = 2.979 Å, b = 3.740 Å) show good agreement with the values reported by Sambi23 (a = 3.02 Å, b = 3.73 Å).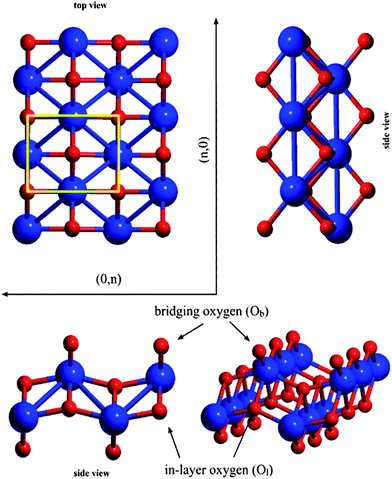 | ||
| Fig. 1 Directions and notation of atoms on the lepidocrocite-like TiO2 layer. The lepidocrocite elementary cell is highlighted. | ||
Two types of oxygen atoms can be distinguished: two-coordinated bridging oxygen atoms (Ob) and four-coordinated in-layer (Ol) oxygens; Ob atoms possess lower negative Mulliken net charges (qOb = −1.01 au) and shorter Ob–Ti distance (dOb–Ti = 1.813 Å) than Ol –s (qOl = −1.29 au and dOl–Ti = 1.966 and 2.174 Å), which show higher ionic character.
Unlike the graphenenanotubes, the 2D lepidocrocite sheet's rectangular unit cell gives different structures in the (n,0) and (0,n) cases, so we have investigated three types; (n,0),(0,n) and (n,n) nanotubes. See ref. 22 for a detailed discussion concerning the nanotube construction.
(n,0) structures
Geometries of the n = 16, 20, 28, 36 and 48 (D = 18.0–45.5 Å) nanotubes were fully optimized. In the case of the (n,0) rollup, the bridging oxygen rows of the lepidocrocite slab form concentric rings on the internal and external surface of the nanotube perpendicular to the tube axis (see representative rollups in this direction in Fig. 2). The curvature of the tube elongates the bonds of the bridging oxygens on the external surface, Obe, while compressing those on the internal surface Obi, creating a considerable strain. Calculated geometrical and electronic parameters as well as strain energies are compiled in Table 1. Strain energies, ES (calculated as the difference between the energy of one TiO2 unit in the fully optimized nanotube and the energy of one such unit in the optimized flat layer) and E′S(calculated employing the energy of the rolled but not optimized nanotube) plotted against the tube diameter, D (calculated as the mean distance of the inner and outer surface bridging oxygen atoms on opposite sides of the nanotube), can be seen on Fig. 3. At small D the difference between ES and E′S is large, showing the large energy that can be gained through the reorganization of the atoms on the nanotube surfaces. Accordingly, in sharp contrast to the results given by the DFT-TB calculations of Enyashin,13 tubes of small diameter undergo considerable bond rearrangement to relieve this strain. While according to the calculations of Enyashin the maximum Ti–O bond length difference between the nanotubes and the infinite flat layer is 0.03 Å, our results show that in the case of the (16,0) nanotube (D = 18.0 Å) the oxygen bridges at the external surface break, and the external bridging oxygen atoms Obe form very short bonds dTie–Obe = 1.616 Å, cf. the 1.813 Å of the flat slab) towards one of the pillar Ti atoms, while the distance from the other pillar Ti atom increases to dTie–Obe = 3.393 Å (Table 1, Fig. 2a). Bridging oxygen atoms on the inner surface of the tube follow the asymmetry of the outer layer although to a much smaller extent. The unsaturated Ti and O atoms created this way can play a role in the stabilization of the experimentally observed multilayer structures as was reported for quasi-anatase nanotubes,4 however in contrast to the structure assumed there, the under-coordinated sites occur only on the external surface. Under-coordinated sites can also play an important role in the hydration or hydroxylation of the nanotube surface.24 The elimination of the strain with the increasing diameter of the tube can be traced to the decreasing difference of the Ti–O bond lengths of the bridging oxygen atoms (Table 1). The difference is practically eliminated in case of the (28,0) tube (D = 27.4 Å) for the inner and (36,0) tube (D = 34.3 Å) for the outer surface bridging oxygens. Another, perhaps more sensitive geometrical measure of the strain is provided by: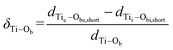 | (1) |
| n | D/Å | E ′S [eV/TiO2] | E s [eV/TiO2] | Tie–Obe,long/Å | Tie–Obe,short/Å | Tii–Obi,long/Å | Tii–Obi,short/Å | q Obe/au | E g/eV |
|---|---|---|---|---|---|---|---|---|---|
| 16 | 18.0 | 2.71 | 0.85 | 3.393 | 1.616 | 1.835 | 1.751 | −0.83 | 5.39 |
| 20 | 20.9 | 1.65 | 0.73 | 2.673 | 1.658 | 1.783 | 1.769 | −0.93 | 5.82 |
| 24 | 24.0 | 1.55 | 0.58 | 2.325 | 1.701 | 1.772 | 1.770 | −1.00 | 5.69 |
| 28 | 27.4 | 0.81 | 0.46 | 2.171 | 1.730 | 1.774 | 1.770 | −1.02 | 5.59 |
| 36 | 34.3 | 0.48 | 0.30 | 1.879 | 1.875 | 1.773 | 1.773 | −1.05 | 5.19 |
| 48 | 45.5 | 0.27 | 0.17 | 1.859 | 1.857 | 1.782 | 1.782 | −1.04 | 5.26 |
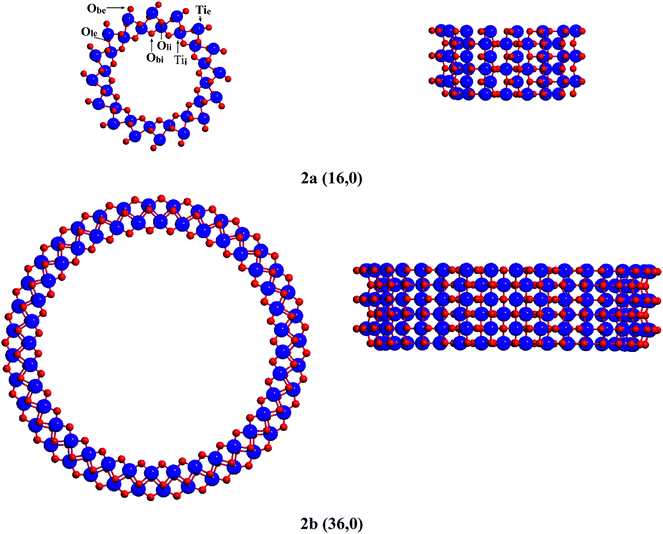 | ||
| Fig. 2 Cross-sectional view of (n,0) lepidocrocitenanotubes. | ||
 | ||
| Fig. 3 Strain energies of lepidocrocitenanotubes. | ||
 | ||
| Fig. 4 δ Ti–Ob (in case of (n,0)and (n,n)) and (δTi–Ol) values. See text for details. | ||
The significant geometrical changes caused by the excessive strain cause changes in the electronic structure of the nanotubes as well. Mulliken net charges on the bridging Ob atoms, qObe, were calculated as a function of the tube diameter (Table 1). Negative charges accumulated at the bridging Obe atoms show an increasing tendency with the tube diameter from qObe = −0.83 au for the (16,0) case until qObe = −1.00 au for the (24,0) case, where they reach the flat slab value, indicating the transfer from a covalent double-bonded oxygen to a more ionic bridge position. Simultaneously, charges of the Ti atoms linked to the Obes (Tie) change from 2.18 to 2.31 au. Mulliken charges on the other atoms show only insignificant variations. The modification in the nature of the Tie–Obe bonding as induced by the geometrical strain is also monitored by the projected density of states (DOS). Similarly to results of ab initio calculations for bulk TiO2rutile and anatase,18 in lepidocrocitenanosheets and nanotubes, the top of the valence bands is dominated by the oxygen 2p states and the conduction bands are characterized by Ti 3d states. However in nanotubes, the electron structure shows considerable variations with D. At small diameters, the (16,0) case, the edge of the valence band is determined by states originating from the oxygen atoms on the external surface of the tube (see DOS plots in Fig. 5). The 2p Obe states are localized in a more narrow range of energies with respect to the 2p Obi bands, and are almost perfectly superimposed on the occupied states of the external Ti, thus reflecting the localized nature of the Tie–Obe double bond. As the Obe move from a “double-bonded” to a “bridging” position with the increase of the tube diameter, the 2p Obe states upshift and widen concomitantly with the increasing ionic character of these atoms and with a simultaneous upshift of all DOS profiles (Fig. 5 and 7). Above the (28,0) tube, further change in the diameter does not influence the occupied band edge significantly.
 | ||
| Fig. 5 Projected densities of states for (n,0) nanotubes. | ||
 | ||
| Fig. 6 Band gaps of lepidocrocitenanotubes. The horizontal line denotes the band gap of the infinite flat layer. | ||
Band gap values (Eg) calculated for the nanotubes (between 5.19 and 5.82 eV) and the flat lepidocrocite-like layer (5.43 eV) are considerably higher than those calculated by Enyashin,13 and higher than expected from the bulk value (since bulk lepidocrociteTiO2 is nonexistent, the calculated bulk value of rutile with the same computational parameters: 4.1 eV is used for comparison). The increase of the band gap compared to the bulk value was earlier observed in the case of nanotubes constructed from anatase layers.15 The band gap follows a discontinuous trend that reflects the variation in the electron structures: from (16,0) to (20,0), the gap increases with the size of the tube up to 5.82 eV; above (20,0) the gap decreases and approaches the value of a lepidocrocitenanosheet (Fig. 6). At the largest investigated diameters (closest to the experimentally observed ones) the (n,0) nanotubes possess a direct band gap, similarly to the infinite flat layer.
 | ||
| Fig. 7 Topmost energies of the valence bands and lowest energies of the virtual bands for lepidocrocitenanotubes. | ||
(0,n) structures
Geometries of the n = 14, 16, 20, 28, 36 and 48 (D = 18.1–57.3 Å) nanotubes were optimized. Strain energies and selected geometrical and electronic parameters are compiled in Table 2. In contrast to the (n,0) nanotubes the bridging oxygens run parallel to the axis of the tube in the (0,n) structures (Fig. 8), so these bonds do not contribute to the strain caused by the bending. dTie–Obe and dTii–Obi distances change by no more than 0.005 Å in the whole diameter range. For the (0,16) nanotubes these distances are 1.817 and 1.808 Å, while for the (0,48) nanotube they are 1.814 and 1.813 Å respectively, practically equal to the flat slab value of 1.813 Å. The strain is caused mainly by the titanium in-layer oxygen bonds, Tie–Ole, perpendicular to the tube axis. The high curvature in the case of the small-diameter tubes causes a bond rearrangement among the in-layer Ti and O atoms: similar to the breaking up of bridging O–Ti bonds in the (n,0) cases, the in-layer Ti–O bonds break up, while one of the Ole–Tie distances increases to 2.699 Å (cf. the flat slab value of 1.966) in the case of the (0,14) nanotube (D = 18.1 Å), the other decreases to 1.842 Å (see Fig. 8a), transforming the originally four-coordinated Ole to a three-coordinated one. This reconstruction is active up to the (0,20) nanotube (D = 24.6 Å), above this diameter the two Ole–Tie distances are practically equal. This extensive rearrangement is again in sharp contrast to the observations made by Enyashin13 on the calculated geometry of these nanotubes. The under-coordinated surface sites formed this way are probably important both for the interlayer bonding in multilayer nanotubes and for water adsorption as well, although to a smaller extent than the (n,0) case.| n | D/Å | E ′S [eV/TiO2] | E s [eV/TiO2] | Tie–Ole,long/Å | Tie–Ole,short/Å | Tii–Oli,long/Å | Tii–Oli,short/Å | q Ole/au | E g/eV |
|---|---|---|---|---|---|---|---|---|---|
| 14 | 18.1 | 0.67 | 0.31 | 2.699 | 1.842 | 1.992 | 1.955 | −1.24 | 5.64 |
| 16 | 20.2 | 0.50 | 0.27 | 2.564 | 1.861 | 1.968 | 1.944 | −1.25 | 5.61 |
| 20 | 24.6 | 0.31 | 0.21 | 2.339 | 1.917 | 1.936 | 1.926 | −1.28 | 5.42 |
| 28 | 33.6 | 0.16 | 0.11 | 2.054 | 2.052 | 1.920 | 1.920 | −1.30 | 5.24 |
| 36 | 43.0 | 0.09 | 0.07 | 2.023 | 2.023 | 1.927 | 1.927 | −1.29 | 5.31 |
| 48 | 57.3 | 0.05 | 0.04 | 2.012 | 2.012 | 1.934 | 1.934 | −1.29 | 5.36 |
 | ||
| Fig. 8 Cross-sectional view of (0,n) lepidocrocitenanotubes. | ||
The strain on the bonds can also be monitored by employing a δTi–Ol indicator, in analogy with δTi–Ob of eqn (1), where the Ti–Ol distances are used instead of Ti–Ob lengths, since, for the (0,n) tubes, these are the distances that show the largest variations. δTi–Ol for the (0,n) tubes is initially smaller than δTi–Ob for the (n,0) cases in Fig. 4, but approaches zero at about the same diameter (D = 33.6 Å for the (0,28) tube, vs.D = 34.1 Å for the (36,0) tube).
Accordingly, ES and the difference between ES and E′S for (0,n) tubes is always smaller than (n,0) showing that at any calculated diameter the (0,n) rollup is energetically preferred over the (n,0) one, Fig. 3. However, since the experimentally observed nanotubes have a diameter of ∼10 nm,5 about 1.7 times than that of our largest calculated ones, an extrapolation of the trend reported in Fig. 3, indicates that at large diameters the ES difference due to the two different rollups becomes insignificant.
The largest changes in the Mulliken charges with the tube diameter are displayed by the Ole atoms: however these changes are small (ranging from qOle = −1.23 in the (0,14) case to qOle = −1.30 au in the (0,28) case) whereas qOl = −1.29 is the value of the flat nanosheet. Seemingly, projected DOS values do not change qualitatively with the tube diameter, the most significant variation is a moderate upshift of the top of the valence band caused by the Ole atoms; however, already from the (0,28) case no further shift can be observed (see Fig. 9). The small changes in the electron structure versus the large changes in geometry described for low-diameter nanotubes (because of the break of the Tie–Ole bonds) can possibly be explained by invoking the high ionic character of the bonding involving Ole: as typical in ionic oxides, in small (0,n) tubes, the reduced coordination from four to three of Ole is compensated by shorter bond distances: 1.842 Å vs. the flat surface value of 1.966 Å for Tie–Ole, and 2.155 Å vs. the flat surface value of 2.174 Å for Ole–Tii.
 | ||
| Fig. 9 Projected densities of state for (0,n) nanotubes. | ||
Unlike the (n,0) case, the plot of the EgversusD for the (0,n) nanotubes (Fig. 6), is shaped mainly by changes in the valence bands, since the lowest energy of the virtual bands shows only insignificant changes in the investigated diameter region (Fig. 7). In addition, the magnitude of the change in Eg due to changes in D is also smaller than in the (n,0) tubes, aligning well with the small changes in the electron structure exhibited by this type of nanotube.
Again, at large diameters these nanotubes possess a direct band gap, similarly to the infinite flat lepidocrocite-like TiO2 layer.
(n,n) structures
Strain energies and selected geometrical and electronic parameters of these nanotubes are compiled in Table 3. Although this structure does not display a larger residual strain energy at small tube diameters than the other two cases, this strain decreases much slower with the increasing tube diameter. During the formation of a nanotube, atoms in the circumferential direction experience the highest initial displacement. In the case of the (n,n) nanotubes, the circumferential direction connects atoms of the same type, so the rolling up creates horizontal “stripes” of Ti and O atoms. As a result, in the internal layers of the nanotube short Ti–Ti (e.g.: 2.864 Å instead of 2.979 Å in the (14,14) case) distances form, causing unfavorable interactions. During the relaxation the minimal Ti–Ti distances increase back to 3.079 Å by the opening of some of the original four-membered rings of the lepidocrocite layer (Fig. 10). The same reconstruction can be observed throughout the entire investigated diameter range. This reconstruction results in tetravalent Ti atoms, consequently the strain energy of the relaxed tube remains high even at relatively high diameters, although this destabilization is not a direct consequence of the curvature, but the rearrangement of the bonds in the nanotube wall. It is clear that while the (0,n) and (n,0) nanotubes at the highest investigated diameters already have surface geometries similar to the infinite flat layer, the (n,n) nanotubes still possess a different bond structure. δTi–Ob for the (n,n) nanotubes is reported in Fig. 4. The small gradient of this curve aligns well with the similar behavior of the strain energies.| n | D/Å | E ′S [eV/TiO2] | E S [eV/TiO2] | Tie–Obe,long/Å | Tie–Obe,short/Å | Tii–Obi,long/Å | Tii–Obi,short/Å | q Obe/au | E g/eV |
|---|---|---|---|---|---|---|---|---|---|
| 14 | 18.1 | 1.86 | 0.77 | 2.327 | 1.708 | 1.880 | 1.791 | −1.03 | 5.39 |
| 16 | 23.8 | 1.77 | 0.72 | 2.285 | 1.716 | 1.889 | 1.786 | −1.04 | 5.35 |
| 20 | 30.0 | 1.68 | 0.66 | 2.209 | 1.731 | 1.899 | 1.786 | −1.06 | 5.28 |
| 24 | 36.0 | 1.62 | 0.63 | 2.160 | 1.741 | 1.906 | 1.786 | −1.07 | 5.25 |
| 26 | 39.0 | 1.61 | 0.62 | 2.140 | 1.745 | 1.909 | 1.787 | −1.07 | 5.24 |
| 30 | 44.5 | 1.58 | 0.60 | 2.115 | 1.751 | 1.915 | 1.787 | −1.08 | 5.23 |
 | ||
| Fig. 10 Cross-sectional view of (n,n) lepidocrocitenanotubes. | ||
The electronic properties of the (n,n) nanotubes also display different behavior from the other two cases; qObe is almost constant for the whole investigated range, displaying only a minute increase with diameter. Band gaps also show the least change with diameter of the three types of tubes, although a small decrease can be observed, owing to minute changes in the band structure. The projected DOS profiles (not shown) do not exhibit significant changes upon increasing D, reflecting the relatively small geometrical changes in this type of nanotube. Unlike the previous two cases, these nanotubes possess an indirect band gap even at the largest investigated diameter, the indirect gap being 0.26 eV smaller than the direct one, indicating that the electronic structure is still far from that of the infinite flat layer at this diameter.
Conclusions
Geometrical and electronic properties of TiO2 nanotubes possessing a lepidocrocite-like structure were investigated in a diameter range (18–57 Å) that was hitherto unavailable by ab initio methods because of computational cost.Of the calculated (n,0), (0,n) and (n,n) structures, the (0,n) rollup was found to be the most stable in the whole investigated diameter range. In the (n,0) and (0,n) cases, strain energies approached zero at the higher end of the investigated diameter range, while the strain in the (n,n) tubes decreased at a smaller rate. Changes in the strain energies could be correlated to geometrical differences between the external and internal tube surfaces.
In case of the (0,n) and (n,0) nanotubes, at diameters smaller than 25 Å, bond reconstruction took place. At the largest calculated diameters both geometries and strain energies were approaching the values corresponding to the infinite flat layer. In case of the (n,n) nanotubes the same large surface reconstruction can be observed in the whole calculated diameter range, and the strain energy remains relatively high even at the largest investigated diameter. These results indicate that while at low diameters (∼5 nm, like in case of the inner walls of multi-walled nanotubes5) the (0,n) rollup is preferred over the other structures, at higher diameters (approaching 10 nm) the (n,0) structure is feasible as well.
All three types of nanotubes as well as the parent lepidocrocite-like TiO2 layer were proven to possess band gaps considerably higher than bulk TiO2 phases. Changes in the band gap with diameter could be traced to states originating from atoms suffering the largest geometry changes during reconstruction.
References
- D. V. Bavykin, J. M. Friedrich and F. C. Walsh, Adv. Mater., 2006, 18, 2807–2824 CrossRef CAS.
- T. Kasuga, M. Hiramatsu, A. Hoson, T. Sekino and K. Niihara, Langmuir, 1998, 14, 3160–3163 CrossRef CAS.
- Y. Q. Wang, G. Q. Hu, X. F. Duan, H. L. Sun and Q. K. Xue, Chem. Phys. Lett., 2002, 365, 427–431 CrossRef CAS.
- Z. V. Saponjic, N. M. Dimitrijevic, D. M. Tiede, A. J. Goshe, X. Zuo, l. X. Chen, A. S. Barnard, P. Zapol, R. Curtiss and T. Rajh, Adv. Mater., 2005, 17, 965–971 CrossRef CAS.
- T. Akita, M. Okumura, K. Tanaka, K. Ohkuma, M. Kohyama, T. Koyanagi, M. Date, S. Tsubota and M. Haruta, Surf. Interface Anal., 2005, 37, 265–269 CrossRef CAS.
- A. Vittadini and M. Casarin, Theor. Chem. Acc., 2008, 120, 551–556 CrossRef CAS.
- F. Alvarez-Ramirez and Y. Ruiz-Morales, Chem. Mater., 2007, 19, 2947–2959 CrossRef CAS.
- Q. Chen, W. Zhou, G. Du and L. Peng, Adv. Mater., 2002, 14, 1208 CrossRef CAS.
- S. Afshar and M. Hakamizadeh, J. Exp. Nanosci., 2009, 4, 77–86 Search PubMed.
- J. Yang, Z. Jin, X. Wang, W. Li, J. Zhang, S. Zhang, X. Guo and Z. Zhang, Dalton Trans., 2003, 3898–3901 RSC.
- Nakahira, W. Kato, M. Tamai, T. Isshiki, K. Nishio and H. Aritani, J. Mater. Sci., 2004, 39, 4239–4245 CrossRef CAS.
- D. H. Kim, Y. H. Jung, D.-K. Choi, S.-J. Kim and K. S. Lee, J. Nanosci. Nanotechnol., 2009, 9, 941–945 CrossRef CAS.
- A. N. Enyashin and G. Seifert, Phys. Status Solidi B, 2005, 242, 1361–1370 CrossRef CAS.
- M. Casarin, A. Vittadini and A. Selloni, ACS Nano, 2009, 3, 317 CrossRef CAS.
- J. Wang, L. Wang, L. Maa, J. Zhao, B. Wang and G. Wang, Phys. E., 2009, 41, 838–842 CrossRef CAS.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arcoand M. Llunell, Crystal 2006 User's Manual, University of Torino, Torino, 2006 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Labat, P. Baranek and C. Adamo, J. Chem. Theory Comput., 2008, 4, 341–352 CrossRef CAS.
- http://www.crystal.unito.it/Basis_Sets/Ptable.html .
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270 CrossRef CAS.
- Xin Dong, MSc thesis, University of Torino, 2009.
- Y. Noel, P. D'arco, R. Demichelis, C. M. Zicovich-Wilson and R. Dovesi, J. Comp. Chem., 2009 DOI:10.1002/jcc.21370.
- T. Orzali, M. Casarin, G. Granozzi, M. Sambi and A. Vittadini, Phys. Rev. Lett., 2006, 97, 156101 CrossRef.
- U. Diebold, Surf. Sci. Rep., 2003, 48, 53–229 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2010 |
