TiO₂ nanotubes and their application in dye-sensitized solar cells

Abstract

The present article reviews the current status of using TiO₂ nanotubes in Grätzel-type, dye-sensitized solar cells and extends the overview with the latest results and findings. Critical factors in tube geometry (length, diameter, top morphology), crystal structure (amorphous, anatase, rutile) as well as factors affecting dye loading or electron mobility are addressed. The highest solar cell efficiencies today for pure nanotube systems reach approximately 4% while for some mixed systems, around 7% has been reported. For both systems significant room for enhancement is anticipated and some key points and strategies for improvement are outlined.

---

Poulomi Roy

Poulomi Roy received her MSc degree in Inorganic Chemistry from Vidyasagar University, India and obtained her PhD degree in Inorganic Nanomaterials from the Indian Institute of Technology, Kharagpur, in 2007. She joined the group of Prof. Patrik Schmuki at the University of Erlangen–Nürnberg, Germany in 2008 as a post-doctoral fellow, where currently she is continuing her research. Her research interests include the synthesis of semiconductor nanomaterials and their application in various energy fields, especially in solar cells.

Doohun Kim

Doohun Kim received his MSc degree from Inha University, Inchon, South Korea in 1999. He then worked at Solartech Corp., Seoul for four years. Currently, he is persuing his PhD degree in Prof. Patrik Schmuki’s lab at the University of Erlangen–Nürnberg, Germany. His research interest includes synthesis of self-organized nanomaterials by electrochemical means and their applications in different energy devices.

Kiyoung Lee

Kiyoung Lee obtained his MSc degree in Chemical Engineering from Inha University, Korea in 2009. He is currently a PhD student under the supervision of Prof. Schmuki at the University of Erlangen–Nürnberg in Germany. His research interests include functional nanomaterial synthesis by electrochemical methods with the direction of application in energy conversion and storage devices.

Erdmann Spiecker

Erdmann Spiecker received his PhD in physics in 1999 from the University of Göttingen. In 2000 he joined the Materials Science Department of the University of Kiel as research associate. He was awarded a Humboldt Fellowship in 2005 and spent over a year at the National Center for Electron Microscopy in Berkeley. In 2007 he received his habilitation from the University of Kiel. Since September 2008 he has been Professor of Materials Science and head of the Electron Microscopy group at the University of Erlangen–Nürnberg. His research focuses on electron microscopy techniques for investigation of nanostructured materials.

Patrik Schmuki

Patrik Schmuki studied physical chemistry at the University of Basel, and obtained his PhD degree from ETH-Zurich in 1992. From 1994–97 he worked at Brookhaven National Laboratory, USA and the Institute for Microstructural Sciences of the NRC, Canada. From 1997–2000 he was an Associate Professor for Microstructuring Materials at EPFL, Switzerland, and since 2000 he is Full Professor and head of the Institute for Surface Science at the Materials Science Department of the University of Erlangen–Nürnberg. His current research interests cover electrochemistry and materials at the nanoscale—with particular focus on functional materials and the control of self-assembly.

---

1. Introduction

1.1 General overview

Currently the majority of commercial solar cells are made of different solid-state junction devices, usually from silicon. These cells reach light-to-electricity conversion efficiencies of ≈ 20% for multicrystalline and ≈ 25% for monocrystalline silicon at reasonable cost, and thus represent the milestone of terrestrial applications.¹ However, several other concepts are explored that are geared to achieve either higher efficiencies, or manufacture at more attractive costs, or are expected to be overall more environmentally friendly. A particularly striking photoelectrochemical concept is based on dye-sensitized TiO₂ – it involves neither expensive semiconductor substrates nor high-level processing steps.

In 1985, Desilvestro et al.² reported TiO₂ nanoparticles onto which suitable organic molecules (Ru-based complexes) were adsorbed. Such electrodes were active under visible-light irradiation and allowed solar energy to be converted to electricity with a quantum efficiency of 80%.³ Later on, Grätzel and O'Regan extended the concept to a full solar cell,^4–6 which is nowadays known as a dye-sensitized solar cell (DSSC). In these DSSCs the hole-transmitting medium is a redox species in an electrolyte, liquid or gel (quasi solid-state). The principle of such a DSSC is described in Fig. 1. The classic DSSC is composed of a layer of nanocrystalline TiO₂ particles on a conducting substrate, a platinum counter electrode, and an adsorbed Ru-dye as a sensitizer and an electrolyte. Using such constructions 11% conversion efficiency has been achieved.⁷ Usually, the TiO₂ nanoparticles are deposited on a conducting glass substrate, and sintered to convert the particles to an anatase crystal phase and to improve the electronic conduction between the conductive glass and the TiO₂ nanoparticles. On the TiO₂ surface adsorbed is a dye, which serves as a light absorber (sensitizer), and is anchored (attached) to the surface of the TiO₂ nanoparticles by specific functional groups. A key requirement for the dye is that the LUMO of the dye molecule is energetically positioned slightly higher than the conduction band of TiO₂. Under irradiation with sunlight, HOMO–LUMO transitions in the dye occur. Excited electrons can then be injected from the LUMO into the conduction band of the semiconductor electrode (Fig. 1B). For typically used Ru-ligand dyes the electron injection from the dye sensitizer to the conduction band of TiO₂ occurs through a metal-to-ligand charge transfer (MLCT) pathway as shown in Fig. 1C.⁸ The oxidized dye is reduced to its original state by electron donation from the redox couple in the electrolyte. Usually the electrolyte is an organic solvent or ionic liquid containing an I₃⁻/I⁻ redox system. After the I₃⁻ ion is oxidized to I⁻, it regenerates the dye (refills the HOMO levels). The resulting I⁻ species can diffuse to the Pt counter electrode where they are regenerated to I₃⁻ by reduction.

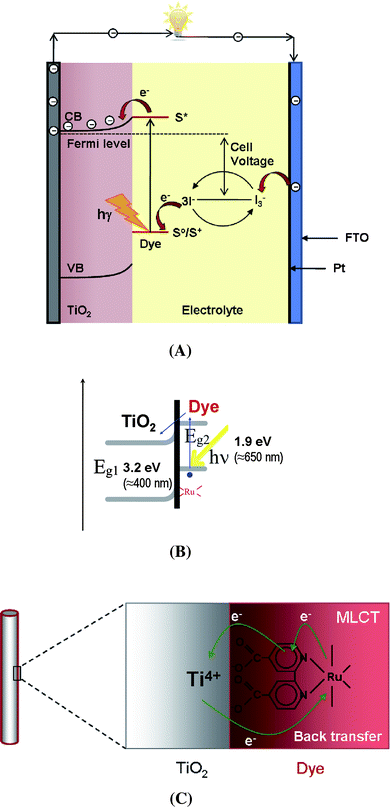Fig. 1 (A) Schematic representation of the principle of a dye-sensitized solar cell. (B) Schematic diagram of the light-induced electron excitation (HOMO–LUMO transition) and injection process from the LUMO of the dye to the conduction band of TiO₂. (C) Excited electron transfer from Ru-metal to the TiO₂ conduction band occurs by the so-called metal-to-ligand charge transfer pathway (MLCT).

The potential difference under illumination corresponds to the difference between the Fermi level of the electron in the semiconductor electrode and the redox potential of the electrolyte (i.e., this represents the achievable V_oc).

However, not only energetic (thermodynamic) considerations are crucial but also the reaction kinetics. The rate constant for electron injection from the conduction band has to be faster than the de-excitation of the dye and the regeneration time constant for the dye has to be sufficiently fast to avoid depletion effects^8,9 (Fig. 2A). Generally, the rate-limiting factor is the dynamic competition between the electron transport in the TiO₂ and interfacial recombination of electrons. Typically the electron transport time constants in TiO₂ nanoparticles are comparably slow (due to a trapping/de-trapping type of electron transport).^10,11 Low electron diffusion coefficients within the TiO₂ nanoparticles can be due to defects, surface states, grain boundaries etc. that act as electron trapping sites, thus slowing down electron flow, enhancing recombination and thereby diminishing the electron collection at the back contact.^12,13 In order to considerably improve this behaviour, recently research has been prompted towards the use of one-dimensional nanostructures of TiO₂, such as, nanotubes,^14–19nanorods,^20–23nanowires^24,25etc. These 1D nanostructures are expected to significantly improve the electron transport properties due to a directional smooth electron mobility (limiting random walk in the wide nanocrystalline network) as well as decreased inter-crystalline contacts, thereby accelerating electron transport and lowering the recombination probability as shown in the schematic diagram of Fig. 2B–C.¹⁴

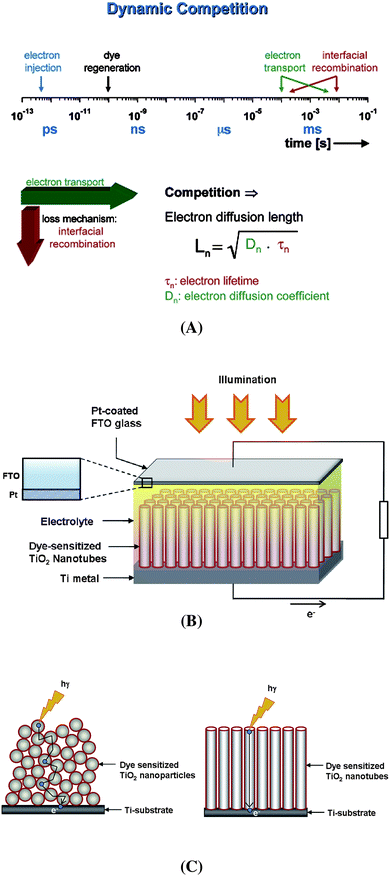Fig. 2 (A) The most relevant kinetic constants involved in the dynamics of the redox processes involving electron injection from the dye into TiO₂, dye regeneration, electron transportation and back-transfer of the electrons to the redox medium. The electron diffusion length (L_n) in TiO₂, one of the key parameters in DSSCs, depends on the diffusion constant (D_n) and the electron lifetime (τ_c) (reproduced with permission from ref. 8. Copyright American Chemical Society, 2005). (B) Schematic representation of typical solar cell construction using TiO₂ nanotubes grown on a Ti substrate. (C) A comparison of the electron pathways through nanoparticulate and nanotubular structured TiO₂ (3D random walk vs. 1D transport).

Various techniques for synthesizing TiO₂ nanotubes and other 1D structures have been reported in recent years, such as sol –gel processes, or hydrothermal approaches.^26–30 Although comparably high-efficiency solar cells have been produced with these chemically synthesized 1D morphologies of TiO₂, a multidirectional orientation of TiO₂ nanotubes or nanorods may not ensure the most efficient unidirectional electron flow along the length of a restricted passage towards the back contact. In principle, as long as the nanotube or nanorod systems are ideal i.e., they provide a highly conductive, rapid electron transport, their orientation on the substrate is of minor importance. This, for example, may hold for single crystalline defect-free nanowires. However, many approaches to grow TiO₂ nanotubes lead to a polycrystalline material with substantial recombination possibilities along the electron path. In this case the optimally increased rate of electron transport and the higher charge collection efficiencies can only be expected for nanotubes vertically aligned with the conductive substrate. Therefore approaches to produce self-ordered titaniananotubes by anodic oxidation of Ti in adequate electrolyte^31,32 have become of a significant interest – the present review will focus on this point in later sections but will first give a brief overview of some general concepts in DSSCs.

1.2 Key factors for DSSCs

More than 2000 papers have been published on dye-sensitized solar cells with the goal of understanding and optimizing key factors, such as, the TiO₂ morphology and structure,^33–36 and the dye and the electrolyte.^37–41 It is beyond the scope of this article to give a detailed review on these topics. However, some of the most important points with reference to further reading shall be briefly outlined. While in the beginning, advances in DSSCs were almost entirely based on experimental findings, for some elementary steps a much higher degree of understanding is achieved through modelling and detailed optical and electrical characterization.^9–16,22 The development of the dye and the electrolyte are still dominated by general guidelines and empirical approaches. The dyes used and explored in DSSCs can be broadly characterized as (1) ruthenium complexes (mostly polypyridyl), or (2) metal-free donor–acceptor systems.^{37,38,42–45} Some typical examples are shown in Fig. 3. Both classes of dyes were recently reviewed, for Ru-dyes see ref. 38, for metal-free dyes see refs. 37 and 42. In addition to Ru, other transition metals, such as, Os, Pt, Cu or Fe have been explored^46–51 and although some metal-free dyes can reach solar cell efficiencies of ∼9%,⁴² still the dominating structures are the Ru-based dyes shown in Fig. 3A–D. For these dyes it is well established that charge transfer from the Ru-dye to the TiO₂ is a two-step process (MLCT).⁸ Ligands not only influence charge separation in the dye and thus can control the kinetics of electron transfer from metal to ligand but also affect the electron injection kinetics to the conduction band of TiO₂.^8,38 Attachment (adsorption) of the dye to the TiO₂ surface is usually achieved via carboxylate groups. Although other coordination groups, such as, phosphates or silanes may even lead to a stronger bond between TiO₂ and the dye,^38,52,53 they usually do not yield as high an efficiency. The reason may be that carboxylate ligands attached to the bipyridine molecule lower the energy of the ligand π^*-orbital – thus giving charge transfer the desired direction. Some room for improvement is believed to be achieved with dyes with a significantly higher molar extinction coefficient.^37,38 This would allow the use of thinner TiO₂ particle layers (as full light absorption could be reached in a shorter path and thus the length for recombination would be reduced too). In this regard, several metal-free organic dyes were found to be very useful in DSSCs and for example, coumarin, squaraine, porphyrin and phthalocyaninedyes in DSSCs with solar cell efficiencies of 6–8% have been reported.^54–58 Due to the wide possibilities of synthetic chemistry it is also reasonable to assume that the absorption spectra of these dyes may be even further tuned and particularly be better extended into the infrared range. A problem in dye design and application is to avoid multilayer formation or non-bound dye residues, simply as this material absorbs light but is not able to inject the carriers to TiO₂ and thus leads to recombination losses. Proper monolayer formation may be supported by co-adsorption for example of deoxycholic acid or by optimized design of the ligands.³⁷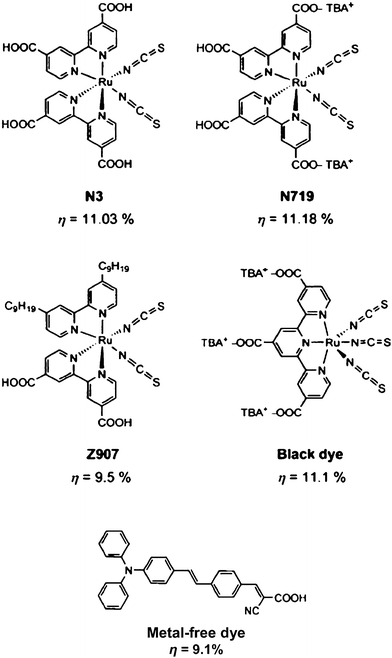

Fig. 3 The most efficient Ru-complex and metal-free dyes with their maximum achieved solar cell efficiencies. (Reproduced with permission from ref. 37. Copyright Wiley-VCH, 2009).

Three different types of electrolytes are usually used in DSSCs:^39–41,59 liquid electrolytes, quasi-solid-state electrolytes, and solid electrolytes. Typically, various nitriles, such as, acetonitrile, valeronitrile, 3-methoxypropionitrile, and esters such as ethylene carbonate, propylene carbonate, γ-butyrolactoneetc. have been used. The active redox couple is almost exclusively I₃⁻/I⁻. The achievable voltage in the solar cell V_oc, depends directly on the redox potential of the redox system. The redox potential should be as positive as possible but still sufficiently negative to be able to regenerate the dye. With regard to the energy level of the most common dyes, it can be assumed that with a suitable redox system V_oc could be improved by ∼0.1 V. Therefore, several researchers tried to change the redox couple. For example, Wang et al.⁶⁰ investigated the role of the redox couple Br⁻/Br₂ as well as I₃⁻/I⁻ on various dyes. And indeed a higher solar cell efficiency was obtained by replacing the I₃⁻/I⁻ redox couple with Br⁻/Br₂ if eosin Y was used as a dye. The use of the Co(II)/Co(III) redox couple as polypyridyl cobalt(II/III) complexes in the electrolyte of the solar cell in presence of Ru-dye (Z316) showed promising activity and may become a rival to I₃⁻/I⁻.^61,62Pseudohalide redox couples, such as, SCN⁻/(SCN)₂- and SeCN⁻/(SeCN)₂-containing electrolytes were also tested in DSSCs.^63,64 Grätzel and his co-workers used a solvent-free, SeCN⁻/(SeCN)₃-based ionic liquid electrolyte and achieved 7.5% conversion efficiency under standard AM 1.5 conditions.⁶⁴ In spite of all of these efforts, to the date the highest efficiency is observed by using a classic Ru-dye (N719) and I₃⁻/I⁻ as the redox couple.

A key consideration regarding the redox couple is the back reaction. Probably still the main efficiency loss mechanism today is interface recombination, i.e., loss by the reaction of electrons already injected into the TiO₂ back to the redox couple in the electrolyte. The kinetics of the back reaction is, among others, determined by interface states at the TiO₂/electrolyte interface. While certain orientations at TiO₂ crystallites may show a lower defect density, there may also be the possibility of blocking reactive interface states by adequate chemical or physicochemical treatments. Additives to the electrolyte such as 4-tert-butyl pyridine are reported to preferentially adsorb at defect sites, thus blocking, to a certain extent, these recombination sites (reducing the dark current) and as a result a higher V_oc is obtained.⁶⁵

In comparison to conventional organic solvent electrolytes, ionic liquids have several advantages, but mainly their negligible vapor pressure combined with their high ionic conductivity make them interesting as alternative electrolytes for DSSCs. Recently, Grätzel achieved 7.6% conversion efficiency using 1-propyl-3-methylimidazolium iodide and 1-ethyl-3-methylimidazolium tetracyanoborate as an ionic liquid electrolyte in a TiO₂-based DSSC.⁶⁶ Solid electrolytes are typically based on hole-conducting polymers. While difficulties in complete filling and penetration of the nanoparticulate material with the hole-conducting polymer exist, efficiencies in the range of ∼5% are reported – recent reviews on this topic are provided in refs. 67 and 68.

Very recently, Grätzel reported 8.2% solar cell efficiency using eutectic melts to produce solvent-free liquid redox electrolytes.⁶⁹ As mentioned before, a key factor affecting the overall efficiency of the solar cell is the competition between charge carrier transport and interface recombination. Therefore, approaches that lead to a significantly faster (or shorter) overall transport of electrons from the point of injection to the back contact are highly promising. Therefore nanoscale TiO₂, not present as an extended 3D network, but as a highly directional 1D nanostructure with potentially very fast carrier kinetics, has attracted considerable attention as dye-support material.

As the role of the TiO₂ in DSSCs is solely to act as a good electron conducting semiconductor, harvesting the electrons injected from the dye, various other oxide materials may be considered for this role as an alternative. Semiconducting oxides, having a wide bandgap, such as, ZnO, SnO₂, Nb₂O₅^70–75 have also been explored for DSSCs. Particularly in the case of ZnO, 1D nanostructures also seem attractive and are being explored.⁷⁵ However, up to now TiO₂ is still regarded as by far the best choice.

TiO₂ nanorods, nanowires and nanotubes have been prepared by various approaches, such as, template-assisted growth, sol –gel methods, hydrothermal methods and so on.^26–30 The recent findings of self-ordered growth of vertically aligned TiO₂ nanotube arrays by a simple anodic oxidation reaction on titanium metal attracted wide interest.^31,32 It is believed that these nanotubes will be superior to nanorods or nanowires because of the availability of inner as well as outer wall of tubes for dye adsorption.

In the following we will discuss the current state-of-the-art in dye-sensitized solar cells based on self-organized TiO₂ nanotubes and we will show some results from ongoing research on DSSCs. We will try to discuss the critical factors of DSSC efficiency when using TiO₂ nanotubes, such as, tube morphology, dimensions and annealing. We will also demonstrate how different secondary treatments can affect DSSC performance.

2. Anodic self-organized TiO₂ nanotube arrays

2.1 Growth of layers

Self-organized TiO₂ nanotube layers as shown in Fig. 4 are formed by anodic oxidation of a Ti-metal sheet (illustrated in Fig. 4A). This simple electrochemical process can be carried out in an electrochemical cell with a two- or three-electrode system: Ti-foil as the working electrode (the anode) and for example Pt as the counter electrode, and using a standard voltage source or a high-voltage potentiostat. The key to forming self-ordered nanotube layers on the metal substrate is that samples are anodized under a set of optimized conditions in solutions containing fluoride ions. Reviews of this topic have recently been published.^31,32,76 The process originates from work by Zwilling and co-workers published in 1999, on the anodization of Ti and Ti alloys in chromic acid–HF mixtures.⁷⁷ These authors could grow the first generation of tubes to layers of a thickness of few 100 nm. Later on, this process was used by Gong et al.⁷⁸ and Beranek et al.⁷⁹ to grow organized TiO₂ nanotubular layers in aqueous HF electrolytes or H₂SO₄/HF electrolytes to establish better defined growth conditions. However, although considerable order in wall thickness, diameter and short-range arrangement was established, the tube length remained limited to ∼500 nm and the walls showed considerable disorder (side-wall ripples and other etch effects). Two key steps in improving the geometry were introduced by Macak et al.:^80–82 (i) the use of neutral electrolytes⁸⁰ that allowed, under suitable conditions, significantly longer tubes to be grown,⁸¹ and (ii) the use of non-aqueous electrolytes that allowed to significantly improve the tube wall roughness (smooth, high aspect ratio nanotubes).⁸² Using such an an anodization procedure in non-aqueous electrolytes, not only very thick TiO₂ nanotube layers (several 100 μm) can be grown but they also show a very smooth wall⁸³ and can be grown to show an almost ideal hexagonal arrangement⁸⁴ (Fig. 4C).

Fig. 4 (A) Schematic diagram of a electrochemical set-up and anodic growth of TiO₂ nanotubes on a Ti-metal sheet. (B) SEM images of the self-organized nanotubeTiO₂ layer formed in aqueous electrolyte (1 M Na₂SO₄/0.14 M NaF electrolyte). (C) SEM images of TiO₂ nanotube layers formed by the anodic oxidation of Ti-metal in non-aqueous electrolyte (cross section, top view and bottom view) and also showing a very high-aspect-ratio nanotube layer (several hundred μm).

Nowadays, even more advanced geometries of TiO₂ nanotubes can be prepared by altering the voltage during growth.^15,85,86 For example, by regular voltage cycling a ‘bamboo-type’ morphology of TiO₂ nanotubes can be grown in HF-containing ethylene glycol electrolyte^15,85 (Fig. 5A). By using different AV pulse durations the distance between the ‘bamboo rings’ can be adjusted. Voltage stepping furthermore allows the growth of branched tubes (tube multilayers) or some 2D TiO₂ networks (nanolaces).^85,87–89

Fig. 5 Example of advanced geometries of self-organized TiO₂ nanotube layers: (A) A ‘bamboo-type’ nanotube layer (inset: half broken tube); (Reproduced with permission from ref. 85. Copyright Wiley-VCH, 2008). (B) Double-walled TiO₂ nanotube structure; (Reproduced with permission from ref. 90. Copyright Wiley-VCH, 2008). (C) Nanograss formation at TiO₂ tube tops under normal anodization conditions (left) and after pre-conditioning (Reproduced with permission from ref. 16. Copyright Elsevier, 2008). (D) ₂nanotubes grown by rapid breakdown anodization; (Reproduced with permission from ref. 94. Copyright Elsevier, 2007).

Recently we reported that adequate heat treatment of some TiO₂ nanotubes leads to the characteristic double-wall structure shown in Fig. 5B.⁹⁰ The smooth tubes are grown in ethylene glycol electrolytes and then, by rapid thermal annealing, the tubes are separated in two separate entities. As shown in Fig. 5B, the inner wall has a very high porosity providing a high surface area and the outer wall of the tubes is comparably smooth. A common feature is observed, if self-organized tubes are grown for extended periods of time: ‘grass’ formation at the tube top occurs. Although several times attributed to the formation of nanorods, nanospikes, or nanowires,⁹¹ this feature simply originates from the continuous thinning of the tube walls in the fluoride electrolyte. These ‘grassy’ tube tops may interfere with the defined electron transfer through nanotubes but in any case the disorder at the tube top may hamper optimized solar cell performance. In order to avoid this problem, various approaches have been developed to achieve ordered and open tube tops (Fig. 5C)^15,18,92,93 and effects on the solar cell performance will be discussed in next section.

Another electrochemical approach to form high aspect nanotubes is so called rapid breakdown anodization (RBA).^94–96 Such tubes form very rapidly (within seconds), if Ti is anodized under breakdown conditions in chloride or perchlorate containing electrolytes. This rapid process leads to formation of flower-like bundles of nanotubes as shown in Fig. 5D, with very high aspect ratio of tubes having lengths of 3–50 μm within some minutes. These structures have also been reported to show a good performance in DSSC.^96,97

2.2. Modification and characterization of TiO₂ nanotubes

2.2.1 Annealing . As-prepared TiO₂ nanotubes are amorphous in nature and by thermal treatment they can be converted to anatase or rutile, or mixtures of anatase and rutile phases depending on the annealing temperature as shown in Fig. 6.^31,32,90 The crystallinity of TiO₂ has a significant effect on solar cell performance. If amorphous TiO₂ (nanocrystallites or tubes) is annealed at 300–450 °C in air, the anatase phase of TiO₂ can be obtained. At 500 °C, a trace of rutile is typically observed, and on increasing the annealing temperature the percentage of the rutile phase increases. Typically the material can be converted completely to its rutile phase at 900 °C. However, at high temperatures (800–900 °C), the structure of the tubes collapses.⁹⁰ Typically the anatase phase of TiO₂ turns out to be the most efficient for solar cell performance. A certain amount of rutile phase present in the nanotube layers typically has a detrimental effect on the solar cell, which may be ascribed to the approximately 10×lower electron mobility in rutile compared with anatase as reported in ref. 98. Along these lines it is also interesting to note that the group of Frank reported an approximately 10× higher electron diffusion constant for anatase than for rutile in particulate solar cells.⁹⁹ Other than the annealing temperature, the ramping speed also has great influence on the tube morphology, crystal structure, and finally solar cell performances. There are several findings that are very relevant considering the annealing procedure. Generally, annealing of the TiO₂ nanotubes does not lead to single crystalline material but very large scale grains (≈ 20 nm) can be observed (Fig. 6C)¹⁰⁰ that do not depend on the annealing temperature very much. In other words, the grain size as such is considerably larger than the size of Grätzel-type nanoparticles (≈ 10 nm) and therefore higher electron mobilities could be expected. However, at higher annealing temperatures (such as 450 °C) nanoscale cracks in the tube walls become apparent,¹⁰⁰ such as shown in Fig. 6B. Moreover, annealing at temperatures >400 °C will cause some thermal oxidation of the underlying Ti-metal foil to rutile, i.e., thin rutile layers are present underneath the nanotube layers as illustrated in Fig. 6C. These layers can only be observed if XRD sufficiently penetrates the TiO₂ nanotube layers (tubes shorter than 10 μm length). Some results on the effect of thermal treatment of TiO₂ nanotubes on the solar cell performance will be discussed in section 2.3.4. It may be noteworthy that by annealing the TiO₂ nanotube in NH₃ or acetylene successful N- or C-doping can be achieved^101–103 or even conductive TiO₂ nanotubes can be formed.¹⁰⁴

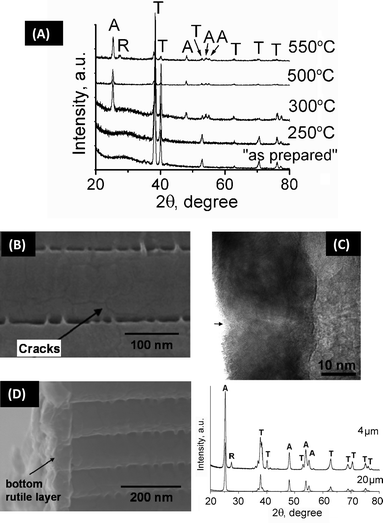Fig. 6 (A) XRD analysis of TiO₂ nanotube layers at different annealing temperatures, revealing the amorphous ‘as-prepared’ material and anatase ‘A’ or rutile ‘R’ formation after the heat treatment. (B)–(C) SEM and TEM images of TiO₂ nanotubes after annealing at 450 °C showing the crack lines and the grains present in the tube wall, respectively. (D) SEM image of TiO₂ nanotubes after annealing at 450 °C showing the bottom rutile layer underneath the nanotubes. Inset: XRD of short tubes (4 μm) and long tubes (20 μm), indicating the rutile peak only for short tubes.

2.2.2 Photoresponse. The typical electrochemical photoresponse of neat TiO₂ nanotubes is summarized in Fig. 7. For illumination with energies larger than the bandgap of TiO₂ (rutile, E_g = 3.0 eV; anatase, E_g = 3.2 eV; amorphous, E_g = 3–3.6 eV) clearly non-annealed (amorphous) nanotubes show a low and hardly higher photoresponse than corresponding compact layers, due to the high recombination rate of carriers in the amorphous material.¹⁰⁵ In other words, in order to “switch on” the tube walls, the tubes need to be annealed to a crystallite form. The voltage dependence of the photocurrent seems to follow essentially the Gärtner model.¹⁰⁶ The photocurrent increases from the flatband voltage (ca. −0.2 to −0.5 V_SCE in neutral electrolytes) but reaches saturation under comparably mild anodization conditions (ca. +0.5 V_SCE). For anodic TiO₂ layers, frequently comparably high doping densities are found that are attributed to defect structure, to non-stoichiometry (Ti_xO_y) or hydroxide content.¹⁰⁷ Even after annealing, doping levels – typically determined by Mott–Schottky analysis – in the range of 10¹⁹ cm⁻³ are obtained.^108,109 This level of doping is likely due to oxygen vacancies or Ti³⁺ formation under the present annealing conditions.¹¹⁰ This indicates that the heavily doped nanotube material [N_d ∼10¹⁹ cm⁻³] can expand a space charge layer with applied voltage but at voltages of 0.5 V or higher the tube wall is completely depleted in carriers. The situation becomes comparable to the case of nanoparticulate TiO₂ films, where all evidence indicates that band bending effects are negligible, and it is believed that the charge separation must be under thermal (diffusion) control.¹¹¹ Under typical conditions in these TiO₂nanostructures, the reaction of a photogenerated hole with a hole acceptor is assumed to be fast, whereas the recombination of a photoexcited electron with an electron acceptor is assumed to be slow. For UV excitation in aqueous electrolytes, this has been recently investigated by Lynch et al.¹⁰⁷ Most striking is that estimates of the electron diffusion length (L_el) for tubes differ strongly from nanoparticulate layers. For nanoparticulate layers of the Grätzel type, Södergren et al. deduced, L_el ∼0.9 μm.¹¹² For nanotubular layers for UV illumination L_el depends strongly on their morphology; while the first-generation tubes (such as in Fig. 4B) yield L_el ∼2–5 μm. For the second-generation smooth tubes (such as in Fig. 4C) L_el >20 μm is obtained.¹¹³ These findings on UV-induced electron transport in an aqueous electrolyte support the high expectations on improved carrier transport properties in a nanotube morphology compared with nanoparticulate layers.

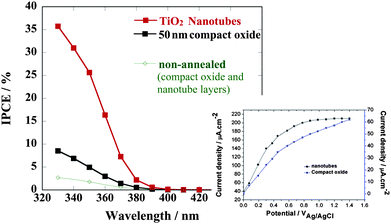Fig. 7 Photoelectrochemical behavior of TiO₂ nanotubes and compact oxide layers on annealing (photocurrent spectra taken in 0.1M Na₂SO₄ at 500 mV vs. Ag/AgCl. Inset: voltage dependence of the photocurrent measured at a wavelength of 350 nm for the annealed samples).

2.3 Tubes in DSSCs

2.3.1 Overview. In 2005, the first report on dye-sensitized TiO₂ nanotubes appeared¹¹⁴ and investigated the first-generation tube layers such as those shown in Fig. 4B. The photoelectrochemical investigations were carried out with TiO₂ nanotubes with a diameter of 100 nm and length of 500 nm to 2.5 μm using Ru-dye (N3) as the sensitizer. The maximum incident photon-to-energy conversion (IPCE) value in the visible range was of the order of 1.6–3.3%. Such tubes show, in solar cell constructions such as Fig. 2B, efficiencies of 0.036%. However, the use of the geometrically more defined nanotubes of the second generation – either produced in glycerol or ethylene glycol electrolytes – drastically improved the reported efficiencies. Meanwhile for plain tubes (not further modified with TiCl₄, TiO₂etc.), several independent articles^14–19,115 find overall solar cell efficiencies of 2–3% under AM 1.5 illumination. Factors that affect the efficiency and means to improve it will be discussed in the following sections. It should be mentioned, however, that many of the results reported by different groups are difficult to compare due to two reasons. First, many groups used mixtures of tubes and nanoparticles,^116–118 and in many cases it is not clear that the reported efficiency value indeed can be ascribed to the presence of TiO₂ nanotubes or if similar efficiencies could be obtained simply by using the nanoparticles alone. Second, in full solar cell constructions (that may look as in Fig. 2A) not only the intrinsic tube properties determine the efficiency but to a large extent the solar cell engineering parameters such as the distance between the Pt counter electrode and tubes or the investigated tube area (i.e., active area of the solar cell). For example it has been shown that with a change in the geometry of the active area, the overall efficiencies may easily vary by a factor of 2.^92,119 This illustrates the need for standardized testing and shows that absolute efficiency values in literature should be carefully considered when relating them to tube geometry or material properties. In other words, the discovery of material-specific efficiency enhancing effects can only be reasonably compared within one work (one solar cell construction approach) and assuming that proper reference experiments were carried out. Furthermore, one should mention some variations from using self-organized tubes grown on Ti-metal sheets used in solar cells.

For example, Kang and his group²⁹ fabricated highly ordered TiO₂ nanotubes using a nanoporous alumina templating method. Such nanotubes with 15 μm lengths were heat treated at 500 °C for 30 min and soaked in N3 dye for 24 h, which afterwards showed a solar cell efficiency of 3.5%. Some efforts are directed towards using completely anodized sputter-deposited layers on conductive glass^117,120 but claims such as conversion efficiency of 2.9% fabricated on an only 360-nm-thick TiO₂ nanotube arrays on conductive glass substrates remain unconfirmed and somewhat questionable.¹¹⁷ In particular, sputtering or evaporating a >10 μm thick Ti-metal layer on conductive glass to convert it to TiO₂ nanotubes or lift-off processes seem not economically competitive. On the other hand, recent reports on hydrothermally fabricated nanorods such as the work by Liu et al.¹²¹ may provide valuable alternatives. Recently, Grätzel and his co-workers¹⁹ fabricated a flexible dye-sensitized solar cell from highly ordered TiO₂ nanotube layers further treated with TiCl₄. They used the conductive polymer Pt/ITO-PEN as the counter electrode in combination with an ionic liquid electrolyte. The solar cell performance depends on the thickness of the nanotube layers, and the highest energy conversion efficiency of 3.6% at AM 1.5 simulated full sunlight was obtained for 14 μm long tubes.

Also, RBA tubes (shown in Fig. 5D) were used in DSSCs (in a similar arrangement to Fig. 2B). The growth process leads to the advantage that high-aspect-ratio nanostructures (several dozens of μm in length vs. several dozens of nm in diameter) in the form of nanobundles can be prepared in a very short time (minutes). Some points regarding these tubes will be discussed in section 2.3.9.

2.3.2 Electron dynamics and lifetime of electrons in nanotubes. In nanoparticulate DSSCs the electron lifetime in the conduction band of TiO₂ after electron injection from the dye and the electron diffusion through the TiO₂ films can be calculated using a multiple trapping model.^9,14,107 The electrons can recombine through surface trap sites or directly from the conduction band with the I⁻/I₃⁻ redox couple in the electrolyte. In case of nanoparticulate films, it has been found that the diffusion coefficient (D) of electrons increases and the electron recombination lifetime (τ) decreases with an increase in the particle size up to 32 nm.¹² The τ value usually is influenced by the surface area, which determines the effective electron acceptor density for recombination. The electron dynamics were considered by Frank and his co-workers⁹³ who also compared tubes to classical nanoparticle layers. It was proposed that the nanotube and nanoparticle films showed similar transport times, whereas recombination was 10× slower in the nanotube films, leading to a significantly enhanced charge collection efficiency for the nanotube photoelectrodes. Interestingly, it was reported that lifetimes do not strongly depend on tube length. Along these lines, Frank et al. reported a significant effect of tube top geometry on transport times²⁵ as will be discussed more in section 2.3.7.

The most detailed study on charge carrier behaviour in dye-sensitized TiO₂ nanotube arrays stems from Jennings et al.¹⁴ It was shown that at about 20 μm tube length, IPCE values close to 100% could be obtained (Fig. 8A) when corrected for reflection losses. The measured and calculated IPCE values for 20 μm long nanotubes show good agreement. Most remarkable is that the electron diffusion length, based on experimental results to determine the diffusion coefficient and lifetime of the photoinjected electrons is of the order of 100 μm in the titania nanotube cells (Fig. 8B). This means a value of L that is significantly larger than 20 μm and 100% collection of electrons (without recombination) could be achieved with significantly longer tubes. The value of L_el = 100 μm seems to be in contrast to a value of L_el ≈ 30 μm obtained from data in the work by Zhu et al.^18,25 However, it seems that tube properties are sensitive to the preparation procedure as mentioned in the next section, as for the differently prepared nanotubes considerable differences in L_el were obtained. The study of Jennings et al.¹⁴ also revealed a substantial discrepancy between the shapes of the electron trap distributions measured experimentally using charge extraction techniques and those inferred indirectly from transient current and voltage measurements.

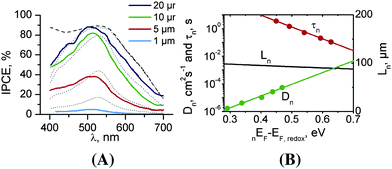Fig. 8 (A) Comparison of measured (solid line) and calculated (dotted line) IPCE values for different thicknesses of TiO₂ nanotube layers; dashed line – the calculated IPCE spectrum for 20 μm long nanotubes without including the absorption loss due to I3 in the electrolyte. (B) Estimation of electron diffusion length (L_n) of 20 μm long TiO₂ nanotubes from the experimental values of D_n and τ_c by taking the quasi Fermi level (QFL) into account. (Reproduced with permission from ref. 14. Copyright American Chemical Society, 2008).

2.3.3 Tube length and diameter. Several authors have investigated the influence of tube length on the conversion efficiency (IPCE) and on the final solar cell performance.^14,16–18 Typical results for the IPCE are shown in Fig. 8A. As mentioned above, the internal conversion efficiency reaches a maximum for tubes of a length of approximately 20 μm. These findings are consistent if the measurements are performed in a photoelectrochemical or in a solar cell set-up. Typical more recent results are shown in Fig. 9 and are obtained with a commercial R50 electrolyte from Solaronix. From the characteristic I–V curve it can be seen that the short-circuit current (I_sc) increases with an increase in the thickness of nanotubes from 8 to 24 μm and for the first-generation tubes (1–2 μm long) very small I_sc values are observed. This very low efficiency for the first-generation tubes may be attributed to their highly irregular tube wall structure, which in the non-sensitized tubes, also has a very detrimental effect on the electron lifetime. For the second-generation tubes, on increasing the tube thickness, the surface area increases and more dye is adsorbed onto the tube wall surfaces allowing an increase in light harvesting. The open-circuit voltage (V_oc) values decreases from 0.68 V to 0.62 and 0.58 V on increasing the tube thickness from 16 to 24 and 32 μm, respectively. This may be due to the fact that at 20 μm an optimum collection is reached, although the electron diffusion length is ∼100 μm.¹⁴ This, in fact, may suggest that for tubes >20 μm, the overall properties may not be the same. For example, a lower collection efficiency may be due to the previously mentioned thinning of the tube walls when tubes are grown for extended times (grass formation on the tube surface). This factor, that tube top morphology is crucial, has been addressed several times in literature and will be discussed in section 2.3.7. By considering all the factors, 16–25 μm is found to be the optimum tube length for attaining the highest energy conversion efficiency (typically reaching ∼2.5%). It should be noted that low short-circuit current values for >30 μm long tubes may also be due to an increasing probability of loss of attachment between tube bottom and the Ti-foil for the long tubes. Up to now the most comprehensive work on solar cell performances has been provided by Ghicov et al.¹⁷ This is particularly important as measurements on solar cell efficiencies vary strongly from various groups, i.e., comparable consistent data is only obtained when identical solar cell constructions and measurement conditions are used. Moreover, different characterization tools and methods are used and the comparison of tubes is done frequently in different terms, such as, diffusion constants, transport time constants and recombination lifetimes. The work of Ghicov et al.¹⁷ suffers to some extent from comparably poor fill factors (due to a simple solar cell construction).^122,123 Furthermore, in the work of Ghicov et al.,¹⁷ a simple electrolyte such as an 0.1 M lithium iodide +0.05 M iodine was used and a maximum 1.6% efficiency at 20 μm tube length was obtained. However, the addition of 0.6M tert-butyl pyridine (BP) increased the efficiency to 2.4%.¹⁷Tert-butyl pyridine was added as an agent to the electrolyte in order to block surface states by preferential adsorption, thereby decreasing the chance of recombination.¹⁷ However, the overall trend of maximum efficiency at a tube length ≈ 20 μm was not changed.

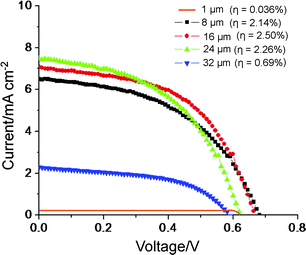Fig. 9 I–V characteristics measured for the solar cell configuration of Fig. 2B for different lengths of TiO₂ nanotube layers after annealing at 450 °C for 1 h using commercial R50 as electrolyte and dye soaking (N719) for 1 day.

The tube diameter also has significant effect on the solar cell performance. It was found that for the same thickness of nanotube layers, smaller diameter tubes show a higher energy conversion efficiency.¹⁷Fig. 10 compiles a series of results obtained for several different tube geometries. Although some details such as the electrolyte or solar cell geometry vary slightly in different articles, the clear trend that a smaller diameter (at the same length) increases the solar cell response is observed as indicated in the inset. These findings overall correlate with the trend that an increase in the surface area of tubes increases the specific dye loading. This holds for decreasing the diameter or increasing the length of the nanotubes. In several cases this finding was confirmed by dye desorption measurements.^14,17 As a bottom line for the tubes: though a better electrical performance is provided than in nanoparticulate layers, the lower specific surface area [BET_tubes ≈ 30 m² g⁻¹; BET_{nanoparticles} ≈ 80 m² g⁻¹] lowers the dye loading and thus reduces the efficiency. Some measures against this will be discussed in sections 2.3.5 and 2.3.8.

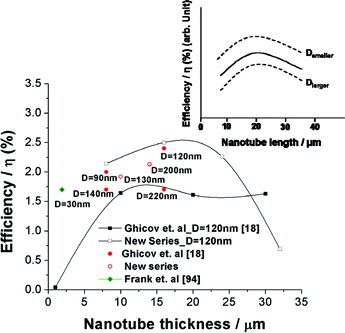Fig. 10 Influence of tube geometry: Comparison of solar cell efficiencies from literature and unpublished data, illustrating the effect of TiO₂ nanotube length and diameter. All of the new series of experiments were carried out using R50 as electrolyte and N719 dye soaking for 1 day. Inset: Schematic trend of solar cell performances of TiO₂ nanotube layers with tube length and diameter.

2.3.4 Annealing . Other than the tube geometry, the annealing temperature, duration and ramping also has significant effect on dye loading, electron transport time and in the end the electron collection efficiency. The as-prepared TiO₂ nanotubes are amorphous in nature and show negligible energy conversion efficiency in solar cells. The nanotubes convert to anatase phase of TiO₂ after annealing at 300 °C (compare Fig. 6), and depending on the annealing temperature anatase, rutile or a mixture of phases is obtained. From the XRD data can be observed that at 450–500 °C the pure anatase phase of TiO₂ is obtained. However, at 550 °C or above, a mixture of anatase and rutile phases is formed. An overview of results for different annealing temperatures and times is compiled in Fig. 11. In this case, all the samples were annealed in a rapid thermal annealing chamber with a ramping speed of 30 °C min⁻¹. In all the experiments the samples were dye-sensitized with Ru-based N719 dye for 1 day at room temperature. The I–V characteristic curves for different annealing temperatures reveal that the short-circuit current and the open-circuit voltage increase with increasing annealing temperature. This may be due to the increase in crystallinity, thereby promoting the connectivity between grains and consequent improvement in electron diffusion coefficients and lifetimes.^17,90 At higher annealing temperatures the efficiency decreases. This observation can be explained because of the detrimental effect of rutile phase formation at high annealing temperatures. However, other key points, as outlined in section 2.2.1, are that annealing of the tubes at higher temperatures leads to cracks visible in the SEM and TEM images¹⁰⁰ and this effect may drastically reduce electron mobility. Additionally, as also outlined in a previous section, higher temperature annealing of the TiO₂ nanotubes on their Ti substrate leads typically to the formation of a thermal oxide of a rutile type (Fig. 6c) underneath the nanotubes which can also affect the electron mobility. This would in turn explain why Zhu et al.²⁵ find an electron mobility in TiO₂ nanotubes that is similar to particulate systems. A maximum solar cell efficiency of 2.95% is obtained after annealing at 450 °C for 3 h. Figs. 11B and C show the I–V curves of TiO₂ nanotubes for different annealing durations and different ramping speeds at 450 °C. The higher I_sc value for 3 h annealed sample results in the highest energy conversion efficiency of ∼3%. This increase in efficiency due to longer annealing times may be due to better crystallization of the anatase phase. Besides different annealing temperature and durations, also using a different ramping speed of annealing at 450 °C showed significant effect on solar cell performances. It is observed that very fast ramping shows a lower solar cell efficiency. This might be due to the fact that very fast ramping affects the tube morphology drastically as shown in work by Albu et al.⁹⁰

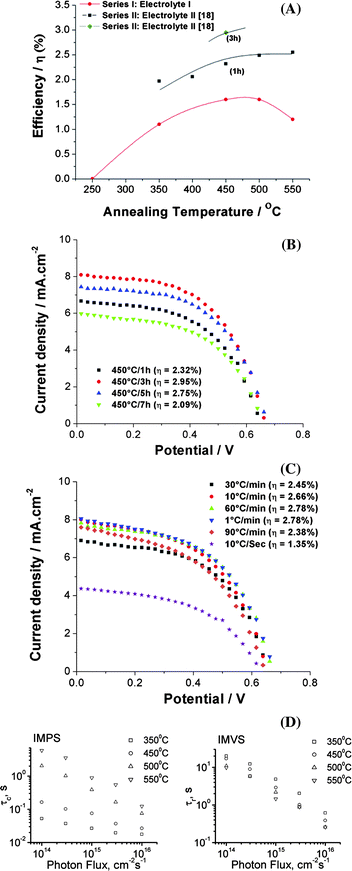Fig. 11 Influence of tube annealing: (A) Compilation of solar cell efficiencies of 16 μm TiO₂ nanotube layers at different annealing temperatures (Series I measurements were carried out with 0.1 M lithium iodide +0.05 M iodine containing 0.6M tert-butyl pyridine as electrolyte I and Series II measurements were carried out using R50 as electrolyte II and N719 as dye for both cases). (B) I–V characteristics of 16 μm TiO₂ nanotube layers annealed at 450 °C for different durations; (C) I–V characteristics of 16 μm TiO₂ nanotube layers annealed at 450 °C for different annealing ramping speeds. (D) Electron transport (τ_c) and recombination time (τ_r) constants calculated from IMPS and IMVS curves for 16 μm TiO₂ nanotube layer-based DSSCs at different annealing temperatures (reproduced with permission from ref. 17. Copyright Wiley-VCH, 2009).

Very remarkable is a recent finding by Ghicov et al.¹⁷ that the electron transport properties through nanotubes can strongly depend on the annealing temperature. The electron recombination (τ_r) and transport time constants (τ_c) can be evaluated by intensity-modulated photocurrent spectroscopy (IMPS) and intensity-modulated photovoltage spectroscopy (IMVS) measurements as shown in Fig. 11D (from ref. 17). Extracting the transport time constants shows that τ_c is 10× smaller for tubes annealed at 350 °C compared with tubes annealed at 450 °C, which means the electron transport is drastically faster in the tubes annealed at 350 °C. This may be attributed to many fewer cracks induced at this annealing temperature¹⁰⁰ or less rutile formation underneath the tubes. Although the finding of high rate constants at lower annealing temperatures is extremely promising for further research, the authors point out in their article that for these tubes a significantly lower dye loading was attained. The reasons for this at the current stage are unclear and further work is required to possibly exploit these effects.

2.3.5 TiCl₄ treatment. The above findings show clearly that for tubes a very crucial factor is simply the surface area, as it determines the amount of dye adsorbed on the tubes.¹⁷ In other words, in order to improve the overall solar cell efficiency, the amount of dye adsorbed by a unit solar cell volume needs to be higher. One way to achieve a higher surface area is to use a treatment well established for nanoparticulate DSSCs: the so-called TiCl₄ treatment.^124–129 Typical results obtained for nanotube layers before and after this treatment are shown in Fig. 12(A)–(B).¹²⁹ The inner as well as the outer wall of TiO₂ nanotubes are covered with a ∼25 nm thick nanoparticle coating of TiO₂ nanoparticles having 3 nm, as shown in Fig. 12(C). This leads to a significant increase in surface area and therefore more dye can be adsorbed to the nanotube walls. Attempts to carry out TiCl₄ treatments directly on as-grown or amorphous nanotube layers resulted in a lift-off of nanotube layers from the Ti substrate. In order to avoid this problem, double annealing was carried out: The first time to anneal the tubes, and the second time after TiCl₄ tratment of nanotubes to convert the deposited nanoparticles to a crystalline structure. After decoration with TiO₂ nanoparticles, the I_sc as well as the V_oc values increases indicating high light harvesting due to the larger amount of dye loading and the increase in the porosity of material. All these factors help to achieve an energy conversion efficiency of ∼3.8% after TiCl₄ treatment as shown in Fig. 12(D). The first preliminary results on further optimization of the process, however, show efficiencies of >5%.¹³⁰ For less well defined tubes and particle mixtures efficiencies up to 7% have been reported¹¹⁸ but as mentioned before, the effective contribution of tubes remains unclear.

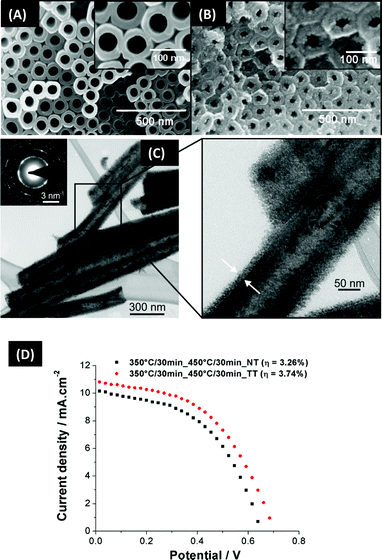Fig. 12 Influence of TiCl₄ treatment: (A)–(B) SEM images of TiO₂ nanotubes before and after TiCl₄ treatment, showing tube decoration with TiO₂ nanoparticles (reproduced with permission from ref. 129. Copyright Elsevier, 2009). (C) TEM and HRTEM of TiO₂ nanotubes after TiCl₄ treatment. (D) I–V curve for non-treated (NT) and treated tubes (TT).

2.3.6 Dye sensitization duration. Several experiments have been carried out in order to optimize the dye sensitization duration. In this context it should be noted that also the dye sensitization temperature plays a significant role. Dye sensitization at 40 °C in a closed container in the dark leads to very fast anchoring of –COOH group at the TiO₂ surface due to possibly a faster dehydration reaction. Some results from various experimental series are compiled in Fig. 13. First results from Ghicov et al. for TiO₂ nanoparticle free nanotubes showed that classic dye sensitization in the case of tubes can take significantly longer for tubes (3–5 days soaking to reach saturation) than usually needed for nanoparticulate layers (some hours to one day). This may on the one hand be ascribed to a slightly different surface reactivity of tubes (see e.g., ref. 131) but may also be due to the fact that the tubes represent a closed porous system, and in some cases a delayed wetting of the tube insides has been mentioned.¹³² The fact that for more than 5 days dye sensitization the efficiency decreases may be associated with dye agglomeration on the tube surface. Clearly, dye sensitization at elevated temperature such as at 40 °C leads to a faster dye adsorption and thus a significant improvement in solar cell performance. E.g., improvement from 1.3% to 3% for non-particle treated tubes and up to 4% for TiO₂ nanoparticle decorated tubes could be achieved [in short sensitization times (24 h)]. Although these results give a general idea about important effects in the dye sensitization of nanotubes, and reveal some differences to nanoparticulate layers, considerable room for optimization seems to exist particularly regarding the interplay with TiO₂ nanoparticle decorated tube walls.

Fig. 13 Influence of dye soaking time: An overview graph for non-treated (TiCl₄) as well as treated tubes for different dye soaking durations.

2.3.7 Top morphology. Most tube tops prepared in conventional ethylene glycol electrolytes are not entirely ideal. Due to chemical etching during growth of the nanotubes, the overall tube wall thickness is thinner at the top than at the bottom.^84,90 At the top region the tube walls can become very thin so that tube upper parts may collapse and form bundles, or form needle-like structures apparent as ‘grass’ on the top of the tubes. Such a ‘grassy’ morphology on the top of the tubes may inhibit smooth electron transport in one direction and thus affect the solar cell performance.

In order to avoid these problems, or at least reduce it, several approaches have been developed by various researchers. Frank and his co-workers²⁵ improved the solar cell efficiency from 1.6% to 1.9% by modifying the cleaning and drying step using supercritical CO₂ drying of tube layers. This approach leads to bundle-free and crack-free nanotube films. The positive effect on the solar cell efficiency was ascribed to an enhancement of the total surface area and making the tube tops more accessible to dye molecules. According to these authors, the inter-tube connection in the compact nanotube bundle effects the electron transport mechanism from the expected one-dimensional pathway to a mixture of one- and three-dimensional pathways. By making bundle-free and crack-free nanotubes, the one-dimensional transport shortens the transport pathway and reduces multiple electron trapping events.

Another approach to making ‘nanograss-free’ TiO₂ nanotubes is by polishing the Ti-foil prior to anodization.¹⁶ A protective top layer can be formed on polished Ti samples, which delays the chemical attack of the tube ends and thus the formation of ‘nanograss’ and tube bundling can be avoided. Additionally, the layer seems also to act as a stratification against disorder induced by the drying process. Such highly aligned, ordered, and ‘nanograss’-free geometries show higher solar cell efficiencies than the conventional nanotubes (see Fig. 14). The maximum energy conversion efficiency is obtained again for 20 μm thick nanotube layers. The open-circuit voltage of nanograss-free nanotubes is found to be higher than that for ‘grassy’ tubes. This may be due to the fact that in more ordered grass-free tubes the electron lifetime is higher due to the presence of fewer defects.

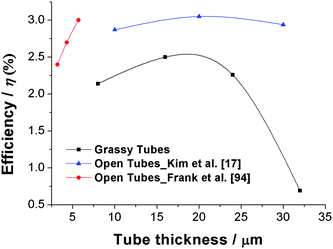Fig. 14 Influence of tube top morphology: A comparative study of solar cell performances of ‘nanograss-free’ and ‘grassy’ tube tops of TiO₂ layers.

Another approach to create top ordered layer was reported by Song et al.⁹³ In this approach a thermal rutile layer is first formed on the Ti metal surface and tubes are then grown underneath. This treatment was found to be very effective to produce defined tubetops up to considerable length of >50 μm.⁹³ Clearly, such tubes are very promising in view of achieving defined tube tops. Most recently also direct growth approaches in optimized electrolytes are being explored to avoid “grass” formation.⁹² However, it should be noted that smooth and regular tube tops may not represent the most ideal case as the disorder has an anti-reflection effect which helps high light harvesting as evident from the high I_sc values.

2.3.8 Advanced geometries. In order to modify the tube geometry, in particular to achieve larger surface areas, modified morphologies such as bamboo tubes (Fig. 5A)⁸⁵ or double-walled structures (Fig. 5B)⁹⁰ are being explored in DSSCs.¹⁵ For example, ‘bamboo-type’ geometry tubes with rings lead to a more optimized volume filling of the TiO₂nanostructure with a higher surface area per unit volume of the solar cell. Bamboo tubes were compared with conventional smooth-walled tubes of the same thickness. The I–V characteristics revealed that the short-circuit current significantly increases in comparison with the conventional smooth-walled tubes, due to the chemisorption of a large number of dye molecules that can cover the interior and exterior of TiO₂ nanotube walls. In particular, the rings of bamboo-type tubes may act as spacers at the exterior of the nanotube walls, which promote the enhanced dye loading.

2.3.9 RBA tubes. As mentioned in section 2.3.1, RBA-type TiO₂ nanotubes can be prepared from fluoride-free electrolytes and long nanotube bundles of 30 μm thickness can be prepared in a very short time (seconds to few minutes). These bundles on the Ti-substrate can be mounted in similar solar cell structures as shown in Fig. 2B. Due to the high surface area of these bundles of nanotubes and porous structures, already in very early experiments some comparably good performances have been obtained.^95,96Fig. 15B shows an I–V curve of RBA tubes with and without ethanol in the electrolyte during growth of the tubes. Ethanol leads to a higher bundle density. Therefore, the higher surface area available for dye anchoring of highly dense bundles of nanotubes leads to higher energy conversion efficiencies in RBA-EtOH tubes, yielding overall a solar cell efficiency of 2.4%.

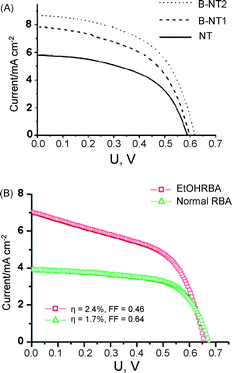Fig. 15 Influence of tube morphology modifications: I–V characteristics for DSSCs of different advanced geometries of TiO₂ nanotubes. (A) Bamboo nanotube (B-NT) with different ring distance and normal nanotubes (NT) (reproduced with permission from ref. 15. Copyright American Chemical Society, 2008). (B) RBA tubes formed in aqueous electrolyte and in ethanolic electrolyte.

2.4 Conclusions

The present article tries to give an overview of the current state of using TiO₂ nanotubes in DSSCs. It is remarkable that since the first results in 2005 with efficiencies of 0.04%, reproducible results in the order of 4–5% efficiency have since been obtained. This although a number of parameters, such as, tube annealing, dye optimization and solar cell geometry, are far from optimized. Exciting results involve the finding of much higher electron diffusion length in tubes than in particles, and the finding that the tube geometry strongly affects electron lifetime – in optimized tubes electron diffusion lengths of ∼100 μm have been observed. The fact that annealing conditions strongly affect electron collection values give room for significant improvement as here one of the crucial loss mechanisms in DSSCs (recombination with the electrolyte) can be reduced. While some higher efficiencies up to 7% have been reported in literature for mixing tubes with nanoparticles, one has to carefully judge if these effects are indeed due to tubes or must be ascribed primarily to the effect of the nanoparticles.

However, from the current state of investigations it is clear that specific dye loading in the tubes need to be improved – i.e., TiO₂ structures with a larger surface area need to be created. This may be achieved in various ways by modifying the tube walls with porous materials (double-walled tubes), TiO₂ nanoparticle decoration or creating defined ‘bamboo-type’ rings. Also, several issues relating to practical solar cell construction, such as, front- or backside illumination, optimized layout, surface reflectivity, or designed light absorption are further open research areas and exciting new findings can also be expected in the development in these “technology” areas.

References

1. F. Pfisterer, Photovoltaic Cells, Ullmann's Encyclopedia of Industrial Chemistry, 2002,Wiley-VCH, Germany.
2. J. Desilvestro, M. Grätzel, L. Kavan and J. Moser, J. Am. Chem. Soc., 1985, 107, 2988.
3. N. Vlachopoulos, P. Liska, J. Augustynski and M. Grätzel, J. Am. Chem. Soc., 1988, 110, 1216.
4. B. O'Regan and M. Grätzel, Nature, 1991, 353, 737.
5. M. Grätzel, Nature, 2001, 414, 338.
6. M. K. Nazeeruddin, F. D. Angelis, S. Fantacci, A. Selloni, G. Viscardi, P. Liska, S. Ito, B. Takeru and M. Grätzel, J. Am. Chem. Soc., 2005, 127, 16835.
7. Y. Chiba, A. Islam, Y. Watanabe, R. Komiya, N. Koide and L. Han, Jpn. J. Appl. Phys., 2006, 45, L638.
8. M. Grätzel, Inorg. Chem., 2005, 44, 6841.
9. S. E. Koops, B. C. O'Regan, P. R. F. Barnes and J. R. Durrant, J. Am. Chem. Soc., 2009, 131, 4808.
10. J. Nelson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 15374 LP.
11. J. Bisquert, Phys. Rev. Lett., 2003, 91, 010602.
12. S. Nakade, Y. Saito, W. Kubo, T. Kitamura, Y. Wada and S. Yanagida, J. Phys. Chem. B, 2003, 107, 8607.
13. L. M. Peter, J. Phys. Chem. C, 2007, 111, 6601.
14. J. R. Jennings, A. Ghicov, L. M. Peter, P. Schmuki and A. B. Walker, J. Am. Chem. Soc., 2008, 130, 13364.
15. D. Kim, A. Ghicov, S. P. Albu and P. Schmuki, J. Am. Chem. Soc., 2008, 130, 16454.
16. D. Kim, A. Ghicov and P. Schmuki, Electrochem. Commun., 2008, 10, 1835.
17. A. Ghicov, S. Albu, R. Hahn, D. Kim, T. Stergiopoulos, J. Kunze, C.-A. Schiller, P. Falaras and P. Schmuki, Chem.–Asian J., 2009, 4, 520.
18. K. Zhu, N. R. Neale, A. Miedaner and A. J. Frank, Nano Lett., 2007, 7, 69.
19. D. Kuang, J. Brillet, P. Chen, M. Takata, S. Uchida, H. Miura, K. Sumioka, S. M. Zakeeruddin and M. Grätzel, ACS Nano, 2008, 2, 1113.
20. S. H. Kang, S.-H. Choi, M.-S. Kang, J.-Y. Kim, H.-S. Kim, T. Hyeon and Y.-E. Sung, Adv. Mater., 2008, 20, 54.
21. M. Y. Song, D. K. Kim, K. J. Ihn, S. M. Jo and D. Y. Kim, Nanotechnology, 2004, 15, 1861.
22. S. Pavasupree, S. Ngamsinlapasathian, Y. Suzuki and S. Yoshikawa, J. Nanosci. Nanotechnol., 2006, 6, 3685.
23. Y. Ohsaki, N. Masaki, T. Kitamura, Y. Wada, T. Okamoto, T. Sekino, K. Niihara and S. Yanagida, Phys. Chem. Chem. Phys., 2005, 7, 4157.
24. M. Adachi, Y. Murata, J. Takao, J. Jiu, M. Sakamoto and F. Wang, J. Am. Chem. Soc., 2004, 126, 14943.
25. K. Zhu, T. B. Vinzant, N. R. Neale and A. J. Frank, Nano Lett., 2007, 7, 3739.
26. H.-H. Ou and S.-L. Lo, Sep. Purif. Technol., 2007, 58, 179.
27. X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891.
28. D. V. Bavykin, J. M. Friedrich and F. C. Walsh, Adv. Mater., 2006, 18, 2807.
29. T.-S. Kang, A. P. Smith, B. E. Taylor and M. F. Durstock, Nano Lett., 2009, 9, 601.
30. G. R. Patzke, F. Krumeich and R. Nesper, Angew. Chem., Int. Ed., 2002, 41, 2446.
31. A. Ghicov and P. Schmuki, Chem. Commun., 2009, 2791.
32. J. M. Macak, H. Tsuchiya, A. Ghicov, K. Yasuda, R. Hahn, S. Bauer and P. Schmuki, Curr. Opin. Solid State Mater. Sci., 2007, 11, 3.
33. M. J. Cass, A. B. Walker, D. Martinez and L. M. Peter, J. Phys. Chem. B, 2005, 109, 5100.
34. N. G. Park, J. van de Lagemaat and A. J. Frank, J. Phys. Chem. B, 2000, 104, 8989.
35. H. Lindström, A. Holmberg, E. Magnusson, S. E. Lindquist, L. Malmqvist and A. Hagfeldt, Nano Lett., 2001, 1, 97.
36. H. Lindström, E. Magnusson, A. Holmberg, S. Sodergren, S. E. Lindquist and A. Hagfeldt, Sol. Energy Mater. Sol. Cells, 2002, 73, 91.
37. A. Mishra, M. K. R. Fischer and P. Bauerle, Angew. Chem., Int. Ed., 2009, 48, 2474.
38. N. Robertson, Angew. Chem., Int. Ed., 2006, 45, 2338.
39. M. Grätzel, Progr. Photovolt.: Res. Appl., 2006, 14, 429.
40. M. Grätzel, J. Photochem. Photobiol., A, 2004, 164, 3.
41. P. Bonhôte, A.-P. Dias, N. Papageorgiou, K. Kalyanasundaram and M. Grätzel, Inorg. Chem., 1996, 35, 1168.
42. S. Hwang, J. H. Lee, C. Park, H. Lee, C. Kim, C. Park, M.-H. Lee, W. Lee, J. Park, K. Kim, N.-G. Park and C. Kim, Chem. Commun., 2007, 4887.
43. M. K. Nazeeruddin, A. Kay, I. Rodicio, R. Humpbry-Baker, E. Miiller, P. Liska, N. Vlachopoulos and M. Grätzel, J. Am. Chem. Soc., 1993, 115, 6382.
44. M. K. Nazeeruddin, P. Pechy and M. Grätzel, Chem. Commun., 1997, 1705.
45. M. K. Nazeeruddin, S. M. Zakeeruddin, R. Humphrey-Baker, M. Jirousek, P. Liska, N. Vlachopoulos, V. Shklover, C.-H. Fischer and M. Grätzel, Inorg. Chem., 1999, 38, 6298.
46. D. Kuciauskas, M. S. Freund, H. B. Gray, J. R. Winkler and N. S. Lewis, J. Phys. Chem. B, 2001, 105, 392.
47. R. Argazzi, G. Larramona, C. Contado and C. A. Bignozzi, J. Photochem. Photobiol., A, 2004, 164, 15.
48. A. Islam, H. Sugihara, K. Hara, L. P. Singh, R. Katoh, M. Yanagida, Y. Takahashi, S. Murata and H. Arakawa, Inorg. Chem., 2001, 40, 5371.
49. E. A. M. Geary, L. J. Yellowlees, L. A. Jack, I. D. H. Oswald, S. Parsons, N. Hirata, J. R. Durrant and N. Robertson, Inorg. Chem., 2005, 44, 242.
50. N. Alonso-Vante, J.-F. Nierengarten and J.-P. Sauvage, J. Chem. Soc., Dalton Trans., 1994, 1649.
51. P. M. Jayaweera, S. S. Palayangoda and K. Tennakone, J. Photochem. Photobiol., A, 2001, 140, 173.
52. P. Wang, C. Klein, J.-E. Moser, R. Humphry-Baker, N.-L. Cevey-Ha, R. Charvet, P. Comte, S. M. Zakeeruddin and M. Grätzel, J. Phys. Chem. B, 2004, 108, 17553.
53. H. Park, E. Bae, J.-J. Lee, J. Park and W. Choi, J. Phys. Chem. B, 2006, 110, 8740.
54. K. Hara, Z.-S. Wang, T. Sato, A. Furube, R. Katoh, H. Sugihara, Y. Dan-oh, C. Kasada, A. Shinpo and S. Suga, J. Phys. Chem. B, 2005, 109, 15476.
55. S. Alex, U. Santhosh and S. Das, J. Photochem. Photobiol., A, 2005, 172, 63.
56. T. Horiuchi, H. Miura, K. Sumioka and S. Uchida, J. Am. Chem. Soc., 2004, 126, 12218.
57. W. M. Campbell, A. K. Burrell, D. L. Officer and K. W. Jolley, Coord. Chem. Rev., 2004, 248, 1363.
58. Q. Wang, W. M. Campbell, E. E. Bonfantani, K. W. Jolley, D. L. Officer, P. J. Walsh, K. Gordon, R. Humphrey-Baker, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. B, 2005, 109, 15397.
59. M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145.
60. Z.-S. Wang, K. Sayama and H. Sugihara, J. Phys. Chem. B, 2005, 109, 22449.
61. H. Nusbaumer, J.-E. Moser, S. M. Zakeeruddin, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. B, 2001, 105, 10461.
62. S. A. Sapp, C. M. Elliott, C. Contado, S. Caramori and C. A. Bignozzi, J. Am. Chem. Soc., 2002, 124, 11215.
63. G. Oskam, B. V. Bergeron, G. J. Meyer and P. C. Searson, J. Phys. Chem. B, 2001, 105, 6867.
64. P. Wang, S. M. Zakeeruddin, J.-E. Moser, R. Humphry-Baker and M. Grätzel, J. Am. Chem. Soc., 2004, 126, 7164.
65. G. Boschloo, L. Haggman and A. Hagfeldt, J. Phys. Chem. B, 2006, 110, 13144.
66. D. B. Kuang, C. Klein, Z. P. Zhang, S. Ito, J. E. Moser, S. M. Zakeeruddin and M. Grätzel, Small, 2007, 3, 2094.
67. J.-H. Yum, P. Chen, M. Grätzel and M. K. Nazeeruddin, Chem. Sus. Chem., 2008, 1, 699.
68. H. J. Snaith and L. Schmidt-Mende, Adv. Mater., 2007, 19, 3187.
69. Y. Bai, Y. Cao, J. Zhang, M. Wang, R. Li, P. Wang, S. M. Zakeeruddin and M. Grätzel, Nat. Mater., 2008, 7, 626.
70. A. B. F. Martinson, J. W. Elam, J. T. Hupp and M. J. Pellin, Nano Lett., 2007, 7, 2183.
71. N. N. Dinh, M.-C. Bernard, A. H.-L. Goff, T. Stergiopoulos and P. Falaras, C. R. Chim., 2006, 9, 676.
72. K. Tennakone, G. R. R. Kumara, I. R. M. Kottegoda and V. S. P. Perera, Chem. Commun., 1999, 15.
73. K. Sayama, H. Suguhara and H. Arakawa, Chem. Mater., 1998, 10, 3825.
74. F. Lenzmann, J. Krueger, S. Burnside, K. Brooks, M. Grätzel, D. Gal, S. Rühle and D. Cahen, J. Phys. Chem. B, 2001, 105, 6347.
75. J. B. Baxter and E. S. Aydil, Appl. Phys. Lett., 2005, 86, 053114.
76. P. Schmuki, in Electrochemistry at the Nanoscale, ed. P. Schmuki and S. Virtanen, Springer, New York, 1st edn, 2009, pp. 435–466.
77. V. Zwilling, E. Darque-Ceretti, A. Boutry-Forveille, D. David, M. Y. Perrin and M. Aucouturier, Surf. Interface Anal., 1999, 27, 629.
78. D. Gong, C. A. Grimes, O. K. Varghese, Z. Chen and E. C. Dickey, J. Mater. Res., 2001, 16, 3331.
79. R. Beranek, H. Hildebrand and P. Schmuki, Electrochem. Solid-State Lett., 2003, 6, B12.
80. J. M. Macak, K. Sirotna and P. Schmuki, Electrochim. Acta, 2005, 50, 3679.
81. J. M. Macak, H. Tsuchiya, L. Taveira, S. Aldabergerova and P. Schmuki, Angew. Chem., Int. Ed., 2005, 44, 7463.
82. J. M. Macák, H. Tsuchiya and P. Schmuki, Angew. Chem., Int. Ed., 2005, 44, 2100.
83. S. P. Albu, A. Ghicov, J. M. Macak and P. Schmuki, Phys. Status Solidi RRL, 2007, 1, R65.
84. J. M. Macak, S. P. Albu and P. Schmuki, Phys. Status Solidi RRL, 2007, 1, 181.
85. S. P. Albu, D. Kim and P. Schmuki, Angew. Chem., Int. Ed., 2008, 47, 1916.
86. W. Chanmanee, A. Watcharenwong, C. R. Chenthamarakshan, P. Kajitvichyanukul, N. R. Tacconi and K. Rajeshwar, J. Am. Chem. Soc., 2008, 130, 965.
87. Y.-Y. Song, F. Schmidt-Stein, S. Bauer and P. Schmuki, J. Am. Chem. Soc., 2009, 131, 4230.
88. J. M. Macak, S. Albu, D. H. Kim, I. Paramasivam, S. Aldabergerova and P. Schmuki, Electrochem. Solid-State Lett., 2007, 10, K28.
89. K. Yasuda and P. Schmuki, Electrochem. Commun., 2007, 9, 615.
90. S. P. Albu, A. Ghicov, S. Aldabergenova, P. Drechsel, D. LeClere, G. E. Thompson, J. M. Macak and P. Schmuki, Adv. Mater., 2008, 20, 4135.
91. J. H. Lim and J. Choi, Small, 2007, 3, 1504.
92. K. Lee, D. Kim, P. Roy and P. Schmuki, unpublished work.
93. Y.-Y. Song, R. Lynch, D. Kim, P. Roy and P. Schmuki, Electrochem. Solid-State Lett., 2009, 12, C17.
94. R. Hahn, J. M. Macak and P. Schmuki, Electrochem. Commun., 2007, 9, 947.
95. K. Nakayama in: 208th ECS Meeting, California, 2005, abstract 819 and abstract 843.
96. K. Ishibashi, R. Yamaguchi, Y. Kimura and M. Niwano, J. Electrochem. Soc., 2008, 155, K10.
97. R. Hahn, T. Stergiopoulus, J. M. Macak, D. Tsoukleris, A. G. Kontos, S. P. Albu, D. Kim, A. Ghicov, J. Kunze, P. Falaras and P. Schmuki, Phys. Status Solidi RRL, 2007, 1, 135.
98. H. Tang, K. Prasad, R. Sanjinbs, P. E. Schmid and F. Levy, J. Appl. Phys., 1994, 75, 2042.
99. N.-G. Park, J. van de Lagemaat and A. J. Frank, J. Phys. Chem. B, 2000, 104, 8989.
100. S. P. Albu, H. Tsuchiya, S. Fujimoto and P. Schmuki, Chem. Phys. Lett., 2009 , to be submitted.
101. R. P. Vitiello, J. M. Macak, A. Ghicov, H. Tsuchiya, L. F. P. Dick and P. Schmuki, Electrochem. Commun., 2006, 8, 544.
102. J. M. Macak, A. Ghicov, R. Hahn, H. Tsuchiya and P. Schmuki, J. Mater. Res., 2006, 21, 2824.
103. R. Hahn, A. Ghicov, J. Salonen, V.-P. Lehto and P. Schmuki, Nanotechnology, 2007, 18, 105604.
104. R. Hahn, F. Schmidt-Stein, J. Salonen, S. Thiemann, Y. Y. Song, J. Kunze, V.-L. Lehto and Patrik Schmuki, Angew. Chem., Int. Ed., 2009, 48, 7236.
105. R. Beranek, H. Tsuchiya, T. Sugishima, J. M. Macak, L. Taveira, S. Fujimoto, H. Kisch and P. Schmuki, Appl. Phys. Lett., 2005, 87, 243114.
106. W. W. Gärtner, Phys. Rev., 1959, 116, 84.
107. J. W. Schultze and M. M. Lohrengel, Electrochim. Acta, 2000, 45, 2499.
108. L. V. Taveira, A. A. Sagües, J. M. Macak and P. Schmuki, J. Electrochem. Soc., 2008, 155, C293.
109. H. Tsuchiya, J. M. Macak, A. Ghicov, A. S. Räder, L. Taveira and P. Schmuki, Corros. Sci., 2007, 49, 203.
110. U. Diebold, Surf. Sci. Rep., 2003, 48, 53.
111. A. Hagfeldt, U. Björksten and M. Gra1tzel, J. Phys. Chem., 1996, 100, 8045.
112. S. Södergren, A. Hagfeldt, J. Olsson and S.-E. Lindquist, J. Phys. Chem., 1994, 98, 5552.
113. R. Lynch, A. Ghicov and P. Schmuki, J. Electrochem. Soc., submitted.
114. J. M. Macak, H. Tsuchiya, A. Ghicov and P. Schmuki, Electrochem. Commun., 2005, 7, 1133.
115. T. Stergiopoulos, A. Ghicov, V. Likodimos, D. S. Tsoukleris, J. Kunze, P. Schmuki and P. Falaras, Nanotechnology, 2008, 19, 235602.
116. K.-M. Lee, V. Suryanarayanan, J.-H. Huang, K. R. J. Thomas, J. T. Lin and K.-C. Ho, Electrochim. Acta, 2009, 54, 4123.
117. G. K. Mor, K. Shankar, M. Paulose, O. K. Varghese and C. A. Grimes, Nano Lett., 2006, 6, 215.
118. J. H. Park, T.-W. Lee and M. G. Kang, Chem. Commun., 2008, 2867.
119. W. J. Lee, E. Ramasamy and D. Y. Lee, Sol. Energy Mater. Sol. Cells, 2009, 93, 1448.
120. S. Berger, A. Ghicov, Y.-C. Nah and P. Schmuki, Langmuir, 2009, 25, 4841.
121. B. Liu, E. S. Aydil and J. Am, J. Am. Chem. Soc., 2009, 131, 3985.
122. V. Yong, S.-T. Ho and R. P. H. Chang, Appl. Phys. Lett., 2008, 92, 143506.
123. J. Nelson, The Physics of Solar Cells, Imperial College Press, London, 2003, ch. 1.
124. L. Kavan, B. O'Regan, A. Kay and M. Grätzel, J. Electroanal. Chem., 1993, 346, 291.
125. M. K. Nazeeruddin, A. Kay, I. Rodicio, R. Humpbry-Baker, E. Miiller, P. Liska, N. Vlachopoulos and M. Grätzel, J. Am. Chem. Soc., 1993, 115, 6382.
126. N.-G. Park, G. Schlichthrl, J. van de Lagemaat, H. M. Cheong, A. Mascarenhas and A. J. Frank, J. Phys. Chem. B, 1999, 103, 3308.
127. S. Ito, P. Liska, P. Comte, R. Charvet, P. Pechy, U. Bach, L. Schmidt-Mende, S. M. Zakeeruddin, A. Kay, M. K. Nazeeruddin and M. Grätzel, Chem. Commun., 2005, 4351.
128. B. C. O'Regan, J. R. Durrant, P. M. Sommeling and N. J. Bakker, J. Phys. Chem. C, 2007, 111, 14001.
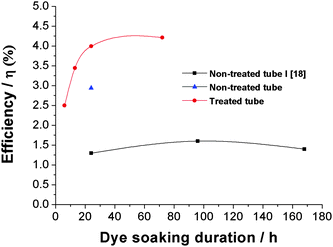
129. P. Roy, D. Kim, I. Paramasivam and P. Schmuki, Electrochem. Commun., 2009, 11, 1001.
130. P. Roy, D. Kim, K. Lee, E. Spiecker and P. Schmuki, unpublished work.
131. S. Funk, B. Hokkanen, U. Burghaus, A. Ghicov and P. Schmuki, Nano Lett., 2007, 7, 1091.
132. D. Kim, J. M. Macak, F. Schimidt-Stein and P. Schmuki, Nanotechnology, 2008, 19, 305710.

---