Stability and cooperativity of hydrogen bonds in dihydroxybenzoic acids

Abstract

Multiple temperature single crystal neutron diffraction studies of a new polymorphic form of 2,4-dihydroxybenzoic acid, and of the isomer 2,5-dihydroxybenzoic acid, are presented, together with static and dynamic solid-state density functional theory calculations. The studies present an unambiguous analysis of the potential for cooperativity and hydrogen atom disorder in the hydrogen bond network of both materials. The neutron diffraction experiments establish clearly that there is no disorder, and hence that no hydrogen bond cooperativity is present in either system at temperatures up to 150 K. The findings are supported by DFT calculations, from which lattice and hydrogen bond configuration energies are also obtained, together with computed vibrational spectra.

---

Introduction

Hydrogen bonds (HBs) in the solid-state are varied and complex interactions. The architecture of hydrogen bonding in crystal lattices can be, at least partially, controlled by taking starting materials of known structural inclination (e.g. a tetrahedral core) and combining them with specific intermolecular bonding substituents (e.g. COOH groups). The details of the HBs involved, and the frequent competition between possible hydrogen bonding schemes governing such architectures, can often be subtle, and recent studies of hydrogen bonding using multi-temperature (multi-T) single crystal neutron diffraction, X-ray diffraction and solid-state simulations have begun to reveal the potential for variation in the bonding energies and topologies of HB networks by changing external thermodynamic parameters such as temperature and pressure.¹ In effect, such perturbations can be viewed as tuning the ‘chemistry’ (and energetics) of the HB network,² as evinced by changes in bond orders and the redistribution of electron density. Infrequently, within compounds in which the proton affinities and structure are favourable, a change in temperature or pressure may instigate proton migration or disorder.

Multi-condition studies of short HBs have permitted such effects to be followed in detail,³ and have revealed that the chemistry of these materials in the solid-state may be more varied than was previously suspected. Disordered hydrogen atom positions within a double well potential have also been widely observed in longer HBs, e.g. in substituted benzoic acids.⁴ Similar findings have also been reported in a comprehensive series of studies by Gilli et al. (and references therein).⁵

The latter authors have also investigated a number of materials bearing intramolecular HBs, in which proton transfer involves tautomerism, and therefore a degree of cooperativity, between the hydrogen and chemical bonds.⁶ On the basis of this work, Gilli et al. have further developed the concepts of charge- (CAHB) and resonance- (RAHB) assisted hydrogen bonding.

Ongoing interest in hydrogen atom disorder in carboxylic acid dimers has prompted further investigation of the possibility of cooperative effects in materials containing both intra- and intermolecular HBs. As a part of this work, a recent study highlighted a previously unknown polymorph of 2,4-dihydroxybenzoic acid (2,4-DHBA).⁷ The 2,4-DHBA structure was characterised by multi-T X-ray diffraction and preliminary solid-state DFT calculations. As the representation in Fig. 1 shows, the material manifests a HB network that is suggestive of cooperativity between the intermolecular (COOH)₂ dimer-forming and intramolecular HBs. The presence of any hydrogen atom disorder within these HBs would support such a cooperative model, but initial X-ray studies proved to be inconclusive in this regard. However, calculations on the three potential end-point tautomers (Fig. 1) indicated that the dominant, crystallographically observed configuration (form I) is at least 9 kJ mol⁻¹ lower in energy than the other forms, indicating that no disorder should be expected. The current work expands upon this initial study, also extending it to the 2,5-dihydroxybenzoic acid (2,5-DHBA) isomer and adding, in particular, the results obtained from multi-T neutron diffraction experiments, with their ability to locate accurately and precisely the nuclear positions associated with the hydrogen atoms in molecular structures. These experimental measurements are supported by more extensive calculations, including dynamics simulations.

Fig. 1 The three possible tautomeric forms of the 2,4-DHBA dimer.

Two polymorphs of 2,5-DHBA are known⁸ and their structures have been determined by X-ray diffraction. The first (form 1) is an ordered monoclinic form and the second (form 2) contains a disordered HB involving the 5-substituted hydroxyl group. This disorder is constrained to exist by the presence of an inversion centre along the HB. In addition to multi-T neutron diffraction studies of 2,4-DHBA, the evolution in the structure of form 1, an ordered polymorph of 2,5-DHBA, is also investigated by means of multi-T X-ray and neutron single crystal diffraction.

X-Ray diffraction study of 2,5-DHBA

Multi-T X-ray diffraction data for form 1 of 2,5-DHBA were collected over temperatures ranging from 100 to 350 K in 50 K intervals. The evolution in the geometry of the HB network was followed closely. The molecules (Fig. 2) are found to condense into a lattice (Fig. 3) characterised by a planar ribbon arrangement, and containing three crystallographically-unique HBs: namely, two intermolecular (A and C; Fig. 3) and one intramolecular (B) bond. The carboxylic acid group (C7, O8, O9 and H1; Fig. 2) borne by each molecule participates in an intermolecular HB with an adjacent molecule, forming dimers with inversion centres located at the midpoint of the (COOH)₂ linkages. The non-protonated oxygen (O8) of each COOH group also acts as a hydrogen acceptor for the intramolecular HB (B) extending from the ortho-OH group (O2H2). The meta-OH group (O5H5) participates in an intermolecular HB (C; Fig. 3) with the equivalent group on a neighbouring molecule, leading to the formation of continuous HB chains along the b-axis of the cell.

Fig. 2 Structure and atom labels in the 2,5-DHBA molecule.

Fig. 3 Top: The crystal structure of 2,5-DHBA in the plane of a ribbon, highlighting the intermolecular dimer-forming (A), intramolecular (B) and intermolecular chain-forming (C) HBs. Bottom: The crystal structure of 2,4-DHBA in the plane of a layer, highlighting the intermolecular dimer-forming (D), intramolecular (E) and intermolecular (F) HBs.

In keeping with the previous results for 2,4-DHBA,⁷ examination of the X-ray difference Fourier maps proves inconclusive, in the sense that the presence of small secondary electron density peaks associated with each HB cannot be excluded with complete certainty (Fig. 4), although there is certainly little compelling evidence for such density. The peaks locating the electron density associated with the hydrogen bonded hydrogen atoms are well defined at low temperature, but the noisier higher temperature maps are slightly ambiguous in their localisation of the hydrogen atom density.

Fig. 4 Difference Fourier maps derived from the X-ray diffraction study of 2,5-DHBA, plotted in the plane of the C7, O8 and O9 atoms, with atoms H1 and H2 removed from the structural model. Left to right: 100, 150, 200 and 350 K. The (COOH)₂ dimerisation link is at the top.

Neutron diffraction studies

Crystals of both materials were grown by slow evaporation from acetone solutions. Large single crystals suitable for neutron diffraction studies were obtained, and data subsequently collected on the SXD instrument at the ISIS spallation neutron source (see the Experimental and theoretical methods section).

The 2,4-DHBA structures obtained from our neutron diffraction experiments confirm the results of the previous X-ray diffraction study,⁷ yielding lattices in which the usual (COOH)₂-bonded (D, Fig. 3) dimers are linked into undulating layers by intermolecular (F) HB linkages. Intramolecular HBs (E) are also present, linking the ortho-OH and COOH groups. The relevant crystallographic data are presented in the Experimental and theoretical methods section, while the evolution in the structure of the 2,4-DHBA molecule with temperature is depicted in Fig. 5.

Fig. 5 The neutron diffraction structure of 2,4-DHBA at 20 (top) 90 (middle) and 150 (bottom) K, visualised with 50% ellipsoids.

The previous study by Parkin et al.⁷ offered some evidence in support of the lack of cooperative disorder in the dimer-forming (D) and intramolecular (E) HB linkages. The difference Fourier maps derived from the present multi-T neutron diffraction (shown in the plane of atoms C7, O8 and O9 in Fig. 6) establish clearly that there is no proton disorder in any of the HBs up to the highest temperature accessed in our study (150 K). The atomic displacement parameters of the hydrogen atoms increase in magnitude with temperature as expected, but their shapes remain close to spherical in each case. The C–O, C=O, O–H and O⋯O distances determined from the nuclear densities also remain invariant throughout the temperature range studied. This constitutes an important null finding, effectively ruling out any cooperativity in the HB network of this material and supporting the conclusion of the related X-ray study.

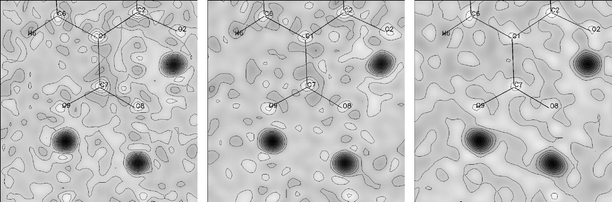Fig. 6 Difference Fourier maps derived from the neutron diffraction study of 2,4-DHBA, plotted in the plane of the C7, O8 and O9 atoms with protons H1 and H2 removed from the structural model. 20 (left), 90 (middle) and 150 (right) K. Note that these maps are in a different orientation from those in Fig. 4, with, in this case, the (COOH)₂ dimerisation link at the bottom.

The results obtained for 2,5-DHBA are similar, in that, while the thermal ellipsoids increase in size with temperature, no proton disorder is observed within any of the HBs up to 200 K. The structures and Fourier difference maps obtained from the neutron data are similar to those of 2,4-DHBA, and are consequently not discussed here, although they are included together with the CIFs derived from the neutron refinements within the accompanying ESI.†

Theoretical studies

First principles electronic structure calculations were performed to establish the relative energies of the 2,4-DHBA tautomers (Fig. 1), both in isolation and in the condensed phase. Total energies were obtained from solid-state density functional calculations within the plane-wave pseudopotential formalism, as embodied in the CASTEP code.⁹ Deformation electron densities were also obtained from calculations using the CRYSTAL06 code.¹⁰ Full details of the theoretical methods applied are presented in the Experimental and theoretical methods section.

The strengths of the intermolecular dimer-forming (D) HBs, E_HB, are easily obtained from the difference in total energies per molecule of isolated molecules and dimers. Plane-wave basis sets are well suited to this task, for they are free of the superposition errors that are manifested in atom-centred representations. Similarly, the stabilisation of the dimers arising out of their interaction with the crystalline environment, E_DS, may be obtained from the differences in total energies per molecule of the isolated dimer and crystal cells. It can be anticipated that the latter energies will be dominated by the longer intermolecular (F) HBs linking the proton donating and accepting O atoms at the para- (O4) and ortho- (O2) positions, respectively. Clearly, the intramolecular (E) HB strengths cannot be obtained in the same fashion, for these HBs do not link units that are chemically stable in isolation. Insight into the strengths of these bonds in the various tautomers is instead sought by comparing the respective ν_OH stretching frequencies, as obtained from molecular dynamics simulations upon isolated form I and form III dimers.

Previous calculations sought to estimate the relative energies of the three tautomeric forms of the 2,4-DHBA lattice.⁷ Form I was found to be the most stable configuration, with form III lying some 8.6 kJ mol⁻¹ higher in energy. Tautomer II was shown to be unstable; all attempts to optimise into this structure resulted in relaxation back to the form I configuration. The energy of this tautomer was instead estimated by combining the explicit calculation of the intramolecular (E) HB potential with a harmonic model for the relaxation of the ortho C2–O2 and acid C7=O8 bonds, yielding an energy approximately 51 kJ mol⁻¹ higher than that of form I.⁷ The current study expands upon this earlier work, seeking in particular some insight into the influence of the crystalline and dimer environments on the relative energies of the stable tautomers, alongside the strengths of the interactions binding the molecules into their lattices.

Table 1 presents the energies per molecule of forms I and III of 2,4-DHBA in various environments. Crystals composed of the form I tautomer constitute the most stable configuration, while it should be noted that the form III tautomer is higher in energy in each environment. The energy difference might, at first sight, be attributed to a simple variation in the charges of the intramolecular (E) HB acceptors, but this cannot be the case, for the calculations reveal that the acid group hydroxyl O9 atom has a population 0.14e higher than the carboxyl atom O8, which would be expected to lead to an increase in the stability of form III through a strengthening of the intramolecular (E) HB. A more plausible model emerges from a consideration of the tetrahedral and planar orientations of the O atom lone pairs, revealed by plots of the deformation electron density [ρ_molecule(r) − Σρ_atoms(r); Fig. 7], arising from the sp³ and sp² hybridization of orbitals within the acid O9–H1 and C7=O8 groups, respectively. Thus, it is suggested that, in form I, the carboxyl oxygen atom O8 acts as a more effective acceptor of the intramolecular (E) HB, for its lone pairs lie in the molecular plane, while the hydroxyl oxygen atom O9 is less effective in this regard in form III, for its lone pairs point out of the plane. The Mulliken overlap populations shown in Table 2 support this model, revealing that the intramolecular (E) HB H2⋯O population is 0.05e lower in form III as compared with form I.

Table 1 The relative energies, E, per molecule of forms I and III of 2,4-DHBA in various environments, the energy splitting between forms I and III, ΔE_{Form III − Form I}, the intermolecular (D) HB strengths, E_HB, and the stabilisation energies of dimers in the lattice, E_DS. All energies are in kJ mol⁻¹

Environment	E (Form I)	E (Form III)	ΔEForm III − Form I
Crystal	0.00	8.64	8.64
Isolated dimer	19.65	29.23	9.58
Isolated molecule	55.12	76.67	21.55
E HB	35.47	47.44	—
E DS	19.65	20.60	—

---

Fig. 7 The theoretical deformation electron density [ρ_def(r) = ρ_molecule(r) − Σρ_atoms(r)] of the isolated form I monomer of 2,4-DHBA obtained from B3LYP/6-311G** calculations. Solid, dashed and dot-dashed lines indicate positive-, negative- and zero-valued contours, respectively.

Table 2 The Mulliken overlap populations, O(e), between atoms comprising the intramolecular (E) and intermolecular (D) HBs

	O Intra O2–H2		O Intra H2⋯O		O Inter O9–H1		O Inter H1⋯O8′
	Form I	Form III	Form I	Form III	Form I	Form III	Form I	Form III
Monomer	0.49	0.52	0.12	0.07	0.49	0.48	—	—
Dimer	0.50	0.51	0.12	0.09	0.47	0.42	0.16	0.23

---

It is interesting that the formation of the intermolecular (D) HBs in the dimer reduces the form I–III energy difference. The effect can be tentatively attributed to two mechanisms, namely: the increase in the O9–H1 distance of the intermolecular (D) HB and the redistribution of charge from the latter bond into the partial H1⋯O8′ bonds (O8′ on an adjacent molecule and related by an inversion centre), both of which could conceivably permit the lone pairs borne by oxygen O9 some degree of relaxation from a tetrahedral configuration. Thus, in this model, the energy of the form III tautomer in the dimer will be lowered by two additional contributions that do not occur in the monomer. Firstly, there is an increase in the strength of the intramolecular (E) HBs caused by the partial reorientation of the hydroxyl oxygen lone pairs discussed above, and secondly, there is an increase in the strength of the intermolecular (D) HBs, arising from the transfer of charge from the O9–H1 bond to the H1⋯O8′ bond. Again, there is support for this model in the results presented in Table 1 and Table 2, which reveal that the intermolecular (D) HBs are stronger in form III than in form I, while the form I and form III intramolecular (E) HB H2⋯O overlap populations differ by 0.03e in the dimer and by 0.05e in the isolated molecule. However, it must be noted that the subtlety of the foregoing effects necessitate that they be regarded with caution, particularly with regard to the computed Mulliken charges, the absolute values of which vary sensitively with basis set size and local geometry. Nevertheless, it is emphasised that the focus here is always upon relative charges and total energies, and that the use of a plane-wave basis removes any contributions to the latter arising out of superposition error.

The packing of dimers into the crystalline environment changes the form I–III energy difference very little, emphasising that it is an essentially intradimer effect. The stabilisation of dimers in the crystal, E_DS, is appreciable, and, given that the intermolecular (F) HBs and weaker interactions possess near identical geometries, is of similar magnitude in both forms. The intermolecular (F) HBs also seem to adopt geometries that permit the tetrahedrally-oriented lone pairs on oxygen atom O2 to act as effective acceptors. The energies of the dimer-forming (D) HBs are within the approximate range of 15–60 kJ mol⁻¹ suggested by Emsley for moderate strength bonds,¹¹ while, if the majority of the dimer stabilisation energy, E_DS, is attributed to the presence of the intermolecular (F) HBs, the latter are found to possess strengths at the low end of this range.

Finally, the effects revealed in the static calculations have been investigated further by performing low temperature molecular dynamics simulations on isolated dimers of the form I and form III tautomers. Fig. 8 presents the vibrational spectra obtained from these calculations for the ortho- (H2), para- (H4) and acid (H1) hydroxyl group protons. The spectra for the para- (H4) protons can be considered as convenient benchmarks, for this group does not participate in hydrogen bonding in the isolated dimer. The ν_OH peaks for this group occur at the same frequency of approximately 3760 cm⁻¹ in both tautomers. Discussing form I first, the most readily apparent effect of hydrogen bonding is a strong red-shifting of the stretching frequencies, yielding peaks at 3110 cm⁻¹ for the ortho-hydroxyl proton (H2), and at 2650 and 2760 cm⁻¹ for the acid proton (H1). The latter two peaks most likely correspond to the symmetric (g) and asymmetric (μ) stretching modes of the (COOH)₂ linkage, respectively. Tautomerisation into the form III structure induces a further red-shifting of approximately 500 cm⁻¹ and a broadening of the acid proton (H₁) stretching band, in keeping with the increased intermolecular (D) HB strength found in the static calculations. However, the ortho-proton (H2) modes apparently blue-shift by approximately 300 cm⁻¹, in support of the earlier conclusion that the intramolecular (E) HB is weakened by conversion to form III.

Fig. 8 The vibrational spectra of protons in the para- (black), ortho- (blue) and acid- (red) OH groups in forms I ([thick line, graph caption]) and III ([dash dash, graph caption]) of the isolated dimer of 2,4-DHBA.

Conclusions

Representations of the electron density of hydrogen atoms involved in hydrogen bonding in the form of Fourier difference maps by X-ray diffraction can provide additional insight into the behaviour of hydrogen atoms involved in hydrogen bonds (HBs). In the cases of both 2,4-dihydroxybenzoic acid (2,4-DHBA)⁷ and 2,5-dihydroxybenzoic acid (2,5-DHBA), these representations provided an ambiguous picture, showing limited evidence for the possibility of a cooperative effect between the intra- and intermolecular HBs, and hence hydrogen disorder as a function of variable temperature. Neutron diffraction provides the definitive unambiguous identification of such effects, and in these cases showed no evidence for any disorder of the nuclear density in these systems up to 150 K in the case of 2,4-DHBA and 200 K for 2,5-DHBA. This is consistent with the observations from the X-ray data, where the Fourier difference maps only started to show an unusual shape of the electron distributions at higher temperatures. This, however, also corresponds to temperatures where there is inevitably more noise in the Fourier difference maps.

Theoretical calculations were also utilised in the form of static models, from which lattice and HB configuration energies could be extracted, together with theoretical deformation densities, providing further insight into the electronic structure local to the hydrogen bonding regions. These suggested that no cooperative effect in the HBs or disorder should be expected, confirming the observations obtained through the neutron diffraction data. The alternative tautomers were found to be significantly higher in energy than those found from calculations on the experimentally observed tautomeric form. Molecular dynamics calculations were also used to calculate the vibrational spectra of isolated dimers of the form I and form III tautomers, which in turn assisted in rationalising the relative variations in the strengths of the inter- and intramolecular HBs in the isolated dimers, and in the crystalline environment. Again, the data obtained were consistent with the structural interpretations advanced.

Finally, a comment on the complementarity of the X-ray and neutron diffraction, and periodic DFT calculations, in locating the HB protons, is worthwhile. While the most generally accurate and useful of these techniques undoubtedly remains variable temperature neutron diffraction, X-ray diffraction and static calculations might be expected to offer useful insights into moderate and weak strength HBs, in which the protons remain well-localised. The increasing dominance of quantum effects and covalency in short and strong HBs poses more severe problems for the latter two techniques, and while the direct access to the potential for proton motion afforded by total energy calculations offers a means by which to account for such effects, there remains, as yet, no generally applicable theoretical method by which to include the potentially important coupling of proton motion to low frequency vibrational modes, such as donor–acceptor stretching and rocking motions.

Experimental and theoretical methods

Crystallisation

Both materials were purchased from Sigma-Aldrich and recrystallised by slow evaporation from an acetone solution.

X-Ray diffraction

Single crystal X-ray diffraction data for 2,5-DHBA were collected on a Bruker-Nonius Kappa CCD diffractometer and modelled at 100, 150, 200, 250, 300 and 350 K. The structures were solved using SIR92¹² and refined against all collected data within WinGX.¹³ The crystallographic data at 100 K can be found in Table 3 and CIFs for all other temperatures have been deposited.†

Table 3 Crystallographic data for 2,4-DHBA and 2,5-DHBA

Formula	2,4-DHBA	2,5-DHBA	2,5-DHBA
	C7H6O4	C7H6O4	C7H6O4
M/g mol^−1	154.12	154.12	154.12
T/K	20	20	100
Radiation	Neutron	Neutron	X-Ray
Space group	P21/n	P21/n	P21/n
a/Å	3.656(2)	5.545(3)	5.5591(2)
b/Å	22.329(11)	4.877(3)	4.8698(2)
c/Å	8.009(4)	23.3506(11)	23.3593(9)
β (°)	99.76(4)	93.62(3)	93.448(2)
V/Å^3	644.4(6)	630.1(5)	631.23(4)
Z	4	4	4
ρ c/g cm^−3	1.569	1.623	1.600
Reflections collected	8839	8671	10859
Independent reflections			1463
Observed > 2σ(I)	8839	8671	1064
R int			0.0724
Parameters	264	263	124
GooF	1.048	1.429	0.867
R 1 (observed)	0.0789	0.0927	0.0430
R 1 (all)	0.0789	0.0927	0.0674
wR2 (all)	0.2129	0.2903	0.1284
ρ max,min/e Å^−3	0.50, −0.32	0.71, −0.47	0.26, −0.33

---

Neutron diffraction

Single crystal neutron diffraction data for both 2,4-DHBA and 2,5-DHBA were collected on SXD,¹⁴ the single crystal diffraction instrument at ISIS, UK using the time-of-flight Laue diffraction method.

A total of 10 frames, each consisting of data from the 11 detectors, with an exposure length of approximately 400 μamp h (approx. 2.5 h), were collected at each temperature. In the case of 2,4-DHBA, temperatures of 20, 90 and 150 K were measured, and for 2,5-DHBA, 20, 100 and 200 K.

The unit cell was refined from the X-ray cell individually for each frame and an average taken for the refinement of each temperature. Processing of the data was completed using SXD2001. The final refinement was done using SHELXL¹⁵ within the program WinGX¹³ with initial atomic co-ordinates taken from the X-ray structure. All hydrogen positional and anisotropic thermal parameters were fully refined. Difference Fourier maps were computed (without the hydrogen atoms under investigation) in the plane generated by the atoms C7, O8 and O9. Molecular structure images were produced using XP¹⁶ and Fourier difference maps by the program MAPVIEW within WinGX.¹³

Crystallographic data for the 20 K data sets for both 2,4-DHBA and 2,5-DHBA can be found in Table 3. CIFs have been deposited for all other temperatures.†

Theoretical methods

The exchange correlation functional of Perdew, Burke and Ernzerhof¹⁷ was used throughout, along with consistent ultrasoft pseudopotentials. The accuracy of the total energies was ensured by the application of a plane-wave cutoff of 450 eV. The calculations in the crystalline cells employed a Monkhorst–Pack mesh,¹⁸ with spacing of points along the reciprocal lattice vectors of 0.05 Å⁻¹ or less. The isolated molecule and dimer calculations were performed in cuboidal supercells with lengths (a,b,c) of (14,10,10) and (22,10,10) Å, respectively, using Γ-point reciprocal space sampling. The initial structures of forms I, II and III of the crystal were set manually, and optimisation of the atomic positions proceeded within the fixed experimental cells until the forces on all atoms were less than 0.01 eV Å⁻¹. Mulliken charges were obtained from a projection of the wavefunction in the plane-wave representation onto a set of localised atomic orbitals via the Sanchez-Portal technique.¹⁹ The molecular dynamics simulations were performed within the NVT ensemble, with sampled trajectories of length 2 ps and a time-step of 0.4 fs. The temperature was maintained at an average value of 20 K in each case by use of a chain of five Nosé-Hoover thermostats. The first 0.4 ps of each trajectory was discarded to allow for equilibration, and the vibrational power spectra obtained by Fourier transformation of the atom-projected force autocorrelation function was derived from the remaining 1.6 ps of each trajectory. Similar analyses using the atom-projected velocity autocorrelation functions (see ESI†) yielded essentially identical positioning of the relevant spectral features. The deformation electron density of the form I molecule of 2,4-DHBA was obtained from B3LYP/6-311G** calculations within the CRYSTAL06 code.¹⁰

Acknowledgements

This work was part-funded by the EPSRC under grant GR/T21615. C. K. L. was funded by the CPOSS Basic Technology project. ISIS beam time was provided by STFC. M. S. A. was funded by the University of Glasgow and the STFC Centre for Molecular Structure and Dynamics.

References

1. C. C. Wilson, Crystallogr. Rev., 2007, 13, 143–198.
2. A. Parkin, S. M. Harte, A. E. Goeta and C. C. Wilson, New J. Chem., 2004, 28, 718–721.
3. C. C. Wilson, K. Shankland and N. Shankland, Z. Kristallogr., 2001, 216, 303–306; T. Steiner, C. C. Wilson and I. Majerz, Chem. Commun., 2000, 1231–1232; T. Steiner, I. Majerz and C. C. Wilson, Angew. Chem., Int. Ed., 2001, 40, 2651–2654.
4. G. A. Sim, J. M. Robertson and T. H. Goodwin, Acta Crystallogr., 1955, 8, 157–164; J. A. Kanters, G. Roelofsen and J. Kroon, Nature, 1975, 257, 625–626; G. Bruno and L. Randaccio, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 1711–1712; P. Fischer, P. Zolliker, B. H. Meier, R. R. Ernst, A. W. Hewat, J. D. Jorgensen and F. J. Rotella, J. Solid State Chem., 1986, 61, 109–125; R. Destro, Chem. Phys. Lett., 1991, 181, 232–236; R. Feld, M. S. Lehmann, K. W. Muir and J. C. Speakman, Z. Kristallogr., 1981, 157, 215–231; C. C. Wilson, N. Shankland and A. J. Florence, Chem. Phys. Lett., 1996, 253, 103–107; C. C. Wilson, N. Shankland and A. J. Florence, J. Chem. Soc., Faraday Trans., 1996, 92, 5051–5057; C. C. Wilson, Recent Res. Dev. Chem. Phys., 2002, 3, 119–147; C. C. Wilson and A. E. Goeta, Angew. Chem., Int. Ed., 2004, 43, 2095–2099; C. C. Wilson, X. Xu, A. J. Florence and N. Shankland, New J. Chem., 2006, 30, 979–981; A. Parkin, C. C. Seaton, N. Blagden and C. C. Wilson, Cryst. Growth Des., 2007, 7, 531–534.
5. P. Gilli, V. Bertolasi, L. Pretto, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 2004, 126, 3845–3855.
6. G. Gilli, F. Bellucci, V. Ferretti and V. Bertolasi, J. Am. Chem. Soc., 1989, 111, 1023–1028; V. Bertolasi, V. Ferretti, P. Gilli, G. Gilli, Y. M. Issa and O. E. Sherif, J. Chem. Soc., Perkin Trans. 2, 1993, 2223–2228; V. Bertolasi, P. Gilli, V. Ferretti and G. Gilli, Chem.–Eur. J., 1996, 2, 925–934.
7. A. Parkin, M. Adam, R. I. Cooper, D. S. Middlemiss and C. C. Wilson, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 303–308.
8. M. Haisa, S. Kashino, S.-I. Hanada, K. Tanaka, S. Okazaki and M. Shibagaki, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 1480–1485; D. E. Cohen, J. B. Benedict, B. Morlan, D. T. Chiu and B. Kahr, Cryst. Growth Des., 2007, 7, 492–495.
9. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and C. M. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
10. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, Ph. D’Arco and M. Llunell, CRYSTAL06 User’s Manual, University of Torino, Torino, 2006.
11. J. Emsley, Chem. Soc. Rev., 1980, 9, 91.
12. A. Altomare, G. Cascarano, G. Giacovazzo, A. Guagliardi, M. C. Burla, G. Polidori and M. Camalli, J. Appl. Crystallogr., 1994, 27, 435–436.
13. J. L. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838.
14. D. A. Keen, M. J. Gutmann and C. C. Wilson, J. Appl. Crystallogr., 2006, 39, 714–722.
15. G. M. Sheldrick, SHELXL-97, Program for refinement of crystal structures, University of Göttingen, Germany, 1997.
16. XP, Bruker AXS Inc., Madison, Wisconsin, USA, 2005.
17. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
18. H. J. Monkhorst and D. J. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
19. D. Sanchez-Portal, E. Artacho and M. J. Soler, Solid State Commun., 1995, 95, 685–690.

---

Footnote

† Electronic supplementary information (ESI) available: Structures and Fourier difference maps from 2,5-dihydroxybenzoic acid neutron data, proton vibrational spectra derived from Fourier transforms of the atom projected velocity autocorrelation functions for isolated dimers of the form I and form III tautomers. CCDC 747937–747948. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/b9nj00353c

---