A kinetic investigation, supported by theoretical calculations, of steric and ring strain effects on the oxidation of sulfides and sulfoxides by dimethyldioxirane in acetone

Abstract

The oxidations of alkyl 4-nitrophenyl, and dialkyl, sulfides and sulfoxides by dimethyldioxirane in acetone occur by concerted mechanisms but the sulfides respond differently from the sulfoxides to variation in the alkyl group. The reactions of the sulfides are inhibited by the steric effects of alkyl groups and these predominate over their inductive effects. By contrast, the reactions of these limited sets of sulfoxides are insensitive to alkyl steric effects but there is an indication of steric acceleration when a broader set of sulfoxides is considered. This behaviour is rationalised in terms of the differences in dipolar charge and its solvation between the ground state and transition state for the two types of substrate. The oxidations of cyclic sulfides and sulfoxides also exhibit contrasting behaviour. The reactivity of the sulfides is insensitive to ring strain but is explicable in frontier orbital terms whereas that of the sulfoxides is partly dependent upon the change in ring strain between reactant and product on oxidation, a difference rationalised in terms of the relative positions of the transition states in the reaction coordinates of the two oxidations. The reactivity of 4-, 5- and 6-membered cyclic sulfoxides is also dependent on a ring-size related property of the transition state. Calculations at the B3-LYP/6-31G* level of density functional theory on both ground states and transition states, including simulation of solvation by acetone, strongly support the mechanistic conclusions reached in this and earlier work.

---

Introduction

For over two decades dioxiranes have been known to be efficient electrophilic oxidants for a wide range of organic substrates.^1,2 Dimethyldioxirane, 1a, and the more reactive (trifluoromethyl)methyldioxirane, 1b, (Scheme 1) prepared in situ in acetone and trifluoroacetone, respectively, by oxidation of the solvent with peroxomonosulfate, have been the most frequently used. Their volatility permits the concentration of both dioxiranes by distillation from their respective ketone oxidation mixtures.³ Latterly, both reagents have also been extracted into, and used in, chloromethane solvents.⁴

Scheme 1

As oxidants of sulfides, the dioxiranes display variants of two distinct mechanisms. Conversion of a sulfide into the corresponding sulfoxide, 3 (Scheme 1), may occur in a single step, via transition state 2, in which the transfer of oxygen from 1 to the sulfide is concerted with elimination of one molecule of ketone MeC(O)R₁.^1a,b,5,6 Given a stoichiometric excess of the dioxirane, the resulting sulfoxide, 3, may, in turn, undergo a comparable, but slower, concerted reaction, via transition state 4, to give the sulfone, 5, also with one molecule of ketone (n = 1). This mechanism prevails when the oxidant is 1a in acetone or in mixtures of acetone with aprotic co-solvents of greater or lesser polarity. However, in aqueous acetone of sufficient water content (20% v/v) the mechanism for sulfides changes to a two-step process in which the intermediate sulfonium betaine, 6a, occurs; this then fragments to give 3 and a molecule of acetone; any subsequent oxidation of sulfoxide to sulfone remains a concerted process.⁶ When the dioxirane is 1b, the corresponding betaine intermediate 6b forms more readily than 6a as the anionic centre is stabilised by the powerful electron-withdrawing effect of the CF₃ group. If formed in chloromethane solvents in which the anionic centre is not stabilised by hydrogen bonding, 6b cyclises to another intermediate, the dioxathietane, 7b, that reacts with a second molecule of 1b to give sulfone 5 and two molecules of MeC(O)CF₃ (n = 2) at a rate faster than the initial rate of reaction of 1b with the sulfide.⁷ Thus, depending on the particular dioxirane and on the composition of the solvent in which the reaction is performed, the oxidation of a sulfide by one equivalent of a dioxirane can lead to sulfoxide alone, to partial oxidation to sulfone alone, or to a mixture of sulfoxide and sulfone.

There has been relatively little previous investigation of steric or ring-size effects on the oxidations of sulfur compounds. Modena and co-workers⁸ reported the trends in rate constants, caused by structural variation of alkyl groups, for the oxidations of sulfides by H₂O₂/H⁺ in aqueous ethanol (6% v/v H₂O) and of sulfoxides by perbenzoic acid in 50% v/v aqueous dioxane, and Ruff and Kucsman⁹ have reported oxidations of aralkyl, dialkyl and cyclic sulfides by periodate ion in 50% aqueous ethanol in which steric effects are considered.

This paper concludes our investigations into the oxidation of sulfides and sulfoxides by dimethyldioxirane, 1a; in particular, the kinetic consequences are described of alkyl moiety variation in oxidations of alkyl 4-nitrophenyl sulfides and sulfoxides and dialkyl sulfides and sulfoxides, and of ring-size variation in cyclic sulfides and sulfoxides, all of which, in acetone, proceed by concerted mechanisms. In addition, we also describe the results of MO calculations that give insight into the nature of the transition states formed by aryl methyl sulfides and sulfoxides on oxidation by 1a, amplifying prior physical-organic reasoning.

Results and discussion

1 Alkyl 4-nitrophenyl substrates

1.1 Rate constants and alkyl group variation. In Table 1 are presented the rate constants, measured spectrophotometrically, for the oxidations of alkyl 4-nitrophenyl sulfides, 8, and sulfoxides, 9, by dimethyldioxirane, 1a, in acetone. The procedures for sulfide oxidation under second order conditions and for sulfoxide oxidation under first order conditions have been described previously.^6b The molar absorbances of substrates and products required for the former conditions are given in ESI† 1, Table S1. The sec-butyl sulfide, being racemic, will give a mixture of diasteroisomeric sulfoxides on oxidation and this mixture, on further oxidation, will give a racemic sulfone. Neither oxidation behaved differently from the oxidations of the achiral substrates and single constants were obtained for both processes.

Table 1 Rate constants^a for the oxidation of alkyl 4-nitrophenyl sulfides and sulfoxides by 1a in acetone

R	10^−2k2(R)S/dm^3 mol^−1 s^−1	10^2kobs(R)SO/s^−1	10^3[1a]/mol dm^−3	k 2(R)SO/dm^3 mol^−1 s^−1
	at 291.3 K	at 294.6 K		at 294.6 K
a Uncertainties are 95% confidence intervals.
Me	5.45 ± 0.11	4.55 ± 0.18	5.48 ± 0.13	8.30 ± 0.54
Et	6.99 ± 0.08	6.94 ± 0.18	5.43 ± 0.13	12.8 ± 0.6
i-Pr	6.54 ± 0.18	—	—	—
n-Bu	6.81 ± 0.22	6.07 ± 0.12	5.36 ± 0.16	11.3 ± 0.6
s-Bu	5.19 ± 0.08	6.54 ± 0.24	5.45 ± 0.11	12.0 ± 0.7
t-Bu	4.86 ± 0.21	11.0 ± 0.3	5.35 ± 0.11	20.5 ± 1.0

---

1.2 Sulfides. The rate constants of the sulfides, k₂(R)_S, vary with the alkyl group increasing from Me to Et then decreasing, in the order n-Bu > i-Pr > s-Bu > t-Bu, to values less than that of Me. This variation suggests that, in the electrophilic oxidation, the reaction-promoting, electron-donating (+I) effects of the groups larger than Et are outweighed by their reaction-hindering steric effects.

In a first attempt to evaluate quantitatively the separate electronic and steric effects of the alkyl groups we applied the Taft–Pavelich eqn (1):¹⁰

log [k₂(R)_S/k₂(Me)_S] = ρ*σ*_(T) + δE_s (1)

where σ*_(T) and E_s are Taft’s polar and steric substituent constants and ρ* and δ the respective reaction constants (see ESI† 2, Table S2 for substituent constants); the correlation is poor: R² = 0.870. The recasting of eqn (1) as eqn (2) which allows variation in the intercept {from [log k₂(Me)_S/dm³ mol⁻¹ s⁻¹]} results in a marginal improvement (R² = 0.8895) but the correlation remains indifferent.

log [k₂(R)_S/dm³ mol⁻¹ s⁻¹] = ρ*σ*_(T) + δE_s + C (2)

Since the work of Taft and Pavelich, other scales of both inductive and steric substituent constants have been proposed (see ESI† 2, Table S2). A systematic survey of the possible pairings of the various inductive and steric constants (see ESI† 2, Table S3) has shown that the sulfide data in Table 1 are best expressed by eqn (3):

log [k₂(R)_S/dm³ mol⁻¹ s⁻¹] = ρσ_I(L) + δE_s + C (3)

where σ_I(L) is Levitt and Widing’s inductive scale based on gas-phase ionisation potentials.¹¹ This results in the regression coefficients and intercept of eqn (4) (R² = 0.9787):

log [k₂(R)_S/dm³ mol⁻¹ s⁻¹] = −(10.17 ± 3.94)σ_I(L) + (0.226 ± 0.065)E_s + (2.27 ± 0.14) (4)

It should be noted that, whereas the σ_I(L) scale is referred to H, the E_s scale is referred to Me; the raw regression coefficients found here cannot therefore be taken as the respective reaction constants. Even if both scales were referred to a common standard substituent, the raw coefficients still would not adequately reflect the relative importance of the two substituent effects because the ranges of the various inductive scales are considerably less than those of the steric scales (see ESI† 2, Table S2). This problem can be mitigated by a standardisation of the data that applies unit normal scaling to the variate and both explanatory variables (each is assigned a mean value of zero and a standard deviation of 1).¹² The manipulation also eliminates the intercept so allowing comparison of coefficients of substituent constants referred to different groups; the correlation then takes the form of eqn (5),

{log [k₂(R)_S/dm³ mol⁻¹ s⁻¹]}_Std = β_Iσ_I(L)Std + β_sE_sStd (5)

in which {log [k₂(R)_S/dm³ mol⁻¹ s⁻¹]}_Std is the standardised variate, σ_I(L)Std and E_sStd are the standardised inductive and steric substituent constants and β_I and β_s are the corresponding standardised regression coefficients. Eqn (6) gives their values:

{log [k₂(R)_S/dm³ mol⁻¹ s⁻¹]}_Std = −(1.509 ± 0.444)σ_I(L)Std + (2.054 ± 0.444)E_sStd (6)

It is seen that the steric effect has the coefficient of larger absolute magnitude as expected from the trend in the rate constants. (The signs of the regression coefficients differ because the σ_I(L) values for alkyl groups are negative and their inductive effects (+I) act to increase the reaction rate whilst the steric regression coefficient is positive because the alkyl E_s values are also negative but the steric effects reduce the reaction rate). The ratio |β_s/β_I| = 2.054/1.509 = 1.36 showing the steric effect to be 36% greater than the inductive effect or, put alternatively, the overall substituent effect of the alkyl groups on the oxidation of alkyl 4-nitrophenyl sulfides by 1a comprises a minor electronic component (42.5%) and a major steric component (57.5%), so quantifying the steric predominance inferred above.

In our previous work⁶ it was inferred that the activation process for the oxidation of sulfides by 1a is characterised by a significant separation of charge, positive charge increasing on S with negative charge accumulating on the distal oxygen atom of 1a (see 10). In a polar aprotic solvent the stabilisation of these charges depends on the intramolecular interactions of the different substituents and on intermolecular interactions with solvent dipoles. The alkyl groups, R, being directly attached to S, are able to stabilise its increased positive charge by their +I effects. This is indicated by the observation k₂(Et)_S > k₂(Me)_S. The increase in charge separation on activation would be expected to cause electrostriction of the solvent; however, such increased interaction with the solvation shell is hindered by bulky alkyl groups and hence the transition states in their cases are deprived of the stabilisation the interaction would afford. This is shown by the sequence noted previously, k₂(Et)_S > k₂(n-Bu)_S > k₂(i-Pr)_S > k₂(s-Bu)_S > k₂(t-Bu)_S where the increase in α-branching governs the maximum extent of the hindrance and β-chain-extension within the primary and secondary examples augments the effect. A maximum rate constant occurs (for Et) because, as a function of the ramification of alkyl group structure, the steric effect increases faster than the inductive effect.

1.3 Sulfoxides. Results sharply contrasting with those above were obtained on attempts to correlate values of log [k₂(R)_SO/dm³ mol⁻¹ s⁻¹] using alkyl inductive and steric substituent constants. Paired with any of the scales of inductive constant (see ESI† 2, Table 2), all steric constants were statistically insignificant at the 0.1 level of probability. In the oxidations by 1a of the alkyl 4-nitrophenyl sulfoxides examined, the alkyl groups clearly have no effects that are quantifiable by any of their steric substituent constants.

Table 2 Rate constants at various temperatures with derived activation parameters for the oxidation of sec-butyl 4-nitrophenyl sulfide and sulfoxide by 1 in acetone^a

T/K	10^−2k2(s-Bu)S/dm^3 mol^−1 s^−1	T/K	k 2(s-Bu)SO/dm^3 mol^−1 s^−1
a Uncertainties are the 95% confidence intervals. b Values for the methyl analogue (data from ref. 6b and Table 1) for comparison. c At 298.2 K.
291.3	5.19 ± 0.08	—	—
294.8	5.40 ± 0.11	294.6	12.0 ± 0.7
301.1	6.56 ± 0.10	301.4	20.7 ± 0.8
306.5	8.02 ± 0.20	306.5	26.5 ± 0.7
312.4	9.77 ± 0.42	311.5	34.2 ± 0.8
317.5	11.3 ± 0.5	317.2	43.1 ± 0.9
ΔH^‡S/kJ mol^−1	23.2 ± 1.7	ΔH^‡SO/kJ mol^−1	40.8 ± 10.1
	(22.9 ± 1.9)^b		(42.6 ± 3.9)^b
ΔS^‡S/J K^−1 mol^−1	−114.0± 5.5	ΔS^‡SO/J K^−1 mol^−1	−84.9 ± 33.0
	(−113.7± 6.2)^b		(−83.0 ± 13.3)^b
ΔG^‡S/kJ mol^−1	57.2± 2.3^c	ΔG^‡SO/kJ mol^−1	66.2 ± 10.3^c
	(56.8± 2.6)^bc		(67.3 ± 5.6)^bc

---

The 4-nitrophenyl and S^δ+–O^δ− moieties ensure that these sulfoxides are highly polarised molecules. Our earlier work with aryl methyl sulfoxides in mixed solvents⁶ showed that, in acetone–hexane mixtures, the degree of stabilisation of the ground state by solvation is an important factor in determining their relative rates of oxidation by 1a and, in aqueous acetone mixtures, a Kamlet–Taft analysis¹³ showed the absolute rate constants for oxidation of methyl 4-nitrophenyl sulfoxide by 1a to depend only on the polarity of the mixed solvent, as measured by the parameter π*, and not on the specific solvating properties of the aqueous component (α and β). These observations suggest that interaction between methyl 4-nitrophenyl sulfoxide and acetone will result in electrostriction of the solvent. However, comparable ordering of the solvent-shell around alkyl 4-nitrophenyl sulfoxides in which the alkyl group is bulky will be sterically impeded and, consequently, their ground states are expected to be less stabilised by solvation than the methyl case.

The SO bonds of sulfones are, in general, less polar than those of sulfoxides and, as a consequence, in transition states for the concerted oxidation of sulfoxides to sulfones by 1a there is a dispersal of charge (see 11). It is envisaged that as the dipolarity of the initial sulfoxide SO bond diminishes, some negative charge is transferred mainly to the distal oxygen atom of 1a. There is thus a redistribution of negative charge between the oxygen centres compensated by positive charge on S. The activation process for oxidation of a sulfoxide by 1a would therefore be expected to reduce the prior electrostriction of solvent caused by the ground state. Two opposed consequences of the steric effects of bulky alkyl groups can therefore be envisaged: rate-enhancement, relative to the methyl case, arising from reduced solvation of the ground state and rate-retardation arising from hindrance to the solvation of the transition state (as in the case of sulfide oxidation). If these opposing effects should be similar in magnitude, and hence cancel, the lack of dependence of observed rate constants upon steric parameters can be understood (see Sections 2 and 5 below for further discussion).

2 Activation parameters

Table 2 presents the second order rate constants found for the oxidation of sec-butyl 4-nitrophenyl sulfide and sulfoxide at various temperatures together with the activation parameters derived via Eyring plots (Fig. 1); activation data for the methyl analogue^6b are given for comparison. The individual activation parameters are similar for both alkyl groups but there are differences between sulfides on the one hand and sulfoxides on the other. The enthalpy of activation of the sulfoxides is larger than that of the sulfides by 10–20 kJ mol⁻¹. This is consistent with a significant difference, between the two types of substrate, in the energy of the nucleophilic sulfur lone pair orbital that attacks 1a. The partial positive charge on sulfoxidic S confers a greater electronegativity than that of sulfidic S with a resultant relative stabilisation of the sulfoxidic S lone pair. That this difference in a ground state property of the reactants is important, suggests that the transition states occur relatively early in the reaction coordinates of both oxidations, consistent with the high reactivity of the oxidant.

Fig. 1 Comparison of Eyring plots for the oxidation of methyl and sec-butyl 4-nitrophenyl sulfides and sulfoxides by dimethyldioxirane in acetone.

As bimolecular processes, the oxidations of both types of substrate result in a loss of entropy on formation of the corresponding transition state but the loss for the sulfides is about 30 J K⁻¹ mol⁻¹ larger than that for the sulfoxides. The greater entropy loss for sulfides can be explained by the ordering inherent in the electrostriction of solvent caused by the development of a transition state 10 of increased polarity relative to the reactant 8. Conversely, a lesser entropy loss for the sulfoxides can be accounted for by the relaxation of solvent electrostriction between a highly dipolar reactant ground state 9 and a transition state 11 in which the negative charge is dispersed.

The relative dispositions of the Eyring plots in Fig. 1 illustrate these suggestions. Over the temperature range examined, the sec-butyl 4-nitrophenyl sulfide is less reactive than its methyl analogue reflecting the steric hindrance by the bulkier alkyl group to the stabilising solvation of the polarised transition state. By contrast, sec-butyl 4-nitrophenyl sulfoxide is more reactive than its methyl analogue as a consequence of the larger +I effect of the sec-butyl group and the fact that the ground state of the methyl sulfoxide is strongly solvated relative to its derived transition state, whereas the solvation differences between ground and transition state cancel for the larger group as discussed above.

3 Dialkyl substrates

Although the changes in oxidation rate constants of alkyl 4-nitrophenyl substrates that occur as a result of alkyl group variation have been rationalised, they are relatively small and it was felt that investigation of the larger changes expected for dialkyl substrates could provide confirmatory evidence. As the latter substrates lack the 4-nitrophenyl chromophore that enabled spectrophotometric monitoring, a protocol of competitive kinetics was adopted like that used in earlier Hammett studies of aryl methyl sulfides and sulfoxides.^6a

The substrates selected were (n-Pr)₂S, (n-Pr)₂SO, (t-Bu)₂S and (t-Bu)₂SO. These choices were convenient not only for product separation and quantification by GC but also on account of the disparate steric and inductive effects exhibited by the two alkyl groups (see ESI† 2, Table S2). When the two sulfides competed in large excess, in acetone solution, for a limiting amount of 1a, the molar ratio of sulfoxide products enabled the relative rate constant to be evaluated [eqn (7)].

k₂(n-Pr)_2,S/k₂(t-Bu)_2,S = (3.96 ± 0.15) (7)

As both the inductive and steric effects are larger for t-Bu than for n-Pr, the magnitude of the relative rate constant (>1) is consistent only with a predominant contribution of steric hindrance to the net effect of each group. Explained as steric hindrance of the solvation of the polar transition state, this accords with the behaviour of the alkyl 4-nitrophenyl sulfides described above. In the absence of a measured rate constant, k₂(n-Pr)_S, for the oxidation of n-propyl 4-nitrophenyl sulfide, we interpolate a value of (646⁺⁶⁰⁹₋₃₃₈) dm³ mol⁻¹ s⁻¹viaeqn (4). Taking the higher value of k₂(n-Pr)_S and the lower value of k₂(t-Bu)_S (Table 1), the upper limit of the relative rate constant in the 4-nitrophenyl series k₂(n-Pr)_S/k₂(t-Bu)_S then becomes (646 + 609)/(486 − 21) = 2.7, i.e. <(3.96 ± 0.15); the steric hindrance in the dialkyl series is consequently greater than that in the 4-nitrophenyl series as expected.

On similar competition of the two dialkyl sulfoxides the measured molar ratio of sulfone products led to the relative rate constant [eqn (8)].

k₂(n-Pr)_2,SO/k₂(t-Bu)_2,SO = (0.34 ± 0.02) (8)

The net substituent effect here is very different from that in the oxidation of sulfides but the explanation is less clear-cut as its magnitude (<1) could be explained either by the inductive effect operating alone or by a combination of the I effect and steric hindrance with the former predominant. If the mean of the Et and n-Bu values, i.e. (12.0 ± 0.43) dm³ mol⁻¹ s⁻¹, is taken as an approximation of the rate constant for oxidation of n-propyl 4-nitrophenyl sulfoxide, k₂(n-Pr)_SO, the relative rate constant k₂(n-Pr)_SO/k₂(t-Bu)_SO in the 4-nitrophenyl series is estimated as (0.58 ± 0.04). As the steric effect here was found to be insignificant, this figure represents the ratio of the two inductive terms. Had the steric effect become significant, but not predominant, in the dialkyl series, the outcome would be a reduction of both numerator and denominator [in eqn (8)] with the greater effect in the latter. The expected consequence would be that k₂(n-Pr)_SO/k₂(t-Bu)_SO < k₂(n-Pr)_2,SO/k₂(t-Bu)_2,SO. As this is not the case, the inference is that the steric effect is insignificant in the dialkyl series too.

4 Cyclic substrates

4.1 Rate constants and ring size. With a view to discovering any effects of ring strain, we have investigated oxidations of saturated cyclic sulfides and sulfoxides by 1a. Competition experiments were run from which rate constants were found for various cyclic sulfides relative to (CH₂)₅S and to (n-Pr)₂S, and for the corresponding sulfoxides relative to (CH₂)₅SO and to (n-Pr)₂SO (Table 3). The rate constants of (CH₂)₅S relative to PhSMe and of (CH₂)₅SO relative to PhSOMe were also measured [(7.2 ± 0.1) and (2.9 ± 0.1), respectively]. By employing the absolute rate constants of the aromatic substrates [(2.35 ± 0.24) × 10³ dm³ mol⁻¹ s⁻¹ and (28.6 ± 5.1) dm³ mol⁻¹ s⁻¹, respectively],^6b absolute second order rate constants were then evaluated for all the cyclic substrates and for (n-Pr)₂S and (n-Pr)₂SO. Absolute second order rate constants for (t-Bu)₂S and (t-Bu)₂SO were derived from the latter by use of eqn (7) and eqn (8). The second order constants are presented in Table 4.

Table 3 Relative rate constants for the oxidation of cyclic sulfides and sulfoxides by dimethyldioxirane in acetone at 293 K

Ring size, x	[k(x)/k(6)]S	[k(x)/k(n-Pr)2]S	Ring size, x	[k(x)/k(6)]SO	[k(x)/k(n-Pr)2]SO
3	0.14 ± 0.02	0.09 ± 0.01	3	0.17 ± 0.01	0.11 ± 0.01
4	0.81 ± 0.02	0.52 ± 0.02	4	0.23 ± 0.01	0.15 ± 0.01
5	1.71 ± 0.04	1.08 ± 0.04	5	0.36 ± 0.01	0.23 ± 0.01
6	1.00 ± 0.00	0.64 ± 0.02	6	1.00 ± 0.00	0.64 ± 0.02
7	0.99 ± 0.02	0.63 ± 0.02	7	2.39 ± 0.11	1.52 ± 0.08
8	2.32 ± 0.10	1.48 ± 0.07	8	2.50 ± 0.09	1.59 ± 0.08
(n-Pr)2S	1.57 ± 0.04	1.00 ± 0.00	(n-Pr)2SO	1.57 ± 0.05	1.00 ± 0.00

---

Table 4 Second order rate constants for the oxidation of cyclic and other sulfides and sulfoxides by dimethyldioxirane in acetone at 293 K

Ring size, x	10^−3k2(x)S/dm^3 mol^−1 s^−1	Ring size, x	10^−1k2(x)SO/dm^3 mol^−1 s^−1
3	2.37 ± 0.42	3	1.41 ± 0.27
4	13.7 ± 1.5	4	1.91 ± 0.36
5	28.9 ± 3.1	5	2.99 ± 0.55
6	16.9 ± 1.7	6	8.29 ± 1.51
7	16.8 ± 1.8	7	19.8 ± 3.7
8	39.1 ± 4.4	8	20.7 ± 3.8
(n-Pr)2S	26.6 ± 2.8	(n-Pr)2SO	13.0 ± 2.4
(t-Bu)2S	6.72 ± 0.75	(t-Bu)2SO	38.2 ± 7.4

---

Fig. 2 shows plots against ring size, x, of the relative rate constants k(x)_S/k(n-Pr)_2,S and k(x)_SO/k(n-Pr)_2,SO for oxidations by 1a (cf. Table 3) and the corresponding constants for the oxidation of sulfides by NaIO₄ in 50% v/v aqueous ethanol. The latter data are taken from Ruff and Kucsman⁹ apart from that for the oxidation of thiirane which was measured for this work (see Experimental). The oxidation of sulfoxides exhibits a relatively simple sigmoid curve (plot 1) whereas the two oxidations of sulfides (plots 2 and 3) show a more complex dependence on ring size with the rate constants passing through maxima at x = 5. The periodate oxidation involves an electrophilic attack on S by the oxidant with a concerted O-atom transfer comparable to oxidation by 1a. The similarity of the profiles found for the two independent sulfide oxidations (for the five ring sizes in common) is persuasive evidence that in neither case is the shape accidental but, rather, that both oxidations respond in essentially the same way to a ring size-dependent property.

Fig. 2 Variation with ring size of the rate constants for oxidations of cyclic sulfides and sulfoxides relative to (n-Pr)₂S and (n-Pr)₂SO, respectively. Plot 1 (filled squares) sulfoxides oxidised by dimethyldioxirane in acetone at 293 K; plot 2 (open circles) sulfides oxidised by dimethyldioxirane in acetone at 293 K; plot 3 (open diamonds) sulfides oxidised by NaIO₄ in 50% v/v aqueous ethanol at 298 K; + is the reference point for all plots.

4.2 Ring strain. For the compounds of present interest conventional, thermochemically-derived ring strain energies are limited to cyclic sulfides with ring sizes of 3–6, inclusive.¹⁴Table 5 compares the conventional ring strain energies of these sulfides with those of the corresponding cycloalkanes; the smaller E_rs(conv) values found for the sulfides relative to cycloalkanes of the same ring size are ascribed to the fact that C–S are longer than C–C bonds.¹⁴

Table 5 Comparison of conventional ring strain energies of cycloalkanes and cyclic sulfides^a

Ring size, x	Cycloalkane^b	Cyclic sulfide^c
	E RS(conv)/kJ mol^−1	E RS(conv)/kJ mol^−1
a Data are from tables in ch. 7 of ref. 14. b Table 39. c Table 41.
3	115.1	83.3
4	110.9	82.5
5	25.9	8.4
6	0.0	−0.8
7	25.9	—
8	40.2	—
9	52.7	—

---

Owing to the lack of available heat of formation data for cyclic sulfoxides and sulfones we have obtained theoretical ring strain values for sulfides, sulfoxides and sulfones via molecular orbital calculations carried out by means of the Gaussian 98 suite of programs.¹⁵ Using the B3-LYP/6-31G* level of density functional theory (DFT),^16,17 the geometries of the 3- to 8-membered cyclic sulfides, sulfoxides and sulfones were fully optimised without geometry constraints. The validity of this method in producing accurate results for these types of S-containing substrate, for the oxidant 1a [and for their derived transition states (see later)] has been well established.^18–24 The energies calculated were treated in the manner of Dudev and Lim.²⁵ The ring strain E_rs of an x-membered cyclic compound relative to an r-membered cyclic reference compound of the same type is given by eqn (9),

E_rs = E_x − E_r − (x − r)E_CH2 (9)

where E_x and E_r are the energies of the two compared cyclic compounds and E_CH2 is the energy of a strain-free CH₂ fragment, (x − r) of which differentiate the two rings. The value of E_CH2 was taken as the difference in energy between the all-trans-conformers of hexane and pentane. The ring strain of a monocyclic compound can also be expressed relative to an acyclic reference with the same number of like, contiguous non-H atoms; in this case, it is given by eqn (10),

E_rs = E_cyclo − E_acyclo + E_2H (10)

where E_2H = 2E_C–H − E_C–C compensates for the C–C bond lost and the two C–H bonds gained between the cyclic compound and its acyclic reference. The latter two energies were defined by eqn (11) and eqn (12), respectively. The fragment energies cited in eqn (9)–(12) are given in Table 6.

E_C–H = E_CH3CH3 − E_CH3CH2˙ (11)

E_C–C = E_CH3CH3 − 2E_CH3˙ (12)

Table 7 gives the results of calculations of the total energies and derived ring strain energies for cyclic sulfides of ring sizes 3–8, relative to that in the 6-membered cyclic sulfide. In Fig. 3 the values of E_rs(DFT)S are plotted, together with thermochemically-derived E_rs(conv) values for cyclic sulfides and cycloalkanes (cf. Table 5),¹⁴ against ring size. It is clear that, despite the disparity in magnitude between the DFT energies on the one hand and heats of atomisation used in the calculation of conventional values¹⁴ on the other (2–3 orders of magnitude), the agreement between the theoretical and thermochemical values for sulfides is quite good for the four ring sizes in common; indeed, they are linearly related: E_rs(DFT)S = 0.9147 × E_rs(conv)S with R² = 0.998. Equally, for the 6- to 8-membered rings, the comparability of E_rs(DFT)S values with E_{rs(conv)Cycloalk} is also close. These agreements give confidence in the values of E_rs(DFT) obtained for the cyclic sulfides and the sulfoxides and sulfones for which there are no thermochemical values. Ring strain energies for all three families of heterocycle, now relative to the acyclic references (n-Pr)₂S, (n-Pr)₂SO and (n-Pr)₂SO₂, as appropriate, are given in Table 8. Also given are the changes in ring strain on oxidation of sulfides to sulfoxides, ΔE_rs(I), and of sulfoxides to sulfones, ΔE_rs(II).

Fig. 3 Variation with ring size, x, of ring strain energies relative to the six-membered ring for cycloalkanes and cyclic sulfides. Plot 1 (open circles) thermochemically-derived values for cycloalkanes; plot 2 (open squares) thermochemically-derived values for sulfides; plot 3 (filled diamonds) theoretically-derived (DFT) values for sulfides.

Table 6 Fragment energies (B3-LYP/6-31G* DFT) for ring strain evaluation

Antecedent species	E/Hartrees per particle	10^−5E/kJ mol^−1	Fragment energies/kJ mol^−1
All-trans-CH3(CH2)4CH3	−237.085 51	−6.224 54
All-trans-CH3(CH2)3CH3	−197.771 78	−5.192 38
			E CH2	−1.032 16 × 10^5
CH3CH3	−79.830 42	−2.095 90
CH3CH2˙	−79.157 87	−2.078 24
CH3˙	−39.838 29	−1.045 93
			E C–H	−1.765 74 × 10^3
			E C–C	−4.038 79 × 10^2
			E 2H	−3.127 60 × 10^3

---

Table 7 Total energies for cyclic sulfides and derived ring strain energies relative to that of C₅H₁₀S

Ring size, x	10^−6 × E(x)DFT/kJ mol^−1	E rs(DFT)S/kJ mol^−1^a
a Calculated as E(x)DFT + 1.56149 × 10^6 − (x − 6) × 1.03216 × 10^5cf. eqn (9) and Table 6.
3	−1.251 77	74.23
4	−1.354 98	77.37
5	−1.458 27	7.10
6	−1.561 49	0.00
7	−1.664 68	30.03
8	−1.767 88	43.30

---

Table 8 Ring strain energies, E_rs(DFT), for cyclic sulfides, sulfoxides and sulfones calculated relative to the corresponding acyclic di-(n-propyl) reference compound

Ring size, x	E rs(DFT)S/kJ mol^−1	E rs(DFT)SO/kJ mol^−1	E rs(DFT)SO2/kJ mol^−1	ΔErs(I)/kJ mol^−1^a	ΔErs(II)/kJ mol^−1^a
a ΔErs(I) = Ers(DFT)SO − Ers(DFT)S and ΔErs(II) = Ers(DFT)SO2 − Ers(DFT)SO.
3	105.5	118.3	212.2	12.8	93.9
4	108.7	100.3	115.5	−8.4	15.2
5	38.4	47.4	56.3	9.0	8.9
6	31.3	36.5	35.7	5.2	−0.8
7	61.3	66.3	60.0	5.0	−6.3
8	74.6	84.7	74.3	10.1	−10.4

---

4.3 Sulfoxides. Both k(7)_SO/k(n-Pr)_2,SO and k(8)_SO/k(n-Pr)_2,SO > 1 (cf.Table 3 and Fig. 2, plot 1), i.e. the 7- and 8-membered cyclic sulfoxides are more reactive than the unstrained acyclic reference compound (n-Pr)₂SO on reaction with 1a. In Sections 1.2 and 3 above it was shown that the oxidation of sulfoxides by 1a is insensitive to the steric effects of alkyl substituents on S. Furthermore, in cyclic sulfoxides the conformational freedom of the carbon ligands on S is restricted relative to that in dialkyl sulfoxides, it is therefore unlikely that the ring structure, as such, will exert any significant steric influence on oxidation for ring sizes ≤8. The polymethylene chains in (CH₂)₆SO and (CH₂)₇SO are expected to exert inductive effects similar to that of two n-propyl groups (see ESI† 2.2 and Table S5) so the fact that these cyclic sulfoxides react 50% faster than the acyclic comparator does not arise from significantly enhanced inductive promotion. However, the values of ΔE_rs(II) in Table 8 show that whilst there is a large increase in ring strain between thiirane 1-oxide, (CH₂)₂SO, and its derived sulfone, for larger rings the magnitudes of the corresponding increases decline with increasing ring size and eventually become negative, i.e. ring strain is significantly reduced on oxidation of sulfoxide to sulfone for x ≥ 7. If the activation energies for the oxidation were sensitive to these changes in ring strain, the behaviour of k(x)_SO/k(n-Pr)_2,SO as a function of ring size can be understood: the smaller rings are oxidised more slowly than the acyclic reference because reaction increases ring strain but, for x ≥ 7, the relief of ring strain enhances the relative rates of oxidation. With the exception of the 3-membered system, there is a linear correlation, ‘fair’ by Exner’s criterion,²⁶ between log [k₂(x)_SO/dm³ mol⁻¹ s⁻¹] and the change in ring strain [eqn (13)] (see ESI† 2, Table S7 for statistical detail),

log [k₂(x)_SO/dm³ mol⁻¹ s⁻¹] = 1.915 − 0.044ΔE_rs(II) (13)

The deviation of the point for (CH₂)₂SO from the correlation line is such that eqn (13) underestimates k₂(x)_SO by more than two orders of magnitude. Later (see Section 5.1) we shall find that ring strain change between the reactant and product ground state does not, alone, fully explain the behaviour of 4- to 6-membered cyclic sulfoxides.

4.4 Sulfides. Although the steric effects of bulky alkyl groups were found to outweigh their +I effects on the oxidation of alkyl 4-nitrophenyl and dialkyl sulfides by 1a (see Sections 1.1 and 3 above), it is unlikely that, in similar oxidations, the polymethylene chains in 4- to 8-membered cyclic sulfides will exert steric effects that are much different from each other, the reason being that the steric effects of linear alkyl groups are essentially constant [e.g. E_s′ = −0.31 for n-Pr, n-Bu and n-Pe²⁷ (see ESI† 2, Table S2)] and the cyclic structure restricts the conformational freedom, and hence the capacity for hindrance, of the polymethylene chain relative to that of linear alkyl groups. Also, the inductive effect is expected to increase regularly with the length of polymethylene chain, similar to that of linear alkyl groups¹¹ (see ESI† 2.2 and Table S5). The irregular variation of k(x)_S/k(n-Pr)_2,S with ring size (see Table 6 and Fig. 2) cannot therefore be accounted for in terms of steric and inductive effects either alone or in combination. Furthermore, the finding that both k(5)_S/k(n-Pr)_2,S and k(8)_S/k(n-Pr)_2,S > 1 shows that these relative rate constants are not influenced by the change in ring strain on oxidation for, after the 3-membered ring, the 5- and 8-membered rings have the largest positive values of ΔE_rs(I) (see Table 8). As ΔE_rs values measure the difference in ring strain between a substrate and its oxidation product, a relationship between oxidation rate constants and ΔE_rs values implies the transition state to have developed some product-character; such was the case with the oxidation of sulfoxides. The lack of relationship between oxidation rate constants and ΔE_rs(I) therefore implies product-character to be poorly developed in the case of sulfide oxidation: the transition states for sulfide oxidation evidently occur earlier in their reaction coordinate than those of sulfoxide oxidation [though the latter still occur relatively early, see Section 2 and later 6.2]. The frontier-orbital approach to the explanation of reactivity²⁸ considers transition states in terms of the reactants’ orbital interactions and hence is particularly relevant for reactions that proceed via early transition states. A major determinant of reactivity is the reciprocal of the frontier-orbital energy difference, i.e. Φ = 1/(E_HOMO − E_LUMO) where E_HOMO is the energy of the highest occupied molecular orbital of the nucleophilic reactant and E_LUMO is the energy of the lowest unoccupied orbital of the electrophilic reactant. This term represents a stabilisation attenuating the larger, filled-orbital repulsions that give rise to the energy of activation of the reaction. Table 9 reports the relevant frontier-orbital energies for the reaction of cyclic sulfides with 1a and Fig. 4 compares log [k₂(x)_S/dm³ mol⁻¹ s⁻¹] with Φ/eV⁻¹.

Fig. 4 Plot 1 (open squares), variation with ring size, x, of log k₂(x)_S for the oxidation of cyclic sulfides by dimethyldioxirane in acetone at 293 K; the filled square is the value for (n-Pr)₂S. Plot 2 (open circles), variation with ring size of Φ/eV⁻¹, the reciprocal of the difference in corresponding frontier orbital energies; the filled circle is the value for (n-Pr)₂S.

Table 9 Frontier orbital energies (B3-LYP/6-31G* DFT)

Reactant	Frontier orbital energy/eV		Φ = [1/(EHOMO − ELUMO)]/eV^−1
	LUMO
Dimethyldioxirane, 1a		−0.4773
	HOMO
(CH2)2S,		−6.1354	−0.1767
(CH2)3S		−5.8736	−0.1853
(CH2)4S		−5.7517	−0.1896
(CH2)5S		−5.8137	−0.1874
(CH2)6S		−5.7767	−0.1887
(CH2)7S		−5.7435	−0.1899
(n-Pr)2S		−5.7685	−0.1889

---

It is clear that there is an inverse relationship between the two. The order of reactivity of the cyclic sulfides predicted by the frontier-orbital term is k₂(8)_S > k₂(5)_S > k₂(7)_S ≈ k₂(n-Pr)_2,S > k₂(6)_S > k₂(4)_S > k₂(3)_S. The experimental order is k₂(8)_S > k₂(5)_S > k₂(n-Pr)_2,S > k₂(7)_S ≈ k₂(6)_S > k₂(4)_S > k₂(3)_S, i.e. only k₂(7) is out of sequence, being less than predicted. In view of the expected similarity of +I effects (see ESI† 2, Table S5) and of steric effects for (CH₂)₆ and (n-Pr)₂ (see ESI† 2.3) and independence of the ring strain given by eqn (10), k₂(7)_Sis less than expected. The reason is not obvious but the similar behaviour of the value of k₂(7)_S for oxidation by periodate⁹ (Fig. 2) indicates the effect to be real.

5 Overall correlation of reactivities

Here we seek to correlate the reactivities towards 1a of all the substrates examined in our previous and present work (i.e. aryl methyl, dialkyl, alkyl 4-nitrophenyl and cyclic sulfides and sulfoxides) and to identify the parameters required to do so. The data used are the logarithms of rate constants reported previously^6b or given above (Table 1 and Table 4) for reactions in acetone at 293 ± 2 K, and the explanatory variables we have considered are: Σσ* and ΣE_s′, respectively, the sum of the σ* and E_s′ values of the two carbon ligands on S; q_S/e, the Mulliken charge²⁹ at S (e = 1.602 177 ×10⁻¹⁹ C); Φ/eV⁻¹, the inverse of the difference between the energy of the HOMO of the substrate and the LUMO of 1a; c_S²_H, the square of the 3p_z component of the HOMO at S, taken as a measure of electron density at the reaction centre; and ΔE_rs/kJ mol⁻¹, the change in ring strain, if any, between the reactant and the product. The σ* values for 3- and 4-substituted-phenyl groups were calculated by means of an algorithm from ref. 30, those for alkyl groups and the polymethylene chain in cyclic substrates were calculated from the carbon connectivity as described in ESI† 2; E_s′ values are taken from Dubois and co-workers,²⁷ or assumed (see ESI† 2.3), and the quantum mechanical parameters, q_S/e, Φ/eV⁻¹ and c_S²_H are from our calculations at the B3-LYP/6-31G* level of density functional theory as are the ΔE_rs values already given in Table 8 (see ESI† 2, Table S6). A probability level not greater than 0.01 was specified for each explanatory variable. Correlations using the raw variables were run with, and without, an intercept. In general, those obtained with an intercept are statistically the more precise and require fewer variables; none involved c_S²_H. Since the variables have widely differing ranges and are not referred to a common standard, the chemical significance of the intercept is unclear but this uncertainty is circumvented by standardisation of the variables and reactivity data [cf. discussion of eqn (5)]¹² (see ESI† 2, Table S7 for statistical detail).

Previous work showed that oxidations, in acetone solution, of methyl 3- and 4-substituted-phenyl sulfides and sulfoxides by 1a, though differing in rate constants by 2–3 orders of magnitude, exhibit very similar Hammett reaction constants.^5,6 As a consequence, a common Hammett plot produces two essentially parallel lines separated by 2–3 ordinate units and the same is true if σ* values for the substituted-phenyl groups are used, as these are proportional to the Hammett σ_m and σ_p constants.³¹Fig. 5a shows the logarithms of the rate constants of aryl methyl sulfides and sulfoxides plotted against calculated values given by eqn (14). The data for the two subsets are accommodated by a single line, spanning 2–3 ordinate units:

log [k₂/dm³ mol⁻¹ s⁻¹]_calc = 4.336 − 3.061q_S/e − 0.949Σσ* (14)

This result implies that the difference in reactivity, towards 1a in solution, between the sulfides and sulfoxides arises from variation, within a single mechanism, of the polarity of the sulfur function. When the regression is standardised,¹² the percentage weightings of the two parameters are q_S/e, 80.6% and Σσ*, 19.4% (see ESI† 2, Table S7). The line of eqn (14) provides a reference against which other data may be compared. For example, Fig. 5a also includes points for the dialkyl sulfides (n-Pr)₂S and (t-Bu)₂S and the corresponding sulfoxides. The points for the two sulfoxides and for (n-Pr)₂S lie close to the line but that for (t-Bu)₂S does not. If the close-lying points are included in the correlation, eqn (14) is modified to eqn (15).

log [k₂/dm³ mol⁻¹ s⁻¹]_calc = 4.324 − 3.086q_S/e − 0.922Σσ* (15)

When this regression is standardised, the percentage weightings of the two parameters in the correlation are q_S/e, 70.0% and Σσ*, 30.0% (see ESI† 2, Table S7). The non-correlation of the point for (t-Bu)₂S confirms the conclusion in Section 3 that the oxidation of bulky dialkyl sulfides is sterically inhibited whereas the correlation of the point for (t-Bu)₂SO confirms the contrary for bulky sulfoxides.

Fig. 5 (a) Plot of log [k₂/dm³ mol⁻¹ s⁻¹] for aryl methyl, and dialkyl, sulfides and sulfoxides versus values calculated for the aryl methyl compounds by eqn (14). (b) Plot of log [k₂/dm³ mol⁻¹ s⁻¹] for all the sulfides studied versus values calculated by eqn (16); the definition of the line excludes (CH₂)₂S.

Fig. 5b is the plot of the values of log [k₂/dm³ mol⁻¹ s⁻¹] for the oxidation of all the sulfides that we have considered versus the calculated value given by eqn (16):

log [k₂/dm³ mol⁻¹ s⁻¹]_calc = 2.991 − 0.648Σσ* + 0.289ΣE_s′ − 7.190Φ/eV⁻¹ (16)

On standardisation, the percentage weightings of the variables in the correlation are found to be Σσ*, 51.7%; ΣE_s′, 36.4% and Φ/eV⁻¹, 11.9%. This line is essentially equivalent to that in Fig. 5a in the collinearity of the data for ArSMe and (n-Pr)₂S but the point for (t-Bu)₂S is now also correlated on account of the inclusion of ΣE_s′. Also well correlated are the points for the alkyl 4-nitrophenyl sulfides for which the importance of the steric effect of the alkyl group was found above (see Section 1.2). Among the cyclic sulfides, the only seriously deviant point is that due to (CH₂)₂S (not included in the definition of the line) but the remainder lie close to the line near the point for (n-Pr)₂S. This clustering justifies the values of Σσ* and ΣE_s′ assigned to polymethylene chain, (CH₂)_3–7 (see ESI† 2.2 and 2.3) and the absence of dependence on ΔE_rs confirms the inference that cyclic sulfide oxidation is independent of ring strain change. The correlation also implies the frontier-orbital term Φ/eV⁻¹ to be significant for sulfides generally and not just for the cyclic sulfides for which it was inferred in Section 4.4 above.

In Fig. 6a are plotted the values of log [k₂/dm³ mol⁻¹ s⁻¹] for the oxidation of all the sulfoxides we have investigated as a function of calculated values given by eqn (17):

log [k₂/dm³ mol⁻¹ s⁻¹]_calc = 1.857 − 0.967Σσ* − 0.0056ΔE_rs − 0.0576ΣE_s′ (17)

In defining the line, the points for the three cyclic sulfoxides (CH₂)_3–5SO are excluded so ensuring the points for ArSOMe and the two dialkyl sulfoxides are collinear as in Fig. 5a. The points for the remaining 3-, 7- and 8-membered cyclic sulfoxides are well correlated as are those of the alkyl 4-nitrophenyl sulfoxides. Standardisation leads to the following weightings of the variables in the correlation: Σσ*, 76.1%; ΔE_rs, 16.6% and ΣE_s′, 7.3%. Interestingly, not only is ΣE_s′ significant but here its negative coefficient implies the reaction rate to be sterically accelerated. This contrasts with the situation in Sections 1.3 and 3 above where, in considering, separately, the limited subsets of alkyl 4-nitrophenyl sulfoxides and dialkyl sulfoxides, there was no evidence of any alkyl steric effect. In explaining this apparent lack, two opposed consequences of the steric effects of bulky alkyl groups were envisaged: rate-enhancement, relative to the methyl case, arising from hindered solvation of the substrates’ ground states and rate-retardation arising from hindered solvation of their transition states. These opposing effects were suggested to be similar in magnitude and hence to cancel. The correlation by eqn (17) implies the rate-enhancing term to be marginally bigger in the extended data set. Although ΔE_rs is significant, it is insufficient to ensure correlation of (CH₂)_3–5SO (cf. 4.3).

Fig. 6 (a) Plot of log [k₂/dm³ mol⁻¹ s⁻¹] for all the sulfoxides studied versus values calculated by eqn (17); the definition of the line excludes (CH₂)_3–5SO. (b) Plot of log [k₂/dm³ mol⁻¹ s⁻¹] for all the sulfides and sulfoxides studied versus values calculated by eqn (18); the definition of the line excludes (t-Bu)₂S, (CH₂)₂S and (CH₂)_3–5SO.

Fig. 6b shows the variation of log [k₂/dm³ mol⁻¹ s⁻¹] for all of our substrates as a function of calculated values given by eqn (18); the percentage weightings of the standardised variables allow comparison of their relative importance as follows: q_S/e, 60.9%; Σσ*, 31.2% and ΔE_rs, 7.9%. The definition of the line excludes the points for (t-Bu)₂S, (CH₂)₂S and (CH₂)₃₋₅SO. Eqn (18) is thus a refinement of eqn (15) accommodating the change in ring strain of the included cyclic compounds [the points for (CH₂)₆SO and (CH₂)₇SO coincide].

log [k₂/dm³ mol⁻¹ s⁻¹]_calc = 4.287 − 3.027q_S/e − 0.928Σσ* − 0.00885ΔE_rs (18)

If the data for (t-Bu)₂S are included in the correlation, ΣE_s′ becomes significant at a level of probability <0.01, with a positive coefficient [eqn (19)] and the following percentage weightings of the standardised variables: q_S/e, 59.0%; Σσ*, 25.9%; ΔE_rs, 9.0% and ΣE_s′, 6.0%.

log [k₂/dm³ mol⁻¹ s⁻¹]_calc = 4.375 − 2.961q_S/e − 0.753Σσ* − 0.01027ΔE_rs + 0.110ΣE_s′ (19)

However, the precision deteriorates relative to eqn (18) (see ESI† 2, Table S7). The added point still does not fall on the line and, as a consequence of the different signs of the coefficient of ΣE_s′ for the sulfide and sulfoxide subsets discerned above, points for other t-Bu derivatives are displaced from the line and the strict collinearity of the ArSMe and ArSOMe subsets is also lost. Eqn (19) is not therefore an improvement on eqn (18).

5.1 Non-correlated points. The correlation line in Fig. 6b [eqn (18)] overestimates log [k₂/dm³ mol⁻¹ s⁻¹] for (t-Bu)₂S and (CH₂)₂S by similar amounts. As seen above, the cause is steric for (t-Bu)₂S but this cannot be the case for (CH₂)₂S which has the least encumbered sulfur centre of all the substrates. Nor can the non-correlation be reasonably explained in terms of Σσ*: it would require a value 5–6 times greater than that used (1.0–1.2 rather than 0.2, see ESI† 2.2) to correlate the point by eqn (16) and eqn (18) [see also ESI† 2, comments on Table S7, eqn (S24)]. Evidently, the three-membered cyclic sulfide is unique and not directly comparable with the remaining cyclic sulfides in its reaction with 1a. Given this fact, we investigated the effect of removing the (correlated) point for the 3-membered cyclic sulfoxide, (CH₂)₂SO, from the definition of the line in Fig. 6a to see whether the non-correlated points for (CH₂)_3–5SO are then brought into line. To a certain extent this is the case: all the sulfoxides, excluding (CH₂)₂SO, are correlated but the correlation is poorer than eqn (17) [see ESI† 2, comments on Table S7, eqn (S25)] and log [k₂/dm³ mol⁻¹ s⁻¹] for (CH₂)₂SO is then underestimated by almost 3 orders of magnitude similar to the case with eqn (13). If the point for (CH₂)₂SO is also excluded from the definition of eqn (18), those for (CH₂)_3–5SO are not better correlated than when it is included. Eqn (18) thus represents the best overall correlation of the full data set with the minimum number of exclusions (5 out of 45). The displacement of the points for the 4- to 6-membered cyclic sulfoxides from the correlation line is greater the smaller is the ring. There is clearly a ring-size effect which is not adequately expressed by ΔE_rs, the difference in ring strain between the ground states of the reactant and product. Presumably, the displacements have their origin in a transition state property such as increased eclipsing strain within the ring caused by the proximity of the oxidant; the degree of such strain would be expected to depend on the flexibility of the polymethylene chain and hence be greater the smaller the ring size. We have not, however, performed the calculations on the transition states of the oxidations of cyclic sulfoxides by 1a which could support or disprove this hypothesis.

6 Calculations on the reactants, products and transition states in the oxidation of aryl methyl sulfides and sulfoxides by 1a

Calculations of the optimised ground state geometries of the reactants and products of the oxidations of aryl methyl sulfides and sulfoxides were performed using the Gaussian 98 suite of programs, revision A.3¹⁵ and the B3-LYP/6-31G* level of density functional theory;^16,17 the transition state calculations employed revision A.7.³² The effects of solvation (by acetone) were simulated at the B3-LYP/6-31G* level by single point self consistent reaction field (SCRF) calculations with Tomasi’s polarised continuum model³³ (PCM) using the gas-phase B3-LYP/6-31G*-optimised geometries. The output of all calculations was visualised, as appropriate, using the program Molekel.³⁴

6.1 Reactants and products. In Table 10 are given enthalpies and other descriptors of the ground states of compounds that are reactants or products of oxidations by 1a for which optimised transition state structures have been found (see Section 6.2 below). Each SO bond lowers the molecular enthalpy ostensibly by a similar amount irrespective of whether it is a sulfoxide or sulfone bond: for the tabulated compounds the mean enthalpy of sulfonic SO bonds exceeds that of sulfoxidic SO bonds by only 0.05% but, because the calculated enthalpies are so large, this nevertheless corresponds to a greater exothermicity of sulfonic SO bonds of ∼104 kJ mol⁻¹. The Mulliken charges on S and O are more obviously characteristic of the species. The increment in positive charge on S when sulfide is oxidised to sulfoxide is about twice as large as that when sulfoxide is oxidised to sulfone and the negative charge on each sulfonic O atom is less by 0.09e relative to that on the O of its sulfoxide precursor. The bond lengths show variations consistent with these charge variations: sulfonic SO bonds are shorter than sulfoxidic SO bonds owing to their less dipolar, more double-bonded, character.

Table 10 Enthalpies and other characteristics of the optimised ground state structures of various methyl 4-substituted-phenyl sulfur compounds, their oxidant and co-product as calculated using B3-LYP/6-31G* DFT

Species	Enthalpy, 10^−6H°/kJ mol^−1^a	Mulliken charge qS/e^b	Mulliken charge qOso/e^b	Bond length rS–O/Å^c	Molecular dipole moment, μ/D^d
a Sum of total electronic and thermal enthalpies at 298.15 K and 1 atmosphere, corrected for zero-point energy. b e = 1.602177 × 10^−19 C. c 1 Å = 10^−10 m. d 1 D = 3.336 × 10^−30 C m. e Mulliken charge on oxygen.
4-MeOPhSMe (syn)	−2.059105	0.127	—	—	2.676
(anti)	−2.059104	0.126	—	—	0.871
4-MeOPhSOMe (syn)	−2.256477	0.762	−0.635	1.514	3.800
(anti)	−2.256476	0.760	−0.635	1.514	5.276
PhSMe	−1.758427	0.133	—	—	1.413
PhSOMe	−1.955794	0.765	−0.631	1.513	3.917
PhSO2Me	−2.153265	1.098	−0.540	1.471	5.137
4-O2NPhSMe	−2.295350	0.168	—	—	5.459
4-O2NPhSOMe	−2.492707	0.780	−0.619	1.511	4.191
4-ClPhSOMe	−3.162460	0.771	−0.628	1.513	3.218
4-ClPhSO2Me	−3.359930	1.100	−0.537	1.471	4.009
4-NCPhSOMe	−2.197974	0.778	−0.622	1.511	4.124
4-NCPhSO2Me	−2.395440	1.104	−0.532	1.470	3.701
Me2CO2, 1a	−0.704349	—	−0.318^e	—	3.373
Me2C=O	−0.507139	—	−0.426^e	—	2.816

---

The variation in molecular dipole moments is more complex. The Mulliken charges at S for the unsubstituted compounds show that consecutive oxidations of the sulfur function will result in an increasing polarisation of the attached aromatic ring, a fact conveniently expressed by the Hammett σ_p constants^31a of the sulfur functional groups: σ_p(SMe) = 0, σ_p(SOMe) = 0.49 and σ_p(SO₂Me) = 0.72. Although individual molecular geometry has a key role in determining the precise molecular dipole moment, the pattern of the tabulated values, where the substituent X is an electron-withdrawing group, may be largely explained on the assumption that the transfer of polarisation by the π-system of the aromatic ring is responsible for the major part of the variation between 4-substituted structures. In Fig. 7 the dipole moments of Table 10 are plotted versus Hammett’s σ_p(X), now taken as an index of the substituents’ electronic character.

Fig. 7 Molecular dipole moments calculated for 4-X-substituted-phenyl methyl sulfides, sulfoxides and sulfones plotted against σ_p(X). Sulfides, open squares; sulfoxides, open circles; sulfones, filled diamonds.

A substituent with σ_p(X) = σ_p(SOMe) would negate the polarisation due to the SOMe group and reduce the dipole moment to zero. As σ_p(Cl) = 0.23 (i.e. 0 < σ_p(Cl) < 0.49),^31a the dipole moment of 4-chlorophenyl methyl sulfoxide is reduced relative to PhSOMe but to a value greater than zero. Similar reasoning may be applied to 4-chlorophenyl methyl sulfone where the Cl substituent reduces the dipole moment to a value between those of PhSO₂Me and the chlorinated sulfoxide. Both the CN and NO₂ groups have values of σ_p > 0.49 (i.e. 0.66 and 0.78, respectively);^31a the ring polarisation in the corresponding sulfoxides will therefore be reversed relative to that in the unsubstituted sulfoxide. The dipole moments of the two substituted sulfoxides are then not directly comparable with that of the unsubstituted molecule but they are expected to be less than those of PhNO₂ and PhCN, which is the case (experimental gas-phase values 4.17 D and 4.23 D, respectively).^35a Since σ_p(SOMe) < σ_p(CN) < σ_p(SO₂Me), a reversal of ring polarisation is expected between 4-cyanophenyl methyl sulfoxide and its derived sulfone. The ring of the sulfone is therefore polarised in the same sense as that of 4-chlorophenyl methyl sulfone (see Fig. 7) but, as σ_p(CN) > σ_p(Cl), the cyano-sulfone has the smaller dipole moment. Methyl 4-nitrophenyl sulfide exhibits a molecular dipole moment larger than PhNO₂ owing to the direct conjugation between the ring substituents represented by 12 [here the electronic effect of the SMe group is better represented by σ_p⁺ (−0.6)³⁶ than by σ_p (0)]; on oxidation, this conjugation is lost and the SOMe group attenuates the polarisation due to the NO₂ group.

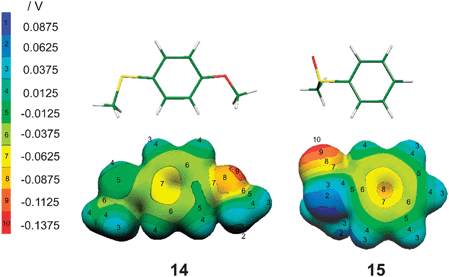
4-OMe is a net electron donor [σ_p(OMe) < 0] and, furthermore, rotation about the ring-C–O_Me bond allows the lone pair of OMe to conjugate with the aromatic π-system in two coplanar conformations that give rise to syn and anti conformers when the ring also carries another unsymmetrical group. Thus both 4-methoxyphenyl methyl sulfoxide and sulfide exhibit syn–anti conformers which lie close in energy but differ in dipole moment (Table 10). The dipole moment of syn 4-methoxyphenyl methyl sulfoxide seems anomalous in being slightly less than that of PhSOMe: a substituent which is an electron donor is expected to enhance the ring polarisation produced by the SOMe group (see structure 13) as occurs with the anti-conformer. This no doubt occurs because the orientation of the O–Me bond dipole modulates the net ring-polarisation pattern. In the case of 4-methoxyphenyl methyl sulfide, neither substituent is electron withdrawing [σ_p(OMe) = −0.27, σ_p(SMe) = 0].^31a The dipole moment calculated for the syn-conformer is close to the sum of the experimental values for PhOMe and PhSMe [1.38 D (gas phase)^35a and 1.38 D (benzene),^35b respectively] suggesting that it is determined by an order of electronegativities, within the molecule, of O > C > S and that minor polarisations of the ring induced by the heteroatoms are not countervailing but coincident. Structure 14 shows the syn-conformation found for 4-methoxyphenyl methyl sulfide as a stick diagram (in which O is red, S is yellow, C is green and H is white); the associated molecular electrostatic potential (MEP) illustrates the distribution of charge.³⁴ By contrast, the dipole moment of only 0.871 D calculated for the anti-conformer shows the sensitivity of the measure to the rotameric state of the molecule when the ring is not strongly polarised.

In order to investigate the differences between sulfides and sulfoxides in more detail a natural bond order (NBO) analysis was carried out for PhSMe and PhSOMe within the Gaussian 98 package utilising Gaussian NBO version 3.1.³⁷ Details for S are given in Table 11. The non-equivalence of the sulfidic lone pairs is evident. The pair of higher energy is in an atomic 3p_z-orbital which accords with the geometry found for the aryl methyl sulfides in which the S–Me bond is coplanar with the aromatic ring (see 14) so allowing stabilising overlap of the lone pair with the aromatic π-system. [This is expressed in the corresponding molecular orbital of PhSMe in which the coefficient at S of the HOMO, c_S,H, is 0.541 whereas those for saturated sulfides, in general, exceed 0.6 (see ESI† 2, Table S6 for values of c_S²_H for aryl methyl, dialkyl and cyclic sulfides).] Given that, for PhSMe, the 3p_z-orbital is occupied by the lone pair of higher energy, the three hybrid orbitals formed by the 3s, 3p_x and 3p_y orbitals accommodate the lone pair of lower energy and contribute to the bonds to C. The orbital of the latter lone pair accounts for 66.9% of the 3s orbital and 33.1% of the two 3p orbitals, the S–C_Ph and S–C_Me bonds thus account for 17.6% and 15.8% of s-character and 81.6% and 83.4% p-character, respectively, which confers a C_PhSC_Me angle of 103.6°. The polarisation of each bond to S is indicated by the NBO percentages.

Table 11 Natural bond order analysis at sulfur

	Energy/eV	NBO percentage			Angle/°	Electronic character percentage
		S	C	O		s	p	d
PhSMe
1st S lone pair	−6.31	—	—	—	—	0.00	99.96	0.04
2nd S lone pair	−16.54	—	—	—	—	66.89	33.09	0.02
S–CPh	—	45.44	54.56	—	—	17.61	81.63	0.75
S–CMe	—	46.88	53.12	—	—	15.85	83.44	0.68
∠CPhSCMe	—	—	—	—	103.62	—	—	—
PhSOMe
S lone pair	−14.72	—	—	—	—	52.33	47.64	0.03
S–CPh	—	44.86	55.14	—	—	15.28	83.67	1.05
S–CMe	—	46.25	53.75	—	—	14.27	84.71	1.03
S–O	—	35.92	—	64.08	—	18.98	80.00	1.02
∠CPhSCMe	—	—	—	—	96.28	—	—	—
∠CPhSO	—	—	—	—	107.20	—	—	—
∠CMeSO	—	—	—	—	106.89	—	—	—

---

On oxidation of PhSMe to PhSOMe, the sulfidic second lone pair orbital, on becoming the sulfoxidic lone pair orbital, undergoes a reduction in s- and an increase in p-character with a concomitant increase in energy by almost 2 eV (Table 11). The reaction of the first lone pair in the oxidation of a sulfide thus potentiates the nucleophilic character of the second lone pair. The change in hybridisation of the lone pair entrains corresponding changes in the contributions of S to the bonds to its C and O ligands which narrow the C_PhSC_Me angle to 96.3° while according the CSO angles values ∼107°. It is the resultant pyramidal disposition of the sulfur ligands, rather than delocalisation of the lone pair, that sterically determines the conformation adopted by PhSOMe (see 15): the oxygen and Me groups are positioned so as to minimise their interaction with ortho-H atoms of the aromatic ring. Equally, the pyramidal geometry at S and the single-bond character of the sulfoxidic bond also prevents mesomeric delocalisation of aromatic π-electrons on to the SOMe group.³⁸

6.2 Transition states. Transition states were located by a scanning procedure in which the distance between the S atom of a substrate and the proximal O atom of the oxidant was varied stepwise between 3 Å and 1.5 Å. At each fixed separation, the geometry was optimised by the B3-LYP/6-31G* method, so generating a separation-dependent potential energy curve exhibiting a maximum at the approximate separation of the moieties in the required transition state. This distance was then used as the starting point for optimising the geometry of the transition state. All the transition state structures were found to be first order saddle-points on the potential energy surface characterised by a single imaginary frequency which, on visualisation using the Molekel program,³⁴ corresponded in every case to a vibration between the sulfur atom and the proximal oxygen of the oxidant. The method was validated by repeating, with excellent agreement, B3-LYP/6-31G* calculations that had been reported by Baboul and co-workers²⁴ for the oxidation of H₂S and H₂SO by dioxirane (see Table 12).

Table 12 Reaction energetics and key features of the transition states formed by various substrates on oxidation by 1a as calculated by B3-LYP/6-31G* DFT

Substrate	ΔrH°/kJ mol^−1^a	ΔH^‡/kJ mol^−1^b	r ^‡ (S–Op)/Å^c	r ^‡ (Op–Od)/Å^d	r ^‡ (C–Op)/Å^e	ξ ^f	μ/D^g
a Standard enthalpy of reaction, calculated as the difference between the sum of combined electronic and thermal enthalpies of the products at 298.15 K and 1 atmosphere, corrected for zero point energy, and the sum of the similar entropies of the substrate and oxidant. b Enthalpy of activation, calculated as the difference between the combined electronic and thermal enthalpies of the transition state at 298.15 K and 1 atmosphere, corrected for zero point energy, and the sum of the similar entropies of the substrate and oxidant. c The length of the partial bond between the S atom of the substrate and the proximal (transferred) O atom of the oxidant. d The length of the partial bond between the proximal and distal O atoms of the oxidant. e The length of the partial bond between the ring-C and the proximal O atoms of the oxidant. f The extent of reaction at the transition state calculated by eqn (20). g The gas-phase dipole moment of the transition state. h The oxidant was dioxirane instead of dimethyldioxirane. i Derived from values reported by Baboul and co-workers in kcal mol^−1 (ref. 24).
4-MeOPhSMe	−162.6	33.2	2.022	1.930	1.482	0.455	5.986
PhSMe	−157.5	40.9	2.011	1.935	1.487	0.463	6.453
4-O2NPhSMe	−146.9	56.9	1.986	1.946	1.506	0.481	6.020
PhSOMe	−261.7	37.2	2.032	1.885	1.475	0.403	5.246
4-ClPhSOMe	−260.3	39.4	2.019	1.889	1.482	0.411	3.765
4-NCPhSOMe	−256.5	43.3	2.003	1.894	1.491	0.421	3.374
H2S^h	−73.3 (−73.2)^i	81.0 (81.2)^i	1.888	2.017	1.520	0.572	6.922
H2SO^h	−228.3 (−228.4)^i	44.9 (44.8)^i	1.933	1.902	1.457	0.456	3.012

---

The transition state structures were very similar to those found by the same authors. At the reaction centre the transition state 16 formed by PhSMe and 1a was characterised by the following angles (the values²⁴ for the transition state formed by Me₂S and 1a are given in parentheses for comparison): ∠SOO, 169.16° (168.54°); ∠SOC, 126.11° (125.92°). Avoidance of the lone pairs on O by the nucleophile reduces ∠SOO from 180°. It is also apparent in 16 that activation involves the rotation of the SMe group from co-planarity with the ring (cf.14) so decoupling the S lone pair from conjugation with the aromatic π-system. In transition state 17 formed by PhSOMe and 1a the geometry of the nucleophile is closer to that of its ground state 15 as the S lone pair is not conjugated. The angles at the reaction centre are similar to those found²⁴ in the transition state formed by Me₂SO and 1a ∠SOO, 172.80° (172.56°); ∠SOC, 129.39° (128.43°).

The reaction enthalpies, Δ_rH°, show that the oxidation of a sulfoxide to sulfone is more exothermic than the oxidation of a sulfide to a sulfoxide by ∼104 kJ mol⁻¹, consistent with the molecular enthalpy differences noted in Table 10. In addition, it is clear that in both oxidations the exothermicity increases the more electron-donating is the substituent; on the other hand, the trend in the enthalpies of activation, ΔH^‡, is the opposite. The enthalpy data together thus constitute examples of the Bell–Evans–Polanyi principle:³⁹ for each class of substrate, the stronger the bond being formed, the lower is the activation barrier to its formation and vice versa. In general, the gas-phase oxidations of sulfoxides exhibit lower activation energy barriers than the oxidation of sulfides, a result that has also been obtained with other levels of theory.^24,40 For the O-atom transfer, the extent of reaction, ξ, may be defined by eqn (20):⁴¹

in which r^‡_(Op⋯Od) is the length of the partial bond between the proximal and distal O atoms in the dimethyldioxirane moiety of the transition state; r^R_(Op−Od) is the length of the Op–Od bond in the reactant (oxidant), i.e. 1.506 Å; r^‡_(S⋯Op) is the length of the partial bond between S and the proximal O atom in the transition state and r^P_(S–Op) is the length of the SO bond in the product (see Table 10). The values of ξ tabulated for the aryl methyl substrates indicate that, in the gas phase, both oxidations have relatively early transition states (ξ < 0.5), as in solution (see Section 2, above); that in each class, the more reactive substrates manifest the earlier transition states and that the transition states for sulfoxide oxidation occur earlier in their reaction coordinate than those of sulfide oxidation (ξ_SO < ξ_S). The behaviour of the substrates and their derived transition states, summarised in Table 12, thus accords with the Hammond postulate:³⁹ the more exothermic a reaction, the more its transition state resembles the reactants in energy and geometry.

An expected consequence of ‘Hammond behaviour’ is that, in the same reaction conditions, on comparing the reactivities of different substrates, the reactivity–selectivity principle should apply; e.g. in Hammett correlations, the more reactive substrates should give reaction constants of smaller absolute magnitude than the less reactive. On the reasonable assumption that, for gas-phase bimolecular processes, the entropy of activation differences will be negligible, log [k₂(X)/k₂(H)]_S and log [k₂(X)/k₂(H)]_SO can be evaluated from the calculated activation enthalpies for sulfides and sulfoxides given in Table 12; these give the (three-point) Hammett correlations eqn (21) and eqn (22). As expected, the less reactive sulfides do show the reaction constant of larger absolute magnitude.

log [k₂(X)/k₂(H)]_S = −3.7σ_p, R² = 0.986 (21)

log [k₂(X)/k₂(H)]_SO = −1.9σ_p, R² = 0.996 (22)

Table 13 gives additional calculated data concerning gas-phase transition states. On formation of transition states with 1a there are large percentage increases in the Mulliken charges on sulfidic S together with increases in negative charge on the O atoms of the dioxirane moiety, especially the distal O atom. These increases are responsible for the large dipole moments found for the sulfide-derived transition states (Table 12). The sulfoxides show similar charge changes on the proximal O atom to those of the sulfides on transition state formation but the changes at S and the distal O atom are smaller consistent with their lesser dipole moments (Table 12) and the negative charges on the sulfoxidic O atoms decrease due to their transformation into sulfonic O atoms. The increases in charge separation in transition states formed by both sulfides and sulfoxides indicate that the formation of the S–O bond and breakage of the O–O bond are further advanced than the changes to C–O bonds and that the asynchrony is more marked for sulfides than sulfoxides. Comparison of changes to bond lengths bears this out: the percentage extensions of the O–O bond length of the dimethyldioxirane moiety are 4–5 fold greater than the corresponding changes to the C–O bond lengths in the oxidation of both sulfides and sulfoxides. The S–O bond lengths in transition states formed by both sulfides and sulfoxides average 2.01 Å (Table 12) but, expressed as percentage extensions of S–O bonds in the reaction products, they appear different because sulfonic bonds are shorter than sulfoxidic bonds (Table 10); the important point is that the relatively short partial bond length, however expressed, indicates significant S–O bonding in both types of transition state. The extent of O–O bond cleavage in transition states that are sulfide-derived indicates that even in the gas phase, the distribution of charge and bonding has a tendency towards the sulfonium betaine structure 6a (Scheme 1).

Table 13 Percentage changes in Mulliken charges and bond lengths in transition states^a

Substrate	ΔqS^b	ΔqOp^c	ΔqOd^d	ΔqOso^e	ΔrSOp^f	Δr(Op–Od)^g	ΔrCOp^h	ΔrCOd^i
a Percentages are calculated relative to the ground state parameter in each case; positive values are increases and negative values are decreases in the absolute magnitude of the parameter. b Increase in positive charge on S. c Increase in negative charge on the proximal O atom of 1a. d Increase in negative charge on the distal O atom of 1a. e Decrease in negative charge on the sulfoxidic O atom. f Extension in the length of the product S–O bond. g Increase in the O–O bond length of 1a. h Increase in length of the C to proximal O bond of 1a. i Decrease in length of the C to distal O bond of 1a.
4-MeOPhSMe	239.4	45.9	63.5	—	33.2	28.3	5.6	−5.6
PhSMe	232.3	47.2	63.2	—	32.9	28.5	6.0	−5.7
4-O2NPhSMe	180.8	50.6	61.6	—	31.4	29.2	7.3	−6.1
PhSOMe	25.6	49.1	55.0	−11.7	38.1	25.2	5.1	−4.9
4-ClPhSOMe	25.6	50.6	54.4	−11.6	37.3	25.4	5.6	−3.4
4-NCPhSOMe	25.6	52.5	53.8	−11.6	36.3	25.8	6.3	−5.2

---

6.3 Modelling transition state solvation. The Hammett reaction constants for sulfides and sulfoxides, −3.7 and −1.9, respectively, found above from calculations for gas-phase reactions, contrast with the experimental values of −0.76 and −0.78 found for sulfides and sulfoxides, respectively, for reactions in acetone solution;^6a moreover, the sulfoxides were found to be less reactive than sulfides.^6b In order to gain insight into these differences, the effects of solvation by acetone were simulated at the B3-LYP/6-31G* level by single point self-consistent reaction field (SCRF) calculations with Tomasi’s polarised continuum model³³ (PCM) using the gas-phase B3-LYP/6-31G* optimised geometries as implemented in Gaussian 98. Caution is required in the interpretation of these results as they relate to single point calculations on the optimised gas-phase structures and not to re-optimisations in the simulated medium; for this reason no bond lengths or derived ξ values for the solution phase are given. In view of the inversion in relative reactivity of sulfides and sulfoxides between the theoretical gas phase and the experimental solution phase, the PCM calculations investigated the influence of the medium on the activation barriers to the oxidations of PhSMe and PhSOMe by 1a.

Table 14a gives relevant enthalpy changes. For a reaction in a particular phase, the datum from which the enthalpy of reaction, Δ_rH°, and the enthalpy of activation, ΔH^‡, are measured is, of course, the total enthalpy of the reactants in their ground states (the initial state, IS); on the other hand, the datum for the enthalpies of transfer of any state from the gas phase to solution in acetone is the total enthalpy of the particular state in the gas phase. Fig. 8 illustrates how the absolute magnitudes of these enthalpy changes are related. For both substrates, the enthalpy of activation for reaction in solution, ΔH^‡_s, is given, in terms of absolute magnitudes, by eqn (23).

Fig. 8 Enthalpy changes calculated for oxidations by dimethyldioxirane (a) PhSMe; (b) PhSOMe.

Table 14 (a) Comparison of various enthalpies for reactions of PhSMe and PhSOMe with 1a in the gas phase and acetone solution as calculated by B3-LYP/6-31G* DFT. (b) Comparison of changes in Mulliken charges in the transition states of the reactions of PhSMe and PhSOMe with 1a in the gas phase and in acetone solution as calculated by B3-LYP/6-31G* DFT. (c) Comparison of the molecular dipole moments of PhSMe and PhSOMe and their derived transition states with 1a and of their changes on transfer from the gas phase to acetone solution and on oxidation

(a) Reactants	Phase	ΔrH°/kJ mol^−1^a	ΔH^‡/kJ mol^−1^b	Δg→s(H°)IS/kJ mol^−1^c	Δg→s(H°)TS/kJ mol^−1^d	Δg→s(H°)FS/kJ mol^−1^e
PhSMe + 1a	Gaseous	−157.5	40.9	—	—	—
PhSMe + 1a	Solution	−162.3	30.4	−16.9	−27.3	−21.7
PhSOMe + 1a	Gaseous	−261.7	37.2	—	—	—
PhSOMe + 1a	Solution	−270.4	31.9	−22.1	−27.3	−30.7

---

(b) Reactants	Phase	ΔqS/e^f	Percent^g	ΔqOp/e^h	Percent^i	ΔqOd/e^j	Percent^k	ΔqOso/e^l	Percent^m
PhSMe + 1a	Gaseous	0.309	232	−0.150	47.2	−0.201	63.2	—	—
PhSMe + 1a	Solution	0.362	329	−0.137	41.0	−0.249	74.5	—	—
PhSOMe + 1a	Gaseous	0.196	25.6	−0.156	49.1	−0.175	55.0	0.074	−11.7
PhSOMe + 1a	Solution	0.205	27.0	−0.143	42.8	−0.212	63.5	0.086	−13.2

---

(c) Substrate	Phase	μ IS/D^n	Δg→s(μIS)/D^n	ΔS→SOΔg→s(μIS)/D^n	μ TS/D	Δg→s(μTS)/D	ΔS→SOΔg→s(μTS)/D
a Standard enthalpy of reaction, calculated as the difference between the sum of combined electronic and thermal enthalpies of the products at 298.15 K and 1 atmosphere, corrected for zero point energy, and the sum of the similar entropies of the substrate and oxidant. b Enthalpy of activation, calculated as the difference between the combined electronic and thermal enthalpies of the transition state at 298.15 K and 1 atmosphere, corrected for zero point energy, and the sum of the similar entropies of the substrate and oxidant. c Change in combined standard enthalpies of the initial state (reactants) on transfer from the gas phase to solution in acetone. d Change in standard enthalpy of the transition state on transfer from the gas phase to solution in acetone. e Change in combined standard enthalpies of the final state (products) on transfer from the gas phase to solution in acetone. f Change relative to the ground state value of the organo-sulfur substrate (PhSMe: qSg = 0.133e, qSs = 0.110e; PhSOMe: qSg = 0.765e, qSs = 0.759e). g Percentage increase in positive charge on S. h Change relative to an O atom of 1a (qOg = −0.318e, qOs = −0.334e). i Percentage increase in negative charge on the proximal O atom of 1a. j Change relative to an O atom of 1a (qOg = −0.318e, qOs = −0.334e). k Percentage increase in negative charge on the distal O atom of 1a. l Change relative to the sulfoxidic O atom of PhSOMe (qOso,g = −0.631e, qOso,s = −0.653e). m Percentage decrease in negative charge on the sulfoxidic O atom of PhSOMe. n Here the initial state excludes 1a.
PhSMe	Gaseous	1.413	—	—	6.453	—	—
PhSMe	Solution	1.733	0.320	—	8.401	1.948	—
PhSOMe	Gaseous	3.917	—	—	5.246	—	—
PhSOMe	Solution	4.641	0.724	0.404	6.758	1.512	−0.436

---

ΔH^‡_s = ΔH^‡_g + Δ_g→s(H°)_IS − Δ_g→s(H°)_TS (23)

The attenuation of the gas-phase activation enthalpy ΔH^‡_g to the solution value thus depends on the magnitudes of the phase-transfer enthalpies of the initial and transition states. Fortuitously, for both substrates, the phase-transfer enthalpies of the transition state, Δ_g→s(H°)_TS, are equal, hence their relative reactivity depends on the difference in their gas-phase activation enthalpies and in the phase-transfer enthalpies of their initial states eqn (24):

{[ΔH^‡_s]_SO − [ΔH^‡_s]_S} = {[ΔH^‡_g]_SO − [ΔH^‡_g]_S} + {[Δ_g→s(H°)_IS]_SO − [Δ_g→s(H°)_IS]_S} (24)

Since the sulfoxide has the lower gas-phase activation barrier (Table 14a), the inversion in relative reactivity found for reaction in solution (where [ΔH^‡_s]_SO > [ΔH^‡_s]_S) must arise from a positive difference in the phase-transfer enthalpies of their initial states out-weighing the negative difference in their gas-phase activation enthalpies. As the initial states each comprise one mole of 1a and one mole of substrate, the difference in the phase-transfer enthalpies stems from the difference in ground state solvation of the two substrates: the inversion in relative reactivity of PhSMe and PhSOMe between the two phases occurs because solvation of the sulfoxide is more exothermic than that of the sulfide.

This conclusion depends on the equality of Δ_g→s(H°)_TS for these two substrates and it is relevant to enquire why this should occur. At first sight, it might be expected that the transition state difference [Δ_g→s(H°)_TS]_SO − [Δ_g→s(H°)_TS]_S should be greater than zero, as in the case of the initial-state difference, owing to solvation of the S⁺–O⁻ bond, but this ignores the large increase in charge separation on passage from the ground state to the transition state in the case of the sulfide. As shown in Table 14b, the percentage increase in Mulliken positive charge on S is 232% for the gas phase rising to 329% in solution with corresponding negative charge increases of 63.2% and 74.5% on the distal oxygen atom. There is thus an increase of ∼100% in the positive charge on S and ∼10% in the negative charge on distal O on transfer of the transition state from the gas phase to solution. This change in charge distribution is reflected in the dipole moments (Table 14c). Comparison of the changes in dipole moments shows increases for both substrates on transfer from the gas to solution phase with the greater increase for the sulfoxide, i.e. Δ_S→SOΔ_g→s(μ_IS)/D is +0.40. This is consistent with the larger magnitude of Δ_g→s(H°)_IS calculated for the sulfoxide. The transition states also show an increase in dipole moment on transfer from the gas to solution phase, consistent with their stabilisation by solvation but, in the case of the sulfoxide-derived transition state, the increase is smaller than that of the sulfide-derived transition state, i.e. Δ_S→SOΔ_g→s(μ_TS)/D is negative (−0.44) by a similar amount to the positive difference found for the initial state. The solvation of the relatively enhanced dipole of the sulfide-derived transition state will therefore negate that of the S⁺–O⁻ bond in the sulfoxide-derived transition state so reducing [Δ_g→s(H°)_TS]_SO − [Δ_g→s(H°)_TS]_S to zero. It does not necessarily follow, however, that the comparable difference is zero for all other ArSMe and ArSOMe.

In solution, the aryl methyl sulfoxides are less reactive towards 1a than the corresponding sulfides [e.g. values of k₂(X)_S/k₂(X)_SO lie in the range 81–86]^6bi.e. [ΔH^‡_s]_SO > [ΔH^‡_s]_S hence the inequality (25), comprising three differences, follows from eqn (23).

{[ΔH^‡_g]_SO − [ΔH^‡_g]_S} + {[Δ_g→s(H°)_IS]_SO − [Δ_g→s(H°)_IS]_S} − {[Δ_g→s(H°)_TS]_SO − [Δ_g→s(H°)_TS]_S} > 0 (25)

In terms of absolute magnitudes, the first difference is negative (Table 14a) and it is probable that the second difference is positive for many pairs of substrates (as in the case for PhSOMe and PhSMe) on account of the polarity of the S⁺–O⁻ bond but, in cases of direct conjugation between SMe and a 4-substituent of −M type, it may be that the dipole moment of the sulfide is greater than that of the like-substituted sulfoxide (see 12 and Table 10) with the possibility that [Δ_g→s(H°)_IS]_S > [Δ_g→s(H°)_IS]_SO and the second difference may then be negative. On activation, sulfides show the greater changes in Mulliken charges (Table 13) thus, notwithstanding the zero value of the third difference for PhSMe and PhSOMe, it is probable, generally, that [Δ_g→s(H°)_TS]_S > [Δ_g→s(H°)_TS]_SO and the third difference makes a positive contribution to the inequality. The value of k₂(NO₂)_S/k₂(NO₂)_SO is 85.7,^6b the largest ratio observed for any substituent. If the second difference in inequality (25) is negative for this −M substituent, the negative sum of the first two differences is clearly more than compensated by a positive third difference. The reversal of relative reactivity of sulfoxides and sulfides towards 1a between the gas and solution phases thus stems from a combination of factors, the principal of which are a greater ground state stabilisation by solvation in the case of sulfoxides due to their polar S⁺–O⁻ bonds and a greater transition state stabilisation by solvation in the case of sulfides, the latter made possible by the enhanced charge separation that develops as a consequence of more asynchronous bond scission.

6.4 Anti-Hammond behaviour. Above (Section 6.2), calculations showed that in the gas phase the oxidations of sulfides and sulfoxides by 1a exhibit Hammond behaviour. The inversion of relative reactivity in solution therefore must result from a switch to ‘anti-Hammond’ behaviour by at least one of them; such a switch is usually explained in terms of factors that displace a transition state away from the reaction coordinate between reactants and products.³⁹

Fig. 9 is a qualitative potential energy-surface (PES) diagram^39,42 for the gas-phase oxidation of PhSMe by 1a; the actual energy coordinate is not given explicitly being perpendicular to the page. The abscissa represents decrease in the bond length between the ring-C atom and the distal O atom of 1a and the ordinate represents decrease in the distance between the S atom and the proximal O atom of 1a. The lower left corner (origin) corresponds to the reactants in their ground state and is thus an energy minimum; the upper right corner corresponds to the products in their ground states and is also an energy minimum. Four pathways between reactants and products are indicated (two two-step paths aa′, bb′ and two concerted paths c and d). Change along the abscissa (path a) is accompanied by a steep increase in energy followed by a shallow decrease as 1a undergoes fragmentation to acetone and the high-energy intermediate oxene. Change along the ordinate (path b) also marks an increase in energy followed by a shallow decrease as the charges of the intermediate sulfonium betaine separate. Concerted reaction coordinates pass directly from the lower left to the upper right. If all the bonding changes were to occur in synchrony (at the same rate), the saddle-point of the synchronous transition state, TS_syn, would occur in the centre of the diagonal (path c, ξ = 0.500). However, our calculations have shown that formation of the S–O bond and breaking of the O–O bond are in advance of the changes to bonding at C, hence the saddle-point of the asynchronous transition state, TS_asyn, occurs displaced towards the upper left corner and at a distance less than half-way along the reaction coordinate, path d (ξ = 0.463, Table 12). Our previous studies of the reaction in acetone solution⁶ have shown that the introduction of an aqueous component to the solvent increases the betaine-like character of the transition state by lone pair donation at S and hydrogen bonding at O so enhancing the anti-Hammond behaviour: the absolute magnitude of the Hammett reaction constant is increased (from −0.76 in acetone to −1.33 in 5% v/v aqueous acetone) and a decrease in the value of ξ is expected. Ultimately, with the addition of sufficient water (20% v/v), the betaine 6a is sufficiently stabilised to occur as a real reaction intermediate (path bb′). In terms of Fig. 9, specific aqueous solvation of the betaine converts the shallow energy minimum of the upper left corner into a deeper minimum with the energy maximum between the two left-hand corners decreasing and receding towards the origin.

Fig. 9 Qualitative potential energy-surface diagram for the oxidation of PhSMe by dimethyldioxirane.

The PES diagram for the gas-phase oxidation of PhSOMe by 1a is similar to Fig. 9: the bonding changes are asynchronous (ξ = 0.403, Table 12). However, the changes on transfer of the reaction to acetone solution differ from those of PhSMe. Although the gas-phase TS_asyn has some betaine-like character, the response of the PES to solvent variation is different. Solvation of the polar S⁺–O⁻ bond results in a deepening of the energy minimum at the origin, a change which will shift TS_asyn along the reaction coordinate towards the products with an associated increase in the magnitude of ξ, i.e. Hammond-behaviour. Experimentally, a 20% v/v addition of water has scant effect on the Hammett reaction constant (it is reduced in magnitude from −0.78 to −0.70)^6a and there is no specific stabilisation to produce a real sulfoxonium betaine intermediate, PhS⁺(O)OCMe₂O⁻.^6b The upper left corner of the diagram stays high in energy relative to the saddle-point of TS_asyn and the reaction remains concerted. Owing to the mentioned limitations of our PCM calculations we cannot give modified ξ values but in Section 4.4 we inferred that, in solution, sulfides manifest earlier transition states than sulfoxides (i.e. ξ_S < ξ_SO). The modelling of the effect of solvation by acetone thus strongly supports the inferences drawn from our present and prior experimental mechanistic studies.

Conclusions

1. The rate constants for the oxidation of alkyl 4-nitrophenyl and dialkyl sulfides by 1a are sensitive to variation in alkyl group structure. In both series of sulfides alkyl groups, by their +I effects, assist the development of a transition state which is more polarised than the reactants but, sterically, they hinder its solvation; for bulky groups the hindrance outweighs the stabilisation.

2. The rate constants for the oxidation of alkyl 4-nitrophenyl and dialkyl sulfoxides by 1a are also sensitive to the +I effects of alkyl groups as both ground states and transition states are polar. The polarity of both states leads to their solvation but this is hindered by bulky alkyl groups. Hindrance to solvation of the ground state is rate-enhancing whereas hindrance to that of the transition state is rate-inhibiting. For the subsets of alkyl 4-nitrophenyl sulfoxides and dialkyl sulfoxides these hindering factors cancel but, when the range of sulfoxides is expanded to include other aryl methyl sulfoxides and cyclic sulfoxides, a steric acceleration of oxidation may be discerned statistically.

3. Comparisons of activation parameters show that, on oxidation by 1a, alkyl 4-nitrophenyl sulfides exhibit lower activation enthalpies than sulfoxides owing to the difference in energy of their nucleophilic sulfur lone pairs. Activation entropy differences between sulfides and sulfoxides reflect the difference in the solvation patterns for the two oxidations.

4. The oxidation of saturated cyclic sulfides by 1a is independent of ring strain energies and the pattern of rate constants is well accounted for in frontier orbital terms. By contrast, rate constants for the oxidation of analogous cyclic sulfoxides show a dependence on the change in ring strain energy between reactant and product but there is also statistical evidence that an additional ring size-dependent factor affects the transition states for 4- to 6-membered rings.

5. Calculations at the B3-LYP/6-31G* level of density functional theory have been performed on a range of 4-substituted-phenyl alkyl, dialkyl and cyclic sulfides and sulfoxides. The reactivities of 40 of these have been correlated using a combination of quantum mechanical and empirical parameters (Mulliken charge on S, q_S; substituent effects, Σσ*; and ring strain differences between reactant and product, ΔE_rs). Sulfides and sulfoxides must be treated separately in order to account for steric effects, ΣE_s′ and the reciprocals of the frontier orbital energy differences, Φ/eV, are relevant only to sulfides.

6. Calculations at the B3-LYP/6-31G* level of density functional theory have been performed for the transition states formed by three aryl methyl sulfides and three aryl methyl sulfoxides on oxidation by 1a and the nature of charge and bonding changes explored. For both types of substrate, formation of the S–O bond and scission of the O–O bond occur ahead of bonding changes at C but these changes are more marked for sulfide-derived transition states. The calculations indicate sulfoxides to be more reactive than sulfides in the gas phase.

7. The application of Tomasi’s PCM model to the gas-phase transition state structures allows simulation of solvation by acetone. It is shown how solvation accentuates differences between sulfides and sulfoxides by inducing anti-Hammond behaviour in the former, and inverting their relative reactivity. The calculations give strong support to the conclusions reached by physical-organic reasoning.

Experimental

Instrumental methods

Our previous papers⁶ give details of the instrumentation and procedures used in the characterisation of reactants and products. The procedures include the determination by GC of relative rate constants from the product ratios of competitive oxidations of sulfides and sulfoxides by 1a, and the spectrophotometric determination of absolute rate constants for the oxidations of substrates bearing a 4-nitrophenyl chromophore under both pseudo-first order and second order conditions.

Acquired materials

Organic solvents were supplied by Fisher and were of analytical or HPLC grade. Methyl phenyl sulfide, its 4-nitro-derivative, ethylene sulfide (thiirane), tetramethylene sulfide (tetrahydrothiophen, thiolane), pentamethylene sulfide (thiane), di-(n-propyl) sulfide, di-(tert-butyl) sulfide and other reagents were purchased in the highest available purity (Aldrich, Fluka or Lancaster); liquid sulfides were distilled before use. Methyl phenyl sulfoxide and sulfone (Aldrich) were further purified by column chromatography (silica, 10% v/v acetone in CH₂Cl₂). The water used was deionised.

Synthetic materials

Dimethyldioxirane, 1a, was prepared and handled as previously described.^6a Alkyl 4-nitrophenyl sulfides and unavailable (or costly) cyclic sulfides were synthesised by established methods as were their derived sulfoxides and, where required, sulfones. In general these were known compounds and their synthetic details are given in ESI† 3.

Spectrophotometric rate measurements

UV-Vis spectra were recorded on a Hewlett Packard HP8453 diode array spectrophotometer with Chemstation Rev. A.02.05 data processing. Quartz cuvettes of 1 cm path-length were used for the recording of spectra in acetone in the range 300–500 nm, a blank measurement on the solvent being obtained before each experimental run. Solutions of the alkyl nitrophenyl sulfide or sulfoxide (2 cm³) were thermostated in the cuvette at the required temperature for at least 15 min then a solution of 1a was added by syringe and the mixture thoroughly shaken. For the oxidation of sulfoxides under pseudo-first order conditions, a 12-fold excess of 1a (3 − 6 × 10⁻³ mol dm⁻³) over substrate (2.5 − 5 × 10⁻⁴ mol dm⁻³) was used and absorbance decay profiles were recorded at 330 nm for 10 min. For oxidations under second order conditions, the alkyl nitrophenyl substrate concentration was 1 × 10⁻⁴ mol dm⁻³ with 1a 2.5 × 10⁻⁵ mol dm⁻³. The decay of absorbance was monitored over 10 min; the monitoring wavelengths being 330 nm for sulfoxides and 350 nm or 342 nm for sulfides. Data for both first and second order conditions were analysed by the methods given in ref. 6b.

Competitive oxidation of (CH₂)₅S and (CH₂)₂S by NaIO₄ in 50% v/v aqueous ethanol at 298 K

To a mixture of (CH₂)₅S (1.0 cm³, 1.5 × 10⁻² mol dm⁻³) and (CH₂)₂S (1.0 cm³, 5.3 × 10⁻² mol dm⁻³) in aqueous ethanol (25% v/v H₂O) was added an aqueous solution of NaIO₄ (1.0 cm³, 4.5 × 10⁻³ mol dm⁻³). After shaking, the mixture was allowed to stand overnight (ca. 16 h) at 298 K and the sulfoxide product ratio was then found by GC with 1,4-dibromobenzene as internal standard and used to evaluate k(3)_S/k(6)_S as previously described.^6a The oxidation was repeated 3 times and the average value of k(3)_S/k(6)_S found to be (0.43 ± 0.03). This value together with those for k₂(6)_S and k₂(n-Pr)_2,S [0.399 dm³ mol⁻¹ s⁻¹ and 0.237 dm³ mol⁻¹ s⁻¹, respectively (cf. ESI† 4, Table S8)],⁹ allows evaluation of k(3)_S/k(n-Pr)_2,S for periodate oxidation as 0.72 (see Fig. 2) and also k₂(3)_S as 0.17 dm³ mol⁻¹ s⁻¹.

Acknowledgements

We thank AstraZeneca for a studentship (RAAJH) and Dr A. M. Davis and Dr N. Gensmantel for their interest and encouragement. We are grateful to Professor J. E. McGrady for the provision of facilities, help and advice with the DFT calculations and to Dr A. C. Whitwood for advice and help with IT.

References and notes

1. (a) W. Adam, R. Curci and J. O. Edwards, Acc. Chem. Res., 1989, 22, 205; (b) R. W. Murray, Chem. Rev., 1989, 89, 1187; (c) R. Curci, in Advances in Oxygenated Processes, ed. A. L. Baumstark, JAI Press, Greenwich, 1990, ch. 1, vol. 2; (d) W. Adam, L. P. Hadjiarapoglou, R. Curci and R. Mello, in Organic Peroxides, ed. W. Ando, Wiley, New York, 1992.
2. (a) A. R. Gallopo and J. O. Edwards, J. Org. Chem., 1981, 46, 1684; (b) G. Cicala, F. Curci, M. Fiorentino and O. Larichiutta, J. Org. Chem., 1982, 47, 2670; (c) S. E. Denmark, D. C. Forbes, D. S. Hays, J. S. Depue and R. G. Wilde, J. Org. Chem., 1995, 60, 1391; (d) D. Yang, M. K. Wong and Y. C. Yip, J. Org. Chem., 1995, 60, 3887; (e) A. Lévai, ARKIVOC, 2003, (xiv), 14.
3. (a) L. Cassidei, M. Fiorentino, R. Mello, O. Sciacovelli and R. Curci, J. Org. Chem., 1987, 52, 699; (b) R. Mello, M. Fiorentino, C. Fusco and R. Curci, J. Am. Chem. Soc., 1989, 111, 6749; (c) W. Adam, L. P. Hadjiarapoglou and A. K. Smerz, Chem. Ber., 1991, 124, 227; (d) W. Adam, G. Asensio, R. Curci, M. E. González-Núñez and R. Mello, J. Am. Chem. Soc., 1992, 114, 8345.
4. (a) W. Adam, R. Curci, M. E. González-Núñez and R. Mello, J. Am. Chem. Soc., 1991, 113, 7654; (b) K.-P. Zeller, M. Kowallik and P. Haiss, Org. Biomol. Chem., 2005, 3, 2310.
5. (a) R. W. Murray and R. Jeyaraman, J. Org. Chem., 1985, 50, 2847; (b) R. W. Murray, R. Jeyaraman and M. K. Pillai, J. Org. Chem., 1987, 52, 746.
6. (a) P. Hanson, R. A. A. J. Hendrickx and J. R. Lindsay Smith, Org. Biomol. Chem., 2008, 6, 745; (b) P. Hanson, R. A. A. J. Hendrickx and J. R. Lindsay Smith, Org. Biomol. Chem., 2008, 6, 762.
7. (a) G. Asensio, R. Mello and M. E. González-Núñez, Tetrahedron Lett., 1996, 37, 2299; (b) M. E. González-Núñez, R. Mello, J. Royo, J. V. Ríos and G. Asensio, J. Am. Chem. Soc., 2002, 124, 9154.
8. (a) G. Modena, Gazz. Chim. Ital., 1959, 89, 834; (b) A. Cerniani and G. Modena, Gazz. Chim. Ital., 1959, 89, 843; A. Cerniani, G. Modena and P. E. Todesco, Gazz. Chim. Ital., 1960, 90, 3.
9. F. Ruff and A. Kucsman, J. Chem. Soc., Perkin Trans. 2, 1985, 683.
10. (a) W. A. Pavelich and R. W. Taft, J. Am. Chem. Soc., 1957, 79, 4935; (b) R. W. Taft, in Steric Effects in Organic Chemistry, ed. M. S. Newman, Wiley, New York, 1956, ch. 13.
11. L. S. Levitt and H. F. Widing, Prog. Phys. Org. Chem., 1976, 12, 119.
12. D. D. Steppan, J. Werner and R. P. Yeater, Essential Regression add-in for Microsoft Excel, 1998 and 2006, freely available at http://www.geocities.com/jowerner98/index.html; Essential Regression, Erbbook, pp. 13.
13. M. J. Kamlet, J.-L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877.
14. J. D. Cox and G. Pilcher, in The Thermochemistry of Organic and Organometallic Compounds, Academic Press, London, New York, 1970, ch. 7. The NIST webbook and DETHERM on-line databases cite the same original sources as Cox and Pilcher.
15. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Ciolowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98, Revision A.3, Gaussian Inc., Pittsburgh, PA, 1998.
16. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
17. C. Lee, W. Lang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785.
18. J. O. Morley, Int. J. Quantum Chem., 1998, 66, 141.
19. D. V. Deubel, J. Org. Chem., 2001, 66, 2686.
20. V. M. Bzhezovskii, E. G. Kapustin and N. N. Il’chenko, Russ. J. Gen. Chem., 2000, 70, 745.
21. K. Miaskiewicz and D. A. Smith, J. Am. Chem. Soc., 1998, 120, 1872.
22. W. Sander, K. Schroeder, S. Muthusamy, A. Kirschfeld, W. Kappert, R. Boese, E. Kraka, C. Sosa and D. Cremer, J. Am. Chem. Soc., 1997, 119, 7265.
23. M. Freccero, R. Gandolfi, M. Sarze-Amade and A. Rastelli, Tetrahedron, 1998, 54, 6123.
24. A. G. Baboul, H. B. Schlegel, M. N. Glukhovtsev and R. D. Bach, J. Comput. Chem., 1998, 19, 1353.
25. T. Dudev and C. Lim, J. Am. Chem. Soc., 1998, 120, 4450.
26. (a) O. Exner, Collect. Czech. Chem. Commun., 1966, 31, 3222; (b) J. Shorter, in Correlation Analysis of Organic Reactivity, Research Studies Press (Wiley), Chichester, 1982, ch. 7.
27. J. A. MacPhee, A. Panaye and J.-E. Dubois, Tetrahedron, 1978, 34, 3553.
28. I. Fleming, in Frontier Orbitals and Organic Chemical Reactions, Wiley-Interscience, Chichester, 1978, ch. 2.
29. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833.
30. Advanced Chemistry Development, PhysChem Batch, Version 6.00, Advanced Chemistry Development, Inc., Toronto, ON, Canada, 2002, http://www.acdlabs.com.
31. (a) C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165 table 1; (b) We find: σ*(3-XPh)_ACD = 0.67σ_m(X) + 0.59 and σ*(4-XPh)_ACD = 0.72σ_p(X) + 0.58; 3-CN and 4-COCH₃ were omitted from these correlations to preserve their precision.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Ciolowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98, Revision A.7., Gaussian Inc., Pittsburgh, PA, 1998.
33. (a) S. Miertuš and J. Tomasi, Chem. Phys., 1982, 65, 239; (b) S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117.
34. S. Portmann, Molekel, CSCS/ETHZ, Geneva, 2002.
35. (a) CRC Handbook of Chemistry and Physics, ed. R. C. Weast, CRC Press, Boca Raton, 63rd edn, 1982 table E-61; (b) A. L. McClellan, Tables of Experimental Dipole Moments, W. H. Freeman and Company, San Francisco, 1963.
36. See ref. 31a, table V.
37. E. D. Glendening, A. E. Reid, J. E. Carpenter and F. Weinhold, Gaussian NBO Version 3.1, Gaussian Inc., Pittsburgh PA, 1998.
38. For previous discussion of the relationship of the various substituent constants for the SOMe group to its geometry see ref. 6a.
39. A. Pross, in Theoretical and Physical Principles of Organic Reactivity, Wiley, New York, 1995, ch. 5.
40. J. J. W. McDouall, J. Org. Chem., 1992, 57, 2861.
41. An analogous equation has been given for O-atom transfer in epoxidation: D. V. Deubel, J. Org. Chem., 2001, 66, 3790.
42. (a) E. R. Thornton, J. Am. Chem. Soc., 1967, 89, 2915; (b) W. J. Albery, Prog. React. Kinet., 1967, 4, 353; (c) R. A. More O’Ferrall, J. Chem. Soc. B, 1970, 274; (d) W. P. Jencks, Chem. Rev., 1972, 72, 705; (e) D. A. Winey and E. R. Thornton, J. Am. Chem. Soc., 1975, 97, 3102; (f) W. P. Jencks, Acc. Chem. Res., 1980, 13, 161.

---

Footnotes

† Electronic supplementary information (ESI) available: 1. Molar absorbances. 2. Connectivity-derived substituent constants for hydrocarbon moieties; statistical analysis of correlated data. 3. Synthetic materials. 4. Published rate constants for comparison. See DOI: 10.1039/b9nj00452a

‡ Present address: Department DMPK & Bio-analysis, AstraZeneca, AB 221 87, Lund, Sweden. E-mail: ramon.hendrickx@astrazeneca.com

---