Rubrene micro-crystals from solution routes: their crystallography, morphology and optical properties

Abstract

A series of rubrene micro-crystals (MCs) with controllable sizes and shapes, ranging from one-dimensional (1D) ribbons to 2D rhombic and hexagonal plates, have bee prepared by employing the reprecipitation method. Based on X-ray diffraction analysis, the crystal structures of 1D ribbons and 2D plates have been identified to be triclinic and monoclinic phases, respectively, rather than the commonly reported orthorhombic phase for vacuum-deposited rubrene crystals. In our system, adjustment of the monomer concentration of rubrene, which in turn determines the supersaturation (β) for crystallization, paved the way for kinetic control over the nucleation and growth processes. Combining with theoretical calculations, we found that transformation from a triclinic phase at low supersaturation to a monoclinic phase at high supersaturation was responsible for the morphology change from 1D ribbons to 2D plates. Both ensemble and single-particle spectroscopy clarifies that 1D ribbons and 2D plates show distinct optical properties, probably related to their different solid-state structures in triclinic and monoclinic crystals. Moreover, scanning near-field optical microscopy reveals that the ribbons show waveguiding along a 1D direction, and the plates in a 2D plane.

---

1. Introduction

In recent years, organic micro-crystals (MCs) have attracted increasing research interest, due to their potential use in optoelectronics,¹ nonlinear optics,² and photonics.³ Many efforts have been paid on molecule design to gain desired function.⁴ Nonetheless, when the building units of organic molecules constitute into solid-state materials, their molecular-stacking arrangement^5,6 and micro/nano-structured morphology^7,8 also largely influence their performance. In this sense, the fact that organic crystals usually possess polymorphs is both a chance and a challenge. As a chance, the variety in polymorphs offers more possibilities for various morphology and properties. Especially for the organic semiconductor materials, their optical and electrical characteristics are totally different in different polymorphs,⁶ and their external crystal morphology directly influences the device performance.⁸ As a challenge, a polymorph makes the controlled growth of organic crystals more difficult to achieve.^5,9 How to prepare organic crystals with a particular crystal phase and morphology becomes the hindrance to further exploitation of polymorphous organics.

Rubrene is one of the superstars in organic semiconductors. Its fluorescence quantum efficiency in solution is near 100%,¹⁰ attractive for applications in organic light emitting diodes (OLED).¹¹ Meanwhile, the organic field-effect transistor (OFET) fabricated by vacuum-deposited orthorhombic rubrene single crystals show p-type characteristics with high mobility up to 20 cm²/Vs.¹² Besides, the orthorhombic rubrene crystals reveal optical waveguide properties, with propagating emission polarized along short backbone axis.¹³ Nevertheless, all these studies of rubrene crystals are based on the same crystallogaraphic phase, i.e., the base centered orthorhombic crystals, which are usually grown by the physical vapor deposition method (PVD).^12–15 In addition, triclinic and monoclinic forms of rubrene have been also reported previously,¹⁶ however, their preparation as well as crystal structures, such as detailed atom coordinates, remain largely unclear. In this paper, by the method of reprecipitation, we prepared a series of rubrene micro-crystals (MCs), from the triclinic ribbons to monoclinic plates separately, with uniformity in both internal crystal structure and external morphology. Based on X-ray diffraction analysis, the crystal structures of 1D ribbons and 2D plates have been identified to be triclinic and monoclinic phases, respectively, rather than the commonly reported orthorhombic phase for vacuum-deposited rubrene crystals. By adjusting the monomer concentration of rubrene, consequently, the supersaturation for crystallization, the nucleation and growth processes are kinetically controlled. Combining with theoretical calculations, we found that transformation from triclinic phase at low supersaturation to monoclinic phase at high supersaturation was responsible for the morphology change from 1D ribbons to 2D plates. Both ensemble and single-particle spectroscopy clarifies that 1D ribbons and 2D plates show distinct optical properties, probably related to their different solid-state structures in triclinic and monoclinic crystals. Moreover, scanning near-field optical microscopy reveals that the ribbons show waveguiding along the 1D direction, while the plates are in a 2D plane. This work achieved the controlled growth of rubrene MCs in different polymorphs, and disclosed the connection of their crystallography, morphology and optical properties. This might be helpful for broadening the implication of rubrene in optic and opto-electronic devices.

2. Experimental

Materials

Rubrene was purchased from Aldrich, and used without further treatment. The solvents chloroform (CHCl₃, A. R.), dichloromethane (CH₂Cl₂, A. R.) and methanol (MeOH, A. R.) were purchased from Beijing Chemical Co. China.

Preparation

(a) The rubrene MCs were prepared by the reprecipitation method in a 25 °C thermostated container. In our experiment, 50 µL of 30 mM rubrene stock solution in CHCl₃ was quickly injected into different volumes of MeOH (0.1, 0.4, 1.5 mL, for example). Within 2 h, orange solids of rubrene MCs formed from the mixed solvents.

(b) The bulk crystals for single crystal X-ray diffraction (SCD) analysis were cultivated by the solvent diffusion method at the liquid–liquid interface between CH₂Cl₂ and MeOH. Usually, there are two kinds of products, block-like and plate-like crystals, respectively, which are analyzed to be monoclinic and triclinic crystals, respectively. Their crystallographic data have been deposited as No. 726175, 726176, respectively in Cambridge Crystallographic Data Centre (CCDC†).

Measurements

The chemical composition of as-prepared MCs were firstly confirmed by matrix-assisted laser desorption/ionization time-of-flight (MALDI-TOF) mass spectroscopy (Bruker Daltonics Inc. BIFLEX III). Subsequently, the morphology of rubrene MCs was characterized by scanning electron microscopy (SEM, Hitachi S-4300), and transmission electron microscopy (TEM, JEOL JEM-1011). Their crystal structures were determined by means of powder X-ray diffraction (XRD, X'Pert RPO).

The steady-state absorption spectra were measured on a Perkin-Elmer Lambda 35 spectrometer with a scanning speed of 480 nm/min and a slit width of 1 nm. The stationary fluorescence spectra were performed on a Hitachi F-4500 fluorescence spectrophotometer. Slits were set to provide widths of 5 nm for both the excitation and the emission monochromators. The fluorescence decay of rubrene MCs was measured by the ps time-resolved fluorescence spectrometer, which has been described in detail elsewhere.¹⁷ Briefly, the 800 nm laser pulses generated from a Ti:sapphire regenerative amplifier (Spitfire, Spectra Physics) were frequency doubled and used as the excitation pulses. The excitation pulse energy was ∼100 nJ/pulse at a pulse repetition rate of 1 kHz which was focused onto a spot ∼0.5 mm in diameter. Photoluminescence (PL) collected with the 90 degree geometry was dispersed by a polychromator (250is, Chromex) and collected with a photon-counting type streak camera (C5680, Hamamatsu Photonics). The data detected by digital camera (C4742-95, Hamamatsu) were routinely transferred to computer for analysis with HPDTA software. The spectral resolution was 2 nm, and the temporal resolution was 2–100 ps, depending on the delay-time-range setting. Furthermore, fluorescence microscopy images were obtained by laser confocal scanning microscope (Olympus FV1000-1X81). The micro-area microscopy images of single rubrene MCs were obtained by near-filed scanning optical microscopy (NSOM). For the collection of PL spectra, single MCs were excited with a continuous-wave He–Cd laser (λ = 442 nm). PL spectra were then collected using an objective coupled into an optical fiber and a liquid nitrogen cooled charge-coupled device (CCD). All the spectroscopic measurements were carried out at room temperature.

Calculation

The growth morphologies of triclinic and monoclinic crystals were calculated by using the Materials Studio software,¹⁸ based on the attachment energy theory.¹⁹ The molecule structure is firstly optimized based on the experimental crystal structure using the Discover module. The attachment energies of low-index faces were calculated using the method given in ref. 19. The force fields of COMPASS²⁰ are used during the calculation. Moreover, the lattice energies of triclinic and monoclinic structures have been also calculated, as shown in Table S1 (ESI†.

3. Results

Rubrene MCs were prepared through a facile reprecipitation route combined with a self-assembly technique. In a typical preparation, 50 µL of 30 mM rubrene solution in chloroform was injected into varying volumes of methanol (V_MeOH). The turbulent mixing of good and poor solvents changes the solvent surroundings, inducing the nucleation and growth of rubrene MCs. In our system, the total amount of the growth units of rubrene molecules is the same, so the concentration of rubrene molecules (C) is easily adjusted as a function of V_MeOH, according to C = 0.05 × 30/(0.05 + V_MeOH) mM, paving the way for manipulating the growth kinetics of rubrene MCs. Interestingly, we found that the sizes and morphologies of as-prepared rubrene MCs exhibited strong dependence on the value of C.

Electron microscopy characterization of morphology

Fig. 1A presents the SEM images of rubrene MCs formed at C = 1.0 mM. It can be seen that 1D ribbon-like structures have been prepared on a large scale. The rather straight ribbons have a length of 100–200 µm, a width of ∼2 µm, and a thickness of ∼300 nm. The TEM image in Fig. 1B shows that the surfaces of the 1D ribbons are clean and smooth. The 1D ribbons are single-crystalline rather than polycrystalline, as revealed by the sharp spots in the corresponding selected area electron diffraction (SAED) patterns (Fig. 1C). When the value of C is larger than 2.0 mM, 2D rhombic plates are the dominant products (Fig. 2). Moreover, the sizes of rhombic plates can be tuned by adjusting the value of C in the range 2.0 mM < C < 4.0 mM. For example, the average edge lengths of rhombic plates prepared at C = 2.3, 2.7 and 3.3 mM are 21.5 ± 1.4 (Fig. 2A), 10.6 ± 0.6 (Fig. 2B), and 5.1 ± 0.4 µm (Fig. 2C), respectively, while their thicknesses are around 1–2 µm. Interestingly, if the value of C is further increased to be larger than 6.0 mM, hexagonal plates (Fig. 3), instead of rhombic plates, are formed. Moreover, the edge lengths of hexagonal plates also decrease by increasing the value of C, for example, 17.2 ± 1.3 µm at C = 7.1 mM (Fig. 3A), 10.1 ± 0.8 µm at C = 8.8 mM (Fig. 3B), and 6.8 ± 0.5 µm at C = 10.0 mM (Fig. 3C). The thicknesses of the hexagonal plates are around 1 µm. The SAED pattern of a single hexagonal plate in Fig. 3D is different from that of a 1D ribbon, indicating that they might have different internal crystal structures. In any event, these results demonstrated that control over the sizes and morphologies of rubrene MCs have been simply achieved by adjusting the starting concentration of rubrene growth units in the system.

Fig. 1 (A) SEM images, (B) TEM images, and (C) SAED patterns of ribbons, prepared when the final concentration of rubrene after injection C is 1.0 mM. Insert: SEM images in high magnification.

Fig. 2 SEM images of rhombic plates in low magnification, prepared when C is (A) 2.3 mM, (B) 2.7 mM, and (C) 3.3 mM. Insert: the histogram of size distribution, by randomly measuring the edge lengths of 50 particles in a batch.

Fig. 3 SEM images of hexagonal plates, prepared when C is (A) 7.1 mM, (B) 8.8 mM, and (C) 10.0 mM. Insert: the histogram of size distribution, by randomly measuring the edge lengths of 50 particles in a batch. (D) SAED pattern of hexagonal plate.

Crystallographic characterization and attribution

Fig. 4 depicts the XRD patterns of as-prepared MCs of rubrene. The XRD peaks of rhombic (curve 3) and hexagonal plates (curve 4) are almost identical, but different from those of ribbons (curve 2). Nonetheless, none of them are similar to the XRD pattern of the commercial powder, which can be perfectly indexed to the reported orthorhombic crystal structure of rubrene (curve 6).¹⁵ Note that MALDI-TOF MS results of as-prepared MCs re-dissolved in chloroform (Fig. S1, ESI†) verify that there was not any chemical reactions during the reprecipitation process, therefore, the 1D ribbons and 2D plates should be attributed to other crystal forms. Besides orthorhombic, monoclinic and triclinic crystal forms had also been reported previously,¹⁶ however, the detailed atomic coordinates in the latter two polymorphs remain unclear.

Fig. 4 XRD patterns of as-prepared rubrene MCs: ribbons (curve 2), rhombic (curve 3) and hexagonal (curve 4) plates, compared with the calculated XRD of triclinic (curve 1), monoclinic (curve 5) and orthorhombic (curve 6) powders.

We cultivated bulk crystals by a solvent diffusion method at the interface between CH₂Cl₂ and MeOH. Two kinds of products, i.e., block- and plate-like crystals, are formed. Based on SCD analysis, they are attributed to monoclinic and triclinic phases, respectively. The crystallographic data of monoclinic and triclinic crystals are listed in Table 1. For comparison, the data of orthorhombic crystal reported by Jurchescu et al. is also included.¹⁵

Table 1 Crystallographic data and experimental details

	Monoclinic	Triclinic	Orthorhombic^a
a The data of orthorhombic crystal is reported by Jurchescu et al.^15
empirical formula	C42H28	C42H28	C42H28
Formula weight	532.64	532.64	532.68
Temperature (K)	173(2)	173(2)	150
Crystal system	monoclinic	triclinic	orthorhombic
Space group	P2(1)/c	P-1	Cmca
a (Å)	8.7397(17)	7.0196(14)	26.775(4)
b (Å)	10.125(2)	8.5432(17)	7.1680(10)
c (Å)	15.635(3)	11.948(2)	14.258(2)
Alpha(deg)	90	93.04(3)	90
Beta(deg)	90.98(3)	105.58(3)	90
Gamma(deg)	90	96.28(3)	90
Volume(Å^3)	1383.3(5)	683.5(2)	2736.4(7)
Z	2	1	4
Calculated density (Mg/m^3)	1.279	1.294	1.293
Crystal size (mm)	0.36 × 0.30 × 0.16	0.25 × 0.24 × 0.08	0.51 × 0.45 × 0.03

---

Returning to Fig. 4, it is clear that the ribbons are in triclinic crystal structure, while the rhombic and hexagonal plates belong to a monoclinic crystal phase. In the case of triclinic ribbon (curve 2), diffraction peaks corresponding to (001), (011̄)and (012) crystal planes are clearly observed, while other peaks in the simulated powder spectrum (curve 1) are missing. Combined with the SAED pattern in Fig. 1C, the preferential growth of 1D ribbon is determined to be along the [201̄]direction, which is the direction along a-axis in the triclinic crystal form. In the case of rhombic and hexagonal plates, their XRD patterns (curves 3 and 4) exhibit abundant peaks of monoclinic crystal. Among them, the predominate peak is (100) faces. The thickness of rhombic plates is generally above 1 µm, too thick to be suitable for electron diffraction experiments. The ED pattern in Fig. 3D is obtained from a thin hexagonal plate prepared at C = 8.8 mM, proving the edges of hexagonal plate must be bounded by (002)/(002̄), (011)/(01̄1̄), and (011̄)/(01̄1) faces, while the flat top/bottom surfaces must be bounded by (100)/(1̄00) faces, consistent with the XRD results. In our experiments, we also observed truncated rhombic plates at an intermediate condition of C = 5.0–6.0 mM (Fig. S2, ESI†), suggesting that the hexagonal plates originate from rhombus with truncation along [001].

Predicted morphology

Based on the calculated attachment energy by Materials Studio, we found that the predicted growth morphologies of triclinic/monoclinic crystals substantially coincide with the observed MC morphologies (Fig. 5). For the triclinic ribbons (Fig. 5B), the flat face of (001) is also the most-abundant face in prediction (Fig. 5A), and the preferential growth along a-axis is also the main stacking direction predicted. For the monoclinic crystals, the prediction morphology (Fig. 5C) remarkably matches with the observed plate-like morphology (Fig. 5D, E), and that the crystal is mainly bounded by (100), (011), (002) and their symmetric faces. These results reveal that the external morphologies of 1D ribbons and 2D plates are mainly governed by their crystal structures.

Fig. 5 (A) Predicted and (B) ribbon morphology of triclinic crystals. (C) Predicted, (D) rhombus, and (E) hexagon morphology of monoclinic crystals.

Besides, according to the calculation of Materials Studio (Table S1, ESI†), the lattice energy of monoclinic crystal is −107.9 kcal/mol with two molecules per unit cell, while the lattice energy of triclinic crystal is −50.9 kcal/mol with one molecule per unit cell. This means that the Gibbs energy of the monoclinic crystal is 107.9 − 50.9 × 2 = 6.1 kcal lower than the triclinic crystal every two mol of molecules. That is, the monoclinic crystal phase should be more thermodynamically stable than the triclinic phase.

Optical spectroscopic characterization

Fig. 6A displays the fluorescence excitation spectra. The slight shift between solution and MCs is similar to the results of absorption spectra (Fig. S3, ESI†). But for their emission spectra in Fig. 6B, different samples exhibit obvious distinctions. In solution, emission peaks with vibration structures¹⁰ locate at 560 nm (2.21 eV) and 598 nm (2.07 eV). For monoclinic rhombic and hexagonal plates, the emission peaks are 574 nm (2.16 eV) and 613 nm (2.02 eV). The energy gap of the two bands is consistent with the C–C stretching vibration,²¹ moreover, the excitation and fluorescence decays of the two bands are measured to be nearly the same (Fig. S5, ESI†), so these two emission bands should be vibronic bands. Comparing the emission from solution to monoclinic plates, the vibronic structure remained the same, the 0–0 band red shifted 14 nm, and the ratio of the 0–1 band decreased. For the triclinic ribbons, the emission is a little further red shifted to 577 nm, and becomes structureless. For comparison, we also detected the purchased rubrene powders, which were proved to be orthorhombic by XRD. The collected emission is a structurelss peak above 600 nm. In the literature, the emission of orthorhombic single crystals at room temperature is also dominated by peaks above 610 nm.^13,21,22 While the slight shift in absorption and excitation reveals weak intermolecular interactions of ground state in solid aggregation,¹³ the remarkable difference in PL spectra might reflect a substantial change of exciton activities during relaxation,²¹ in different rubrene solid samples.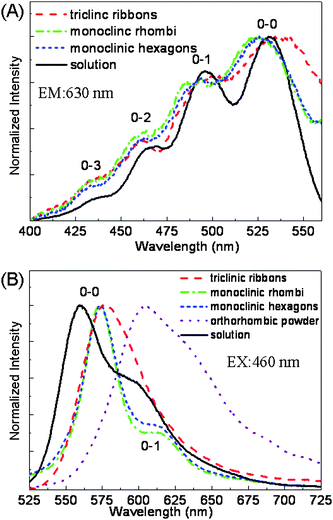

Fig. 6 (A) Normalized fluorescence excitation and (B) emission spectra of rubrene MCs: triclinic ribbons (dash line), monoclinic rhombic (dash dot line) and hexagonal (short dash line) plates, compared with that of rubrene solution (solid line) in chloroform (10⁻⁴ M) and purchased orthorhombic powder (dot line).

Fig. 7 exhibits the normalized fluorescence decays. Rubrene solution exhibits monoexponential decay with a lifetime of 13 ns. But for solid samples, the emission obviously follows multiexponential decay. While the emission bands of different time range are observed to be nearly the same, whether in peak position or in shape (Fig. S5, ESI†), the emissions must originate from the same emission species, what we have attributed to a vibration-resonated molecular exciton. The decay curves of solid samples were well fitted by three exponents, as listed in Table 2. Comparing their short-lifetime components, we found that orthorhombic powders have the fastest decay, 0.3 ns and 2.8 ns; triclinic ribbons follows, 0.4 ns and 3.1 ns; and monoclinic plates are the slowest, 0.8 ns and 4.9 ns. Probably, the short-lifetime components originate from the self-quenching phenomenon, which is a common and serious problem in solid-state aggregation for red-emissive materials.²³ Furthermore, Fig. S6 (ESI†) exhibits the closest molecular packing²⁴ of rubrene molecules in three crystal structures, proving that the intermolecular π–π stacking in monoclinic crystal is weaker than other two crystals. This might be the main reason for the changes in emission peaks and decay dynamics between monoclinic plates, triclinic ribbons, and purchased orthorhombic powders.

Table 2 Fitting results of fluorescence lifetime

	α1	τ1 (ns)	α2	τ2 (ns)	α3	τ3 (ns)
Solution						13.37
Orthorhombic powders	0.966	0.27	0.018	2.81	0.016	64.40
Triclinic ribbons	0.926	0.43	0.060	3.15	0.014	27.54
Monoclinic plates	0.925	0.85	0.059	4.90	0.015	20.15

---

Fig. 7 Normalized fluorescence decays of rubrene samples: triclinic ribbons (solid triangle), monoclinic plates (hollow triangle), orthorhombic powder (hollow circle) and solution in chloroform of 10⁻⁴ M (solid circle). The decays of monoclinic rhombic and hexagonal plates are nearly the same, so the data is labeled as monoclinic plates. The scatter spots are experimental data, and the black lines are corresponding fitted curves.

Shape-dependent waveguiding property

Fig. 8 shows the fluorescence microscopy images of rubrene MCs on glass substrates. Under the excitation of ultraviolet light, the MCs exhibit bright orange emission. In CCD, the ribbons show redder emission than plates, consistent with their emission spectra. (The emission spectra of single particles are also collected and found to be similar with that of ensemble samples in Fig. 6B.) At the ends of the ribbons, brighter luminescence spots are observed (Fig. 8A), showing 1D optical waveguides, and the crystals can absorb the excitation light and propagate the emission towards the tips. And for the rhombic (Fig. 8B) and hexagonal (Fig. 8C) plates, the emission is significantly brighter along the edges, revealing the light is propagating within the flat plane. Similarly, the 1D structure gives rise to the waveguide along the 1D direction, the 2D morphology of rubrene crystals shows a 2D optical waveguide that can trap light in the direction of the film thickness, but allow light to spread in the horizontal direction. The direction of optical propagation is successfully confined by the boundary of morphology.

Fig. 8 Fluorescence microscopy images of rubrene MCs: (A) ribbons, (B) rhombic and (C) hexagonal plates, with scale bar of 50 µm. Normalized emission spectra of micro area: (D) ribbons, (E) rhombic and (F) hexagonal plates, collected by NSOM from the laser spot (solid line) and the edge of particles (dash line) separately, while the laser is focused in the middle of the crystals. Insert: Dark-field PL images for single crystals by NSOM, with white scale bar of 10 µm.

Further spatially resolved photoluminescence experiment for single crystalline particles (Fig. 8D–F) confirm their self-guided property, while the laser beam excited only the central part of the particle and the luminescence emitted form the edges, several micrometres away from the illuminated region. As shown in Fig. 8D–F, the emission collected from the edge is a little red shifted than that of laser spot. It is similar to other observations,²⁵ and attributed to re-absorption of waveguided light during propagation. For the rhombic and hexagonal plates, the emission in laser spot shows a shoulder in 545 nm. The shoulder obviously separates from the series of vibronic structures, and locates at even higher energy than the 0–0 band of monomers in solution, which still can not be certainly classified.

Conclusively, similar to the reported waveguide properties of orthorhombic crystals,¹³ the direction of waveguiding propagation is always confined by the boundary of crystal morphology. But for different crystal phases, their emission spectra during propagation are distinct, just like their distinct PL emission in ensemble samples. Our work of controllable crystal phase and morphology of rubrene, enlarges its application on waveguide propagation, not only in different dimensions but also in different spectra areas.

4. Discussion

Kinetic control on nucleation and growth

In our experiment, we change the total volume of mixed solution and then change the final concentration of rubrene C. While the supersaturation can be defined as β = C/C₀, C₀ is the equilibrium concentration, which can be estimated from the optical density of the upper solution after reprecipitation according to the molar extinction coefficient of rubrene (ε = 9.5 × 10³).¹⁰ Variations of crystallography and morphology under different preparing conditions were summarized in Table 3.

Table 3 Summary of the crystallography and morphology control, when 50 µL 30 mM rubrene in chloroform was injected into different volume of methanol

V meOH(mL)	C(10^−3M)	C 0(10^−5M)	β = C/C0	Crystal form	Shape	Edge length (µm)
1.50	1.0	2.6	38	triclinic	ribbon	∼100
0.60	2.3	3.0	77	monoclinic	rhombus	22
0.50	2.7	3.3	82	monoclinic	rhombus	11
0.40	3.3	3.5	94	monoclinic	rhombus	5
0.16	7.1	4.2	169	monoclinic	hexagon	17
0.12	8.8	5.0	176	monoclinic	hexagon	10
0.10	10.0	5.5	182	monoclinic	hexagon	7

---

It can be seen from Table 3 that at relatively low supersaturation of β = 38, the products are triclinic; while at high supersaturation β ≥ 77, the crystals are monoclinic. The formation of different polymorphs as a function of supersaturation is widely observed.^5,26 Here, Fig. 9 draws an energy-reaction coordination diagram^5,9 for understanding the mechanism behind the formation of triclinic and monoclinic crystals at different values of β. The monoclinic crystal form has been calculated to be more thermodynamically stable, and we think the monoclinic crystal might have a higher nucleation barrier than a triclinic one. At low supersaturation, the triclinic phase is kinetically favored, because of the lower nucleation barrier. At high supersaturation, the driving force of the system is high enough to effectively form stable monoclinic nucleus, the products are preferred to be monoclinic crystals.

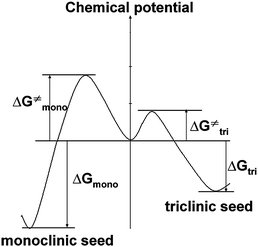Fig. 9 Schematic potential curves of nucleation to show the activated barriers and free energy of polymorphs: monoclinic and triclinic crystals.

As the supersaturation increases from β = 94 to β = 169, the morphology of monoclinic MCs undergoes the transformation from the rhombus to hexagon, revealing a relative shrinkage of growth along [001] at higher supersaturation. It is the supersaturation that influences the relative growth rates of different faces²⁷ and then modifies the shape of grown rubrene monoclinic crystals from rhombus to hexagon.

Furthermore, in a certain range, if the variation in supersaturation is not intensive enough to change the crystal phase of nucleation or the relative growth of crystal faces, the crystal form and the shape of rubrene MCs are maintained. But at higher concentration, there always exists larger numbers of initial nuclei,²⁸ so the grown MCs are generally of smaller size. The modification on crystals size by supersaturation is also shown in Table 3.

In previous reports, rubrene crystals were mainly orthorhombic crystals, prepared from thermal vapor.^12–15 But for the method of reprecipitation from solution routes, our products are triclinic and monoclinic MCs. The solution environment might influence the preferential molecule packing. Besides, the orthorhombic phase might be the most thermodynamic stable phase. During reprecipitation, the crystallization is finished within 2 hours, the nucleation and growth process is kinetically controlled, so the products are kinetically favored triclinic and monoclinic MCs.

5. Conclusions

In summary, a series of rubrene MCs, ranging from triclinic 1D ribbons to monoclinic 2D plates, have been prepared by employing the reprecipitation method. In our system, supersaturation plays the role of control factor in the kinetically dominated crystallization process, thus variation in supersaturation influences both the crystal form and the external morphology of grown crystals. Observed MC morphologies were found to be closely related to the predicted growth morphology, revealing that the different preferential growth in triclinic or monoclinic crystals might be responsible for the morphology change from 1D ribbons to 2D plates. Both emission spectra and decay dynamics clarify that 1D ribbons and 2D plates show distinct optical properties, probably related to their different solid-state structures in triclinic and monoclinic crystals. While as-prepared MCs show a similar self-waveguide property as the orthorhombic rubrene crystals, the confinement of 1D or 2D morphology leads to the confinement of propagation, so the ribbons show waveguiding along the 1D direction, and the plates in the 2D plane. Since waveguide materials, the main components in optical communication and integrated optical circuits, might totally change the current mode of networking and computing, our work of controllable crystallography and morphology of rubrene MCs might further exploit the potential of organic small molecules in optic and opto-electronic devices.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos. 90301010, 20373077, 90606004), the Chinese Academy of Sciences (“100 Talents” program), and the National Research Fund for Fundamental Key Project 973 (2006CB806200).

Notes and references

1. (a) N. Karl, Synth. Met., 2003, 133–134, 649; (b) A. R. Murphy and J. M. J. Fréchet, Chem. Rev., 2007, 107, 1066; (c) S. H. Liu, W. C. M. Wang, A. L. Briseno, S. C. E. Mannsfeld and Z. N. Bao, Adv. Mater., 2009, 21, 1217.
2. (a) J. Zyss and J. F. Nicoud, Curr. Opin. Solid State Mater. Sci., 1996, 1, 533; (b) D. Fichou, S. Delysse and J.-M. Nunzi, Adv. Mater., 1997, 9, 1178; (c) X. Zhu, D. Gindre, N. Mercier, P. Frére and J.-M. Nunzi, Adv. Mater., 2003, 15, 906; (d) M. Ichikawa, R. Hibino, M. Inoue, T. Haritani, S. Hotta, K. Araki, T. Koyama and Y. Taniguchi, Adv. Mater., 2005, 17, 2073.
3. (a) H. Yanagi and T. Morikawa, Appl. Phys. Lett., 1999, 75, 187; (b) I. D. W. Samuel and G. A. Turnbull, Chem. Rev., 2007, 107, 1272.
4. (a) M. D. Hollingsworth, Science, 2002, 295, 2410; (b) C. R. Newman, C. D. Frisbie, D. A. d. S. Filho, J.-L. Brédas, P. C. Ewbank and K. R. Mann, Chem. Mater., 2004, 16, 4436; (c) J. Chen, S. Subramanian, S. R. Parkin, M. Siegler, K. Gallup, C. Haughn, D. C. Martin and J. E. Anthony, J. Mater. Chem., 2008, 18, 1961; (d) E. M. CAlzado, J. M. Villalvilla, P. G. Boj, J. A. Quintana, R. Gómez, J. L. Segura and M. A. Diaz-Garsia, J. Phys. Chem. C, 2007, 111, 13595.
5. J. Bernstein, R. J. Davey and J.-O. Hench, Angew. Chem., Int. Ed., 1999, 38, 3440.
6. (a) H. Yoshida and N. Sato, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235205; (b) Y. L. Liu, Z. Y. Ji, Q. X. Tang, L. Jiang, H. X. Li, M. He, W. P. Hu, D. Q. Zhang, L. Jiang, X. K. Wang, C. Wang, Y. W. Liu and D. B. Zhu, Adv. Mater., 2005, 17, 2953; (c) H. X. Ji, J. S. Hu, L. J. Wan, Q. X. Tang and W. P. Hu, J. Mater. Chem., 2008, 18, 328.
7. Y. S. Zhao, H. B. Fu, A. D. Peng, Y. Ma, D. B. Xiao and J. N. Yao, Adv. Mater., 2008, 20, 2859.
8. (a) R. Ruiz, D. Choudhary, B. Nickel, T. Toccoli, K.-C. Chang, A. C. Mayer, P. Clancy, J. M. Blakely, R. L. Headrick, S. Iannotta and G. G. Malliaras, Chem. Mater., 2004, 16, 4497; (b) S. C. B. Mannsfeld, J. Locklin, C. Reese, M. E. Roberts, A. J. Lovinger and Z. N. Bao, Adv. Funct. Mater., 2007, 17, 1617.
9. G. R. Desiraju, Nat. Mater., 2002, 1, 77.
10. S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814.
11. (a) T.-H. Liu, C.-Y. Iou and C. H. Chen, Appl. Phys. Lett., 2003, 83, 5241; (b) L. Li, J. Yu, X. Tang, T. Wang, W. Li and Y. Jiang, J. Lumin., 2008, 128, 1783.
12. (a) V. C. Sundar, J. Zaumseil, V. Podzorov, E. Menard, R. L. Willett, T. Someya, M. E. Gershenson and J. A. Rogers, Science, 2004, 303, 1644; (b) V. Podzorov, E. Menard, A. Borissov, V. Kiryukhin, J. A. Rogers and M. E. Gershenson, Phys. Rev. Lett., 2004, 93, 086602.
13. S. Tavazzi, A. Borghesi, A. Papagni, P. Spearman, L. Silverstri, A. Yassar, A. Camposeo, M. Polo and D. Pisignano, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245416.
14. D. E. Henn, J. Appl. Crystallogr., 1971, 4, 256.
15. O. D. Jurchescu, A. Meetsma and T. T. M. Palstra, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 330.
16. (a) W. H. Taylor, Z. Kristallogr., 1936, 93, 151; (b) Z. A. Akopyan, R. L. Avoyan and Y. T. Struchkov, Z. Strukt. Khim., 1962, 3, 602.
17. Y. S. Wu, J. Li, X. C. Ai, L. M. Fu, J. P. Zhang, Y. Q. Fu, J. J. Zhou, L. Li and Z. S. Bo, J. Phys. Chem. A, 2007, 111, 11473.
18. Materials Studio, version 3.2, Accelrys Inc.: San Diego, CA, 2005.
19. D. Winn and M. F. Doherty, AIChE J., 2000, 46, 1348.
20. H. Sun, J. Phys. Chem. B, 1998, 102, 7338.
21. O. Mitrofanov, D. V. Lang, C. Kloc, J. M. Wikberg, T. Siegrist, W.-Y. So, M. A. Sergent and A. P. Ramirez, Phys. Rev. Lett., 2006, 97, 166601.
22. H. Najafov and I. Biaggio, Phys. Rev. Lett., 2006, 96, 056604.
23. X. H. Sheng, A. D. Peng, H. B. Fu, Y. Y. Liu, Y. S. Zhao, Y. Ma and J. N. Yao, Nanotechnology, 2007, 18, 145707.
24. D. A. d. S. Filho, E.-G. Kim and J.-L. Brédas, Adv. Mater., 2005, 17, 1072.
25. (a) K. Takazawa, Y. Kitahama, Y. Kimura and G. Kido, Nano Lett., 2005, 5, 1293; (b) Y. S. Zhao, A. D. Peng, H. B. Fu, Y. Ma and J. N. Yao, Adv. Mater., 2008, 20, 1661; (c) Y. S. Zhao, J. J. Xu, A. D. Peng, H. B. Fu, Y. Ma, L. Jiang and J. N. Yao, Angew. Chem., Int. Ed., 2008, 47, 7301; (d) H. Wang, Q. Liao, H. B. Fu, Y. Zeng, Z. W. Jiang, J. S. Ma and J. N. Yao, J. Mater. Chem., 2009, 19, 89.
26. (a) W. Beckmann, J. Cryst. Growth, 1999, 198–199, 1307; (b) S. Datta and D. J. W. Grant, Cryst. Res. Technol., 2005, 40, 233; (c) C. P. M. Roelands, S. Jiang, M. Kitamura, J. H. t. Horst, H. J. M. Kramer and P. J. Jansens, Cryst. Growth Des., 2006, 6, 955.
27. (a) S. X. M. Boerrigter, H. M. Cuppen, R. I. Ristic, J. N. Sherwood, P. Bennema and H. Meekes, Cryst. Growth Des., 2002, 2, 357; (b) M. A. Deij, E. Aret, S. X. M. Boerrigter, L. V. Meervelt, G. Deroover, H. Meeks and E. Vlieg, Langmuir, 2005, 21, 3831; (c) S. Piana, M. Reyhani and J. D. Gale, Nature, 2005, 438, 70.
28. R. B. Hammond, K. Pencheva and K. J. Roberts, Cryst. Growth Des., 2006, 6, 1324.

---

Footnote

† Electronic supplementary information (ESI) available: MALDI-TOF mass spectra of as-prepared rubrene crystals; SEM of truncated rhombic plates; absorption spectra of smashed rubrene crystals; excitation spectra and fluorescence decay near 560 nm and 630 nm; spectral snapshots of different time range; closest molecule packing in different crystals; calculated lattice energy. CCDC reference numbers 726175, 726176. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/b914334c

---