Equivalence versus classical statistical tests in water quality assessments

Abstract

To evaluate whether two unattended field organic carbon instruments could provide data comparable to laboratory-generated data, we needed a practical assessment. Null hypothesis statistical testing (NHST) is commonly utilized for such evaluations in environmental assessments, but researchers in other disciplines have identified weaknesses that may limit NHST's usefulness. For example, in NHST, large sample sizes change p-values and a statistically significant result can be obtained by merely increasing the sample size. In addition, p-values can indicate that observed results are statistically significantly different, but in reality the differences could be trivial in magnitude. Equivalence tests, on the other hand, allow the investigator to incorporate decision criteria that have practical relevance to the study. In this paper, we demonstrate the potential use of equivalence tests as an alternative to NHST. We first compare data between the two field instruments, and then compare the field instruments' data to laboratory-generated data using both NHST and equivalence tests. NHST indicated that the data between the two field instruments and the data between the field instruments and the laboratory were significantly different. Equivalence tests showed that the data were equivalent because they fell within a pre-determined equivalence interval based on our knowledge of laboratory precision. We conclude that equivalence tests provide more useful comparisons and interpretation of water quality data than NHST and should be more widely used in similar environmental assessments.

---

Environmental impact

Environmental research is generally conducted to understand an issue of concern. Such research requires collection, analysis and interpretation of data about the issue. Currently, the majority of environmental data are evaluated using classical statistics which utilize p-values as the standard criterion to indicate significance of the research findings. In this paper, we present equivalence statistical tests as better alternatives to p-values in evaluating an environmental water quality assessment issue. We posit that other environmental issues would benefit from data interpretations that incorporate the practical importance of the research findings. We conclude that equivalence tests offer an alternative to classical statistics' p-values in evaluating whether research findings are or are not of practical importance in understanding any environmental problem.

Introduction

Historically, most water quality data have been interpreted using the null hypothesis statistical tests (NHST). The procedure tests a “null” hypothesis—that differences between treatments are zero—and an alternative hypothesis—that differences are statistically significant. Examples are t-tests, analysis of variance, regression analysis, trend analysis, etc. as well as their nonparametric counterparts. Consider a study of two treatments, A and B. In its most basic form, NHST postulates a null hypothesis (H₀) that there are no differences between A and B and an alternative hypothesis (H_a) that A and B are statistically significantly different at a given significance level (α, usually 0.05 by convention). Then a probability (p) is calculated which is commonly believed to provide evidence that the observed differences are or are not due to chance.

An equivalence test, on the other hand, evaluates whether treatments A and B are close enough to be considered similar. The investigator sets a benchmark, then uses prior knowledge or belief to define a region around the benchmark (equivalence interval) within which the investigator has decided that the difference is unimportant (possibly because the difference falls in a range that is considered trivial). The equivalence interval has to be set a priori. Detailed descriptions of the development and theory of different approaches for testing equivalency are available in the literature.^1–5 One can test for the null hypothesis that 2 (or more treatments) are inequivalent or for the alternative hypothesis that they are equivalent, thereby reversing the traditional tests. This shifts the burden of proof to demonstrating that what is being tested (e.g., water quality) meets certain criteria.

Equivalence tests have been most widely used in pharmacology for approval of generic drugs since 1984.⁶ Before a generic drug is approved, clinical trials have to demonstrate therapeutic equivalence (bioequivalence) to the reference formulation using 20% limits. Equivalence tests have not been widely adopted in environmental studies although their use has been advocated.^7,8

The following equations and discussion explain NHST and its weaknesses:

H₀: A − B = 0 (i.e., A = B) (1)

H_a: A − B ≠ 0 (i.e., A − B < 0 or A − B > 0) (2)

where H₀ is the null hypothesis and H_a is the alternative hypothesis indicating statistically significant differences.

In the above example, if the calculated p is less than 0.05, the H₀ is rejected. The conclusion is that treatments A and B are statistically significantly different at the calculated α level. This is often dismissed by NHST critics. For example, Kirk⁹ stated, “In scientific inference, what we want to know is the probability that the null hypothesis (H₀) is true given that we have obtained a set of data (D); that is, p(H₀|D). What null hypothesis significance testing tells us is the probability of obtaining these data or more extreme data if the null hypothesis is true, p(D|H₀).” In other words, the H₀ infers about (more extreme) data that were never collected.

When compared to other disciplines over the last 70 years, water quality assessments contain few discussions critical of NHST.^10–17 Harlow et al.¹⁸ summarize NHST arguments (for and against). These criticisms of NHST are pertinent to environmental assessments because large sample size can increase statistical significance and a statistically significant result is not necessarily of practical significance.

The following are the main criticisms of NHST in other disciplines:

(1) The basic premise of NHST where the difference between treatments (or whatever is being tested) is assumed to be zero (i.e., H₀: µ₁ − µ₂ = 0) is unrealistic. As Tukey¹⁹ put it, “All we know about the world teaches us that the effects of A and B are always different—in some decimal place—for any A and B.” Some null hypothesis tests have been termed “gratuitous significance testing,” i.e., using statistical significance testing for what is readily obvious or is already known.²⁰ An example from literature is given by Johnson²¹ where a statistically significant test was reported that “the density of large trees was greater in unlogged forest stands than in logged stands (p = 0.02).”

(2) The p-value is arbitrary. Statistical significance has been shown to increase with sample size, i.e., p-value gets smaller as sample size gets larger.^16,22,23 A possible solution is to predetermine a sample size that prevents the test from becoming too powerful. However, this approach is not feasible in long-term environmental monitoring programs where accumulation of data is unavoidable and is actually the main objective.

(3) A statistically significant result does not necessarily indicate magnitude of effect or practical importance.^9,24 In the social sciences, some efforts provide a measure of the practical significance of a statistically significant result using “effect sizes” to indicate the practical importance of the results.^11,16,25 However, these interpretational approaches are largely absent from environmental literature where a small statistically significant p-value is still the gold standard in interpreting research findings.

In this paper, we demonstrate the potential use of equivalence tests as an alternative to NHST in environmental assessments. We present equivalence tests from a practitioner's point of view. In our study, we use organic carbon (OC) data generated by two online field OC instruments each using a different analytical method. We compare a subset of the field instruments' data to grab sample results analyzed in the laboratory. The first objective is to determine if the two field instruments' data are comparable. The second objective is to determine if the two field instruments' data are of comparable precision quality to laboratory-generated data. We will discuss why equivalence tests more than NHST provide more practical interpretation of the data to answer the above objectives.

Materials

The California Department of Water Resources (DWR) has been collecting biweekly OC grab samples and analyzing them at its accredited Bryte Chemical Laboratory (Bryte Lab) since the 1980s. The Sacramento River at Hood station (Hood, 38.382°N, 121.519°W) is about 25 km from DWR's Sacramento headquarters and was established in 1998 to provide a platform for collecting grab samples and to support a secure enclosure for evaluating advanced analytical instruments for online field monitoring of water quality. The platform is approximately 15 meters from the river's bank and 9 meters above the water surface (Fig. 1). Water quality analytical instruments are secured in an air-conditioned wood enclosure affixed on top a steel frame structure. A submersible pump located approximately 1 meter below the Sacramento River surface delivers sample water to the instruments through approximately 21 meters of pressurized (69 kPa maximum) Teflon hoses. The Sacramento River drains a watershed approximately 70 000 km² in size and provides 75% of the freshwater inflows into the Sacramento River-San Joaquin River Delta, the largest estuary on the western coast of the Americas. The estuary is a source of drinking water for about 26 million Californians. It also provides irrigation water to the largest agricultural business in the United States and provides habitat to numerous endangered aquatic organisms. OC is an important constituent in water. During drinking water treatment, OC reacts with disinfectants to form potentially carcinogenic byproducts. OC is an important factor in the fate and transport of pesticides in soil and water and plays a role in climate change through carbon sequestration from air to soil.

Fig. 1 The Sacramento River at Hood station (Hood, 38.382°N, 121.519°W) was established in 1998 to provide a platform for collecting grab samples and to support a secure enclosure for evaluating advanced analytical instruments for online field monitoring of water quality.

A Sievers 800 laboratory-grade OC analyzer (GE Analytical Instruments, Boulder, CO) using ultraviolet (UV) persulfate chemical oxidation analytical method was installed in 1999. A Shimadzu 4100 OC analyzer (Shimadzu Scientific Instruments, Columbia, MD) using high temperature catalytic combustion oxidation (HTC) analytical method was installed in April 2002 to run in tandem with the Sievers 800 (Fig. 2). The two analytical methods are described in Standard Methods.²⁶ The United States Environmental Protection Program (USEPA) has comparable analytical methods. The equivalent USEPA method is 415.3.²⁷ This method describes both HTC and oxidation in the analysis of OC. The Sievers 800 was replaced with a new Sievers 900 instrument in May 2005. (Although the 900 has upgraded hardware and software, its mode of operation is similar to the 800; the data from the two models are not separated in the data analyses in this paper). We use OC collected by the two instruments between April 2002 and April 2007 to demonstrate potential use of equivalence tests over NHST in water quality analysis.

Fig. 2 A Shimadzu 4100 OC analyzer using high temperature catalytic combustion oxidation method runs in tandem with a Sievers 800 organic carbon analyzer using ultraviolet persulfate chemical oxidation method.

The instruments were calibrated and maintained to manufacturers' specifications by DWR field support staff. A Campbell Scientific CR10X data logger (Campbell Scientific, North Logan, Utah) controlled the analytical frequencies and also temporarily stored the OC data. The data were uploaded every two hours by phone modem to the online California Data Exchange Center (CDEC) website (http://cdec.water.ca.gov). The station name is “srh.” Sievers is sensor 101, and Shimadzu TOC is sensor 112.

Methods

From CDEC we downloaded Sievers and Shimadzu OC raw data between April 2002 and April 2007 (the study period) to calculate daily and weekly means and standard deviations. To ensure that each instrument was operational at least 2 hours every day, we removed OC daily data where there were fewer than six individual analyses in any 24-hour period. This procedure eliminated eight Shimadzu and no Sievers daily records. The remaining data represented 1665 dates when both instruments were operational (approximately 95% of the days in the study period). Biweekly and monthly grab samples are still collected (depending on a specific special project) at the Hood station and analyzed at Bryte Lab using an OI Analytical 1010 organic carbon analyzer (OI Analytical, College Station, Texas, USA). The OI 1010 uses chemical oxidation analytical method.

Statistical analyses

We used Minitab Release 15 (Minitab, State College, PA) for all the statistical analyses.

The paired t-test is the standard method (in NHST) for comparing two groups of paired data.²⁸ The Kruskal–Wallis (K-W) analysis of variance (ANOVA) test is one of the options available in NHST for testing more than two sets of data. We used both of these tests for the NHST analyses.

Paired t-test of Sievers versus Shimadzu OC daily average data. First, we performed a paired t-test on the 1665 pairs of daily means of Sievers and Shimadzu OC data. The t-test (α = 0.05) used the customary null hypothesis that there was no difference between Shimadzu and Sievers daily OC means. The alternative hypothesis was that they were statistically significantly different.

Paired equivalence test of Sievers versus Shimadzu OC data. We tested for equivalency using macros written for Minitab 15 statistical software.²⁹ The first macro was analogous to the classical paired t-test and evaluated equivalency using 2 one-sided tests (TOST) on the 1665 pairs of daily means. Each one-sided test (of the TOST) was a t-test (α = 0.05). We set the equivalence interval at 20% using Sievers as the benchmark, which then determined the lower and upper limits of the equivalence interval for Shimadzu data to be equivalent to Sievers data. We selected 20% based on historical precision studies of laboratory OC instruments. Laboratory duplicate analyses of OC in drinking water are considered to be within acceptable limits if their differences are equal to, or less than, 20%. We designated the lower limit (θ₁) as 20% below and the upper limit (θ₂) as 20% above Sievers overall mean. The TOST as described in this paper, assume that sample data are normally distributed (i.e., that they follow a Gaussian distribution). Common tests of normality such as Anderson–Joiner or Shapiro–Wilk are affected by large sample sizes (defined here as n > 70) in the same manner as other classical statistical tests. Thus, testing a large sample size will result in a finding that the data are not normally distributed. We suggest a number of ways to evaluate whether the data are approximately normal. The simplest approaches are to use visual aids such as boxplots or probability plots to provide a graphical view whether the data are skewed or not. If the data are skewed, the logarithmic transformation is probably the most common method in environmental studies to attempt to bring such data to normal distribution. Bootstrapping is an advanced method that can be utilized to generate confidence intervals for the TOST. The method involves sampling (with replacement) the data set to develop the statistics needed to create the confidence intervals, and it does not assume normality of the underlying data. Finally, one can simply invoke the Central Limit Theorem when dealing with large datasets. Simply stated, the theorem postulates that the averages of a large number of independent observations will be normally distributed. In this paper we had over 1000 daily averages (our definition of a large sample size), and we invoked the Central Limit Theorem for purposes of normality.

The macro procedure worked as follows:

Suppose that d̄ was the overall mean difference between the 1665 pairs of Shimadzu and Sievers OC daily average results. The first part of the TOST performed the following hypothesis tests (α = 0.05):

H₀₁: d̄ ≤ θ₁ (3)

H_a1: d̄ > θ₁ (4)

where H₀₁ was the null hypothesis and H_a1 was the alternative hypothesis in the first t-test of the TOST.

The second part of the TOST performed the following hypothesis tests (α = 0.05):

H₀₂: d̄ ≥ θ₂ (5)

H_a2: d̄ < θ₂ (6)

where H₀₂ was the null hypothesis, and H_a2 the alternative hypothesis in the second t-test of the TOST. The macro calculated the t-tests based on methods described by McBride.⁷

Note that in the above procedures (equations 3–6), we were testing the null hypothesis of inequivalence (i.e., the null hypotheses that Shimadzu OC data were not equivalent to Sievers OC data). Shimadzu OC data were equivalent to Sievers OC data only when:

θ₁ < d̄ < θ₂ (7)

If (7) was true, we would conclude that Shimadzu data were equivalent to Sievers OC data.

The TOST is identical to testing whether the 90% confidence interval around d̄ (calculated using 1 − 2α) is entirely contained within the equivalence interval. If equivalence is found to be true in the TOST, the confidence interval must be completely contained within the equivalence interval.^4,30 If any of the null hypotheses was true, the two instruments' data were not equivalent.

Multiple NHST of Sievers, Shimadzu, and Bryte Lab data. We selected Sievers and Shimadzu daily OC averages on the dates that a grab sample from Hood station had been analyzed by Bryte Lab. This resulted in 169 days that had data points for all three instruments. Due to expected autocorrelations of river sample data collected within 24 hours of each other, we considered these 169 to be essentially replicate samples. We used K-W to compare Sievers, Shimadzu, and Bryte Lab data. We then followed with a K-W multiple comparisons test to determine which instrument's data were different from each other. The multiple comparison tests used a Bonferroni adjustment by dividing the alpha level by the number of pairwise comparisons to keep the family error rate at 0.05%.

Multiple equivalence comparisons of Sievers, Shimadzu, and Bryte Lab OC data. We used a second macro to perform multiple equivalence paired comparisons of Sievers, Shimadzu, and Bryte Lab OC data (n = 169). Each paired comparison was essentially the same TOST as before. A Bonferroni adjustment kept the family-wise error rate at 0.05%.

Results

NHST versus equivalence comparisons of paired Sievers and Shimadzu results

The paired t-test indicated that Shimadzu and Sievers daily average field data were statistically significantly different (p < 0.01, n = 1665). On the other hand, the paired equivalence test showed that Shimadzu data were equivalent to Sievers data. Fig. 3 is a graphical output of the classical paired t-test and the equivalence interval test. Fig. 3 shows that the 90% confidence interval for the mean difference between Sievers and Shimadzu OC data was completely contained within the Sievers equivalence interval. Thus, the two instruments' OC data were equivalent.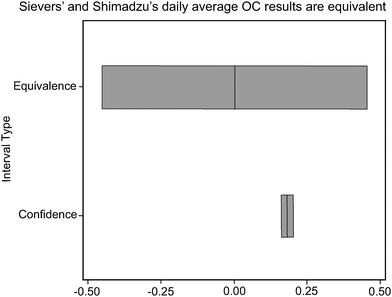

Fig. 3 Sievers and Shimadzu daily average organic carbon results are equivalent.

NHST multiple comparisons of Sievers, Shimadzu, and Bryte Lab OC data

The K-W analysis of variance indicated significant differences (p < 0.01, n = 169) between the 3 instruments' OC data. The K-W multiple comparisons test determined which instruments' results were significantly different from each other. Fig. 4 is a graphical representation of the multiple comparisons. The dotted line (−z to z) denotes the interval outside of which paired differences were statistically significantly different. Shimadzu results were statistically significantly different from both Sievers and Bryte Lab OC data.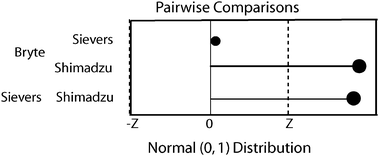

Fig. 4 Kruskal–Wallis pairwise comparisons between instruments. The dotted lines (−z, z) denote the interval outside of which paired differences were statistically significantly different.

Equivalence multiple comparisons of Sievers, Shimadzu, and Bryte Lab OC data

Equivalence multiple comparisons of Sievers, Shimadzu, and Bryte Lab data are graphically shown in Fig 5. The 90% confidence interval limits between all paired differences are within the 20% equivalence interval. Thus Sievers, Shimadzu, and Bryte Lab OC data were all equivalent.

Fig. 5 The confidence interval limits between all paired differences are within the 20% equivalence interval (dotted line); thus Sievers, Shimadzu, and Bryte Lab OC data were all equivalent. We consider the deviations between the instruments to be expected reproducibility differences since all the confidence intervals are contained in the equivalence interval.

Discussion

NHST versus equivalence tests

Because of the large sample size, we were not surprised that the paired t-test indicated that OC results from the two field instruments' data were statistically significantly different from each other, while the equivalence test showed they were equivalent. The same applies to the K-W results indicating significant differences between the field instruments' data and the Bryte Lab data. In large sample sizes, small, sometimes razor-thin non-zero differences will be found to be statistically significant because the calculated p-values become increasingly smaller. For this reason, experimental results can be statistically significantly different but statistically equivalent. Several potential outcomes are possible when NHST methods are compared to equivalence tests in the analysis of a data set: (a) results are statistically significantly different and are not equivalent; (b) results are not statistically significantly different but they are equivalent; (c) results are statistically significantly different and equivalent; and (d) results are not statistically significantly different and are not equivalent.^30,31 Therefore, except for demonstration purposes (as in this paper), it is futile to use both approaches to analyze the same set of data. The very basis for using equivalence tests is to get away from null hypothesis of zero difference.

This study contained a lot of data—more than 1000 OC data pairs. Thus the paired t-test would be likely to detect small negligible differences between the two instruments as statistically significant. High frequency data may present serial correlation problems when used for time series or trend analysis. In method or instrument comparisons a major goal is to block for inter-sample differences, i.e., to keep the aliquots of the replicate samples analyzed in a round-robin study of different classes of instruments as uniform as possible. So we did not consider serial correlation to be an issue in our study. The equivalence test is the appropriate test in this study because we were not interested in small statistically significant differences but in differences of practical significance, i.e., whether two unattended field instruments using different analytical methods can provide data comparable in quality to laboratory-generated results. The equivalence tests demonstrated that the field UV persulfate oxidation and the HTC oxidation generated comparable data to each other at Hood station. Both instruments' data were of equivalent quality to laboratory-generated results. An advantage of using field instruments is that they can generate high frequency data at significantly lower cost compared to laboratory-analyzed data. In addition, the field instruments provide data in near real time; whereas, laboratory analysis of grab samples may take several weeks.

Equivalence tests offer good alternative to tests of significance in environmental assessments because they allow the investigator to incorporate decision criteria that have practical relevance to the study. Most environmental research projects are funded to find a solution to one or more practical problems. It is therefore desirable to use a data analysis technique that can readily indicate the magnitude and/or practical importance of the study results to the project's objectives. In this study, it was logical to use a precision criterion comparable to laboratory duplicate analysis. We were interested in evaluating whether the unattended field instruments could provide data comparable to accepted laboratory quality standards. Equivalence tests provided the mechanism to make these kinds of comparisons. If equivalence tests are preferred in determining the effectiveness of generic drugs for humans, it is our opinion that equivalence tests should be good enough for environmental assessments.

A potential difficulty in using equivalence tests is objectively determining the equivalence interval. Environmental research historically has relied on statistical significance testing for decision-making and does not have a track record of defining quantitative criteria to indicate practical significance of statistically significant test results. Exceptions are where limits are set by a regulatory agency. Practitioners have a number of options to determine a difference of practical significance.³² The first and most straightforward is defining equivalence intervals empirically such as using a regulatory limit (as is the case with generic drugs) or using calculations from previous research. In this paper we set the equivalence interval using our knowledge of laboratory precision of OC analyses, which was an empirical approach. A second approach to constructing the equivalence interval is soliciting (or eliciting) opinions from experts in the area of interest. This approach is more complex than the empirical approach, but in many environmental situations, it may be the only viable alternative.

Conclusions

This study investigated the viability of using laboratory-grade OC instruments for field monitoring of water quality. Our determination that the field instruments' OC data were comparable in precision to laboratory data was made through equivalence testing. We suggest that equivalence tests provide more useful comparisons and interpretation of water quality data than the widely used classical NHST. Equivalence testing would work well in other environmental assessments by requiring such studies to establish a measure of the importance of the results rather than arbitrary p-values.

Acknowledgements

We thank DWR for funding this project. We thank Marilee Talley for technical review of this paper. We thank the many reviewers within and outside DWR who provided useful comments on how to improve the paper.

References

1. S. Anderson and W. W. Hauck, Communications in Statistics - Theory and Methods, 1983, 12, 2663–2692.
2. C. W. Dunnett and M. Gent, Biometrics, 1977, 33, 593–602.
3. M. R. Selwyn, A. P. Dempster and N. R. Hall, Biometrics, 1981, 37, 11–21.
4. W. J. Westlake, Biometrics, 1976, 32, 741–744.
5. W. J. Westlake, Biometrics, 1981, 37, 591–593.
6. FDA, US Department of Health and Human Services, Food and Drug Administration, Center for Drug Evaluation and Research, Office of Pharmaceutical Science, Office of Generic Drugs, 28th edn., 2008, vol. 2008.
7. G. B. McBride, Austral. & New Zealand J. Statist., 1999, 41, 19–29.
8. G. B. McBride, Using statistical methods for water quality management: issues, problems and solutions, John Wiley, Hoboken, N.J., 2005.
9. R. E. Kirk, Educ. Psychol. Meas., 1996, 56, 746–759.
10. J. Berkson, J. Am. Stat. Assoc., 1938, 33, 526–536.
11. R. P. Carver, Harvard Educational Review, 1978, 48, 378–399.
12. J. Cohen, American Psychologist., 1990, 44, 1304–1312.
13. S. J. Evans, P. Mills and J. Dawson, Heart, 1988, 60, 177–180.
14. S. N. Goodman, American Journal of Epidemiology, 1993, 137, 485–496.
15. J. L. Hodges, Jr. and E. L. Lehmann, Journal of the Royal Statistical Society. Series B (Methodological), 1954, 16, 261–268.
16. R. Hubbard and R. M. Lindsay, Theory & Psychology, 2008, 18, 69–88.
17. W. W. Rozeboom, Psychol. Bull., 1960, 57, 416–428.
18. L. L. Harlow, S. A. Mulaik and J. H. Steiger, What if there were no significance tests?, Lawrence Erlbaum Associates Publishers, Mahwah, N.J., 1997.
19. J. W. Tukey, Stat. Sci., 1991, 6, 100–116.
20. R. P. Abelson, in Multivariate applications book series., ed. S. A. M. Lisa L. Harlow, James H. Steiger., Lawrence Erlbaum Associates Publishers, Mahwah, N.J., 1997, pp. 117–141.
21. D. H. Johnson, Journal of Wildlife Management, 1999, 63, 763–772.
22. J. Berkson, J. Am. Stat. Assoc., 1942, 37, 325–335.
23. R. M. Royall, Am. Stat., 1986, 40, 313–315.
24. R. P. Carver, Journal of Experimental Education, 1993, 61, 287–292.
25. J. Cohen, Statistical power analysis for the behavioral sciences, 2nd edn., L. Erlbaum Associates, Hillsdale, N.J., 1988.
26. WEF/AWWA/APHA, Standard Methods for the Examination of Water and Wastewater, 20th edn., Washington, DC, 1998.
27. USEPA. Method 415.3-1: Determination of Total Organic Carbon and Specific UV Absorbance at 254 nm in Source Water And Drinking Water. EPA Document #: EPA/600/R-05/055. Cincinnati, OH: USEPA. 2005.
28. D. R. Helsel and R. M. Hirsch, U.S. Geological Survey, Reston, Va., 2002.
29. D. Helsel and E. Gilroy, http://www.practicalstats.com/ 2008.
30. J. L. Rogers, K. I. Howard and J. T. Vessey, Psychol. Bull., 1993, 113, 553–565.
31. D. J. Schuirmann, J. Pharmacokinet. Biopharm., 1987, 15, 657–680.
32. L. J. Wolfson, J. B. Kadane and M. J. Small, Ecol. Appl., 1996, 6, 1056–1066.

---

Footnotes

† Part of a themed issue dealing with water and water related issues.

‡ Electronic supplementary information (ESI) available: Bryte Lab quality control and accreditation details. See DOI: 10.1039/b912098j

---