Theoretical study of H₂ splitting and storage by boron–nitrogen-based systems: a bimolecular case and some qualitative aspects

Abstract

The experimentally observed reversible hydrogen activation reaction by trans-2,6-dimethyl-2,6-diphenylpiperidine and B(C₆F₅)₃ is modeled at RI-SCS-MP2/aug-cc-pVTZ//B3LYP/6-31G* level. A Morokuma analysis is performed for the transition state and for the product to study the energy contributions. The role of solvent effects, and substitution of ligands is discussed. Some more general points are made on ‘frustration’ (meaning the prevention of B–N bond formation by bulky ligands) and ‘Coulomb pays for Heitler–London’ (meaning that the attraction between the product counterions is comparable with the homolytic splitting energy of H₂). Both ideas refer to hypothetical deviations from the experimental route. A simple NH₃ + H₂ + BH₃ ↔ (NH⁺₄)(BH⁻₄) model reaction is used to estimate the frustration energy and to locate the ionic/covalent crossings of this ‘bimolecular’ model. The ionic structures are stabilised further in oligomers (and crystals), a phenomenon termed as ‘collective Madelung ionisation’ (CMI) and illustrated by a [(NH⁺₄)(BH⁻₄)]₄ tetramer.

---

1. Introduction

The splitting and storage of H₂ is of current interest. A boron–phosphorus-based system was recently synthesised by the group of Stephan.¹ They also suggested, as a contributing factor, a sterically imposed ‘frustration’ against the formation of a B–P covalent bond.^2,3 For the current situation on such ‘frustrated Lewis pairs’ (FLP), see Stephan.⁴ This idea received theoretical support from the group of Pápai.⁵ For related work on the reduction of imines and the effects of ligands, see Rokob et al.^6,7 and Privalov.^8,9

We recently reported the synthesis and theoretical calculation of a monomolecular, boron–nitrogen compound N-TMPN-CH₂C₆H₄B(C₆F₅)₂1, that also reversibly adsorbs hydrogen. Here TMPN = 2,2,6,6-tetramethylpiperidine and ‘N-’ indicates the site of attaching a ligand. Around 110 °C the hydrogen is recovered.^10,11 In the hydrogen-loaded 1 + H₂ → 2, the experimental, X-ray B–N distance was 336 pm.¹⁰ In the same paper we suggested as a further driving force that ‘Coulomb pays for Heitler–London’ (CHL). At such a typical interionic distance of the zwitterion, the Coulomb attraction between the cation and the anion is comparable to the ‘homolytic’ (H₂ → 2H) dissociation energy. (The ‘heterolytic’, H₂ → H⁺ + H⁻ dissociation energy would be much larger.) This ‘ionicity idea’ was verified using a Born–Haber cycle for a split model system. Parenthetically, it should be added that ion-pairing as such is well-known in chemistry.¹² Its effects on H₂ splitting were possibly new.

We also pointed out that, compared to the H₂ dissociation energy of 432 kJ mol⁻¹, the energies due to N–H⋯H–B ‘dihydrogen bonds’ (DHB),^13–15 if defined between neutral fragments, would be much smaller. Therefore it is not evident that the hydrogen⋯hydrogen interactions would be relevant. Moreover, it should be noticed that one new N–H and one new B–H bond are created upon the splitting of the H–H bond.¹⁶

As to the potential use of these compounds, it may mainly be as hydrogenation reagents, where the low H₂ weight percentage and high synthetic costs will not matter. As such, the ΔG and release temperature of these compounds would also suit hydrogen storage applications.

More recently, Sumerin et al.¹¹ obtained a similar, reversible H₂ activation reaction by a bimolecular B–N system, trans-2,6-dimethyl-2,6-diphenylpiperidine 3 and B(C₆F₅)₃4. Since the hydrogen atoms of the split H₂ are now bound to two separate fragments in the product, one on the boron side, and the other on the nitrogen side, a Morokuma energy decomposition analysis will be straightforward compared with the previous monomolecular case, where a hypothetical bimolecular model had to be used. Therefore we here consider the new, experimental bimolecular system. A Born–Haber cycle is also constructed for the product, in order to clarify the role of the new B–H and N–H bonds.

We further introduce a simple model for comparing these views, including the FLP and CHL ideas. The simplest tool chosen is the model system

H₃N + H₂ + BH₃ ↔ (NH₄)⁺(BH₄)⁻ (1)

with the rest of the molecule mimicked by geometrical constraints. Estimates for the frustration and Coulomb energies are given.

2. Methods

The calculations were performed using density functional theory (DFT) with the B3LYP^17–22 exchange–correlation functional and the spin-component-scaled Møller–Plesset second-order perturbation theory²³ with the resolution-of-identity^24,25 approximation (RI-SCS-MP2). The core electrons were left uncorrelated during all RI-SCS-MP2 calculations. The Pople double-ζ split-valence plus polarisation function basis set, 6-31G*^26–28 and the Dunning augmented correlation-consistent triple-ζ basis set, aug-cc-pVTZ²⁹ were employed. The basis set superposition error (BSSE) was corrected by the counterpoise method for the supermolecular RI-SCS-MP2 calculations.^30,31 The B3LYP calculations were done by the Gaussian 03 program package, revision E.01³² and the RI-SCS-MP2 ones with the Turbomole 6.0 program package.³³ The transition state was confirmed by an internal reaction coordinate (IRC) scan.^34,35 The polarized continuum model (PCM)³⁶ was used to estimate solvent effects, and a natural bond orbital (NBO)³⁷ analysis was performed for atomic charges. These were calculated using the Gaussian 09 program package, revision A.1.³⁸ In addition, a Morokuma energy analysis³⁹ was performed using the ADF 2008 program package⁴⁰ with an augmented triple-zeta polarised Slater type basis (ATZP).^41,42 The PBE⁴³ and M06-2X⁴⁴ functionals were also used to test the geometry optimisation for the product 8.

The Gibbs free energies were calculated in the RRHO (rigid-rotor harmonic-oscillator) approximation.

3. Results

3.1 The new, bimolecular system

A new bimolecular boron–nitrogen system was recently synthesised from trans-2,6-dimethyl-2,6-diphenylpiperidine, NC₁₉H₂₃, 3, and B(C₆F₅)₃, 4, in our Department by Sumerin et al.¹¹ We now treat it at the RI-SCS-MP2/aug-cc-pVTZ//B3LYP/6-31G* level in gas phase (without solvent potentials). The notation A//B means a single-point energy at level A, after a structural optimisation at level B. The solvent effect is estimated later at B3LYP/6-31G* level with solvent parameters corresponding to benzene. It lowers the Gibbs free energy of the kinetic barrier by 1.4 kJ mol⁻¹ and that of the whole reaction by 20.3 kJ mol⁻¹. This may be interpreted as an ionic effect. As the product consists of a cation and an anion, each of them will polarise the solvent, while at the transition state the fragments still stay neutral. Notice that in the experiment there will be Coulomb interactions among all the cations and anions of the system, while our simulation only considers one ion pair in benzene. Higher-order effects of Debye–Hückel type are not considered.

The computed reaction mechanism is shown in the Fig. 1. The molecules 3 and 4 first form a hydrogen bonded N–H⋯F(–C) intermediate complex 5 with an R(H⋯F) of 246.4 pm. A similar complex was also found by Rokob et al. in their boron–phosphorus system.⁵ However, the finite-temperature effects arising from entropy will produce a positive Gibbs free energy contribution at 298 K. The role of fluorination is to increase the electronegativity of borane. As one can see in Fig. 2 and Table 1, B(C₆F₅)₃ has a much larger hydride affinity of 501 kJ mol⁻¹ than BH₃ (310 kJ mol⁻¹). Similarly, the NC₁₉H₂₃ has a higher proton affinity of 1029 kJ mol⁻¹ than NH₃ (854 kJ mol⁻¹), due to the alkyl groups.

Fig. 1 The computational reaction mechanism for the experimental, ‘bimolecular’ hydrogen splitting reaction. The lines stand for the electronic energy, E, without solvent corrections.

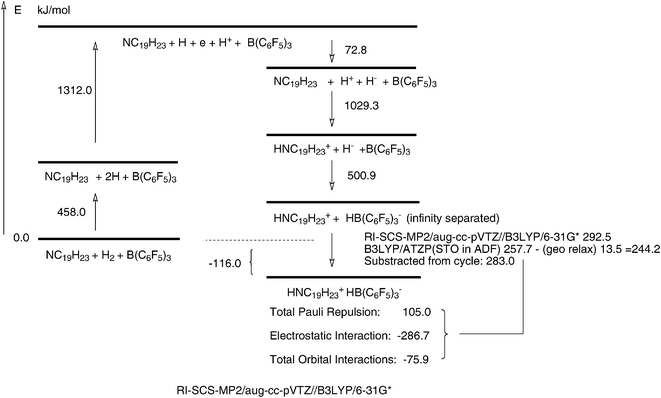Fig. 2 The Born–Haber cycle and Morokuma energy analysis for the hydrogen splitting reaction. The bond energy of hydrogen molecule, the ionisation energy and the electron affinity of the hydrogen atom are taken from experimental data.⁵⁷ The proton affinity of NC₁₉H₂₃ and the hydride affinity of B(C₆F₅)₃ are calculated at RI-SCS-MP2/aug-cc-pVTZ//B3LYP/6-31G* level. No solvent corrections included.

Table 1 Experimental monomer properties of relevant molecules (in kJ mol⁻¹). ‘PA’ = Proton affinity. ‘HA’ = Hydride affinity

System	Property	Value	Ref.
NH3	PA	853.6	55
N(CH3)3	PA	948.9	55
BH3	HA	310(12)	56
B(C2H5)3	HA	290(10)	56

---

As to the intermediates, the presently found intermediate 5 of Fig. 1 is interestingly the same as the first intermediate, suggested in the purely experimental, irreversible bimolecular boron–nitrogen-based hydrogen activation reaction of Sumerin et al.⁴⁵ in their Scheme 3. To the contrary, our calculations show no evidence for their suggested later intermediate 1c′.

After another weak complex, 6, the reaction arrives at a quasi-linear early transition state 7. The bond distances H–H, B–H, and N–H are 83.1, 160.1, and 170.2 pm while the bond angles BHH and NHH are 167.3 and 172.1°, respectively. The reaction barrier is 106 kJ mol⁻¹ in Gibbs free energy. We then present a Morokuma analysis at this transition state, by selecting H₂ and the rest of the complex as the two fragments. The calculated results are given in Table 2. The results indicate that, in the transition state, orbital interactions are important. This is supported by the NBO analysis of Rokob et al.,^5,46 who ascribe the breaking of the H₂ to electron donation to its σ* antibonding orbital.

Table 2 Morokuma energy decomposition analysis for the transition state, 7, at B3LYP/ATZP level. All quantities in kJ mol⁻¹

Geom.relax^a	Pauli repulsion	Electrostatic	Orbital interaction	Total interactions
a The geometry relaxation refers to the equilibrium structures of H2 and the complex, NC19H23⋯B(C6F5)3, calculated at the RI-SCS-MP2/aug-cc-pVTZ//B3LYP/6-31G* level.
32.2	360.0	−108.9	−254.8	28.5

---

For the product 8, a comparison between computational and experimental bond distances is given in Table 3. Our calculations are for a gas-phase ionic complex 8, while the experimental data come from the crystal structure for species number 5 of ref. 11. This difference may be less serious because the active B–H⋯H–N part is hidden inside the system, see Fig. 3. For this extended complex, the B–N distance of nearly 400 pm is 8 pm longer than in the X-ray experiment. Concerning the B–H and N–H distances, the calculated values may be more reliable than the experimental ones, due to the well-known difficulty of seeing H atoms by X-rays. This also makes the experimental H⋯H distance less trustworthy.

Fig. 3 The calculated structure for 8 at B3LYP/6-31G* level. The ADF-GUI software⁵⁸ was used.

Table 3 Experimental and computed structural parameters for the hydrogenated product 8. The 6-31G* basis set is used in all geometry optimisations. The bond distances are in pm and the angles in degree

	Exp.^11	B3LYP	RI-PBE	M06-2X
d(B–N)	388.3	396.3	390.3	374.6
d(B–H)	115.4	121.2	122.6	121.5
d(N–H)	94.4	103.2	104.3	103.4
d(H–H)	189.2	221.7	216.6	198.8
∠BHH	157.4	142.1	140.6	140.1
∠NHH	160.9	120.5	118.6	119.7

---

Concerning the energetics, the electronic energy decrease of the reaction

3 + 4 + H₂ → 8. (2)

in Fig. 1 is −116 kJ mol⁻¹ while the Gibbs free energy goes up +13 kJ mol⁻¹. With the solvation contribution of −20 kJ mol⁻¹, we finally arrive at −6.8 kJ mol⁻¹ in Gibbs free energy, corresponding to a thermodynamically favored reaction at 298 K. Note here that reaction (2) goes from three molecules to a single molecule. The corresponding entropy decrease of −318.4 J K⁻¹ mol⁻¹ consists of translational, rotational and vibrational contributions of −290.6, −145.0 and +117.2 J K⁻¹ mol⁻¹, respectively. The corresponding −TS contribution to G is 94.9 kJ mol⁻¹, as given in Fig. 1.

A Born–Haber cycle and a Morokuma analysis are presented in Fig. 2. As a mutual check on the methods, the interaction energy between HNC₁₉H⁺₂₃ and HBC₆F⁻₅ is evaluated in three different ways: (1) a direct RI-SCS-MP2/aug-cc-pVTZ//B3LYP/6-31G* calculation between the fragments and the product; (2) a Morokuma analysis based on a B3LYP functional, adding geometric relaxation at RI-SCS-MP2/aug-cc-pVTZ//B3LYP/6-31G* level; and (3) subtraction from a Born–Haber cycle. The difference between a direct calculation and a subtraction, i.e. 9.5 kJ mol⁻¹, gives an idea of the accuracy of the RI-SCS-MP2 method for the processes H₂ → 2H, H → H⁺ + e, and H + e → H⁻ since experimental data were adopted for the cycle. The difference between RI-SCS-MP2 and Morokuma analysis with B3LYP functional, i.e. 48 kJ mol⁻¹ may contain dispersion contributions.⁴⁷ Concerning the dominant contribution, the results suggest that the product is mainly bound by the electrostatic interaction of −287 kJ mol⁻¹, if we let the Pauli repulsion and the orbital interaction cancel each other.

Moreover, the formation of the additional B–H and N–H bonds also contributes to the splitting of hydrogen. Corresponding to our calculated proton affinity of 3, the new N–H bond provides −1029 kJ mol⁻¹. Similarly, the calculated hydride affinity of 4 gives an estimate of −501 kJ mol⁻¹ for the energy of the new B–H bond.

3.2 Charge shifts

In Fig. 4 and 5, we show the atomic and fragment NBO charges, q, along the reaction path (2) of the new experimental reaction after the transition state, TS.

Fig. 4 The calculated NBO atomic charges along the reaction path (2) at B3LYP/6-31G* level. The transition state is given by the vertical arrow. The largest changes occur for the atoms B and H(N), given by the thick lines.

Fig. 5 The calculated NBO charges for the boron- and nitrogen-containing fragments along the reaction path (2) at B3LYP/6-31G* level. Note that the charges approach nearly complete ionisation.

As said in Chapter 3.1, at the TS the H₂ is only stretched from 74 pm to 83 pm. This introduces an initial q of +0.2 at the H pointing towards the N. After the TS, the largest changes occur for q(H(N)) and q(B). When dissociation is approached, we observe a transition towards almost complete ionisation, q = ±0.92e, for the fragments HNC₁₉H₂₃ and HB(C₆F₅)₃, containing nitrogen and boron, respectively, in the product. The calculated dipole moment of the product is 6.16 atomic units, corresponding to two opposite unit point charges at a distance of 326 pm.

As discussed earlier, the corresponding Coulomb attraction is comparable with the homolytic dissociation energy of H₂.¹⁰

3.3 Electrostatic potentials

A further way to visualise the driving forces for the reaction (2) is to look for areas of strong electrostatic potentials, V. Those of the reactants are shown in Fig. 6. The red dot of the amine 3 is the nitrogen lone pair and the blue dot of the borane 4 is its 2p vacancy. They indeed form the sites of the opposite extremes of V.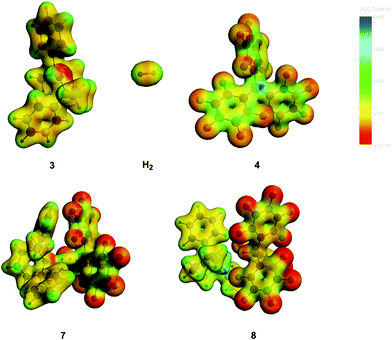

Fig. 6 The electrostatic potentials for the experimental reaction. Note the red nitrogen lone pair of 3 and the blue boron vacancy of 4 for the reactants in the upper part. The transition state is 7 and the product 8. The H₂ molecule is drawn in a larger scale. The ADF-GUI software⁵⁸ was used.

A further observation from this Figure is the N–H⋯F hydrogen bond, observed in the product 8.

We then turn to a qualitative discussion of other aspects, relevant for the hydrogen splitting reaction, using simple models.

3.4 Frustration

A Lewis-acid–Lewis-base pair can form a bond, such as the possible B–N bond between the present reactants. By frustration one means that sterically bulky ligands R are preventing the formation of that, otherwise lower-energy, B–N bond:^2,3

R₃N + B(R′)₃ ↔ R₃N − B(R′)₃. (3)

In Fig. 7 this corresponds to the distance from the symbol ↕ to the well bottom. In a theoretical study this frustration can be simulated just by stopping the B–N bond formation, as illustrated for the simplest case R = R′ = H in Fig. 7.

Fig. 7 Calculated potential curve for reaction (3) at B3LYP/aug-cc-pVTZ level. The ‘frustration energy’ is defined as the remaining one from the stopping point (↕) around B–N of 350 pm to the bottom.

How great is the ‘frustration’? Although we then are discussing a process that is not allowed to happen, we can study the remaining frustration energy from the stopping point to the energy minimum with a full B–N bond. We find that it can be of the order of 100 kJ mol⁻¹, if the B–N distance is maintained at 350 pm as a typical geometry for the FLP.¹¹ For theoretical readers, including the present authors, it might be emphasized that the reactions, leading to B–N bonds, or even to solid boron nitride, are not arbitrary, imaginary deviations but a concrete danger that must be averted at all costs in the experiment, in order to reversibly bind H₂.

3.5 A linear model for ionisation

To illustrate the competing mechanisms we then vary R(B–N) for reaction (1) but keep the N–H–H–B subsystem linear, see Fig. 8. Above R > 450 pm, both a lower-lying trimolecular system and a higher-lying, bimolecular ionic curve are possible, corresponding to the left-hand-side and right-hand-side of eqn (1), respectively. For this simplest model, with shorter R, a crossing is approached but not yet reached. We also add a dashed line for the substituted ammonia, NR₃ with R = Me, whose proton affinity (PA) is 95 kJ mol⁻¹ larger than PA(NH₃) (see Table 1). Then the crossing would be reached already at larger R. This already demonstrates the potential of the Coulomb interaction. In addition, for the experimentally synthesized cases, e.g. B(C₆F₅)₃ and trans-2,6-dimethyl-2,6-diphenylpiperidine, the PA and hydride affinity (HA) can be even larger than those for NMe₃ and BH₃, see Fig. 2. This will favour even more the ionised structure. The point here was that the cross-over from the neutral reactants to the ionised product can already be achieved in this simplest of models.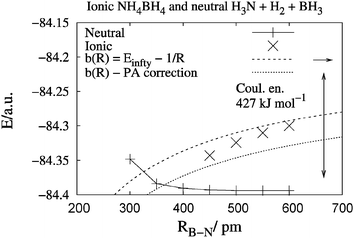

Fig. 8 Ionic NH⁺₄⋯BH⁻₄ (×) versus neutral H₃N + H₂ + BH₃ (+) potential curves calculated at B3LYP/aug-cc-pVTZ level using constrained optimisations for the two quasilinear model systems. Note that the two can coexist outside ca. R_B–N = 450 pm. The upper, rising, dashed curve gives the pure Coulomb-law behaviour towards the calculated ionic dissociation limit. The lower, rising, dotted curve is corrected for the proton affinity (PA) difference between NMe₃ and NH₃. The crosses (×) are quantum chemical points without further fitting.

3.6 ‘Collective Madelung ionisation’

Although the (NH₄)(BH₄) dimer only balances on the brink of ionisation, the solid (NH⁺₄)(BH⁻₄) has been synthesised^48,49 and its cohesive energy has been theoretically estimated. The solid lies 70 kJ mol⁻¹ above BH₃NH₃(s) + H₂.⁵⁰

A qualitatively analogous case are the ammonia–sulfuric acid complexes, where the simplest dimer remains neutral, but larger systems ionise to ammonium(hydrogen)sulfate.⁵¹

Such cases can be lumped together as collective Madelung ionisation (CMI), meaning that the Coulomb potential from a single nearest-neighbour counterion ±q at distance R, or V = −q/R, is multiplied by a Madelung factor, f > 1 in an oligomer or a crystal.⁵² It should be added that in the ammonia–sulfuric acid case, hydrogen bonds influence the stability and that, as stated above, methyl amine has a larger proton affinity than ammonia.

We illustrate this concept by considering a tetrahedral (T_d) tetramer [(NH₄)(BH₄)]₄, 9. If R denotes the interionic distance, taken as the B–N one, a pseudocubic geometry would increase the Coulomb attraction, felt by one ion, by the factor

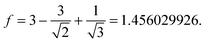The same factor (with one decimal less and without eqn (4)) was given by Baker and Baker⁵³ in a discussion of Madelung factors in nanocrystals. Note that this factor is not so far from those for NaCl or CsCl crystal structures, 1.747565 and 1.762675, respectively.⁵²

The molecular structure of 9, optimised at the RI-SCS-MP2/aug-cc-pVTZ level, is shown in Fig. 9. The structural parameters are given in Table 4. Note that the ammonium ion distorts only slightly, and the borohydride ion hardly at all from their local tetrahedral structure. The ammonium ion prefers having one N–H bond outwards from the corner, and three N–H bonds inwards. The borohydride ion makes the opposite choice. This results in one intramolecular H⋯H distance of 175.6 pm per ion pair.

Fig. 9 The calculated RI-SCS-MP2/aug-cc-pVTZ structure of the ionic tetramer (NH₄BH₄)₄, 9. The ADF-GUI software⁵⁸ was used.

Table 4 Structure of the (NH₄BH₄)₄ tetramer, 9 at RI-SCS-MP2/aug-cc-pVTZ level

Property	Value/pm	Number of hydrogens
R(B–N)	326.1
R(N–H(out))	101.5	1
R(N–H(in))	103.5	3
R(B–H(in))	122.7	1
R(B–H(out))	122.5	3

---

The lowest vibrational frequencies of about 100 cm⁻¹ describe interionic vibrations. The librational motions lie higher.

Energetically the tetramer is 434 kJ mol⁻¹ more stable than four ion pairs NH₄BH₄.

This argument adds to the credibility of the simple ionic (NH₄BH₄) dimer model, pointing out that although it itself is at the brink of existence, the CMI strongly stabilises already the ionic tetramer. The consequence of Madelung stabilisation on the related infinite crystals has been studied for the bulk (XH₄)(YH₄) X = B, Al, Ga and Y = N, P, As by Zuliani et al.⁵⁴ Their calculated B–N distance for a ‘NaCl’ crystal structure of solid NH₄BH₄ is 334 pm, compared with our tetramer value of 326 pm in Table 4. Zuliani et al. do not specify the orientation of their N–H and B–H bonds.

4. Conclusion

Returning to the title, the reversible hydrogen storage in systems of the present type requires a nearly thermoneutral total reaction in Gibbs free energy, with low-lying transition state(s). What happens outside the really existing path, is a bit hypothetical. Stephan’s FLP idea points out that, without the bulky ligands, the formation of a B–N bond between the Lewis acid and Lewis base would take the system energetically further down and leave it there, in a very real sense. We here put a number on this “frustration energy”. In the simplest model it is about 100 kJ mol⁻¹. Our “CHL” idea would take us further up, by 300–500 kJ mol⁻¹ from the actual reaction system, if the ions of the final product were removed to infinity. Both of these hypothetical detours exist. A further aspect is that the formation of one new B–H and one new N–H bond also largely compensates for the splitting and ionisation of the H₂. The three C₆F₅ ligands around boron and the alkyl groups at nitrogen increase the hydride affinity HA and the proton affinity PA, respectively, providing further energy lowering. This is also supported by Lewis acidity and basicity values, compiled by Rokob et al.⁷

Under such circumstances, the relatively tiny dihydrogen bonding contribution also has a potential to influence the process. We hope to have illustrated by these simple estimates the number of different aspects of, or potential explanations for the reversible heterolytic splitting and storage of H₂.

Acknowledgements

We belong to the Finnish Center of Excellence in Computational Molecular Science (2006–2011). The Magnus Ehrnrooth Foundation supported CW and the CSC, Espoo, Finland, provided computational resources. We thank Michael Patzschke for technical advice. The referees helped to improve the clarity of the presentation.

References

1. G. C. Welch, R. R. San Juan, J. D. Masuda and D. W. Stephan, Science, 2006, 314, 1124–1126.
2. J. S. J. McCahill, G. C. Welch and D. W. Stephan, Angew. Chem., Int. Ed., 2007, 46, 4968–4971.
3. D. W. Stephan, Org. Biomol. Chem., 2008, 6, 1535–1539.
4. D. W. Stephan, Dalton Trans., 2009, 3129–3136.
5. T. A. Rokob, A. Hamza, A. Stirling and I. Pápai, Angew. Chem., Int. Ed., 2008, 47, 2435–2438.
6. T. A. Rokob, A. Hamza, A. Stirling and I. Pápai, J. Am. Chem. Soc., 2009, 131, 2029–2036.
7. T. A. Rokob, A. Hamza and I. Pápai, J. Am. Chem. Soc., 2009, 131, 10701–10710.
8. T. Privalov, Dalton Trans., 2009, 1321–1327.
9. T. Privalov, Eur. J. Inorg. Chem., 2009, 2229–2237.
10. V. Sumerin, F. Schulz, M. Atsumi, C. Wang, M. Nieger, M. Leskelä, T. Repo, P. Pyykkö and B. Rieger, J. Am. Chem. Soc., 2008, 130, 14117–14119.
11. V. Sumerin, F. Schulz, M. Nieger, M. Atsumi, C. Wang, M. Leskelä, P. Pyykkö, T. Repo and B. Rieger, J. Organomet. Chem., 2009, 694, 2654–2660.
12. A. Macchioni, Chem. Rev., 2005, 105, 2039–2074.
13. R. H. Crabtree, P. E. M. Siegbahn, O. Eisenstein, A. L. Rheingold and T. F. Koetzle, Acc. Chem. Res., 1996, 29, 348–354.
14. V. I. Bakhmutov, Dihydrogen Bonds. Principles, Experiments and Applications, Wiley, Hoboken, NJ, 2008.
15. D. Hugas, S. Simon, M. Duran, C. Fonseca Guerra and F. M. Bickelhaupt, Chem.–Eur. J., 2009, 15, 5814–5822.
16. D. G. Musaev, Private communication, March, 2009.
17. J. C. Slater, Phys. Rev., 1951, 81, 385–390.
18. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
19. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
20. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1210.
21. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789.
22. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
23. S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102.
24. F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340.
25. F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152.
26. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
27. J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921–2923.
28. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
29. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988.
30. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
31. S. Simon and M. D. and, J. Chem. Phys., 1996, 105, 11024–11031.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, J. T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03 (Revision E.01), Gaussian, Inc., Wallingford, CT, 2008.
33. R. Ahlrichs, M. Bär, M. Häser, H. Hörn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
34. H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918–9924.
35. H. P. Hratchian and H. B. Schlegel, J. Chem. Theory Comput., 2005, 1, 61–69.
36. J. Tomasi, B. Mennucci and E. Cancès, THEOCHEM, 1999, 464, 211–226.
37. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1997, 97, 331–340.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision A.1), Gaussian, Inc., Wallingford, CT, 2009.
39. K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244.
40. ADF2008.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com.
41. E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
42. D. P. Chong, Mol. Phys., 2005, 103, 749–761.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
44. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
45. V. Sumerin, F. Schulz, M. Nieger, M. Leskelä, T. Repo and B. Rieger, Angew. Chem., Int. Ed., 2008, 47, 6001–6003,  DOI:DOI: 10.1002/anie.200800935.
46. A. Hamza, A. Stirling, T. A. Rokob and I. Pápai, Int. J. Quantum Chem., 2009, 109, 2416–2425.
47. X. Xu and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2673–2677.
48. R. W. Parry, D. R. Schultz and P. R. Girardot, J. Am. Chem. Soc., 1958, 80, 1–3.
49. M. Krumpolc, AIP Conf. Proc., 1982, 95, 502–504.
50. D. A. Dixon and M. Gutowski, J. Phys. Chem. A, 2005, 109, 5129–5135.
51. T. Kurtén, V. Loukonen, H. Vehkamäki and M. Kulmala, Atmos. Chem. Phys. Discuss., 2008, 8, 7455–7476.
52. C. Kittel, Introduction to Solid State Physics, Wiley, New York, 4th edn, 1971, pp. 115 and 118.
53. A. D. Baker and M. D. Baker, J. Phys. Chem. C, 2009, 113, 14793–14797.
54. F. Zuliani, A. W. Götz, C. Fonseca Guerra and E. J. Baerends, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165106.
55. E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656.
56. D. J. Goebbert and P. G. Wenthold, Int. J. Mass Spectrom., 2006, 257, 1–11.
57. D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, FL, 80th edn, 1999.
58. ADF-GUI 2008.01, SCM, Amsterdam, The Netherlands, www.scm.com.

---