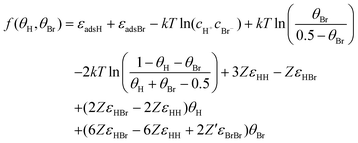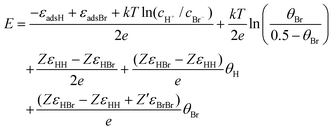A sublattice-model isotherm for the competitive coadsorption of hydrogen and bromide on a Pt(100) electrode
Received
19th June 2009
, Accepted 5th October 2009
First published on
7th November 2009
Abstract
Previous work demonstrated that the Frumkin isotherm is inadequate to model the competitive coadsorption of species with different saturation coverages, such as hydrogen and bromide coadsorption on Pt(100) [N. Garcia-Araez et al., J. Electroanal. Chem., 2006, 588, 1]. Therefore, Monte Carlo simulations were necessary to determine meaningful values of the microscopic parameters (namely, energies of adsorption and interaction). In the present work, an alternative analytical isotherm is developed, by taking into account the occupation of two sublattices, which together compose the whole lattice of adsorption sites. Despite its relatively simple mathematical form, this isotherm presents, under certain conditions, a significant improvement over the classical Frumkin isotherm for the modeling of competitive adsorption processes, thus providing a closer agreement with results from Monte Carlo simulations. Finally, it is demonstrated that the sublattice-model isotherm will be generally applicable to systems in which the formation of segregated adlayers, whose structure is not explicitly taken into account in the model, is energetically unfavorable.
1. Introduction
Modeling adsorption processes on well-defined surfaces has been acknowledged as a powerful tool towards an improved understanding of the elementary processes and interactions that are relevant to heterogeneous catalysis and electrocatalysis. For example, the fit of electrochemical adsorption processes on single-crystal surfaces by means of Monte Carlo simulations or adequate analytical isotherms, allows the evaluation of microscopic parameters such as adsorption energies and interactions.1–16 These results can be used to predict the behavior of more complex systems. In this way, the comparison of the values of the adsorption energies allows to estimate which species would remain stable on the surface, and which would be displaced by others. In addition, the values of the interaction energies play an important role in the structure and reactivity of the adlayer.17
The study of hydrogen and bromide coadsorption on Pt(100) is particularly interesting for the molecular-level understanding of competitive adsorption processes.18 This system is simple and well-defined, since it can be well-described by the coadsorption of two kinds of species that adsorb on the same surface sites of a square lattice, but whose saturation coverages are different (θH,max = 1, θBr,max = 0.5). Previous work demonstrated that the Frumkin isotherm can be used to obtain a satisfactory fit of the experimental data, but the microscopic parameters obtained from such a fit are in fact unrealistic. Therefore, the evaluation of reliable microscopic parameters should be performed by Monte Carlo simulations (which provide the exact solution of a given model). The inadequacy of the Frumkin isotherm was explained by its inability to correctly deal with the presence of strong short-range interactions, inherent to adsorption systems with saturation coverages smaller than unity.
Previous work demonstrated that short-range interactions can be better described, within the mean-field approximation, by the separation of the whole lattice of adsorption sites into several sublattices.19 In particular, short-range interactions leading to saturation coverages smaller than unity, can be introduced by considering that only one of the sublattices can be occupied by a given type of species. In the case of the adsorption of a single type of species, this approach leads to the formulation of the classical Frumkin isotherm, which can be also obtained by considering that more than one adsorption site is effectively blocked by an adsorbed species.13 Nevertheless, in the case of coadsorption processes, the classical Frumkin isotherm is in disagreement with the isotherm obtained by the sublattice mean-field treatment, as will be shown in this work.
STM images revealed the formation of the c(2× 2) structure for bromide adsorption at saturation on long terraces of Pt(100) stepped surfaces.20 Accordingly, a more realistic analytical isotherm can be developed by describing separately the occupation of the two c(2 × 2) sublattices that compose the lattice. This isotherm will be called the “sublattice-model isotherm” in the following. Although this treatment employs the mean-field approach for the evaluation of interactions, it differs from the classical Frumkin isotherm, which considers that hydrogen and bromide occupy one and two adsorption sites, respectively.18 The sublattice-model isotherm constitutes a significant improvement with respect to the classical Frumkin isotherm, although it has still a relatively simple mathematical form. Furthermore, it will also be shown that the sublattice-model isotherm can satisfactorily describe competitive adsorption processes as long as large-scale clustering of adsorbates on the surface is energetically unfavorable.
2. The model
The model assumes that the square (1 × 1) lattice can be subdivided into two c(2 × 2) sublattices, called sublattices (1) and (2), that can be treated separately. We will assume that bromide adsorption takes place only on one of the two c(2 × 2) sublattices, say sublattice (1), while hydrogen adsorption takes place on both sublattices. The assumption of bromide adsorption on only one of the sublattices is unphysical, since in reality, the two sublattices are completely equivalent and both can be occupied simultaneously, leading to, for example, separated c(2 × 2) domains. Nevertheless, this assumption does not lead to major errors in the evaluation of coverages. In order to demonstrate so, one should consider the adsorption of a single type of species on a square lattice with infinite nearest-neighbors interaction (that is, the hard-square model). Previous work demonstrated that, in the absence of other type of interactions, the exact Monte Carlo isotherm is in reasonable agreement with a mean-field isotherm for which only half of the adsorption sites is available.13
Fig. 1A illustrates a possible configuration of adsorbed bromide and hydrogen on the (100) surface, and their corresponding labeling. Arrows indicate the interactions included in the model, which are those between hydrogen and hydrogen and bromine and hydrogen adsorbed on nearest neighbor positions (εHH and εHBr, respectively), and between bromine particles adsorbed on next-nearest neighbor positions (εBrBr). All interactions considered here are repulsive, and accordingly, have positive values. Similarly, the sign criterion for the adsorption energies is that more negative values imply a stronger attraction of the adsorbate to the surface.
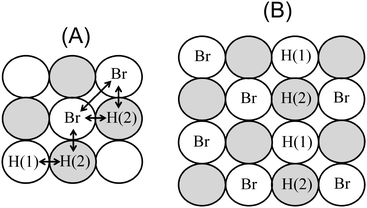 |
| | Fig. 1 (A) Example of a configuration of hydrogen and bromide coadsorbed on a 3 × 3 lattice. The adsorption sites of the sublattices (1) and (2) are depicted as white and gray spheres, respectively. Hydrogen adsorbed on sublattices (1) and (2) are labeled H(1) and H(2), respectively. Arrows indicate the interactions included in the model. (B) Example of the adsorption of a row of hydrogen species at the boundary of bromide c(2 × 2) domains. | |
Effective energies of adsorption can be obtained by considering mean-field interactions, in such a way that the effective interaction energy is considered proportional to the average coverage. Accordingly:
| | | εeffectiveadsH(1) = εadsH + 2ZεHHθH(2) | (1) |
| | | εeffectiveadsH(2) = εadsH + 2ZεHHθH(1) + 2ZεHBrθBr | (2) |
| | | εeffectiveadsBr = εadsBr + 2ZεHBrθH(2) + 2Z′εBrBrθBr | (3) |
where
εadsi is the energy of adsorption of species
i;
εij is the interaction energy between adsorbed species
i and
j; and
Z and
Z′ are the number of nearest and next-nearest neighbors, respectively (
Z =
Z′ = 4 for a square lattice). The factor of 2 in the above equations accounts for the fact that coverages are referred to the total number of sites of the whole lattice, and hence the maximum attainable coverage on each sublattice is 0.5. Taking into account that the coverage of
platinum free sites on each sublattice is:
| | | θ*(1) = 0.5 − θH(1) − θBr | (4) |
the following equilibrium conditions for the adsorption–desorption reactions of H(1), H(2) and Br are obtained:
| |  | (6) |
| |  | (7) |
| |  | (8) |
where
kB,
T and
e have their usual meaning,
ci is the bulk concentration of species
i, and
E is the
electrode potential.
At this point, it should be noted that competitive adsorption processes are characterized by the fact that the amount of free platinum sites are kept at a minimum. In the present system, bromide desorption only takes place due to the strong competition with hydrogen adsorption, and vice versa. Besides, hydrogen adsorption would take place preferentially on the free sites of sublattice (1), rather than on the sublattice (2), since in this way repulsive interactions with bromide adsorbed on nearest neighbors positions are avoided. In conclusion, it is reasonable to assume that the number of free platinum sites in sublattice (1) is negligibly small, so that θH(1) + θBr(1) ≈ 1/2. Accordingly, the hydrogen coverage on each sublattice will be given by:
| | | θH(2) ≡ θH − θH(1) ≈ θH − 0.5 − θBr | (10) |
With this, values of coverages can be calculated by minimizing the square of the following expression [obtained combining
eqn (6)–(10)]:
| | 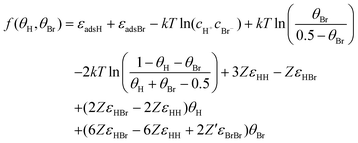 | (11) |
That is, for a given value of coverage of one species (hydrogen or bromide), the coverage of the other species is calculated by numerical minimization of f(θH,θBr), employing a particular set of values for the microscopic parameters [εadH, εadBr, εHH, εHBr, εBrBr]. Finally, the corresponding adsorption potential can calculated from the following expression [obtained from combining eqns (6) and (8)]:
| | 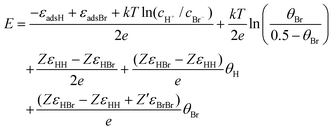 | (12) |
The results of the sublattices model isotherm will be compared to the classical Frumkin isotherm and Monte Carlo simulations. The latter were performed on a square lattice of 256 × 256 sites with periodic boundary conditions using the Dynamic Monte Carlo code CARLOS.21 The details of the simulations have been described elsewhere.18 Finally, the classical Frumkin isotherm is obtained by imposing equilibrium on the adsorption–desorption reactions of hydrogen and bromide adsorption, and including mean-field interactions:18
| | | Br− + 2Pt ↔ Pt2–Br + e− | (14) |
The above equations imply that
hydrogen and
bromide occupy one and two sites, respectively. Taking into account that the number of free
platinum sites is negligible, the hydrogen and
bromide coverages are linked by:
| |  | (15) |
and the overall reaction is:
| | | Br− + 2(Pt–H) ↔ Pt2–Br + 2H+ + 3e− | (16) |
Consequently, the classical Frumkin isotherm can be expressed as a function of either the hydrogen or the bromide coverage:
| |  | (17) |
| |  | (18) |
All calculations, simulations, and experiments in this work are performed at 298 K.
3. Results and discussion
Fig. 2 compares the results of hydrogen and bromide coverages obtained from the sublattice-model isotherm and Monte Carlo simulations, for the sets of microscopic parameters employed in previous work for the modeling of hydrogen and bromide coadsorption on Pt(100),18 summarized in Table 1. The parameters employed in Fig. 2A and B were determined from the fit of voltammetric data for Pt(100) in 0.1 M HClO4 + 10−2 M KBr to a classical Frumkin isotherm, while the parameters corresponding to Fig. 2C and D were evaluated by performing Monte Carlo simulations.18 In both cases, the microscopic parameters for hydrogen adsorption (εadsH and εHH) were predetermined from the modeling of voltammetric data for Pt(100) in 0.1 M HClO4, in the absence of bromide. Then, two reasonable limiting values for the bromide–bromide interaction were taken (εBrBr = 0.055 eV in Fig. 2A and C and εBrBr = 0 in Fig. 2B and D), and the remaining microscopic parameters (εadsH and εHH) were evaluated from the fit of the voltammetric data in the presence of 10−2 M KBr.
 |
| | Fig. 2 Comparison of hydrogen and bromide coverages obtained from Monte Carlo simulations (θMCH, θMCBr) and from the sublattices-model isotherm (θisothH, θisothBr), employing values for the microscopic parameters evaluated in ref. 18 by using the Frumkin isotherm (A, B) and Monte Carlo simulations (C, D), for εBrBr = 0.055 eV (A, C) and εBrBr = 0 (B, D). See text for details. | |
Table 1 Microscopic parameters for hydrogen and bromide coadsorption on Pt(100) employed in the present work
|
ε
adsH/eV |
ε
HH/eV |
ε
BrBr/eV |
ε
adsBr/eV |
ε
HBr/eV |
Fitting method |
Employed in |
| −0.45 |
0.014 |
0.055 |
−0.315 |
0.043 |
Frumkin isotherm |
Fig. 2A
|
| −0.45 |
0.014 |
0.055 |
−0.399 |
0.082 |
MC simulations |
Fig. 2C and 4
|
| −0.45 |
0.014 |
0.055 |
−0.413 |
0.059 |
Sublattice-model isotherm |
Fig. 3A
|
| −0.45 |
0.014 |
0 |
−0.260 |
0.030 |
Frumkin isotherm |
Fig. 2B
|
| −0.45 |
0.014 |
0 |
−0.268 |
0.055 |
MC simulations |
Fig. 2D and 4
|
| −0.45 |
0.014 |
0 |
−0.261 |
0.048 |
Sublattice-model isotherm |
Fig. 3B
|
Its is noteworthy that the application of the sublattice-model isotherm gives results in reasonable agreement with Monte Carlo simulations for the sets of parameters in Fig. 2A and B, which were obtained by the fit of the voltammogram of Pt(100) in 0.1 M HClO4 + 10−2 KBr by means of the classical Frumkin isotherm.18 It should be noted, though, that these sets of parameters do not describe correctly the real system. As demonstrated in previous work with the help of Monte Carlo simulations, these sets of parameter values incorrectly predict that the substitution of the H (1 × 1) adlayer by the Br c(2 × 2) adlayer takes place through the formation of ordered, mixed hydrogen-bromide structures [namely H + Br c(2 × 2) and H + Br p(2 × 2)] that are stable in a relatively wide potential range. Experimentally, it is found that the substitution of hydrogen by bromide on Pt(100) takes place in a narrow potential window (0.17–0.21 V vs. RHE). In conclusion, taking into account that the results in Fig. 2A and B, obtained by means of the sublattice-model isotherm are in reasonable agreement with Monte Carlo simulations, it is demonstrated that this isotherm can be used, in the present case, in order to test the applicability of the classical Frumkin isotherm.
On the other hand, although the results of the sublattice-model isotherm are rather close to Monte Carlo simulations for the set of parameters corresponding to εBrBr = 0 (Fig. 2D); in the case of εBrBr = 0.055 eV (Fig. 2C), marked deviations are observed. In order to explain the origin of these marked deviations, it should be noted that, for the parameter values in Fig. 2D, snapshots of the configuration of the adlayer during Monte Carlo simulations showed the formation of rows of adsorbed hydrogen at the boundary of bromide c(2 × 2) domains, as illustrated in Fig. 1B. This local structure is favored because repulsive interactions between hydrogen and hydrogen, are weaker than those between hydrogen and bromide. As a result, when hydrogen occupies a site on sublattice (1), the adsorption of hydrogen on nearest neighbors positions becomes more favorable (in comparison to the adsorption on nearest neighbors positions of bromide). In conclusion, under these conditions, segregation on the occupancy of the adsorbates takes place, and therefore, the use of mean-field interactions in the derivation of the lattice-model isotherm [eqn (6)–(8)] is inappropriate.
As an additional test of the applicability of the sublattice-model isotherm, we employed this isotherm to fit the voltammetric data for Pt(100) in 0.1 M HClO4 + 10−2 M KBr. This is done by taking into account that the current measured in cyclic voltammetry is given by the derivative of the hydrogen and bromide coverages with potential, according to:
| |  | (19) |
where
ν is the scan rate and
QPt(100) is the charge associated to the adsorption of one monolayer on the Pt(100) surface (
QPt(100) = 109 μC cm
−2). Consequently, from the fit of the
experimental data by means of the sublattice-model isotherm, two new sets of values of the microscopic parameters are obtained (one set corresponding to each predetermined value of
εBrBr). These new estimative values of the microscopic parameters are included in
Table 1, and the results of these fits are compared with the
experimental data in
Fig. 3. This figure also includes the results of the fits obtained by means of Monte Carlo simulations, for the sake of comparison. It is concluded that, although the Monte Carlo simulations are more accurate to describe the system under study, and provide a better fit of the
experimental data; the sublattice-model isotherm provides values of the microscopic parameters in reasonable agreement with Monte Carlo simulations, and thus constitutes a significant improvement over the classical Frumkin isotherm.
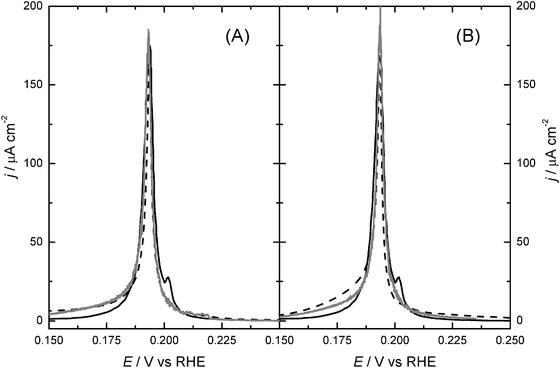 |
| | Fig. 3 Fit of the voltammogram of a Pt(100) in 0.1 M HClO4 + 10−2 M KBr (scan rate: 5 mV s−1, solid line), by using Monte Carlo simulations (grey line) and the sublattice-model isotherm (dashed line), and considering εBrBr = 0.055 eV (A) and εBrBr = 0 (B). | |
A final question to be addressed is for which systems the sublattice-model isotherm would be safely applicable. To answer this question it is helpful to have a close look to the calculations of the ground-state energies of ordered adlayers.3,4Fig. 4 compares the results for the most relevant structures, calculated with the microscopic parameters evaluated by Monte Carlo simulations (also used in Fig. 2C and D). For both sets of parameters, the most stable structures are the H (1 × 1) and Br c(2 × 2) adlayers. However, for the set of parameters with εBrBr = 0.055 eV (Fig. 2C), the structure with hydrogen adsorbed at the boundary of bromide c(2 × 2) domains [here called Br c(2 × 2) + H row] is also very stable. Indeed, as above mentioned, patches of this structure were formed during the Monte Carlo simulations. Conversely, for the set of parameters with εBrBr = 0, this structure is not favored, and instead, mixed adlayers of hydrogen and bromide will preferably have a H + Br c(2 × 2) structure, because its ground-state energy is lower. Noteworthy, while the interaction energy for the H + Br c(2 × 2) structure is correctly calculated within the sublattice-model isotherm, this approach gives incorrect results for the lateral interactions in the presence of hydrogen rows adsorbed at the boundary of Br c(2 × 2) domains. This explains why the sublattice-model isotherm gives results rather close to Monte Carlo simulations for εBrBr = 0 (Fig. 2D), but not for εBrBr = 0.055 eV (Fig. 2C). In conclusion, the sublattice-model isotherm will be generally applicable to systems in which the formation of segregated adlayers, whose structure is not correctly taken into account in the model, is energetically unfavorable.
 |
| | Fig. 4 Ground-state energies of selected ordered structures, obtained with the microscopic parameters evaluated by Monte Carlo simulations, for εBrBr = 0.055 eV (solid lines) and εBrBr = 0 (dashed lines). Grey spheres: adsorbed hydrogen, black spheres: adsorbed bromide, white spheres: empty sites. | |
4. Conclusions
We have described the derivation of an analytical isotherm that considers separately the composition of the two c(2 × 2) sublattices that together compose the whole square lattice of adsorption sites. This isotherm has proven satisfactory for the modeling of the hydrogen and bromide competitive adsorption on Pt(100), under certain conditions. Finally, it is demonstrated that the sublattice-model isotherm will be generally applicable to systems in which the formation of local domains, with ordered structures not correctly included in the model, is unimportant. This can be tested by the calculation of the ground-state energies of the most relevant structures.
Acknowledgements
N. G. thanks the MICINN (Spain) for the award of a postdoctoral fellowship.
References
-
M. A. Habib and J. O. Bockris, in Comprehensive Treatise of Electrochemistry, ed. J. O. Bockris, B. E. Conway and E. Yeager, Plenum Press, New York, 1980, vol. 1, ch. 4 Search PubMed.
-
M. A. Vorotynstev, in The Chemical Physics of Solvation, ed. R. R. Dogonadze, E. Kalman, A. A. Kornyshev and J. Ulstrup, Elsevier, Amsterdam, 1988, Part C Search PubMed.
- J. B. Collins, P. Sacramento, P. A. Rikvold and J. D. Gunton, Surf. Sci., 1989, 221, 277–298 CrossRef CAS.
- P. A. Rikvold, J. B. Collins, G. D. Hansen and J. D. Gunton, Surf. Sci., 1988, 203, 500–524 CrossRef CAS.
- M. Gamboa-Aldeco, P. Mrozek, C. K. Rhee, A. Wieckowski, P. A. Rikvold and Q. Wang, Surf. Sci., 1993, 297, L135–L140 CrossRef CAS.
- J. Zhang, Y. E. Sung, P. A. Rikvold and A. Wieckowski, J. Chem. Phys., 1996, 104, 5699–5712 CrossRef CAS.
- P. A. Rikvold, J. Zhang, Y. E. Sung and A. Wieckowski, Electrochim. Acta, 1996, 41, 2175–2184 CrossRef CAS.
- S. J. Mitchell, G. Brown and P. A. Rikvold, Surf. Sci., 2001, 471, 125–142 CrossRef CAS.
- I. Abou Hamad, T. Wandlowski, G. Brown and P. A. Rikvold, J. Electroanal. Chem., 2003, 554–555, 211–219 CrossRef CAS.
- D. Armand and M. L. Rosinberg, J. Electroanal. Chem., 1991, 302, 191–206 CrossRef CAS.
- L. Blum and D. A. Huckaby, J. Electroanal. Chem., 1994, 375, 69 CrossRef CAS.
- L. Blum, D. A. Huckaby and M. Legault, Electrochim. Acta, 1996, 41, 2207–2227 CrossRef CAS.
- M. T. M. Koper, J. Electroanal. Chem., 1998, 450, 189–201 CrossRef CAS.
- M. T. M. Koper, Electrochim. Acta, 1998, 44, 1207–1212 CrossRef CAS.
- S. J. Mitchell and M. T. M. Koper, Surf. Sci., 2004, 563, 169–182 CrossRef CAS.
- G. S. Karlberg, T. F. Jaramillo, E. Skulason, J. Rossmeisl, T. Bligaard and J. K. Norskov, Phys. Rev. Lett., 2007, 99, 126101 CrossRef CAS.
-
C. G. M. Hermse and A. P. J. Jansen, in Catalysis, ed. J. J. Spivey and K. M. Dooley, The Royal Society of Chemistry, Cambridge, 2006, ch. 19 Search PubMed.
- N. Garcia-Araez, J. J. Lukkien, M. T. M. Koper and J. M. Feliu, J. Electroanal. Chem., 2006, 588, 1–14 CrossRef CAS.
- K. Binder and D. P. Landau, Phys. Rev. B: Condens. Matter, 1980, 21, 1941 CrossRef CAS.
- N. Garcia-Araez, V. Climent, E. Herrero and J. M. Feliu, Surf. Sci., 2004, 560, 269–284 CrossRef CAS.
-
J. J. Lukkien, CARLOS 4.0, Eindhoven University of Technology, 2002.
|
| This journal is © the Owner Societies 2010 |
Click here to see how this site uses Cookies. View our privacy policy here.