The proton dynamics of imidazole methylphosphonate: an example of cooperative ionic conductivity†
Jason W. Traer and Gillian R. Goward*
McMaster University, Department of Chemistry, 1280 Main St. W. Hamilton, ON, Canada L8S 4M1. E-mail: goward@mcmaster.ca; Fax: +1-905-522-2509; Tel: +1-905-525-9140 x24176
First published on 13th November 2009
Abstract
Imidazole methylphosphonate models the hydrogen bonding and dynamics of a potential anhydrous polymer electrolyte. Understanding the behavior of anhydrous electrolytes is crucial to creating polymer materials with better performance in a fuel cell environment. This model salt exhibits ionic conductivity in the solid-state and the method of ion conduction in the solid-state differs depending on the choice of anion and cation pairs. Previous investigation of a sulfonate analogue suggests fast ring dynamics, which contributes to the ionic conductivity. However, 13C CODEX NMR shows that rotation of the imidazole ring is somewhat slower in the methlyphosphonate compound, with a timescale for the two-site ring flip of 31 ± 9 ms at ambient temperature. 31P CODEX and variable temperature 1H MAS NMR spectra confirm that ionic conductivity is facilitated by dynamics at the bifurcated hydrogen bonds between anions, with a timescale of 57 ± 4 ms at ambient temperature for rotation of the phosphonate about the C3v axis. Increasing temperature introduces thermal motion and promotes the rotation of the imidazole ring together with the rotation of the phosphonate group. This leads to a cooperative mechanism of ion conduction between imidazole and the methylphosphonate at higher temperatures, which was unseen in a previous study of the benzimidazole methylphosphonate analogue.
Introduction
Proton exchange membrane based fuel cells would benefit from higher operating temperatures, as this would reduce catalyst poisoning.1–3 However, this requires a reduction in the dependence of the electrolyte membrane on an aqueous phase. The perfluorinated ionomer, Nafion, has an ionic conductivity of 6.0 × 10−2 S cm−1 and operates best under fully hydrated conditions at 80 °C.4 Deviation from this environment in a fuel cell using Nafion as the PEM results in a loss in performance, particularly if a significant amount of hydration is lost.5,6 However, operation of a PEM fuel cell above 120 °C increases catalyst longevity by mitigating the binding of carbon monoxide to the platinum catalyst at high temperatures.7,8 Other benefits of high temperature operation are increased electrode kinetics, less complicated humidification and thermal control systems.9 Thus, other polymer membranes like poly[2,2′-(m-phenylene)-5,5′-bibenzimidazole] (PBI) have been designed to operate in anhydrous environments and at higher temperatures.10,11The ionic conductivity of PBI is closely related to the amount of liquid electrolyte present within the polymer membrane. Large concentrations of phosphoric acid impregnated into PBI have produced conductivities up to 6.2 × 10−2 S cm−1.12,13 However, as the liquid electrolyte leaches out of the membrane, ionic conductivity of PBI is lost. With PBI, high temperature operation was achieved, in this case by trading one leachable liquid phase for another. The next goal in the evolution of the high temperature polymer electrolytes is the elimination of the liquid electrolyte entirely.
A proposed approach to eliminating the liquid electrolyte is to attach the protic groups of the liquid electrolyte to the backbone of the polymer, such that only chemical decomposition would result in a loss of ion carriers.14–22 The chemical structures of several successful copolymer electrolytes are shown in Fig. 1a. The combination of vinylphosphonic acid and 4-vinylimidazole produced a copolymer (VPA-co-4-VIm) with the protogenic groups tethered to the backbone of the polymer.16 The anhydrous copolymer membrane VPA-co-4-VIm achieved ionic conductivities ranging from 10−6 to 10−12 S cm−1 over the temperature range of 5–140 °C using different ratios of vinylphosphonate and vinylimidazole.16 Another example of a dry polymer electrolyte is a copolymer of vinyltriazole and vinylphosphonic acid which had a dry ionic conductivity ranging from 10−3 to 10−4 S cm−1.23 The dry conductivities of these polymer electrolytes are lower than the fully acid-doped PBI at equivalent temperatures. More recently, a similar approach using a tethered triazole ring to a polysiloxane backbone yielded ionic conductivities reaching 10−5 S cm−1 at 140 °C.22 Proton dynamics are achieved through the rotation of the triazole ring, which is facile at high temperatures. Dry polymer electrolytes require significant thermal energy to produce molecular motion, which facilitates long-range transport through the membrane. Thus, the dry polymer electrolytes are particularly favourable for high temperature applications.
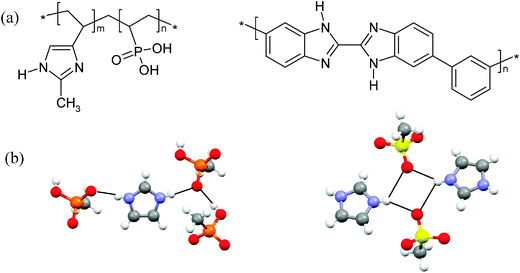 | ||
| Fig. 1 (a) The chemical structures of vinylphosphonic acid and 4-vinylimidazole copolymer (left) and poly benzimidazole (right). (b) The hydrogen bonding in the structures of imidazole methylphosphonate (left) and imidazole methylsulfonate (right). | ||
The disparity in the ionic conductivity between the wet and dry polymer material occurs due to the differences in the mechanisms of ionic conductivity. In PBI, the liquid electrolyte is able to diffuse through the polymer with ease as the phosphoric acid provides an exchange mechanism between molecules of the liquid electrolyte for the conduction of protons.24–26 In contrast, in the dry copolymer membranes, the mechanism of the ionic conductivity is limited to structural diffusion.14,27 The protogenic groups of the dry copolymers form a network of hydrogen bonds that are the pathways for the conduction of protons.23 Transport of the protons therefore occurs via backbone motion of the polymer or rotation of the protogenic groups. The lack of a liquid phase in VPA-co-4-VIm reduces the ionic conductivity, presumably due to the lack of a vehicular transport process and forces the polymer to use a structural mechanism of ionic conductivity.16 The mechanism of proton conduction in phosphoric acid impregnated PBI was investigated by NMR using model compounds, benzimidazole phosphate (Bi-PA) and benzimidazole methylphosphonate (Bi-mPA) to represent the polymer system.11,28 For both Bi-PA and Bi-mPA it was found that the ring does not rotate at room temperature, while the anion does. This current study aims to investigate the mechanism of proton conductivity in imidazole methylphosphonate, a model salt of the VPA-co-4-VIm polymer. The application of solid-state NMR to the model salts will distinguish the contributions of the hydrogen bonding motifs, and identify the role of the anion and cation participants in the proton transport of various polymer electrolytes.
Methodology
Efforts to explain the slow dynamics in the phosphonate and imidazole copolymer begin with choosing a correct model system, which represents the important features in the polymer. Hydrogen bonding plays a crucial role in the anhydrous conductivity of a phosphorous based polymer, thus 1H solid-state NMR is well suited to study a strongly hydrogen-bonded polymer system.15,29 Solid-state NMR is a technique that can probe the local environment of the hydrogen nucleus and provide information on the dynamics and structure of the material on a molecular level.30The chemical shift of the hydrogen-bonded protons is related to the strength of the bonding interaction and often has a resonance frequency above aromatic protons; generally, for a given pair of heteronuclei, a stronger hydrogen bond leads to a higher chemical shift.31 Resolution of the hydrogen bonding protons is often a problem and is overcome with fast magic angle spinning (MAS). The dipolar Hamiltonian (eqn (1)) is attenuated by MAS.
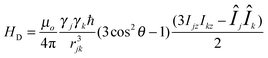 | (1) |
The magnitude of a homonuclear dipolar coupling is inversely related to the cube of the distance between two spins, rjk in eqn (1). One example of a dipolar recoupling experiment, which refocuses the homonuclear dipolar couplings to obtain distance based information, is the back to back (BABA) sequence.32,33 This sequence has two variants: the 2D double quantum correlation spectrum (DQC) correlates homonuclear dipolar coupled spins, and the 1D double quantum filtered (DQF) spectrum recouples resonances that have strong dipolar couplings on the timescale of the rotor period.
In the case of 1H resonances, the major contribution to the linewidth is homonuclear dipolar couplings. Frequency switched Lee–Goldburg (FSLG) homonuclear decoupling schemes reduce the effect of dipolar broadening in the spectrum.34,35 When applied during the t1 evolution period of a heteronuclear correlation, a high-resolution 1H NMR spectrum is observed in the indirect dimension. In many cases, improved chemical shift resolution is achieved. In the case of a disordered material, heterogeneous broadening caused by a chemical shift distribution limits the degree to which the resolution of the spectrum is enhanced by FSLG decoupling. Thus, this pulse sequence is used in the present study to distinguish broadening due to strong couplings from chemical shift dispersion as a result of structural inhomogeneity.
Investigations of dynamics in the model salts included variable temperature 1D NMR spectroscopy, as well as exchange-based experiments. Exchange studies can be effectively used to probe the dynamics of functional groups such as phosphonate, which are known to facilitate ion conduction processes in the solid-state. A particularly useful NMR pulse sequence called center-band only detection of exchange (CODEX) translates the changes in a local chemical environment of a nucleus and into relative intensity data which report on the timescale and type of reorientation.36 The pulse sequence measures the timescale and geometry of the reorientation through the chemical shift anisotropy (CSA). The sensitivity of the CODEX experiment relies on the amount of recoupling applied and presumes that no exchange occurs during the recoupling periods. Therefore, the timescale of dynamics accessible with this method is limited to timescales greater than the rotor period, such that the method is sensitive to millisecond-timescale dynamics. During the mixing time, the CSA tensors may be influenced by molecular reorientations, such that they are no longer recoupled by the π-pulse train following the mixing time. This dephasing of the magnetization occurs as a function of mixing time, allowing the timescale of motion to be determined. Moreover, the geometry of the reorientation determines the plateau reached in the dephasing curve.36 Fast exchange mechanisms like the oscillation of a hydrogen bond inside the potential well of the bond would exceed the timescale capacity of the measurement. Motion of nearby molecules would produce a negligible effect on the CSA of the center being investigated creating a very low amplitude motion requiring very long recoupling times in order to be sampled. The CODEX pulse sequence is susceptible to strong dipolar couplings which will attenuate the signal in a similar fashion to a reorientation.37 This must be considered in the data analysis, as presented below. A series of variable temperature experiments measure a corresponding change in the correlation time which is used to confirm that the measured correlation times are indeed caused by thermally activated molecular dynamics.
Experimental
15N labeled imidazole, natural abundance imidazole, and methylphosphonic acid were purchased from Sigma Aldrich. The imidazolium methylphosphonate powder was prepared by mixing stoichiometric amounts of each ion in the minimum amount of methanol needed to dissolve each component. Evaporation of the solvent yielded clear crystals that were subsequently ground and further dried at 70–80 °C to remove trace amounts of methanol.The NMR experiments were conducted on an Bruker 500 MHz Avance system using double resonance probes that support rotors with an outer diameter of 2.5 mm or 4 mm at 25 kHz and 10 kHz MAS, respectively. All high-resolution 1H NMR was carried out using a 90° pulse width of 2.5 μs on the 2.5 mm probe. The 13C and 31P CODEX experiments were acquired using 8 μs recoupling pulses and 3000 μs contact pulses to ensure saturation of the desired nucleus. 13C CODEX analysis of the 15N labeled sample required long acquisition times of ∼3–6 h per mixing time, due to the limited amount of 15N labeled sample. Isotropic enrichment of the nitrogen atoms in imidazole was used to reduce any additional dephasing caused by dipolar-induced relaxation.37 Additional dephasing could alter the observed correlation time and plateau of the exchange curve.
The on-resonance field for the FSLG decoupling was set to 83.3 kHz while the off-resonance fields were ±58.9 kHz with a 2 kHz asymmetric offset. The scaling factor for the indirect dimension was set to 0.578. Contact pulses of 3000 μs were used to acquire the 1D CPMAS experiments. Temperature calibration of the MAS probes was performed using a sample of samarium stannate.38
An Autolab PGSTAT 30 was used to measure the AC impedance of a two-electrode cell, frequency range used was 500 kHz down to 0.1 Hz. The pellet had a thickness of 0.175 cm with a radius of 0.476 cm. The sample was allowed to equilibrate at a given temperature for a minimum of 4 h between impedance measurements.
Results and discussion
Structure
Imidazole methylphosphonate (Fig. 1b) was chosen to model the hydrogen bonding donor and acceptor sites of the copolymer vinylimidazole vinylphosphonate to gain insight into the relative ionic conductivity of the polymer when compared to other proton exchange membranes. In a previous study, Fischbach et al. investigated the ring flip motion of the imidazole methylsulfonate (IMS) analogue of imidazole methylphosphonate (IMMPA).39 The structural similarity of the two compounds suggests the ring flip mechanism is likely present in the phosphonate derivative, and the ring flip was verified by 13C and 15N variable temperature NMR for IMS.39 However, the number of hydrogen bond acceptor sites is known to play a significant role in the crystal packing. The two salts differ in their hydrogen bonding motifs, with an additional hydrogen bonding donor atom in the methylphosphonate anion compared to a single hydrogen bonding donor atom in methylsulfonate. This results in shared hydrogen bonding protons between multiple sites, and influences the dynamics of the two salts, as seen below.The 1H MAS spectra (above) and DQF spectra (below) are shown in Fig. 2 for the two compounds. The 1H MAS NMR spectra reveal the different proton chemical environments of the salts, IMMPA and IMS. The chemical shift of the two N–H⋯O hydrogen-bonded protons occur at the same position since similar nitrogen to oxygen distances are found in the crystal structures. The chemical shift of a hydrogen bond is determined primarily by the heterogeneous atoms, which control the bond lengths and local packing of the imidazole ring.40 The O–H⋯O hydrogen bond has a lower chemical shift compared to N–H⋯O hydrogen bonds, which arises from reduced hydrogen bond strength.31 Furthermore, the chemical shift assignment is similar to previous investigations on the Bi-PA analogue compound due to their similar number of hydrogen bonding donor and acceptor sites.28
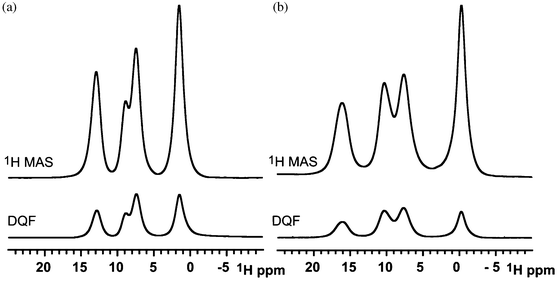 | ||
| Fig. 2 (a) The 1H MAS NMR spectrum of IMS (above) and the corresponding 1H-1H DQF NMR spectrum (below). (b) The corresponding 1H MAS NMR and 1H-1H DQF NMR spectrum for IMMPA. All spectra were acquired at 25 kHz MAS. | ||
Resonances in the 1H-1H DQF spectra arise from double quantum coherence between spins with homonuclear dipolar couplings on the timescale of the MAS frequency. If a spin experiences an attenuated dipolar coupling due to mobility, the reduction in the strength of the dipolar coupling lowers the intensity of the recoupled resonance. For mobile protons, which experience motionally averaged dipolar couplings, the BABA pulse sequence cannot successfully recouple any intensity due to the poor excitation efficiency for weakly coupled species. In Fig. 2 the DQF spectrum closely resembles the 1H MAS spectrum of each compound, respectively. The degree of signal attenuation in the DQF spectra which were recoupled for one rotor period, at 25 kHz MAS, is equivalent. Additional rotor periods of recoupling show a collective decrease in signal suggesting molecular dynamics which lead to attenuated dipolar couplings. Further consideration of the dynamics in these materials is provided below.
The 2D 1H-1H DQC spectrum correlates homonuclear spin pairs and separates the couplings based on the chemical shift of the resonances (Fig. 3). It is not uncommon to observe all possible spin pairs in densely packed organic salts. In this case, IMMPA is a tightly packed lattice, and the observed spin pairs are summarized in Table 1. The table lists the two single quantum chemical shifts that sum to the double quantum chemical shift in the indirect dimension of Fig. 3. A vertical slice taken through the 16 ppm frequency (A resonance) in the single quantum dimension of Fig. 3 corresponds to the two protons on either side of the imidazole ring. Although the hydrogen bonding on either side of the imidazole ring is different, the change in chemical shift for those protons is very small. The small difference in hydrogen bond distances (2.653 versus 2.673 Å, as measured by X-ray diffraction at 173 K) results in nearly identical chemical shifts for these protons, which are not resolved in the 1D 1H MAS spectrum (Fig. 2b) at this field strength. However, in the single quantum projection of the DQC spectrum, Fig. 3, the broad, flattened A resonance reveals that this resonance in fact comprises two closely overlapping lineshapes which suggests two different chemical shifts for the N–H protons. Only one of the A protons is expected to have a strong dipolar coupling to the O–H⋯O hydrogen bond, due to the crystallographic packing. This can be confirmed and assigned by examining the 2D 1H DQC spectrum. The intense AB cross-peak correlation has single quantum chemical shifts of 15.8 (A′) and 9.8 (B) ppm and a double quantum frequency of 25.4 ppm. The A′ frequency is offset from the middle of the broad A resonance to a lower chemical shift (Δ≅ 0.3 ppm). The oxygen atoms involved in the N–HA′⋯O hydrogen bonding also participate in a second O–HB⋯O hydrogen bond, this results in a lengthening of the N–O distance. The oxygen atom in the N–HA⋯O hydrogen bond on the side of the imidazole ring is not bifurcated and causes the hydrogen to be pulled further from the nitrogen which results in a higher 1H chemical shift. This change in chemical shift is small and is only visible through the contours and the projections at this resolution. If both protons experienced the same coupling then the contour would appear as an oval stretched in the single quantum dimension, as is the case for AA′ and AD. The AA′ dipolar coupling at 15.9 ppm in the single quantum dimension or the AD coupling at 15.8 ppm in the single quantum dimension has an oval shape indicating that the dipolar coupling is recoupled for both A protons on either side of the imidazole ring. The lower intensity of the weak AA′ dipolar coupling likely arises due to the long-range packing contact between the two protons.
 | ||
| Fig. 3 The 2D 1H-1H DQC NMR spectrum shows the dipolar connectivity of the protons in the solid-state structure (left). The protons in the structure are labeled from A to D, A and B being hydrogen-bonded protons, C are aromatic protons, D are methyl protons (right). | ||
| Dipolar coupling pair | 1st single quantum chemical shift | 2nd single quantum chemical shift | Double quantum chemical shift |
|---|---|---|---|
| AA′ | 15.9 | 15.9 | 31.7 |
| AB | 15.8 | 9.8 | 25.4 |
| AC | 16.0 | 7.5 | 23.9 |
| AD | 15.8 | −0.4 | 15.2 |
| BB | 10.1 | 10.1 | 19.8 |
| BC | 10.1 | 7.4 | 17.4 |
| BD | 10.2 | −0.5 | 9.5 |
| CC | 7.4 | 7.4 | 14.8 |
| CD | 7.4 | −0.5 | 6.6 |
| DD | −0.5 | −0.5 | −1.2 |
The small difference in hydrogen bond distance and the strong homonuclear dipolar couplings both greatly decrease our ability to resolve these two resonances in a simple 1H MAS spectrum. Moreover, even in the case of the 2D DQC spectra, much of the interpretation is based on distinguishing subtle differences in contour shape among strongly overlapping resonances in the complex hydrogen-bonded structure. Frequency-switched Lee–Goldburg is a homonuclear decoupling scheme that attenuates the strong dipolar couplings between the protons based on a combination of both sample spinning and pulses applied at the magic angle.41 Application of FSLG during the t1-evolution period of a pulse sequence will produce a 2D spectrum with narrow resonances in the indirect dimension that compete and surpass the resolution provided by MAS alone. The heteronuclear 2D 31P-1H FSLG-CPMAS spectrum was acquired, and the sum over the 31P resonance in the direct dimension is shown as Fig. 4. The inset of Fig. 4 shows the increase in resolution achieved using FSLG decoupling under 10 kHz MAS. The overlapping two resonances shown in the inset correspond to the protons in the N–H⋯O hydrogen bonds, A and A′, as above. The linewidths of the A and A′ resonances are 250 Hz each, while the A and A′ resonances extracted from the projection of the DQC spectrum are 900 and 1100 Hz. The A′ proton has a larger linewidth because that proton has an extra dipolar coupling to the nearby proton in the O–HB⋯O hydrogen bond. The FSLG data imply that the timescale of a ring flip in IMMPA that would exchange these two protons is slower than the separation between these two resonances. The separation of 0.48 ± 0.05 ppm (240 Hz) provides an upper limit for the timescale of dynamics, at 4.2 ± 0.4 ms. If the rotation of the imidazole cation had a correlation time below this, a single coalesced resonance for the A protons would be observed. In comparison to IMS where ring dynamics have been observed, the correlation time was 3.6 ± 0.3 ms at ambient temperature, which was derived from 13C CODEX NMR.39 Since the local dynamics of the imidazole ring in IMMPA cannot average these two resonances, the imidazole ring rotation contributes negligibly to proton transport at this temperature.
 | ||
| Fig. 4 A sum over the 31P resonance in the 2D 31P-1H FSLG-CPMAS spectrum results in a 1H-1H decoupled 1H MAS spectrum. The inset shows that the A resonance is resolved as two protons with nearly identical chemical shifts. | ||
Proton dynamics by 1H NMR
The macroscopic ionic conductivity of IMMPA was measured using impedance spectroscopy from room temperature to 115 °C. The room temperature conductivity of IMMPA is 2.0 × 10−9 S cm−1, which is significantly slower than competing hydrated membrane technologies. However, this strongly thermally activated system responds to increased temperature with a substantial increase in conductivity to 1.8 × 10−5 S cm−1 at 115 °C, as shown in Fig. 5. The large change in ionic conductivity correlates to a large activation energy (42 ± 2 kJ mol−1) for the overall process of ion conduction. The modest ionic conductivity observed at ambient temperature suggests that the material conducts protons, although the slow dynamics responsible for this are not evident in the 1D 1H MAS NMR spectrum. Nevertheless, an indication of these dynamics is provided by the comparison to the DQF spectra shown in Fig. 2, where the attenuated signal as a function of recoupling time is consistent with a degree of molecular motion at ambient temperature.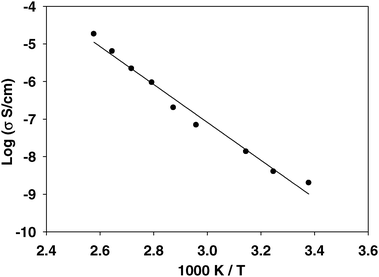 | ||
| Fig. 5 A plot of ionic conductivity measured by impedance spectroscopy versus temperature, showing a steady increase in conductivity. The activation energy for the conduction process is 42 ± 2 kJ mol−1. | ||
Solid-state 1H MAS NMR acquired as a function of temperature is used to probe the mobility of the protons in hydrogen bonds. Fig. 6a shows a series of 1H MAS NMR spectra acquired between 310 and 370 K. The dynamics of the methylphosphonate begin to influence the lineshape of the 1H NMR spectrum at approximately 363 K. Increasing ionic conductivity is proportional to the increasing number of charge carriers. Thus, in light of the conductivity data the new proton resonance in the 1D NMR spectra is assigned to a mobile component, based on both its chemical shift and lineshape, as well as its response to the DQF. These spectra (Fig. 6b) show that the new peak at δ = 11.4 ppm is removed by the DQF sequence, consistent with this species arising from mobile hydrogen-bonded protons within the salt. The chemical shift trend of this proton resonance is also consistent with the mobility of the associated protons, as the increasing frequency represents the changing weighting of an active chemical exchange process (Fig. 7).
 | ||
| Fig. 6 (a) The variable temperature stack plot of the 1H MAS NMR spectra of IMMPA and (b) the corresponding 1H-1H DQF spectra, acquired at 25 kHz MAS, with one rotor periods of recoupling. | ||
 | ||
| Fig. 7 The plot of 1H chemical shift versus temperature for the hydrogen-bonded protons shows a distinct change in slope at 364 K. | ||
Thermal analysis of IMMPA by the differential scanning calorimetry is presented in the ESI.† In the range of 40 to 160 °C a single only thermal transition is observed which corresponds to a melting point at 132 °C. The thermal analysis of IMMPA does not show evidence of any secondary phase transitions prior to melting. This is in contrast to the solid acids such as CsH2PO4, where solid-state phase transitions have been shown to enable sudden increases in ionic conductivity.42 The lack of any transition prior to the melt indicates that structural transitions leading to dynamics within IMMPA are not observable by this method. From this, it is concluded that a constant increase in thermal energy allows faster dynamics within the original crystalline phase, rather than permitting a reorganization of new solid phase at a particular temperature. The onset of the melting transition observed by DSC begins near 120 °C, well above any of the NMR spectra in Fig. 6.
The rapid line narrowing occurs over a narrow temperature range, and corresponds to a large activation energy for the onset of local proton dynamics. Several new resonances are observed upon increasing the temperature. The most significant of these is the resonance initially at 11.2 ppm and 357 K. This is an intermediate resonance between the chemical shifts of the N–H⋯O and O–H⋯O hydrogen bonds. Based on the comparatively low frequency of this new peak, proton dynamics in IMMPA begins between the O–H⋯O and N–H⋯O hydrogen bonds via the rotation of the phosphonate group, similar to the dynamics observed in Bi-mPA.28 As the temperature increases, the rate of exchange increases, thereby averaging the chemical shift of the exchanging protons.43 The average chemical shift between one N–H⋯O and one O–H⋯O is 13.1 ppm, whereas the new resonance in Fig. 6a begins at 11.1 ppm. As the temperature increases, the chance of a successful exchange increases, causing the chemical shift to trend to higher frequency. A plot of chemical shift change versus temperature in Fig. 7 illustrates the movement of the emerging resonance of Fig. 6a with temperature. The change in slope at 364 K suggests that another process is contributing to the coalescence of the resonances above this temperature. As well, above 364 K the narrowing of the aromatic resonances increases, signifying increased mobility of the imidazole ring. Prior to the ring flip motion, the exchange between the bifurcated hydrogen bonds is the only allowed pathway for a proton to cross the solid-state structure. Since the hydrogen bonding in IMMPA is similar to its benzimidazole analogue, Bi-mPA, the conduction of protons was expected to follow the previous example.28 However, with both the ring flip and the rotation of the phosphonate available, exchange between all three hydrogen bonds is possible. This ring flip mechanism is not available in the Bi-mPA salt, due to the greater steric bulk of the cation. In IMMPA, while ring reorientation does take place, the complete coalescence of the three hydrogen-bonded resonances is postulated to occur at the average of the three protons chemical shifts at 14.1 ppm. The largest observed chemical shift in the variable temperature data set was 12.3 ppm, which is well below the average of the three hydrogen-bonded resonances. Therefore, equally weighted population exchange is not observed at the temperatures of these experiments, and is presumed to only be achieved once the salt is molten. Nevertheless, these data provide strong evidence for solid-state proton transport involving contributions of both cation and anion dynamics. This case is similar to the triazole heterocycle case studied by Akbey et al., where triazole dynamics were elucidated by lineshape analysis, providing insight into the equilibria within the hydrogen bonding motif.22 Chemical shift trends in IMMPA indicate a comparable result, where the hydrogen bonding behavior at higher temperatures facilitates the rotation of the phosphonate then the imidazole ring.22 In the case of IMMPA the hydrogen bonding surrounding the phosphonate breaks first, allowing the motion of the phosphonate to occur readily, suggesting that the limiting step in the rotation of the phosphonate is the breaking of the A hydrogen bond. The proton transport mechanism includes, but does not rely on the rotation of the imidazole ring, in contrast with Bi-mPA, where cation dynamics are prohibited.28 Further evidence for this mechanism is provided by the heteronuclear studies of the cations and anions individually.
Heteronuclear NMR studies of ion dynamics
There are two basic mechanisms for proton conduction available for vinylimidazole and vinylphosphonate copolymers: the ring flip motion of imidazole and the rotation of the phosphonate group, both of which are examples of a Grotthus (structural) diffusion mechanism of ion conduction.44 To support the 1H NMR results, heteronuclear studies can be applied. In the 1D 13C CPMAS spectrum of imidazole methylphosphonate, the 4/5 carbon atoms of the imidazole ring share the same chemical shift due to either having equivalent structure or undergoing chemical exchange. In IMS the resonances of the 4/5 carbon atoms of the ring coalesce as the correlation time for ring dynamics is shortened.45 In the case of IMMPA, in particular, lowering the temperature did not cause any significant change in the 1D 13C CPMAS. It did not resolve the overlapping 4/5 13C resonances. This implies that the overlap is due to a similar chemical shift and not ring dynamics. This is consistent with a lack of observable ring flipping at ambient temperature, as seen in the 1H NMR data above.The slow reorientations of solid-state materials have been monitored by using variations in the CSA.46–48 CODEX is a specialized pulse sequence that determines the timescale and the type of motion that is accessible to a functional group or molecule.36,49 Multinuclear CODEX can be used to confirm and quantify both of these mechanisms of solid-state dynamics, since both mechanisms produce a change in the chemical shift anisotropy (31P or 13C) from the variations in the hydrogen bonding environment. For a three-site motion, the expected plateau would be 66%, whereas for a ring flip of either an imidazole or a benzimidazole ring, the expected plateau is 50%.
13C CODEX NMR is used here to characterize dynamics of the imidazole cations. The cation ring flip in IMS and Bi-mPA occurs on very different time scales; in IMS the imidazole ring rotation has a timescale of tens of milliseconds while the benzimidazole ring flip cannot be detected using 13C CODEX NMR.28,39 For IMMPA the imidazole ring flip does occur but is slower than the sulfate analogue. The 13C exchange curve is plotted in Fig. 8. The correlation time of the imidazole ring in IMS is 3.6 ± 0.3 ms at 23 °C while the correlation time for IMMPA is 31 ± 9 ms at 23 °C with a 50% plateau, again consistent with observations from the 1H NMR spectra shown above. Selectively labeling this material with the spin half 15N isotope reduced the probability for any additional dephasing due to the fast relaxation of the quadrupolar nucleus.37 Additional dephasing would obscure any geometry information obtained from the plateau of the exchange curve in Fig. 8. The hydrogen bonding in IMS has one more oxygen atom from the sulfonate to which the hydrogen atoms may bind. This leads to longer hydrogen bonding distances in the crystal structure, Fig. 1b. The longer hydrogen bonds in IMS result in weaker hydrogen bonding around the imidazole ring that allows it to rotate more freely, as evidenced in the relative 13C correlation times for the imidazole cation. The change in hydrogen bonding motif due to the extra hydrogen bonding donor in IMMPA plays a significant role in increasing the strength of the hydrogen bonding and thereby limiting the dynamics of the imidazole ring in this compound.
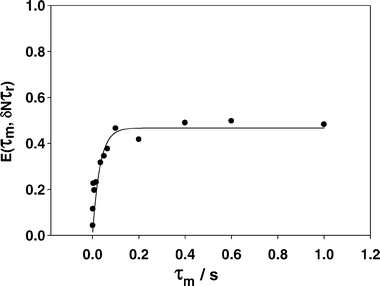 | ||
| Fig. 8 The 13C normalized pure exchange curve for IMMPA, which shows a plateau at 0.5, or 50% intensity, consistent with a two-site rotation around the C2v axis of the imidazole ring. The correlation time for the ring flip is 31 ± 9 ms. | ||
A plot of the 31P normalized pure exchange CODEX NMR signal versus mixing time is shown in Fig. 9a. Fitting the attenuation of the 31P CODEX NMR signal to an exponential function yields a correlation time for the rotation of the phosphonate. The plateau of the 31P CODEX NMR is 10% higher than the expected 66% due to longitude relaxation transmitted through a dipolar coupling.37 By using a double exponential, the motion of the phosphonate and the spin relaxation of the phosphorous spin were fitted. Table 2 shows the correlation times of the exponentials representing the motion of the phosphonate. For room temperature the correlation time is 57 ± 4 ms with a plateau of 53 ± 6% for the exponential representing the motion of the phosphonate. The relaxation portion of the data set is 21 ± 6% with a correlation time of 7 ± 3 ms and when the results are renormalized to include only exchange, the weighting for the second exponential is (52%/(100% − 21%) = 66% which corresponds to a three-fold motion, as expected for this anion.
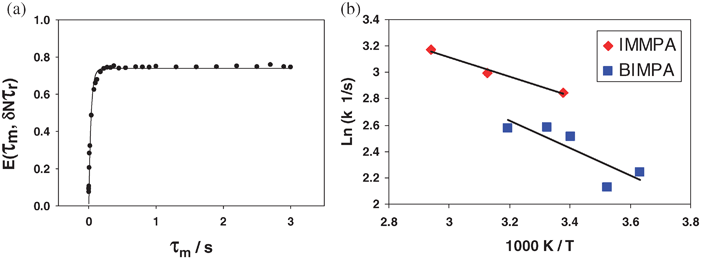 | ||
| Fig. 9 (a) The 31P normalized pure exchange curve for IMMPA and (b) the variable temperate plot of the different rate constants. The exchange curve is used to obtain a correlation time, which is shown to change with temperature indicating that the process observed is related to the motion of the phosphonate. | ||
| Temperature/K | Weight (%) | Correlation time/ms |
|---|---|---|
| 296 | 52 ± 3 | 58 ± 4 |
| 320 | 55 ± 4 | 50 ± 4 |
| 340 | 67 ± 4 | 42 ± 4 |
To justify the weighting of the dynamic process and the spin-diffusion process, the same experiment was performed at different temperatures. The correlation time for the dynamic process changes with temperature, whereas spin-diffusion is temperature independent.37 Using analogous data processing to that above, a temperature increase to 320 K resulted in a correlation time for the phosphonate reorientation of 50 ± 5 ms with a plateau of 55 ± 6%, again with a spin diffusion of 22 ± 6% and time of 7 ± 3 ms. This implies that the correlation time is sensitive to temperature change indicating that the dynamics of the phosphonate is increasing with temperature. Fig. 9b shows a plot of two sets of 31P CODEX correlation times, for the methylphosphonate anion paired with a benzimidazole and with an imidazole cation, respectively. The activation energy for the rotation of the methylphosphonate rotation is quite low at 9 ± 3 kJ mol−1 for the Bi-mPA while for IMMPA the activation energy is 6 ± 3 kJ mol−1 for the phosphonate dynamics. These activation energies are similar to the values obtained from a molecular dynamics study run on CsHSO4 which found an activation energy of 7.5 kJ mol−1 for a rotation of the sulfate around one S–O bond.50 The solid acid family, to which CsHSO4 belongs, is a series of small molecule ion conductors.50–54 The ion conduction in solid acid materials occurs through the hydrogen bonding of the material and is facilitated by the rotation of the anion. The previously reported activation energy is for the rotation of the sulfate in CsHSO4 and matches the magnitude of the activation energy measured for the rotation of the phosphonate in IMMPA. This strongly suggests that the 31P CODEX NMR experiments are probing the reorientation of the methylphosphonate, a slow reorientation in the solid-state on the millisecond timescale at room temperatures.
Conclusion
Anhydrous ionic conductivity in the solid-state for fuel cell electrolytes is a new topic that requires further development. Ion conduction in anhydrous materials follows a different motif than hydrated electrolytes. The ionic conductivity of an anhydrous electrolyte depends more on the solid-state hydrogen bonding and the dynamic range of the ions. For IMMPA, the local mobility of the methylphosphonate is a key component to the ionic conductivity. The 31P CODEX NMR shows that the rotation of the methylphosphonate has a low activation energy and this implies that the motion of the anion is not impeded by the solid-state structure. The smaller imidazole ring exhibits faster reorientation than a benzimidazole cation, but this motion does not yield significant line narrowing in the 1H variable temperature NMR experiments until higher temperatures (>363 K). Chemical exchange, observed through the appearance of a new resonance in the hydrogen bonding region, appears to occur first between phosphonate groups suggesting that proton transport between anions is the preferred pathway at lower temperatures until the imidazole ring dynamics are activated. When the imidazole ring starts to rotate it exchanges both N–H⋯O hydrogen-bonded protons. With the rotation of both the cation and anion, a beneficial cooperative mechanism of ion conduction exists. This is supported by the increase in 1H chemical shift of the mobile hydrogen-bonded resonance, as well as temperature-dependent heteronuclear CODEX studies of the cations and anions individually.Acknowledgements
JWT acknowledges scholarship support through the Ontario Graduate Scholarship program. This research was supported by an NSERC Discovery grant to GRG. The authors are grateful to Bob Berno and Alex D. Bain for their helpful discussions regarding the FSLG experiments.References
- A. Rodrigues, J. C. Amphlett, R. F. Mann, B. A. Peppley and P. R. Roberge, Proceedings of the Intersociety Energy Engineering Conference, The American Institute of Chemical Engineers, New York, NY, 1997 Search PubMed.
- L. Ghassemadeh, M. Marrony, R. Barrera, K. D. Kreuer, J. Maier and K. Muller, J. Power Sources, 2009, 186, 334–338 CrossRef.
- A. Kabasawa, J. Saito, K. Miyatake, H. Uchida and M. Watanabe, Electrochim. Acta, 2009, 54, 2754–2760 CrossRef CAS.
- G. Ye, C. A. Hayden and G. R. Goward, Macromolecules, 2007, 40, 1529–1537 CrossRef CAS.
- P. D. Beattie, F. P. Orfino, V. I. Basura, K. Zychowska, J. Ding, C. Chuy, J. Schmeisser and S. Holdcroft, J. Electroanal. Chem., 2001, 503, 45–56 CrossRef CAS.
- A. V. Anantaraman and C. L. Gardner, J. Electroanal. Chem., 1996, 414, 115–120 CrossRef CAS.
- J. J. Baschuk and X. LI, Int. J. Energy Res., 2001, 25, 695–713 CrossRef CAS.
- K. S. Hwang, M. Yang, Z. Ji, J. Grunes and G. A. Somorjai, J. Mol. Catal. A: Chem., 2003, 204–205, 499–507 CrossRef CAS.
- Q. Li, R. He, J. O. Jensen and N. J. Bjerrum, Chem. Mater., 2003, 15, 4896–4915 CrossRef CAS.
- L. Xiao, H. Zhang, E. Scanlon, L. S. Ramanathan, E.-W. Choe, D. Rogers, T. Apple and B. C. Benicewicz, Chem. Mater., 2005, 17, 5328–5333 CrossRef CAS.
- C. E. Hughes, S. Haufe, B. Angerstein, R. Kalim, U. Mahr, A. Reiche and M. Baldus, J. Phys. Chem. B, 2004, 108, 13626–13631 CrossRef CAS.
- Q. Li, R. He, J. O. Jensen and N. J. Bjerrum, Fuel Cells (Weinheim, Ger.), 2004, 4, 147–159 Search PubMed.
- J. A. Asensio, S. Borros and P. Gomez-Romeroa, J. Electrochem. Soc., 2004, 151, A304–A310 CrossRef CAS.
- U. Akbey, R. Graf, Y. G. Peng, P. P. Chu and H. W. Spiess, J. Polym. Sci., Part B: Polym. Phys., 2009, 47, 138–155 CrossRef CAS.
- Y. J. Lee, B. Bingol, T. Murakhtina, D. Sebastiani, W. H. Meyer, G. Wegner and H. W. Spiess, J. Phys. Chem. B, 2007, 111, 9711–9721 CrossRef CAS.
- A. Bozkurt, W. H. Meyer, J. Gutmann and G. Wegner, Solid State Ionics, 2003, 164, 169–176 CrossRef CAS.
- M. F. H. Schuster, W. H. Meyer, M. Schuster and K. D. Kreuer, Chem. Mater., 2004, 16, 329–337 CrossRef CAS.
- C. C. de Araujo, K. D. Kreuer, M. Schuster, G. Portale, H. Mendil-Jakani, G. Gebel and J. Maier, Phys. Chem. Chem. Phys., 2009, 11, 3305–3312 RSC.
- M. Schuster, K. D. Kreuer, H. Steininger and J. Maier, Solid State Ionics, 2008, 179, 523–528 CrossRef CAS.
- S. Beyazyildirim, K. D. Kreuer, M. Schuster, A. J. Bhattacharyya and J. Maier, Adv. Mater., 2008, 20, 1274–1278 CrossRef CAS.
- H. Steininger, M. Schuster, K. D. Kreuer, A. Kaltbeitzel, B. Bingol, W. H. Meyer, S. Schauff, G. Brunklaus, J. Maier and H. W. Spiess, Phys. Chem. Chem. Phys., 2007, 9, 1764–1773 RSC.
- U. Akbey, S. Granados-Focil, E. B. Coughlin, R. Graf and H. W. Spiess, J. Phys. Chem. B, 2009, 113, 9151–9160 CrossRef CAS.
- S. U. Celik, U. Akbey, R. Graf, A. Bozkurt and H. W. Spiess, Phys. Chem. Chem. Phys., 2008, 10, 6058–6066 RSC.
- R. H. He, Q. T. Che and B. Y. Sun, Fibers Polym., 2008, 9, 679–684 Search PubMed.
- J. R. P. Jayakody, S. H. Chung, L. Durantino, H. Zhang, L. Xiao, B. C. Benicewicz and S. G. Greenbaum, J. Electrochem. Soc., 2007, 154, B242–B246 CrossRef CAS.
- R. H. He, Q. F. Li, J. O. Jensen and N. J. Bjerrum, J. Polym. Sci., Part A: Polym. Chem., 2007, 45, 2989–2997 CrossRef CAS.
- S. U. Celik, U. Akbey, R. Graf, A. Bozkurt and H. W. Spiess, Phys. Chem. Chem. Phys., 2008, 10, 6058–6066 RSC.
- J. W. Traer, J. F. Britten and G. R. Goward, J. Phys. Chem. B, 2007, 111, 5602–5609 CrossRef CAS.
- N. N. Greenwood and A. Thompson, J. Chem. Soc., 1959, 3485–3492 RSC.
- S. P. Brown and H. W. Spiess, Chem. Rev., 2001, 101, 4125–4155 CrossRef CAS.
- G. A. Kumar and M. A. McAllister, J. Org. Chem., 1998, 63, 6968–6972 CrossRef.
- G. Ye, N. Janzen and G. R. Goward, Macromolecules, 2006, 39, 3283–3290 CrossRef CAS.
- M. Feike, D. E. Demco, R. Graf, J. Gottwald, S. Hafner and H. W. Spiess, J. Magn. Reson., Ser. A, 1996, 122, 214–221 CrossRef CAS.
- M. Lee and W. I. Goldburg, Phys. Rev., 1965, 140, A1265–A1271.
- C. Coelho, J. Rocha, P. K. Madhu and L. Mafra, J. Magn. Reson., 2008, 194, 264–282 CrossRef CAS.
- E. R. deAzevedo, W. G. Hu, T. J. Bonagamba and K. Schmidt-Rohr, J. Am. Chem. Soc., 1999, 121, 8411–8412 CrossRef CAS.
- K. Saalwachter and K. Schmidt-Rohr, J. Magn. Reson., 2000, 145, 161–172 CrossRef CAS.
- G.-J. M. P. van Moorsel, E. R. H. Van Eck and C. P. Grey, J. Magn. Reson., Ser. A, 1995, 113, 159–163 CrossRef CAS.
- I. Fischbach, H. W. Spiess, K. Saalwaechter and G. R. Goward, J. Phys. Chem. B, 2004, 108, 18500–18508 CrossRef CAS.
- C. F. Julio, Concepts Magn. Reson., 2004, 20A, 42–69 Search PubMed.
- M. Lee and W. I. Goldburg, Phys. Rev., 1965, 140, A1261–A1271 CrossRef.
- D. A. Boysen, S. M. Haile, H. Liu and R. A. Secco, Chem. Mater., 2003, 15, 727–736 CrossRef CAS.
- H. W. Spiess, Adv. Polym. Sci., 1985, 66, 23–58 CAS.
- C. J. T. Grotthuss, Ann. Chim. (Paris), 1806, 58, 54–74 Search PubMed.
- G. R. Goward, K. Saalwachter, I. Fischbach and H. W. Spiess, Solid State Nucl. Magn. Reson., 2003, 24, 150–162 CrossRef CAS.
- S. P. Brown, Macromol. Rapid Commun., 2009, 30, 688–716 CrossRef CAS.
- I. Fischbach, T. Pakula, P. Minkin, A. Fechtenkotter, K. Mullen, H. W. Spiess and K. Saalwachter, J. Phys. Chem. B, 2002, 106, 6408–6418 CrossRef CAS.
- C. Gervais, C. Coelho, T. Azais, J. Maquet, G. Laurent, F. Pourpoint, C. Bonhomme, P. Florian, B. Alonso, G. Guerrero, P. H. Mutin and F. Mauri, J. Magn. Reson., 2007, 187, 131–140 CrossRef CAS.
- D. J. Harris, T. J. Bonagamba, M. Hong and K. Schmidt-Rohr, Macromolecules, 2000, 33, 3375–3381 CrossRef CAS.
- C. R. I. Chisholm, Y. H. Jang, S. M. Haile and W. A. Goddard(III), Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 134103–134103-134120 CrossRef.
- W. Muench, K. D. Kreuer, U. Traub and J. Maier, Solid State Ionics, 1995, 77, 10–14 CrossRef CAS.
- T. Norby, M. Friesel and B. E. Mellander, Solid State Ionics, 1995, 77, 105–110 CrossRef CAS.
- A. I. Baranov, L. A. Shuvalov and N. M. Schagina, J. Exp. Theor. Phys., 1982, 36, 459–462.
- T. Uda, D. A. Boysen and S. M. Haile, Solid State Ionics, 2004, 176, 127–133.
Footnote |
| † Electronic supplementary information (ESI) available: Differential scanning calorimetry data. See DOI: 10.1039/b917360a |
| This journal is © the Owner Societies 2010 |
