The role of the methyl group in stabilising the weak N–H⋯π hydrogen bond in the 4-fluorotoluene–ammonia complex†
Matthew P. Goslinga, Igor Pugliesib and Martin C. R. Cockett*a
aDepartment of Chemistry, University of York, Heslington, York, UK YO10 5DD. E-mail: mcrc1@york.ac.uk; Fax: +44 (0)1904 432516; Tel: +44 (0)1904 434534
bLehrstuhl für BioMolekulare Optik, Ludwig-Maximilians-Universität, Oettingenstr. 67, D-80538 München, Germany. E-mail: igor.pugliesi@gmail.com
First published on 6th November 2009
Abstract
The 4-fluorotoluene–ammonia van der Waals complex has been studied using a combination of resonant two-photon ionisation (R2PI) spectroscopy, ab initio molecular orbital calculations and multidimensional Franck–Condon analysis. The R2PI spectrum shows two sets of features assignable to two distinct conformers: one in which the ammonia binds between the hydrogen meta to the methyl group and the fluorine atom in a planar configuration and the other a π-bound structure involving one bond between an ammonia hydrogen and the π-system and another between the ammonia lone pair and the slightly acidic hydrogens on the methyl group. Ground state estimated CCSD(T) interaction energies were computed at the basis-set limit: these calculations yielded very similar interaction energies for the two conformers, whilst zero point energy correction yielded a zero point binding energy for the π-complex about 10% larger than that of the in-plane, σ-complex. The results of multidimensional Franck–Condon simulations based on ab initio ground and excited state geometry optimisations and vibrational frequency calculations showed good agreement with experiment, with further improvements achieved using a fitting procedure. The observation of a π-complex in addition to a σ-complex supports the intuitive expectation that electron-donating groups should help to increase π-density and hence stabilise π-proton acceptor complex formation. In this case, this occurs in spite of the presence of a strongly electron-withdrawing fluorine atom.
Introduction
The binding affinity of small molecules with proteins is governed by numerous weak non-covalent interactions, the most ubiquitous of which is the hydrogen bond. Hydrogen bonding is conventionally defined as an attractive interaction between a proton donor and a proton acceptor which in the context of protein–ligand binding, might typically involve an NH group on a protein and a carbonyl group on a ligand. However, in ligands with an aromatic chromophore, the π-system can also potentially act as the proton acceptor and form weak hydrogen bonds with OH, NH or CH groups.1π-Hydrogen bonds have been recognised in the past few years for the important role they play in molecular recognition and association, molecular biology and crystal engineering.2–6 In the context of molecular biology, they have been shown to feature not only in the stabilisation of protein secondary structures1,7,8 but also in the binding of ligands in proteins.3–5 In spite of the large extent to which they feature in molecular association, far less is known about hydrogen bonding to π-systems than conventional hydrogen-bonding and this has undoubtedly resulted in significant gaps in our understanding of the electronic and thermodynamic driving forces behind molecular recognition and association.Electronic effects are commonly used in medicinal chemistry to alter, for example, the basicity of a proton-donating substituent such as an amide group, thereby changing its ability to interact with ionic binding groups. Similarly, in ligands with the potential to act as either π-proton acceptors or conventional proton donor/acceptors, the relative strengths of the different types of hydrogen bond can potentially be controlled using the electron-donating or -withdrawing power of any substituents. In their ab initio fragment molecular orbital study of a number of LCK protein–inhibitor complexes, Ozawa and co-workers reported that the LCK protein is stabilised by C–H⋯π and N–H⋯π hydrogen bonds.9 Furthermore, they were able to achieve a ten-fold increase in the potency of one inhibitor by replacing a 2-chloroaniline ring, containing a strongly electron-withdrawing substituent, with 2,6-dimethylaniline, containing two additional electron-donating substituents.
Model binary van der Waals complexes, studied in the gas phase using supersonic free jet expansion techniques, provide a means of establishing the intrinsic stabilities of different types of hydrogen bond, with the isolated environment of the complex allowing direct comparison with the results of computational calculations. A number of beautiful spectroscopic studies have been made of π-hydrogen bound complexes, most notably by Gotch and Zwier10 in their multiphoton ionisation studies of benzene–water clusters and by Blake and co-workers in their microwave and R2PI spectra of the benzene–water and benzene–ammonia complexes.11,12 The latter work was able to establish unambiguously that the water or ammonia binds above the plane of the benzene ring with one or more of the hydrogens directed towards the π-system.
In a recent study of the fluorobenzene–NH3 complex (FB–NH3), we have used a combination of resonant two-photon ionisation (R2PI) spectroscopy, ab initio electronic structure calculations and multidimensional Franck–Condon analysis to demonstrate that the observed complex is one in which the ammonia binds in the plane of the ring, forming a double-hydrogen-bonded six-membered ring with the fluorine atom.13 The effect of the strongly electron-withdrawing group in this case evidently depletes the π-electron density sufficiently to destabilise the π-bound conformer in favour of an in-plane σ-complex in spite of the inherent weakness of covalently bound fluorine as a hydrogen bond acceptor.14 Pratt and co-workers had previously shown in their analysis of the rotationally resolved S1–S0 electronic spectrum of the water complex of p-difluorobenzene (pDFB) that the complex adopts an in-plane structure, analogous with that proposed for FB–NH3.15 In the case of pDFB, it is perhaps not surprising that the presence of two strongly electron-withdrawing fluorine atoms should strongly favour in-plane binding, but the FB–NH3 result shows that a single electron-withdrawing group in an aromatic complex does appear more generally to mitigate against successful formation of π-hydrogen bond interactions. This conclusion is supported by a more recent study of complexes formed between the nucleobase mimic 2-pyridone and a number of n-fluorobenzenes, in which conventional hydrogen-bonding is found to be favoured over ππ-stacking for all n-fluorobenzenes with n = 1–5.16 Conversely, the presence of a single electron-donating group can greatly favour the formation of π-complexes with proton donor solvents such as ammonia. For example, Li and Bernstein concluded that ammonia binds to toluene with the hydrogen atoms of the ammonia coordinated with the π-system of the aromatic ring.17 However, where electron-donating groups themselves provide additional hydrogen-bonding opportunities, such as an amino group in aniline, the global minimum may well still be the more conventional hydrogen-bound form.
The aim of the present work is to establish whether or not a π-hydrogen bond can be stabilised in 4-fluorotoluene–NH3 (4FT–NH3), a complex containing an electron-donating group in addition to a strongly electron-withdrawing group. The methodology is similar to that employed in the fluorobenzene study, combining R2PI spectroscopy with ab initio and Franck–Condon calculations. The key difference with that work is the very much higher level of theory used here to determine ground state binding energies which provide a view of the relative stability of the different conformers. CCSD(T) single point calculations will be combined with basis-set extrapolation based on counterpoise corrected optimised geometries obtained at the MP2 level. The correlation between geometry change accompanying electronic excitation and vibrational activity in the R2PI spectrum is obtained from a multidimensional Franck–Condon analysis of the S1–S0 electronic transition for each conformer. This requires geometry optimisation and vibrational frequency calculations for both electronic states involved in the transition, conducted at the RICC2 level of theory.
4FT–NH3 has not previously been subject to spectroscopic study although the first electronically excited state of 4-fluorotoluene (4FT) has been studied by fluorescence excitation spectroscopy18 and REMPI spectroscopy19,20 with particular emphasis in some studies on internal rotation of the methyl group. In addition, the cation ground state has been studied by laser photoelectron spectroscopy21 and ZEKE spectroscopy in pump–probe experiments aimed at characterising the vibrational modes of both the S1 state and the cation ground state.22,23 The only van der Waals complex to have been studied spectroscopically is the 4-fluorotoluene–Ar complex which has been studied in its electronic ground state using rotational spectroscopy24 and in its S1 state and cation ground state using REMPI and MATI spectroscopies, respectively.19,25 The nature of the solvent in this case mitigates against binding anywhere other than the π-system because of the dominant role played by the dispersion interaction in binding the argon atom. In the case of 4FT–NH3 the binding of the ammonia will additionally be influenced by the relative strengths of interaction between the partial positive and negative charges on the ammonia and the regions of enhanced or depleted electron density on the aromatic chromophore.
Experimental
The experimental setup is essentially that described in detail elsewhere.26 4FT–NH3 was prepared in the gas phase using a supersonic free jet expansion of 4FT with ammonia and argon, at typical stagnation pressures of between 0.2 and 5 bar and at a typical sample reservoir temperature of 18 °C. Electronic excitation and ionisation was achieved using the Nd:YAG (Continuum Surelite III) pumped, frequency doubled output of one dye laser (Continuum Jaguar using Coumarin 152 and 153) acting as pump, with the frequency doubled output of a second dye laser (Radiant Narrowscan using Rhodamine B and Rhodamine 6G), acting as probe. The pump dye laser was calibrated using a neon optogalvanic lamp. All quoted energies are corrected to vacuum, but intensities of observed features have not been corrected to dye intensity profiles.Computational
Molecular orbital calculations were performed using the GAUSSIAN 03 and TURBOMOLE 5.9 suites of programs.27,28 Counterpoise corrected geometry optimisations and vibrational frequencies were initially performed on the electronic ground states of a number of different conformers of the neutral complexes using second order Møller–Plesset perturbation theory29 with the cc-pVTZ correlation consistent basis set of Dunning. The choice of this basis set for the geometry optimisations derives from the results of Shibasaki et al. who found that the under-representation of the binding determined for π-complexes using the cc-pVTZ basis-set compensates for the over-binding that results from the choice of the MP2 methodology.30 As a result the accuracy of MP2/cc-pVTZ level optimised geometries is actually very high and provides an excellent basis from which to perform higher level single point binding energy calculations.Interaction energies at the basis-set limit, ΔEMP2(limit), were calculated at the MP2 level using Helgaker’s method to extrapolate from counterpoise corrected interaction energies obtained using pairs of adjacent quality basis sets.31,32 In Helgaker’s method, interaction energies calculated at the MP2 level using Dunning’s augmented correlation consistent basis sets are fitted to the form a + bX−3 (where X is 2 for aug-cc-pVDZ, 3 for aug-cc-pVTZ and 4 for aug-cc-pVQZ). The best results are obtained from extrapolations using aug-cc-pVTZ and aug-cc-pVQZ MP2 calculations but where the latter proves intractable, very good results can still be obtained from results obtained using aug-cc-pVDZ and aug-cc-pVTZ bases.
The MP2 method, which includes double electron excitations, overestimates the correlation interaction energies when used with a large basis set.33 The result is that dispersion-bound π-complexes are overstabilised compared to in-plane hydrogen-bound complexes. The least computationally expensive method that is consistently capable of producing quantitatively accurate binding energies for both hydrogen and dispersion-bound complexes is the coupled cluster CCSD(T) method in which the single and double excitations are evaluated iteratively while triple excitations are included in a non-iterative way.34 However, even single point CCSD(T) calculations using large basis sets are completely intractable for the size of system studied here and so the accepted methodology involves applying a CCSD(T) correction to interaction energies computed at a lower level of theory. In the present case, this is achieved by performing counterpoise corrected single point CCSD(T) and MP2 calculations at the MP2/cc-pVTZ optimised geometry using the aug-cc-pVDZ basis set. The difference between CCSD(T) and MP2 interaction energies (ΔECCSD(T)−ΔEMP2) exhibits a relatively small basis-set dependence compared to the MP2 and CCSD(T) energies and so an approximate CCSD(T) interaction energy at the basis-set limit, ΔECCSD(T)(limit), can be computed as a simple correction to ΔEMP2(limit).
The computed interaction energies provide a computational view of the absolute and relative stabilities of different conformers. However, one of the most important additional diagnostics in helping to identify which conformers are observed experimentally is the change in geometry that occurs upon electronic excitation. To this end, geometry optimisation and vibrational frequency calculations were performed on the electronic ground and first excited states of the most stable conformers of the neutral complexes using second order resolution of the identity approximate coupled cluster with singles and doubles (RICC2) theory.35,36 Basis sets included the doubly polarised triple-zeta, def2-TZVPP, basis set of Ahlrichs and co-workers37,38 and the correlation consistent triple-zeta basis sets of Dunning (cc-pVTZ). The results of these calculations were used to generate a multidimensional Franck–Condon simulation which is compared with experiment (see ref. 39 for details of the methodology).
The Franck–Condon calculations were carried out using the coherent state model of Doktorov et al.40 This approach addresses the problem of how to treat the rotation and mixing of the normal modes of one electronic state within the normal mode basis of the other electronic state involved in the transition which would otherwise present considerable difficulties in reducing multidimensional Franck–Condon integrals to simple products of one-dimensional integrals. This problem was first considered by Duschinsky,41 who proposed that the two sets of normal coordinates are related to each other by a linear transformation. Our implementation of this approach allows for the calculation of Franck–Condon factors for progressions of up to 9 quanta in any one vibrational mode.39 Any differences in the standard orientation of the two states (ground and first singlet excited states) are accounted for by the inclusion of a Hougen–Watson axis switching matrix42 into the standard linear Duschinsky normal coordinate transformation procedure.
Results and discussion
1. Experimental: the (1+1′) R2PI spectrum of 4FT–NH3
The first 1000 cm−1 of the mass-resolved two-colour (1+1′) R2PI spectrum of 4FT–NH3 is compared to that of 4FT in Fig. 1. The most intense band in the R2PI spectrum of 4FT (Fig. 1(b)) appears at 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 ± 1 cm−1, in almost perfect agreement with that reported by Okuyama et al.18 To higher energy, the spectrum is characterised by a number of weak vibrational features appearing within the first 350 cm−1 or so, and to higher energy still, two groups of vibrational features of stronger intensity at about 400 cm−1 and 850 cm−1. The weaker features below 350 cm−1 are predominantly due to methyl internal rotation but low frequency benzene ring modes also appear in this region (11 and 15 modes). The bands at about 400 cm−1 are assigned to an overlapping pair of bands at 399.5 cm−1 (9b1 + 16a2)23 and a weaker 6a1 band at 410.4 cm−1 whilst the strong doublet at about 800 cm−1 is due to overlapping 121 and 11 ring fundamentals. The complete vibrational assignments are given in Table 1.
860 ± 1 cm−1, in almost perfect agreement with that reported by Okuyama et al.18 To higher energy, the spectrum is characterised by a number of weak vibrational features appearing within the first 350 cm−1 or so, and to higher energy still, two groups of vibrational features of stronger intensity at about 400 cm−1 and 850 cm−1. The weaker features below 350 cm−1 are predominantly due to methyl internal rotation but low frequency benzene ring modes also appear in this region (11 and 15 modes). The bands at about 400 cm−1 are assigned to an overlapping pair of bands at 399.5 cm−1 (9b1 + 16a2)23 and a weaker 6a1 band at 410.4 cm−1 whilst the strong doublet at about 800 cm−1 is due to overlapping 121 and 11 ring fundamentals. The complete vibrational assignments are given in Table 1. | ||
| Fig. 1 A comparison of the two-colour (1+1′) R2PI spectrum of (a) 4FT–NH3 with that of (b) 4FT. | ||
| 4FT (S1) | 4FT–NH3 (S1) | |||||||
|---|---|---|---|---|---|---|---|---|
| σ-complex | π-complex | |||||||
| One-photon energy/cm−1 | Δ/cm−1 | Assignmenta | One-photon energy/cm−1 | Δ/cm−1 | Assignmentc | One-photon energy/cm−1 | Δ/cm−1 | Assignmentc |
| a 4FT intramolecular mode assignments from ref. 18 unless otherwise indicated.b Assignments from ref. 23.c This work. | ||||||||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 718.1 718.1 | −20.8 | Hot band | ||||||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 859.8 859.8 | 0 | 00 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939.6 939.6 | 0 | 00 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 738.9 738.9 | 0 | 00 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 949.4 949.4 | 9.8 | 2β″ | ||||||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 959.5 959.5 | 19.9 | 4β″ | ||||||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766.2 766.2 | 27.3 | 1βz | ||||||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 913.2 913.2 | 53.4 | 3a1″ | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990.9 990.9 | 51.3 | 3a1″ | |||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 785.2 785.2 | 46.3 | 1βy | ||||||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 789.6 789.6 | 50.7 | 2βz | ||||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012.1 012.1 | 72.5 | 1β″1τ or 1β′ | ||||||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815.9 815.9 | 77.0 | 1σx | ||||||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821.7 821.7 | 82.8 | |||||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 024.1 024.1 | 84.5 | 1σ | ||||||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 826.3 826.3 | 87.4 | 1βy | ||||||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970.0 970.0 | 110.2 | 5e″ | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 044.0 044.0 | 104.4 | 5e″ | |||
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 997.1 997.1 | 137.3 | 111 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075.8 075.8 | 136.2 | 111 | |||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032.1 032.1 | 172.3 | 6a1′ | — | |||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 079.4 079.4 | 219.6 | 151 | — | |||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 116.3 116.3 | 256.5 | 7e″ | — | |||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 142.8 142.8 | 283.0 | 112 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220.7 220.7 | 281.1 | 112 | |||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 169.0 169.0 | 309.2 | 8e′ | — | |||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 259.3 259.3 | 399.5 | 9b1 + 16a2b | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 338.9 338.9 | 399.3 | 9b1 + 16a2 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 141.3 141.3 | 402.4 | 9b1 + 16a2 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270.2 270.2 | 410.4 | 6a1 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 344.2 344.2 | 404.6 | 6a1 | |||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 344.5 344.5 | 484.7 | — | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420.5 420.5 | 480.9 | — | |||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411.6 411.6 | 551.8 | 6b1 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 488.4 488.4 | 548.8 | 6b1 | |||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567.6 567.6 | 707.8 | — | — | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516.2 516.2 | 777.3 | — | ||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653.1 653.1 | 793.3 | 121b | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 729.8 729.8 | 790.2 | 121 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528.2 528.2 | 789.3 | 121 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660.2 660.2 | 800.4 | 11b | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736.9 736.9 | 797.3 | 11 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536.8 536.8 | 797.9 | 11 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673.5 673.5 | 813.7 | |||||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558.1 558.1 | 819.5 | 121 + 1βz | ||||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564.6 564.6 | 826.0 | 11 + 1βz | ||||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 576.3 576.3 | 837.7 | 121 + 1βy | ||||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 702.5 702.5 | 842.7 | |||||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 583.1 583.1 | 844.5 | 11 + 1βy | ||||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 607.4 607.4 | 868.8 | 121 + 1σx | ||||||
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614.2 614.2 | 875.6 | 11 + 1σx | ||||||
The R2PI spectrum of 4FT–NH3 (Fig. 1(a)) is dominated by a strong band origin at 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939 ± 1 cm−1, which appears 80 cm−1 to higher energy than that of 4FT. This spectral blue-shift indicates that the complex binding energy is smaller in the S1 state than in the electronic ground state by 80 cm−1: in other words, electronic excitation has weakened the van der Waals interaction. Spectral blue-shifts are rather less commonly observed in excitation spectra of aromatic van der Waals complexes than spectral red-shifts, because the majority of such complexes are generally dispersion-bound to the π-system. The toluene–NH3 complex, whose structure has been proposed as being π-bound, shows an apparent red-shift of about −30 cm−1,17 whereas ammonia and water complexes of fluorobenzene and p-difluorobenzene all of which have been shown to form in-plane hydrogen-bound structures show spectral blue-shifts ranging from 59 to 117 cm−1.13,15,43,44 A reasonable preliminary assignment of this feature then might be to associate it with an in-plane σ-complex.
939 ± 1 cm−1, which appears 80 cm−1 to higher energy than that of 4FT. This spectral blue-shift indicates that the complex binding energy is smaller in the S1 state than in the electronic ground state by 80 cm−1: in other words, electronic excitation has weakened the van der Waals interaction. Spectral blue-shifts are rather less commonly observed in excitation spectra of aromatic van der Waals complexes than spectral red-shifts, because the majority of such complexes are generally dispersion-bound to the π-system. The toluene–NH3 complex, whose structure has been proposed as being π-bound, shows an apparent red-shift of about −30 cm−1,17 whereas ammonia and water complexes of fluorobenzene and p-difluorobenzene all of which have been shown to form in-plane hydrogen-bound structures show spectral blue-shifts ranging from 59 to 117 cm−1.13,15,43,44 A reasonable preliminary assignment of this feature then might be to associate it with an in-plane σ-complex.
To higher energy, a number of weaker vibrational bands appear up to about 800 cm−1 internal energy, most of which are likely to be associated with either intermolecular (van der Waals) or intramolecular vibrational modes or combinations of the two. A notable feature of the spectrum is the rapid loss of oscillator strength with increasing internal energy compared to that of 4FT: this probably arises either from progressive dissociation in the S1 state to higher energy or from ion–molecule reactions occurring post-ionisation, with the cross-section increasing with increasing two-photon energy. Nevertheless, it appears relatively straightforward to associate the weak features at 399.3 and 404.6 cm−1 with the 9b1 + 16a2 and 6a1 bands seen in the 4FT spectrum, and those at 790.2 cm−1 and 797.3 cm−1 with the 121 and 11 fundamentals, respectively. All but the first of these show small red-shifts compared to 4FT, although the weakness of the features makes it difficult to be sure which of them have shifted and which have lost intensity to below the signal-to-noise floor. One additional group of features centred at about 620 cm−1 internal energy appears not to align obviously with any intramolecular bands seen in the 4FT spectrum, nor can they be associated with van der Waals combination bands. However, one possible explanation is that they are associated with a second isomer of the complex. This point will be discussed further below.
Immediately to the blue of the dominant band origin, the spectrum exhibits additional low-wavenumber vibrational structure which is most reasonably assignable to van der Waals vibrational mode activity. In addition, it is just possible to discern most of the weaker features associated with methyl internal rotation seen in the 4FT spectrum. The van der Waals structure bears a strong similarity to that observed in the FB–NH3 spectrum, with in particular the characteristic doublet of bands at 72 and 85 cm−1 showing strong similarities to the pair seen in the FB–NH3 spectrum at 75 and 86 cm−1. This similarity in the appearance of the low-wavenumber region of the spectrum lends further support to assignment to a σ-complex.
The defining feature of the spectrum, however, is the appearance of bands to lower energy, comprising weaker but more extended vibrational progressions building from an origin about 200 cm−1 to the red of the dominant origin band. Given that no analogous features appear in the FB–NH3 spectrum, which was recorded under very similar experimental conditions, an obvious possible assignment is that these bands are associated with a second conformer, which given the smaller integrated intensity (by a factor of 3.5) is likely to be slightly less stable than that responsible for the dominant origin. Further support for this provisional assignment derives from the group of features centred at 620 cm−1, relative to the origin at 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939.6 cm−1, which lie about 800 cm−1 to the blue of the −200 cm−1 origin. Thus, an assignment of this higher energy group of bands is that they are combination bands involving single quanta excitation in the intramolecular modes 1 and 12 of a second conformer of the complex. The very weak feature at 37
939.6 cm−1, which lie about 800 cm−1 to the blue of the −200 cm−1 origin. Thus, an assignment of this higher energy group of bands is that they are combination bands involving single quanta excitation in the intramolecular modes 1 and 12 of a second conformer of the complex. The very weak feature at 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 141 cm−1 would then align with where the 9b1 + 16a2 and 6a1 intramolecular bands would fall for this conformer. Given its obvious disparity in terms of intensity compared with the other bands in the region, the weak feature appearing 20 cm−1 to the red of the nominal origin band (at 36
141 cm−1 would then align with where the 9b1 + 16a2 and 6a1 intramolecular bands would fall for this conformer. Given its obvious disparity in terms of intensity compared with the other bands in the region, the weak feature appearing 20 cm−1 to the red of the nominal origin band (at 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 718.1 cm−1) is assumed to be a hot band, possibly in the ammonia torsion mode.
718.1 cm−1) is assumed to be a hot band, possibly in the ammonia torsion mode.
2. Ab initio calculations
 | ||
| Fig. 2 Schematic diagrams of the two most stable conformers, (a) σ and (b) π, for the electronic ground state of 4FT–NH3 conducted at the MP2/cc-pVTZ level of theory. The π-complex was determined to be the global minimum. | ||
Zero point energies were obtained from both analytical frequency calculations conducted at the MP2 level using the cc-pVTZ basis set, and from numerical frequencies computed at the RICC2 level using both the def2-TZVPP and cc-pVTZ basis sets. Interestingly, for the σ-complex, the MP2/cc-pVTZ calculations, which only yielded the staggered methyl conformation as a stable structure, resulted in a single imaginary frequency in the ammonia out-of-plane bend. The RICC2/cc-pVTZ calculation yielded a true minimum for the eclipsed structure whilst the RICC2/def2-TZVPP calculation yielded a true minimum for the staggered conformation. The failure to eliminate the imaginary frequency for the σ-complex at the MP2/cc-pVTZ level was attributed to an artifact arising from the choice of the basis set, rather than an indication that this conformer was anything other than a true minimum. Consequently, this structure was chosen as being representative of the true minimum energy structure for the σ-complex for the purposes of the binding energy calculations that followed.
Counterpoise corrected interaction energies at the basis-set limit were computed for these two conformers at the MP2 and CCSD(T) levels of theory using the methodology described in the Computational section above. Table 2 shows the results of extrapolations computed from the aug-cc-pVTZ and aug-cc-pVQZ pair of results for the two most stable complexes of 4FT–NH3. In order to obtain a comparative view of the effects of the methyl group, a similar set of calculations were completed for the FB–NH3 complex, the results of which are also shown in Table 2.
| FB–NH3 | 4FT–NH3 | |||
|---|---|---|---|---|
| π | σ | π | σ | |
| a Computed at the counterpoise corrected MP2/cc-pVTZ optimised geometry.b RICC2/cc-pVTZ. | ||||
| MP2/aug-cc-pVDZ | 733.9 | 916.0 | 1012.2 | 905.3 |
| MP2/aug-cc-pVTZ | 834.9 | 1002.9 | 1114.1 | 990.6 |
| MP2/aug-cc-pVQZ | 863.2 | 1035.1 | 1146.5 | 1022.3 |
| MP2 (limit) | 883.9 | 1058.5 | 1170.2 | 1045.1 |
| CCSD(T)/aug-cc-pVDZ | 623.5 | 909.9 | 875.6 | 907.0 |
| CCSD(T)−MP2/aug-cc-pVDZ | −110.5 | −6.1 | −136.7 | +1.7 |
| CCSD(T)(limit) | 773.4 | 1052.4 | 1033.6 | 1046.9 |
| ΔZPEb | −249.4 | −348.8 | −263.4 | −346.3 |
| D0 (calc) | 524.0 | 703.6 | 770.2 | 700.6 |
The computed differences in zero point energies between complexes and fragments, ΔZPE, allowed zero point binding energies, D0, to be calculated. In spite of the issues over imaginary frequencies obtained from the MP2/cc-pVTZ calculations, the differences in zero point energy corrections obtained from MP2 and RICC2 calculations differed by no more than 10%. For this reason, the zero point energy corrections given in Table 2 are those obtained from the RICC2/cc-pVTZ calculations, which yielded true minima for both conformers.
The results of these calculations are interesting. In the case of FB–NH3, the computed interaction energies and zero point binding energies reveal the σ-complex to be about 35% more strongly bound than the π-bound complex. This result is consistent with the experimental observation of just a single conformer in the R2PI spectrum of FB–NH3, although the very large computed change in geometry predicted for the π-complex would mitigate against its observation in practice for this system.13 Nevertheless, the presence of a single strongly electron-withdrawing group in fluorine in this case clearly greatly weakens the prospects of the ammonia binding to the π-system compared to in-plane binding to the fluorine atom and one of the ortho hydrogens.
In the case of 4FT–NH3, the addition of a single electron-donating methyl group in addition to the fluorine atom appears to have stabilised the π-complex to the extent that it is likely to be at least as stable as the σ-complex. The computed interaction energies for the two complexes are essentially identical, whilst zero point energy correction yields a zero point binding energy for the π-complex that is about 10% larger than that computed for the σ-complex. The extent to which zero point correction further stabilises the π-complex depends to a very great extent on the accuracy of the zero point energy differences computed for each conformer. The frequency calculations are performed within the harmonic approximation and so contributions in particular from the intermolecular and low-wavenumber intramolecular modes to the computed zero point energy are likely to be subject to a significant degree of error. Nevertheless, it is safe to conclude that it is highly likely that both complexes of 4FT–NH3 are comparably stable in the gas phase and in principle should both be observable experimentally.
| Conformer | RICC2/def2-TZVPP | |
|---|---|---|
| S100/ cm−1 | Δ/cm−1 | |
| 4FT | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 204.4 204.4 | 0 |
| 4FT–NH3 (σ) | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 294.4 294.4 | +90.0 |
| 4FT–NH3 (π) | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 934.6 934.6 | −269.7 |
The excited state optimisations reveal the extent of the geometry changes occurring upon electronic excitation: for the σ-complex the orientation of the ammonia with respect to the fluorotoluene ring undergoes relatively modest change, with a small increase in the F−H8 intermolecular separation accompanying small decreases in both the H1–N distance and FH8N bond angles. These cumulatively account for a very small net increase in the distance between the 4FT centre-of-mass, 4FTCOM, and that of the ammonia, NH3COM.
As far as changes in the geometry of the 4FT chromophore are concerned, the most significant from the point of view of low-wavenumber vibrational activity accompanying electronic excitation is the C4C1C7 bond angle which provides a measure of the extent to which the methyl group lies above the aromatic plane. With the methyl group in its staggered orientation, this bond angle undergoes a small but significant decrease from 178.7° in the ground state to 176.6° in the excited state. The only excited state optimisation to converge to an eclipsed methyl conformation in the S1 state was the RICC2/ccpVTZ calculation and this yielded a single imaginary frequency in the methyl internal rotation. The energy of this structure is also less negative than the staggered form at the same level of theory which suggests that this conformation is a genuine saddle point. Nevertheless, it is worth noting that the eclipsed methyl conformers show no change in the C4C1C7 bond angle, remaining at 179.5° in both states. The activity of the 11 mode in the R2PI spectrum of 4FT suggests that there must indeed be some small change along this coordinate upon electronic excitation which lends some support to the staggered conformer being more representative of that observed experimentally.
For the π-complex the geometry undergoes a much more substantial change with the ammonia responding to the changes in π-electron density by shifting its centre of mass closer to the centre of the aromatic ring whilst simultaneously rotating about the ammonia C3 axis. The most significant changes are a reduction of 0.271 Å in the distance between the 4FT and ammonia centres-of-mass, and shifts in position of the ammonia along both the 4FT long and short axes (the former is parameterised in Table 4 through the C1FTCOMNH3COM bond angle). Schematic representations of these changes in geometry are shown in Fig. 3, whilst a selection of geometric parameters for the ground and first excited states of the two most stable conformers are shown in Table 4.
 | ||
| Fig. 3 A comparison of the optimised geometries of (a) the σ- and (b) the π-conformers of 4FT–NH3 in the S0 ground (left) and S1 excited states (right). Both structures were optimised at the RICC2/def2-TZVPP level of theory. | ||
| π | σ | ||||
|---|---|---|---|---|---|
| RICC2/def2-TZVPP (MP2/cc-pVTZ) | |||||
| Parameter | S0 | S1 | Parameter | S0 | S1 |
| FTCOM–NH3COM | 3.342 (3.484) | 3.071 | FTCOM–NH3COM | 4.945 (5.042) | 4.995 |
| N–C7 | 3.625 (3.630) | 3.644 | F–H8 | 2.363 (2.464) | 2.427 |
| FTCOM–H8 | 2.644 (2.782) | 2.748 | H1–N | 2.469 (2.552) | 2.463 |
| C1FTCOMNH3COM | 77.0 (75.8) | 84.6 | FH8N | 144.5 (144.0) | 142.1 |
| C6NH3COM | 3.420 | 3.356 | H9NH1 | 125.3 | 125.5 |
| C4C1C7 | 176.9 (177.3) | 174.4 | C4C1C7 | 178.7 (178.7) | 176.6 |
Harmonic vibrational frequencies were calculated at the RICC2/def2-TZVPP level for the ground and first excited states of both conformers. The frequencies calculated for the complexes can be categorised as either intermolecular modes which essentially describe motion of the ammonia against the 4-fluorotoluene chromophore, or intramolecular modes which map onto the normal modes of 4FT or ammonia.
For the π-complex, the eight lowest calculated S1 state wavenumbers are 32.7, 47.9, 92.5, 99.0, 107.9, 112.9, 127.7 and 197.0 cm−1. Six of these are intermolecular modes and two intramolecular. The first five can be characterised, respectively, as the ammonia long axis bend, βz, the short axis bend βy, the x-axis rock, ρx, the van der Waals stretch, σx, and the NH3 internal rotation, τ. The 112.9 cm−1 mode is the 4FT 11 mode, best described as a long axis ring flap (correlating most closely with the benzene symmetric CH out-of-plane bend), the 127.7 cm−1 mode is the methyl internal rotation fundamental and the last of the six intermolecular modes at 197.0 cm−1 is the y-axis rock, ρy.
For the σ-complex, the six van der Waals modes are characterised as out-of-plane bend, β″ (5.8 cm−1), NH3 internal rotation, τ (52.4 cm−1), in-plane bend, β′ (54.4 cm−1), van der Waals stretch, σ (96.3 cm−1), out-of-plane rock, ρ″ (128.6 cm−1) and in-plane rock, ρ′ (223.2 cm−1). This time, three intramolecular modes occupy positions within the intermolecular region: the methyl internal rotation at 80.3 cm−1, the 11 mode at 108.6 cm−1 and the 16a mode, the diagonal ring twist, at 207.8 cm−1. Schematic representations of the six van der Waals normal mode vibrations of the π- and σ-complexes are shown in Fig. 4 and 5 whilst the computed wavenumbers are presented in Table 5.
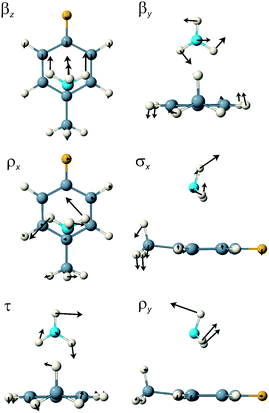 | ||
| Fig. 4 A schematic representation of the six van der Waals normal mode vibrations of the π-complex of 4FT–NH3 in the S1 state. | ||
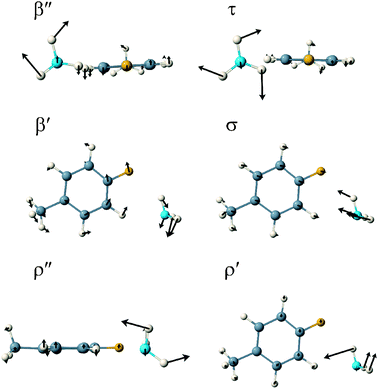 | ||
| Fig. 5 A schematic representation of the six van der Waals normal mode vibrations of the σ-complex of 4FT–NH3 in the S1 state. | ||
| π | σ | ||
|---|---|---|---|
| cm−1 | Assignment | cm−1 | Assignment |
| 32.7 | βz | 5.8 | β″ |
| 47.9 | βy | 52.4 | τ |
| 92.5 | ρx | 54.4 | β′ |
| 99.0 | σx | 80.3 | CH3 int. rot. |
| 107.9 | τ | 96.3 | σ |
| 112.9 | 11 | 108.6 | 11 |
| 127.7 | CH3 int. rot. | 128.6 | ρ″ |
| 197.0 | ρy | 207.8 | 16a |
| 203.4 | 16a | 223.2 | ρ′ |
| 242.1 | — | 239.9 | — |
| 308.4 | C–CH3 in-plane bend | 307.9 | C–CH3 in-plane bend |
| 390.5 | 9b | 394.6 | 9b |
| 409.9 | 6a | 406.3 | 6a |
| 456.4 | — | 450.6 | — |
| 465.3 | 10a | 488.1 | 4 |
| 506.3 | 4 | 492.8 | 10a |
| 549.0 | 17a | 550.4 | — |
| 558.2 | — | 557.5 | 17a |
| 616.8 | — | 622.1 | — |
| 628.7 | 5 | 685.4 | 5 |
| 711.5 | C–CH3 stretch | 709.6 | C–CH3 stretch |
| 813.1 | 1 | 809.6 | 1 |
| 958.5 | — | 958.5 | — |
| 968.6 | 18a, 12 | 968.8 | 18a, 12 |
| 993.2 | — | 999.9 | — |
The simulated spectrum obtained for the σ-complex is compared to the experimental R2PI spectrum in Fig. 6. The simulation shows rather weak intermolecular activity, building from a dominant band origin. This correlates with the small computed change in geometry at the RICC2/def2-TZVPP level and furthermore produces a spectrum that bears a strong similarity to the part of the experimental R2PI spectrum provisionally attributed to the σ-complex.
 | ||
| Fig. 6 A comparison of (a) the higher energy part of the experimental R2PI spectrum of 4FT–NH3 with (b) a Franck–Condon simulation for the σ-complex obtained from ab initio calculations conducted at the RICC2/def2-TZVPP level of theory and (c) a Franck–Condon simulation obtained from a fit to experiment. See text for details. | ||
The lowest wavenumber activity in the simulation is due to overtones in the out-of-plane van der Waals bending mode, β″. This mode is polarised perpendicular to the transition dipole moment and consequently, if we treat the methyl group as a rotationally averaged sphere, we would not expect the fundamentals or even-numbered overtones of these modes to appear with substantial intensities compared, for example, to the stretch or in-plane bend. However, odd-numbered overtones will be polarised in the direction of the transition dipole moment, being of nominal a′ symmetry, and consequently may appear in the spectrum with strong intensity (this also assumes that the 4FT chromophore is planar in both states which it evidently is not according to the geometry optimisations for the staggered methyl conformation). Thus, the simulations predict a short, two member even quanta progression in the out-of-plane bending mode with relatively strong intensity in the first overtone, at 11.6 cm−1, but much weaker intensity in the third overtone at 23.2 cm−1. The fundamental and second overtone appear with non-zero but negligible intensity. To higher energy, a pair of lines appear close together at 96.3 and 108.6 cm−1 with the latter assuming the greater intensity. These bands are due to the van der Waals stretch fundamental, σ and the 11 mode 4FT long axis ring flap fundamental, respectively. The latter appears as a direct consequence of the increase in the extent to which the methyl group moves further out-of-plane in the excited state. The out-of-plane van der Waals bending mode overtone appears again as a combination band with the 11 mode fundamental at 120.1 cm−1. The highest wavenumber van der Waals mode is the in-plane rock, which is predicted to appear weakly at 223.2 cm−1.
The methyl internal rotation appears as a weak fundamental at 80.3 cm−1 and a stronger overtone at 160.6 cm−1. However, the energy levels associated with internal rotation are defined according to both the rotational quantum number of a one-dimensional free rotor as well as the symmetry species of the permutation inversion group isomorphous to the D3h point group. The lowest two internal rotation levels in the electronic ground state are 0a1′ and 1e″ which means that transitions to excited state levels having a1 and e symmetries are allowed, assuming a small enough energy gap between 0a1′ and 1e″ in the ground state. Consequently, the predicted intensities associated with fundamentals and overtones in the methyl internal rotation mode cannot necessarily be taken as representative of what is observed experimentally.
While the simulation shows some obvious differences in band positions and intensities compared with experiment, it does nonetheless bear a striking resemblance to the experimental spectrum. The strong activity in the out-of-plane bend overtones in the simulated spectrum suggests an assignment of the two lowest wavenumber bands in the experimental spectrum at 9.8 and 19.9 cm−1 to the first and third overtones, 2β″ and 4β″, respectively. Clearly the much stronger predicted intensity in the first overtone is somewhat at odds with experiment and must be due to an over-prediction of the extent to which the ammonia moves out of the aromatic plane in the S1 state. The difficulty in eliminating imaginary frequencies from the calculations conducted with cc-pVTZ basis sets in the out-of-plane bending mode lends further support to there being a small deviation from non-planarity in the excited state.
The pair of bands at 72.5 and 84.5 cm−1 in the experimental spectrum correlate logically with the van der Waals stretch fundamental, 1σ, and the 11 ring-mode fundamental, respectively. However, the 11 mode fundamental appears at 137.3 cm−1 in the 4FT spectrum, and there would seem to be no obvious reason why this value should differ significantly in the complex. Indeed, the band at 136.2 cm−1 in the complex spectrum would seem to be an obvious candidate for such an assignment which then leads to a reconsideration of how to assign the two bands at 72.5 and 84.5 cm−1. One logical reassignment attributes the 84.5 cm−1 band to the van der Waals stretch fundamental, on the grounds that its preliminary assignment to the 11 mode was made simply because it appears higher in wavenumber than the van der Waals stretch. The appearance of two such features in this region appears to be a signature of many of the in-plane haloaromatic ammonia complexes. In the case of the FB–NH3 complex, the higher wavenumber of the two bands, appearing in that case at 85.8 cm−1, was assigned, as here, to the van der Waals stretch. On the other hand, the lower energy band at 75.4 cm−1 was tentatively assigned to the 1β″1τ combination, which appeared quite strongly in the simulations conducted using the TZVPP basis set. In the present case, this band also appears in the simulation for 4FT–NH3, but, again, not at an intensity that competes with that of the van der Waals stretch or 11 mode fundamentals. One additional possibility is the in-plane bending mode fundamental, 1β′, whose intensity grows considerably in the simulations conducted for FB–NH3 using the QZVPP basis set, but which in that case was assigned to a lower wavenumber band. A definitive assignment in this case remains difficult and so the 72.5 cm−1 band is tentatively assigned as being due either to 1β″1τ, which is consistent with the assignment made in the case of FB–NH3, or to the in-plane bend fundamental, 1β′, which would require a reconsideration of the assignment made for the FB–NH3 spectrum.
On the basis of the assignments given above, a second Franck–Condon simulation was performed for the σ-complex by fitting the simulated spectrum to the experimental spectrum.45 The resulting simulation is compared to experiment in Fig. 6(c) whilst changes in key geometrical parameters upon excitation are compared to the ab initio values in Table 6. The key parameters showing most significant differences between the ab initio results and those deriving from the fitting procedure are the H1–N and FH8N parameters, both of which reflect in part the shift along the in-plane bend normal mode coordinate, and the C4C1C7 bond angle which reflects the shift along the 11 mode coordinate. It should be emphasised that these changes will be aggregated across both states and should not be taken as in indication of the extent to which the ab initio geometries of one or other state deviate from reality. Nevertheless, the ease with which the fit was obtained lends further confidence in the assignment of these features in the R2PI spectrum to the σ-complex.
| π | σ | ||||
|---|---|---|---|---|---|
| Parameter | Ab initio | Fit | Parameter | Ab initio | Fit |
| ΔFTCOM–NH3COM | −0.271 | −0.236 | ΔFTCOM–NH3COM | +0.05 | +0.047 |
| ΔN–C7 | +0.019 | −0.083 | ΔF–H8 | +0.064 | −0.003 |
| ΔFTCOM–H8 | +0.104 | +0.202 | ΔH1–N | −0.006 | +0.026 |
| ΔC1FTCOMNH3COM | +7.6 | +4.4 | ΔFH8N | −2.4 | −0.7 |
| ΔC6NH3COM | −0.064 | −0.012 | ΔH9NH1 | +0.2 | +1.5 |
| ΔH10NH1 | −0.7 | −1.6 | |||
| ΔH8NH1C2 | +0.8 | −0.62 | |||
| ΔC4C1C7 | −2.5 | −2.3 | ΔC4C1C7 | −2.1 | +0.1 |
The simulated spectrum obtained from the ab initio results for the π-complex is compared to the experimental R2PI spectrum in Fig. 7. In contrast to the spectrum obtained for the σ-complex which is dominated by a strong origin band, in this case we see quite strong intermolecular vibrational activity, with no single dominating feature. Superficially, the simulation shows quite strong similarities to the part of the experimental spectrum lying to the red of the dominant origin band and adds considerable weight to an assignment of these red-most features in the experimental spectrum to a π-complex. However, more detailed scrutiny suggests that the ab initio calculations may be predicting larger changes in geometry than occur in practice. The extent of this overestimate in geometry change may be obtained from a more detailed consideration of the active modes in the simulated spectrum and how this activity maps on to what is observed experimentally.
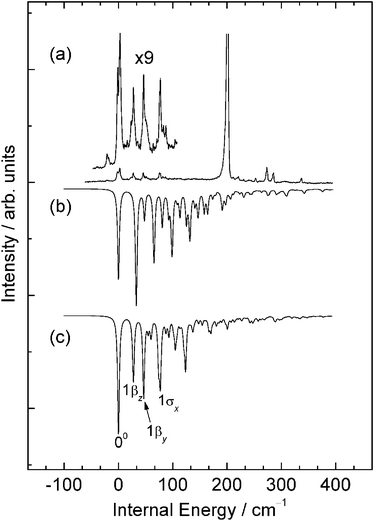 | ||
| Fig. 7 A comparison of (a) the lower energy region of the experimental R2PI spectrum of 4FT–NH3 with (b) a Franck–Condon simulation for the π-complex obtained from calculations conducted at the RICC2/def2-TZVPP level of theory and (c) a Franck–Condon simulation obtained from a fit to experiment. See text for details. | ||
The simulation is dominated by a progression in the long axis van der Waals bending mode, βz, extending to 3 or 4 quanta, with shorter, weaker activity in the short axis van der Waals bend, βy, and the van der Waals stretch, σx. With the first of these features aligned with the strongest experimental band in this region, a provisional assignment of the experimental spectrum becomes possible. Thus, we assign the band at 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 738.9 cm−1 to the band origin, the features at 27.3 and 50.7 cm−1 internal energy to the fundamental and first overtone in the long axis bend, βz, the bands at 46 and 87 cm−1 to the fundamental and first overtone in the short axis bend, βy, and the band at 77 cm−1 to the van der Waals stretch fundamental, σx. Similarly the cluster of features between 800 and 875 cm−1 are then straightforwardly assigned to combination bands involving the same van der Waals modes with the 121 and 11 ring-mode fundamentals. The one feature of the spectrum that proved difficult to assign with any degree of confidence was the splitting evident in the band origin. We suspect that this most likely derives from quantum mechanical tunnelling associated with a greater torsional freedom in the ammonia in the π-complex compared to σ-complex.
738.9 cm−1 to the band origin, the features at 27.3 and 50.7 cm−1 internal energy to the fundamental and first overtone in the long axis bend, βz, the bands at 46 and 87 cm−1 to the fundamental and first overtone in the short axis bend, βy, and the band at 77 cm−1 to the van der Waals stretch fundamental, σx. Similarly the cluster of features between 800 and 875 cm−1 are then straightforwardly assigned to combination bands involving the same van der Waals modes with the 121 and 11 ring-mode fundamentals. The one feature of the spectrum that proved difficult to assign with any degree of confidence was the splitting evident in the band origin. We suspect that this most likely derives from quantum mechanical tunnelling associated with a greater torsional freedom in the ammonia in the π-complex compared to σ-complex.
These assignments were then used to refine the simulation using the same fitting procedure as used for the σ-complex (see Fig. 7(c)). The geometrical parameters showing most significant differences between the ab initio results and those deriving from the fit are in this case the N–C7 and C4FTCOMNH3COM parameters, both of which reflect in part the smaller shift along the long axis bend normal mode coordinate, and the C6NH3COM distance which reflects a change along the short axis bend coordinate. Whilst not a perfect fit, the resulting simulation does now show a striking resemblance to the experimental spectrum and lends a considerably greater degree of confidence in an assignment of these feature to the π-complex. Changes in key geometrical parameters upon excitation are compared to the ab initio values in Table 6.
Conclusions
The experimental and computational results reported in this work provide a strong case for assigning the R2PI spectrum of 4-fluorotoluene–ammonia to a mixture of two conformers: one, a σ-complex, in which the ammonia binds between the hydrogen meta to the methyl group and the fluorine atom and the other a π-complex featuring an NH⋯π hydrogen bond. The more red-shifted bands observed in the spectrum are assigned to the π-complex and the blue-shifted bands to the σ-complex. The main sources of evidence justifying these conclusions are as follows: (1) the computed counterpoise corrected CCSD(T) binding energies show that addition of a methyl group stabilises the π-complex to the extent that it is at least as stable as the σ-complex; (2) the appearance of the part of the spectrum attributed to the σ-complex closely resembles that observed for FB–NH3, a complex adopting an in-plane conformation; (3) the ab initio calculations predict directions of spectral shift for the two complexes upon electronic excitation that are consistent with what is observed experimentally: the σ-complex being blue-shifted relative to 4FT and the π-complex being red-shifted. (4) The results of multidimensional Franck–Condon simulations based on ab initio ground and excited state geometry optimisations and vibrational frequency calculations showed good agreement with experiment and allowed confident assignments of the observed vibrational structure. Refinements of these simulations using a fitting procedure resulted in simulated spectra showing remarkably close agreement with experiment, thereby lending considerable additional weight to the conclusions drawn from the other experimental and computational evidence.The observation of a π-complex in addition to a σ-complex supports the intuitive expectation that electron-donating groups should help to increase π-density and hence stabilise π-proton acceptor complex formation. In this case, this occurs in spite of the presence of a strongly electron-withdrawing group in the fluorine atom. This result suggests that a clear relationship exists between substituent choice, π-electron density and the stabilisation of π-proton acceptor complexes. Electronic effects are commonly used in medicinal chemistry to alter, for example, the basicity of a proton-donating substituent interacting with an ionic binding group. However, it also appears that the electronic character of substituents can be used to tune the relative strengths of different types of non-ionic weak interactions that feature in protein–ligand binding in the relatively solvent free, low polarity encapsulated environments of enzyme active sites.
Acknowledgements
The EPSRC National Service for Computational Chemistry Software is gratefully acknowledged for computing time and access to Turbomole and Gaussian. URL: http://www.nsccs.ac.uk. IP gratefully acknowledges financial support from the Alexander von Humboldt Stiftung and the SFB 749 (Dynamics and Intermediates of Molecular Transformations).Notes and references
- S. K. Panigrahi and G. R. Desirau, Proteins: Struct., Funct., Bioinform., 2007, 67, 128 Search PubMed.
- G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311 CrossRef CAS.
- C. B. Aakeröy and K. R. Seddon, Chem. Soc. Rev., 1993, 22, 397 RSC.
- E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210 CrossRef CAS.
- G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond: In Structural Chemistry and Biology, Oxford University Press, 2001 Search PubMed.
- G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 8342 CrossRef CAS.
- G. Tóth, C. R. Watts, R. F. Murphy and S. Lovas, Proteins: Struct., Funct., Genet., 2001, 43, 373 CrossRef CAS.
- T. Steiner and G. Koellner, J. Mol. Biol., 2001, 305, 535 CrossRef CAS.
- T. Ozawa, E. Tsuji, M. Ozawa, C. Handa, H. Mukaiyama, T. Nishimura, S. Kobayashi and K. Okazaki, Bioorg. Med. Chem., 2008, 16, 10311 CrossRef CAS.
- A. J. Gotch and T. S. Zwier, J. Chem. Phys., 1992, 96, 3388 CrossRef CAS.
- S. Suzuki, P. G. Green, R. E. Bumgarner, S. Dasgupta, W. A. Goddard III and G. A. Blake, Science, 1992, 257, 942 CrossRef CAS.
- D. A. Rodham, S. Suzuki, R. D. Suenram, F. J. Lovas, S. Dasgupta, W. A. Goddard III and G. Blake, Nature, 1993, 362, 735 CrossRef CAS.
- N. M. Tonge, E. C. MacMahon, I. Pugliesi and M. C. R. Cockett, J. Chem. Phys., 2007, 126, 154319 CrossRef.
- D. J. Dunitz and R. Taylor, Chem.–Eur. J., 1997, 3, 89 CrossRef CAS.
- C. Kang, D. W. Pratt and M. Schäfer, J. Phys. Chem. A, 2005, 109, 767 CrossRef CAS.
- R. A. Bachorz, F. A. Bischoff, S. Höfener, W. Klopper, P. Ottiger, R. Leist, J. A. Frey and S. Leutwyler, Phys. Chem. Chem. Phys., 2008, 10, 2758 RSC.
- S. Li and E. R. Bernstein, J. Chem. Phys., 1992, 97, 804 CrossRef CAS.
- K. Okuyama, N. Mikami and M. Ito, J. Phys. Chem., 1985, 89, 5617 CrossRef CAS.
- Y. Hu, X. Wang and S. Yang, Chem. Phys., 2003, 290, 233 CrossRef CAS.
- S. Georgiev, T. Chakraborty and H. J. Neusser, J. Phys. Chem. A, 2004, 108, 3304 CrossRef CAS.
- S. M. Bellm, P. T. Whiteside and K. L. Reid, J. Phys. Chem. A, 2003, 107, 7373 CrossRef CAS.
- K. Takazawa, M. Fujii and M. Ito, J. Chem. Phys., 1993, 99, 3205 CrossRef CAS.
- V. L. Ayles, C. J. Hammond, D. E. Bergeron, O. J. Richards and T. G. Wright, J. Chem. Phys., 2007, 126, 244304 CrossRef.
- J. Rottstegge, H. Hartwig and H. Dreizler, J. Mol. Spectrosc., 1999, 195, 1 CrossRef CAS.
- S. Georgiev, T. Chakraborty and H. J. Neusser, J. Phys. Chem. A, 2004, 108, 3304 CrossRef CAS.
- M. J. Watkins and M. C. R. Cockett, J. Chem. Phys., 2000, 113, 10560 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03 (Revision B.3), Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef CAS.
- K. Shibasaki, A. Fujii, N. Mikami and S. Tsuzuki, J. Phys. Chem. A, 2007, 111, 753 CrossRef CAS.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639 CrossRef CAS.
- A. Fujii, K. Shibasaki, T. Kazama, R. Itaya, N. Mikami and S. Tsuzuki, Phys. Chem. Chem. Phys., 2008, 10, 2836 RSC.
- J. Šponer, K. E. Riley and P. Hobza, Phys. Chem. Chem. Phys., 2008, 10, 2595 RSC.
- P. Hobza and J. Šponer, Chem. Rev., 1999, 99, 3247 CrossRef CAS.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef CAS.
- F. Weigand, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753 CrossRef CAS.
- I. Pugliesi and K. Müller-Dethlefs, J. Phys. Chem. A, 2006, 110, 4657 CrossRef CAS.
- E. V. Doktorov, I. A. Malkin and V. I. Man’ke, J. Mol. Spectrosc., 1977, 64, 302 CrossRef.
- F. Duschinsky, Acta Physicochim. URSS, 1937, 7, 551 Search PubMed.
- J. T. Hougen and J. K. G. Watson, Can. J. Phys., 1965, 43, 298 CAS.
- H.-D. Barth, K. Buchold, S. Djafari, B. Reimann, U. Lommatzsch and B. Brutschy, Chem. Phys., 1998, 239, 49 CrossRef CAS.
- S. Vaupel, B. Brutschy, P. Tarakeshwar and K. S. Kim, J. Am. Chem. Soc., 2006, 128, 5416 CrossRef CAS.
- All Franck–Condon simulations have been carried out using FC-LabII Version 2009.a, a computational package developed by C. Schriever, M.C.R. Cockett and I. Pugliesi. The latest information on program updates, a basic introduction to Franck–Condon simulations and a free download of the software can be found at http://www.fclab2.net/.
Footnote |
| † Electronic supplementary information (ESI) available: Further details of the Franck–Condon fitting procedure are given as well as the Cartesian coordinates for optimised ground and excited state structures of the complex. See DOI: 10.1039/b916815j |
| This journal is © the Owner Societies 2010 |
