Two unusual self-threading frameworks self-assembled from mixed ligands and cobalt/zinc ions

Abstract

Reactions of Co^II or Zn^II nitrate with mixed ligands norfloxacin (H-Norf) and 1,4-benzenedicarboxylic acid (H₂bdc) under hydrothermal conditions afford two isostructural compounds [Co₃(bdc)₂(Hbdc)₂(H-Norf)₂(H₂O)₄] (1) and [Zn₃(bdc)₂(Hbdc)₂(H-Norf)₂(H₂O)₄] (2). An eye-catching structure feature of these two compounds is that each rhombic window within the sheet is threaded by two dangling H-Norf ligands belonging to the sheet itself, showing the self-threading feature. Equally interesting is that the packing of these layers gives rise to a 3D self-threading network if interlayer H-bonds are taken into account. Thermal stability analyses of these two compounds and the magnetic property of complex 1 were also studied in this paper.

---

Introduction

Entangled systems have captivated the attention of chemists not only for their undisputed beauty^1–3 but also for their potential applications arising directly from the intertwining nature of the lattices.⁴ Interpenetration has been the most investigated type of entanglement, as shown by the two comprehensive reviews by Batten and Robson.⁵ More recently, a complete analysis of all 3D interpenetrated structures contained in the CSD database was also carried out with a rationalization and classification of the topology of interpenetration.⁶ The increasing number of coordination polymers reported in the literature has led to new and more complex types of entanglement being recognised^5b,7,8 in polycatenated, polythreaded and polyknotted species, that are reminiscent of molecular catenanes, rotaxanes and knots, respectively. Their local topological features are represented in Scheme 1.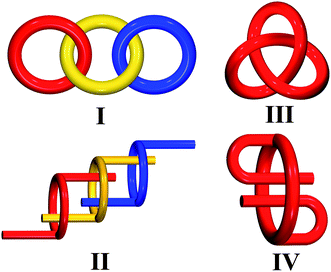

Scheme 1 Local topological features of polycatenation (I), polythreading (II), trefoil knot (III), and self-threading (IV).

According to Ciani and co-workers,⁸ polycatenation differs from interpenetration in that the whole catenated array has a higher dimensionality than that of the component motifs, and that each individual motif is catenated only with the surrounding ones but not with all the others (see I in Scheme 1). Polythreaded structures are characterized by the presence of closed loops, as well as of elements that can thread the loops, and can be considered as extended periodic analogues of molecular rotaxanes and pseudo-rotaxanes (see II in Scheme 1). It is worth underscoring here that this threading mode occurs between different frameworks. Whereas, polyknotting is typical of self-penetrating nets, i.e. single nets having the peculiarity that the smallest topological rings or knots are catenated by other shortest rings belonging to the same net (see III in Scheme 1). Aided by the rapid growth of network-based crystal engineering, another new phenomenon of entanglements has been found recently, whose structural characteristic is shown in IV of Scheme 1. Obviously, this new type of entanglement neither falls in the polythreading nor the polyknotting categories, although it possesses partially inherent features of these two classes. Considering that it is a structural compromise between polythreading and self-penetrating, a new term ‘self-threading’ is employed to define this new threading mode in which closed loops are threaded by components from the network itself. Such a topological nature, owing to being recognized very recently, is merely explicitly described in two recently reported cases; one is a self-threading 2D layered structure⁹ and the other is a chiral 3D self-threading framework.¹⁰ Therefore, much work is still necessary to enrich and develop this branch.

Herein, we report two complexes with self-threading feature, [Co₃(bdc)₂(Hbdc)₂(H-Norf)₂(H₂O)₄] (1) and [Zn₃(bdc)₂(Hbdc)₂(H-Norf)₂(H₂O)₄] (2) by simultaneous use of norfloxacin (H-Norf) and aromatic dicarboxylic ligand having bridging ability 1,4-benzenedicarboxylic acid (H₂bdc). To the best of our knowledge, this remarkable threading topology described here is a second entangled phenomenon found in single nets besides self-penetration.

Results and discussion

Crystal structures

Single-crystal X-ray diffraction reveals that compounds 1 and 2 are isomorphic. For the convenience of depiction, the structure of compound 1 is described representatively.

Compound 1 crystallizes in the monoclinic system, space groupP2₁/c. As shown in Fig. 1, there are one H-Norf ligand, two Co atoms, two H₂bdc ligands and three aqua ligands in the asymmetric unit. Both Co atoms (Co1 and Co2) are six-coordinated and exhibit distorted octahedral geometries. Co(1) atom is surrounded by four carboxyl oxygen atoms from three individual bdc ligands and one Norf ligand (Co(1)–O(9) 2.0412(16) Å, Co(1)–O(4) 2.05792(16) Å, Co(1)–O(5) 2.2164(15) Å, Co(1)–O(8A) 2.1516(15) Å), one hydroxyl oxygen atom from Norf ligand (Co(1)–O(11) 2.0205(16) Å), and one aqua ligand (Co(1)–O(1W) 2.1367(17) Å); Co(2) atom is defined by four planar carboxyl oxygen atoms from different bdc ligands (Co(2)–O(6) 2.0734(14) Å, Co(2)–O(6B) 2.0734(15) Å, Co(1)–O(9) 2.0412(16) Å, Co(2)–O(7A) 2.1046(14) Å, Co(2)–O(7C) 2.1046(14) Å) and two apical aqua ligands (Co(2)–O(2W) 2.0734(14) Å and Co(2)–O(2WB) 2.0734(14) Å). The Co(2) atom lies on a two-fold axis and is linked to two crystallographically equivalent Co(1) atoms by the symmetry operations ‘1 − x, 1 − y, 2 − z’ to give a trinuclear cobalt cluster with a Co⋯Co distance of 4.615(7) Å.

Fig. 1 ORTEP drawing of structural unit in 1 (50% probability ellipsoids). Symmetry codes: A −x + 1, y − 1/2, −z + 3/2, B −x + 1, −y + 1, −z + 2.

It is worth mentioning here that bdc ligands in 1 adopt two different coordination modes: bdc^A act as a tetraconnector to link four cobalt atoms (Scheme 2I), whereas bdc^B only corresponds to a monodentate ligand to link one cobalt atom using one carboxylate group, the para-carboxyl group of which is not engaged in coordination but provides a potential hydrogen-bonding donor (Scheme 2II). Similar with bdc^B, H-Norf ligand only chelates one Co²⁺ ion using carbonyl and carboxyl groups of the quinoline ring but with the N atom of the piperazine ring being protonized that offers potential action point for hydrogen bonds (Scheme 2III). This type of coordination mode leads a torsion angle to be formed between the main body of the rigid ligand and the metal center, thus the H-Norf ligand is considered as having a candy-cane type geometry. Recent work published by us¹¹ and by others¹² has proved that in a neutral or weakly basic solution, the N atom of the piperazine ring can connect the metal ion, while in the weak acidic solution, the N atom of the piperazine ring is protonated and fails to coordinate to the metal ion. Thus this coordination mode of H-Norf ligand presented here is determined by the pH value (6.5) of the reaction solution.

Scheme 2 Coordination modes of the bdc^A (I), bdc^B (II), and H-Norf (III) ligands in 1.

From the above description, it is not difficult to see that neighbouring trinuclear cobalt clusters are actually linked by linear bdc^A spacers to give a 2D layer (ESI, Fig. S1).† Terminal bdc^B ligands protrude from both sides of the sheets in an angle of inclination about 35°. It should be noted that, different from the previously reported 2D layers with side arms,^9,13 the unusual layer structure reported here carries bending elements at the same time, namely Co–H-Norf segments (see Scheme 2III). This remarkable feature is a necessary condition for the formation of self-threading.

To sum up, three factors can be envisaged to play roles in the generation of the ultimate self-threading architecture in 1: (i) the presence of very large rhombic windows within the 2D layer (with dimensions 11.39 × 11.39 Å estimated from the distances between corner metal sites) built up by four pairs of trinuclear cobalt units and four bdc^A ligands, (ii) the existence of dangling H-Norf groups that are disposed in an mutual anti orientation with respect to the layer plane and (iii) the candy-cane type geometry of H-Norf with the effective length of H-Norf of about 12.2 Å (from the coordinated carboxyl oxygen atom to the utmost H atom of the piperazine ring). Under these premises, the dangling H-Norf ligand grafted on the Co(1) atom is threaded into the rhombic void of the 2D layer, which is above the plane of the window about 5.7 Å before it bends back down through the window to the other side, and is below the plane of the window about 5.5 Å after penetrating through the window (Fig. 2a). Each rhombic window is therefore penetrated by two H-Norf ligands belonging to the 2D sheet itself, one entering from one side and the other from the opposite one, as shown in Fig. 2b. The resultant 2D self-threading architecture is schematically presented in Fig. 2c.

Fig. 2 (a) A detail drawing highlighting the penetration depth. (b) Sphere-packing representation of a rhombic unit of the 2D layer, showing the two threading H-Norf ligands. Terminal bdc^B ligands are omitted for clarity. (c) Schematic illustration of the 2D self-threading architecture.

Adjacent layers are stacked in a parallel fashion along the [100] direction with an interlayer separation of 13.85 Å (Fig. 3a). Whilst exploring the acting forces between them, we found that there exist two weak interactions: a π–π stacking arising from the aromatic rings of the bdc^B ligands protruding from the layers (face-to-face distance: 3.39 Å; center-to-center distance: 4.23 Å), and a strong hydrogen bonding involving the uncoordinated carboxyl oxygen atoms (O1) from dangling bdc^B ligand and a coordinated water molecule (O2W) bonded to the Co(2) atom (O1⋯O2W 2.65 Å, Fig. 3c). Interestingly, when these strong hydrogen bonds are taken into account, the resulting structure displays a 3D 6-connected net with α–Po (primitive cubic, pcu) (4¹²6³) topology. A distorted cubelike unit of the resulting α–Po nets shows dimensions of 11.39 × 11.39 × 13.85 Å. As such, the overall architecture can be considered as a 3D supramolecular self-threading framework (Fig. 3b). In addition, the interlayer multiple weaker H-bonds, associated with the coordinated water molecule, protonated nitrogen atom of dangling H-Norf ligand, and carbonyl group of bdc^B [O(1W)⋯O(10) 2.865(3) Å, N(1)⋯O(10)] 2.713(3) Å, N(1)⋯O(2) 2.849(2) Å], further stabilize the 3D self-threading framework.

Fig. 3 (a) Crystal packing of 1 along the [100] direction. (b) A schematic representation of the 3D self-threading network that is formed when H bonds are taken into account. Terminal bdc^B ligands are omitted for clarity. (c) Interlayer hydrogen bonding interactions involving the uncoordinated carboxyl oxygen atoms and coordinated aqua molecules.

In the aforementioned 2D self-threading example,⁹ although terminal 4,4′-bipy ligands insert into the rectangle of the 2D layer in a manner similar to that observed herein, they merely interdigitate, not penetrate, into the void space of the neighbouring layers to generate an interdigitated 3D architecture. The topology is significantly different to the resulting 3D self-threading structure of the coordination polymers described here.

Thermal stability analyses

In order to examine the thermal stability of the two compounds, thermal gravimetric (TG) analyses were carried out for 1 and 2 between 30 and 600 °C (ESI, Fig. S1).† Probably due to the existence of strong hydrogen-bonding interactions in the two compounds that further stabilize the whole structures, they exhibit good thermal stability. For 1, no weight losses were observed up to 200 °C, subsequent to this, significant weight losses occurred and ended at ca. 430 °C, indicating the complete deposition of the complex to form Co₂O₃ as a final product. This conclusion is supported by the percentages of the residues (15.49%), which is in accordance with the expected value (16.09%).

The thermal decomposition behaviour of 2 is much like that observed for 1. A continuous loss stage is observed in the temperature range 200–440 °C, corresponding to the release of coordinated water molecules and organic groups. The remaining weight of 15.50% corresponds to the percentage (15.60%) of Zn and O components, indicating that the final product is ZnO. The whole weight loss (84.50%) is in good agreement with the calculated value (84.40%).

Magnetic properties

The variable-temperature magnetic susceptibility of compound 1 was measured from 2 to 300 K at 1000 Oe and was displayed in Fig. 4, plotted as the thermal variation of χ_MT and χ_M⁻¹. At 300 K, the χ_MT product is 8.99 cm³ K mol⁻¹. As temperature is lowered, the χ_MT value decreases continuously to a value of 5.42 cm³ K mol⁻¹ at 2 K. Such a behaviour of χ_MT curve indicates a mainly antiferromagnetic interaction in 1. The χ_M⁻¹vs. T curve is well fitted by the Curie–Weiss law above 10 K with the Curie constant of 9.23 cm³ K mol⁻¹ (3.08 cm³ K mol⁻¹ for each Co²⁺ ion) and Weiss temperature of −6.78 K, respectively. The Curie constant is larger than that of three isolated spin-only Co²⁺ ions (1.875 cm³ K mol⁻¹, S = 3/2, g = 2.0), indicating that an important orbital contribution is involved.¹⁴ The negative Weiss constant further indicates that there exists an antiferromagnetic interaction in the Co₃ clusters.

Fig. 4 The temperature dependence of the product χT for 1. Inset: plots of reciprocal magnetic susceptibility (χ⁻¹) versus temperature (T). The straight line is a fitted curve with Curie–Weiss law.

Conclusions

In conclusion, we have prepared and characterized two 2D self-threading metal–organic nets, in which each rhombic window within the sheet is threaded by two dangling H-Norf ligands belonging to the sheet itself. The successful isolation of these two species not only provides intriguing examples of chemical topology but also adds new members for the newborn self-threading family.

Experimental

General information

All chemicals purchased were of reagent grade and used without further purification. Elemental analyses (C, H and N) were performed on a Perkin–Elmer 2400 CHN elemental analyzer. TG analyses were performed on a Perkin–Elmer TGA7 instrument in flowing N₂ with a heating rate of 10 °C min⁻¹. Magnetic susceptibility measurements were obtained on finely grounded polycrystalline samples of 1 with the use of a Quantum Design SQUID magnetometer MPMS-XL.

Synthesis

Synthesis of [Co₃(bdc)₂(Hbdc)₂(H-Norf)₂(H₂O)₄] (1). A mixture of Co(NO₃)₂·6H₂O (0.582 g, 2.0 mmol), H-Norf (0.638 g, 2.0 mmol), H₂bdc (0.657 g, 4.0 mmol) in H₂O (15 mL) was adjusted to pH 6.5 with 1 M NaOH solution and then sealed in a 25 mL Teflon-lined stainless steel container, which was heated at 120 °C for 3 d and then cooled down to room temperature at a rate of 5 °C h⁻¹. Red crystals of 1 were collected and washed with distilled water and dried in air to give the product; yield, 52.3% based on Co. Anal. calcd (%) for C₆₄H₆₂Co₃N₆F₂O₂₆ (M_r = 1545.99): C 49.72, H 4.04, N 5.44. Found: C 49.68, H 4.15, N 5.32.

Synthesis of [Zn₃(bdc)₂(Hbdc)₂(H-Norf)₂(H₂O)₄] (2). Similar procedure is performed to obtain colourless crystals of complex 2, except that Zn(NO₃)₂·6H₂O is used instead of Co(NO₃)₂·6H₂O. Yield, 50.8% based on Zn. Anal. calcd (%) for C₆₄H₆₂Zn₃N₆F₂O₂₆ (M_r = 1565.31): C 49.10, H 3.99, N 5.37. Found C 49.12, H 3.82, N 5.40.

X-Ray crystallography

Single crystals of compounds 1 and 2 were glued on a glass fiber. Data collection were performed on a Bruker Smart Apex II CCD diffractometer with graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å) at room temperature. Empirical absorption correction was applied. The structures were solved by the direct method and refined by the full-matrix least-squares method on F² using the SHELXTL crystallographic software package.¹⁵ Anisotropic displacement parameters were applied to all non-hydrogen atoms. The organic hydrogen atoms were generated geometrically; the aqua hydrogen atoms were located from difference maps. The crystal data and structure refinement of compounds 1 and 2 are summarized in Table 1. Selected bond lengths and angles for 1 and 2 are listed in the ESI, Table S1.†

Table 1 Crystallographic data for 1 and 2

	1	2
a R 1 = Σ‖Fo| − |Fc‖/Σ|Fo|. b wR2 = Σ[w(Fo^2 − Fc^2)^2]/Σ[w(Fo^2)^2]^1^/2.
Empirical formula	C64H62Co3N6F2O26	C64H62Zn3N6F2O26
M	1545.99	1565.31
T/K	298(2)	298(2)
λ/Å	0.71073	0.71073
Crystal system	Monoclinic	Monoclinic
Space group	P21/c	P21/c
a/Å	13.853(3)	13.859(3)
b/Å	13.391(3)	13.313(3)
c/Å	18.438(7)	18.894(7)
α/°	90	90
β/°	119.54(2)	119.31(2)
γ/°	90	90
V/Å^3	2975.7(15)	3039.8(15)
Z	2	2
μ/mm^−1	0.932	1.278
R 1 ^a [I > 2σ(I)]	0.0305	0.0736
wR2^b [I > 2σ(I)]	0.0773	0.1943

---

Acknowledgements

This work was financially supported by the National Science Foundation of China (no. 20701006), PhD Station Foundation of Ministry of Education for New Teachers (no. 20070200014/20070200015), the Program for New Century Excellent Talents in University (NCET-10-0282), and the Fundamental Research Funds for the Central Universities (09QNJJ018/09ZDQD003).

References

1. (a) J. P. Sauvage, Molecular Catenanes, Rotaxanes and Knots, A Journey Through the World of Molecular Topology, Dietrich-Buchecker, C. Wiley-VCH, Weinheim, 1999; (b) J. F. Stoddart, Acc. Chem. Res., 2001, 34, 410; (c) K. Kim, Chem. Soc. Rev., 2002, 31, 96; (d) S. J. Loeb, Chem. Commun., 2005, 1511.
2. (a) B. F. Abrahams, S. R. Batten, M. J. Grannas, H. Hamit, B. F. Hoskins and R. Robson, Angew. Chem., Int. Ed., 1999, 38, 1475; (b) K. Biradha and M. Fujita, Chem. Commun., 2002, 1866; (c) Y. H. Li, C. Y. Su, A. M. Goforth, K. D. Shimizu, K. D. Gray, M. D. Smith and H. C. zur Loye, Chem. Commun., 2003, 1630; (d) M. L. Tong, X. M. Chen and S. R. Batten, J. Am. Chem. Soc., 2003, 125, 16170; (e) B. Moulton, H. Abourahma, M. W. Bradner, J. Lu, G. J. McManus and M. J. Zaworotko, Chem. Commun., 2003, 1342; (f) M. Xue, S. Q. Ma, Z. Jin, R. M. Schaffino, G. S. Zhu, E. B. Lobkovsky, S. L. Qiu and B. L. Chen, Inorg. Chem., 2008, 47, 6825.
3. (a) D. L. Long, R. J. Hill, A. J. Blake, N. R. Champness, P. Hubberstey, C. Wilson and M. Schröder, Chem.–Eur. J., 2005, 11, 1384; (b) M. Du, X. J. Jiang and X. J. Zhao, Chem. Commun., 2005, 5521; (c) J. He, Y. G. Yin, T. Wu, D. Li and X. C. Huang, Chem. Commun., 2006, 2845; (d) A. L. Cheng, N. Liu, Y. F. Yue, Y. W. Jiang, E. Q. Gao, C. H. Yan and M. Y. He, Chem. Commun., 2007, 407; (e) B. Xu, J. Lü and R. Cao, Cryst. Growth Des., 2009, 9, 3003; (f) R. Feng, F. L. Jiang, L. Chen, C. F. Yan, M. Y. Wu and M. C. Hong, Chem. Commun., 2009, 5296.
4. (a) J. S. Miller, Adv. Mater., 2001, 13, 525; (b) C. Janiak, Dalton Trans., 2003, 2781; (c) M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469; (d) B. Kesanli, Y. Cui, M. R. Smith, E. W. Bittner, B. C. Bockrath and W. Lin, Angew. Chem., Int. Ed., 2005, 44, 72; (e) D. F. Sun, S. Q. Ma, Y. X. Ke, D. J. Collins and H. C. Zhou, J. Am. Chem. Soc., 2006, 128, 3896; (f) B. L. Chen, S. Q. Ma, F. Zapata, F. R. Fronczek, E. B. Lobkovsky and H. C. Zhou, Inorg. Chem., 2007, 46, 1233; (g) J. P. Zhang, S. Horike and S. Kitagawa, Angew. Chem., Int. Ed., 2007, 46, 889; (h) T. Maji, R. Matsuda and S. Kitagawa, Nat. Mater., 2007, 6, 142.
5. (a) S. R. Batten and R. Robson, Angew. Chem., Int. Ed., 1998, 37, 1460; (b) S. R. Batten, CrystEngComm, 2001, 3, 67.
6. V. A. Blatov, L. Carlucci, G. Ciani and D. M. Proserpio, CrystEngComm, 2004, 6, 378.
7. L. Carlucci, G. Ciani and D. M. Proserpio, Coord. Chem. Rev., 2003, 246, 247.
8. L. Carlucci, G. Ciani and D. M. Proserpio, CrystEngComm, 2003, 5, 269.
9. X. Y. Cao, J. Zhang, Z. J. Li, J. K. Cheng and Y. G. Yao, CrystEngComm, 2007, 9, 806.
10. C. Qin, X. L. Wang, L. Yuan and E. B. Wang, Cryst. Growth Des., 2008, 8, 2093.
11. (a) D. R. Xiao, E. B. Wang, H. Y. An, Z. M. Su, Y. G. Li, L. Gao, C. Y. Sun and L. Xu, Chem.–Eur. J., 2005, 11, 6673; (b) S. V. Ganesan and S. Natarajan, Inorg. Chem., 2004, 43, 198.
12. Z. F. Chen, R. G. Xiong, J. Zhang, X. T. Chen, Z. L. Xue and X. Z. You, Inorg. Chem., 2001, 40, 4075.
13. (a) C. Qin, X. L. Wang, L. Carlucci, M. L. Tong, E. B. Wang, C. W. Hu and L. Xu, Chem. Commun., 2004, 1876; (b) X. L. Wang, C. Qin, E. B. Wang, Y. G. Li, Z. M. Su, L. Xu and L. Carlucci, Angew. Chem., Int. Ed., 2005, 44, 5824.
14. X. H. Bu, M. L. Tong, Y. B. Xie, J. R. Li, H. C. Chang, S. Kitagawa and J. Ribas, Inorg. Chem., 2005, 44, 9837.
15. (a) G. M. Sheldrick. SHELXS-97. A Program for the Solution of Crystal Structures from X-ray Data. University of Göttingen, Germany, 1997; (b) G. M. Sheldrick, SHELXL-97. A Program for the Refinement of Crystal Structures from X-ray Data. University of Göttingen, Germany, 1997.

---

Footnote

† Electronic supplementary information (ESI) available: TG curves for compounds 1 and 2, Fig. S1, and Table S1. CCDC reference numbers 768676 and 768677. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c004065g

---