The relative strength and role in crystal packing of I⁻⋯π and CH⋯I⁻ interactions in iminium salts

Abstract

The relative energy and importance of Hal⁻⋯π and CH⋯Hal⁻ interactions were studied basing on the crystal structures of iminium salts with different I⋯C distances. DFT calculations of the corresponding cations and ionic pairs were performed in an isolated state, accompanied by PW-DFT calculations of the crystals. The QTAIM methods in conjunction with the Espinosa–Lecomte correlation scheme were used to estimate the energies of C⋯I and H⋯I interactions both in isolated and in solid state. A detailed CSD survey was performed to estimate the relative abundance of these interactions in iminium salts.

---

Introduction

Ionic liquids (ILs) are low melting (<100 °C) salts consisting of a bulky organic cation and an organic or inorganic anion. ILs are a subject of intensive research due to their unique properties as solvents—they are non-volaile, non-flammable, and their use as reaction media instead of traditional organic solvents can alter the reaction products and increase the reaction speed.

1,3-Dialkylimidazolium halides were among the first ionic liquids discovered, and remain in active use today. A common method employed to study the structure and organization of ILs is X-ray diffraction (XRD) analysis of corresponding crystals, as their crystal packing bears considerable similarity to relative arrangement of cations and anions in liquid.^1,2 In a recent study³ it has been shown that crystals of 1-isopropyl-3-methylimidazolium (iPmim) and 1-propyl-3-methylimidazolium (Pmim) feature similar highly-directed Br⁻⋯π contacts, along with the C–H⋯Br⁻ ones. The shortest distances between the atoms of the aromatic rings and the bromide anion were 3.34 Å (iPmim) and 3.48 Å (Pmim), corresponding to a quite weak, if any, interaction. However, such interactions can be possible in case of different substituents in the imidazolium ring and may play some role in crystal packing and organization of molecules in liquid.

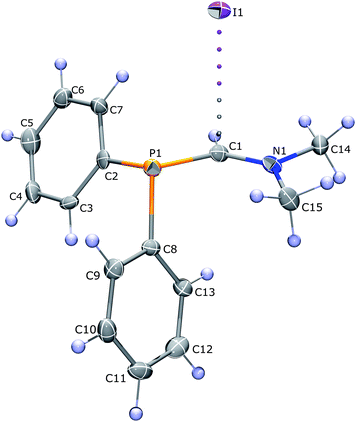
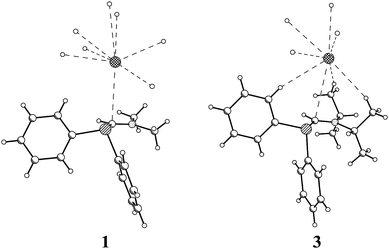
At the same time, the study of such interactions based on crystallographic data of ionic liquids is difficult because even small alterations in imidazolium substituents tend to completely alter the crystal packing of the compounds. However, an alternative approach to study such interaction is to find an ionic crystal with similar contacts. Indeed, in the three salts 1, 2, and 3 recently studied by some of us⁴ the C⋯I interaction in a similar P–C=NR₂⁺ system exhibited a notable directionality, with the I⋯C vector being nearly perpendicular to the P–C–N plane, forming an angle from 86 to 88° to it in all three compounds, independent from the variation of substituents at the nitrogen atom (see Fig. 1). It should be noted that the I⋯C distance in compounds 1–3 according to XRD varied considerably: from 3.526(5) to 3.927(3) Å, in the latter case being significantly longer than the sum of iodine and carbon van der Waals radii (3.75 Å).⁵ If we take into account the van der Waals radius of iodine being by 0.15 Å bigger than that of bromine,⁵ Hal⁻⋯π interaction in compound 1 should be stronger than the one observed in iPmim—if this interaction is bonding at all and is not forced by numerous C–H⋯I⁻ ones. Thus, compounds 1, 2, and 3 were chosen as a useful model for quantitative investigation of the relative strength and importance of Hal⁻⋯π interactions.

Fig. 1 General view of a tight ionic pair in crystal 1 according to ref. 4.

The aim of our study is to check if the aforementioned geometrical properties of this ionic pair are caused by any “residual” bonding between carbon and iodine, or they are forced by effects of crystal packing, i.e. C–H⋯I⁻ contacts. The appropriate framework for such study is Bader's quantum theory of atoms in molecules (QTAIM),⁶ which allows to find and quantitatively estimate weak intermolecular bonds by studying the topology of the total electron density ρ(r). The weak intermolecular bonds within the QTAIM theory can be estimated using the Espinosa–Lecomte^7,8 correlation linking the potential energy density in the bond critical point (BCP) to the bond energy. This approach is especially useful for ionic compounds where the traditional methods of bond energy estimation usually fail.^9–11

Although the I⋯C distances in 1–3 vary widely (Table 1) the C(1) atom in all cations is characterized by planar configuration. Thus we could not estimate the amount of charge transfer between iodide and cation exclusively from the X-ray structural data. At the same time the P–C bond in ethyl (2) and isopropyl (3) derivatives (1.838(3) Å) was by 0.03 Å longer than in the crystal of the methyl one (1.807(3) Å). However, the B3LYP/6-311G* calculation of the isolated cations revealed that the variation of P–C remained for compounds 1, 2 and 3 in the absence of intermolecular contacts: the C–P bonds in cations 2 and 3 were elongated by 0.01 Å (see Table 1). Thus, we could suggest that the variation of the P–C bond in 1–3 is a consequence of the phosphorous electron lone pair (Lp) conjugation with C=NR₂⁺ double bond.

Table 1 Selected interatomic distances (Å) in the crystal and gas phase according to XRD and DFT calculations

	XRD data^a	Cation in an isolated state	Ionic pair in an isolated state	PW-DFT crystal calculation
a The X-ray diffraction data for 1–3 are taken from ref. 4.
Compound 1
C(1)⋯I(1)	3.526(5)	—	2.608	3.482
P(1)-C(1)	1.807(6)	1.812	1.887	1.804
N(1)-C(1)	1.289(7)	1.301	1.348	1.302
Compound 2
C(1)⋯I(1)	3.782(5)	—
P(1)-C(1)	1.839(5)	1.824
N(1)-C(1)	1.291(6)	1.298
Compound 3
C(1)⋯I(1)	3.927(3)	—	2.811	3.922
P(1)-C(1)	1.838(3)	1.825	1.877	1.822
N(1)-C(1)	1.286(4)	1.296	1.325	1.299

---

In order to study the role of this conjugation for the stabilization of the cation a relaxed scan of C(2)-P(1)-C(1)-N(2) torsion angle was performed at B3LYP/6-311G* level with a step size of 10° in cation 1 (see Fig. 2). The global minimum of 1, where the corresponding torsion angle is equal to −173°, was chosen as the starting point.

Fig. 2 The plot of l (P–C bond length) against ω (C(2)–P(1)–C(1)–N(2) torsion) in a relaxed potential energy surface scan by ω in cation 1.

The shortest bond length (l = 1.799 Å) is observed at ω = 27°, which corresponds to Lp–P–C–N torsion angle of ∼90°, the longest (l = 1.901) at ω = −53° (Lp–P–C–N torsion angle of ∼180°). The position of phosphorus Lp was evaluated according to VSEPR theory.¹² This clearly shows that the variation of the P–C bond during the rotation can be attributed purely to conjugation of the phosphorus lone pair with C=NR₂⁺ double bond. The ellipticity in the BCP of P–C bond (a measure of π-electron density contribution to the bond¹³) equals 0.4 for ω = 27° and decreases to 0.15 for ω = −53°, supporting this suggestion. At the same time, the C=N bond length stays almost unaffected by conjugation: its variation does not exceed 0.01 Å, and ellipticity in the corresponding BCP also varied only slightly in the range 0.06–0.09.

The estimated rotation barrier is ∼11.9 kcal mol⁻¹ with a maximum energy in the case of ω = −53° (Fig. 2). It should be noted that the C–P bond length during the rotation correlates with the molecular energy with correlation coefficient 0.79, and the total energy extrema correspond to those for the P–C bond length. This correlation shows that the phosphorus Lp conjugation with C=NR₂⁺ double bond plays the main role in the stabilization of a particular conformer.

The P–C bond length is, however, notably affected by steric effects: two minimal bond lengths at ω = −163° (1.810 Å) and ω = 27° (1.800 Å) differ by 0.01 Å only due to different interactions of the methyl substituents at the nitrogen atom with the phenyl rings. Thus, the observed lengthening of the P–C bond in cations 2 and 3 in the gas phase should be attributed to the increase of steric repulsion between the nitrogen and phosphorus substituents that is more pronounced for ethyl and isopropyl groups.

As we can see, the inherent properties of the cations studied could be reproduced and explained in an isolated state without consideration of interionic contacts in the crystal. This fact leads to the suggestion that the interactions between organic cation and iodide in the crystals of 1, 2 and 3 are not accompanied by any significant charge transfer to the cation.

However, to check how the geometry of the cation would be altered if this interaction were more pronounced, we studied the case of the strongest C–I interaction possible in this system: cation-iodide ionic pair in an isolated state. The diethyl derivative 2 was not involved in this analysis, as its properties were considered as an intermediate between those for methyl and isopropyl ones based on experimental and calculated data.

The cation–anion interaction in the gas phase was strong enough for the C–I bond to form; however, its length was 2.533 Å in the methyl derivative (compared to 2.12 Å in CH₃I) and 2.811 Å in the isopropyl one. The C(1) atom notably pyramidalized, deviating from the P(1)–N(1)–H(1) plane by 0.27 Å in the tight ion pair 1 and by 0.22 Å in 3, correlating with the weakening of the interaction upon the increase of I⋯C(1) distance. Correspondingly, the bond order of C–N bond significantly decreased, leading to lengthening of both conjugated P–C and C–N bonds (see Table 1) and deviation of the N(1) atom from substituents plane (0.24 Å in 1 and 0.07 Å in 3). However, the torsion angles and the overall conformation of the cation were not seriously affected by the interaction with the iodide anion, if compared to the crystal data (see ESI, Fig. S1 and S2†).

The origin of the C–I bond being so weak is the Lp-N-C–I stereoelectronic interaction, i.e. the charge transfer from the N(1) Lp to the antibonding C–I orbital. Such interactions are usually very strong in systems containing a donor of electron lone pair and a polar bond with a good leaving group.¹⁴ The analysis of the Cambridge Crystallographic Structure Database version 5.30, November 2008¹⁵ (further CSD) shows that the compounds containing R₂N–CR₂–I fragment exist in the crystal only in ionic form, except for N-benzoyl-1-iodo-7-azabicyclo(2.2.1)heptane,¹⁶ where the conformation of rigid 7-azabicyclo(2.2.1)heptane bicycle makes the N–C–I stereoelectronic interaction impossible. At the same time, this system can be considered a special case of nucleophilic addition reaction intermediate, with I⁻ attacking the C=NR₂⁺ bond and I–C–N angle (110.1°) being close to the Bürgi-Dunitz angle of 107°.¹⁷

The analysis within the QTAIM framework has shown that the properties of the corresponding BCP for C–I bonds are typical of so-called intermediate interactions¹³: the Laplacian of ρ(r) in these points is positive, while the electron energy density (h_e(r)) is negative (Table 2). The studied ionic pairs, besides the C–I critical point, contained also C–H⋯O critical points corresponding to closed-shell interactions (see Fig. 3 and 4). The properties of these critical points are summarized in Table 2. The lengthening of the C–I bond in compound 3 can be attributed exclusively to steric repulsive interactions between the iodide anion and the isopropyl groups. The charge transfer, measured as 1 + q(I), where q(I) is the QTAIM charge of the iodine atom, was 0.60 and 0.54 for ion pairs 1 and 3, respectively, which is certainly in line with weakening of the cation–anion interaction: according to the Espinosa–Lecomte correlation,^7,8 the total energy of the iodide-cation contacts is 10.0 kcal mol⁻¹ for 1 and 9.0 kcal mol⁻¹ for 3 (see Table 2).

Table 2 Topological parameters^a in the cation–anion critical points (3,−1) in tight ion pairs 1 and 3 in an isolated state

	ρ(r)/e Å^−3	∇^2ρ(r)/e Å^−5	h e(r)/a.u.	v(r)/a.u.	E /kcal mol^−1
a Estimated within the Espinosa–Lecomte correlation scheme (ref. 7 and 8).
Compound 1
C(1)-I	0.350	0.727	−0.010	−0.027	−8.39
H(7)-I	0.072	0.674	0.001	−0.005	−1.60
Compound 3
C(1)-I	0.246	0.868	−0.004	−0.017	−5.3
H(13)-I	0.075	0.708	0.001	−0.005	−1.7
C(15)-I	0.045	0.473	0.001	−0.003	−1.0
H(19C)-I	0.048	0.426	0.001	−0.003	−1.0

---

Fig. 3 Molecular graph with bond paths for ionic pair 1 in an isolated state according to topological analysis of the electron density function. Critical points (3,−1) and (3,+1) are depicted by red and yellow balls, correspondingly.

Fig. 4 Molecular graph with bond paths for ionic pair 3 in an isolated state according to the topological analysis of the electron density function. The critical points (3,−1) and (3,+1) are depicted by red and yellow balls, correspondingly.

The comparison of atomic charges in cations and ionic pairs displayed a more detailed picture of charge displacement: in both systems 1 and 3, the most significant charge (>0.15 e) transferred to P(1) and other charge was delocalized in the molecule. Interestingly, in ionic pair 1 the charge transfer to carbon C(1) was notably high (0.1 e), while in 3 it was comparable to those for other carbon atoms in the molecule (0.027 e). This fact clearly corresponds to the increased role of C⋯I interaction in 1.

Indeed, in the gas phase where the geometry of the cation is notably altered due to partial formation of the C—I bond, the I⁻⋯π interactions are significantly stronger than the I⋯CH₃ ones. However, the formation of CH₃⋯I⁻ contacts leads to weakening of I⁻⋯ π interaction even in an isolated state, and the total energy of the three CH⋯I⁻ interactions (3.7 kcal mol⁻¹) in the case of 3 becomes comparable to the I⁻⋯π one (Table 2). Thus, we can suggest that in a crystal where the geometry of the cation is very close to those for the isolated cation, the comparative role of I⋯π bonding is even smaller. However, for the analysis of these interactions in a crystal we can employ some study of CSD and check if C⋯I contacts are widespread and directed, or they appear in the database only occasionally.

From a geometrical point of view, the I(1)⋯C(1) distance in the crystal of compound 1 (3.526(2) Å) is less than the sum of I and C van der Waals radii (3.68 Å), while in compounds 2 (3.782 Å) and 3 (3.928 Å) it exceeds the formal limit value. However, the definition of the van der Waals radii for the iodide anion is unclear, as the van der Waals radii are defined only for uncharged compounds.⁵ Moreover, the definition of a nonbonded interaction between iodine and the sp² carbon atom meets the problems of steric hindering of the carbon: according to ref. 5, the statistical analysis of CSD shows that the optimal distance for X₃C⋯I contact is 3.90 Å, significantly bigger than 3.68 Å, arising from the sum of the van der Waals radii.

We performed a search for [NR₂-C(sp²)-X]⋯I⁻ fragments, where X is a non-hydrogen atom, R is any substituent and the C⋯I distance lies in the range 3.2⋯4.5 Å. For analysis of the found fragments two parameters were chosen: the I⋯C distance (d) and the distance from carbon to perpendicular dropped from iodine atom to this plane (p). The parameters d and p fully characterize the interaction, and the lower values of p correspond to more directed cases of the I⋯C interaction. The d value of 4.5 Å was chosen as an upper limit for the interaction distance. As the typical bond length for C(sp²)-X, where X is not a hydrogen, is bigger than 1.2 Å, the value of 0.5 Å for p can be chosen as a cutoff for highly-directed C⋯I interactions, i.e. for the cases when the iodide is closer to sp² carbon atom than to its neighbors. The values of p for compounds 1, 2 and 3 lie in the range from 0.15 to 0.25 Å, the compounds are marked on the scattergram by stars.

As we can see from Fig. 5, highly-directed C(sp²)⋯I interactions in the crystals are rare. They appear in the cases of C⋯I distances from 3.44 Å (refcode IALXZN10) to 4.42 Å (refcode BPYACU), correspond only to 68 contacts of total 2296 found in CSD and there is no observable threshold between “directed” and “undirected” ones. The latter, marked on the scattergram by the lower ellipsis, are, however, quite common (∼1000 contacts of a total of 2296). A good example of such interaction can be found in the crystal of MEPRIC, where the iodide is located above the middle of the C–N bond and forms 3 contacts shorter than 4.5 Å (p changing from 0.7 to 1.9 Å) with ring carbons. The values of p close to d (upper ellipsis) represent the C(sp²)–H⋯I⁻ contacts which appear to be more specific and directed than I⁻⋯π ones, in good agreement with recent analysis of anion-π interactions performed by Hay and Custelcean.¹⁸

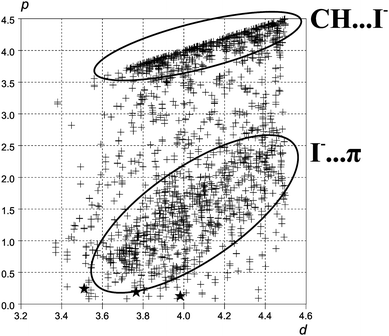Fig. 5 Scattergram of p against d. Each cross on the scattergram corresponds to one fragment found in the CSD with I⋯C distance between 3.2 and 4.5 Å. The positions of the stars correspond to the contacts observed in compounds 1, 2 and 3.

The information obtained from CSD shows that the mere existence of C(sp²)⋯I interaction in the crystal is questionable. The geometrical properties of the C–I bond, as has been shown above, indicate that in the gas phase its strength is significantly overestimated. To model the interaction in the crystal more precisely, we performed a PW-DFT calculation of crystals 1 and 3 using experimental geometry and cell dimensions as the starting point.

The calculated geometries were very similar to those observed in the corresponding crystals, the differences between experimental and calculated covalent bonds not exceeding 0.02 (see Table 1). The calculated C(1)⋯I(1) distance was 3.482 Å in compound 1 and 3.922 Å in 3, shorter than the experimental one by 0.04 and 0.006 Å, respectively. According to the topological analysis of ρ(r) in both calculated crystals, each iodide anion formed interactions mostly with the hydrogen atoms of the surrounding molecules (see Fig. 6). However, the analysis unambiguously shows that the C(sp²)⋯I⁻ interactions appear among others in the crystals. Their estimated energies (1.5 kcal mol⁻¹ for 1 and 0.5 kcal mol⁻¹ for 3) depend on the C⋯I distance and are comparable to those of I⁻⋯H interactions (0.8–2.2 kcal mol⁻¹), but their fraction in the overall energy of iodine contacts is too small to make significant changes in the crystal lattice (see ESI, Table S1†). The total energy of interactions per one iodine anion, calculated as the sum of all I⋯C and I⋯H interaction energies, is −12.45 kcal mol⁻¹ for 1 and–8.95 for 3. These interaction energies are close to those observed in the gas phase (−10.0 and −9.0 kcal mol⁻¹, respectively), but the charge transfer (see above) in the crystal is significantly smaller, namely 0.32 for 1 and 0.29 e for 3, which shows that the C⋯I interactions transfer more charge than the I⋯H ones of equal strength.

Fig. 6 The environment of iodide in crystals 1 and 3 according to topological analysis of the electron density obtained by means of PW-DFT calculations.

Conclusions

The comparative consideration of I⁻⋯π and I⁻⋯H contacts has shown that the I⁻⋯π interaction contributes only a small fraction of the total cation–anion interaction energy in the crystal. However, while the C⋯I interaction energy is small, this interaction can be found even in the case of C⋯I distances exceeding 3.9 Å, which are usually overlooked in the analysis of crystal packing using conventional programs like CCDC Mercury. Based on the data presented in the paper, we can conclude that the directed Hal⁻⋯π contacts observed in some crystal structures actually correspond to attractive interactions with energy comparable to C–H⋯Hal⁻ ones. It should be noted that the I⁻⋯π interactions result in significantly higher charge transfer than I⁻⋯H ones with an equal energy.

Computational details

All calculations of isolated systems were performed using Gaussian03 E.01¹⁹ at B3LYP/6-311G*//B3LYP/6-311G* level. For iodine, the 6-311G* basis set by Radom and coworkers was used.²⁰ The increase of the basis set on light atoms to 6–311+G** for one conformer of ionic pair 1 did not significantly alter the properties of BCPs (see ESI, Table S3†), and the change in charge transfer upon the expansion of the basis set did not exceed 0.01 a.u. The QTAIM analysis of isolated systems was performed using the AIMAll package.²¹ PW-PBE calculations of crystal structures 1 and 3 were carried out using the VASP 4.6.31 code.^22–25 A conjugated gradient technique was used for optimizations of the atomic positions, cell vectors and minimization of the total energy. Experimental atomic coordinated and cell parameters were taken as a starting point. The projected augmented wave (PAW) method was applied to account for core electrons while valence electrons were approximated by plane-wave expansion with 400 eV cutoff. The exchange and correlation terms of total energy were described by the PBE exchange–correlation functional.²⁶ Kohn–Sham equations were integrated using Γ-point approximation. At a final step of our calculations atomic displacements converged better than 0.01 eV Å⁻¹, as well as the energy variations were less than 10⁻⁴ eV. In order to perform the topological analysis, the electron density distribution functions were calculated on dense FFT (fast Fourier transformation) grid 240 × 192 × 180 and 192 × 240 × 210 points for 1 and 3, respectively, using PAWs with the smallest core radii. The topological analysis was carried out by the AIM program (part of the ABINIT software²⁷).

Acknowledgements

This study was financially supported by the Foundation of the President of the Russian Federation (Federal Program for the Support of Young Doctors, Grants MD-172.2008.3 and Leading Scientific Groups SS-3019.2008.3)

References

1. J. Dupont, J. Braz. Chem. Soc., 2004, 15, 341–350.
2. C. S. Consorti, P. A. Z. Suarez, R. F. de Souza, R. A. Burrow, D. H. Farrar, A. J. Lough, W. Loh, L. H. M. da Silva and J. Dupont, J. Phys. Chem. B, 2005, 109, 4341–4349.
3. D. Golovanov, K. Lyssenko, Y. Vygodskii, E. Lozinskaya, A. Shaplov and M. Antipin, Russ. Chem. Bull., 2006, 55, 1989–1999.
4. E. E. Nifant'ev, V. P. Morgaliuk, P. V. Petrovskii and K. A. Lyssenko, Russ. Chem. Bull., 2007, 56, 2131–2132.
5. R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384–7391.
6. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, USA, 1994.
7. E. Espinosa, C. Lecomte and E. Molins, Chem. Phys. Lett., 1999, 300, 745–748.
8. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
9. Y. V. Nelyubina, M. Y. Antipin and K. A. Lyssenko, CrystEngComm, 2007, 9, 632–635.
10. Y. V. Nelyubina, M. Y. Antipin and K. A. Lyssenko, J. Phys. Chem. A, 2009, 113, 3615–3620.
11. Y. V. Nelyubina, K. A. Lyssenko, D. G. Golovanov and M. Y. Antipin, CrystEngComm, 2007, 9, 991–996.
12. R. J. Gillespie and I. Hargittai, The Vsepr Model of Molecular Geometry, Allyn & Bacon, 1991.
13. R. F. W. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061–5068.
14. A. J. Kirby, The anomeric effect and related stereoelectronic effects at oxygen, Springer Berlin, 1983.
15. F. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388.
16. A. Avenoza, J. H. Busto, C. Cativiela and J. M. Peregrina, Tetrahedron, 2002, 58, 1193–1197.
17. A. S. Cieplak, in Structure Correlation, eds. H. B. Bürgi and J. D. Dunitz, Verlag Chemie, Weinheim, 1994, pp. 205–302.
18. B. P. Hay and R. Custelcean, Cryst. Growth Des., 2009, 9, 2539–2545.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople, Gaussian 03, Revision E.01, Gaussian, Inc., Wallingford, CT, 2004.
20. M. N. Glukhovtsev, A. Pross, M. P. McGrath and L. Radom, J. Chem. Phys., 1995, 103, 1878–1885.
21. T. A. Keith, AIMAll, Version 09.04.23, 2009, http://aim.tkgristmill.com.
22. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
23. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
24. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
25. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
27. X. Gonze, J.-M. Beuken, R. Caracas, F. Detraux, M. Fuchs, G.-M. Rignanese, L. Sindic, M. Verstraete, G. Zerah, F. Jollet, M. Torrent, A. Roy, M. Mikami, P. Ghosez, J.-Y. Raty and D. C. Allan, Comput. Mater. Sci., 2002, 25, 478–492.

---

Footnote

† Electronic supplementary information (ESI) available: Comparison of calculated and experimental geometries (Fig. S1 and S2), the summary of X⋯I bonding contacts in crystals of compounds 1 and 3, according to PW-DFT calculation (Tables S1 and S2), and comparison of BCP properties for ionic pair 1 in different basis sets (Table S3). See DOI: 10.1039/b908500a

---