Classification of polymer groups by means of a new polymer testing instrument, the identiPol QA, coupled with pattern recognition techniques
Bozena M.
Lukasiak
* and
John C.
Duncan
Triton Technology Ltd., 3 The Courtyard, Main Street, Keyworth, Nottinghamshire, NG12 5AW, UK. E-mail: bozena@triton-technology.co.uk
First published on 13th October 2010
Abstract
An original instrument for thermo-mechanical polymer testing has been developed. This article describes the process of data acquisition, preprocessing and classification into 11 main polymer groups. The following polymer groups are used: polystyrene, acrylonitrile–butadiene–styrene, polycarbonate, low density polyethylene, polypropylene, high density polyethylene, polyamide 4.6, polyamide 6, polyamide 6/6, polybutylene terephthalate and polyethylene terephthalate. Three pattern recognition techniques of increasing complexities are applied in order to assess their suitability for the automated categorisation of polymer samples: k-nearest neighbours, various combinations of Q- and D-statistics (sometimes referred to as Soft Independent Modelling of Class Analogy, SIMCA) and Back-propagation Neural Networks. It is found that all the three methods categorise the materials into the correct polymer groups irrespective of their complexity. Methods based on the correlation structure in the data prove more beneficial than methods based on distance due to particular characteristics in the data. Best results are obtained using an adequate combination of two coefficients: one based on correlation and another based on distance.
Introduction
The work presented here describes an original combination of techniques for the classification of thermoplastic materials. It is based upon measurements recorded using a novel thermo-mechanical device and the processing of those measurements using chemometric data analysis methods.Most polymers are largely chemically inert and have very similar physical properties and characteristics, e.g. thermal conductivity and Young's Modulus.1 Therefore simple chemical tests are ineffective in identifying or differentiating between samples. Equally mechanical property tests tend to be more complex than those used for metals, e.g. hardness testing, and generally less informative, mainly due to the viscoelastic properties of polymeric materials. Mechanical tests are very specific, e.g. what is the breaking strength, but they are not so good for differentiating between materials. They also have the disadvantage that they need to be performed on finished components or special test pieces must be moulded from the raw material. Therefore they do not make a good quality control check for raw material, which is usually in the form of plastic granules approximately 20–30 mg in weight.
Naturally, instrumentation for testing all kinds of polymer properties is plentiful. Typically they are specialised and only yield a particular piece of information about the sample being analysed. They are usually expensive apparatus and require a skilled scientific operator. The spectroscopic equipment (Fourier Transform Infrared, Mid-infrared, and Near Infrared)2 is excellent for chemical group identification, e.g. for differentiating between PVC and PE, but is not so good at distinguishing between two very similar grades of poly(ethylene) for example. They are usually confounded by black plastics, since the carbon black filler is a strong infra-red absorber. X-Ray3 results are specific to the crystalline form of the plastic. It is expensive and it can be hard to interpret the results. It makes a poor QC tool. The Solid-state Nuclear Magnetic Resonance (NMR)4 device provides detailed structural and deformational information on any polymer sample. It is almost certainly the most comprehensive analysis technique, however, it is a pure research tool. Costs are over several hundred thousands of pounds and a purpose built laboratory with a skilled operator is required to run analyses and interpret data. Gel Permeation Chromatography (GPC)5 is a very specific test, yielding molecular weight information. Again this makes a poor QC test for all other properties.
Of all the techniques, the thermal analysis methods usually give the best performance for polymer analysis, based upon speed of test, amount of information obtained and relative cost of equipment. The following thermal analysis techniques are commonly applied:
- Differential Scanning Calorimetry (DSC, measures melting point,6 glass transition,7 and crystallinity6).
- Dynamic Mechanical Analysis (DMA, measures modulus,8 damping (tan δ6), glass transition,7 and melting point6).
- Thermo-Mechanical Analysis (TMA, measures coefficient of thermal expansion,6 glass transition,7 and melting point6).
Two types of instruments, commonly used to perform mechanical thermal analysis, are thermo-mechanical analyser (TMA)6 and dynamic mechanical analyser (DMA).6,8 The former, TMA, carries out a simple test, which allows for measuring various transitions occurring in the material. The second, DMA, is more complex, as it measures two parameters responsible for the viscoelastic behaviour of a polymer. The first is complex modulus, which determines the stiffness of the material, while the other is related to the amount of damping the material can provide and determines the energy it can absorb (tan δ6). Studies on the classification of polymer groups based on the DMA dataset have been reported previously.9 The disadvantage of both instruments is that average plastics processing facility may not be able to afford such equipment, nor the personnel to run it and generally it would be too slow for the production environment. Consequently the polymer processing industry has never had a simple and cost effective device available for rapid and definitive quality control purposes.
The identiPol QA measures a fingerprint of a material's thermo-mechanical properties in a rapid test. Typically this takes about seven minutes, with an equal amount of time for sample preparation, from either raw material or a finished product. It is limited to thermoplastic materials, but such materials account for a £74 billion market in Europe alone. This measurement, combined with the automated chemometrics data interpretation, means that an inexperienced operator can make reliable quality control measurements with little training. It complements melt flow index (MFI) data1 and density test data,10 which are the only scientific tests routinely employed by the plastics processing industry and which also yield little information on subtle differences between materials.
The data from several different polymer types are used to provide a database that the chemometric techniques described here automatically interrogate to identify and check new plastic samples before their use in a production process. A quick and correct automatic classification of 11 main polymer groups (Table 1) is achieved.
| No | Polymer groups | Number of grades | Shortcuts | Number of samples | Number of samples in the training set | Number of samples in the validation set |
|---|---|---|---|---|---|---|
| 1 | Polystyrene | 5 | PS | 219 | 164 | 55 |
| 2 | Acrylonitrile–butadiene–styrene | 3 | ABS | 79 | 59 | 20 |
| 3 | Polycarbonate | 2 | PC | 158 | 118 | 40 |
| 4 | Low density polyethylene | 5 | LDPE | 98 | 73 | 25 |
| 5 | Polypropylene | 7 | PP | 202 | 151 | 51 |
| 6 | High density polyethylene | 3 | HDPE | 165 | 124 | 41 |
| 7 | Polyamide 4.6 | 1 | PA 4.6 | 12 | 9 | 3 |
| 8 | Polyamide 6 | 2 | PA 6 | 35 | 26 | 9 |
| 9 | Polyamide 6/6 | 1 | PA 6/6 | 42 | 31 | 11 |
| 10 | Polybutylene terephthalate | 1 | PBT | 26 | 19 | 7 |
| 11 | Polyethylene terephthalate | 6 | PET | 169 | 127 | 42 |
| Total | 1205 | 901 | 304 |
Experimental
Instrumentation
Data were collected using identiPol QA produced by Triton Technology (Fig. 1). IdentiPol QA measures visco-elastic properties of the polymer as the temperature is rapidly increased to the point when the sample melts or softens. IdentiPol QA consists of two working stages. One is the sample preparation stage and the other is the sample analysis stage. The sample preparation stage uses the left hand side of the heater block, the moulding section on which the empty sample holder is placed (Fig. 1). The sample analysis stage uses the right hand side of the heater block, the testing section on which the prepared sample holder is placed. The drive motor, mounted below the right-hand side of the heater block, also contains the displacement sensor (Fig. 2). | ||
| Fig. 1 IdentiPol QA. | ||
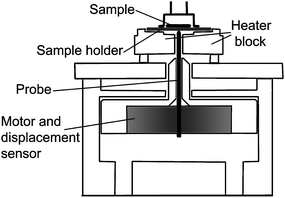 | ||
| Fig. 2 A schematic of the testing section of identiPol (a cross-section running from the front to the back of the instrument). | ||
Data acquisition
Between 20 and 30 mg (one or two plastic granules) of each polymer sample are loaded onto the sample holder,11 mounted on the moulding section of the machine (Fig. 1). The sample preparation stage is then initiated by closing the lid with a spring-loaded plunger pressing down on the sample. On closing it automatically starts to heat. As the plastic softens, the plunger squashes the sample, moulding it uniformly into the sample holder. At this point heating stops and a cooling fan is turned on. This automatically switches off when the sample reaches a predefined temperature and indicates that the sample holder may be removed.The novel sample holder allows material in pellet or other forms, such as powder or parts cut from a finished product, to be moulded consistently, whilst at the same time providing a heat transfer lattice throughout the prepared sample enabling rapid heat transfer.11 The composite of a sample and holder creates a complex geometry, which does not correspond to any of the standard DMA modes.
The composite of a sample and holder is transferred to the analysis stage on the right-hand side. The composite is rapidly heated while the motor applies force to it by means of a probe and measures the change in resistance to the applied force (Fig. 2 and 3). The heating rate is user-defined (maximally 100 °C min−1). The maximum temperature of the identiPol QA is 350 °C.
 | ||
| Fig. 3 A schematic of the phase difference between the applied stress and sample response. | ||
In the current study the heating rate of 70 °C min−1 is employed and the sinusoidal force is applied at a frequency of 55 Hz (Fig. 3). The data are collected approximately every 0.25 °C, and the output data are linearly interpolated in order to obtain equidistant temperature datapoints at exactly 1 °C intervals. The temperature range studied is from 45 °C up until the temperature at which the sample is totally viscous and no further useful data can be collected.
The entire measuring procedure using identiPol QA takes about 15 minutes (depending on the melting temperature of the polymer), which is generally faster than the existing DMA methods.
Thermal analysis
Mechanical properties of polymers, which are the most important in the commercial applications of these materials, depend on the temperature. Therefore in order to determine the behaviour of polymer in various conditions it is necessary to perform a temperature ramp test, where the properties of the material are examined, while the temperature is rising. This experiment can be performed using the identiPol QA. The measurement is based upon Dynamic Mechanical Analysis (DMA).8 A sinusoidal force is applied to the sample and the resulting sinusoidal displacement is measured (Fig. 3). The response is phase shifted with respect to the applied force; this phase difference is called δ. The ratio of the applied stress and resultant strain (deformation) can be resolved into two components: an in-phase component (in-phase stiffness, S′), which is proportional to the elastic contribution of the sample's response, and an out-of-phase component (out-of-phase stiffness, S″),12 proportional to the viscous contribution.1 Tan δ6 is the ratio of S″ to S′. In this paper tan δ parameter is employed in the classification procedure. A typical tan δ trace is presented in Fig. 4. A semi-crystalline polymer, represented by a line, features a small peak at about 90 °C. At this temperature the crystalline phase of the material is undergoing the glass transition.7 This feature is the most important in the classification procedure. Classifiers based on the correlation structure of the dataset aim to distinguish polymer groups on the basis of the glass transition position. The rise in the tan δ slope above 260 °C corresponds to the process of melting. An amorphous polymer, represented by (○), is distinguished by a much higher glass transition peak. This polymer does not melt. | ||
Fig. 4 An example of identiPol QA signal (tan δ) for a semi-crystalline polymer (![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) ) and for an amorphous polymer (○). ) and for an amorphous polymer (○). | ||
Dataset
The identiPol QA polymer dataset consists of 11 polymer groups, each group consisting of between 1 and 7 polymer grades, in total 1205 samples (Fig. 4 and Table 1). The diversity in the number of samples measured for each of the polymer groups adds another challenge to the classification problem tackled in this work. Each sample is described using between 150 and 280 datapoints depending on its melting point.6 Each datapoint corresponds to the value of tan δ6 at an interpolated temperature.Every polymer sample is measured at least up to the point when the sample melts (in the case of semi-crystalline polymers) or softens (in the case of amorphous polymers). At the temperature where polymer is completely soft it does not influence the measurement significantly. At this point only sample holder is measured, and since its stiffness changes insignificantly with rising temperature, the measured parameter S′ also does not change, which can be detected using its derivative. This point is defined as the End Point temperature, Ep.
Every polymer group is characterised by a different Ep. In order to obtain a rectangular data matrix all temperature traces used in this publication are cut off at the End Point, and extrapolated to the longest temperature trace, replacing values above Ep with 0. It should be highlighted though that this procedure can only be applied if Ep is detected completely automatically, independent of the users knowledge, otherwise the data processing procedure may overfit the data and bias the classification result.
Ep is defined separately for each sample as a datapoint 15 °C higher than the temperature where both the absolute value of the first derivative of S′ drops below 5 and the value of S′ drops below 1/8 of the total range of S′, according to the equation:
| S′ < (S′max − S′min)/8 + S′min | (1) |
Software
Data acquisition is performed by means of in-house routines written in the Microsoft® Visual Basic™ environment. Subsequent data visualisation and processing are performed using in-house developed scripts run using the Matlab environment (R2009a, The MathWorks, Cambridge, UK). Matlab routines for neural network analysis are kindly provided by the chemometrics group of the Chemistry Department at the Sapienza University of Rome.Data analysis
Outlier removal
Generally, identiPol QA results for the same material are highly repeatable, but certain circumstances can produce unrepeatable results. For example, this can occur when the material being tested consists of two (or more) different kinds of pellets made from different polymer grades. In this case different sample preparation techniques are required, but these are not discussed here as they do not affect the aspects of the analysis being presented here.All samples in this work affected by an obvious experimental error are removed from the dataset. Table 1 describes data obtained after this procedure. All the other potentially outlier samples, where the reason for outlying is not obvious, are included in the dataset in order to test the robustness of the automatic data processing methods. In the classification stage of this work samples with a low probability of belonging to any of the classes are considered outliers.
Validation and optimisation
An important data processing step is to make sure that the goal of the research, which in this particular case is polymer classification, can be obtained with the same accuracy (i.e. the same percentage of correctly classified samples, %CC) by the user, who will apply the described instrumentation and pattern recognition methods at his or her workplace. A high %CC may be obtained by trained statisticians on their carefully gathered dataset, thanks to their expertise, manual outlier detection, or even more accurate sample preparation. The factory employee in the manufacturing plant, on the other hand, has to rely on the automatic procedure. Therefore in this paper an emphasis is put on finding a data processing routine which will be completely automatic, independent of the user expertise, robust and not result in overly optimistic results (overfitting).In order to prevent overfitting a 3-way split validation procedure is applied. Firstly, data are split into a validation and training set using duplex.13,14 This procedure is referred to as external validation. The training set is used for building and optimisation of the classification models, which are then applied to the validation set. The optimisation of the classification models is performed by repeated divisions of the training set into internal test and internal training sets using 5-fold cross-validation13,15 (internal validation).
The percentage of correctly classified samples, which gives the prediction ability of the model (%CC), is calculated for the validation set. The classification results are reported additionally in confusion tables. A confusion table consists of rows corresponding to the true polymer group of the samples whereas the columns represent the group to which the analysis method assigned the samples. For perfect classification only the diagonal would be greater than zero, i.e. one to one correspondence. Numbers appearing off the diagonal represent misclassifications.
Classification
The effectiveness of three classification methods of various complexities is compared, namely: the k-nearest neighbour (k-NN) method,15,16 several combinations of Q- and D-statistics17 and Back-propagation Neural Networks (BPNN).18In the case of a multidimensional dataset, k-NN often suffers from the curse of dimensionality.20,21 The multidimensionality of data may cause some problems for the k-NN classifier because redundant information in the training set usually influences the classification ability.21 Therefore a feature reduction method, such as principal component analysis (PCA),15,22 is usually performed before the classification procedure, and PCA scores are often used in the classification instead of raw variables. In this study two options are compared: with and without the application of PCA.
Principal component model (PC model) is produced using the training set and applied to the validation set, as described previously.15,23 PCA scores are then used in the k-NN procedure. A simple method of optimising the component number is employed, namely the number of components which include at least 95% of the training set variance is applied.23
Mean centering is a standard technique employed before PCA. In this study, mean centering is applied in order to reduce both the size of the first principal component and the optimal number of components. Before the application of PCA, each variable in the training set is mean centred, and the means calculated using the training set are applied to the validation set.
The nearest neighbour of a sample can be defined using any similarity or distance measure appropriate for the dataset. In this paper only Euclidean distance15,23 is applied for simplicity.
Both statistics are based on a principal component model (PC model) and the combination of them is often called SIMCA.17 The D-statistic is based on the popular Mahalanobis distance, whereas the Q-statistic is based on the similarity between the shapes of various temperature traces (which are related in a way to the correlation structure of the dataset). Please refer to the Appendix for more information. It is not the primary purpose of this paper to describe the Q- and D-statistics, which are standard procedures discussed in depth elsewhere.17 Here we focus only on these aspects of the methodology, which are applied in an unusual way. Therefore the following topics are discussed: classification criterion, calculation of the two statistics for this application and methods for combining the two statistics together.
The usual method of implementing Q- and D-statistics is to define a threshold encompassing 95% or 99% of the modelled class (Qlimit) and reject or include the samples based on comparison with this threshold. This approach is based on the fact that first implementations of Q- and D-statistics were in the area of multivariate statistical process monitoring, where the new sample was assumed to be in or out of control. This is in fact a one-class classification problem.24,25 However this approach does not help in the case of more complex classification problems with multiple classes, where a sample can belong to various classes with various confidences. In this case it is better to calculate the similarity to each of the classes separately and then classify the sample to the one which gives highest similarity.15,26 In some cases this method is called disjoint hard modelling,26 however, in our application we do not require samples to be unambiguously assigned to a specific group, therefore soft modelling is a more appropriate name in our case.
Therefore, the standard equations, presented by Tracy27 and Jackson et al.28,29 and summarised by Westerhuis,25 are rearranged in order to obtain a number related to the confidence that the unknown sample belongs to a specific class (please refer to the Appendix). In the practical application this number can be interpreted in terms of the quality of the measured material. In this paper we call it the D- or Q-statistic score (αD and αQ).
The D-statistic score is calculated by superimposing the unknown sample on the PC model. The Q-statistic shows how suitable is this PC model for describing the unknown sample. The D- and Q-statistics are therefore complementary. They are often treated as independent and therefore usually the values calculated using them are interpreted separately. However in order to produce an automatic algorithm for polymer classification, giving a definite answer which can then be evaluated using standard parameters, such as %CC or confusion tables, it is necessary to find a way of combining these two statistics into one classification score.
Many ways of combining the two confidence limits obtained using Q- and D-statistics have been proposed in the literature.30–32 However here, instead of using the confidence limits directly, the D- and Q-statistics scores (αQ and αD) are employed without setting the limits (see Appendix). For this reason it is easier to apply other methods in this project, namely: (a) the geometric average 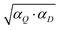 , (b) the average (αD + αQ)/2 and (c) the minimum (min(αD, αQ)).15,26,33 For a comparison additionally αQ and αD are applied individually. Samples which obtain the classification score below a threshold for all the classes are considered outliers. The threshold of 1 out of 100 is applied for all the options described above.
, (b) the average (αD + αQ)/2 and (c) the minimum (min(αD, αQ)).15,26,33 For a comparison additionally αQ and αD are applied individually. Samples which obtain the classification score below a threshold for all the classes are considered outliers. The threshold of 1 out of 100 is applied for all the options described above.
The optimisation of the principal components number is based on the ratio of the predictive residual error sum of squares (PRESS) and the residual sum of squares (RSS).15,23,34 When the ratio of PRESS using J + 1 components over RSS using J components is higher than 1, J is the optimal number of components.
| Δw(t) = −η(δE/δw) + γΔw(t − 1) | (2) |
Variation of the weight (w) at the tth iteration depends on two parameters: the partial derivative of the total error with respect to that weight and its own variation during the previous iteration. These two relations are determined by η (learning rate) and γ (momentum). The origins of the term Back-propagation Neural Networks are linked to the way in which the prediction error is distributed backward between the neurons of the hidden layers.
The algorithm applied here is described by Bridle,36 where a hyperbolic tangent is chosen as the activation function36 in the hidden layer, while softmax output is used. The output is a value between 0 and 100 for each modelled class, where a higher number indicates a higher probability that the tested sample belongs to a particular class. The learning rate is set to 0.003 and no momentum is added (that is to say that momentum is equal to 0). The optimisation of the number of learning iterations and number of hidden neurons is based on the average classification ability of the internal validation set. Firstly the neural network is trained with the internal training set, using a certain number of learning iterations and certain number of hidden neurons. Then the classification model is applied to the internal validation set. This procedure is repeated for various numbers of hidden neurons (between 5 and 30) and learning iterations (up till 1000), and every time a separate %CC is calculated. This %CC is then averaged over all cross-validation splits and the number of hidden neurons and learning iterations corresponding to the best %CC is chosen. The optimal value of hidden neurons and learning iterations is then applied to the validation set. Samples which obtain the classification score below 5 (out of 100) for all the classes are considered outliers.
Results and discussion
In general all the classification methods perform very well, which indicates that the thermo-dynamic dataset contains enough information to differentiate between polymer groups, using various data processing methods (Table 2). Below differences between classification methods are explained in detail.| SIMCA | α Q | α D | min(αQ, αD) | (αQ + αD)/2 |
|
|---|---|---|---|---|---|
| 98.93 (outliers: 1.0%) | 75.42 (outliers: 7.6%) | 100.00 (outliers: 13.8%) | 88.78 (outliers: 0.3%) | 100.00 (outliers: 6.9%) | |
| k-NN | k = 1 | k = 2 | k = 3 | k = 4 | |
| Unreduced dataset | 99.01 | 99.01 | 98.68 | 99.01 | |
| PCA scores | 99.01 | 99.01 | 98.68 | 98.68 | |
| BPNN | 99.34 (no outliers) | ||||
A comparison of BPNN and combinations of Q- and D-statistics
At the first sight the most accurate classification is obtained using two classifiers: the geometric average of the Q- and D-statistics scores and the minimum of the Q- and D-statistics scores (min(αD, αQ)). In both cases no sample is misclassified, however, the criterion min(αD, αQ) identifies 13.8% of the samples as outliers, whereas the criterion
and the minimum of the Q- and D-statistics scores (min(αD, αQ)). In both cases no sample is misclassified, however, the criterion min(αD, αQ) identifies 13.8% of the samples as outliers, whereas the criterion 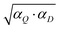 identifies 6.9% of the samples as outliers (Table 2). On the other hand, in the case of BPNN no sample is identified as an outlier and only 0.66% of validation set samples are misclassified. One HDPE sample is misclassified to PP and one PA 6 sample is misclassified to PBT, which gives two misclassified samples out of 304 samples in the validation set for BPNN. This means that there are many samples, which are assumed to be outliers by Q- and D-statistics, and are not classified to any group, whereas BPNN classifies them correctly. This suggests the superiority of BPNN for the problem in hand. It additionally highlights the fact that in the evaluation of classification methods using %CC the user shall take into account also the number of outliers identified by various methods.
identifies 6.9% of the samples as outliers (Table 2). On the other hand, in the case of BPNN no sample is identified as an outlier and only 0.66% of validation set samples are misclassified. One HDPE sample is misclassified to PP and one PA 6 sample is misclassified to PBT, which gives two misclassified samples out of 304 samples in the validation set for BPNN. This means that there are many samples, which are assumed to be outliers by Q- and D-statistics, and are not classified to any group, whereas BPNN classifies them correctly. This suggests the superiority of BPNN for the problem in hand. It additionally highlights the fact that in the evaluation of classification methods using %CC the user shall take into account also the number of outliers identified by various methods.
The difference between Q- and D-statistics and BPNN could be a result of the fact that the process of neural network training is based on highlighting the differences between classes, in contrast to Q- and D-statistics, where the modelling process aims at capturing the variance within each class separately (D-statistic) or the variance of the unknown sample “to the model” (Q-statistic). Therefore BPNN are designed to obtain best separation, whereas both Q- and D-statistics aim at modelling. Some polymer groups consist of a number of grades, which can be very different from each other. It is assumed that the PC model consisting of an optimal number of components is supposed to account for the variability in the polymer group, but still in our study big polymer groups consisting of many grades contain more outliers than small groups. Both Q- and D-statistics build a general model, including all the polymer grades involved, and assuming that the PCA scores are distributed normally, which can be perceived as a way of “averaging” various grades. Therefore certain samples which do not follow the main trend in the polymer group obtain a low classification score and can be selected as outliers. This can explain why the application of Q- and D-statistics to big polymer groups (like: ABS and PP), which are build of many grades, identifies more outliers, whereas no outlier is identified in small groups, consisting of only one, or two very consistent polymer grades, like: PA 4.6, PA 6, PA 6/6 or PBT. On the other hand the process of neural network training, due to its non-linearity, allows for modelling each particular cluster, giving a better fit to all the grades in the validation set.
The superiority of BPNN in this particular situation does not mean that this method will always give the best solution for polymer classification. In order to prevent overfitting there must be a balance between adjusting the classifier to the dataset and generalisation. An interesting test for the future would be to challenge the classifier using a polymer group which was not presented in the learning process.
A comparison Q- and D-statistics
Comparison of the results for Q- and D-statistics shows that distance to the centroid of the polymer group (D-statistic) is not the best classification parameter. This information is relevant for the future studies of the thermo-mechanical polymer data. D-Statistic is based on a very well known and widely used Mahalanobis distance, and it shall be stressed that the application of this popular measure is not always beneficial for the classification or other judgment of our data. Usually the application of a parameter linked to the correlation structure of the dataset (like Q-statistic) gives better classification. However combination of Q- and D-statistics gives the best result.The average of αD and αQ gives bad prediction. This is a reasonable outcome, taking into account that averaging a good classifier (Q-statistic) with a bad classifier (D-statistic) shall result in averaging the classification power of the model. On the other hand the application of the minimum of Q- and D-statistics or geometric average gives the best prediction, better than Q-statistic alone. This suggests that in some cases a sample, which would be misclassified using only Q-statistic, can be classified correctly when D-statistic is applied additionally, even if on its own D-statistic is a bad classification criterion. A good example here is the misclassification of LDPE samples to PA 6 group by means of Q-statistic alone (Table 3). LDPE is a semi-crystalline polymer melting at a low temperature, which does not resemble PA 6, and the only reason why 4% of LDPE samples are classified to PA 6 by Q-statistic is that the End Point of LDPE, where its tan δ slope decreases, corresponds to the decreasing of tan δ slope of PA 6 group after the glass transition.7 Application of additionally the D-statistic solves this problem. D-Statistic highlights the huge difference in the value of tan δ between these two very different polymers (as opposed to the correlation structure). However this improvement can be achieved only if the confidence value is restricted by both criterions, for example if the minimum of Q-statistic and D-statistic, or the geometric mean is applied, and not in the case when the average value is used.
| α D | Predicted group (%) | Outliers (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PS | ABS | PC | LDPE | PP | HDPE | PA 4.6 | PA 6 | PA 6/6 | PBT | PET | |||
| Actual group | PS | 92.7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.8 | 5.5 |
| ABS | 0.0 | 85.0 | 0.0 | 0.0 | 0.0 | 0.0 | 10.0 | 0.0 | 0.0 | 0.0 | 5.0 | 0.0 | |
| PC | 0.0 | 0.0 | 35.0 | 0.0 | 0.0 | 0.0 | 35.0 | 0.0 | 0.0 | 0.0 | 30.0 | 0.0 | |
| LDPE | 0.0 | 0.0 | 0.0 | 96.0 | 0.0 | 0.0 | 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| PP | 0.0 | 0.0 | 0.0 | 0.0 | 51.0 | 0.0 | 49.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| HDPE | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 75.6 | 24.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| PA 4.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| PA 6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 22.2 | 77.8 | 0.0 | 0.0 | 0.0 | 0.0 | |
| PA 6/6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | |
| PBT | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 14.3 | 0.0 | 0.0 | 85.7 | 0.0 | 0.0 | |
| PET | 0.0 | 0.0 | 0.0 | 0.0 | 2.4 | 0.0 | 9.5 | 0.0 | 0.0 | 0.0 | 88.1 | 0.0 | |
| α Q | Predicted group (%) | Outliers (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PS | ABS | PC | LDPE | PP | HDPE | PA 4.6 | PA 6 | PA 6/6 | PBT | PET | |||
| Actual group | PS | 90.9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 9.1 |
| ABS | 0.0 | 85.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 15.0 | |
| PC | 0.0 | 0.0 | 92.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 7.5 | |
| LDPE | 0.0 | 0.0 | 0.0 | 88.0 | 0.0 | 0.0 | 0.0 | 4.0 | 0.0 | 0.0 | 0.0 | 8.0 | |
| PP | 0.0 | 0.0 | 0.0 | 0.0 | 92.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 7.8 | |
| HDPE | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 87.8 | 0.0 | 0.0 | 2.4 | 0.0 | 0.0 | 9.8 | |
| PA 4.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| PA 6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| PA 6/6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | |
| PBT | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | |
| PET | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2.4 | 0.0 | 92.9 | 4.8 | |
When Q- and D-statistics are applied many outliers are identified in the polypropylene (PP) group. PP is a relatively numerous group in our dataset, containing 202 samples. The glass transition7 of this polymer occurs at a low temperature, and in the range measured this material does not express any distinctive features. Consequently the signal to noise ratio is low and any erroneous artefact on the temperature trace is highlighted. Due to this, even if in general PP can be easily distinguished from other polymers using any of the classification methods presented here, this polymer group cannot be easily modelled using Q- and D-statistics, and the group contains many outliers.
It is detected that certain techniques deal worse with certain polymer groups, for example Q-statistic mistakes PET for PA 6/6, whereas D-statistic classifies them correctly, misclassifying PET and PP instead (Table 3). Therefore in the practical applications it could be beneficial to adjust the classification method to the types of polymers being measured, if possible.
k-NN classification
An interesting conclusion relates to k-NN which works with accuracy comparable with the more sophisticated methods. Simple methods often outperform complex classification algorithms,38 and additionally k-NN often deals well with non-linear data. Even very complex boundaries can be correctly defined using a simple k-NN model, in the case when the classes do not overlap to a high extent. However obtaining a suitable confidence value based on the k-NN classifier is not trivial (although there are examples in the literature19). Due to this, k-NN does not deal well with the situation when the unknown sample is situated outside the boundaries of the dataset (it is more suitable for interpolating than extrapolating problems), and in our application it is not possible to set a threshold for outliers. Nevertheless only one sample out of 304 is misclassified by k-NN (k = 1).Another comparison performed in this project aims to find out how the multidimensionality of the data obtained from identiPol QA affects the division between polymer groups. k-NN classifier is applied to the raw dataset as well as to the reduced dataset (PCA scores). Examination of the total polymer groups classification (%CC) does not provide any answer, since both with and without the application of PCA a high %CC is obtained. This confirms our previous conclusion: data produced using identiPol allow for a correct polymer classification in general. Looking at the confusion tables allows for a more detailed study. For certain polymer groups there is a slight improvement after the application of PCA, whereas in other cases better result is obtained without PCA. This suggests that it is beneficial to apply a custom made classification model, depending on which kind of polymer is being analysed. However it shall be indicated that due to the particularity of the thermo-mechanical data, in general the k-NN classifier does not suffer from the curse of dimensionality,21 when applied to this multidimensional dataset.
Various numbers of nearest neighbours are tested and all the options allow for the correct categorisation of samples. This confirms again that the classification problem is not difficult. Approaching a more complex classification dilemma, for example polymer grades classification (classification of subgroups instead of groups), could provide us with insight as to the optimal k.
Conclusions
An alternative polymer classification method is presented in this publication. This method allows for a correct classification of polymer groups (%CC = 100 with 6.9% of outliers), and proves to be a good solution for plastic product manufacturers, who would not be able to afford or operate a DMA.6,8The method employs a new machine, indentiPol QA, which produces a unique fingerprint of how the properties of a plastic change as a function of increasing temperature.
The new instrumentation provides a new challenge in the field of pattern recognition. Several classification strategies are described, and the reported results suggest that all methods, irrespective of whether they are simple, like k-NN, or sophisticated, like Back-propagation Neural Networks, give good classification results. This suggests a good quality of the data gathered using identiPol QA. However even if the classification decision is correct, it was noticed that certain polymer groups produce many outliers. This happens if the modelling is done by means of specific data analysis techniques (like for example a classification criterion: min(αD, αQ)). These groups do not undergo many relaxations in the temperature range of the measurement (like for example PP).
Additionally k-NN studies suggest that the curse of dimensionality21 does not always apply to the identiPol QA polymer dataset, probably due to the smoothness of the curves.
Various combinations of Q- and D-statistics are applied and it is concluded that due to the particularity of the presented dataset, methods based on the correlation structure of the data are especially beneficial for the polymer classification, in contrast to the very popular classifiers based on the distance to mean, like for example the Mahalanobis distance.
Appendix
In our application the original equations for Q- and D-statistics25,27–29 are rearranged in order to obtain Q- or D-statistic score, a number which can be related to the confidence that the unknown sample belongs to a specific class.15 The following procedure is applied.Firstly a PC model of the training set samples from polymer group A is built.39
| XA = TA·PTA + EA | (A1) |
The validation set sample b is projected onto this model in order to test whether or not it is modelled well by the PCA based on class A. A new set of scores and residuals is obtained:39
![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) bA = PTAmxbA bA = PTAmxbA | (A2) |
ebA = mxbA − PA![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) bA bA | (A3) |
![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) bA is the new set of scores, mxbA is a data vector for sample b mean centered using the averages of class A, and ebA is the residuals vector for sample b produced using model from class A.
bA is the new set of scores, mxbA is a data vector for sample b mean centered using the averages of class A, and ebA is the residuals vector for sample b produced using model from class A.
The D-statistic value is defined in the following way:39
Dvalue,bA = ![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) TbA·(S−1A) TbA·(S−1A)![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) bA bA | (A4) |
The confidence limits for the D-statistic at a confidence level α are obtained using the F-statistic:39
 | (A5) |
Using eqn (A4) and (A5) a D-statistic score is calculated:15
 | (A6) |
The Q-statistic value is defined as:
 | (A7) |
The confidence limit for the Q-statistic is calculated as follows28
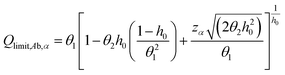 | (A8) |
 and Zα is the standardised normal variable with (1 − α) confidence level.
and Zα is the standardised normal variable with (1 − α) confidence level.
Using eqn (A7) and (A8) a number relating to the confidence α that the tested sample b belongs to the class A is obtained:28
 | (A9) |
Both αbA,D and αbA,Q are sometimes interpreted as the probability that the unknown sample belongs to the class being modelled, however, this interpretation is not entirely valid. Therefore in this paper we prefer using the term similarity, or score.
Louwerse and Smilde41 concluded that the control limits for the Q- and D-statistics should be calculated using the leave-one-out procedure. It shall be reminded that in this case the leave-one-out procedure does not have anything to do with the procedure of the validation of the classification results. It was later concluded that leave-one-out is more suitable for Q than for D-statistic,39 and therefore in this paper we apply it only to Q-statistic. The reason is the following: Q-statistic is applied to the validation set samples which were not used for building the PC model. Therefore it is a fair assumption that the residuals of the PC model (EA) used for the calculation of the control limits (eqn (A8)) shall be calculated in the same manner. The residual matrix EA is obtained using the leave-one-out method in the following way. Sample c is removed from the training set for group A. A PC model is produced using the residual training set samples for group A (eqn (A1)). The modelling error is calculated for sample c using the leave-one-out PC model (according to eqn (A3), where sample c is substituted for sample b). The procedure is repeated for all the samples in the training set group A and the corresponding errors are included in the residual matrix EA.
Acknowledgements
The author would like to thank to Phil Preen from Triton Technology for fruitful discussions.References
- B. J. Hunt and M. I. James, Polymer Characterisation, Blackie Academic and Professional, Glasgow, 1993 Search PubMed.
- T. Huthfehre, J. Mol. Struct., 1995, 348, 143 CrossRef CAS; R. Sattmann, I. Monch, H. Krause, R. Noll, S. Couris, A. Hatziapostolou, A. Mavromanolakis, C. Fotakis, E. Larrauri and R. Miguel, Appl. Spectrosc., 1998, 52, 456 CAS.
- N. Kasai and M. Kadudo, X-Ray Diffraction by Macromolecules, Springer, Tokyo, 2005 Search PubMed; P. Cebe, B. S. Hsiao and D. J. Lohse, Scattering from Polymers: Characterization by X-Rays, Neutrons, and Light, American Chemical Society Publication, 2000 Search PubMed.
- P. A. Mirau, A Practical Guide to Understanding the NMR of Polymers, John Wiley and Sons, New Jersey, 2004 Search PubMed; L. J. Mathias, Solid State NMR of Polymers, Springer, New York, 1991 Search PubMed.
- J. Cazes, Liquid Chromatography of Polymers and Related Materials, CRC Press, 1981 Search PubMed; W. W. Yau, J. J. Kirkland and D. D. Bly, Modern Size-Exclusion Liquid Chromatography: Practice of Gel Permeation and Gel Filtration Chromatography, John Wiley and Sons, 1979 Search PubMed.
- Principles and Applications of Thermal Analysis, ed. P. Gabbott, Blackwell Publishing, Singapore, 2008 Search PubMed.
- E. Donth, The Glass Transition, Springer, Berlin, 2001 Search PubMed.
- J. C. Duncan, in Mechanical Properties and Testing of Polymers, ed. G. M. Swallowe, Kluwer Academic Publishers, Dordrecht, 1999, pp. 43–48 Search PubMed; B. E. Read, G. D. Dean and J. C. Duncan, Determination of Dynamic Moduli and Loss Factors, Physical Methods of Chemistry, John Wiley and Sons, New York, 1991, vol. 7, pp. 1–70 Search PubMed; D. M. Price, Principles of Thermal Analysis and Calorimetry, Royal Society of Chemistry Paperbacks, Cambridge, 2002, pp. 94–128 Search PubMed.
- B. M. Lukasiak, S. Zomer, R. G. Brereton, R. Faria and J. C. Duncan, Analyst, 2006, 131, 73–80 RSC; B. M. Lukasiak, S. Zomer, R. G. Brereton, R. Faria and J. C. Duncan, Chemom. Intell. Lab. Syst., 2007, 87, 18–25 CrossRef CAS; R. Faria, J. C. Duncan and R. G. Brereton, Polym. Test., 2007, 26, 402–412 CrossRef CAS; G. R. Lloyd, R. G. Brereton, R. Faria and J. C. Duncan, J. Chem. Inf. Model., 2007, 47, 1553–1563 CrossRef CAS; G. R. Lloyd, R. G. Brereton and J. C. Duncan, Analyst, 2008, 133, 1046–1059 RSC; D. Li, G. R. Lloyd, J. C. Duncan and R. G. Brereton, J. Chemom., 2010, 24, 273–287 CAS.
- R. P. Brown, Handbook of Polymer Testing—Short-Term Mechanical Tests, Rapra Technology, New York, 1997 Search PubMed.
- Patent pending: International Patent Application No. PCT/EP2008/063556.
- N. G. McCrum, B. E. Read and G. Williams, Anelastic and Dielectric Effects in Polymeric Solids, John Wiley and Sons, London, 1967, pp. 238–574 Search PubMed.
- R. D. Snee, Technometrics, 1977, 19, 415–428.
- I. Stanimirova and B. Walczak, Talanta, 2008, 76, 602–609 CrossRef CAS.
- B. Lukasiak, PhD thesis, University of Bristol, 2009.
- B. R. Kowalski and C. F. Bender, Anal. Chem., 1972, 44, 1405–1411 CrossRef CAS.
- E. N. M. van Sprang, H. J. Ramaker, H. F. M. Boelens, J. A. Westerhuis, D. Whiteman, D. Baines and I. Weaver, Analyst, 2003, 128, 98–102 RSC; T. Kourti and J. F. MacCregor, Chemom. Intell. Lab. Syst., 1995, 28, 3–21 CrossRef CAS.
- F. Marini, in Comprehensive Chemometrics, ed. S. D. Brown, R. Tauler and B. Walczak, Elsevier, Oxford, 2009, vol. 3, pp. 477–505 Search PubMed.
- D. Coomans and D. L. Massart, Anal. Chim. Acta, 1982, 135, 153–165 CrossRef CAS , part 1 T. M. Cover and P. E. Hart, IEEE Trans. Inf. Theory, 1967, IT-13, 21–27 Search PubMed.
- R. O. Duda, P. E. Hart and D. G. Stork, Pattern Classification, John Wiley and Sons, Chichester, 2001, pp. 117–121 Search PubMed.
- M. O'Farrell, E. Lewis, C. Flanagan, W. Lyons and N. Jackman, Sens. Actuators, B, 2005, 107, 104–112 CrossRef.
- S. Wold, K. Esbensen and P. Geladi, Chemom. Intell. Lab. Syst., 1987, 2, 37–55 CrossRef CAS.
- R. G. Brereton, Chemometrics: Data Analysis for the Laboratory and Chemical Plant, John Wiley and Sons, Chichester, 2003 Search PubMed.
- J. V. Kresta, J. F. MacGregor and T. E. Marlin, Can. J. Chem. Eng., 1991, 69, 35–47 CrossRef CAS.
- J. A. Westerhuis, S. P. Gurden and A. K. Smilde, Chemom. Intell. Lab. Syst., 2000, 51, 95–114 CrossRef CAS.
- B. M. Lukasiak, R. G. Brereton and J. C. Duncan, Use of Subclustering to Improve Classification Abilities of Inhomogeneous Sample Groups: Application to Classification of Plastics using Dynamic Mechanical Analysis, unpublished work.
- N. D. Tracy, J. C. Young and R. L. Mason, J. Qual. Technol., 1992, 24, 88–95 Search PubMed.
- J. E. Jackson and G. S. Mudholkar, Technometrics, 1979, 21, 341–349.
- J. E. Jackson and R. H. Morris, J. Am. Stat. Assoc., 1957, 52, 186–199 CrossRef.
- A. Raich and A. Cinar, AIChE J., 1996, 42, 995–1009 CrossRef CAS.
- S. J. Qin, J. Chemom., 2003, 17, 480–502 CAS.
- D. Li, G. R. Lloyd, J. C. Duncan and R. G. Brereton, J. Chemom., 2010, 24, 273–287 CAS.
- G. Lloyd, PhD thesis, University of Bristol, 2010.
- B. G. M. Vandeginste, D. L. Massart, L. M. C. Buydens, S. De Jong, P. J. Lewi, J. Smeyers-Verbeke, Handbook of Chemometrics and Qualimetrics, Elsevier, Amsterdam, 1998 Search PubMed.
- D. E. Rumelheart, G. E. Hinton and R. J. Williams, Learning Internal Representations by Error Back-Propagation, in Parallel Distributed Processing. Explorations in the Microstructure of Cognition, ed. D. E. Rumelheart and J. L. McClelland, MIT Press, Cambridge, MA, 1986, pp. 318–362 Search PubMed; Backpropagation: Theory, Architectures and Applications, ed. Y. Chauvin and D. E. Rumelheart, Lawrence Erlbaum, New Jersey, 1995 Search PubMed; D. E. Rumelhart, G. E. Hinton and R. J. Williams, Nature, 1986, 323, 533–536 Search PubMed.
- J. S. Bridle, Probabilistic Interpretation of Feedforward Classification Network Outputs with Relationships to Statistical Pattern Recognition in Neuro-computing: Algorithms, Architectures and Applications, in NATO ASI Series in Systems and Computer Science, ed. F. Fogelman-Soulie and J. Herault, Springer, 1989, pp. 227–236 Search PubMed.
- F. Marini, A. L. Magrì and R. Bucci, Chemom. Intell. Lab. Syst., 2007, 88, 118–124 CrossRef CAS.
- M. J. Charlesworth, Philos. Stud. (Ireland), 1976, 6, 105–112 Search PubMed.
- H.-J. Ramaker, E. N. M. van Sprang, J. A. Westerhuis and A. K. Smilde, Chemom. Intell. Lab. Syst., 2004, 73, 181–187 CrossRef CAS.
- Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, ed. M. Abramowitz and I. A. Stegun, Dover, New York, 1972 Search PubMed.
- D. J. Louwerse and A. K. Smilde, Chem. Eng. Sci., 2000, 55, 1225–1235 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2010 |

