Progress curve analysis of enzyme reactions by flow microcalorimetry: Use of a pseudo-first order approximation
Jean
Debord
*a,
Michel
Harel
b,
Jean-Claude
Bollinger
c and
Thierry
Dantoine
d
aService de Pharmacologie-Toxicologie, Hôpital Dupuytren, 2 Avenue Martin-Luther-King, F-87042, Limoges, France. E-mail: jean.debord@unilim.fr
bInstitut de Mathémathiques de Toulouse (UMR CNRS 5219), F-31062, Toulouse, France
cGroupement de Recherche Eau, Sol, Environnement, Université de Limoges, Faculté des Sciences, 123 Avenue Albert Thomas, F-87060, Limoges, France
dService de Gérontologie clinique, Hôpital Dupuytren, 2 Avenue Martin-Luther-King, F-87042, Limoges, France
First published on 8th October 2010
Abstract
We describe a method for determining the pseudo-first order rate constant of a chemical reaction by flow microcalorimetry operating in the flow-through mode. The impulse response of the instrument was described by a Gamma distribution and the equation of the thermogram was computed analytically. The resulting equation was fitted to the data by simulated annealing. The method was applied to an enzyme reaction following Michaelis–Menten kinetics by means of a new empirical equation relating the apparent rate constant to the kinetic parameters Vmax and Km. The method was exemplified by a kinetic study of horse serum butyrylcholinesterase.
1 Introduction
Microcalorimetry has proved to be a useful tool for the study of enzyme kinetics.1,2 For instance, flow microcalorimetry, operated in the flow-through mode, makes it possible to record the progress curve of a reaction which has been initiated outside the calorimeter. While enzyme reactions are governed by complex kinetic laws, it is often possible to use a pseudo-first order approximation with an apparent rate constant k. If the time scale of the reaction (1/k) is much higher than the time constant τ of the instrument, graphical methods or linear regression can be used to determine the rate constant from the terminal part of the recorded curve (thermogram).3 However, if the previous condition is not fulfilled, or if the initial part of the thermogram needs to be analysed, it will be necessary to take into account the response function of the calorimeter. Here we present a method which allows the determination of k by nonlinear regression applied to an analytic expression of the thermogram. In addition, we propose a new equation relating the apparent rate constant of an enzyme reaction to its maximal velocity and Michaelis constant. The method is exemplified by a kinetic study of horse serum butyrylcholinesterase.2 Theory
2.1 Determination of rate constants
We consider a chemical reaction for which the reaction rate at time t is given by:| v(t) = v0exp(−kt) = k[S]0exp(−kt) | (1) |
If the reaction is studied with a microcalorimeter, the recorded e.m.f. E(t)is the convolution product of the reaction rate v(t) with the impulse response I(t) of the instrument:
 | (2) |
In the case of the flow microcalorimeter used in this work, we have shown previously4,5 that the impulse response could be described by a Gamma distribution function:
 | (3) |
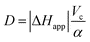 | (4) |
As we have shown previously,5 the convolution integral (2) can be computed analytically if the rate v(t) varies according to eqn (1) and if k < ω. We obtain:
 | (5) |
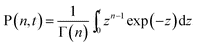 | (6) |
If n is integer, by integration by part, this function can be expressed in terms of exponential functions. In the simplest case (n = 2) we have:
| P(2,t) = 1−(1 + t)exp(−t) | (7) |
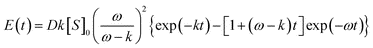 | (8) |
So, if D is known, it is possible to determine k by fitting eqn (5) or eqn (8) to the data.
2.2 Application to enzyme reactions
For an enzyme reaction following Michaelis–Menten kinetics, the rate at time t is given by: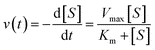 | (9) |
It has been shown6,7 that the analytical solution of this differential equation can be expressed in terms of Lambert's W-function:
 | (10) |
Using the simulation procedure described in the Appendix, we have found that the previous equation could be approximated by the pseudo-first order equation:
| [S] = [S]0exp(−kt) | (11) |
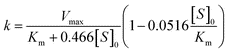 | (12) |
So, if the apparent rate constant k is determined at several values of [S]0, the kinetic parameters Km and Vmax can be estimated by fitting eqn (12) to the data.
3 Experimental
3.1 Reagents
Butyrylcholinesterase (EC 3.1.1.8) from horse serum (about 1700 U mg−1 protein) and Butyrylcholine iodide were purchased from Sigma. All compounds were at the highest purity grade available. The solutions were prepared in Tris buffer, 0.1 M, pH 7.5 at 37 °C3.2 Microcalorimetry
The flow microcalorimeter (LKB 10700-1) was operated in the flow-through mode at 37 °C. The signal from the detectors was amplified and transferred to a microcomputer as described previously.4,8 The flow rate was 6.8 μL s−1. The apparent volume Vc of the cell, which is a function of the flow rate, was estimated at 0.62 mL from the data of O'Neill et al.9 The electrical calibration gave α = 17μW/μV and τ = 75 s, so that ω = 1/τ = 0.0133 s−1 = 0.8 min−1. The apparent reaction enthalpy for the hydrolysis of butyrylcholine in our conditions was |ΔHapp| = 35.2 kJ mol−1 from our previous work.4 The value of D was therefore 1.28 μV s μM−1, from eqn (4).3.3 Progress curve study
The reaction was initiated outside the calorimeter in a thermostated vessel. The reaction mixture contained the enzyme (BuChE at constant concentration) and substrate (BuCh at variable concentration) in Tris buffer. This solution was infused into the flow-through cell of the calorimeter. There was a lag time of about 180 s before the solution reached the detector. The signal was then recorded for about 780 s.3.4 Treatment of data
All computations were done on a PC computer with our own programs. Eqn (5) and (8) were fitted to the thermograms by simulated annealing. A program written in BASIC (for the open source compiler FreeBASIC10) is freely available at our web site.11Since the reaction was started outside the calorimeter, a fraction of the substrate was hydrolysed during the lag time before the reacting mixture reached the detector. So, the `initial' substrate concentration [S]0 (which is in fact the concentration at the beginning of the detection) was treated as an adjustable parameter, as well as the rate constant k.
Simulated annealing requires an initial starting range for each parameter. The range for k was 1% to 99% of ω (in agreement with the condition k < ω) and the range for [S]0 was 1% to 99% of the substrate concentration present at the start of the reaction. When eqn (5) was fitted to the data, the range for n was 1.01 to 4 to fulfill the condition n > 1.
Eqn (12) was fitted to the data by nonlinear regression using Marquardt's method.12 This method requires the partial derivatives of the regression function with respect to the parameters. These derivatives were computed as follows:
 | (13) |
 | (14) |
 | (15) |
4 Results and discussion
Thermograms for the hydrolysis of butyrylcholine catalysed by butyrylcholinesterase at 37 °C and pH 7.5 were recorded for substrate concentrations ranging from 0.058 to 0.75 mM. Eqn (5) was fitted to each curve by simulated annealing. In this step, the exponent n of the Gamma distribution was treated as an adjustable parameter. Since the values of n so obtained were very close to 2, each curve was then analysed with the simplified eqn (8) which assumes n = 2. According to Table 1, the results of the two methods were very similar. The results given by the simplified equation were therefore used for the subsequent analyses.| General equation | Simplified equation | |||
|---|---|---|---|---|
| [S]0 | k | n | [S]0 | k |
| 0.058 | 0.50 | 2.0 | 0.058 | 0.52 |
| 0.13 | 0.44 | 2.0 | 0.13 | 0.46 |
| 0.25 | 0.26 | 2.1 | 0.26 | 0.25 |
| 0.39 | 0.19 | 2.0 | 0.40 | 0.19 |
| 0.79 | 0.10 | 1.9 | 0.75 | 0.11 |
Fig. 1 shows an example of the fit obtained at the lowest substrate concentration. The quality of the fit was very good, especially since the measured e.m.f. was very low at this concentration. The residual error of the fit was about 7.5 nV, corresponding to about 0.13 μW.
 | ||
| Fig. 1 Thermogram of the hydrolysis of butyrylcholine (0.058 mM) by butyrylcholinesterase at 37 °C and pH 7.5. The curve was fitted by simulated annealing according to eqn (8). | ||
The results displayed in Table 1 show that the apparent rate constant k varied between 0.11 and 0.52 min−1 while the ω parameter was 0.80 min−1. So, the condition k < ω was always fulfilled. The value of ω corresponds to the highest rate constant which can be measured with this technique. Higher rate constants could be measured by decreasing the time constant of the calorimeter or using the mixing cell of the instrument.13
The values of k were then plotted against the substrate concentration and eqn (12) was fitted to the data by nonlinear regression (fig. 2). The kinetic parameters Km and Vmax are displayed in Table 2.
![Variation of the pseudo first order rate constant k with the substrate concentration [S]0. The curve was fitted by nonlinear regression according to eqn (12).](/image/article/2010/AY/c0ay00223b/c0ay00223b-f2.gif) | ||
| Fig. 2 Variation of the pseudo first order rate constant k with the substrate concentration [S]0. The curve was fitted by nonlinear regression according to eqn (12). | ||
| V max/mM min−1 | 0.093 ± 0.006 |
| K m/mM | 0.072 ± 0.008 |
The Michaelis constant determined by this method for horse serum butyrylcholinesterase was in agreement with the value obtained by Lockridge14 for the human enzyme (Km = 0.091 mM), and with our own spectrophotometric determination15 for Electrophorus electricus acetylcholinesterase (Km = 0.05 mM) It must be noted, however, that butyrylcholinesterase is an allosteric protein, so that Km depends of the substrate concentration range. For instance, by using substrate concentrations up to 50 mM we have determined an apparent Km of 3.3 mM by flow microcalorimetry operated in the flow-mix mode.4
We have described a computer method to determine a pseudo-first order rate constant when the impulse response of the calorimeter corresponds to a Gamma distribution. The early work of Sargent and Moeschler16 examined the case of an impulse response described by a sum of exponentials. These authors constructed calibration curves relating the rate constant to the maximal e.m.f. for various values of the calorimeter time constant. This method does not seem to have been widely applied, but in the field of enzymology Beezer et al.3 have discussed several ways to analyse the terminal part of the thermogram, when the distortion due to the instrumental response is negligible.
Due to the ability of present day microcomputers it is now possible to apply nonlinear regression techniques, and especially stochastic optimization algorithms like simulated annealing, to analyse the whole thermogram, including the initial part in which the influence of the instrumental response cannot be neglected. In our case, this goal was reached by computing an analytic expression of the thermogram based on the incomplete Gamma function. This function is often used in Statistics, and computer programs for its evaluation are widely available.17 It can be assumed that the Gamma distribution is versatile enough to apply to a wide range of calorimeters. On the other hand, when the exponent of the Gamma distribution is an integer, the incomplete Gamma function can be expressed in terms of the more familiar exponential functions.
The method has been successfully applied to a kinetic study of butyrylcholinesterase. It has been classically assumed in enzyme kinetics that the pseudo-first order approximation holds only for the lowest substrate concentrations ([S]0 ≪ Km). However, by means of the empirical eqn (12) we have been able to extend the validity of this approximation to substrate concentrations exceeding the Michaelis constant.
The use of eqn (12) is of course a simplified approach. A more general procedure would involve the numerical evaluation of the convolution integral 2 using the reaction rates computed from eqn (10). Another possibility would be to approximate the reaction rate by a sum of exponentials. Such methods are currently being studied in our laboratory.
5 Appendix
The simulation of eqn (10) was performed with the following set of nondimensional variables: | (16) |
In the system of nondimensional variables, eqn (10) becomes:
| S = W{S0exp(S0 − T)} | (17) |
This equation was simulated by computing S as a function of T (up to T = 10) for 50 values of S0. An exponential was then fitted to each curve S = f(T) by nonlinear regression according to the equation:
| S = S0exp(−ηT) | (18) |
The 50 values of η obtained by this procedure were plotted against the corresponding S0 values (data not shown). Inspection of the plot suggested a rational fraction, and the following empirical equation was selected by nonlinear regression:
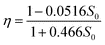 | (19) |
Turning back to the original variables, this equation was converted to eqn (12).
References
- M. L. Bianconi, Biophys. Chem., 2007, 126, 59–64 CrossRef CAS.
- M. J. Todd and J. Gomez, Anal. Biochem., 2001, 296, 179–187 CrossRef CAS.
- M. A. A. O'Neill, A. E. Beezer, J. C. Mitchell, J. Orchard and J. A. Connor, Thermochim. Acta, 2004, 417, 187–192 CrossRef CAS.
- J. Debord, B. Verneuil, J. C. Bollinger, L. Merle and T. Dantoine, Anal. Biochem., 2006, 354, 299–304 CrossRef CAS.
- J. Debord, M. Harel, B. Verneuil, J. C. Bollinger and T. Dantoine, Anal. Biochem., 2009, 389, 97–101 CrossRef CAS.
- S. Schnell and C. Mendoza, J. Theor. Biol., 1997, 187, 207–212 CrossRef CAS.
- C. T. Goudar, J. R. Sonnad and R. G. Duggleby, Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol., 1999, 1429, 377–383 Search PubMed.
- J. Debord, C. Laubarie and T. Dantoine, Anal. Biochem., 2008, 373, 247–252 CrossRef CAS.
- M. A. A. O'Neill, A. E. Beezer, C. Labetoulle, L. Nicolaides, J. C. Mitchell, J. Orchard, J. A. Connor, R. B. Kemp and D. Olomolaiye, Thermochim. Acta, 2003, 399, 63–71 CrossRef CAS.
- http://www.freebasic.net/ .
- http://www.unilim.fr/pages_perso/jean.debord/articles/calk.bas .
- D. W. Marquardt, SIAM J. Appl. Math., 1963, 11, 431–441 CrossRef.
- R. E. Johnson and R. L. Biltonen, J. Am. Chem. Soc., 1975, 97, 2349–2355 CrossRef CAS.
- O. Lockridge, Pharmacol. Ther., 1990, 47, 35 CrossRef CAS.
- J. C. Bollinger, J. Levy-Serpier, J. Debord and B. Pénicaut, J. Enzyme Inhib. Med. Chem., 1990, 3, 211–217 Search PubMed.
- D. F. Sargent and H. J. Moeschler, Anal. Chem., 1980, 52, 365–367 CrossRef CAS.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes, Cambridge University Press (Cambridge, USA), 2007 Search PubMed.
| This journal is © The Royal Society of Chemistry 2010 |
