DOI:
10.1039/C0AY00408A
(Paper)
Anal. Methods, 2010,
2, 1514-1521
Spectrophotometric determination of acidity constants by mean centering of ratio spectra
Received
27th June 2010
, Accepted 27th July 2010
First published on
6th September 2010
Abstract
In this work, an application of mean centering of ratio spectra is proposed to resolve the two-way pH-spectral data and acquire the acidity constants of diprotic acids. The method is based on the mean centering of ratio spectra in order to obtain a pH profile of the intermediate component. After recording the electronic absorbance spectra of the acids at different pH values, the contributions of H2A and A2− are eliminated from the absorbance data using a mean centering of ratio spectra method, which made feasible the determination of two successive acidity constants by computational fitting of the obtained pure pH profile of HA−1. Given the acidity parameters (pKas), the absorption spectrum of the intermediate can be reached through least squares regression. The applicability of the proposed method was evaluated by using model data. The pH-spectral data of Eriyochrome Black T (acid–base indicator) as a real system was also studied by the proposed method.
1. Introduction
Studies on the acid/base properties of organic reagents are important for understanding their biological activity, mechanism of action of certain pharmaceutical preparations, solvent extraction, complex formation etc.1–3 Therefore, the accurate determination of acidity constant values is often required in various chemical and biochemical areas. Of the several physicochemical methods for studying the protonation equilibria in solution, UV–vis spectrophotometry under broad experimental conditions is in general highly sensitive, and with subsequent computer treatment of the data is a very powerful method.3–19 When the components involved in protonation equilibrium have distinct spectral responses, their concentrations can be measured directly, and the determination of the dissociation constant is trivial. In many cases, however, the spectral responses of two or sometimes more components overlap considerably, and analysis is no longer straightforward. Much more information can be extracted if multivariate spectroscopic data are analyzed by means of appropriate multivariate data analysis methods.14,16,20 On the other hand, protonation equilibria sometimes involve minor changes in the electronic spectra, which make it difficult to employ spectrophotometry for determination of dissociation constants.
Hard modeling methods include traditional least-squares curve fitting approaches, based on a previous postulation of a chemical model, i.e. the postulation of a set of species defined by their stoichiometric coefficients and formation constants, which are then refined by least-squares minimization. These mathematical procedures require the fulfilment of the mass-balance equations and the mass-action law. The most relevant algorithms are SQUAD21–29 and SPECIFIT.30–33 On the other hand, soft modeling techniques, such as multivariate curve resolution methods based on factor analysis, work without any assumption of a chemical model, and do not have the requirement of compliance with the mass-action law.
Combinations of hard and soft strategies have also been applied to resolve and determine the thermodynamic stability constants.34 In particular, mean centering of ratio spectra is used to remove the contribution of absorbing known components from the data matrix exactly.35–38 Mean centering of ratio spectra has been presented by Afkhami and Bahram36 and applied to the simultaneous analysis of binary and ternary mixtures.35–38 Also recently, mean centering of ratio spectra was applied to resolve the two-way kinetic–spectral data of consecutive reactions and to acquire the rate constants and the spectrum of the intermediate component.39 This preprocessing strategy was also applied by Bahram et.al. for pretreatment of the kinetic-spectrophotometric data prior to rank annihilation factor analysis method.40 This work presents a new application of mean centering of ratio spectra method for estimation of acidity constants of diprotic acids.
To two-way pH-spectral data measured by a titration process, the pure spectrum of H2A and A2− (the spectra in completely low and high pH values can be related to the pure spectra of fully acidic and basic forms of each acid) can be reached, while that of the intermediate (HA−) usually remains unknown. Also the concentration profiles of each species in the reaction are not directly available, but they do change conforming to a certain kinetics function. Knowing the spectra of H2A and A2−, the determination of the consecutive acidity constants of the diprotic acids is deduced by mean centering of ratio spectra. In particular, it is used to remove the contribution of H2A and A2− components from the data matrix exactly. In the first stage, the goal of this work is removing the contribution of known components from the data matrix such that a reduced data set, which belongs to the contribution of the intermediate component (which is assumed as unknown component), is obtained. In the second step, the acidic constants are calculated using least squares. In this paper, a theoretical formulation of mean centering of ratio spectra in order to eliminate the contribution of H2A and A2− from the pH-spectral data of the diprotic acid titration is presented. Several two-way pH-spectrophotometric data were simulated and the mean centering of ratio spectra of them, which gives the pure response of the intermediate component of the pH-titration (HA−), are calculated. Then a computational fitting is used to simply estimate the consecutive acidity constants. Given the acid/base dissociation parameters, the absorption spectrum of the intermediate (HA−) can be obtained through least squares regression. The applicability of the proposed method was also investigated by studying the protonation reaction of Eriyochrome Black T (acid–base indicator) as a real diprotic acid and it was proven that this approach can be successfully applied to the analysis of practical systems as well.
2. Mathematical description
Suppose that the following two-step consecutive dissociation reaction of H2A, defined by chemical equilibria, is considered:| |  | (1) |
| | 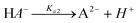 | (2) |
The corresponding stepwise acidity constants are
| |  | (3) |
| |  | (4) |
According to classical analytical chemistry, the variation in the concentration profile of species of a diprotic acid, H2A, HA− and A2− can be calculated according to the following equations:
| |  | (5) |
| |  | (6) |
| |  | (7) |
where
Ct is the total concentration of the diprotic acid. An
experimental data matrix
D, whose elements (
di,j) are absorbances at
ith pH and
jth wavelength, is obtained by spectrophotometric–pH-metric
titration (by recording the
absorbance spectrum at each pH). This data matrix can be considered as the sum of the contributions of the protogenic species:
D = D
H2A +
DHA− + D
A2−| | | D = qH2AeTH2A + qHA−eTHA− + qA2−eTA2− = QET | (8) |
where
qi is the pH profile (column vector) and
eTi is the
absorption spectrum (row vector, superscript T denotes the transpose of a matrix or vector). Bold letters
E and
Q represent matrices formed by the pure
spectrum and the pH profile of each species, respectively. In highly acidic media the recorded
spectrum is the pure
spectrum of H
2A and in highly basic media the recorded
spectrum is the pure
spectrum of A
2−. Therefore their pure
spectra are known, while usually, that of the intermediate (
eHA−) in the pH-titration of a diprotic acid is unknown. By using ternary mean centering (MC) of ratio
spectra method
21–24 the pH profile of the intermediate species (
qHA−) can be simply resolved.
For two-way pH-spectral data of Dif the elements of rows (D(i,:)) are divided by the elements of eH2A corresponding to the spectrum of H2A, the first ratio spectra are obtained in the form of (for the possibility of dividing operation, the zero values of eH2A should not be used in the divisor):
| | 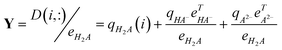 | (9) |
If the matrix D, row mean centered, would be obtained:
| |  | (10) |
By dividing each row of MC(Y), shown as MC(Y)(i,:) in eqn (11), by MC(eA2−/eH2A), element by element, corresponding to the mean centering of the ratio of the spectra of reactants H2A and A2−, the second ratio spectra is obtained:
| |  | (11) |
Now if eqn (12) is row mean centered, eqn (7) would be obtained:
| |  | (12) |
Each row of matrix L has a response that only depends on the concentration of product (qp), and therefore plotting every column of Lversus time will give a pure kinetic profile of the intermediate. Finally, the rate constants of the reactions can be simply obtained by curve fitting (non-linear optimization).
Under the conditions that the two successive acidity constants, or the concentration profile of species of a diprotic acid (H2A, HA− and A2− (Q)) were calculated, the pure absorption spectrum of each component (especially the intermediate, HA−) can be obtained by means of least squares regression:
The principle of the proposed method shows that this approach can be applied to the systems where all three components absorb, or H2A, HA− or A2− do not absorb. When one of H2A or A2− has no absorbance in the studied wavelength or pH range, binary mean centering22,23 can be simply used, and the pure concentration profile, and subsequently the spectrum of the intermediate (HA−), can be obtained. Also, in the case that the intermediate component (HA−) has no absorbance in the studied conditions, using binary mean centering the concentration profiles of H2A and A2− (and therefore the acidity constants) can be obtained.
3. Software
All calculations in the computing process were done in Matlab7.0.1 and Microsoft Excel for Windows. The programs for simulation of data and mean centering of ratio spectra were written in Matlab7.0.1. Fitting of kinetic profiles was done in MATLAB using fminsearch command.
4. Results and discussion
4.1. Simulated data
To evaluate the performance of the proposed method, it was applied to analyze the simulated data sets. Several simulated data with different acidity constants of protogenic species (i.e. H2A, HA− and A2−) (Table 1) were prepared. For preparation of each data set, a data matrix (Qsim) composed of the concentrations of the protogenic species as a function of pH was calculated using the pKa1 and pKa2 values represented in Table 1. This matrix has a dimension of (n × 3), where n is the number of imaginary solutions whose pH are fixed at predefined values. The pH of solutions was varied between 1 and 14 in 0.2 unit intervals. Therefore, n is equal to 56. In addition, a data matrix of the pure absorbance spectra (Esim) of the protogenic species was simulated (450–600 nm with 1 nm intervals). The simulated absorbance spectra (Dsim) of each data set were then calculated by post-multiplication of Qsim with Esim![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dsim = Qsim × Esim. The matrix Dsim has a dimension of (n × m), where m is the number of wavelengths at which absorbences were calculated (here m = 151) and n is number of pH values as defined previously (n = 56). To more rigorously test the method, random errors equal to the 0.005 absorbance values were added to the simulated data. Fig. 1 represents case simulated spectra, concentration profiles of protogenic species (i.e. H2A, HA− and A2−) for pKa1 = 5 and pKa2 = 6.5 and the obtained data. The results that have been obtained by applying the proposed method for analyzing this data set are shown in Fig. 2. The pure response of the intermediate component of the diprotic acid pH-titration (concentration profile of HA−) is also shown in Fig. 2(e). The result of fminsearch fitting for a case data set is also presented in Fig. 3.
Dsim = Qsim × Esim. The matrix Dsim has a dimension of (n × m), where m is the number of wavelengths at which absorbences were calculated (here m = 151) and n is number of pH values as defined previously (n = 56). To more rigorously test the method, random errors equal to the 0.005 absorbance values were added to the simulated data. Fig. 1 represents case simulated spectra, concentration profiles of protogenic species (i.e. H2A, HA− and A2−) for pKa1 = 5 and pKa2 = 6.5 and the obtained data. The results that have been obtained by applying the proposed method for analyzing this data set are shown in Fig. 2. The pure response of the intermediate component of the diprotic acid pH-titration (concentration profile of HA−) is also shown in Fig. 2(e). The result of fminsearch fitting for a case data set is also presented in Fig. 3.
Table 1 The results for applying the proposed method on several simulated diprotic acid with different pKa1 and pKa2
| No. |
Simulated pKai |
Predicted (without noise) |
Predicted (with noise) |
RSE (%)a |
| pKa1 |
pKa2 |
pKa1 |
pKa2 |
pKa1 |
pKa2 |
pKa1 |
pKa2 |
|
: relative standard error.
|
| 1 |
3 |
9 |
3 |
9 |
2.98 |
9 |
−0.67 |
0.00 |
| 2 |
2 |
6 |
2 |
6 |
2 |
5.99 |
0.00 |
−0.17 |
| 3 |
9 |
11 |
9 |
11 |
8.99 |
11.03 |
−0.11 |
0.27 |
| 4 |
2.5 |
4 |
2.5 |
4 |
2.51 |
3.95 |
0.40 |
−1.25 |
| 5 |
7.5 |
9 |
7.5 |
9 |
7.49 |
9.01 |
−0.13 |
0.11 |
| 6 |
4.5 |
6 |
4.5 |
6 |
4.51 |
6.02 |
0.22 |
0.33 |
| 7 |
5.5 |
7 |
5.5 |
7 |
5.5 |
7.02 |
0.00 |
0.29 |
| 8 |
3 |
5 |
3 |
5 |
2.99 |
5.01 |
−0.33 |
0.20 |
| 9 |
8 |
10.5 |
8 |
10.5 |
7.98 |
10.5 |
−0.25 |
0.00 |
| 10 |
4 |
5 |
4 |
5 |
4 |
5.02 |
0.00 |
0.40 |
| 11 |
3 |
7 |
3 |
7 |
2.99 |
7.01 |
−0.33 |
0.14 |
| 12 |
5 |
9 |
5 |
9 |
5.01 |
8.99 |
0.20 |
−0.11 |
| 13 |
3.5 |
4 |
3.5 |
4 |
3.51 |
3.99 |
0.29 |
−0.25 |
| 14 |
3 |
5.5 |
3 |
5.5 |
3.02 |
5.49 |
0.67 |
−0.18 |
| 15 |
6 |
10 |
6 |
10 |
6.01 |
9.96 |
0.17 |
−0.40 |
| 16 |
4 |
6.5 |
4 |
6.5 |
3.99 |
6.49 |
−0.25 |
−0.15 |
| 17 |
6.5 |
9 |
6.5 |
9 |
6.5 |
9 |
0.00 |
0.00 |
| 18 |
7.5 |
11 |
7.5 |
11 |
7.49 |
11.01 |
−0.13 |
0.09 |
| 19 |
8 |
10 |
8 |
10 |
8 |
10.04 |
0.00 |
0.40 |
| 20 |
5 |
8 |
5 |
8 |
5 |
7.99 |
0.00 |
−0.12 |
 |
| | Fig. 1 Case simulated spectra, concentration profiles of protogenic species (i.e. H2A, HA− and A2−) and the obtained data of modeled diprotic acid with pKa1 = 5 and pKa2 = 6.5. | |
 |
| | Fig. 2 (a): The ratio profiles obtained by dividing the simulated data by the spectrum of H2A (eH2A), (b): The mean centering of ratio profiles, (c): Second ratio profiles were obtained by dividing by MC(eA2−/eH2A), (d): Mean centering of these vectors and (e): The concentration profile of HA−. | |
 |
| | Fig. 3 The results of applying the proposed method for the analysis of case simulated pH-spectral data (the calculated concentration profile and the spectra (♦) and the simulated ones (—)). The spectrum of protogenic species (i.e. H2A, HA− and A2−) was estimated by least squares regression (projection) of concentration profiles (Q) on experimental data (eqn (8)). | |
As mentioned, under the conditions in which the two successive acidity constants, or the concentration profile of species of the diprotic acid, H2A, HA− and A2− (Q), were calculated, the pure absorption spectrum of each component (especially the intermediate, HA−) can be obtained by means of least squares regression using eqn (8). Fig. 3(b) shows that the spectra of H2A, HA− and A2− obtained by the proposed method are in agreement with those of simulated ones.
To investigate the effects of the degree of overlap, a series of pH profiles and spectra were chosen, which are shown in Fig. 4. In columns A to C, different degrees of overlap were simulated. In rows 1 to 3, different pKa(s) values were used to build pH profiles of diprotic acid components.
 |
| | Fig. 4 The effect of the degree of overlap in spectral and pH mode of pH-spectral two-way data. The simulated data are shown as continuous lines and the calculated ones as dotted lines. | |
The simulated and calculated profiles of the intermediate component (HA−) by applying the proposed method are shown in Fig. 4. The results confirm the adequacy of our strategy for finding the pure response of the intermediate component of a diprotic acid in a pH-titration (concentration profile of HA−).
All real data are noisy. Therefore, it is important to consider whether the experimental error has an influence on the results obtained by the proposed strategy. Randomly a homoscedastic noise matrix was generated using MATLAB®randn function with zero mean and different relative standard deviation values. Six different trials were used with simulated measurement error scaled to 0.01%, 0.02%, 0.05%, 0.1%, 0.2% and 0.5% of the average intensity of the measured signal for each data matrix considered. Table 2 represents the effect of different levels of noise (0.02, 0.1 and 0.5%) on the results of the proposed method. The results were all satisfactory. The simulated data with a high degree of studied noise (0.5%) are presented in Table 1 together with noise-free results.
Table 2 The effect of different values of noise on the results.
|
|
Simulated pKa |
Predicted values |
%RSE |
| Without noise |
0.02% noise |
0.1% noise |
0.5% noise |
0.02% noise |
0.1% noise |
0.5% noise |
| pKa1 |
3.00 |
3.00 |
2.98 |
3 |
3.04 |
−0.67 |
0.00 |
1.33 |
| pKa2 |
5.00 |
5.00 |
4.97 |
4.99 |
5.03 |
−0.60 |
−0.20 |
0.60 |
| pKa1 |
4.50 |
4.50 |
4.50 |
4.48 |
4.53 |
0.00 |
−0.44 |
0.67 |
| pKa2 |
7.00 |
7.00 |
6.96 |
7.02 |
6.97 |
−0.57 |
0.29 |
−0.43 |
| pKa1 |
6.00 |
6.00 |
6 |
5.98 |
6.10 |
0.00 |
−0.33 |
1.67 |
| pKa2 |
10.00 |
10.00 |
9.98 |
9.97 |
9.96 |
−0.20 |
−0.30 |
−0.40 |
In order to examine the applicability of the method, it was applied for determination of acidity constants of Eriyochrome Black T (EBT) (acid–base indicator) as experimental data. In this study, the spectra of 10−4 mol L−1 EBT were monitored between 400–700 nm with 2 nm increments at 23 different pH values in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethanol–water solution (25 °C). The size of the obtained pH-titration data set of EBT was therefore 151 × 23. Fig. 5(a) shows the monitored spectra at different pH values. In highly acidic media (pH ≤ 1) the recorded spectrum was used as the pure spectrum of H2A and in highly basic media (pH ≥13) the recorded spectrum was used as the pure spectrum of A2− (Fig. 5(b)). The matrix of absorption data was processed by the proposed method. The spectrum of H2A and A2− were used as divisors according to eqn (9)–(12). Fig. 5(c–f) represents the results obtained by the proposed method.
1 ethanol–water solution (25 °C). The size of the obtained pH-titration data set of EBT was therefore 151 × 23. Fig. 5(a) shows the monitored spectra at different pH values. In highly acidic media (pH ≤ 1) the recorded spectrum was used as the pure spectrum of H2A and in highly basic media (pH ≥13) the recorded spectrum was used as the pure spectrum of A2− (Fig. 5(b)). The matrix of absorption data was processed by the proposed method. The spectrum of H2A and A2− were used as divisors according to eqn (9)–(12). Fig. 5(c–f) represents the results obtained by the proposed method.
 |
| | Fig. 5 (a): Absorption spectra for 1 × 10−4 mol L−1 EBT at pH; 0.98, 2.13, 2.37, 3, 3.1, 3.37, 3.78, 3.98, 4.48, 4.49, 5.04, 5.77, 5.87, 6.29, 6.8,7, 8.53, 9.51, 10.76, 11, 11.5, 11.99, 13.29, (b): The spectra of EBT at highly acidic and basic pH (0.98 and 13.29) used as divisors, (c): The ratio profiles which were obtained by dividing the spectral data by the spectrum of H2A (eH2A), (d): the mean centering of ratio profiles, (e): Second ratio profiles were obtained by dividing by MC(eA2−/eH2A), (f): Mean centering of these vectors and (g): The concentration profile of HA−. | |
The singular value decomposition of the obtained data matrix showed that there are 3 significant components. Also the singular value decomposition of the mean centered ratio spectra (MC(Y) and L) indicated that the number of significant principal components for first mean centered ratio spectra (MC(Y)) is two and that of 2nd ratio spectra (L) is one. These results indicate that by using mean centering of ratio spectra the contribution of H2A and A2− forms of EBT have been completely eliminated from the data and the final response can be used as the pure response of the intermediate component of EBT pH-titration (concentration profile of HA−). This pure response is shown in Fig. 5(e). The result of fminsearch fitting for this concentration profile is also presented in Fig. 6(a). Using the proposed method, the pKa1 and pKa2 values for EBT were estimated as 6.70 and 11.45, respectively, which are in agreement with those reported in literature.20,41Table 3 represents a comparison between different methods to calculate the pKa values of EBT.
 |
| | Fig. 6 The results of applying the proposed method for the analysis of EBT pH-spectral data; (a): The calculated concentration profile (♦) and the fitted ones (—), (b): Reconstruction of the concentration profiles using estimated pKa1 and pKa2 and (c): The spectra of protogenic species obtained by least squares. | |
Table 3 Comparison of the results obtained by different methods for calculation of acidity constants of Eriyochrome Black T (acid–base indicator).
|
|
Hard model |
Tow-RAFA20,41 |
Reported value41 |
MCR42 |
Proposed method |
| pKa1 |
6.12 |
6.88 |
6.30 |
6.7 |
6.50 |
| pKa2 |
11.39 |
11.36 |
11.55 |
11.5 |
11.45 |
| Comment |
Based on a previous postulation of a chemical model. There is no need for the spectra of the components to be known. |
The spectrum of H2A or A2− in combination with a known model is used to subtract its contribution from the data. |
|
In the first step the data is resolved to concentration and spectra profiles. For this step usually no model is necessary (soft method). Some constraints such as non-negativity, uni-modality and cluster should be applied to obtain meaningful results. The obtained concentration profile is then subject to pKa(s) calculation. |
By mean centering of ratio spectra the contribution of known components are eliminated from the data and the pure response of HA− is used in the fitting step. |
After estimation of two successive acidity constants and consequently construction of the concentration profile of protogenic species of EBT (Fig. 6(b)), the pure absorption spectrum of each component (especially the intermediate, HA− form of EBT) can be obtained by means of least squares regression using eqn (13). Fig. 6(c) represents the spectra of H2A, HA− and A2− forms of EBT obtained by the proposed method.
5. Conclusion
In the first stage, the goal of this work was removing the contribution of known components from the data matrix to obtain reduced data, which belongs to the contribution of an unknown component (intermediate component of a diprotic acid). In the second step, the acidity constants are calculated using least squares. Although there are many different strategies, algorithms and/or software such as SQUAD, HYPERSQUAD, SPECIFIT,21–33 MCR-ALS,42 Rank annihilation factor analysis41 and Hard-soft methods34 available, this study showed that the proposed method (mean centering of ratio spectra) is useful and can be an alternative to obtain acidity constants, concentration profiles and the spectra of the components which exist in a suitable pH range for a diprotic acid. The proposed algorithm is simple, very sensitive and easy to understand and apply. Several simulated data as well as the pH-spectral data of Eriyochrome Black T (acid–base indicator) as a real system were evaluated by the proposed method. The results are all satisfactory. The proposed method can also be applied to the pH-titration data where H2A, HA− or A2− form a non-absorbing species, using binary mean centering. In addition, the method can be used to obtain the pKa value of a monoprotic acid with highly overlapped spectra. The contribution(s) of known component(s) can be removed from any data by using the proposed method. Knowing the reduced data, a least squares (fitting) will be simply useful. The least squares step (fitting) is a common step in all mentioned methods while the first stage of the proposed method (mean centering of ratio spectra) is a preprocessing step which can be used as a pretreatment step prior to any other software in order to increase the convergence rate, decrease the time of analysis and improve the accuracy of the results. Finally, it should be noted that the proposed method in the current manner might not be applicable in the presence of external unknown interferences, but coupling mean centering of ratio spectra with the soft or hard models may reduce the possible ambiguities. Our future work focuses on the study of the effect of mean centering of ratio spectra as a preprocessing step on the results of multivariate curve resolution method.
References
- V. E. Modest and J. F. Butterworth, Chest, 1995, 108, 1373 CrossRef CAS.
- S. C. Sealfon, H. Weinstein and R. P. Millar, Endocr. Rev., 1997, 18, 180 CrossRef CAS.
- M. Meloun and M. Pluhařová, Anal. Chim. Acta, 2000, 416, 55 CrossRef CAS.
- M. Meloun and P. Cernohorský, Talanta, 2000, 52, 931 CrossRef CAS.
-
D. J. Leggett (Ed.), Computational Methods for the Determination of Formation Constants, Plenum Press, New York, 1985, pp. 99–157 Search PubMed.
-
D. J. Leggett (Ed.), Computational Methods for the Determination of Formation Constants, Plenum Press, New York, 1985, pp. 291 Search PubMed.
-
J. Havel, M. Meloun and D. J. Leggett (ed.), Computational Methods for the Determination of Formation Constants, Plenum Press, New York, 1985, p. 19 Search PubMed.
-
J. Havel, M. Meloun and D. J. Leggett (ed.), Computational Methods for the Determination of Formation ConstantsPlenum Press, New York, 1985, p. 221 Search PubMed.
- M. Meloun, M. Javůrek and J. Havel, Talanta, 1986, 33, 513 CrossRef CAS.
- D. J. Leggett and W. A. E. McBryde, Anal. Chem., 1975, 47, 1065 CrossRef CAS.
- D. J. Leggett, Anal. Chem., 1977, 49, 276 CrossRef CAS.
- D. J. Leggett, S. L. Kelly, L. R. Shine, Y. T. Wu, D. Chang and K. M. Kadish, Talanta, 1983, 30, 579 CrossRef CAS.
- J. J. Kankare, Anal. Chem., 1970, 42, 1322 CrossRef CAS.
- M. Meloun, J. Capek, P. Miksik and R. G. Brereton, Anal. Chim. Acta, 2000, 423, 51 CrossRef CAS.
- M. Meloun, D. Burkonova, T. Syrovy and A. Vrana, Anal. Chim. Acta, 2003, 486, 125 CrossRef CAS.
- H. Abdollahi and F. Nazari, Anal. Chim. Acta, 2003, 486, 109 CrossRef CAS.
- M. Meloun, T. Syrovy and A. Vrana, Anal. Chim. Acta, 2003, 489, 137 CrossRef CAS.
- M. Meloun, T. Syrovy and A. Vrana, Talanta, 2004, 62, 511 CrossRef CAS.
- Y. Kin, K. Tam and Takacs-Novak, Anal. Chim. Acta, 2001, 434, 157 CrossRef CAS.
- B. Hemmateenejad, A. Abbaspour, H. Maghami and A. Foroumadi, Anal. Chim. Acta, 2008, 607, 142 CrossRef CAS.
-
D. J. Leggett (Ed.), Computational Methods for the Determination of Formation Constants, Plenum Press, New York, 1985, pp. 99–157 Search PubMed.
-
D. J. Leggett (Ed.), Computational Methods for the Determination of Formation Constants, Plenum Press, New York, 1985, pp. 291–353 Search PubMed.
- M. Meloun, Anal. Chim. Acta, 2007, 584, 419 CrossRef CAS.
-
J. Havel, M. Meloun, in: D. J. Leggett (Ed.), Computational Methods for the Determination of Formation Constants, Plenum Press, New York, 1985, p. 221 Search PubMed.
- M. Meloun, M. Javůrek and J. Havel, Talanta, 1986, 33, 513 CrossRef CAS.
- D. J. Leggett and W. A. E. McBryde, Anal. Chem., 1975, 47, 1065 CrossRef CAS.
- D. J. Leggett, Anal. Chem., 1977, 49, 276 CrossRef CAS.
- D. J. Leggett, S. L. Kelly, L. R. Shiue, Y. T. Wu, D. Chang and K. M. Kadish, Talanta, 1983, 30, 579 CrossRef CAS.
- J. J. Kankare, Anal. Chem., 1970, 42, 1322 CrossRef CAS.
- P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739 CrossRef CAS.
- H. Gampp, M. Maeder, Ch.J. Meyer and A. Zuberbuhler, Talanta, 1985, 32, 95 CrossRef CAS.
- H. Gampp, M. Maeder, Ch.J. Meyer and A. Zuberbühler, Talanta, 1985, 32, 251 CrossRef.
- H. Gampp, M. Maeder, Ch.J. Meyer and A. Zuberbühler, Talanta, 1985, 32, 1133 CrossRef CAS.
- L. Blanchet, C. Ruckebusch, J. P. Huvenne and A. de Juan, Hybrid hard- and soft-modeling applied to difference spectra, Chemom. Intell. Lab. Syst., 2007, 89, 26 CrossRef CAS.
- A. Afkhami and M. Bahram, Talanta, 2005, 66, 712 CrossRef CAS.
- A. Afkhami and M. Bahram, Anal. Chim. Acta, 2004, 526, 211 CrossRef CAS.
- A. Afkhami and M. Bahram, Talanta, 2006, 68, 1148 CrossRef CAS.
- A. Afkhami, T. Madrakian, M. Bahram and J. Haz, Mater, 2005, 123, 250 Search PubMed.
- M. Bahram, Anal. Chim. Acta, 2007, 603, 13 CrossRef CAS.
- M. Bahram and M. Mabhooti, Anal. Chim. Acta, 2009, 639, 19 CrossRef CAS.
- A. Afkhami, F. Khajavi and H. Khanmohammadi, Anal. Chim. Acta, 2009, 634, 180 CrossRef CAS.
-
A. de Juan, E. Casassas and R. Tauler, in: R. A. Myers (Ed.), Encyclopedia of Analytical Chemistry, vol. 11, Wiley, Chichester, 2002, pp. 9800–9837 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2010 |
Click here to see how this site uses Cookies. View our privacy policy here. 
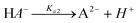





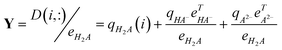



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dsim = Qsim × Esim. The matrix Dsim has a dimension of (n × m), where m is the number of wavelengths at which absorbences were calculated (here m = 151) and n is number of pH values as defined previously (n = 56). To more rigorously test the method, random errors equal to the 0.005 absorbance values were added to the simulated data. Fig. 1 represents case simulated spectra, concentration profiles of protogenic species (i.e. H2A, HA− and A2−) for pKa1 = 5 and pKa2 = 6.5 and the obtained data. The results that have been obtained by applying the proposed method for analyzing this data set are shown in Fig. 2. The pure response of the intermediate component of the diprotic acid pH-titration (concentration profile of HA−) is also shown in Fig. 2(e). The result of fminsearch fitting for a case data set is also presented in Fig. 3.
Dsim = Qsim × Esim. The matrix Dsim has a dimension of (n × m), where m is the number of wavelengths at which absorbences were calculated (here m = 151) and n is number of pH values as defined previously (n = 56). To more rigorously test the method, random errors equal to the 0.005 absorbance values were added to the simulated data. Fig. 1 represents case simulated spectra, concentration profiles of protogenic species (i.e. H2A, HA− and A2−) for pKa1 = 5 and pKa2 = 6.5 and the obtained data. The results that have been obtained by applying the proposed method for analyzing this data set are shown in Fig. 2. The pure response of the intermediate component of the diprotic acid pH-titration (concentration profile of HA−) is also shown in Fig. 2(e). The result of fminsearch fitting for a case data set is also presented in Fig. 3.




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethanol–water solution (25 °C). The size of the obtained pH-titration data set of EBT was therefore 151 × 23. Fig. 5(a) shows the monitored spectra at different pH values. In highly acidic media (pH ≤ 1) the recorded spectrum was used as the pure spectrum of H2A and in highly basic media (pH ≥13) the recorded spectrum was used as the pure spectrum of A2− (Fig. 5(b)). The matrix of absorption data was processed by the proposed method. The spectrum of H2A and A2− were used as divisors according to eqn (9)–(12). Fig. 5(c–f) represents the results obtained by the proposed method.
1 ethanol–water solution (25 °C). The size of the obtained pH-titration data set of EBT was therefore 151 × 23. Fig. 5(a) shows the monitored spectra at different pH values. In highly acidic media (pH ≤ 1) the recorded spectrum was used as the pure spectrum of H2A and in highly basic media (pH ≥13) the recorded spectrum was used as the pure spectrum of A2− (Fig. 5(b)). The matrix of absorption data was processed by the proposed method. The spectrum of H2A and A2− were used as divisors according to eqn (9)–(12). Fig. 5(c–f) represents the results obtained by the proposed method.


