Rapid estimation of overall mass-transfer coefficients in liquid chromatography
Ivett
Bacskay
and
Attila
Felinger
*
Department of Analytical and Environmental Chemistry, University of Pécs, Ifjúság útja 6, H-7624, Pécs, Hungary. E-mail: felinger@ttk.pte.hu
First published on 27th October 2010
Abstract
The stochastic or microscopic model of chromatography has been applied to determine overall mass-transfer coefficients from peak shapes recorded in reversed-phase liquid chromatography. The stochastic model of chromatography describes the separation process at the molecular level by probabilistic terms. This microscopic model is rather straightforward and it can furnish direct answers when one tries to understand the development of chromatographic peaks. In this study we demonstrate that this model can be rather simply used to estimate the fundamental mass-transfer characteristics of the separation process. The only information needed to obtain the mass-transfer coefficients is the first and the second moments of the chromatographic peak.
1 Introduction
Chromatographic processes are usually described with either equilibrium or kinetic macroscopic models. The modeling usually consists in formulating a proper differential mass balance equation that describes the physico-chemical processes of chromatography with a desired detail.1,2 The mass balance models usually assume instantaneous equilibrium between the mobile and the stationary phases or use kinetic rate constants to characterize the resistance to mass transfer or adsorption–desorption.A number of kinetic models of various degree of complexity have been introduced in chromatography. The most detailed kinetic model is the general rate model.3 The solution of that model has been studied by several authors.4,5 The moments calculated from the general rate model allow the derivation of a detailed plate height equation for both particulate and monolith columns.6
Lapidus and Amundson7 introduced a simple nonequilibrium model, the lumped kinetic model, which has been used in various forms. The reaction-dispersive model attributes the nonequilibrium state to slow adsorption and desorption processes while the transport-dispersive model assumes that the adsorption–desorption is fast, but the mass-transfer kinetics is slow.
The lumped pore model8 is the result of a different simplification of the general rate model. It seems to be more detailed than the lumped kinetic model because, similarly to the general rate model, it takes into consideration the difference between the mobile phase percolating through the interparticle space (or the through-pores of a monolithic column) and the mobile phase stagnant in the stationary phase pores. However, it ignores the radial concentration gradient within a stationary phase particle.
The microscopic – or stochastic – models depict the chromatographic processes at a molecular level via the random migration of the individual molecules.
The stochastic model of chromatography was introduced by Giddings and Eyring.9 In their model, they assumed that while migrating along the column, a molecule performs a random number of adsorption and desorption steps characterized by a Poisson distribution. Furthermore, once a molecule is adsorbed on the stationary phase, the time spent until desorption – the sojourn time in the stationary phase – is a random variable, too. This latter random variable follows an exponential distribution. A significant effort has been devoted to the extension of the stochastic model to heterogeneous surfaces in the 1960s, but the handling of the problem in time domain resulted in rather complex expressions, inadequate for practical calculations.10,11
The characteristic function (CF) approach remarkably facilitates the use of the stochastic model of chromatography.12,13 The use of CF facilitated the extension of the stochastic theory to two-site14 or to generic multiple-site heterogeneous surfaces15 that are very complex to handle otherwise.9,16,17 Thus, the CF approach of the stochastic theory is able to model the band profile that is due to any unimodal or multimodal distribution of sorption energies. The stochastic model was further extended to describe the effect of mobile phase dispersion and size exclusion effects as well.18–20
By means of the CF method, closed form expressions are obtained in Fourier domain for the band profiles, thus the statistical moments can directly be calculated even if the transformation into time domain is possible numerically only.21,22
The dispersion in the mobile phase is very often neglected in the stochastic models. In some studies the contribution of the mobile phase dispersion was modeled simply with a Gaussian distribution12,18,23 or by first-passage density calculated from the diffusion equation.16,24
There have been some attempts to compare the microscopic and the macroscopic models of chromatography. Usually this is restricted to the comparison of the first and the second moments. Cavazzini et al. showed that the number of theoretical plates calculated by either the microscopic or the macroscopic kinetic models of chromatography agree as long as the mobile phase dispersion is neglected.15 Felinger et al. considered the mobile phase dispersion by a Gaussian peak and proved that the first and the second moments of the stochastic-dispersive and the lumped kinetic models are identical.18 Later, Felinger et al. showed that not only the first and the second moments but also the whole peak shape obtained with the stochastic-dispersive and with the lumped kinetic models are identical.24
In the present study, we will show a simple method to characterize the solute transfer between the mobile and stationary phases by using the stochastic model of liquid chromatography.
2 Theory
In the stochastic model of chromatography,9 a distribution is determined for a given molecule describing the probability that the molecule can be found at location z within the column at time t. It is assumed that the ka mass-transfer coefficient is a rate constant that represents the probability that a solute molecule will transfer from the mobile to the stationary phase. A similar kd rate constant describes another mass-transfer coefficient – the solute transfer from the stationary to the mobile phase. The ka constant represents the probability that a solute molecule will transfer to stationary phase during one second. The similar kd rate constant describes the first-order process for the stationary-to-mobile phase transfer.9In a similar manner, during a random walk of a molecule through the chromatographic bed, two mass-transfer time constants are defined. τm indicates the average time a molecule spends in the mobile phase between two visits to the stationary phase, and τs is the average time spent in the stationary phase during a single visit. These time constants can directly be related to the above introduced rate constants of the adsorption – or transfer from the mobile to the stationary phase – and desorption – or transfer from the stationary to the mobile phase – kinetics:
| τm = 1/ka | (1) |
| τs = 1/kd | (2) |
Thus the void time and the adjusted retention time can be expressed by the average mobile and stationary phase sojourn times and by the average number of mass-transfer events (n)
| t0 = nτm | (3) |
| t′R = nτs | (4) |
| σ2s = 2nτ2s | (5) |
3 Experiments
An Agilent 1100 liquid chromatograph with a dual solvent delivery system, an auto sampler, a column thermostat, a multi-wavelength UV detector and Chemstation software was used for all measurements. A Waters Symmetry C18 column was used (150 × 4.6 mm, average particle size 5 μm). Thiourea, toluene, ethylbenzene, propylbenzene, butylbenzene were purchased from Sigma-Aldrich; pentylbenzene was purchased from Fluka. Scharlau HPLC grade methanol and Baker water was used for all experiments.Different flow rates were used, 0.25 mL min−1, 0.50 mL min−1, 1.00 mL min−1, and 1.50 mL min−1. The column thermostat was set at the following temperatures: 10 °C, 20 °C, 30 °C and 40 °C. Each measurement was executed with methanol–water (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, v/v) solution as mobile phase. The standard mixture contained 0.8 μg mL−1 of toluene, ethylbenzene, propylbenzene, butylbenzene, pentylbenzene and 1.6 μg mL−1 thiourea. The hold-up time of the column was determined from the elution time of thiourea. 20 μL of the standard mixture was injected in all measurements. The components were detected at 254 nm.
20, v/v) solution as mobile phase. The standard mixture contained 0.8 μg mL−1 of toluene, ethylbenzene, propylbenzene, butylbenzene, pentylbenzene and 1.6 μg mL−1 thiourea. The hold-up time of the column was determined from the elution time of thiourea. 20 μL of the standard mixture was injected in all measurements. The components were detected at 254 nm.
4 Calculations
In order to estimate the overall mass-transfer coefficients, the first and the second moments of the peaks must be determined. The first moment, or expectation of a transient signal is calculated as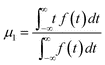 | (6) |
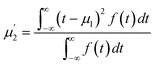 | (7) |
The exponentially modified Gaussian (EMG) function is one of the most frequently used asymmetrical models to describe peak profiles in chromatography. Although the peak shape parameters of the EMG model have no direct physical meaning, the moments of the recorded peak can be determined after the fitting procedure with sufficient accuracy. The following EMG model was fitted to the experimental peak profiles of thiourea and alkylbenzenes:
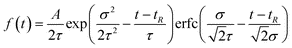 | (8) |
The first moment and the second central moment of the EMG model are:
| μ1 = tR + τ | (9) |
| μ′2 = σ2 + τ2 | (10) |
At this point we have to emphasize that the EMG model is purely empirical and cannot be used to estimate kinetic or mass-transfer coefficients. Chromatographers often use this peak shape model, as it can mimic many experimental peaks. The τ parameter of the EMG model, however, has nothing to do with mass-transfer or adsorption–desorption kinetics. There are several reasons why one observes tailing peaks in HPLC. One of those reasons is indeed slow mass-transfer or sorption kinetics. However, kinetics must be extremely slow to have an effect on the peak asymmetry. In reversed-phase liquid chromatography, kinetics is fast enough and the number of mass-transfer events is high enough to observe symmetrical peaks. We only use the EMG model to assure accurate estimation of the moments.
5 Results and discussion
We applied the previously described theory to HPLC experiments, in order to determine overall mass-transfer coefficients. The reversed-phase separation of neutral compounds on a C18 silica-based stationary phase was studied. Samples of mixture of thiourea and alkylbenzenes were injected at flow rates between 0.25 and 1.5 mL min−1, using aqueous solution of methanol with 80% methanol as mobile phase, under chromatographic conditions described in experimental section. Fig. 1 shows the chromatogram recorded at 10 °C and 0.25 mL min−1 flow rate.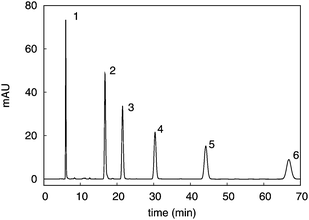 | ||
| Fig. 1 Chromatogram of the standard mixture. Peaks: 1: thiourea, 2: toluene, 3: ethylbenzene, 4: propylbenzene, 5: butylbenzene, 6: pentylbenzene. | ||
The first step of the calculations is to eliminate the effect of mobile phase dispersion and extra-column broadening from the peaks using the moments calculated from the peak shape of an unretained marker. The peak shape and the moments of the unretained marker carry the influence of the extra-column and mobile phase processes, therefore they can be utilized for correction and to obtain moments characteristic for the stationary phase process. Thus Δμ1 = μ1 − μ01 and Δμ′2 = μ′2 − μ′02 are obtained, where μ01 is the first moment and μ′02 is the second central moment of the thiourea peak.
We used two sets of data to calculate the mass-transfer coefficients. The moments of the chromatographic peaks were calculated by two different ways: (i) using the moments reported by the Chemstation software and (ii) by fitting the exponentially modified Gaussian function, eqn (8). The Chemstation software calculates the moments by numerical integration, using a discretized form of eqn (6) and (7).
Tables 1 and 2 show a selected example from series of results for calculation of n, τs and τm. The average number of mass-transfer events (n) is calculated from the first moment and the second central moment corrected by the respective moments of thiourea using eqn (4) and (5):
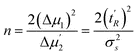 | (11) |
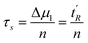 | (12) |
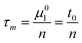 | (13) |
| Thiourea | Toluene | Ethyl-benzene | Propyl-benzene | Butyl-benzene | Pentyl-benzene | |
|---|---|---|---|---|---|---|
| μ 1 (s) | 362.22 | 1004.6 | 1291.3 | 1823.2 | 2653.6 | 4014.7 |
| μ ′2 (s2) | 19.71 | 77.45 | 123.63 | 244.85 | 519.39 | 991.14 |
| Δμ1 (s) | 642.42 | 929.04 | 1461.0 | 2291.4 | 3652.4 | |
| Δμ′2 (s2) | 57.75 | 103.93 | 225.14 | 499.69 | 971.43 | |
| n | 14293 | 16610 | 18962 | 21015 | 27465 | |
| τ s (ms) | 44.9 | 55.9 | 77.1 | 109.0 | 133.0 | |
| τ m (ms) | 25.3 | 21.8 | 19.1 | 17.2 | 13.2 | |
| Thiourea | Toluene | Ethyl-benzene | Propyl-benzene | Butyl-benzene | Pentyl-benzene | |
|---|---|---|---|---|---|---|
| μ 1 (s) | 362.3 | 1005.4 | 1291.4 | 1823.2 | 2653.3 | 4011.2 |
| μ ′2 (s2) | 22.39 | 96.07 | 134.76 | 267.98 | 569.3 | 1311.1 |
| Δμ1 (s) | 643.02 | 929.09 | 1460.9 | 2290.9 | 3648.8 | |
| Δμ′2 (s2) | 73.68 | 112.37 | 245.59 | 546.9 | 1288.7 | |
| n | 11224 | 15363 | 17380 | 19192 | 20663 | |
| τ s (ms) | 57.3 | 60.5 | 84.1 | 119.4 | 176.6 | |
| τ m (ms) | 32.3 | 23.6 | 20.8 | 18.9 | 17.5 | |
Fig. 2 shows the comparison of the experimental and theoretical profiles along the time axis for the calculation of the zeroth, first and the second central moments. The theoretical distribution was calculated from the fitting of the EMG function. The experimental data are the respective f(t), tf(t), and (t − μ1)2f(t) series calculated from the chromatograms. Those terms are to be integrated when the moments are determined by numerical integration of the peaks in the chromatogram, as it is shown by eqn (6) and (7).
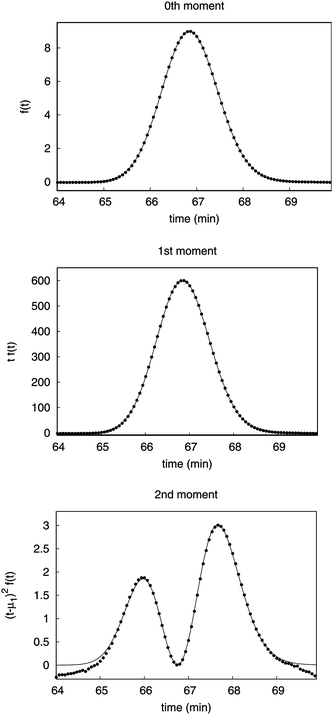 | ||
| Fig. 2 Plots of the contributions of the signals to the moments versus the time. Symbols are the numerical integration data and the solid line is the theoretical data based on the EMG function, respectively. | ||
The experimental data and the theoretical data are in excellent agreement for the zeroth and first moments. The experimental data set for second central moment diverges from the theoretical data. Accordingly, it is difficult to make an accurate evaluation from the experimental data of the second central moment, since one cannot accurately determine where to start and stop the numerical integration.
We can express – using eqn (12) and (13) – the average stationary phase and mobile phase residence times for one mass-transfer event (τs and τm), respectively. The results summarized in Table 2 show that the stationary phase residence time ranges between τs = 57–177 ms, and the mobile phase sojourn time is in the range of τm = 17–33 ms for the given temperature and flow rate†. The average sojourn time in the stationary phase increases with the increase of the retention, and the average time a molecule spends in the mobile phase between leaving the stationary phase and the subsequent return there is decreasing.
Fig. 3 shows the significant decrease of the τs values with the increase of temperature and a slight decrease of the τm values with flow rate. The changes of sojourn times in the stationary phase are more significant for the strongly retained components than for the weakly retained ones. We can notice that when the flow rate is increased, the values of the average stationary phase sojourn times and the average time a molecule spends in the mobile phase are decreased.
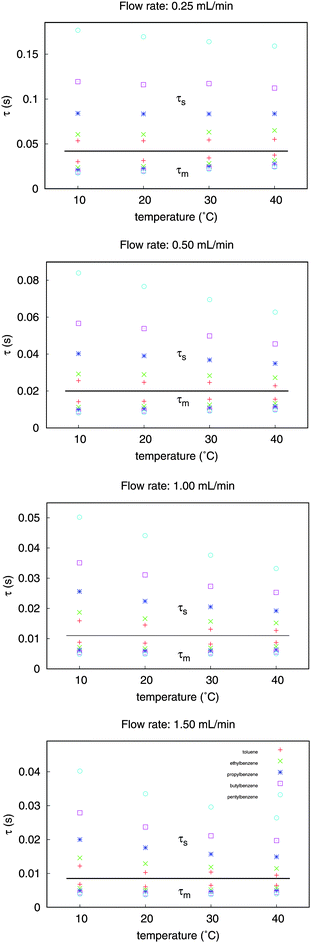 | ||
| Fig. 3 Plot of the mass-transfer time constants versus temperature at different flow rates, calculated by stochastic model of liquid chromatography. | ||
As it is expected, the mobile phase sojourn times are independent of the solute. For one set of experimental conditions, the solute molecules show identical mobile phase sojourn times, with a very small temperature dependence. On the other hand, the stationary phase time constants strongly depend on temperature and on the retention of the solute. Since selectivity arises from the stationary phase processes, therefore this is the expected behavior. In a similar manner, the weaker retention observed at higher temperatures is due to the decrease of the τs time constant that characterizes the stationary phase sojourn time.
6 Conclusions
The stochastic model of chromatography offers a rather interesting view of the chromatographic process. The determination of the stationary phase sojourn times and the number of mass-transfer events gives a practical view of the molecular process of separation. From the first moment and the second central moment, the overall mass-transfer coefficients can easily be determined. All the information needed to calculate the mass-transfer coefficients is the first and second moments of the peaks. That information is easily conveyed by the data handling software of an HPLC instrument.The analysis of a reversed phase HPLC separation shows that the typical time constants are the stationary phase residence time ranges between τs = 10–180 ms, and the mobile phase sojourn time is in the range of τm = 5–20 ms, depending on solute, temperature, and flow rate.
The typical numbers of mass-transfer events is in the range of n = 15000–25000, i.e. on the average, every molecule enters and leaves the stationary phase that many times during the migration along the chromatographic column. The enormous separation power of chromatography arises from the differences in the stationary phase sojourn time combined with the large number of mass-transfer events.
Acknowledgements
This work was supported by grants GVOP-3.2.1-0168, RET 008/2005, OTKA 75717, and OTKA-NKTH 68863.References
- G. Guiochon, A. Felinger, D. G. Shirazi and A. M. Katti, Fundamentals of Preparative and Nonlinear Chromatography, Academic Press, Amsterdam, 2nd edn, 2006 Search PubMed.
- G. Guiochon and B. Lin, Modeling for Preparative Chromatography, Elsevier, Amsterdam, 2003 Search PubMed.
- E. Kučera, J. Chromatogr., A, 1965, 19, 237–248 CrossRef CAS.
- M. Suzuki and J. M. Smith, Adv. Chromatogr., 1975, 13, 213–263 CAS.
- A. M. Lenhoff, J. Chromatogr., A, 1987, 384, 285–2990 CrossRef CAS.
- K. Miyabe and G. Guiochon, J. Phys. Chem. B, 2002, 106, 8898–8909 CrossRef CAS.
- L. Lapidus and N. R. Amundson, J. Phys. Chem., 1952, 56, 984–988 CrossRef CAS.
- M. Morbidelli, A. Servida, G. Storti and S. Carrà, Ind. Eng. Chem. Fundam., 1982, 21, 123–131 CrossRef CAS.
- J. C. Giddings and H. Eyring, J. Phys. Chem., 1955, 59, 416–421 CrossRef CAS.
- J. C. Giddings, Anal. Chem., 1963, 35, 1999–2002 CrossRef CAS.
- J. C. Giddings, Dynamics of Chromatography, Marcel Dekker, New York, 1965 Search PubMed.
- D. A. McQuarrie, J. Chem. Phys., 1963, 38, 437–445 CrossRef CAS.
- F. Dondi and M. Remelli, J. Phys. Chem., 1986, 90, 1885–1891 CrossRef CAS.
- A. Cavazzini, M. Remelli and F. Dondi, J. Microcolumn Sep., 1997, 9, 295–302 CrossRef CAS.
- A. Cavazzini, M. Remelli, F. Dondi and A. Felinger, Anal. Chem., 1999, 71, 3453–3462 CrossRef CAS.
- G. H. Weiss, Sep. Sci. Technol., 1970, 5, 51–62 CrossRef CAS.
- G. H. Weiss, Sep. Sci. Technol., 1982, 17, 1609–1622 CrossRef CAS.
- A. Felinger, A. Cavazzini, M. Remelli and F. Dondi, Anal. Chem., 1999, 71, 4472–4479 CrossRef CAS.
- F. Dondi, A. Cavazzini, M. Remelli, A. Felinger and M. Martin, J. Chromatogr., A, 2002, 943, 185–207 CrossRef CAS.
- L. Pasti, F. Dondi, M. Van Hulst, P. J. Schoenmakers, M. Martin and A. Felinger, Chromatographia, 2003, 57, S171–S186.
- A. Felinger, Data Analysis and Signal Processing in Chromatography, Elsevier, Amsterdam, 1998 Search PubMed.
- A. Felinger, J. Chromatogr., A, 2008, 1184, 20–41 CrossRef CAS.
- J. H. Beynon, S. Clough, D. A. Crooks and G. R. Lester, Trans. Faraday Soc., 1958, 54, 705–714 RSC.
- A. Felinger, A. Cavazzini and F. Dondi, J. Chromatogr., A, 2004, 1043, 149 CrossRef CAS.
Footnote |
| † The retention of toluene is the weakest, so the width of the toluene peak is mostly affected by mobile phase dispersion and not stationary phase processes. Therefore the time constants obtained for toluene are prone to error. |
| This journal is © The Royal Society of Chemistry 2010 |
