A kinetic method in simultaneous thermal analysis
Yi
Cheng
*
Nanjing University of Science and Technology, Nanjing, 210094, P.R.China. E-mail: chengyi20@yahoo.com.cn
First published on 2nd July 2010
Abstract
Ordinarily, Thermogravimetry (TG) or Differential Thermal Analysis (DTA) or Differential Scanning Calorimetry (DSC) can describe only the change of α or △T or q with T(t), and Simultaneous Thermal Analysis (STA) provides two curves, (α∼ T(t) curve and △T or q∼ T(t) curve, in a single test (T is temperature; q is the heat flow; t is time). This work proposes a Simultaneous Kinetic Method, or simply SKM method aimed at STA tests. In the SKM method, the values of the activation energy (E) and reaction mechanism function can be calculated and determined by a trial and error method using the differential kinetic equation. When the values of αm at the different heating rate are different, for example the heat degradation of polyamide 6 (PA6), the SKM method provides a more accurate activation energy than that calculated by the Kissinger equation.
Introduction
In 1958, Paulik1 introduced a multi-purpose method by which thermogravimetric TG and DTA curves could be obtained from a single analysis, a technique called simultaneous thermal analysis (STA). Historically the Mettler-Toledo Company developed the first commercial equipment to achieve STA in 1964. Until now, STA can be carried out in many types of machines, such as the TGA/SDTA851e (Mettler-Toledo), DSC/TGAQ600 (TA Instruments), DTG-60/60H (Shimadzu) and STA449 series (Netzsch).The Kissinger method2 is a well known differential method in thermal analysis. The main supposition is that ln[−f′(αp)] is zero or constant. But many researchers have proved that ln[−f′(αp)] is not a constant.3–9Ref. 10 suggests the use of differential methods when the experimental curve is fluctuating.
Since the values of αp and Tp can be obtained directly from STA, a differential method similar to the Kissinger method, but even more exact than that, is proposed here.
Theoretical consideration
Generally, the kinetic equation of a chemical reaction undergoing linear heating may be described by the basic rate equation as follows: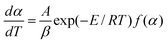 | (1) |
At a peak temperature (Tp) of a curve of either differential thermal analysis DTA or differential scanning calorimetry DSC, d2α/dT2 = 0, the differential rate equation, eqn (1), may be expressed as:
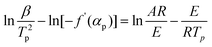 | (2) |
Usually, because f(α)is unknown and the value of αp cannot be obtained directly from just a DTA or DSC curve, eqn (2) cannot be solved.
Kissinger1 suggested that choosing f(α) = (1 − α)n and assuming n(1 − αp)n−1 ≈ 1, then ln[−f′(α)] = 0. Hence, eqn (2) can be re-expressed as:
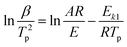 | (3) |
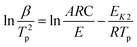 | (4) |
In fact, n(1 − αp)n−1 ≠ 1 or f′(αp) ≠ C1(constant) in many reactions. Hence, the activation energy can not calculated exactly by Kissinger eqn (3) and (4) for many reactions.
Now, with the development of thermal analysis techniques, the STA technique can give TG and DTA (or DSC) curves in one experimental set-up, which are α ∼ T(t) and either ΔT ∼ T(t) or q ∼ T(t) (q is the heat flow mw/mg). In this case, the values of Tp and corresponding αp can easily be determined.
By varying the linear heating rate, a series of αp and Tp values are obtained. From any of the f(α), the reaction active energy (E) can be calculated from eqn (2). The f(α) can assume any reaction mechanism function, such as the reaction order equation, Johnson–Mehl–Avrami equation, the one-dimensional diffusion equation, the two-dimensional diffusion equation, Jander equation, Ginstling–Brounshtein equation, random equation, etc.10 From the different f(α), we can get a series of E values. Comparing the deviation of E for different f(α) and analyzing the rationality of f(α), E and f(α) can be determined. This method is called the Simultaneous Kinetic Method (SKM).
To illustrate SKM's application, it is applied to analysis degradation of polyamide 6.
Experimental
The STA analysis was performed on a Mettler-Toledo TGA/SDTA851 with selected heating rates of 5, 10 and 20 K min−1 in the range 30–600 °C. Samples of polyamide 6 (PA6), all of mass 8 mg, were put in alumina 30 ul pans in an atmosphere of dry nitrogen at a flow rate of 20 ml min−1.Results and discussion
TG-DTA curve of PA6 degradation
The TG-DTA curves of PA6 are shown in Fig.1. It can be found that PA6 has two peaks on DTA curves: the first peak is the melting of PA6; the second peak is the main degradation reaction. The values of αp and Tp of the second peak are listed in Table 1. It is clear that the values of αp at the different heating rates are not constant or even quasi-constant. The TG data are listed in Table 2.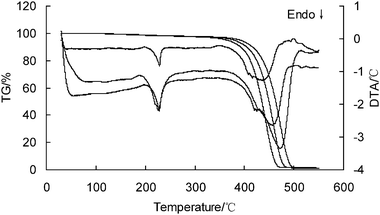 | ||
| Fig. 1 The STA curves of PA6 at 5, 10 and 20 K min−1 (the heating rate increasing from left to right). | ||
| β/K min−1 | 5 | 10 | 20 |
|---|---|---|---|
| 1 − αp | 0.431 | 0.372 | 0.333 |
| T p/K | 712.24 | 729.65 | 745.48 |
| β T/K | α | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | |
| 5 | 665.5 | 685.2 | 695.2 | 702.5 | 708.5 | 713.9 | 719.0 | 724.4 | 731.0 |
| 10 | 677.7 | 698.2 | 709.0 | 716.5 | 722.9 | 728.2 | 733.4 | 738.5 | 745.0 |
| 20 | 689.5 | 710.5 | 721.9 | 729.9 | 736.2 | 741.9 | 747.2 | 752.5 | 758.9 |
The kinetic calculation of PA6 by SKM
If f(α) = (1 − α)n, eqn (2) can be re-expressed as follows: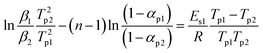 | (5) |
| ln(β/T2p) − ln(2 − 2αp) = ln(AR/Es2) − Es2/RTp (L = 2) | (6-1) |
| ln(β/T2p) − ln(6αp − 6α2p) = ln(AR/Es2) − Es2/RTp (L = 3) | (6-2) |
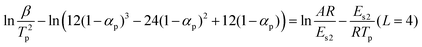 | (6-3) |
By the SKM method, the activation energies for different reaction orders and reaction mechanism functions can be calculated separately.
ΔEmax is the maximum deviation between the activation energy at same reaction order. From Table 3, ΔEmax is seen to decrease with increasing n when f(α) = (1 − α)n. Usually, it is impossible for n to exceed 5, so it is unsuitable to assume f(α) = (1 − α)n in describing the thermal degradation of PA6. For the alternative f(α) function, the smallest value of ΔEmax was obtained when L = 2 and the value of Es of PA6 should then be 206.79 kJ mol−1.
| n | L | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 2 | 3 | 4 | |
| E 5/10(kJ mol−1) | 160 | 197 | 233 | 270 | 307 | 197 | 172 | 148 |
| E 5/20(kJ mol−1) | 172 | 206 | 241 | 275 | 309 | 206 | 185 | 164 |
| E 10/20(kJ mol−1) | 186 | 217 | 249 | 281 | 312 | 217 | 200 | 183 |
| ΔEmax(kJ mol−1) | 26 | 21 | 16 | 11 | 6 | 21 | 28 | 35 |
| E s/kJ mol−1 | 173 | 207 | 241 | 275 | 309 | 207 | 186 | 165 |
The kinetic calculation of PA6 by Ozawa and Kissinger method
To compare the kinetic results calculated by the SKM method with that of other methods, the kinetic parameters of PA6 are also calculated by Ozawa11 and the Kissinger method.The Ozawa equation is given below:
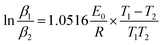 | (7) |
The activation energy of PA6 calculation by Ozawa, Kissinger and SKM method are listed in Table 4 and 5. Where E0 is calculated by Ozawa method according to the data in Table 2; Ek is calculated by Kissinger method according to the data in Table 1; Es is calculated by SKM method according to the data in Table 1.
| E/kJ mol−1 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 |
|
|---|---|---|---|---|---|---|---|---|---|---|
| E 5/10 | 203 | 202 | 196 | 197 | 195 | 199 | 201 | 208 | 213 | 201 |
| E 5/20 | 210 | 212 | 206 | 205 | 206 | 207 | 209 | 213 | 218 | 209 |
| E 10/20 | 217 | 221 | 217 | 214 | 219 | 216 | 218 | 218 | 223 | 218 |
| E/kJ mol−1 |
|
E k | E s1(n = 5) | E s2 (L = 2) |
|---|---|---|---|---|
| E 5/10 | 201 | 160 | 307 | 197 |
| E 5/20 | 209 | 172 | 309 | 207 |
| E 10/20 | 218 | 186 | 312 | 217 |
| ΔEmax | 17 | 26 | 6 | 21 |
| E average | 210 | 173 | 309 | 207 |
Because the Ozawa equation is a model-free kinetic equation, the value of Eo is considered reasonable, implying that the value of Es2 in Table 3 is also reasonable. Furthermore, it can be determined from Table 3 that the reaction mechanism function for PA6 degradation is f(1 − α) = (α)L−1[1 + (L − 1) × (1 − α)], the reaction order is L = 2, while the activation energy is about 207 KJmol−1. Apparently, both Ek and Es1 have larger deviations.
Conclusions
For the calculation of activation energy from Kissinger equation, some large errors were displayed when values of αp which are not constant. Based on the STA technique, a new analytic method, called SKM, was provided. For the degradation of PA6, the calculated results showed that a more accurate value of activation energy was obtained using SKM instead of the Kissinger equation. Moreover, the reaction mechanism function f(α) also can be determined easily from SKM.Acknowledgements
The author gratefully acknowledges the assistance of Mr. Urs Jörimann, Mettler-Toledo GmbH in obtaining the PA6 test data, and is also grateful to his students, Zuo Jinqiong and Li Yanchun.References
- F. Paulik, J. Paulik and L. Erdey, Der Derivatograph, Fresenius’ J. Anal. Chem., 1958, 16(4), 241–252 CrossRef
.
- H. E. Kissinger, Reaction Kinetics in Differential Thermal Analysis, Anal. Chem., 1957, 29(11), 1702–1706 CrossRef CAS
.
- H. H. Horowitz, Gershon Metzger, A New Analysis of Thermogravimetric Traces, Anal. Chem., 1963, 35(10), 1464–1468 CrossRef CAS
.
- T. Ozawa, Kinetic analysis of derivative curves in thermal analysis, J. Therm. Anal., 1970, 2(3), 301–324 CrossRef CAS
.
- Takeo Ozawa, Estimation of activation energy by isoconversion methods, Thermochim. Acta, 1992, 203, 159–165 CrossRef CAS
.
- Xiang Gao, Dun Chen, David Dollimore, The correlation between the value of α at the maximum reaction rate and the reaction mechanisms: A theoretical study, Thermochim. Acta, 1993, 223, 75–82 CrossRef CAS
.
- J. Llópiz, M. M. Romero, A. Jerez and Y. Laureiro, Generalization of the Kissinger equation for several kinetic models, Thermochim. Acta, 1995, 256, 205–211 CrossRef CAS
.
- C. Popescu and E. Segal, Critical considerations on the methods for evaluating kinetic parameters from nonisothermal experiments, Int. J. Chem. Kinet., 1998, 30, 313–327 CrossRef CAS
.
- P. Budrugeac, The Kissinger law and the IKP method for evaluating the non-isothermal kinetic parameters, J. Therm. Anal. Calorim., 2007, 89, 143–51 CrossRef CAS
.
- C. F. Dickinson and G. R. Heal, A review of the ICTAC kinetics project, 2000Part 2. Non-isothermal results, Thermochim. Acta, 2009, 494, 15–25 CrossRef CAS
.
- Takeo Ozawa, Anew Method of Analyzing Thermogravimetric Data, Bull. Chem. Soc. Jpn., 1965, 38(11), 1881–1886 CAS
.
| This journal is © The Royal Society of Chemistry 2010 |