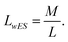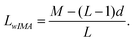Automatic lane detection and separation in one dimensional gel images using continuous wavelet transform
Akbar
Akbari
*a,
Fritz
Albregtsen
a and
Kjetill S.
Jakobsen
b
aDepartment of Informatics, University of Oslo, POB 1080, Blindern, N-0316, Oslo, Norway. E-mail: akbara@ifi.uio.no; fritz@ifi.uio.no; Fax: (+47) 22 84 24 01
bCentre for Ecological and Evolutionary Synthesis (CEES), Department of Biology, University of Oslo, Norway. E-mail: k.s.jakobsen@bio.uio.no
First published on 10th August 2010
Abstract
This work presents new methods which automatically detect and separate the lanes in one dimensional electrophoresis gel images. The motivation is to present algorithms which can be applied on one dimensional gel images produced from separation of DNA, RNA, (including PCR products), proteins, etc. In addition, a one dimensional intensity profile for each separated lane analogous to capillary electrophoresis (CE) profiles is provided. Experiments are performed on ten multi- and ten single-locus DNA gel images, where the number of lanes, resolution and image quality are highly variable. The Elder & Southern (ES) semi-automatic lane detection method, followed by two new methods: an iterative moving average filter (IMA) and a continuous wavelet transform (CWT) with Morlet wavelet are presented and applied on the test images. The accuracy of the results obtained by applying these methods on a set of 10 multi-locus gel images was 91.7% with the ES, 94.4% with the IMA and 99.5% with the CWT; in the set of 10 single-locus images it was 100% with the ES, 94.8% with the IMA and 97.8% with the CWT; for both sets combined (20 images) it was 96.1% with the ES, 94.7% with the IMA and 98.7% with the CWT. Two lane separation methods are presented; the first is based on a K-neighbouring points algorithm, while a half-width algorithm is applied in the second method. Every separated lane from a gel image can be transferred into a sub-image and further into a one dimensional intensity profile.
1. Introduction
In many applications such as forensic studies, paternity analysis, protein profile comparison and population genetic analysis, bands in a lane within a gel image (an image obtained from a separation technique called gel electrophoresis) will be compared to the bands from other lanes within, or between, gel images (e.g., refs 1–5 and references therein).One dimensional gel images usually contain multiple lanes, and the location of the lanes will often be recomputed every time the analysis is performed. Detection and separation of the lanes would make the process of analysis and comparison easier, and would also give a significant reduction of the storage space.
There are a number of image processing packages and methods available, applying different approaches to detect the lanes in a gel image. KODAK 1D,6 uses features such as isomolecular weight lines to optimize lane detection, while in Image,7 the correlation between adjacent lines (columns) across the image is used to detect the lanes. In ImageJ,8 lanes are manually selected, starting from the first lane. Methods presented in ref. 9 use algorithms based on frequency domain filtering, min and max, while the method in ref. 10 uses the average intensity profile to detect lanes. The method proposed by Elder and Southern11 is semi-automatic and based on equispaced lanes with constant width. However, these methods depend on the image resolution and quality, and may fail to detect the lanes with only very weak bands or eventually no bands. In addition, they may require user interaction and preprocessing operations on the gel images.
In this work, the performance of the semi-automatic lane detection method presented by Elder and Southern11 (ES), applied on the test images is evaluated. Then, two new automatic lane detection methods, followed by two automatic lane-width estimation and separation algorithms are presented. The separated lanes are then transferred to sub-images and then into one dimensional profiles. We assume that the images are geometrically corrected using standard image processing algorithms,13,12 if necessary. The projected intensity profile in the direction along the lanes in a gel image will be used as the input to the new lane detection methods. Further, the output of the lane detection methods is used as the input to the boundary estimation and separation algorithms.
The first automatic lane detection method is based on an iterative moving average (IMA) algorithm presented in Section 2.1.2. The IMA depends on the image quality and is also sensitive to the distance between two adjacent lanes in a gel image (depending on the image resolution), which is used as input parameter. To improve the lane detection for lower quality images and to eliminate the sensitivity due to the image resolution, a continuous wavelet transform (CWT) algorithm based on the continuous Morlet wavelet is introduced in Section 2.1.3.
A common input parameter to all three lane detection methods, is the number of lanes given by the user. Counting the number of lanes in a gel image automatically, could be possible for high quality images with lanes containing sufficient number of high intensity bands. If so, an appropriate low pass filter on the intensity profile obtained by eqn (1) followed by a peak detection algorithm, or correlation between adjacent columns across the image could be used to count the number of lanes. Since the quality of multi-locus images are highly variable, and the lanes (except the lanes loaded with standards) in single-locus images contain very few and relatively weak bands, the application of the automatic counting of lanes would be very limited. Therefore it has not been considered in this work.
Further, the lane positions computed by the CWT algorithm will be employed to estimate the boundaries for the corresponding lanes in the gel image followed by the transferral of each lane into a sub-image. To perform this task, two automatic lane separation methods will be employed. The first method in Section 2.2.1 is based on the K-neighbouring points, while the second method in Section 2.2.2 is based on the half width power point.
Each lane in a gel image can be presented by an intensity profile analogous to capillary electrophoresis (CE) profiles by computing the average of each row (along the axis parallel to the DNA bands) in the sub-image corresponding to each lane. The computed profile analogous to CE corresponding to each lane can be analysed for its number of bands. Separated lanes containing no band could have been left empty (non-loaded) by intention and may be ignored in future analysis.
Finally, the included standard markers in the corresponding gel image can be used to convert the peak positions of DNA bands in the intensity profile for each lane into molecular weights (MW),15 which may be stored in an appropriate database for further analysis.
2. Methods
2.1 Lane detection methods
Ideally, the lanes in one dimensional gel images are approximately equidistant. In practice, the distance between lanes and the lane-widths vary due to different sources of noise. This makes the process of lane detection and separation complicated. In some cases, smiling artefacts and deformations are produced due to the high voltage and current6 in addition to the handling of the gel. It is also common for molecular biologists to skip loading the first and last lanes of a gel, as those lanes tend to be most susceptible to distortions from high current voltage effects. If the image contains non-loaded lanes, they will be removed after the process of lane detection and separation, which is presented in this work. If the deformations in the image are significant, a geometrical algorithm13 could be applied to correct the image, using the information in the lanes with known standards as grid control points across the image. Throughout this work, we assume that the images are geometrically corrected in case of deformations.The test images in this work are obtained by scanning X-ray films generated from one dimensional electrophoresis gel images,† using a Microtek ScanMaker 4 scanner with the transparency scanning function, and deal with one spectral bands, i.e., images with grey levels between 0 (black) and 255 (white).
The images experimented within this work are tiff format (readable in Matlab14), while other formats could also be applicable. The methods described here are only related to the location and separation of the lanes in a gel image and have no concern with image compression.
Both multi- and single-locus gel images of various quality and resolution and with different numbers of lanes have been used as test images. Examples are shown in Fig. 1(a) and (b) respectively.
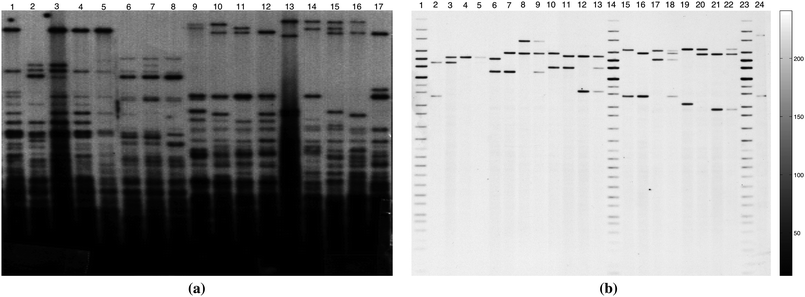 | ||
| Fig. 1 Examples of one dimensional DNA gel images. (a) A 317 × 327 (150 dpi) multilocus DNA gel image. (b) A 1857 × 1650 (300 dpi) single-locus DNA gel image. | ||
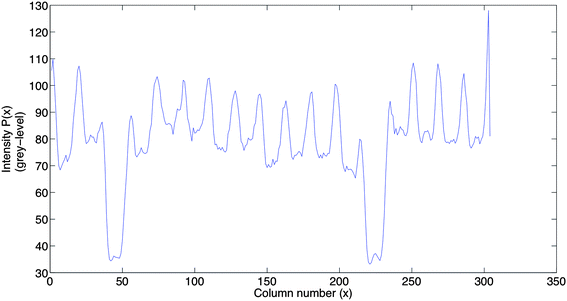
The algorithms presented in sections 2.1.2 and 2.1.3 are based on the intensity profile obtained by the projection of column intensities in the image onto the horizontal axis (axis perpendicular to the lanes in the image). The projection P(x) of image I(x, y) of size M × N (where M is the number of rows and N is the number of columns in the image) onto the horizontal axis is obtained by averaging the grey level values on each column in the image.
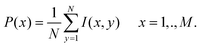 | (1) |
The intensity profile obtained by applying eqn (1) on the image in Fig. 1(a) is shown in Fig. 2.
In order to identify the lane positions in a gel image, the corresponding projected intensity profile P(x) (referred to as the intensity profile) will be used as input to the IMA and CWT algorithms.
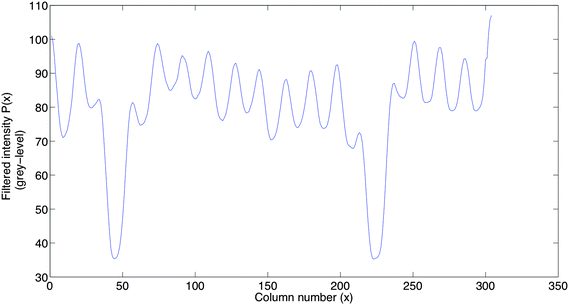
The approximated lane width LwES and the image width M are used to compute the center of the lanes in the image.
 | ||
| Fig. 3 The smoothed intensity profile is the result of applying the IMA algorithm (Section 2.1.2) on the intensity profile in Fig. 2 in one iteration. | ||
The image width M, the number of lanes L (including lanes with weak or no bands), and the approximate distance d (given by the user) between adjacent lanes give an approximate lane width LwIMA:
The size of the moving window initialized for the first iteration of the low pass filter W0, is computed as
| W0 = aLwIMA, a < 1 | (2) |
There is an analogy between the iterative moving average filter and the pyramid KNN smoothing presented by Mastin.16 The reason for applying an iterative moving average filter with an updated window size in each iteration is the unknown number of iterations needed to stop the filtering process.
The algorithm to perform the filtering process with the moving average filter is as follows:
1. Initialize the size of the window for the moving average filter: (Wn) for n = 0, as stated in eqn (2).
Compute the intensity profile P(eqn (1)) for the gel image.
2. Initialize Sn for n = 0, S0 = P. Where Sn will represent the filtered intensity profile regarding n iterations.
3. Run the moving average filter (Wn) (weight coefficients 1.0) on the profile Sn to compute Sn+1 which will be Sn+1 = WnSn. Increase the number of iterations by 1, (n = n + 1).
4. Count the number of minima NMin on the filtered intensity profile S, resulting from step 3.
5. Compare the number of lanes (L) with NMin in step 4. If NMin ≤ L, set P equal to the filtered profile S from step 3 and exit. Otherwise continue to step 6.
6. Update the size of the filter by: (Wn = aWn–1), and go back to step 3. The reason of reducing the filter size after each iteration is to keep the narrow peaks representing lanes with weak edges.
The first point in the image should be the approximated start of the first lane in the image and the image end point should be the end of the last lane in the image.
In the test images, scanned at 150 and 300 dpi, the distance between adjacent lanes varies and depends on the scanning resolution.
The IMA algorithm is sensitive to the parameter d since it is an approximation to the true distance. The number of lanes in a gel image should be accurate since it is easily obtained by counting the lanes, including the lanes with very weak or eventually no bands.
In some images, the IMA algorithm will not be able to detect all the lanes even with different values of d. This could be due to the high intensity contrast between the unidentified lane and its adjacent lanes, which makes the algorithm filter out the minimum corresponding to the lane that remains undetected.
The development of wavelet analysis began with Morlet.17 Wavelets are defined in reference to a kernel function ψ(x) of a real variable x. The kernel function ψ(x) is called “mother wavelet”. A mother wavelet can be used to generate modified functions which are called “daughter wavelets” by translation and scaling as shown in eqn (3),
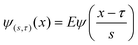 | (3) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) is the translation factor. The factor E is for energy normalization in different scales and will keep the energy of the daughter wavelets equal to the energy of the original mother wavelet.
is the translation factor. The factor E is for energy normalization in different scales and will keep the energy of the daughter wavelets equal to the energy of the original mother wavelet.
Applying this theory to the intensity profile from eqn (1), the number of lanes is the parameter to be used for choosing the scale of the wavelet coefficient that gives the desired frequency range.
In the case of lane position detection, the scale which isolates the correct details from a particular frequency band should be selected. For an orthogonal wavelet, we are limited to a discrete set of scales while for non-orthogonal wavelet analysis, we can use an arbitrary set of scales which is more appropriate in this case. The complex Morlet wavelet as defined in eqn (4), consists of a plane wave modulated by a Gaussian and is known to provide a better resolution than other wavelets,
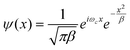 | (4) |
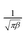 ensures that the wavelet has unit energy. In eqn (4), the variance will be set to β = 1 based on the arguments in ref. 18 about Morlet wavelet, and the center frequency is set to ωc = 5 based on the values proposed in refs 19,20.
ensures that the wavelet has unit energy. In eqn (4), the variance will be set to β = 1 based on the arguments in ref. 18 about Morlet wavelet, and the center frequency is set to ωc = 5 based on the values proposed in refs 19,20.
Based on this, only the real part of the Morlet wavelet in eqn (4) with the bandwidth β = 1 will be applied further in this work. By dilation with scale a and translation with b, a daughter wavelet acquired from the real part of the wavelet in eqn (4) is shown in the following equation
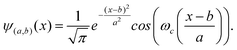 | (5) |
The flow chart of the CWT algorithm to detect the lanes in a gel image is illustrated in Fig. 4.
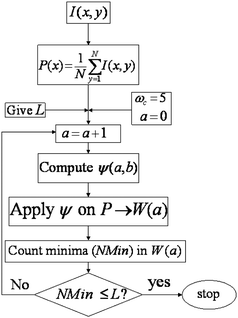 | ||
| Fig. 4 Flow chart of the CWT algorithm to detect the lanes in a gel image. | ||
The CWT method requires the number of lanes (L) in a gel image as the only input parameter. As we shall see later, the results obtained by CWT applied on 20 test images (totally 456 lanes) show a significant improvement in the detection of lanes in gel images (see Table 2), independent of image quality and resolution. Based on these experiments, the output of the CWT algorithm will be used as input to the lane separation methods in Section 2.2.
As an example, the positions of the lanes detected by applying the ES, IMA and CWT methods on the image in Fig. 1(b) are shown in Fig. 5. The magnified points between 350 and 580 of the signals in Fig. 5(b), (c) and (d) are shown in Fig. 6 to illustrate the false detected and undetected band positions with ES and IMA respectively.
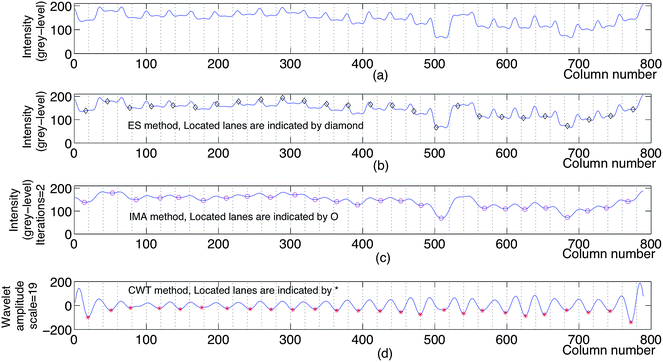 | ||
| Fig. 5 (a) The intensity profile obtained by applying the eqn (1) on a multilocus gel image (an image similar to the image in Fig. 1(b), not shown here). (b) The positions of the lanes detected by the ES method applied on the gel image. (c) The positions of the lanes detected by the IMA method applied on the intensity profile in (a). (d) The positions of the lanes detected by the CWT method applied on the intensity profile in (a). | ||
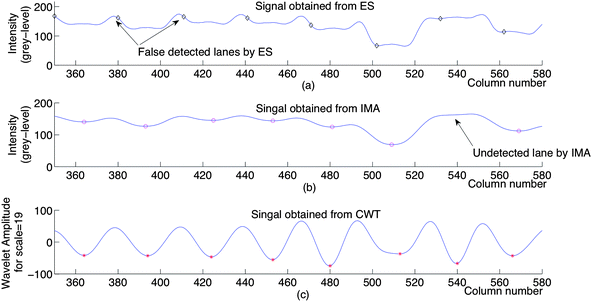 | ||
| Fig. 6 The points between 350 and 580 of the signals in Fig. 5(b), (c) and (d) magnified to illustrate the false detected and undetected band positions with ES, IMA and CWT respectively. | ||
2.2 Lane separation
In this section, two alternative techniques, K-neighbours and half width will be presented to estimate the boundaries of the lanes in a gel image. Once the positions of the minima corresponding to the lanes in a gel image are computed, lane boundaries can be estimated. The estimated lane boundaries will be used to separate the lanes from the gel image and generate a sub-image for each lane, where the intensity, position and width of the bands are preserved.To illustrate that a lane in a one dimensional gel image may be represented by K-neighbouring columns of its central part, a small part of an arbitrary lane containing three DNA bands shown in Fig. 7(a) will be analysed here. A two-sided variance (variances outward to the left and right sides of the center pixel in each band) is computed (as an increasing number of neighbouring pixels are included) from the lane center and outward on each row of a band, as shown in Fig. 7(b). Three, five and seven rows are included for the three bands, respectively. The resulting variance plots show the homogeneity of the central part on each row in the bands. Experiments on a number of DNA bands extracted from various gel images gave similar results.
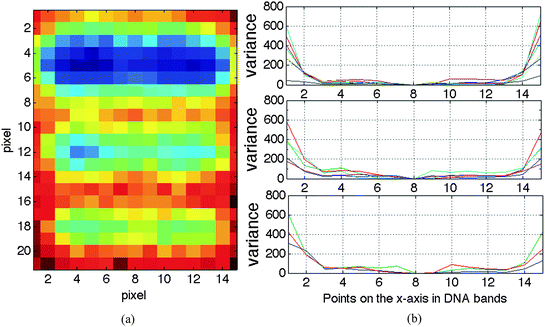 | ||
| Fig. 7 Illustration of the homogeneity in the central part of each row in DNA bands. (a) The image is extracted from a lane in a multi-locus gel image with 150 dpi. (b) Two-sided variance plots computed as an increasing number of neighbouring pixels are included. | ||
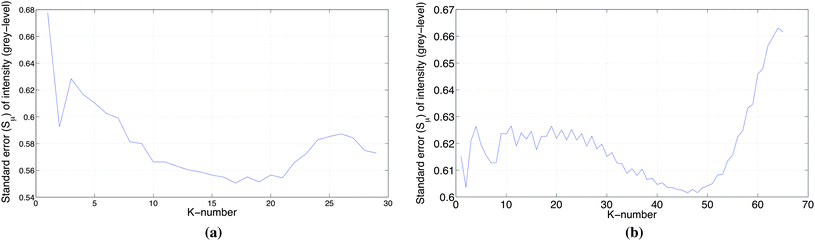
Assuming that lanes within a set of gel images of the same type and resolution have approximately the same width, the K-neighbours representation may be applied on all the lanes in the image set. To obtain the K-neighbours, we have analysed the standard errors (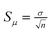 ) of the intensity, position and width of a peak as a function of K. For this, we have employed two sets of 20 bands of approximately the same type, in which the first set has been extracted from different lanes in a multi-locus gel image with a resolution of 150 dpi and the other set from a single-locus gel image with the resolution of 300 dpi. The results are illustrated in Fig. 8.
) of the intensity, position and width of a peak as a function of K. For this, we have employed two sets of 20 bands of approximately the same type, in which the first set has been extracted from different lanes in a multi-locus gel image with a resolution of 150 dpi and the other set from a single-locus gel image with the resolution of 300 dpi. The results are illustrated in Fig. 8.
 | ||
| Fig. 8 Standard error for peak intensity as a function of K-neighbours in a lane. The bands in this experiment have approximately the same intensity (light background) and size extracted from a gel image. (a) The results obtained using a set of 20 bands of approximately the same type, extracted from a multi-locus gel image with resolution of 150 dpi. (b) The results obtained using a set of 20 bands approximately the same type, extracted from a single-locus gel image with resolution of 300 dpi. | ||
The procedure to obtain a K-neighbours representation of a lane in a gel image could be as follows:
• The detected lane minima from applying the CWT on the projection P(x) of the image on the x-axis are used to compute the temporary lane boundaries with an arbitrary value of K-neighbours to the minima.
• Projecting the rows of the lane onto y-axis, the DNA bands of that lane are located by applying the MVR algorithm described in ref. 21 on the resulting intensity profile.
• A set of bands with approximately the same intensity and size are selected from different lanes in the image and the average standard errors for intensity, position and width of the selected bands are computed for a range of K-Values.
• The average standard error of intensity could then be employed to select new lane boundaries and the resulting value of K.
The minimum in the standard error of the peak intensity around 15 ≤ K ≤ 20 for the multi-locus image (Fig. 8(a)) corresponds to the homogeneous part of the two-sided variance plot of (Fig. 7(b)). This optimal range of K is supported by corresponding minima in plots of the standard error of peak position and peak width for the multi-locus image with a resolution of 150 dpi. For the single-locus image with a resolution of 300 dpi, the optimal range of K seems to be around 40 ≤ K ≤ 50, based on the standard error of peak intensity (Fig. 8(b)). In this case, the confirmation by the standard error of peak position and peak width are less clear.
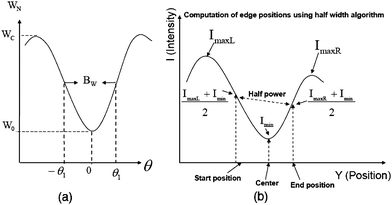 | ||
| Fig. 9 (a) Using the half power points to compute the half width of the signal. (b) Applying eqn (6) and eqn (7) with q = 2, outlined in Section 2.2.2 to compute the boundaries. | ||
For a non-symmetric signal (Fig. 9(b)), eqn (6) and eqn (7) can be used to compute the boundary intensity values for each lane in a gel image,
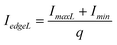 | (6) |
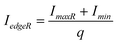 | (7) |
However, the boundary points of each lane can be moved toward the center of the lane by choosing q > 2. Increasing the value of q will result in a lane with smaller width and reducing the storage space. Applying q ≠ 2 will no longer result in the “half width” since the “power” is non-linear. This argument is in analogy to the choice of neighbouring columns in the central part of a lane outlined in Section 2.2.1. In a gel image, bands may exhibit deformations such as smiling or rotation along their main axis due to the electrical field, overloading,24 gel inhomogeneities, etc. The lane width of the separated lanes obtained by the half-width algorithm could be affected if deformations exhibited by the bands in a lane are significantly high. In such cases, the image should be geometrically corrected before the computation of intensity profile in eqn (1) and lane detection algorithms IMA and CWT. If the deformations are not significant, their effects on the lane width could be ignored since they are reduced due to the projection of the columns in the image onto the axis perpendicular to the lanes (eqn (1)).
3. Results
To evaluate the performance of the methods presented in this work, we have used 20 test images (totally 456 lanes) of both single- and multi-locus DNA, of various quality and resolution and with different number of lanes. The ES, IMA and the CWT methods are applied to detect the lane positions in each test image.The example shown in Fig. 5 indicates that the computed lane positions by the ES method requires manual adjustments before being employed as input to the K-neighbours algorithm, as well as additional filtering of the intensity profile, before being used as input to the half-width algorithm.
The computed lane positions by the CWT method may be employed directly as input to both K-neighbours and half-width lane separation algorithms. This could also be true for the lane positions obtained by the IMA method, if the image quality is good and the results are satisfactory. The test images have been arranged into two sets, as summarized in Table 1.
| Image set | No. of images | Total lanes | Resolution | |
|---|---|---|---|---|
| Multi-locus | Single-locus | |||
| First | 10 | 219 | 150 dpi | |
| Second | 10 | 237 | 300 dpi | |
It is worth mentioning that the multi-locus images in the first set are highly variable due to the noise, number of lanes and intensity of the bands in each lane, as well as non-uniform spacing between the lanes within and between images (see Fig. 1(a) as an example), while the single-locus images in the second set are similar to the image in Fig. 1(b) regarding the number of bands in each lane and spacing between the lanes. The results obtained by applying the ES, IMA, and CWT methods on each image set in Table 1 and the combination of both image sets are summarized in Table 2.
| Test images | Method | No. of Lanes | |||
|---|---|---|---|---|---|
| Correctly detected (TP) | False detected (FP) | Undetected (FN) | Between lanes (TN) | ||
| All images (20): | ES | 439 | 17 | 17 | 409 |
| multi-locus and single-locus | IMA | 417 | 8 | 39 | 428 |
| CWT | 450 | 6 | 6 | 430 | |
| Multi-locus images (10) | ES | 202 | 17 | 17 | 175 |
| IMA | 201 | 5 | 18 | 187 | |
| CWT | 218 | 1 | 1 | 191 | |
| Single-locus images (10) | ES | 237 | 0 | 0 | 227 |
| IMA | 216 | 3 | 21 | 224 | |
| CWT | 232 | 5 | 5 | 222 | |
An example of scoring the results in Table 2 is illustrated in Fig. 10, where the white vertical lines correspond to detected projection minima. Scoring of the results in Table 2 has been performed manually, because an automated method would require the true width of the lanes as a priori information.
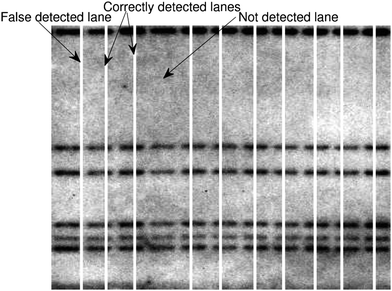 | ||
| Fig. 10 A section of a multi-locus image where its lanes are located by the IMA method (Section 2.1.2) is shown to illustrates the scoring results in Table 2. | ||
Results obtained by the lane detection algorithms applied on gel images where the lanes are significantly deformed and irregular would be strongly affected. The image in Fig. 11(a) where some lanes on the left side are significantly deformed and irregular illustrates this problem. The results obtained by applying the ES, IMA, and CWT methods on the image in Fig. 11(a) are shown in Fig. 11(b), Fig. 11(c), and Fig. 11(d) respectively. The white lines along the images indicate the lanes detected by each method. The first few lanes on the right side of the image are correctly detected by the CWT method, while the detected lanes on the left side are false due to the deformations. The importance of having better quality gel images could be seen by comparing the few correctly detected lanes on the right side in Fig. 11(d) with the falsely detected lanes on its left side. Although not shown here, problems with deformations, quality and irregularities in gel images could in principle be solved by applying methods such as geometrical correction and/or dividing the image into sections and analysing each section, prior to the lane detection.
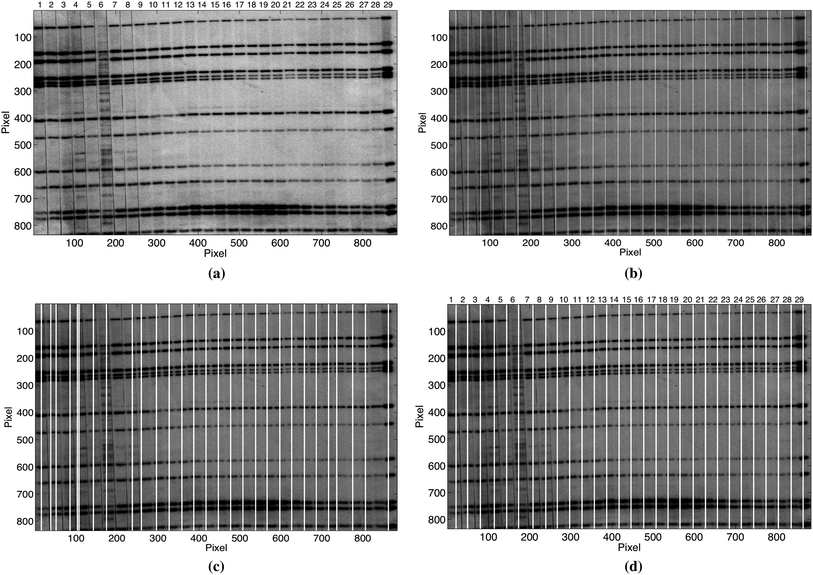 | ||
| Fig. 11 (a) Example of a gel image with significant deformations and irregularities. The results obtained by applying the ES, IMA, and CWT methods on the image in (a) are shown in (b), (c), and (d) respectively. White lines along the images in (b), (c) and (d) illustrate the detected lanes and the effect of deformations and irregularities in image in (a). | ||
The fraction of correctly detected lanes in the first image set was 92.24% with the ES, 91.78% with the IMA, and 99.54% with the CWT, while in the second image set it was 100.0% with the ES, 91.14% with the IMA, and 97.90% with the CWT.
The sensitivity of the ES, IMA and CWT methods applied on both image sets in Table 1 is shown in the ROC space (Receiver Operating Characteristic space, is a graphical plot of the true positive rate (sensitivity) versus the false positive rate (1-specificity). It has four classes: True Positive, False Positive, True Negative, False Negative. TPR = TP/(TP + FN), FPR = FP/(FP + TN)), illustrated in Fig. 12. For a better visualization of the data points, only the upper left hand corner of the ROC space is shown in Fig. 12.
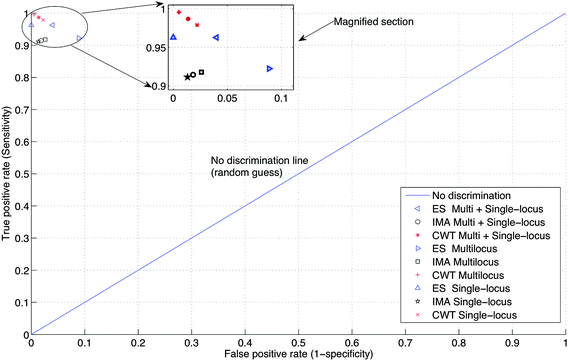 | ||
| Fig. 12 ROC space defined by TPR (sensitivity) against FPR (1-specificity). The upper left hand corner of the complete ROC space is shown for better visualization of the data points. | ||
In ROC space, the optimum values will be in the upper-left-hand corner. Fig. 12 indicates that the precision of locating the lanes by the ES method depends on the image type, where it is high for the single-locus images, but is relatively low for the multi-locus images and for all images as a whole. For the IMA method, the precision of locating the lanes is relatively low, but approximately the same for both image types. In the case of CWT, the precision of the lane location is relatively high, and approximately the same for both image types. Thus, for the image sets considered in this work, the performance of the CWT method is better than the ES and IMA methods.
Table 3 summarizes the accuracy (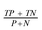 ) of the ES, IMA and CWT methods applied on both image sets and their combination. Based on the accuracy of the methods listed in Table 3, results obtained by the CWT method should be used as input to the lane separation algorithms described in Section 2.2.1 or Section 2.2.2.
) of the ES, IMA and CWT methods applied on both image sets and their combination. Based on the accuracy of the methods listed in Table 3, results obtained by the CWT method should be used as input to the lane separation algorithms described in Section 2.2.1 or Section 2.2.2.
| ES | IMA | CWT | |
|---|---|---|---|
| All images (20) | 96.1% | 94.7% | 98.7% |
| Multi-locus images (10) | 91.7% | 94.4% | 99.5% |
| Single-locus images (20) | 100.0% | 94.8% | 97.8% |
The lanes obtained by the separation methods outlined in Section 2.2.1 with K = 40 (based on the average standard error for the intensity shown in Fig. 8(b)) and Section 2.2.2 with q = 2, using the lane positions from applying the CWT method on the image in Fig. 1(b) are shown in Fig. 13(a) and 13(b) respectively. Separation of the lanes in a gel image and transferring each lane into a sub-image will reduce the storage space significantly. For example, the image size (with unsigned byte pixel) in Fig. 1(b) is 1857 × 1650 ≃ 2.93 Mb, with 24 lanes. Extracting the central part of the lanes using K-neighbours algorithm with K = 40, the storage space will be reduced by more than 50% to ≃1.51 Mb. The storage space saved by applying the separation method in Section 2.2.2 will depend on the width of the separated lanes.
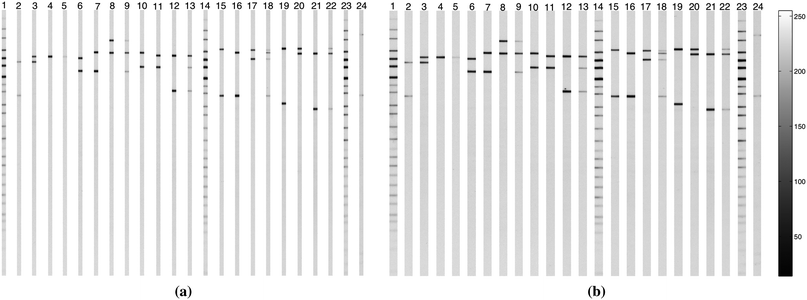 | ||
| Fig. 13 Applying the lane detection method described in Section 2.1.3 followed by the lane separation methods in Section 2.2 on the image in Fig. 1(b). (a) Separated lanes by using K-neighbours algorithm with K = 40. (b) Separated lanes by using the half-width algorithm with q = 2. | ||
Separated lanes from gel images which have been transferred into sub-images can be presented by an intensity profile analogous to the profiles produced by CE. The intensity profile for each lane can be obtained by applying the equivalent of eqn (1) to project the rows in the corresponding sub-image on the axis perpendicular to the band's major axis (y-axis). A common way of showing a lane is its intensity profile (electropherogram), which could be used in the quantitative evaluation of the bands' intensity.
A magnified section of the intensity profile corresponding to the first lane in Fig. 13(a) with q = 2 and (b) with K-neighbours where different values of K (K = 3, 40, 65) is shown in Fig. 14 to illustrate the effect of using different values of K-neighbours on the intensity profiles. We assume that the intensity profiles produced by applying the half-width algorithm with q = 2 on the sub-images corresponding to the separated lanes in a gel image represent the approximate true values of peak position and intensity of the DNA bands. Based on this assumption, using low values of K-neighbours (e.g. K = 3) will result in intensity profiles where the peak intensity and position of the DNA bands could be influenced by both additive and multiplicative noise.25 On the other hand, using high values of K-neighbours (e.g. K = 65) which include the edges of the lanes will reduce the peak intensity of the bands, whereas applying the K-neighbours within the range 40 ≤ K ≤ 50, as suggested in Section 2.2.1, will preserve the peak intensity and position as well as reduce the noise.
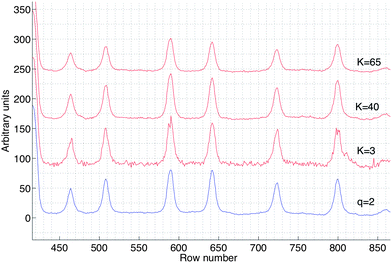 | ||
| Fig. 14 A magnified section of the intensity profiles corresponding to the first lane in Fig. 13(a) with q = 2 and (b) with K-neighbours where different values of K (K = 3, 40, 65) have been applied. | ||
When the profiles generated by CE and gel images are prepared using the same primer and converted into the MW domain,26 they may be stored in an appropriate database and used in analyses such as band comparison.
4. Discussion
To detect and analyse lanes in gel images, there are a number of image processing packages available. Based on the simplicity and performance, we have selected to implement and evaluate the lane detection method presented by Elder & Southern (ES) along with the new algorithms IMA and CWT presented in this work. In addition, two lane separation algorithms, K-neighbour and half-width have been presented. We have evaluated a total of 20 gel images – representing 10 multi- and 10 single-locus gels (Southern blots), as shown in Table 1 (and further “dessicated” in Table 2). The images are derived from different series of real experiments using DNA extracted from field collected mammals (moose and voles) and humans. Test images were chosen “randomly” to give a realistic and statistically sound data collection in the analyses. As can be seen in Fig. 11 bands were distorted (irregular) in several ways; uneven intensities, uneven migration, and variation of intensities within a single band.The performance of the ES method depends on the equispacing criterion. The IMA is sensitive to the parameter d and therefore it may fail to locate all lanes in a gel image. The CWT method performs significantly better and is less sensitive to noise and image quality. Using the K-neighbour algorithm to separate the detected lanes requires an optimal K value, while the half-width algorithm with q = 2 will give approximately true value for lane width. Each separated lane is transferred into sub-image and then into a one dimensional profile. Peak positions in one dimensional profiles can be transferred into molecular weight domain using the included standard markers in the corresponding gel image. The resulting one dimensional profiles and their corresponding computed molecular weights could be saved and managed in a proper database. Despite the ongoing and fast development of new protein, RNA and DNA separation techniques as well as new (high throughput) DNA sequencing27,28 and microarray29,30 techniques, one dimensional gel separation is still a major tool for a great deal of applications – such as clinical and microbial diagnostics, forensic medicine, tissue typing and food safety to mention some. Although methods exist for image analysis of gels, very often gels are analysed by manual and non-standardized visual inspection. There is therefore a need for fast, simple and accurate methods for automatic gel and band analyses. On the other hand, CE and lab-on-a-chip methods – generating intensity profiles rather than images – are becoming increasingly important. Our method allows a simple and accurate transformation of gel images into intensity profiles – in principle directly comparable to the CE and chip intensity profile data. Furthermore, since gel images take up a considerable storage space, conversion to intensity profiles is very convenient – and absolutely required in most high throughput analyses such as microarrays and second generation sequencing. Although not directly investigated here the approach we have taken is likely to be applicable for high throughput methods as well.
5. Acknowledgments
We are grateful to Nils C. Stenseth (CEES), John E. Stacy (Department of Biology, University of Oslo, Norway) and the Forensic Medicine Laboratory for their help and support in addition to the production of gel images. We are also grateful to Jan T. Lifjeld (Natural History Museum, University of Oslo, Norway) for fruitful discussions about CE profiles. The authors would like to thank Jayne Lambrou (CEES), for reading and commenting on this manuscript. We would also thank the anonymous reviewers for helpful comments.References
- A. J. Jeffreys, M. Thurner and P. Debenham, The efficiency of multilocus DNA fingerprint probes for individualization and establishment of family relationships, determined from extensive casework, Am. J. Hum. Genet., 1991, 48, 824–840 CAS.
- J. E. Stacy, U. H. Refseth, M. Thoresen, R. A. Ims, N. C. Stenseth and K. S. Jakobsen, Genetic variability among root voles (Microtus oeconomus) from different geographic regions: populations can be distinguished by DNA fingerprinting, Biol. J. Linn. Soc., 1994, 52, 273–286 Search PubMed.
- T. M. Gabrielsen, K. Bachmann, K. S. Jakobsen and C. Brochmann, Glacial survival does not matter: RAPD phylogeography of Nordic Saxifraga oppositifolia, Mol. Ecol., 1997, 6, 831–842 CrossRef CAS.
- U. H. Refseth, C. L. Nesbø, J. E. Stacy, L. A. Vøllestad, E. Fjeld and K. S. Jakobsen, Genetic evidence for different migration routes of freshwater fish into Norway revealed by analysis of current perch (Perca fluviatilis) populations in Scandinavia, Mol. Ecol., 1998, 7, 1015–1027 CrossRef CAS.
- B.-E. Sæther, E. J. Solberg, M. Heim, J. E. Stacy, K. S. Jakobsen and R. Olstad, Offspring sex ratio in moose Alces alces in relation to paternal age: an experiment, Wildlife Biol., 2004, 10, 51–57 Search PubMed.
- J. Pizzonia, Electrophoresis Gel Image Processing and Analysis Using the KODAK 1D Software, BioTechniques, 2001, 30, 1316–1320 CAS.
- Image – The fingerprint image analysis system, http://www.sanger.ac.uk/Software/Image.
- T. A. Ferreira and W. Rasband, The ImageJ User Guide (http://rsbweb.nih.gov/ij/docs/user-guide.pdf), April 2010, pp. 139–140 Search PubMed.
- A. M. C. Machado, M. F. M. Campos, A. M. Siqueira and O. S. F. De Carvalho, An iterative algorithm for segmenting lanes in gel electrophoresis images, Computer Graphics and Image Processing, IEEE Proceedings, X Brazilian Symposium, Oct. 1997, pp. 140–146 Search PubMed.
- V. S. António, L. A. Rui, A. M. Mendonça and C. C. Aurólio, Automatic Lane and Band Detection in Images of Thin Layer Chromatography, Image Analysis and Recognition, International Conference, ICIAR 2004, Porto, Portugal, Sep. 29–Oct. 1 2004, Proceedings, Part II, pp. 158–165 Search PubMed.
- J. K. Elder and E. M. Southern, Computer-aided analysis of one-dimensional restriction fragment gels, in Nucleic acid and protein sequence analysis, ed. M. J. Bishop and C. J. Rawlings, IRL Press 1987, pp. 165–172 Search PubMed.
- J. K. Elder, D. K. Green and E. M. Southern, Automatic reading of DNA sequencing gel autoradiographs using a large format digital scanner, Nucleic Acids Res., 1986, 14(1), 417–424 CrossRef CAS.
- W. Niblack, An Introduction to Digital Image Processing, Printice Hall International (UK) Ltd., 3rd edn, 1986.
- The MathWorks™, http://www.mathworks.com/.
- A. Akbari, F. Albregtsen and O. C. Lingejaerde, Adaptive weighted least squares method for the estimation of DNA fragment lengths from agarose gels, Electrophoresis, 2002, 23(2), 176–181 CrossRef CAS.
- G. A. Mastin, Adaptive filters for digital image noise smoothing: An evaluation, Computer Vision Graphics and Image Processing, 1985, 31, 103–121 Search PubMed.
- J. Morlet, Sampling theory and wave propagation, in NATO ASI Series, Issues in Acoustic Signal/Image Processing and Recognition, Ed. C. Chen, Springer, 1983, pp. 233–261 Search PubMed.
- A. Teolis, Computational signal processing with wavelets, Birkhäuser, 1998, pp. 59–88 Search PubMed.
- I. Daubechies, Ten Lectures on Wavelets, CBMS-NSF, SIAM, Philadelphia, 1992 Search PubMed.
- P. Goupillaud, A. Grossmann and J. Morlet, Cycle-octave and related transforms in seismic signal analysis, Geoexploration, 1984, 23, 85–102 CrossRef.
- A. Akbari and F. Albregtsen, Automatic segmentation of DNA bands in one dimensional gel images produced by hybridyzing tecchniques, Proceedings of the 26th Annual International Conference of the IEEE EMBS, San Francisco, CA, USA, September, 2004, pp. 2852–2855 Search PubMed.
- A. V. Oppenheim, A. S. Willsky and I. T. Young, Signals and Systems, Prentice Hall International Inc., 1983, pp. 277–278 Search PubMed.
- M. B. Priestley, Spectral Analysis and Time Series, Probability and Mathematical Statistics, Academic Press, London, England, 1989, pp. 517–528 Search PubMed.
- P. Gill, I. W. Evett, S. Woodroffe, J. E. Lygo, E. Millicam and M. Webster, Databases, quality control and interpretation of DNA profiling in the Home Office Forensic Science Service, Electrophoresis, 1991, 12, 204–209 CAS.
- A. Akbari and F. Albregtsen, Evaluation of noise in DNA fingerprint images produced by hybridization techniques, Proceedings of the 6th Nordic Signal Processing Symposium, NORSIG-2004, Espoo, Finland, June 2004, pp. 61–64 Search PubMed.
- A. Akbari, G. Marthinsen, J. T. Lifjeld, F. Albregtsen, L. Wennerberg, N. C. Stenseth and K. S. Jakobsen, Improved DNA fragment length estimation in capillary electrophoresis, Electrophoresis, 2008, 29(6), 1273–1285 CrossRef CAS.
- M. Ronaghi, M. Uhlen and P. Nyren, A sequencing method based on real-time pyrophosphate, Science, 1998, 281, 363–365 CrossRef CAS.
- A. Ahmadian, B. Gharizadeh, A. C. Gustafsson, F. Sterky, P. Nyren, M. Uhlen and J. Lundeberg, Single-nucleotide polymorphism analysis by pyrosequencing, Anal. Biochem., 2000, 280, 103–110 CrossRef CAS.
- D. V. Nguyen, A. B. Arpat, N. Wang and R. J. Carroll, DNA microarray experiments: biological and technological aspects, Biometrics, 2002, 58(4), 701–17 CrossRef.
- T. Wilkes, H. Laux and C. A. Foy, Microarray data quality – review of current developments, OMICS, 2007, 11(1), 1–13 CrossRef CAS.
Footnote |
| † Images in this work were partly provided by the Department of Biology, and partly by the Institute of Forensic Medicine, University of Oslo, Norway. |
| This journal is © The Royal Society of Chemistry 2010 |