Laser induced breakdown spectroscopy for rapid identification of different types of paper for forensic application
Arnab
Sarkar
,
Suresh K.
Aggarwal
* and
D.
Alamelu
Fuel Chemistry Division, Bhabha Atomic Research Centre, Trombay, Mumbai, 400 085, India. E-mail: skaggr@barc.gov.in; skaggr2002@rediffmail.com; Fax: +91-22-25505151; Tel: +91-22-25593740
First published on 11th November 2009
Abstract
The goal of this work was to examine the probability of instant identification of confidential documents for forensic application by comparison with a spectral library generated using laser induced breakdown spectroscopy (LIBS). The library consisted of representative spectra from different types of papers used for official (governmental) work. Statistical methods using linear and rank correlations were applied to identify the unknown paper. Both correlation methods yielded probabilities of correct identification close to unity for all the studied samples. The approach would have applications in forensic science.
1. Introduction
Identification of documents of various qualities, forms and sizes (e.g. will paper, badges, passports, credit cards etc.) is required for various applications. Examples of documents forged include driver permits, cheques, health care cards for accessing expensive medical services from hospitals and physicians, passports for illegal entry into countries and partial tampering of will paper or “last-wish” paper. Recent advances in desk-top publishing equipment and color copiers pose an increasing threat to the security of these documents.In governmental confidential documents, replacing one of the pages of the document is the easiest forgery case. Currently, important government documents rely on special paper, ink and water marking to prevent forgery. The elemental profile of paper of the same quality varies from company to company and even with the time of production. This is because of variation in the soil quality as well as environment in the forests from where trees are used by the paper producing company. During confidential document printing, all the pages will generally belong to paper from a single company and same production time. Hence if a few particular pages are replaced by the forger at a later stage, it should be possible to identify the forgery by elemental profiling. Neutron activation analysis (NAA) has been used to obtain elemental profiling.1 Laser induced breakdown spectroscopy (LIBS) is a promising alternative technique for rapid identification of forged document instead of NAA which is time consuming and depends upon the availability of a nuclear reactor or a neutron source.
Gornushkin et al.2,3 have shown that simple statistical correlation methods, such as linear and rank correlations, can be successfully applied for the identification of solid and particulate materials without trace or bulk quantifications. A near 100% reliable identification was achieved based on the use of thousands of data points (pixels) representing the sample spectrum in a relatively large spectral window. Anzano et al.4 employed this methodology for characterization of post-consumer commercial plastic waste widely used for household and industrial purposes. Jurado-López et al.5 used a rank correlation method for the rapid identification of alloys used in the manufacture of jewellery. Mateo et al.6 showed the capability of linear correlation method for depth profiling by LIBS. Rodriguez-Celis et al.7 compared glass spectra from car windows using linear and rank correlation methods and showed effective discrimination at a 95% confidence level. In this paper, we demonstrate the application of parametric (linear) and non-parametric (rank) correlations for identification of several confidential papers using LIBS.
2. Experimental
2.1. Materials
The paper samples used in the present work were those used for Yearly Confidential Report (YCR) writing in the Department of Atomic Energy (DAE), India. YCR paper pages were collected for the last 10 years (1999–2008) for analysis. The pages were initially classified according to the year of YCR writing. Among the YCR writing pages of a particular year, some contained watermarks, which were different for different years. Those pages which contained watermark were used as library samples for the particular year printed on it and the rest of the pages of that particular year without watermark were used as unknown. Tables 1 and 2 gives details of the paper used for generating a library and used as unknown samples.| Sample No. | Year of use | Watermark |
|---|---|---|
| L1 | 1999 | RAJAMANI |
| L2 | 2000 | CARD |
| L3 | 2001 | SYMBOLIC |
| L4 | 2002 | ASHOK |
| L5 | 2003 | BALLARPURI |
| L6 | 2004 | CENPULP |
| L7 | 2005 | ANDHRA |
| L8 | 2006 | SIRPUR |
| L9 | 2007 | SIMPLEX LEDGER |
| L10 | 2008 | SUDARSHAN CHKRA |
| Sample No. | Year of use |
|---|---|
| X1 | 1999 |
| X2 | 2000 |
| X3 | 2001 |
| X4 | 2002 |
| X5 | 2003 |
| X6 | 2004 |
| X7 | 2005 |
| X8 | 2006 |
| X9 | 2007 |
| X10 | 2008 |
2.2. Instrumentation
The equipment used for the experiment has been described in detail previously.8,9 Spectrolaser 1000M, from M/s. Laser Analysis Technologies Pvt. Ltd. (now known as XRF Scientific), Victoria, Australia was used. The instrument is an integrated analysis system comprising of a high power Q-switched Nd:YAG laser which yields upto 200 mJ of pulse energy at the fundamental wavelength of 1064 nm in a 7 ns pulse-width with a repetition rate of 10 Hz. The laser pulse is focused onto the sample by a plano-convex lens having a focal length of 5 cm. The laser spot area is estimated to be 1.96 × 10−7 m2. The sample is located on a fast XY-translational stage, which moves the sample between two successive laser pulses, exposing a new and fresh region of the sample for analysis. The radiated emission from the laser induced plasma is focused to an end of a fiber optic fiber (core diameter 200 µm) having a collimating lens (0–45° field of view) placed at an angle of 45° to the direction of the plasma expansion, which carries the emission light to the entrance slit of spectrographs in Czerny–Turner (C–T) configuration. Four separate optical cables connected to four separate spectrographs are present in the instrument and these are individually calibrated for specific wavelength range, 180–320 nm, 320–460 nm, 460–620 nm and 620–850 nm, giving a total spectral range coverage of 180–850 nm.2.3. Sample preparation
A little sample preparation was necessary; the results are increased throughput and greater convenience. The papers were cut into small circles (diameter ∼3 cm) which were placed on a double-sided tape stuck to a glass slide which was placed in the sample holder. Care was taken so that the piece of paper was firmly stuck to the slide in order to avoid any air gap between them.2.4. LIBS spectral library
A library of LIBS spectra from 10 different papers was generated for identification of different YCR papers having no watermark. The library spectrum of YCR paper was obtained by performing LIBS on 10 different pieces of paper, obtained by cutting the particular paper at random positions. The spectra were obtained by averaging 10 laser shots spectra with laser energy of 50 mJ (i.e. irradiance of 3.6 GW/cm2), acquisition delay of 2 µs and a repetition rate of 1 Hz. These 10 spectra were averaged to construct the library spectrum for that particular YCR paper. All spectra were stored in a computer and used on a day-to-day basis without renewing. It was found that the last two channels of CCDs (460–620 nm and 620–850 nm) do not provide much of the elemental information except for C2 swan-bands and Na doublet at 588 nm. Hence these were not included in generation of the library. Gornushkin et al10 have shown that masking of the spectrum in correlation analysis improves the analytical result, but in our case it was not considered as it makes the method time consuming, and our aim was to develop a rapid method for identification.For each of the unknown paper samples, similar to the library samples, LIBS spectra were recorded on 10 different pieces of paper, obtained by cutting each unknown YCR paper at random positions.
An inbuilt program for correlation analysis in Microsoft Excel 2003 was used for computation of correlation coefficients between the LIBS spectrum of unknown and library spectra.
3. Results & discussion
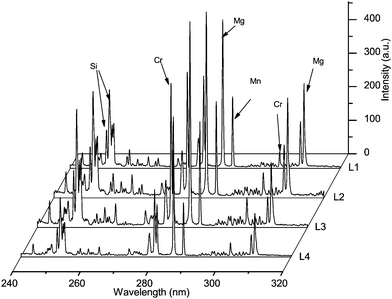
Paper when exposed to intense laser radiation sufficient for breakdown produced atomization of all the elements present. From the produced plasma, emission lines were recorded. A part of the spectra obtained by LIBS for library papers (L1, L2, L3 and L4) are shown in Fig. 1. The spectra are almost identical, since the main matrix composition is the same for all papers, suggesting the need to use powerful statistical methods for detection of the very small differences present in the paper materials. It is a Departmental policy of DAE to purchase fresh YCR paper in bulk every year preferably from a different supplier to minimize the possibility of forging. It is known that the geographical origin of raw material for paper production has sufficient effect on trace profiling of paper materials, thereby generating different spectral patterns in LIBS. The YCR papers are stored in both pre- and post-used stages in ambient conditions to avoid any unnecessary contamination.Each channel consisted of 2048 pixels. Hence from two channels, 4096 data points were available, which are enough to permit statistical analysis like linear correlation and non-parametric rank correlation. Linear correlation measures the similarity in trend and the correlation coefficient “r” is expressed as,
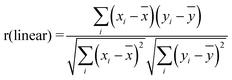 | (1) |
![[x with combining macron]](https://www.rsc.org/images/entities/char_0078_0304.gif) is the mean of xi's, and ȳ is the mean of yi's. The value of “r” lies between −1 and 1; r = 1 corresponds to complete positive correlation. Non-parametric rank correlation coefficient is another statistical approach which shows the similarity of the measurements. The equation for non-parametric rank correlation is the same as eqn (1) with x and y replacing their corresponding ranks R's and S's, respectively:
is the mean of xi's, and ȳ is the mean of yi's. The value of “r” lies between −1 and 1; r = 1 corresponds to complete positive correlation. Non-parametric rank correlation coefficient is another statistical approach which shows the similarity of the measurements. The equation for non-parametric rank correlation is the same as eqn (1) with x and y replacing their corresponding ranks R's and S's, respectively: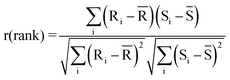 | (2) |
As before, xi (or its corresponding rank Ri) stands for the intensity of light detected by pixel i in the detector spectrum for stored library YCR paper, whereas yi (or its corresponding rank Si) stands for the intensity at the same pixel i of the unknown spectrum. The ranks are numbers 1, 2, 3, …, N, where N is the total number of data points (or pixels in the present case, 4096), which replaces the true values of x and y in accordance with their magnitudes. For example, the most intense pixel in the spectrum obtained in the present study was assigned the number 4096 with number 1 assigned to the least intense pixel, i.e., the rank increases with increase in intensity. It is important to emphasize that if a correlation is proven non-parametrically, then it really exists.11
We applied both the correlation methods for the identification of the unknown YCR papers. Typical correlation plots for the above mentioned two correlation methods are shown in Fig. 2. All the 10 LIBS spectra of each of the 10 unknown YCR papers were correlated with 10 library spectra and the average correlation coefficient values are shown in Fig. 3a for linear correlation and in Fig. 3b for rank correlation. Table 3 shows results obtained when library paper L4 was linearly correlated with spectra of unknown YCR papers X1, X2, X3 and X4. From Figs. 3(a) and (b), it is clear that the identical pair of samples are (L1–X1), (L2–X2), (L3–X3), (L4–X4), (L5–X5), (L6–X6), (L7–X7), (L8–X8), (L9–X9) and (L10–X10). From Tables 1 and 2, it is evident that the observed identical pair of paper actually belongs to the same year YCR paper branch, i.e., 100% identification is achieved.
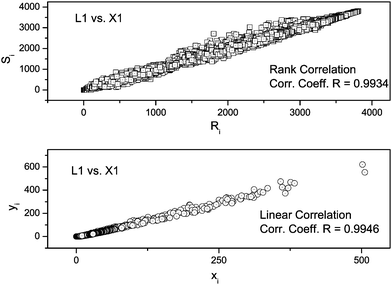 | ||
| Fig. 2 Linear and rank correlation plots for the sample LI (library) vs. unknown X1. | ||
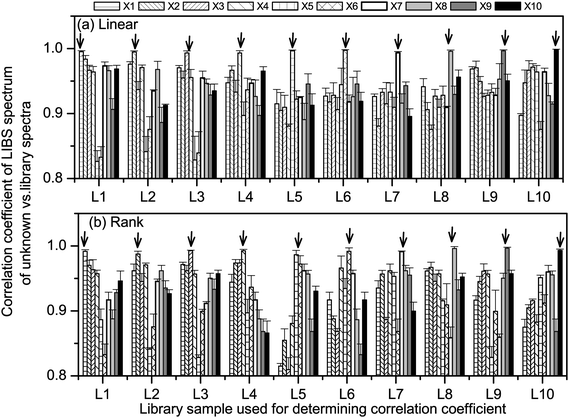 | ||
| Fig. 3 Linear (a) and rank (b) correlation coefficients for the YCR papers. Arrows indicate samples showing the best correlation coefficients. If identification is correct, the indicated sample is the same as the library sample given on the x-axis. | ||
| Sample No. | Linear correlation coefficient (r) | |||
|---|---|---|---|---|
| L4 vs. X1 | L4 vs. X2 | L4 vs. X3 | L4 vs. X4 | |
| 1 | 0.9642 | 0.9683 | 0.9629 | 0.9901 |
| 2 | 0.9517 | 0.9696 | 0.9497 | 0.9956 |
| 3 | 0.9388 | 0.9693 | 0.9515 | 0.9934 |
| 4 | 0.9396 | 0.9617 | 0.9473 | 0.9938 |
| 5 | 0.9441 | 0.9682 | 0.9277 | 0.9962 |
| 6 | 0.9550 | 0.9658 | 0.9248 | 0.9941 |
| 7 | 0.9414 | 0.9539 | 0.8997 | 0.9948 |
| 8 | 0.9381 | 0.9781 | 0.9318 | 0.9836 |
| 9 | 0.9488 | 0.9732 | 0.9185 | 0.9959 |
| 10 | 0.9539 | 0.9592 | 0.9230 | 0.9944 |
| Mean | 0.9476 | 0.9667 | 0.9337 | 0.9932 |
| Standard deviation | 0.0086 | 0.0070 | 0.0190 | 0.0038 |
Apart from the difference in the average values of correlation coefficients, other statistical tests were also performed. Initially an F-test was done between the distributions of correlation coefficient values and the significance of the F-test was calculated. When the calculated significance of F was less than 0.1, the difference in variances was considered as significant and the Student t-test was applied assuming unequal variance from which the probability that two distributions of correlation coefficients had different means was calculated. For the other scenario, the Student's t-test was performed assuming equal variance performed. Tables 4 and 5 show the probability of the two distributions of correlation coefficients had different means.
| Unknown paper samples↓ | Library paper sample → | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | L10 | |
| X1 | 0 | 0.9998 | 1 | 1 | 1 | 1 | 0.9997 | 1 | 1 | 1 |
| X2 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| X3 | 1 | 1 | 0 | 1 | 0.9999 | 1 | 1 | 1 | 0.9999 | 1 |
| X4 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0.9998 | 1 | 1 |
| X5 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| X6 | 1 | 1 | 0.9997 | 1 | 1 | 0 | 1 | 1 | 1 | 0.9998 |
| X7 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| X8 | 1 | 1 | 1 | 0.9998 | 1 | 1 | 1 | 0 | 1 | 1 |
| X9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| X10 | 0.9997 | 1 | 1 | 1 | 1 | 0.9996 | 1 | 1 | 1 | 0 |
| Unknown paper samples ↓ | Library paper sample → | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | L10 | |
| X1 | 0 | 1 | 0.9999 | 1 | 0.9999 | 1 | 0.9999 | 1 | 0.9999 | 0.9999 |
| X2 | 1 | 0 | 0.9963 | 1 | 0.9963 | 0.9963 | 0.9963 | 0.9963 | 1 | 1 |
| X3 | 1 | 0.9998 | 0 | 0.9995 | 1 | 1 | 1 | 1 | 1 | 1 |
| X4 | 0.9999 | 1 | 1 | 0 | 0.9999 | 0.9999 | 1 | 1 | 0.9999 | 1 |
| X5 | 1 | 1 | 1 | 1 | 0 | 0.9963 | 0.9963 | 0.9963 | 0.9963 | 0.9963 |
| X6 | 1 | 0.9999 | 1 | 0.9999 | 1 | 0 | 1 | 1 | 1 | 1 |
| X7 | 0.9963 | 1 | 0.9963 | 1 | 0.9999 | 1 | 0 | 0.9999 | 1 | 0.9979 |
| X8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0.9963 | 0.9963 |
| X9 | 1 | 0.9999 | 0.9999 | 0.9999 | 1 | 0.9963 | 0.9999 | 1 | 0 | 1 |
| X10 | 0.9963 | 0.9963 | 0.9963 | 1 | 0.9999 | 1 | 0.9963 | 0.9999 | 1 | 0 |
The diagonal elements in Table 4 correspond to the correlation (using linear correlation coefficient) of the sample with itself, all exhibiting a zero probability of difference. The same is also given in Table 5 using rank correlation coefficient. All the probabilities given in Tables 4 and 5 as 1.0, differ from 1.0 by a negligibly small value, less than 10−8. As can be seen from Tables 4 and 5, almost 100% matching is achieved using both the linear and rank correlations. It is well known that if a correlation is proven non-parametrically, i.e., by rank correlation, then it really exists.11 For the application and methodology discussed in this work, there was no significant difference between the two approaches i.e. linear and rank correlation.
4. Conclusion
Laser-induced breakdown spectroscopy methodology has been developed for instant reliable classification of different types of paper materials by using statistical correlation analysis. Linear and non-parametric (rank) correlations were both used for classification of spectral data with approximately the same results. The robustness of the technique was demonstrated by the near 99% reliable identification of almost all the analyzed papers. The most attractive features of the technique are its simplicity, non-destructiveness, low cost and a good potential for identification of various kinds of paper, provided that the spectral library is available for the same variety of papers. The analysis time is minimal (about a few minutes) and the technique has excellent potential for on-line, real-time forensic analysis.Acknowledgements
The authors are thankful to Dr. V. Venugopal, Director, Radiochemistry and Isotope Group, B.A.R.C. for his constant support and encouragement in LIBS work.References
- N. D. Chattopadhyay, A. K. Basu, A. B. R. Tripathi, C. A. Bhadkambekar and S. K. Shukla, Proceedings of DAE –BRNS discussion meeting on current trends and future perspective of neutron activation analysis (CFNAA), BARC, India, 2006, pp. 137 Search PubMed.
- I. B. Gornushkin, A. Ruoaz-Medina, J. M. Anzano, B. W. Smith and J. D. Winefordner, J. Anal. At. Spectrom., 2000, 15, 581–586 RSC.
- I. B. Gornushkin, B. W. Smith, H. Nasajpour and J. D. Winefordner, Anal. Chem., 1999, 71, 5157–5164 CrossRef CAS.
- Jesús Anzano, María-Esther Casanova, María-Soledad Bermúdez and Roberto-Jesús Lasheras, Polym. Test., 2006, 25, 623–627 CrossRef CAS.
- A. Jurado-López and M. D. Luque de Castro, Spectrochim. Acta, Part B, 2003, 58, 1291–1299 CrossRef.
- M. P. Mateo, G. Nicolas, V. Pinon and A. Yanez, Surf. Interface Anal., 2006, 38, 941–948 CrossRef CAS.
- E. M. Rodriguez-Celis, I. B. Gornushkin, U. M. Heitmann, J. R. Almirall, B. W. Smith, J. D. Winefordner and N. Omenetto, Anal. Bioanal. Chem., 2008, 391, 1961–1968 CrossRef CAS.
- A. Sarkar, D. Alamelu and S. K. Aggarwal, Appl. Opt., 2008, 47, G58–G64 CrossRef CAS.
- A. Sarkar, D. Alamelu and S. K. Aggarwal, J. Nucl. Mater., 2009, 384, 158–16 CrossRef CAS.
- I. B. Gornushkin, U. Panne and J. D. Winefordner, Spectrochim. Acta, Part B, 2009, 64, 1040–1047 CrossRef CAS.
- W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical Recipes: the Art of Scientific Computing, Cambridge University Press, New York, 1986, pp. 381–497 Search PubMed.
| This journal is © The Royal Society of Chemistry 2010 |