Some thoughts on superhydrophobic wetting

Abstract

Surface roughness has a profound influence on the wetting properties of a material. This fact is especially true with respect to the wetting of superhydrophobic surfaces. As a result of a special surface structure, a drop of water brought into contact with such a material forms an almost perfect sphere and even a very slight tilting of the superhydrophobic object is sufficient to cause the drop to roll off. For the description of the behavior of drops on rough surfaces two theories, namely those of Cassie and Wenzel, are often employed. However, it is currently becoming well established that both models explain the wetting behavior more from a qualitative or practical point of view rather than giving a quantitative description. For a prediction of actual contact angles, a more complex description is required that, next to thermodynamics, takes into account the kinetics of wetting. In this article, we focus on a few key aspects of superhydrophobic wetting, namely the characterization of superhydrophobic surfaces, models for the movement of drops, transitions between the Cassie and Wenzel states, and the behavior of superhydrophobic materials under condensation.

---

Christian Dorrer

Christian Dorrer holds a diploma in microsystems engineering. He recently completed his PhD work at Freiburg's Institute of Microsystems Technology, under the guidance of Prof. Jürgen Rühe. He is now with sensor company Robert-Bosch GmbH, Stuttgart. Dorrer's research interests include wetting and condensation as well as the modelling and experimental characterization of microfluidic and lab-on-a-chip systems.

Jürgen Rühe

In 1999, Jürgen Rühe accepted a professor position at IMTEK, University of Freiburg, where he heads the Laboratory for Chemistry and Physics of Interfaces. His research interests include the generation of tailor-made surfaces and micro- and nanostructured thin films, and the application of such surfaces in microsystems engineering, especially for chip-based bioanalytical devices.

---

Introduction

The wettability, that is, how liquids behave on a surface, is one of the fundamental properties of every solid and, thus, important for a wide range of natural systems as well as in many technical applications. As far as the latter are concerned, wetting phenomena for instance play a role in the painting and coating industries or when designing windshields, waterproof clothing and other consumer products. In microengineering, surface tension effects govern the spreading of resists on silicon wafers, control glueing and soldering processes, influence the movement of liquids in microfluidic channels and lab-on-a-chip systems, and may be used for microfabrication by fluidic self-assembly.^1–5

From a theoretical point of view, Young's equation, formulated around 200 years ago,⁶ remains the fundamental equation in the science of wetting. Assuming an ideal solid surface, it relates the contact angle of a drop on a surface to the specific energies of the solid–gas, the liquid–gas, and the solid–liquid interfaces.^6,7 From Young's equation, the spectrum of possible contact angles ranges from 0° (complete wetting or superwetting) to 180° (complete dewetting).

One aspect of wetting—situated at the hydrophobic extreme of the above wettability spectrum—that has recently received considerable scientific interest is superhydrophobicity (sometimes called ultrahydrophobicity).^8–16 Drops that come into contact with a superhydrophobic material retain a nearly spherical shape, with the contact angles in general larger than 150° and close to 180° in some cases.^8,17 A high drop mobility is a second important characteristic of a superhydrophobic surface:^11,18 due to greatly decreased contact angle hysteresis, drops easily move around even if only very small forces are applied, such as by slightly tilting the substrates or blowing gently across the surfaces. Superhydrophobic properties lead to an interesting side-effect: if water drops are brought onto a superhydrophobic material as, for example, rain or by spraying, the moving drops pick up and thus remove dust and dirt particles that loosely adhere to the substrate. Such “self-cleaning” properties could be interesting for a variety of applications: examples are non-soiling clothing or wall paints, but also other self-cleaning structures such as windows or satellite dishes. Above, we have placed the term “self-cleaning” in quotation marks to point out that, in a strict view, this notation is not fully correct: as has been remarked, it is of course the water that performs the cleaning and not the surface by itself.^19,20 Further applications of ultra-water-repellent materials include microfluidic systems, where superhydrophobic surfaces could for instance be used for the reduction of drag in microchannels.^2,8,9,19,20

From various natural materials, superhydrophobicity has been a well-known phenomenon for thousands of years. The lotus leaf, to give just one prominent example, is a traditional symbol of purity in buddhist societies because it repels dirt and mud (Fig. 1a).²¹ In a pioneering study, biologists Neinhuis and Barthlott performed electron microscopy studies of the leaf, linking its water-repellent properties to the pronounced roughness of the leaf's surface and coining the term “lotus effect”.^22,23 However, it is important to note that superhydrophobicity is not a curiosity resticted to the lotus leaf alone, but actually fairly common in nature: numerous other plant species exhibit similar characteristics,^22–24 among them the lady's mantle (Fig. 1b). Also, many animals are equipped with superhydrophobic body parts:^25–29 the Stenocara beetle, for instance, holds a structured superhydrophobic back into the Namib desert's morning wind to collect drinking water it cannot otherwise obtain in its extremely arid habitat (Fig. 1c).²⁵ The water strider would drown pitifully were it not for its superhydrophobic legs (Fig. 1d).¹³ The wings of many butterflies have superhydrophobic properties because capillary forces would otherwise cause them to stick together and prevent the animals from taking to the air (Fig. 1e).²⁹

Fig. 1 Natural superhydrophobic surfaces: (a) the leaf of the lotus plant, (b) the lady's mantle, (c) the Stenocara beetle, (d) the water strider and (e) butterfly wings. Reproduced with permission from ref. 49 (b), 13 (d), 29 (e). (c) is from ref. 25 and has been reprinted with permission from Macmillan Publishers Ltd.

Again from the theoretical side, two parameters work together in determining the wetting properties of a material: one factor is the chemical composition of the surface, the second is the surface roughness.^7,30,31 Depending on the interplay between these two characteristics, one of two distinct wetting states manifests itself: in the first case, which is frequently referred to as Wenzel wetting, drops penetrate and engulf the surface features (Fig. 2a).³⁰ In the second case (which is termed Cassie or composite wetting), drops rest on top of the roughness features, with air trapped underneath (Fig. 2b).³¹ Both Wenzel's and Cassie's models as well as their application to the problems treated in this report will be discussed in detail below. Cassie wetting is often found for surfaces with hydrophobic surface chemistries and high degrees of roughness. Superhydrophobic properties (Fig. 2c) are associated exclusively with the Cassie state of wetting: in this regime, the fact that the drop's footprint is partially in contact with air leads to a balling up of the drop to a more or less spherical shape and—in many cases—an increased droplet mobility.^23,32,33

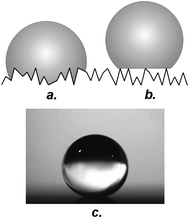Fig. 2 Wetting states on rough surfaces: (a) Wenzel state, (b) Cassie state, (c) drop on a superhydrophobic surface.

In this report we want to review some selected aspects of the unusal wetting properties of superhydrophobic surfaces. Our short review is not intended to give an in depth overview of the vast body of literature that has been published. Rather, we want to highlight some key points which we consider interesting. After presenting some general background information on wetting, a brief classification of current synthetic strategies for the generation of artificial superhydrophobic materials is given. We then focus on the measurement of superhydrophobic contact angles and the mechanisms of drop motion in the composite state. A section is devoted to transitions between the Cassie and Wenzel wetting states, before the condensation behavior of superhydrophobic materials is finally discussed.

Theoretical background

Young's equation

Young's equation relates the thermodynamic equilibrium contact angle θ_Y of a drop on an ideal solid to the specific energies of the solid–liquid (γ_sl), solid–gas (γ_sg) and liquid–gas (γ_lg) interface, where γ_ij is a function of the chemical structure of the respective interface:⁶

γ_lgcosθ_Y = γ_sg − γ_ls (1)

As illustrated in Fig. 3, eqn (1) may be interpreted as an equilibrium of forces at the three-phase contact line. It is critical to note that Young's equation refers to a system in its state of thermodynamic equilibrium. Even though this condition appears trivial at first view, it is difficult to realize experimentally because non-equilibrium processes can have a rather important influence on the details of the wetting process. Evaporation, for instance, will take place even in a saturated vapor atmosphere because the vapor pressure of the liquid phase will be slightly higher than that of the gaseous phase due to the curvature of the drop's surface.³⁴ With decreasing drop size, this problem will become more pronounced. From an oversaturated vapor, in contrast, condensation will occur. At best, non-equilibrium processes can be neglected at the time scale of the respective experiment.³⁴ Young's equation is sometimes modified to include the effect of line tension (τ = the energy associated with a unit length of contact line) on θ:³⁵

where R is the radius of curvature of the contact line. τ has been found to be very small, so that its effect is in general considered negligible except for drops smaller than 1 µm.^36–38

Fig. 3 Drop on a surface with the contact angle θ and the interfacial energies γ_ij indicated.

Non-ideal surfaces

Eqn (1) and (2) make the assumption of an ideal solid surface, which means that roughness, chemical heterogeneity, surface reconstruction, swelling and dissolution are neglected.^7,34 It was realized at an early stage that surface roughness may lead to a deviation of the contact angle from the value predicted by Young's equation.^30,31 To predict the effect of this parameter, two models are commonly employed:

(1) Wenzel model. Wenzel observed that roughness leads to an amplification of the wetting properties of the smooth material if a drop wets a surface in such a way that it follows the roughness features (Fig. 2a).³⁰ In this situation, the area of the drop's solid–liquid interface is enlarged by a factor r. Wenzel proposed that the contact angle on the rough surface, θ_W, then follows as:

cosθ_W = rcosθ_Y (3)

According to eqn (3), a hydrophobic surface (θ_Y>90°) will become more hydrophobic with increasing degree of roughness, while a hydrophilic surface (θ_Y<90°) will become more hydrophilic if the same type of roughness is introduced. A contact angle of 0° (complete wetting or superwetting) will result if r becomes larger than a critical value given by 1/cosθ_Y.

(2) Cassie/Baxter model. Cassie and Baxter looked at the effect of chemical heterogeneities in the surface on the equilibrium contact angle.³¹ In their model, averaging over the surface energies of the respective area fractions, ϕ_i, led to the following expression:In eqn (4), θ_C is the equilibrium contact angle on the heterogeneous surface and θ_i is the angle belonging to area fraction i (we note that Σϕ_i = 1). On rough materials characterized by very hydrophobic surface chemistries and/or pronounced degrees of roughness, drops often prefer to rest on top of the roughness features, with air trapped underneath (Fig. 2b).^11,23,32 In this composite state of wetting, drops are supported by a composite surface composed of solid and air, where the “airy” parts of the surface can be considered perfectly non-wetting. For this case, eqn (4) becomes:

cosθ_C = ϕcosθ_Y + ϕ − 1 (5)

where ϕ is now the solid fraction, i.e., the fraction of the drop's footprint in contact with the solid. Eqn (3) and (5) have sometimes been combined to a more general form:³⁹

cosθ_R = rϕcosθ_Y + ϕ − 1 (6)

where θ_R is the contact angle on the rough surface and r refers to the degree of roughness of those parts of the solid that are in contact with liquid. Both Wenzel's and Cassie's model are valid only if the drop size is large relative to the size of the roughness features. Also, according to a recent discussion, conditions at the contact line much more than those under the entire drop probably determine the contact angle, so that the local values r(x, y) and ϕ(x, y) in the vincinity of the contact line should be used in eqn (3)–(6).^40–42

(3) Contact angle hysteresis. On most surfaces, as a result of, e.g., chemical heterogeneities and/or roughness, a phenomenon commonly referred to as contact angle hysteresis is observed:^43–46 drops are prevented from reaching the minimum-energy state described by Wenzel's and Cassie's models by kinetic barriers.^44,47 As a result, a (more or less wide) range of “static” contact angles is possible, each of which corresponds to an energetically metastable state. Which state a drop finds itself in depends then on its history, for instance on how it was deposited, what forces have been acting on it, or for how long it has been left to evaporate. The maximum/minimum values appear for a liquid front that has been advanced/receded over a surface and are termed the advancing/receding angles (θ_Adv and θ_Rec); the contact angle hysteresis is given as the difference between the two (Δθ = θ_Adv − θ_Rec).

Superhydrophobic surfaces

Most natural superhydrophobic surfaces have as a common feature that they are equipped with a multiscale surface roughness, typically a spectrum of micro- and nanostructures.²³ Recent research has shown that roughness at the nanoscale plays an important role and that, for example, the lotus leaf will loose its water-repellent properties if the nanostructure is removed.⁴⁸ Plants such as the Lady's mantle, which belong to a second class of natural superhydrophobic materials, rely on microscale hairs for their superhydrophobic properties.^23,49 With a few exceptions,⁵⁰ recent research has focused on mimicking the structure of the lotus leaf by combining hydrophobic surface chemistries with high degrees of surface roughness.^8,10,13–15 Current “superhydrophobic” materials can be broadly classified into two categories: (1) surfaces with a controlled design and (2) surfaces with an arbitrary surface structure. Here, we have placed the term “superhydrophobic” in quotation marks because, as we will see in the following, it is often used in a rather loose sense and not all surfaces to which it is applied can be called superhydrophobic in the strict sense.

Surfaces with a controlled design

For this type of surface, the roughness features are precisely defined, most often by lithography and silicon micromachining (Fig. 4a and b).^{33,42,51–57} A mask pattern is first transferred into a thin layer of photoresist that has been coated onto a silicon wafer. Subsequently, the resist is developed and the patterns are transferred into the bulk silicon by anisotropic etching. This process is frequently employed for the generation of post-like structures, where the posts are often quadratic in shape (other shapes such stars or cylinders have also been realized).^51,58 Hydrophobization of the microstructures is carried out in a separate step by, for instance, depositing fluorosilanes in the form of self-assembled monolayers (SAMs).⁵¹ As an alternative, pre-synthesized fluoropolymers can be immobilized at the surfaces,^55,59–61 or fluoropolymers can be grown in situ through a surface-initiated polymerization.⁶¹ The latter processes have been optimized to result in extremely hydrophobic surface coatings, with surface energies even lower than those of Teflon®.^59,62 Variations of the micromachining process include using polymers as structural materials or employing various micromolding techniques.^33,58,62

Fig. 4 Man-made superhydrophobic surfaces: (a) and (b) are post-type structures, (c) is a fractal superhydrophobic surface structure obtained by the solidification of a wax melt, (d) is a superhydrophobic carbon nanotube forest, and (e) is a superhydrophobic surface obtained by the laser ablation of silicon and subsequent hydrophobization. From ref. 52 (a), 68 (c), 72 (d) and 74 (e), respectively, reproduced with permission.

For purely microstructured surfaces, the hysteresis usually remains considerable (a range of 15–25° is typical);^33,51,55 these materials can therefore not be called “truly” superhydrophobic, even if composite wetting is observed. Only recently has microtechnology progressed to a state where nanoscale posts with a controlled geometry could be realized.^63–67 A common advantage of the surfaces discussed in this section is that, since the roughness topography is well-defined, a theoretical analysis of the wetting behavior is more readily performed.

Materials with an arbitrary surface structure

This group includes all superhydrophobic surfaces for which the roughness structure is not controlled, which means that the precise shape and location of the roughness features is statistical (Fig. 4c–e). Various topologies have been realized, from fractal to fibrous.^17,68 Fabrication processes include the etching of fluoropolymer layers,⁶⁹ chemical synthesis,^17,70 solidification,⁶⁸carbon nanotube deposition,^71,72 and various other physical processes.^73–76 The literature on this topic is extensive and would go beyond the scope of this report; the interested reader is referred to several recent reviews.^8,10,13–16

Characterization of superhydrophobic surfaces

The sessile drop method, where a small drop of liquid is placed on a surface, is currently the most popular technique for the characterization of superhydrophobic materials. The drop under analysis is observed in the side view; modern systems then employ a camera and computer for detecting the droplet shape and extracting the contact angle. The size of the drop must be chosen such that, on the one hand, the effect of evaporation on the drop shape can be neglected on the time scale of the experiment. This condition limits the minimum drop size. On the other hand, the drop must be small enough so that it is not significantly deformed due to gravitational forces. The latter point is usually considered satisfied if the drop's diameter is below the capillary length of the respective liquid.^7,11 The capillary length, λ_C, is defined as:⁷where ρ is the liquid density and g is the gravitational acceleration. For drop diameters below λ_C, surface forces are normally assumed to dominate. The capillary length for water is 2.7 mm, which thus represents the upper limit in size for unperturbed water drops.

For the case of superhydrophobic wetting, the approximation explained in the previous paragraph breaks down: as the contact angle of a drop on a surface increases, the circular patch which forms the contact area between liquid and solid successively becomes smaller.⁷⁷ The gravitational force exerted by a drop of given volume is thus concentrated onto a progressively smaller area. Ultimately, for a contact angle of 180°, the contact area would vanish and the pressure on the contact area would become infinite, which is physically not possible. Instead, the contact line is pushed outwards and the drop is deformed from the ideal spherical cap shape even for drop diameters below λ_C. This feature is illustrated in Fig. 5, where the shape of a drop on a superhydrophobic material (contact angle = 178°) was simulated with and without gravity acting on it. It can easily be seen that gravity leads to a significant deformation of the drop. To summarize this paragraph, the effect of gravity should not be neglected when drops on superhydrophobic surfaces are characterized.

Fig. 5 Surface Evolver simulation of a drop on a superhydrophobic surface (drop diameter = 2 mm, θ = 178°). For the computation of the drop shape shown in dark grey, gravity was set to zero. The shape shown in light grey was obtained by setting gravity to 9.81 m s⁻². The simulation results illustrate that gravity led to a deformation of the drop base even though the drop's diameter was below the capillary length of water.

From a practical point of view, several authors have recently remarked that the application of the sessile drop method is problematic when contact angles in the superhydrophobic regime are measured, even when fitting algorithms based on the Laplace–Young equation that take into account the effect of gravity on the drop shape are employed.^55,78–80 At high contact angles, drops have an almost spherical shape, and the meniscus will come very close to the substrate before actually making contact at the three-phase contact line. Therefore, the region around the contact line will often appear blurred due to diffraction and scattering and, with increasing contact angle, the small slit between the meniscus and the surface will become ever more difficult to resolve. Dorrer and Rühe attributed discrepancies between theoretical models and experimental results to such problems and suggested that values obtained by the sessile drop method be treated with caution.⁵⁵ As a possible alternative to the sessile drop method, Gao and McCarthy recently used a superhydrophobic surface to contact a sessile drop from above, judging the degree of superhydrophobicity by how strongly the drop was deformed as the surface was pulled away from the liquid.⁷⁹ However, with respect to a quantitative measurement, this procedure in our opinion does not remove the problem from a fundamental point of view, as it just leads to an inversion of the gravitational force. We can therefore expect values similar to those obtained from the standard procedure, only with a slight over- instead of an underestimation of the contact angle. Following an approach similar to that proposed by Gao and McCarthy, de Souza et al. recently attempted a quantitative measurement by detemining the force–separation curves for capillary bridges between two parallel plates.⁸¹ Their analysis, however, did not extend into the superhydrophobic regime.

Mechanisms of superhydrophobic wetting

Cassie's theory, as it is essentially a thermodynamic model, makes no statement about hysteresis. It simply predicts an increasing “most stable” (in Marmur's notation)⁸² equilibrium angle with decreasing solid fraction ϕ. Experimentally, the contact angle hysteresis often tends to decrease with decreasing solid fraction but, as has also been found, drops may behave very differently on two surfaces of identical ϕ;⁵⁵ thus, the solid fraction cannot be the only parameter that determines the contact angle hysteresis. Chen et al. suggested that the roughness topology plays an important part in determining the advancing and receding angles.¹⁸ These authors concluded that the contact angle hysteresis should be increased for a composite surface where the contact line comes into continuous contact with the roughness features, as is the case for a mesh-like or porous structure (Fig. 6a). For a surface consisting of isolated roughness features (e.g., posts, Fig. 6b), they assumed that the energy barriers between metastable states should be decreased, leading to a lowered hysteresis. Öner and McCarthy followed the same line of thought, highlighting the importance of “destabilizing the contact line” in order to obtain a superhydrophobic material.⁵¹

Fig. 6 Configurations of the contact line on surfaces with different topologies (reprinted with permission from ref. 18). For surface (a), a continuous contact line can be formed, and the hysteresis will be higher than for surface (b).

A quantitative prediction of the advancing and receding angles in the composite state has so far remained elusive. Early attempts were focused on deriving the contact angle hysteresis from the r and ϕ parameters, which, as discussed above, seems problematic. Miwa et al., for instance, tried to relate the sliding angle of a drop on a superhydrophobic surface to a constant k that was related to the “interaction energy” between liquid and solid.⁸³k in turn was a function of r and ϕ. Miwa's concept was criticized by Roura and Fort, who emphasized the fact that without contact angle hysteresis, an equilibrium of drops on a tilted plane is not possible and that for this reason the advancing and receding angles must be different.⁸⁴ For a spike structure that was wetted in the composite mode, these authors argued that the advancing angles are given by the Cassie equation [eqn (6)], i.e., follow from:

cosθ_C.Adv = rϕcosθ_Y + ϕ − 1 (8)

Assuming that the receding meniscus left behind a thin liquid film on the surface, Roura and Fort then computed the receding angle according to:

cosθ_C,Rec = rϕ + ϕ − 1 (9)

In another attempt, McHale et al. introduced the concept of gain factors, where the gain factor described how the contact angle of a drop on a rough surface reacted to small changes in the contact angle of the smooth material, θ_S, around an “operating point”.⁸⁵ The gain factor for the Cassie state, G_C, was defined as:

Unfortunately, none of the above equations [eqn (8)–(10)] has been substantiated to a sufficient degree.

Extrand recently presented a methology for the calculation of the advancing and receding angles in the Cassie state where he looked at the fraction of the contact line supported by solid, λ_P.^78,86 He proposed the following equations:

θ_C.Adv = λ_P(θ_S.Adv + ω) + (1 − λ_P)180^∘ (11)

θ_C,Rec = λ_Pθ_S,Rec + (1 − λ_P)180^∘ (12)

where θ_S,i is the respective contact angle on the smooth material and ω is the slope angle of the asperities. Although Extrand's model agrees with some experimental series,⁷⁸ disagreement with others has been found.⁵⁵ For a drop on a specific (post-type) geometry, Li and Amirfazli computed an energy landscape, finding a parabolic profile and comparing their results to experimental data.⁸⁷

Many recent models for the motion of drops in the composite state remain qualitative and emphasize the importance of pinning effects. An important finding was the observation that superhydrophobic drops roll rather than slide, as Richard and Quere proved in experiments where they traced the path of a bubble that was trapped inside a drop moving over a fibrous, superhydrophobic surface (Fig. 7).⁸⁸ This “rolling” mechanism of motion firstly implies that the advancing contact line is pinned on roughness edges and remains stationary while the advancing meniscus bulges forward and comes down onto neighboring roughness features from above (Fig. 8).^55,78,89,90 Second, on the receding side, the meniscus is forced to lift off from the roughness features (Fig. 8). According to theoretical considerations, in contrast to the advancing motion, this step is associated with an energy barrier.^55,77,91,92 The dewetting event may therefore be seen as the rate-determining step for the motion of drops in the composite state. The meniscus is likely to recede in a zipping fashion, with a dewetting front moving along the length of the contact line (Fig. 9).⁵⁵ If we assume that the energy barrier for dewetting from one asperity is ΔG, then the energy barrier for dewetting from n asperities is nΔG following the mechanism illustrated in Fig. 9a, but only ΔG for the mechanism shown in Fig. 9b. Such a mechanism would agree with mechanisms of contact line motion observed for chemically heterogeneous surfaces, where it was found that it is preferable for the contact line to jump piecewise.^93,94

Fig. 7 Trajectory of an air bubble trapped inside a drop rolling over a superhydrophobic surface (reproduced with permission from ref. 88).

Fig. 8 Mechanism of motion of a drop on a composite surface. (a) On the receding side, the meniscus lifts off from the roughness features. This step is associated with an energy barrier ΔG. (b) On the advancing side, the meniscus comes down onto neighboring roughness features from above.

Fig. 9 Instead of dewetting from several roughness features at once, the meniscus dewets from one asperity at a time, with a dewetting front moving along the length of the contact line (from ref. 55).

Experimental data support the assumption that the receding motion dominates the movement of drops in the composite state: Morra et al. prepared superhydrophobic surfaces by submitting poly(tetrafluoroethylene) to successive oxygen plasma treatments.⁶⁹ The advancing contact angles on their surfaces remained relatively independent of the duration of the treatment, while the receding angles increased with an increasing degree of roughness (Fig. 10). Dettre and Johnson's data show a similar trend.⁴⁶ Gao and McCarthy prepared microposts where the post tops were smooth in the first and equipped with an additional nanostructure in the second case (Fig. 11).⁷⁹ The advancing contact angles on both surfaces were identical, while differences in the receding angles were observed. Dorrer and Rühe showed that, for hydrophobicized micromachined post surfaces where the geometry was systematically varied, the advancing angles remained approximately constant.⁵⁵ The receding contact angles, in contrast, were a function of the roughness geometry. In particular, the size scale of the surface had a much more prominent influence than the solid fraction (Fig. 12).

Fig. 10 Advancing (○) and receding (●) contact angles on plasma-etched poly(tetrafluoroethylene) as a function of treatment time. The three pairs of datapoints to the right correspond to the Cassie wetting regime. Here, the advancing angles remain constant, while the receding angles vary with the treatment time (reproduced with permission from ref. 69).

Fig. 11 SEM image of a surface with microposts where the tops of the microposts have been coated with a hydrophobic polymer network (reproduced with permission from ref. 79).

Fig. 12 Contact angle hysteresis on hydrophobicized silicon post surfaces as a function of the post width. The solid fractions were constant for each curve: ϕ = 25% (a), 11% (b), and 4% (c). Lines are guides to the eye.

Simulations have recently shown that the base of a drop that is resting on a superhydrophobic material is strongly deformed from the ideal spherical cap shape by the underlying surface pattern.^95–102 The contact line (here defined as the line in space where the meniscus leaves the plane of the composite surface; in the traditional definition, in contrast, we have multiple closed contact lines around the top of each wetted roughness feature) is strongly distorted from the circular shape and may assume different configurations depending on the position of the advancing/receding meniscus. Both features depend on the topology of the respective substrate in a complicated way. This fact implies that an analytical quantification of the advancing and receding contact angles will in general not be feasible (except for strongly simplified model geometries).^46,103 However, numerical solutions should be possible, and first attempts in this direction have been made by analyzing simulated side views of the liquid–air interface of drops on various superhydrophobic materials.^99,104,105

Wetting transitions

On some rough surfaces, drops in the Wenzel and Cassie states can coexist, with the actual wetting state depending on how the respective drop was deposited.^{12,33,53,106–108} From theory, for a given r and ϕ, the Wenzel state is energetically favored if the contact angle on the smooth material, θ_Y, is below a critical value θ_Crit. θ_Crit follows by equating the Wenzel and the Cassie equation [eqn (3) and (6)]:^109,110

rcosθ_Crit = ϕcosϕ_Crit + ϕ − 1 (13)

In reality, kinetic barriers may lead to a stabilization of drops in a wetting situation that is not the minimum-energy state.^{108,111–114} As a consequence, drops in both wetting states (Cassie and Wenzel) may appear on one and the same material. Patankar studied the Cassie-to-Wenzel transition theoretically for a model surface composed of regularly arranged posts.¹¹¹ For a hydrophobic surface (i.e., θ_Y>90°), he found the initial impalement of a drop on the post structure to be associated with an increase in interfacial energy. Energy was then recovered as the drop made contact with the bottom of the post surface and liquid–air was replaced by liquid–solid interface. Following similar considerations, Nosonovsky and Bhushan derived an energy diagram for the Cassie-to-Wenzel transition where both states were separated by an energy barrier.¹¹⁴

A transition of drops from the Cassie to the Wenzel state can be induced by exerting pressure on the drops,^{33,53,106,110} vibrating the substrate,¹¹⁵ applying an electrical voltage,^66,67 or having droplets evaporate.^114,116,117 All these methods lead to an increased Laplace pressure ΔP across the drops' liquid–air interfaces, which can thus be seen as the driving force for the transition.¹¹⁸ The pressure difference ΔP stems from the surface tension, γ_lg, and other forces such as gravity. ΔP and the radius of the meniscus are related by the Laplace equation:⁷

A transition occurs once the meniscus is so strongly curved that either (i) direct contact with the bottom of the surface is made according to the mechanism shown in Fig. 13a or (ii) the advancing angle on the sidewalls of the roughness features is reached so that the meniscus can slide down into the structure (Fig. 13b). In drop impact experiments, Bartolo et al. recently determined the energy necessary for inducing a Cassie-to-Wenzel transition on a microstructured post surface as a function of the post height.¹¹⁹ For a transition according to the first mechanism, Bartolo et al. found an approximately linear increase in the energy barrier with increasing post height. Above a critical post height, the increase in the energy barrier levelled off because the transition now proceeded according to the sliding model illustrated in Fig. 13b. In a recent experimental series, the same authors investigated the shape of the drop footprint during the transition and found agreement with the model described above.¹¹⁶ For a similar post-type structure, Zheng et al. computed the hydraulic pressure at which a transition begins, ΔP_Crit, as:¹²⁰

where λ is the cross-sectional area of a post divided by its perimeter. Extrand, in contrast, suggested that ΔP_Crit increases with an increase in the λ_P-parameter.¹²¹ Liu and Lange investigated the critical pressure for a model surface composed of regularly arranged, microscale spheres.¹²²

Fig. 13 According to the mechanism illustrated in (a), the transition from the Cassie to the Wenzel state occurs as the meniscus makes contact with the bottom of the surface while it is still pinned at the post edges. In (b), the advancing angle on the post sidewalls is reached and the meniscus slides into the structure. From ref. 119, reproduced with permission.

As an important aspect, recent experimental studies and simulations indicate that the transition from the Cassie to the Wenzel state takes place not over the entire drop footprint at once, but rather proceeds starting from one or more nucleation sites (Fig. 14).^{94,97,115,123,124} How the transition proceeds is then determined by how easily the meniscus can move within the surface structure.

Fig. 14 Schematic depiction of the Cassie-to-Wenzel transition with the transition proceeding from a nucleation site at the center of the drop footprint (reproduced with permission from ref. 123). (a) Cassie, (b) intermediate, and (c) Wenzel state.

While the Cassie-to-Wenzel transition has been studied extensively, the Wenzel-to-Cassie transition has received much less attention. The Cassie-to-Wenzel transition is in general assumed to be irreversible for the case where the Wenzel state is at the absolute energy minimum.^105,112,113 Results reported in a recent study, however, seem to indicate that Wenzel-to-Cassie transitions are possible when the Wenzel state is metastable, and the Cassie state energetically preferred.¹⁰⁸ It is known that the condensation of water onto microscale post-type surfaces leads to the formation of both Wenzel, Cassie, and mixed Wenzel–Cassie drops.^107,108 In one series of experiments it was found that, in the course of the coalescence events that accompany such a condensation process, Wenzel drops could sometimes make a transition to the Cassie state either entirely or over part of their footprint area.¹⁰⁸ Here, the Wenzel state was separated from the Cassie state by an energy barrier and the coalescence of two drops (that were either both mixed Cassie–Wenzel or where one was a Cassie and the other a Wenzel drop) and the concomitant elimination of liquid–air interfacial area introduced enough energy into the system for this energy barrier to be overcome.

Condensation resistance

The question of how water that is condensed onto a superhydrophobic material behaves is important for a variety of applications. It is essential to know, for instance, how water-repellent windshields respond to fogging. Breathable, waterproof clothing represents another example where superhydrophobic surfaces could be exposed to water vapor.

The leaf of the lotus plant is a well-known example of a natural surface with strong superhydrophobic properties. When Cheng and Rodak condensed water onto a cooled lotus leaf, they found that the leaf's structure was penetrated by liquid (Fig. 15a); “sticky” droplets were formed.¹²⁵ The leaf's superhydrophobic properties were thus lost. With respect to the practical application of superhydrophobic materials, such a scenario is of course highly undesirable since the water-repellency of the surface is lost. In contrast to Cheng and Rodak’s results, Zheng et al. recently observed that drops condensed onto a lotus leaf ended up suspended on top of the papillae that cover the leaf's surface (Fig. 15b).¹²⁶

Fig. 15 The upper two images show the condensation of water onto a lotus leaf. (a) Cheng and Rodak observed that the leaf's structure was penetrated by liquid (reproduced with permission from ref. 125), while (b) Zheng et al. found that condensed drops ended up in the Cassie state of wetting (reused with permission from ref. 126). On microstructured post surfaces (c), condensation leads to drops that are partly in the Wenzel (indicated by arrows) and partly in the Cassie state (image reproduced with permission from ref. 107).

Further systematic studies related to the condensation behavior of superhydrophobic surfaces have mainly concentrated on micromachined geometries. For this type of material, it has been found that condensation in general leads to an at least partial penetration of water into the surface structure.^{107,108,127–129} Narhe and Beysens found that Wenzel drops condensed onto an otherwise superhydrophobic spike structure grew following similar laws, as do drops on planar surfaces.¹²⁷ For post-type surfaces, the formation of combined Cassie–Wenzel drops (i.e., drops that are partly in the Cassie and partly in the Wenzel mode) has been observed (Fig. 15c).^107,108

In contrast to the purely microstructured surfaces discussed in the previous paragraph, recent research indicates that certain artificially prepared nanostructured materials may exhibit condensation-resistant properties. By condensation-resistant, we mean that condensed drops do not penetrate the surface structure, but end up in the Cassie state. Lau et al. observed that drops condensed onto superhydrophobic carbon nanotube forests retained a perfectly spherical shape.⁷¹ This property was a strong indication that the drops were in the Cassie state of wetting. Also for a surface equipped with nanotubes, Chen and coworkers reported a similar effect,¹³⁰ as did other authors for a surface equipped with nanoscale silicon spikes.⁷⁶ With respect to the condensation resistance of a superhydrophobic material, the size scale of the roughness features in relation to the size of the smallest stable drops is probably a critical parameter. For large surface features, condensation will at first proceed as on a smooth surface and drops in the Wenzel state will form. If, in contrast, the roughness features are on the same size scale as the smallest drops, drops will probably transition to the Cassie state at an earlier stage.

Conclusions and outlook

To summarize a few important points, the movement of drops in the superhydrophobic state is governed by how easily the meniscus can recede across the superhydrophobic surface. The receding motion can thus be seen as the rate-determining step, with the size scale and topology of the surface as the most important parameters. The drop shape and morphology of the contact line depend on the geometric and chemical properties of the respective substrate in a complicated way. Since, as a result, a quantification of the contact angle hysteresis involves the computation of a very complicated energy landscape, an analytical description of the wetting properties is possible only for extremely simplified topographies. Numerical solutions should in general be possible in particular for surfaces where the roughness is regular; however, such solutions are in turn valid only for a specific roughness geometry.

While the theoretical understanding of superhydrophobic wetting has greatly improved in the past few years, three major issues remain on the agenda as far as the practical application of superhydrophobic surfaces is concerned: first, the long-term stability of superhydrophobic materials against contamination is an often overlooked, yet no less important challenge. If, for example, hydrocarbons or surface-active substances adsorb at a water-repellent surface over time, the surface energy of the material in question will increase. Once a critical surface coverage is reached, the Wenzel state will become the preferred wetting situation. This situation implies nothing less than a complete loss of the superhydrophobic properties. From a chemical point of view, the minimum surface energy that is attainable is that of a surface consisting of closest-packed CF₃-moieties (such surfaces have been realized by a number of research groups). With respect to surface chemistry, it thus seems that a limit has been reached. One remaining path towards increased robustness against contamination could be the generation of oleophobic, i.e., undercut or mushroom-like structures that maintain the Cassie state of wetting even if the initial low-energy surface coating is partly covered by high-energy-contaminants.

Unfortunately, undercut and especially nanoscale structures have a low mechanical stability and are easily damaged when mechanically challenged. This feature is the second prominent problem related to the practical application of most, if not all superhydrophobic materials: as smaller and smaller (and eventually nanoscale) structures become involved, even relatively small mechanical forces may destroy the intricate surface texture and lead to a (local) destruction of the superhydrophobic properties: drops then no longer roll off but stick to the damaged areas. As far as self-cleaning is concerned, this scenario leads to a catastrophic failure, because it causes an accumulation of dirt in the damaged areas. As a possible solution to this lack of mechanical ruggedness, we could imagine materials that mimic living systems by having the ability to “heal” from damage, for instance by successively exposing fresh layers of superhydrophobic compounds upon wear. As an alternative, microstructures could be integrated into a nanostructure as protective elements that carry most of the mechanical load in tribologically demanding situations.

The third problem we want to mention here is the condensation resistance of superhydropobic surfaces, as for current materials condensation often leads to the formation of drops that are (at least partly) in the Wenzel state. Here, many aspects have remained unclear, even though first results indicate that small (that is, nanoscopic) surface size scales and certain roughness geometries (hairs and spikes) promote condensation-resistant properties.

From many model studies published in the literature, it seems that a wide spectrum of practical applications for superhydrophobic surfaces are right at the doorstep. We however have to remember that, in many of these applications, superhydrophobic materials will be exposed to harsh environmental conditions and that a number of problems still remain to be solved.

References

1. S. K. Cho, K. Moon and C.-J. Kim, J. Microelectromech. Syst., 2003, 12, 70.
2. C.-H. Choi and C.-J. Kim, Phys. Rev. Lett., 2006, 96, 06601.
3. M.-H. Wu and G. M. Whitesides, J. Micromech. Microeng., 2002, 12, 747.
4. W. Mönch and H. Zappe, J. Opt. A: Pure Appl. Opt., 2004, 6, 330.
5. C. Dorrer, O. Prucker and J. Rühe, Adv. Mater., 2007, 19, 456.
6. T. Young, Philos. Trans. R. Soc. London, 1805, 95, 65.
7. H.-J. Butt, K. Graf, M. Kappl, Physics and Chemistry of Interfaces, Wiley-VCH, Weinheim, 2003.
8. A. Nakajima, K. Hashimoto and T. Watanabe, Monatsh. Chem., 2001, 132, 31.
9. G. McHale, N. J. Shirtcliffe and M. I. Newton, Analyst, 2004, 129, 284.
10. I. P. Parkin and R. G. Palgrave, J. Mater. Chem., 2005, 15, 1689.
11. D. Quere, Rep. Prog. Phys., 2005, 68, 2495.
12. M. Callies and D. Quere, Soft Matter, 2005, 1, 55.
13. X. Feng and L. Jiang, Adv. Mater., 2006, 18, 3063.
14. X.-M. Li, D. Reinhoudt and M. Crego-Calama, Chem. Soc. Rev., 2007, 36, 1350.
15. A. Solga, Z. Cerman, B. F. Striffler, M. Spaeth and W. Barthlott, Bioinsp. Biomim., 2007, 2, 126.
16. P. Roach, N. J. Shirtcliffe and M. I. Newton, Soft Matter, 2008, 4, 224.
17. L. Gao and T. J. McCarthy, Langmuir, 2007, 23, 9125.
18. W. Chen, A. W. Fadeev, M. C. Hsieh, D. Öner, J. Youngblood and T. J. McCarthy, Langmuir, 1999, 15, 3395.
19. P. Gould, Mater. Today, 2003, 11, 44.
20. R. Blossey, Nat. Mater., 2003, 2, 301.
21. W. E. Ward, J. Aes. Art Crit., 1952, 11, 135.
22. C. Neinhuis and W. Barthlott, Ann. Bot., 1997, 79, 667.
23. W. Barthlott and C. Neinhuis, Planta, 1997, 202, 1.
24. P. Wagner, R. Fürstner, W. Barthlott and C. Neinhuis, J. Exp. Bot., 2003, 54, 1295.
25. A. R. Parker and C. R. Lawrence, Nature, 2001, 414, 33.
26. T. Wagner, C. Neinhuis and W. Barthlott, Acta Zool., 1996, 3, 213.
27. W. Lee, M. K. Jin, W. C. Yoo and J. K. Lee, Langmuir, 2004, 20, 7665.
28. X. Gao and L. Jiang, Nature, 2004, 432, 36.
29. Q. Cong, G.-H. Chen, Y. Fang and L.-Q. Ren, J. Bionics Eng., 2004, 1, 249.
30. R. N. Wenzel, Ind. Eng. Chem., 1936, 28, 988.
31. A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546.
32. S. Herminghaus, Europhys. Lett., 2000, 52, 165.
33. J. Bico, C. Marzolin and D. Quere, Europhys. Lett., 1999, 47, 220.
34. H.-J. Butt, D. S. Golovko and E. Bonaccurso, J. Phys. Chem. B, 2007, 111, 5277.
35. G. Wolansky and A. Marmur, Langmuir, 1998, 14, 5292.
36. T. Pompe and S. Herminghaus, Phys. Rev. Lett., 2000, 85, 1930.
37. J. Drelich, J. L. Wilbur, J. D. Miller and G. M. Whitesides, Langmuir, 1996, 12, 1913.
38. A. Marmur, J. Colloid Interface Sci., 1997, 186, 462.
39. A. Marmur, Langmuir, 2003, 19, 8343.
40. L. Gao and T. J. McCarthy, Langmuir, 2007, 23, 3762.
41. G. McHale, Langmuir, 2007, 23, 8200.
42. M. Nosonovsky, Langmuir, 2007, 23, 9919.
43. P. G. deGennes, Rev. Mod. Phys., 1985, 57, 827.
44. R. E. Johnson and R. H. Dettre, J. Phys. Chem., 1964, 68, 1744.
45. J. F. Oliver, C. Huh and S. G. Mason, Colloids Surf., 1980, 1, 79.
46. R. H. Dettre and R. E. Johnson, Adv. Chem. Ser., 1964, 43, 136.
47. R. H. Dettre and R. E. Johnson, Adv. Chem. Ser., 1964, 43, 112.
48. Y.-T. Cheng, D. E. Rodak, C. A. Wong and C. A. Hayden, Nanotechnology, 2006, 17, 1359.
49. A. Otten and S. Herminghaus, Langmuir, 2004, 20, 2405.
50. U. Mock, R. Förster, W. Menz and J. Rühe, J. Phys.: Condens. Matter, 2005, 17, 639.
51. D. Öner and T. J. McCarthy, Langmuir, 2000, 16, 7777.
52. Z. Yoshimitsu, A. Nakajima, T. Watanabe and K. Hashimoto, Langmuir, 2002, 18, 5818.
53. B. He, N. A. Patankar and J. Lee, Langmuir, 2003, 19, 4999.
54. J. Jopp, H. Grüll and R. Yerushalmi-Rozen, Langmuir, 2004, 20, 10015.
55. C. Dorrer and J. Rühe, Langmuir, 2006, 22, 7652.
56. A. Shastry, M. J. Case and K. F. Böhringer, Langmuir, 2006, 22, 6161.
57. N. Anantharaju, M. V. Panchagnula, S. Vedantam, S. Neti and S. Tatic-Lucic, Langmuir, 2007, 23, 11673.
58. N. J. Shirtcliffe, S. Aquil, C. Evans, G. McHale, M. I. Newton, C. C. Perry and P. Roach, J. Micromech. Eng., 2004, 14, 1384.
59. J. D. S. Samuel and J. Rühe, Langmuir, 2004, 20, 10080.
60. J. D. S. Samuel, P. Ruther, H.-P. Frerichs, M. Lehmann, O. Paul and J. Rühe, Sens. Actuators, B, 2005, 110, 218.
61. J. Pahnke and J. Rühe, Macromol. Rapid Commun., 2004, 25, 1396.
62. D.-H. Jung, I. J. Park, Y. K. Choi, S.-B. Lee, H. S. Park and J. Rühe, Langmuir, 2002, 18, 6133.
63. C. Marzolin, S. P. Smith, M. Prentiss and G. M. Whitesides, Adv. Mater., 1998, 10, 571.
64. E. Martines, K. Seunarine, H. Morgan, N. Gadegaard, C. D. W. Wilkinson and M. O. Riehle, Nano Lett., 2005, 5, 2097.
65. R. Fürstner and W. Barthlott, Langmuir, 2005, 21, 956.
66. T. N. Krupenkin, J. A. Taylor, T. M. Schneider and S. Yang, Langmuir, 2004, 20, 3814.
67. T. N. Krupenkin, J. A. Taylor, P. Kolodner and M. Hodes, AT&T Bell Laboratories Technical Journal, 2005, 10, 161.
68. S. Shibuichi, T. Onda, N. Satoh and K. Tsujii, J. Phys. Chem., 1996, 100, 1951.
69. M. Morra, E. Occhiello and F. Garbassi, Langmuir, 1989, 5, 872.
70. M. Nicolas, F. Guittard and S. Geribaldi, Langmuir, 2006, 22, 3081.
71. K. K. S. Lau, J. Bico, K. B. K. Teo, M. Chhowalla, G. A. J. Amaratunga, W. I. Milne, G. H. McKinley and K. K. Gleason, Nano Lett., 2003, 3, 1701.
72. C. Journet, S. Moulinet, C. Ybert, S. T. Purcell and L. Bocquet, Europhys. Lett., 2005, 71, 104.
73. Y. Matsumoto and M. Ishida, Sen. Actuators, 2000, 83, 179.
74. T. Baldacchini, J. E. Carey, M. Zhou and E. Mazur, Langmuir, 2006, 22, 4917.
75. X. Li, Z. Cao, F. Liu, Z. Zhang and H. Dang, Chem. Lett., 2006, 35, 94.
76. C. Dorrer and J. Rühe, Adv. Mater., 2008, 20, 159.
77. L. Mahadevan and Y. Pomeau, Phys. Fluids, 1999, 11, 2449.
78. C. W. Extrand, Langmuir, 2002, 18, 7991.
79. L. Gao and T. J. McCarthy, Langmuir, 2006, 22, 2966.
80. G. R. J. Artus, S. Jung, J. Zimmermann, H.-P. Gautschi, K. Marquardt and S. Seeger, Adv. Mater., 2006, 18, 2758.
81. E. J. de Souza, L. Gao, T. J. McCarthy, T. Arzt and A. J. Crosby, Langmuir, 2008, 24, 1391.
82. A. Marmur, Soft Matter, 2006, 2, 12.
83. M. Miwa, A. Nakajima, A. Fujishima, K. Hashimoto and T. Watanabe, Langmuir, 2000, 16, 5754.
84. P. Roura and J. Fort, Langmuir, 2002, 18, 566.
85. G. McHale, N. J. Shirtcliffe and M. I. Newton, Analyst, 2004, 129, 284.
86. C. W. Extrand, Langmuir, 2004, 20, 5013.
87. W. Li and A. Amirfazli, J. Colloid Interface Sci., 2005, 292, 195.
88. D. Richard and D. Quere, Europhys. Lett., 1999, 48, 286.
89. F. E. Bartell and J. W. Shepard, J. Phys. Chem., 1953, 57, 455.
90. J. P. Youngblood and T. J. McCarthy, Macromolecules, 1999, 32, 6800.
91. L. Gao and T. J. McCarthy, Langmuir, 2006, 22, 5998.
92. L. Gao and T. J. McCarthy, Langmuir, 2006, 22, 6234.
93. L. Schwartz and S. Garoff, J. Colloid Interface Sci., 1985, 106, 422.
94. L. Schwartz and S. Garoff, Langmuir, 1985, 1, 219.
95. A. Dupuis and J. M. Yeomans, Langmuir, 2005, 21, 2624.
96. A. J. Briant, A. J. Wagner and J. M. Yeomans, Phys. Rev. E, 2004, 69, 031602.
97. D. Chatain, D. Lewis, J.-P. Baland and W. C. Carter, Langmuir, 2006, 22, 4237.
98. A. Porcheron and P. A. Monson, Langmuir, 2006, 22, 1595.
99. H. Kusumaatmaja and J. M. Yeomans, Langmuir, 2007, 23, 6019.
100. J. Hyväluoma, A. Koponen, P. Raiskinmäki and J. Timonen, Eur. Phys. J. E, 2007, 23, 289.
101. M. Lundgren, N. L. Allan and T. Cosgrove, Langmuir, 2007, 23, 1187.
102. C. Dorrer and J. Rühe, Langmuir, 2007, 23, 3179.
103. R. H. Dettre and R. E. Johnson, Adv. Chem. Ser., 1964, 43, 112.
104. R. Seemann, M. Brinkmann, E. Kramer, F. Lange and R. Lipowsky, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 1848.
105. J. Zhang and D. Y. Kwok, Langmuir, 2006, 22, 4998.
106. A. Lafuma and D. Quere, Nat. Mater., 2003, 2, 457.
107. K. A. Wier and T. J. McCarthy, Langmuir, 2006, 22, 2433.
108. C. Dorrer and J. Rühe, Langmuir, 2007, 23, 3820.
109. J. Bico, U. Thiele and D. Quere, Colloids Surf., A, 2002, 206, 41.
110. D. Quere, A. Lafuma and J. Bico, Nanotechnology, 2003, 14, 1109.
111. N. A. Patankar, Langmuir, 2004, 20, 7097.
112. C. Ishino, K. Okumura and D. Quere, Europhys. Lett., 2004, 68, 419.
113. L. Barbieri, E. Wagner and P. Hoffmann, Langmuir, 2007, 23, 1723.
114. M. Nosonovsky and B. Bushan, Nanoletters, 2007, 7, 2633.
115. E. Bormashenko, R. Pogreb, G. Whyman and M. Erlich, Langmuir, 2007, 23, 6501.
116. S. Moulinet and D. Bartolo, Eur. Phys. J. E, 2007, 24, 251.
117. H. Kusumaatmaja, M. L. Blow, A. Dupuis and J. M. Yeomans, Europhys. Lett., 2008, 81, 36003.
118. M. Reyssat, J. M. Yeomans and D. Quere, Europhys. Lett., 2008, 81, 26006.
119. D. Bartolo, F. Bouamrirene, E. Verneuil, A. Buguin, P. Silberzan and S. Moulinet, Europhys. Lett., 2006, 74, 299.
120. Q.-S. Zheng, Y. Yu and Z.-H. Zhao, Langmuir, 2005, 21, 12207.
121. C. W. Extrand, Langmuir, 2006, 22, 1711.
122. B. Liu and F. F. Lange, J. Colloid Interface Sci., 2006, 298, 899.
123. C. Ishino and K. Okumura, Europhys. Lett., 2006, 76, 464.
124. M. Sbragaglia, A. M. Peters, C. Pirat, B. M. Borkent, R. G. H. Lammertink, M. Wessling and D. Lohse, Phys. Rev. Lett., 2007, 99, 156001.
125. Y.-T. Cheng and D. E. Rodak, Appl. Phys. Lett., 2005, 86, 144101.
126. Y. Zheng, D. Han, J. Zhai and L. Jiang, Appl. Phys. Lett., 2008, 92, 084106.
127. R. D. Narhe and D. A. Beysens, Phys. Rev. Lett, 2004, 93, 076103.
128. R. D. Narhe and D. A. Beysens, Europhys. Lett., 2006, 75, 98.
129. C. C. Yung and B. Bushan, J. Microsc., 2008, 229, 127.
130. C.-H. Chen, Q. Cai, C. Tsai, C.-L. Chen, G. Xiong, Y. Yu and Z. Ren, Appl. Phys. Lett., 2007, 90, 173108.

---