DOI:
10.1039/B810134E
(Paper)
Soft Matter, 2009,
5, 203-207
Elasticity of two-dimensional crystalline monolayers of fatty acid salts at an air–water surface
Received
17th June 2008
, Accepted 18th August 2008
First published on 15th October 2008
Abstract
The elastic properties of organic–inorganic two-dimensional crystals floating at the water surface have been fully characterized by grazing incidence X-ray diffuse scattering and high-resolution diffraction. We show that the strong interaction between the organic molecules and the inorganic divalent cations is enough for these nm thick crystals to behave like true solids, with a residual tension of 1 × 10−4–10−3N m−1. Their bending rigidity is renormalized as κ(q) ∝ q−ηk with ηk = 0.25 ± 0.07 and a microscopic value ≈ 100 kBT at q = 1 × 109 m−1. The in-plane elastic constants behave like qηu with ηu = 1.41 ± 0.2, obeying the scaling relation ηu = 2 − 2ηk. These results are consistent with a long-range phonon-mediated interaction between out-of-plane fluctuations but the values of the exponents differ from those generally obtained in numerical simulations.
1 Introduction
Two-dimensional solid membranes are expected to exhibit very unusual elastic and mechanical properties like vanishing elastic moduli, diverging bending rigidity at long wavelength or a negative Poisson ratio.1 These properties have in particular been recently invoked to explain how graphene2 could be stabilized by gentle crumpling in the third dimension though the Landau–Peierls instability does not allow two-dimensional crystals to exist.3Graphene is a striking example of a perfect one-atom thick crystal, but layered materials like nacre can also be found in nature whose remarkable elastic and mechanical properties do not result only from the strength of their bonds but rather from the synergy between the organic and inorganic parts in a composite structure.4 Amphiphilic molecules coupled to divalent cations at the water surface are the thinnest of such organic–inorganic stratified structures, where both the van der Waals forces between the organic moieties and electrostatic interactions between headgroups and cations contribute to build strong self-assembled two-dimensional structures. Whereas Langmuir films of simple amphiphiles usually make mesophases which do not exhibit the elasticity of solid membranes,5 the coupling to the cations Mg2+, Mn2+ (Fig. 1), Cd2+ and Pb2+ leads to nanometre thick structures, freely floating at the water surface which exhibit a remarkably high crystallinity.6–8 Interestingly, only minute concentrations of ions are necessary to get the two-dimensional composite crystals, e.g. only 1.4 Mg2+ ion per behenic acid molecule at pH 10.59 in which the fatty acid and ionic lattices are commensurate (the ionic lattice is a 2 × 2 superstructure of the organic lattice in the case of Mg2+ or a 1 × 2 in the case of Mn2+7).
 |
| | Fig. 1 Schematic view of the scattering geometry with the Langmuir trough. Inset: Brewster angle microscopy image of behenic acid on a MnCl2 subphase (5 Mn2+ per headgroup) at pH 7.5. | |
One of the most interesting theoretical predictions concerning crystalline or “tethered” membranes is the existence of a long-range interaction between out-of-plane fluctuations (capillary waves) due to the in-plane elasticity (phonons)10,11 which is not present in usual, fluid membranes. This interaction leads to a renormalization of the bending rigidity κ(q) ∝ q−ηk (see ref. 1) which is accompanied by a softening of elastic constants λ(q), µ(q) ∝ qηu at large distances (λ and µ are the Lamé coefficients). Simple integration shows that the roughness exponent ζ defined as 〈z2〉 ∝ L2ζ, where z is the transverse fluctuation of the membrane of size L is such that 2ζ = 2 − ηk. Rotational invariance yields the scaling relation:
| |  | (1) |
More precisely, this equation has to be obeyed in order to preserve the form of the strain when renormalizing the in-plane and normal components of the fluctuations.12 In most of the numerous numerical simulations of the flat phase of tethered membranes, the results are in the range ζ = 0.58–0.65 which implies that ηk ≈ 0.7–0.84 and ηu ≈ 0.32–0.6.11,13 Apart from graphene,3 only two kinds of experimental realization of solid membranes have been reported so far. Light scattering and small angle X-ray scattering of the red blood cell cytoskeleton yielded ζ = 0.6514 and a fractal dimension of 2.15 was obtained by freeze fracture electron microscopy and light scattering in the case of graphitic oxide sheets.15 In none of these experiments was the scaling relation eqn (1) verified as ηu could not be measured.
We show here that the out-of-plane fluctuations of the above mentioned organic–inorganic monolayers are governed by bending rigidity over a large q range, a unique feature at the water surface which can be tuned by changing the concentration in cations. Using grazing incidence diffuse scattering to measure ηk and grazing incidence diffraction to measure ηu, we show that their bending rigidity is renormalized and that the exponents are consistent with the scaling relation eqn (1).
2 Experimental
Behenic acid [CH3(CH2)20COOH] (Fluka, purity > 99%) was dissolved in chloroform (Merck, analytical grade) and spread on a solution of MgCl2 or MnCl2 (Sigma purity 99.99%) in ultra-pure de-ionized water from a Milli-Q 185 + Millipore system contained in a home-made Teflon trough mounted on an active antivibration system for the X-ray experiments. Concentrations of 1.88 × 10−5 mol l−1MgCl2 (20 ions per behenic acid molecule), 1.88 × 10−6 mol l−1MgCl2 (2 ions per behenic acid molecule) and 8.46 × 10−5 mol l−1MnCl2 (90 ions per behenic acid molecule) were used, above the threshold for fast crystal formation which is 1.4 ions per behenic acid molecule for MgCl2 at pH = 10.5 (fixed using KOH) and 7 ions per behenic acid molecule for MnCl2 at pH = 7.5 (fixed using NaHCO3).9 After solvent evaporation, the monolayer was gently compressed to ≈ 22 Å2 molecule−1 in order to maximize the coverage by crystals but stay at zero surface pressure (measured using a Wilhelmy balance) in order to avoid exerting constraints on them. During X-ray measurements, the Langmuir trough was translated by 0.5 mm every minute in order to avoid radiation damage. The experiments reported here used an 8.00 keV X-ray beam (wavelength λ = 0.155 nm) at the Troika II beamline of the European Synchrotron Radiation Facility (ESRF). The scattering geometry is described in Fig. 1. The monochromatic incident beam was first extracted from the polychromatic beam of the undulator source using a two-crystal diamond (111) monochromator. Higher harmonics were eliminated using two palladium coated glass mirrors, also used to set the grazing angle of incidence θin = 1.7 mrad below the critical angle for total external reflection θc (which occurs for X-rays since the refractive index of the matter is less than 1). The effective penetration length of the evanescent wave was ≈ 4.6 nm. The grazing incidence diffraction (GID) experiments were performed either using Soller slits in front of the gas-filled position sensitive detector (PSD) (low resolution mode Δq|| = 6.43 × 107 m−1 for structure determination) or using a Ge (111) crystal analyzer (high-resolution mode Δq|| = 1.47 × 106 m−1 for Bragg peak analysis). For diffuse scattering measurements, the resolution was set by 100 µm slits placed in front of the PSD and 600 mm from it, giving an in-plane resolution Δq|| = 6.7 × 106m−1. Extreme care was taken to minimize the background. The incident and scattered beams travelled through vacuum paths and the measurements were performed under a water saturated helium atmosphere. The residual background was recorded and subtracted by lowering the trough and scanning around the direct beam.16
3 Results and discussion
The diffuse scattering data were analyzed using for the differential scattering cross-section (intensity scattered per unit solid angle Ω in the direction ksc per unit of incident flux in the direction kin):| |  | (2) |
q|| and qz are the in-plane and vertical components of the wavevector transfer. A is the illuminated area and re ≈ 2.818 × 10−15 m is the classical electron radius which is the scattering length of electrons for elastic photon scattering. tin (resp.: tsc) is the Fresnel transmission coefficient between air and water, for the grazing angle of incidence θin (resp.: the scattering angle θsc). The coefficient tin represents a good approximation to the actual field at the interface while tsc describes how the scattered field propagates to the detector.17tsc is responsible for the peaks at low θsc in Fig. 2 (the so-called Yoneda peak). cos2ψ (see Fig. 1) is a polarisation factor (here close to 1). 〈z(0)z(r||)〉 is the height–height correlation function, and 〈z2〉 ≡ 〈z(0)2〉 the surface r.m.s. roughness. δρ(z) is the electron density profile of the film of thickness l minus the electron density of waterρw. Eqn (2) is finally multiplied by the incident flux and integrated over the detector solid angle to get the scattered intensity. The approximation| | 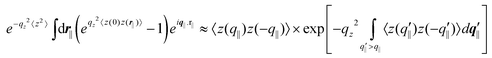 | (3) |
which is valid for small qz2〈z2〉 values was used to perform numerical calculations with| | | 〈z(q||)z(−q||)〉 = kBT/[Δρg + γq||2 + κ(q||)q||4] | (4) |
 |
| | Fig. 2 Scattered intensity along the position sensitive detector as a function of the scattering angle θsc for ψ = 0.08°. Behenic acid on a 1.88 × 10−5 mol l−1MgCl2 subphase (20 ions per headgroup) at pH = 10.5 (filled squares). Behenic acid on a 8.46 × 10−6 mol/l MnCl2 subphase (90 ions per headgroup) at pH = 7.5 (filled circles). Best fits are indicated by solid lines. Inset: corresponding electron density profiles. Behenic acid on a 1.88 × 10−5 mol l−1MgCl2 subphase (20 ions per headgroup) at pH = 10.5. | |
In addition to the renormalized bending rigidity, it has been taken into account in eqn (4) that in our system capillary waves will always be limited by gravity at very long wavelengths (Δρ is here the density difference between water and air) and also that the crystals might have a residual tension γ. Eqn (3) was carefully checked in the case of a constant κ for which an analytical expression for 〈z(0)z(r||)〉 is available.
Experimental results for the diffuse scattering are represented on Fig. 2 and 3. In Fig. 3 numerical integration was performed between θsc = 12.6 × 10−3 and θsc = 21.1 × 10−3 rad, whereas the z-dependence of the scattered intensity along the position sensitive detector for q|| = 5.65 × 107 m−1 (ψ = 0.08 degrees) is given in Fig. 2. As can be seen on Fig. 3, the scattering is dramatically enhanced when the organic–inorganic crystals are present at the surface. Such an enhanced scattering was previously observed in the case of ferric stearate, but on compressed films exhibiting no crystallinity.18 Starting at large q|| values where all curves merge, the scattering from the water surface increases with the q||−2 power law characteristic of capillary waves limited by surface tension. All curves for the organic–inorganic two-dimensional crystals first increase with a much larger exponent, close to 4. This is to our knowledge the first time such a clear signature for bending limited fluctuations is observed at the air–water interface.
![Diffuse scattering differential cross-section dσ/dΩ as a function of the wavevector transfer q||. Pure water (empty squares). Behenic acid on a 1.88 × 10−5 mol l−1MgCl2 subphase (20 ions per headgroup) at pH = 10.5 (filled squares). Behenic acid on a 1.88 × 10−6 mol l−1MgCl2 subphase (2 ions per headgroup) at pH = 10.5 (empty circles). Behenic acid on a 8.46 × 10−6 mol l−1MnCl2 subphase (90 ions per headgroup) at pH = 7.5 (filled circles). Best fits are indicated by solid lines. The long-dashed line has ηk = 0[(q||−4) power law] and the short-dashed line has ηk = 0.65.](/image/article/2009/SM/b810134e/b810134e-f3.gif) |
| | Fig. 3 Diffuse scattering differential cross-section dσ/dΩ as a function of the wavevector transfer q||. Pure water (empty squares). Behenic acid on a 1.88 × 10−5 mol l−1MgCl2 subphase (20 ions per headgroup) at pH = 10.5 (filled squares). Behenic acid on a 1.88 × 10−6 mol l−1MgCl2 subphase (2 ions per headgroup) at pH = 10.5 (empty circles). Behenic acid on a 8.46 × 10−6 mol l−1MnCl2 subphase (90 ions per headgroup) at pH = 7.5 (filled circles). Best fits are indicated by solid lines. The long-dashed line has ηk = 0[(q||−4) power law] and the short-dashed line has ηk = 0.65. | |
All fits of the diffuse scattering curves or Bragg peak profiles were performed by systematically exploring all parameter values on a grid, therefore avoiding local χ2 minima. The error bars were estimated by changing the value of a given parameter and fitting the other parameters until χ2 reaches its minimum value plus 1. Results of the fit are given in Table 1. Interestingly, all curves can be fitted with similar values of ηk. We also give in Table 1κ(q|| = 1 × 109 m−1) which can be understood as the “microscopic” bending rigidity as 1 × 109 m−1 is smaller than 2π/(intermolecular distance) and ηk is small (therefore the exact q|| value is unimportant). κ(q|| = 1 × 109m−1) is of the order of 100 kBT, a value which lies in between the bending rigidities of lipid bilayers in the fluid phase (20–30 kBT) and in the gel phase (300 kBT)19 and is therefore not extremely large. This is indeed the in-plane cohesion and elasticity which is responsible for the large effects at small q. In all cases ηk is different from zero and also from 0.65 found in most numerical simulations of tethered membranes.11 The effect of renormalization is sizeable; for example we have for the Mg2+ case κ(q|| = 1 × 109m−1) = 110 kBT and κ(q|| = 1 × 108m−1) = 170 kBT. In contrast to the exponent and microscopic rigidity, very different values of the tension are obtained for the different curves. In particular, the value of the tension for Mg2+ with 2 ions per headgroup is larger than that for 20 ions per headgroup which is consistent with the idea of a lower cohesion when less cations are present in the membrane. Following this line of interpretation, cohesion is also lower for Mn2+ at pH = 7.5 than for Mg2+ at pH = 10.5.
Table 1 Bending rigidity exponent ηk, surface tension γ and microscopic value of the bending rigidity κ(q|| = 1× 109m−1) for organic–inorganic two-dimensional crystals
| |
ηk
|
γ/mN m−1 |
κ (q|| = 1 × 109 m−1)/kBT |
|
Mg2+ 20 ions head−1 |
0.18 ± 0.06 |
0.45 ± 0.07 |
110 ± 12 |
|
Mg2+ 2 ions head−1 |
0.29 ± 0.06 |
2.2 ± 0.25 |
110 ± 11 |
|
Mn2+ 90 ions head−1 |
0.30 ± 0.08 |
6.5 ± 0.6 |
88 ± 30 |
In order to further investigate the possibility that our non zero ηk could be due to long-range phonon-mediated interactions, we have performed high-resolution diffraction measurements. The diffraction data were first analyzed by correcting the apparent diffraction angle on the detector for the diffraction from the analyzer crystal: due to diffraction, ψ is shifted by arcsin(sinθB/ cos θsc) − θB, where θB is the Bragg angle of the analyzer crystal.20,21q|| and qz were then calculated using this corrected value, and the signal was finally integrated along qz. The Bragg peak profile results from elastic fluctuations. In order to obtain the experimentally measured intensity, we also need to take into account the finite size of the domains and their random orientation ϕ. We finally get for the differential scattering cross-section in the neighborhood of a reciprocal space vector:22,23
| | 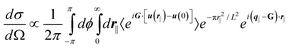 | (5) |
where
G is a reciprocal lattice vector,
u a small displacement and
L the average domain size. For a hexagonal lattice, 〈
eiG·[u(r∥) − u(0)]〉 ∝
r−ηG∥ with
ηG = (
kBT|
G|
2/4π) (3
µ +
λ)/
µ(2
µ +
λ), which implies that
ηG ∝
G(2 − ηu). The integration on
r|| gives
| | 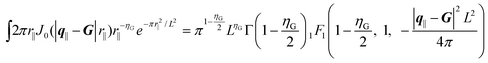 | (6) |
where
Γ is the incomplete Gamma function and
1F1 the confluent hypergeometric Kummer function used in
eqn (5) for the numerical calculation of the scattering cross-section which is finally convoluted with the experimental resolution function to obtain the scattered intensity. From the fit to the experimental data, we obtain
ηG and from the dependence of
ηG on
G, we obtain
ηu.
Experimental data and best fits are given in Fig. 4 for the (01) and (02) reflections of behenic acid on a 1.88 × 10−5 mol l−1MgCl2 subphase (20 ions per headgroup) at pH = 10.5. Obviously, the ηG values which describe the long-range decay of the intensity differ with ηG = 0.29 ± 0.3 for the (01) reflection and ηG = 0.43 ± 0.1 for the (02) reflection. By fitting these values and corresponding exponents for the (01) (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) (
) (![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) and (02) reflections for behenic acid on a 8.46 × 10−5 mol l−1MnCl2 subphase (90 ions per headgroup) at pH = 7.5 to ηG ∝ Gηu, we find ηu = 1.35 ± 0.18 in the Mg2+ case and ηu = 1.47 ± 0.18 in the Mn2+ case. The value expected from the scaling relation ηu = 2 − 2ηk with ηk ≈ 0.25 ± 0.07 is ηu = 1.5 ± 0.14 and is in good agreement with the experimental values.
1) and (02) reflections for behenic acid on a 8.46 × 10−5 mol l−1MnCl2 subphase (90 ions per headgroup) at pH = 7.5 to ηG ∝ Gηu, we find ηu = 1.35 ± 0.18 in the Mg2+ case and ηu = 1.47 ± 0.18 in the Mn2+ case. The value expected from the scaling relation ηu = 2 − 2ηk with ηk ≈ 0.25 ± 0.07 is ηu = 1.5 ± 0.14 and is in good agreement with the experimental values.
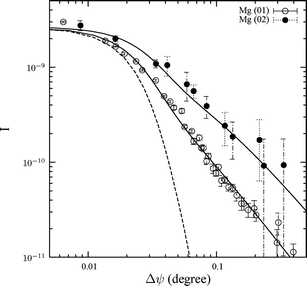 |
| | Fig. 4 Bragg singularity profiles for the (01) (empty circles) and (02) (filled circles) reflections and best fits (lines). The dashed line represents the resolution function. | |
4 Concluding remarks
In this paper, we have determined the exponents governing the bending rigidity ηk = 0.25 ± 0.07 and the elastic constants ηu = 1.41 ± 0.2 for organic–inorganic two-dimensional crystals. These crystals have a microscopic bending rigidity ≈ 100 kBT at q|| = 1 × 109 m−1 consistent with that of organic amphiphiles under similar conditions. Remarkably, this is the crystallinity brought by the interaction between the organic molecules and the inorganic divalent cations which leads to a strenghtening of the nm thick membranes at larger length scales. This interaction also determines the residual tension which is chemistry dependent. Whereas the exponents obey the scaling relation ηu = 2 − 2ηk, supporting our interpretation that we observe the phonon-mediated interaction between capillary waves expected in crystalline membranes, the values we find differ from most of the values found in numerical simulations (ηk ≈ 0.25 ± 0.07 instead of 0.7–0.84 for the simulated value and ηk ≈ 1.3–1.5 instead of 0.32–0.6 for the simulated value). This discrepancy, which requires further analysis, could be due to the tension absent in the simulations; electrostatic interactions could also play a role.
Acknowledgements
Funding by the ACI-nanosciences program under grant NR0106 is gratefully acknowledged.
References
- D. R. Nelson and L. Peliti, Fluctuations in membranes with crystalline and hexatic order, J. Phys., 1987, 48(7), 1085–1092 CAS.
- A. K. Geim and K. S. Novoselov, The rise of graphene, Nat. Mater., 2007, 6, 183–191 CrossRef CAS.
- J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, T. J. Booth T. J. and S. Roth, The structure of suspended graphene sheets, Nature, 2007, 446, 60–63 CrossRef CAS.
- K. Okumura and P. G. de Gennes, Why is nacre strong? Elastic theory and fracture mechanics for biocomposites with stratified structures, Eur. Phys. J. E, 2001, 4(1), 121–127 CrossRef.
- S. Mora, J. Daillant, D. Luzet and B. Struth, X-Ray surface scattering investigation of Langmuir films: phase transitions and elastic properties, Europhys. Lett., 2004, 66, 694–700 CrossRef CAS.
- F. Leveiller, D. Jacquemain, M. Lahav, L. Leiserowitz, M. Deutsch, K. Kjaer and J. Als-Nielsen, Crystallinity of the double-layer of cadmium arachidate films at the water-surface, Science, 1991, 252(5012), 1532–1536 CrossRef CAS.
- J. Kmetko, A. Datta, G. Evmenenko and P. Dutta, The effects of divalent ions on Langmuir monolayer and subphase structure: a grazing-incidence diffraction and Bragg rod study, J. Phys. Chem. B, 2001, 105(44), 10818–10825 CrossRef CAS.
- J. Kmetko, A. Datta, G. Evmenenko, M. K. Durbin, A. G. Richter and P. Dutta, Ordering in the subphase of a Langmuir monolayer: X-ray diffraction and anomalous scattering studies, Langmuir, 2001, 17(16), 4697–4700 CrossRef CAS.
- V. Dupres, S. Cantin, F. Benhabib, F. Perrot, P. Fontaine, M. Goldmann, J. Daillant and O. Konovalov, Superlattice formation in fatty acid monolayers on a divalent ion subphase: role of chain length, temperature, and subphase concentration, Langmuir, 2003, 19(26), 10808–10815 CrossRef CAS.
-
Proceedings of the Jerusalem Winter School for Theoretical Physics on Statistical Mechanics of Membranes and Surfaces, ed. D. R. Nelson, T. Piran, and S. Weinberg, World Scientific, Singapore, 2004 Search PubMed.
- M. J. Bowick and A. Travesset, The statistical mechanics of membranes, Phys. Rep., 2001, 344(4–6), 255–308 CrossRef CAS.
-
P. M. Chaikin and T. C. Lubensky, Principles of Condensed Matter Physics, Cambridge University Press, Cambridge, 1995 Search PubMed.
- G. Gompper and D. M. Kroll, Network models of fluid, hexatic and polymerized membranes, J. Phys.: Condens. Matter, 1997, 9(42), 8795–8834 CrossRef CAS.
- C. F. Schmidt, K. Svoboda, N. Lei, I. B. Petsche, L. E. Berman, C. R. Safinya and G. S. Grest, Existence of a flat phase in red-cell membrane skeletons, Science, 1993, 259(5097), 952–954 CrossRef CAS.
- M. S. Spector, E. Naranjo, S. Chiruvolu and J. A. Zasadzinski, Conformations of a tethered membrane: crumpling in graphitic oxide?, Phys. Rev. Lett., 1994, 73(21), 2867–2870 CrossRef CAS.
- S. Mora, J. Daillant, K. Mecke, D. Luzet, A. Braslau, M. Alba and B. Struth, X-Ray synchrotron study of liquid–vapor interfaces at short length scales: effect of long-range forces and bending energies, Phys. Rev. Lett., 2003, 90, 216101 CrossRef CAS.
- J. Daillant and M. Alba, High-resolution X-ray scattering measurements: I. surfaces, Rep. Prog. Phys., 2000, 63(10), 1725–1777 CrossRef CAS.
- A. Datta, S. Kundu, M. K. Sanyal, J. Daillant, D. Luzet, C. Blot and B. Struth, Dramatic enhancement of capillary wave fluctuations of a decorated water surface, Phys. Rev. E, 2005, 71(4) Search PubMed.
- J. Daillant, E. Bellet-Amalric, A. Braslau, T. Charitat, G. Fragneto, F. Graner, S. Mora, F. Rieutord and B. Stidder, Structure and fluctuations of a single floating lipid bilayer, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(33), 11639–11644 CrossRef CAS.
- C. Zakri, A. Renault, J.-P. Rieu, M. Vallade, B. Berge, J.-F. Legrand, G. Vignault and G. Grübel, Determination of the in-plane elastic tensor of crystalline decanol monolayers on water by X-ray diffraction, Phys. Rev. B, 1997, 55(21), 14163–14172 CrossRef CAS.
- D. M. Smilgies, High resolution grazing-incidence scattering using a combination of analyzer crystal and linear detector, Rev. Sci. Instrum., 2003, 74(9), 4041–4047 CrossRef CAS.
- B. Jancovici, Infinite susceptibility without long-range order: the two-dimensional harmonic “solid”, Phys. Rev. Lett., 1967, 19(1), 20–22 CrossRef CAS.
- D. R. Nelson and B. I. Halperin, Dislocation-mediated melting in two dimensions, Phys. Rev. B, 1979, 19(5), 2457–2484 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2009 |
Click here to see how this site uses Cookies. View our privacy policy here. 


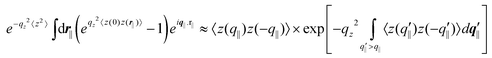

![Diffuse scattering differential cross-section dσ/dΩ as a function of the wavevector transfer q||. Pure water (empty squares). Behenic acid on a 1.88 × 10−5 mol l−1MgCl2 subphase (20 ions per headgroup) at pH = 10.5 (filled squares). Behenic acid on a 1.88 × 10−6 mol l−1MgCl2 subphase (2 ions per headgroup) at pH = 10.5 (empty circles). Behenic acid on a 8.46 × 10−6 mol l−1MnCl2 subphase (90 ions per headgroup) at pH = 7.5 (filled circles). Best fits are indicated by solid lines. The long-dashed line has ηk = 0[(q||−4) power law] and the short-dashed line has ηk = 0.65.](/image/article/2009/SM/b810134e/b810134e-f3.gif)
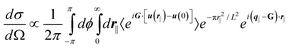
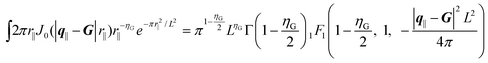
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) (
) (![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) and (02) reflections for behenic acid on a 8.46 × 10−5 mol l−1MnCl2 subphase (90 ions per headgroup) at pH = 7.5 to ηG ∝ Gηu, we find ηu = 1.35 ± 0.18 in the Mg2+ case and ηu = 1.47 ± 0.18 in the Mn2+ case. The value expected from the scaling relation ηu = 2 − 2ηk with ηk ≈ 0.25 ± 0.07 is ηu = 1.5 ± 0.14 and is in good agreement with the experimental values.
1) and (02) reflections for behenic acid on a 8.46 × 10−5 mol l−1MnCl2 subphase (90 ions per headgroup) at pH = 7.5 to ηG ∝ Gηu, we find ηu = 1.35 ± 0.18 in the Mg2+ case and ηu = 1.47 ± 0.18 in the Mn2+ case. The value expected from the scaling relation ηu = 2 − 2ηk with ηk ≈ 0.25 ± 0.07 is ηu = 1.5 ± 0.14 and is in good agreement with the experimental values.
