DOI:
10.1039/B811288F
(Paper)
Soft Matter, 2009,
5, 193-202
Received
3rd July 2008
, Accepted 20th August 2008
First published on 16th October 2008
Abstract
We have investigated the self-assembly and gelation properties of a set of four octa-peptides: AEAEAKAK, AEAKAEAK, FEFEFKFK and FEFKFEFK. The phenylalanine based peptides adopt β-sheet conformations in solution and the alanine based peptides form α-helices. No self-assembly in solution was observed for AEAKAEAK but AEAEAKAK was found to self-assemble forming thick, rigid fibres with a diameter of ∼6 nm. These fibres were composed of two fibrils aggregating side by side to form “pearl-necklace” morphologies. No gelation was observed for AEAEAKAK in the concentration range investigated (0 to 100 mg ml−1). In contrast, both phenylalanine based peptides were found to self-assemble in solution and to form hydrogels at an initial concentration of ∼8 mg ml−1. Similar morphologies were observed for both peptides corresponding to a relatively homogeneous dense network of semi-flexible fibres with a mesh size of ∼15 to 30 nm depending on the concentration. The fibre diameter was found to be ∼4 nm in good agreement with models found in the literature. TEM micrographs clearly showed that these fibres have a helicoidal or twisted structure. Comparison of TEM with AFM data highlighted the influence of substrate chemistry on the macromolecular assembly of small peptides. In contrast small angle neutron scattering (SANS) approaches, which allow for the probing of hydrogel morphology and structure without the need for sample preparation on solid substrates, provide vital data on hydrogel morphology in solution.
Introduction
Molecular self-assembly is a powerful mechanism for the preparation of materials with a wide variety of chemical and physical properties. The importance of this mechanism is evidenced by the abundant examples of protein self-assembly which exist in nature.1–5 Recently much research effort has been focused on using short peptides to create a new generation of self-assembled materials for use in biomedical applications.6–12Peptides are particularly promising as building blocks for a number of reasons. The natural amino acid pool consists of 20 members with different physical properties including polar, non-polar, acidic, basic and aromatic groups. In addition, an infinite number of artificial amino acids can be designed in the laboratory. These amino acids, both natural and artificial, can be combined in numerous ways to produce a wide variety of building blocks with different physical properties. The theoretical understanding of the molecular interactions and self-assembly rules in these materials is still, however, limited; consequently the fundamental links between building block structure, mesoscopic structure and material properties have not yet been elucidated.
Hydrogels formed from self-assembling peptides have attracted considerable attention in the past decade. These hydrogels are based on the self-assembly of short peptides into supra-molecular fibres that entangle or associate to form three dimensional networks and, ultimately, self-supporting hydrogels. Excluding amphiphilic peptides, which can self-assemble and form similar phases to traditional surfactants, there are two main categories of peptides used to form networks: α-helix and β-sheet forming peptides.6,8,13–16 In this article we compare the self-assembly and gelation properties of four octa-peptides inspired from the work of Zhang and co-workers that form either α-helix or β-sheet rich fibres.10,17–22 These authors have mainly focused their investigations on the self-assembly properties of longer peptides typically containing 12 to 16 amino acids. Their work suggests that most of the systems investigated self-assemble and form β-sheet rich structures. Less attention has been dedicated to the gelation properties of these peptides, in particular the structural characterisation of the gels, in relation to the conformation adopted by the peptide which is the subject of this article. The octa-peptides investigated here are based on four different amino acids: alanine (A), phenylalanine (F), lysine (K) and glutamic acid (E). Alanine and phenylalanine are both non-charged amino acids with the latter being the more hydrophobic. These two amino acids were used to modify the overall hydrophobicity of the octa-peptides. Lysine and glutamic acid are charged amino acids which carry a positive and a negative charge respectively at neutral pH. Four octa-peptides were synthesised using these four amino acids: AEAEAKAK, AEAKAEAK, FEFEFKFK and FEFKFEFK (Fig. 1). These octa-peptides are based on the alternation of one charged and one non-charged amino acid. The overall charge of the peptide was kept neutral in order to obtain a pH between 6 and 7 when dissolved in pure water. The self-assembly and gelation properties of our peptides were investigated using small angle neutron scattering (SANS), Fourier transform infrared spectroscopy (FTIR), atomic force microscopy (AFM) and transmission electron microscopy (TEM) combined with single particle averaging (SPA).
 |
| | Fig. 1 Molecular structures of the four peptides investigated: (a) AEAEAKAK; (b) AEAKAEAK; (c) FEFEFKFK; (d) FEFKFEFK. | |
Experimental section
Synthesis
The amino acid activator (HCTU) and Wang resin were purchased from Novabiochem (Merck) and used as received. All other reagents and solvents were purchased from Aldrich and used without further purification. The octa-peptides were synthesised by standard solid-phase methods using a ChemTech ACT 90 peptide synthesiser (Advance ChemTech Ltd, Cambridgeshire, UK). After cleavage from the resin and deprotection of the side groups and N-terminus using a TFA–anisole (95/5) mixture, the peptides were recovered in cold ether, centrifuged and freeze-dried. The synthesis yields ranged from 90 to 95%. HPLC, mass spectrometry and NMR were used to confirm the peptide structure and estimate their purity. The purity of all the octa-peptides synthesised was estimated by HPLC and MALDI-ToF to be >90%, the impurities corresponding mainly to shorter peptides sequences. The peptides were used without further purification.
Atomic force micoscopy (AFM)
Muscovite mica and metal AFM support stubs were obtained from Agar Scientific (Stansted, Essex, UK). Olympus high aspect ratio etched silicon probes with a nominal spring constant of 42 N m−1 were obtained from Veeco Instruments S.A.S (Dourdan, France). Peptide assemblies were imaged by AFM using a Veeco Multimode Scanning Probe Microscope with a Nanoscope IIIa controller. The resolution of the instrument in the x–y-axis is limited by the radius of curvature of the probe tip, the scan size and the number of sampled points per scan line. Using Olympus high aspect ratio etched silicon probes (radius of curvature <10 nm) to capture 2 × 2 µm images at 512 points per line, the effective x–y resolution equates to a pixel size of 3.9 nm. The instrumental resolution in the z-direction is less than 1 Å. Samples were prepared by incubating 100 µl of the peptide solution on a freshly cleaved mica sheet attached to an AFM support stub. The sample was left to gel overnight in a closed environment before being washed with 1 ml of distilled water. It was then allowed to air dry prior to imaging. Samples were imaged in intermittent contact mode in air. Cantilever oscillation varied between 300 and 350 kHz whilst the drive amplitude was determined by the Nanoscope software. Height and phase images were captured at a scan rate of 1.49 Hz with scan sizes of 5 or 2 µm2. The setpoint was adjusted to just below the point at which tip–sample interaction was lost and all images were captured at a relative humidity of <45%. The instrument was periodically calibrated using a grating with 180 nm deep, 10 µm2 depressions and tip deconvolution was performed using 10 nm gold particles deposited on mica. Height data was first-order flattened, and mean diameters were determined using the software package WSxM (Nanotec Electronica S.L.; http://www.nanotec.es). Correction for the over estimation of lateral dimensions due to tip geometry (tip broadening) was performed as reported in Sherratt et al.23 The true width (Wt) of a cylindrical polymer imaged by an AFM tip with a radius R can be calculated from the measured width at half maximum height (Wm):| |  | (1) |
Carbon-coated copper grids (no. 400) were glow discharged for 5 s and placed shiny side down on the surface of a 10 µl droplet of sample for fewer than 5 s. Loaded grids were immediately placed on a 10 µl droplet of double deionised water for 60 s and subsequently blotted. Washed grids were then placed on a 10 µl droplet of freshly prepared and filtered uranyl acetate solution (4% w/v) for 60 s for negative staining and then blotted continuously against double folded Whatman 50 filter paper. Data were recorded in a Tecnai 10 TEM operating at 100 keV (calibrated magnification of 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600×) onto Kodak SO-163 film. Images were subsequently scanned using a UMAX2000 transmission scanner providing a specimen level increment of 0.366 nm pixel−1.
ATR-FTIR experiments were performed on a Thermo Nicolet 5700 spectrometer using a Smart multi-Bounce ARK accessory (Thermo Nicolet) equipped with a zinc selenide crystal. Solutions and hydrogel samples were prepared by dissolving the desired amount of peptide in deuterated water at 90 °C in a small vial and then transferred onto the crystal for analysis. A background spectrum was subtracted from all the samples' spectra. Spectra were acquired in the 4000 to 400 cm−1 range with a resolution of 2 cm−1 over 128 scans.
600×) onto Kodak SO-163 film. Images were subsequently scanned using a UMAX2000 transmission scanner providing a specimen level increment of 0.366 nm pixel−1.
ATR-FTIR experiments were performed on a Thermo Nicolet 5700 spectrometer using a Smart multi-Bounce ARK accessory (Thermo Nicolet) equipped with a zinc selenide crystal. Solutions and hydrogel samples were prepared by dissolving the desired amount of peptide in deuterated water at 90 °C in a small vial and then transferred onto the crystal for analysis. A background spectrum was subtracted from all the samples' spectra. Spectra were acquired in the 4000 to 400 cm−1 range with a resolution of 2 cm−1 over 128 scans.
Small angle neutron scattering (SANS)
SANS experiments were performed at the Forshungszentrum Jülich (FRJ-2) on diffractometer KWS-2. The white beam was monochromated with a velocity selector by Dornier. The neutron wavelength was λ = 0.48 nm with a wavelength distribution characterised by a full width at half maximum Δλ/λ = 0.1. Samples were irradiated on an area of 0.8 × 0.8 cm2. The beamline was equipped with a two-dimensional detector with a 50 × 50 cm2 active area with a spatial resolution of 0.8 × 0.8 cm2 (further details are available on request at Forshungszentrum Jülich). By varying the sample–detector distance, the available momentum transfer vector (q) was in the range 0.1 < q (nm−1) < 2.4, with q = (4π/λ)sin(θ/2), where θ is the scattering angle. The collected data were corrected for the detector efficiency and dark current background. Counter normalization was achieved by using the incoherent scattering of an amorphous hydrogenous poly(methyl methacrylate) secondary standard. After ensuring the scattering was isotropic, the data were radially averaged to obtain a one-dimensional scattering curve. Under these conditions the normalized intensity scattered by a sample is:| |  | (2) |
where I(q), δ, and T are the normalized measured intensity, the thickness, and the transmission of the sample (s) and the empty cell (e) respectively. To extract the coherent intensity scattered by the peptides, we subtracted the coherent intensity scattered by the solvent and the incoherent intensity scattered by the peptide and the solvent from the total scattered intensity. The coherent intensity scattered by the peptides in absolute units is then:| |  | (3) |
where ID(q) is the normalized intensity scattered by the deuterated solvent, CP the peptide concentration in g cm−3, Ib the background scattering mainly due to the incoherent scattering of the hydrogenous peptides and K the contrast factor expressed as:24| |  | (4) |
where ap and as are the scattering lengths of the peptides and the solvent respectively, Yps the molar volume ratio (vp/vs) between the protein and the solvent, NA the Avogadro number and mp the peptide molar mass. The peptides’ molar volumes were estimated by adding the molar volume values reported by Jacrot and Zaccai for each amino acid in the sequence and the peptides’ scattering lengths were calculated using the scattering lengths listed by Jacrot and Zaccai for each amino acid at pH 7 assuming that all labile hydrogens on the peptides were exchanged with deuterium.25 The background scattering, Ib, was estimated using the Porod law which gives the scattered intensity of a two phase system at high q values:24,26,27| |  | (5) |
where KP is the Porod constant. Ib was estimated by fitting the last 10 data points of the scattering curves using a Porod representation (q4I(q)vs. q4). To estimate the influence of Ib subtraction on the overall shape of the scattering curve error bars have been calculated by varying the value of Ib by ±5%. For clarity purposes the SANS data presented in this article are limited to the q region where the coherent scattering is dominant, typically 0 to 1.6 nm−1, while Ib was evaluated at high q values, typically 2.0 to 2.4 nm, where the background scattering is dominant. Solutions and hydrogel samples for neutron experiments were prepared by dissolving the desired amount of peptide in deuterated water at 90 °C directly in HELLMA quartz cells with an optical path length of 2 and 5 mm depending on the sample concentration. Deuterated water (D2O) was used instead of hydrogenated water to increase the contrast between the peptides and the solvent. Samples were prepared on site and annealed for 2 h at room temperature prior to collecting data.
Results and discussion
The exact definition of a gel is still a matter of debate in the literature.1 Here, we define a gel as a material that can be extracted from its container without losing its shape and that is self-supporting when placed on a flat surface. In order to investigate the self-assembly and gelation properties of our peptides, solutions with varying concentrations were prepared in pure water at high temperature (∼90 °C) and subsequently cooled to room temperature. Gelation, which occurred on cooling, was dependent on the peptide and the concentration used.
For phenylalanine based peptides (FEFEFKFK and FEFKFEFK) transparent gels were obtained for concentrations higher than ∼8 mg ml−1 and clear transparent viscous solutions for lower concentrations. For alanine based peptides (AEAEAKAK and AEAKAEAK) no gels were obtained in the concentration range investigated: 0 to 100 mg ml−1. For the AEAEAKAK peptide transparent viscous solutions were obtained. The viscosity of the solution was found to increase with increasing concentration suggesting that, although no gelation is observed, this peptide self-assembles. For the AEAKAEAK peptide no significant increase in viscosity in comparison with pure water was observed even at high concentrations suggesting that this peptide does not self-assemble in water and remains fully dissolved at room temperature.
The SANS curves obtained for the alanine based peptide solutions at different concentrations are shown in a Kratky representation [q2I(q)vs. q] in Fig. 2. As can be seen, the coherent scattering obtained for the AEAKAEAK peptide is very low and independent of q confirming our earlier postulation that this peptide does not self-assemble in solution. On the other hand “bell-shaped” scattering curves with linear slopes at low q were obtained for the AEAEAKAK peptide. Such linearity at low q is characteristic of the scattering of rod-like structures in solution.1,24,26–29
![Kratky [q2IA(q)vs. q] plot of the intensity scattered at room temperature by 10 (○) and 80 (●) mg ml−1AEAEAKAK solutions and 10 (◇) and 40 (◆) mg ml−1AEAKAEAK solutions prepared in D2O.](/image/article/2009/SM/b811288f/b811288f-f2.gif) |
| | Fig. 2 Kratky [q2IA(q)vs. q] plot of the intensity scattered at room temperature by 10 (○) and 80 (●) mg ml−1AEAEAKAK solutions and 10 (◇) and 40 (◆) mg ml−1AEAKAEAK solutions prepared in D2O. | |
For a rod-like structure with cylindrical symmetry in the q range investigated the scattered intensity can be written as:1,24,26,27
| | | q2IA(q) = πqCpµLf(qRσ) + Cst | (6) |
where
µL is the mass per unit length of the rod in g mol
−1 nm
−1,
Cp the
peptide concentration in g cm
−3 and
f(
qRσ) represents the cross-section scattering of the rod,
Rσ being the cross-section radius of gyration of the rod.
Cst is a constant term taking into account inter-scattering effects. For
qRσ < 1
eqn (6) reduces to:
1,24,26,27| |  | (7) |
If the scattering observed is of the form described by eqn (7) then at low q a linear curve should be obtained in a ln[qIA(q)] vs. q2 representation. From the slope and the intersection between the curve and the y-axis Rσ and µL can be estimated respectively. The scattering curves obtained for the AEAEAKAK peptide at 40 and 80 mg ml−1 are presented in Fig. 3 by mean of a ln[qI(q)]vs. q2 representation. As can be seen linear curves are obtained at low q for both concentrations confirming that the peptide has self-assembled into rod-like structures. The following values were estimated for Rσ and µL by fitting the linear part of the curves using relation (7):
![ln[qI(q)]
vs. q2 plot of the intensity scattered at room temperature by 10 (○) and 80 (●) mg ml−1AEAEAKAK solutions prepared in D2O. Dotted lines represent the best fit obtained using eqn (7) (see text for details).](/image/article/2009/SM/b811288f/b811288f-f3.gif) |
| | Fig. 3
ln[qI(q)]
vs. q2 plot of the intensity scattered at room temperature by 10 (○) and 80 (●) mg ml−1AEAEAKAK solutions prepared in D2O. Dotted lines represent the best fit obtained using eqn (7) (see text for details). | |
As can be seen similar values were obtained for Rσ and µL at both concentrations suggesting that the same self-assembled rod-like structures are formed across the concentration range investigated.
At low resolution the scattering of rod-like structures or fibres can be approximated by the scattering of infinitely long cylinders. In this case f(qr) is a function of ρ(r), the density of scattering centres across the cylinder cross-section:30
| |  | (8) |
J0 being the zero order Bessel function. For a homogeneous plain-cylinder of radius
rpc,
ρ(
r) = 1 for 0 <
r <
rpc and
ρ(
r) = 0 for
r >
rpc. Therefore:
| |  | (9) |
where
r is the radius of the cylinder and
J1 the first-order Bessel function and the intensity scattered by a plain-cylinder is:
30| |  | (10) |
This relation was used to fit our
experimental data. The scattered intensities obtained for the AEAEAKAK
peptide at 40 and 80 mg ml
−1 scale with concentration and the scattering curves go through the origin (
Fig. 2) therefore we assume
Cst = 0. The
peptide concentration
Cp being known, there are only two fitting parameters for this model the linear mass,
µL, and the radius,
r. The absolute scattered intensities of AEAEAKAK
peptide solutions are presented with the best fit obtained in
Fig. 4. As can be seen, very good fits were obtained at both concentrations using this plain-cylinder model. From the fitting the radius and the linear mass of the rods were estimated:
![Kratky [q2IA(q)vs. q] plot of the intensity scattered at room temperature by 10 (○) and 80 (●) mg ml−1AEAEAKAK solutions prepared in D2O. Dotted lines represent the best fit obtained using eqn (10) (see text for details).](/image/article/2009/SM/b811288f/b811288f-f4.gif) |
| | Fig. 4 Kratky [q2IA(q)vs. q] plot of the intensity scattered at room temperature by 10 (○) and 80 (●) mg ml−1AEAEAKAK solutions prepared in D2O. Dotted lines represent the best fit obtained using eqn (10) (see text for details). | |
The values obtained for µL are in good agreement with the values obtained above. The linear mass obtained is roughly three times the molar mass of the peptide (816 g mol−1). It should be kept in mind that µL is very sensitive to the normalization of the intensity and therefore to the assumptions made in the calculation of the contrast factor. In addition the concentration term Cp in eqn (10) was taken assuming all peptide molecules present in the sample self-assemble into fibres. The presence of some dissolved peptide in the water phase would result in an over estimation of the concentration term Cp and therefore in an under estimation of the true linear mass of the fibres. The linear mass µL obtained through this methodology should therefore be seen as a lower limit for the real linear mass, more than as an exact value. For a plain-cylinder model the cross-section radius of gyration, Rσ, and radius, r, are related through:
| |  | (11) |
For
r = 3.3 nm a value of 2.3 nm is obtained for
Rσ which is in very good agreement with the value obtained previously. When evaluating
Rσ in the low
q region no assumption was made on the overall internal structure of the fibres (
e.g.: plain or hollow). On the other hand when the plain cylindrical model was used to fit the scattering curves over the full
q range available the assumption that the fibres are plain was made. The relation between
Rσ and
r depends on the fibre internal structure and is different for a hollow fibre. The good agreement between the values of
Rσ derived from both approaches shows that the plain cylindrical model used is self-consistent suggesting that the fibres are indeed plain.
In order to confirm the presence of rod-like structures, or, in other words, fibres, microscopy experiments were performed using AFM and TEM. A typical AFM height micrograph obtained for the AEAEAKAK peptide is presented in Fig. 5a. No fibrillar structures were observed; instead numerous isolated “disc-like” peptide islands with an average diameter of ∼34 nm and an average height of ∼0.6 nm were present. In contrast the TEM micrograph in Fig. 5b clearly shows the presence of long rigid fibres with an average width of 7 to 9 nm. This value is slightly larger than the one obtained viaSANS. This difference is probably due to the fact that with TEM we observe the width of the fibres as they lie flat on the substrate, while in SANS the diameter measured is the average apparent diameter of the fibres which depends on both their width and thickness. Image analysis of the fibres reveals the presence of an internal structure (insert Fig. 5b). The fibres seem to be formed by the lateral association of two smaller fibrils with “pearl-necklace” like (string of “spherical” domains joined together) morphologies. The fibres observed viaTEM seem to have a relatively long persistence length (several millimetres long) and there is no clear evidence of branching.
 |
| | Fig. 5 (a) AFM micrograph of a freshly prepared AEAEAKAK solution (0.25 mg ml−1) dried on a negatively charged mica sheet and (b) TEM micrograph of a freshly prepared AEAEAKAK solution (2 mg ml−1) dried on a discharged carbon-coated copper grid (inset: high magnification image of a single fibre). | |
The difference between the morphologies observed viaAFM and TEM underline the important effects that peptide–surface interactions have on the self-assembly of peptides. In the case of AFM the solutions were dried slowly directly onto a non treated, highly negatively charged mica surface.31 Our peptides carry polar groups and are expected therefore to interact strongly with charged surfaces through electrostatic interactions. In the case of the AEAEAKAK peptide this evidently results in an unfavourable interaction between the fibre in solution and the mica surface resulting in the system wanting to minimise the interaction with the surface. This probably results in either the self-assembled fibres being destroyed during the drying process and the peptide lying on the surface in small “islands” or the fibres simply coiling forming Gaussian coils lying on the surface in a similar manner to polymers.32,33
To confirm the dramatic role that surface charge can have on peptide self-assembly AFM and TEM images were obtained (Fig. 6) for the AEAKAEAK peptide. Although no self-assembly was observed in solution by SANS for this peptide, the AFM micrograph, Fig. 6a, clearly shows the presence of self-assembled structures. Short, stiff rods are observed with an average width of ∼6 nm and an average height of ∼0.7 nm. Branching of the rods can be observed. The absence of any self-assembly in solution as shown by SANS suggests that the rod structure observed in the AFM image probably result from a surface induced self-assembling process. These structures are reminiscent of self-assembled elastin-like peptides on HOPG.34–36 The TEM micrograph on the other hand reveals the presence of a very small number of fibres of varying diameter suggesting that some self-assembly can also be induced by the TEM grid and/or the drying process. It should be noted that no clear internal structure can be observed in this case in comparison to AEAEAKAK suggesting a very different self-assembled structure.
 |
| | Fig. 6 (a) AFM micrograph of a freshly prepared AEAKAEAK solution (0.025 mg ml−1) dried on a negatively charged mica sheet and (b) TEM micrograph of a freshly prepared AEAEAKAK solution (2 mg ml−1) dried on a discharged carbon-coated copper grid. (Inset: high magnification image of single fibre.) | |
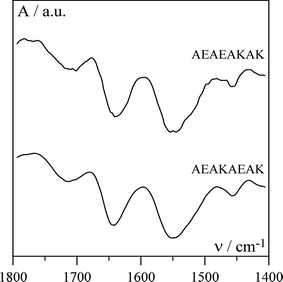
To probe the conformation adopted by the peptides each solution was examined using FTIR and typical spectra obtained for AEAEAKAK and AEAKAEAK solutions are given in Fig. 7. The presence of a broad band at 1643 cm−1 suggests that the backbones of both peptides adopt an α-helical conformation (Fig. 8).37 This is expected as alanine, lysine and glutamic acid are among the strongest α-helix forming amino acids.38 α-Helices are known to self-assemble through hydrophobic interactions to form supra-molecular structures. A large variety of these types of structures have been found in protein conformations and range in size from dimers to much larger aggregates that can involve tens of helices.39–41 α-Helix forming peptides can also be designed to form a variety of fibre morphologies as shown by Woolfson.9 As can be seen from Fig. 8 both our alanine based peptides present two hydrophobic “patches” on opposite sides along the long axes of the α-helix suggesting that both peptides have the ability to self-assemble to form long aggregated chains.39 The main difference between these two peptides is the arrangement of their polar groups. For the AEAEAKAK peptide one lysine and one glutamic acid side group are present on each side of the helix (Fig. 8). The lysine and glutamic acids carry opposite charges and are expected to interact with each other resulting in the stabilisation of the α-helical structure.42 In addition these side chains will be driven away from the hydrophobic “patches” allowing the α-helices to aggregate to form supra-molecular fibres through hydrophobic interactions. On the other hand for the AEAKAEAK peptide both lysine and glutamic acid residues are present on the same sides of the helix (Fig. 8). In this case the two side chains are expected to interact with each other resulting in the destabilisation of the α-helical structure.42 In this case the side chains are being driven away from each other and towards the hydrophobic “patches” interfering with the α-helix–α-helix hydrophobic interactions and disrupting the self-assembly of this peptide in solution. Although hydrophobic interactions have been shown to be key to the coil–coil self-assembly of α-helices, the distribution of polar groups along the helix can also have a dramatic effect on the self-assembly and gelation properties of these peptides.9 The exact internal structure of the observed fibres is not known at this point in time and additional work is under way to try to elucidate this.
 |
| | Fig. 8 Schematic representation (left—side view; right—top view) of the alanine based peptides α-helices. Shaded areas represent the hydrophobic “patches” formed by the alanine residues on each side of the helices (for more details see text). | |
Pheylalanine based peptides FEFEFKFK and FEFKFEFK
SANS was also used to investigate the phenylalanine based peptides. The intensities scattered by these peptides at different concentrations are presented in Fig. 9. In this case the results obtained for the two peptides, FEFEFKFK and FEFKFEFK, are similar. As stated previously the critical gelation concentration for these peptides was found to be ∼8 mg ml−1. For concentrations higher than the critical gelation concentration an intensity maxima is observed (Fig. 9) suggesting the presence of a relatively regular dense network morphology. Neutron scattering is sensitive to the difference in scattering density between phases, here the scattering density difference between the peptide-rich phase, the network, and the peptide-poor phase, the solvent. Scattering patterns for multiphase systems at high concentrations are a complex function of the structure and the arrangement of the different scattering phases. A rigorous interpretation of the origin of a single scattering peak in a SANS curve can be made only for specific arrangements and structures. In our case only an estimated value of the average size of the scattering density fluctuation of the observed morphology, d, can be obtained from the position of the peak maximum, through the Bragg relation:| |  | (12) |
were q* is the position of the intensity maxima. d can be seen as an estimate of the gel network mesh size.24,27 As expected d decreases with increasing concentration for both phenylalanine based peptides from 30 ± 3 nm for the 10 mg ml−1 sample to 15 ± 3 nm for the 40 mg ml−1 sample. Provided that the network structure is the same across the concentration range investigated the network mesh size is expected to decrease with increasing concentration due to an increase in fibre density. These results show that concentration can be used to control the mesh size and porosity of these gels.
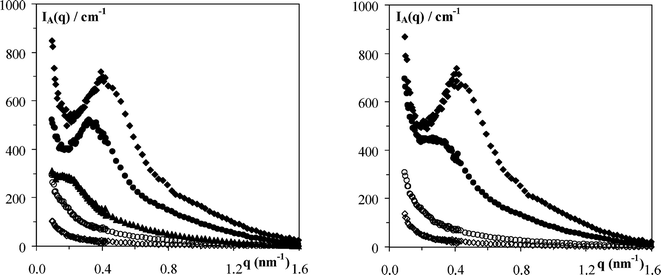 |
| | Fig. 9
I
A(q)
vs. q plot of the intensity scattered at room temperature for: left 2 (◇), 5 (○), 10 (▲), 30 (●) and 40 (◆) mg ml−1FEFEFKFK solutions/gels and right 2(◇), 5 (○), 20 (●) and 40 (◆) mg ml−1FEFKFEFK solutions/gels prepared in pure D2O. | |
For the scattering patterns obtained at concentrations below the critical gelation concentration the same analysis as performed for the alanine based peptides can be applied provided the inter-scattering terms are negligible. The scattering curves obtained for the two peptides at concentrations of 2 and 5 mg ml−1 are presented in a Kratky representation in Fig. 10. For both peptides the scattered intensity scales with concentration and the curves are found to go through the origin suggesting that the inter-scattering terms are indeed negligible and Cst = 0. Eqn (10), which describes the scattering of a plain-cylinder, was therefore used again to fit the scattering curves obtained (Fig. 10). The following values were estimated for the linear mass, µL, and the radius, r, of the fibres:
![Kratky [q2IA(q)vs. q] plot of the intensity scattered at room temperature for: left 2 (◇) and 5 (○) mg ml−1FEFEFKFK solutions and right 2 (◆) and 5 (○) mg ml−1FEFEFKFK solutions prepared in pure D2O. Dotted lines represent the best fit obtained using eqn (10) (see text for details).](/image/article/2009/SM/b811288f/b811288f-f10.gif) |
| | Fig. 10 Kratky [q2IA(q)vs. q] plot of the intensity scattered at room temperature for: left 2 (◇) and 5 (○) mg ml−1FEFEFKFK solutions and right 2 (◆) and 5 (○) mg ml−1FEFEFKFK solutions prepared in pure D2O. Dotted lines represent the best fit obtained using eqn (10) (see text for details). | |
The fibre diameter (2r) obtained is roughly equal to the width of a single octa-peptide molecule in its fully extended conformation (∼3 nm) and is half the diameter obtained for the AEAEAKAK peptide fibres. The linear mass obtained in this case is roughly twice the molar mass of a single peptide molecule (1136 g mol−1). Again it should be kept in mind that the linear mass obtained through this should be seen as a lower limit value for the true linear mass of the fibre, rather than as an exact value.
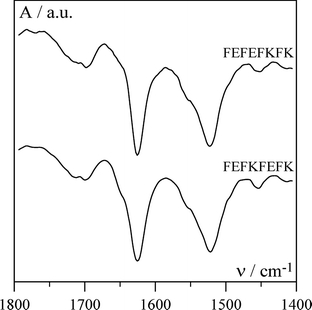
AFM and TEM were used to confirm the presence of fibres and the micrographs obtained for FEFEFKFK are given in Fig. 11. Essentially identical micrographs were obtained for FEFKFEFK (data not shown). As can be seen the micrographs obtained using these two microscopy techniques are similar suggesting that in this case the peptide–surface interactions are less prominent and do not affect the morphology of the fibres. A relatively regular dense network of fibres with diameters of 4–5 nm is observed which is in good agreement with the type of morphology suggested by our SANS experiments. The fibres forming the network seem to be relatively homogeneous in size and no large “bundles” are observed. These results are in agreement with Leon et al. who investigated the same system using SEM.43 Typical FTIR spectra obtained for our samples are presented in Fig. 12. As can be seen a strong absorption band is observed at 1625 cm−1 with a weaker band present at 1695 cm−1. These two bands are characteristic of the presence of anti-parallel β-sheets.37,44 This result indicates that phenylalanine based peptides form anti-parallel β-sheet rich fibres as already shown by Zhang and co-workers.43,45 These authors have performed an extensive investigation on the self-assembly properties of β-sheets forming ionic complementary peptides.46 A molecular model of a flat anti-parallel β-sheet formed by our FEFEFKFK peptides is presented in Fig. 13. As can be seen the width of such a structure (∼4 nm) is in very good agreement with the fibre sizes obtained viaSANS and TEM. All the phenyl rings are located on the same side of the β-sheet (Fig. 13) while the polar groups are located on the opposite side resulting in the β-sheet having a hydrophobic and a hydrophilic face. This results in two β-sheets coming together in order to bury their hydrophobic faces.45,46 Aggeli and co-workers have developed a model describing the self-assembly of the β-sheet rich fibres, referred to as nanotapes by these authors, and showed that with increasing concentration the formation of helical or twisted structures is expected.47,48 Additional examination of the AFM and TEM micrographs revealed alternating bright and dark “patches” running along the fibre axis. A projected average of the fibre observed in the TEM micrographs (Fig. 11b insert) presented a periodic alternation of electron density with a pitch of ∼55° and a repeat distance along the fibre axes of ∼4.5 nm. This is consistent with the formation of a regular helical fibre or twisted structure.
 |
| | Fig. 11 (a) AFM micrograph of a freshly prepared FEFEFKFK solution (0.25 mg ml−1) dried on a negatively charged mica sheet and (b) TEM micrograph of a freshly prepared FEFEFKFK solution (2 mg ml−1) dried on a discharged carbon-coated copper grid. (Inset: high magnification image of single fibre.) | |
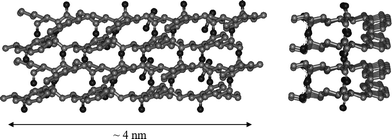 |
| | Fig. 13 Schematic representation (left—top view; right—side view) of four FEFEFKFK peptides in an anti-parallel β-sheet. | |
Conclusion
We have investigated the self-assembly and gelation properties of a set of four octa-peptides: AEAEAKAK, AEAKAEAK, FEFEFKFK and FEFKFEFK. Phenylalanine based peptides adopt a β-sheet conformation in solution while alanine based peptides adopt an α-helix conformation instead. No self-assembly in solution was observed for AEAKAEAK. AEAEAKAK was found to self-assemble and form thick rigid fibres with a diameter of ∼6 nm. The fibres were formed from two laterally aggregated fibrils which exhibited “pearl-necklace” morphologies. No gelation was observed for this peptide in the concentration range investigated (0 to 100 mg ml−1). Phenylalanine based peptides were found to self-assemble in solution and they formed hydrogels for concentrations higher than ∼8 mg ml−1. Similar morphologies were observed for both peptides; a relatively homogeneous dense network of semi-flexible fibres with a mesh size ∼15 to 30 nm which decreased with increasing concentration. The fibre diameter was found to be ∼4 nm in good agreement with the models proposed by Aggeli et al.47 and Zhang et al.49 of two β-sheets aggregating together to bury their hydrophobic faces. TEM micrographs clearly showed that these fibres have a helical or twisted structure.
AFM and TEM have been extensively used to characterise the self-assembling behaviour of short peptides.13,17,18,50–56Microscopy techniques which rely on adsorption onto surfaces can induce conformational changes in probed molecules. AFM, in particular, due to its high sensitivity has been extensively used to identify surface induced conformational changes in biomacromolecules.23,57SANS was shown to be a key complementary tool in the investigation of our peptide systems as it allows probing the morphology and structure of hydrogels directly in solution with no need for any sample preparation.
It is interesting to note that the morphology observed viaAFM for alanine based peptides, that form α-helix rich fibres in solution, is strongly affected by peptide–surface interactions. On the other hand the morphology observed viaAFM for phenylalanine based peptides, that form β-sheet rich fibres, doesn't seem to be affected by the charged surface used and was in good agreement with the morphology suggested by our TEM and SANS experiments. In addition, for alanine based peptides the position of the polar groups along the peptide was found to have a strong effect on the self-assembly properties of the peptide while this was not the case for the phenylalanine based peptide. This marked difference is probably due to the very different nature of the intra-fibre interactions that drive the self-assembly of the peptides into fibres. For β-sheet rich fibres the self-assembly is driven by strong hydrogen bonding interactions along the fibre axes. These interactions are highly directional and link each peptide in the β-sheet to the previous and the next one in the chain creating a very stable structure. As a consequence, in this system the position of the polar group does not play a key role in the self-assembly mechanism of the peptide. In the case of alanine based peptides, self-assembly of the α-helices into fibres occurs through hydrophobic interactions. The position of the hydrophobic “patches” along the α-helix plays a key role in the ability of the peptide to self-assemble into long fibres. The strength of the inter-peptide interactions holding the fibre together are weaker resulting in these systems being more sensitive to charged surfaces and polar group positions. As a result, additional cooperative interactions to stabilise the structure are needed, which results in a higher peptide aggregation order (i.e. a higher number of peptides per fibre repeat unit). As a consequence more complex internal fibre structures are observed. The alanine based peptides also tend to form thicker and more rigid fibres probably resulting in a higher critical gelation concentration.58
Acknowledgements
The authors are grateful to the Leverhulme Trust (research grant F/00 120/AR), the Royal Society (research grant 24184) and the European Commission 6th Framework Programme (Key Action: Strengthening the European Research Area, Research Infrastructures. Contract no.: RII3-CT-2003-505925) for financial support. M.J. Sherratt is a Research into Ageing Senior Research Fellow.
References
-
J.-M. Guenet, Thermoreversible Gelation of Polymers and Biopolymers, Academic Press, London, 1992 Search PubMed.
- W. S. Gosal, A. H. Clark, P. D. A. Pudney and S. B. Ross-Murphy, Langmuir, 2002, 18, 7174–7181 CrossRef CAS.
- H. Yan, H. Frielinghaus, A. Nykanen, J. Ruokolainen, A. Saiani and A. F. Miller, Soft Matter, 2008, 4, 1313–1325 RSC.
- H. Yan, A. Saiani, J. E. Gough and A. F. Miller, Biomacromolecules, 2006, 7, 2776–2782 CrossRef CAS.
- Y. Takeuchi, H. Uyama, N. Tomoshige, E. Watanabe, Y. Tachibana and S. Kobayasi, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 671–675 CrossRef CAS.
- R. J. Mart, R. D. Osborne, M. M. Stevens and R. V. Ulijn, Soft Matter, 2006, 2, 822–835 RSC.
- I. W. Hamley, Angew. Chem., Int. Ed., 2007, 46, 8128–8147 CrossRef CAS.
- R. P. Nagarkar, R. A. Hule, D. J. Pochan and J. P. Schneider, J. Am. Chem. Soc., 2008, 130, 4466–4474 CrossRef CAS.
-
D. N. Woolfson, in Fibrous Proteins: Coiled-Coils, Collagen and Elastomers, 2005, vol. 70, pp 79 Search PubMed.
- S. G. Zhang, Biotechnol. Adv., 2002, 20, 321–339 CrossRef CAS.
- F. Gelain, A. Horii and S. G. Zhang, Macromol. Biosci., 2007, 7, 544–551 CrossRef CAS.
- P. Chen, Colloids Surf. A.: Physicochemical and Engineering Aspects, 2005, 261, 3–24 Search PubMed.
- S. G. Zhang, Nat. Biotechnol., 2003, 21, 1171–1178 CrossRef CAS.
- R. V. Ulijn and A. M. Smith, Chem. Soc. Rev., 2008, 37, 664–675 RSC.
- A. Tinti, M. Di Foggia, P. Taddei, A. Torreggiani, M. Dettin and C. Fagnano, J. Raman Spectrosc., 2008, 39, 250–259 CrossRef CAS.
- R. Gambaretto, L. Tonin, C. Di Bello and M. Dettin, Biopolymers, 2008 DOI:10.1002/bip.21030.
- Y. S. Hong, R. L. Legge, S. Zhang and P. Chen, Biomacromolecules, 2003, 4, 1433–1442 CrossRef CAS.
- S. Jun, Y. Hong, H. Imamura, B. Y. Ha, J. Bechhoefer and P. Chen, Biophys. J., 2004, 87, 1249–1259 CrossRef CAS.
- M. R. Caplan, P. N. Moore, S. G. Zhang, R. D. Kamm and D. A. Lauffenburger, Biomacromolecules, 2000, 1, 627–631 CrossRef CAS.
- M. R. Caplan, E. M. Schwartzfarb, S. G. Zhang, R. D. Kamm and D. A. Lauffenburger, J. Biomater. Sci., Polym. Ed., 2002, 13, 225–236 CrossRef CAS.
- M. R. Caplan and D. A. Lauffenburger, Ind. Eng. Chem. Res., 2002, 41, 403–412 CrossRef CAS.
- M. R. Caplan, E. M. Schwartzfarb, S. G. Zhang, R. D. Kamm and D. A. Lauffenburger, Biomaterials, 2002, 23, 219–227 CrossRef CAS.
- M. J. Sherratt, D. V. Bax, S. S. Chaudhry, N. Hodson, J. R. Lu, P. Saravanapavan and C. M. Kielty, Biomaterials, 2005, 26, 7192–7206 CrossRef CAS.
-
J. S. Higgins and H. C. Benoit, Polymer and Neutron Scattering, Clarendon Press, Oxford, 1994 Search PubMed.
- B. Jacrot and G. Zaccai, Biopolymers, 1981, 20, 2413–2426 CrossRef CAS.
-
R.-J. Roe, Methods of X-Ray and Neutron Scattering in Polymer Science, Oxford University Press, New York, 2000 Search PubMed.
-
A. Guinier and G. Fournet, Small-Angle Scattering of X-Rays, John Wiley & Sons, Inc., New York, 1955 Search PubMed.
- A. Saiani and J. M. Guenet, Macromolecules, 1997, 30, 966–972 CrossRef CAS.
- A. Saiani and J. M. Guenet, Macromolecules, 1999, 32, 657–663 CrossRef CAS.
- G. Oster and D. P. Riley, Acta. Crystallogr., 1952, 5, 272–276 CrossRef CAS.
- M. J. Sherratt, C. Baldock, A. Morgan and C. M. Kielty, Matrix Biol., 2007, 26, 156–166 CrossRef CAS.
- S. S. Sheiko and M. Moller, Chem. Rev., 2001, 101, 4099–4123 CrossRef CAS.
- C. Rivetti, M. Guthold and C. Bustamante, J. Mol. Biol., 1996, 264, 919–932 CrossRef CAS.
- G. C. Yang, K. A. Woodhouse and C. M. Yip, J. Am. Chem. Soc., 2002, 124, 10648–10649 CrossRef CAS.
- S. V. Patwardhan, R. Maheshwari, N. Mukherjee, K. L. Kiick and S. J. Clarson, Biomacromolecules, 2006, 7, 491–497 CrossRef CAS.
- H. G. Cui, V. Krikorian, J. Thompson, A. P. Nowak, T. J. Deming and D. J. Pochan, Macromolecules, 2005, 38, 7371–7377 CrossRef CAS.
- A. Barth and C. Zscherp, Q. Rev. Biophys., 2002, 35, 369–430 CrossRef CAS.
- P. Y. Chou and G. D. Fasman, Trends Biochem. Sci., 1977, 2, 128–131 CrossRef CAS.
- J. Walshaw and D. N. Woolfson, Protein Sci., 2001, 10, 668–673 CrossRef CAS.
- J. Liu, Y. Q. Deng, Q. Zheng, C. S. Cheng, N. R. Kallenbach and M. Lu, Biochemistry, 2006, 45, 15224–15231 CrossRef CAS.
- J. Liu, Q. Zheng, Y. Q. Deng, C. S. Cheng, N. R. Kallenbach and M. Lu, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15457–15462 CrossRef CAS.
- T. M. Iqbalsyah and A. J. Doig, Biochemistry, 2005, 44, 10449–10456 CrossRef CAS.
- E. J. Leon, N. Verma, S. G. Zhang, D. A. Lauffenburger and R. D. Kamm, J. Biomater. Sci., Polym. Ed., 1998, 9, 297–312 CrossRef CAS.
- A. Barth, Prog. Biophys. Mol. Biol., 2000, 74, 141–173 CrossRef CAS.
- S. G. Zhang, T. Holmes, C. Lockshin and A. Rich, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 3334–3338 CAS.
- W. M. Hwang, D. M. Marini, R. D. Kamm and S. Q. Zhang, J. Chem. Phys., 2003, 118, 389–397 CrossRef CAS.
- A. Aggeli, I. A. Nyrkova, M. Bell, R. Harding, L. Carrick, T. C. B. McLeish, A. N. Semenov and N. Boden, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 11857–11862 CrossRef CAS.
- C. W. G. Fishwick, A. J. Beevers, L. M. Carrick, C. D. Whitehouse, A. Aggeli and N. Boden, Nano Lett., 2003, 3, 1475–1479 CrossRef CAS.
- D. M. Marini, W. Hwang, D. A. Lauffenburger, S. G. Zhang and R. D. Kamm, Nano Lett., 2002, 2, 295–299 CrossRef CAS.
- A. Aggeli, M. Bell, N. Boden, J. N. Keen, P. F. Knowles, T. C. B. McLeish, M. Pitkeathly and S. E. Radford, Nature, 1997, 386, 259–262 CrossRef CAS.
- R. P. W. Davies, A. Aggeli, A. J. Beevers, N. Boden, L. M. Carrick, C. W. G. Fishwick, T. C. B. McLeish, I. Nyrkova and A. N. Semenov, Supramol. Chem., 2006, 18, 435–443 CrossRef CAS.
- L. Carrick, M. Tassieri, T. A. Waigh, A. Aggeli, N. Boden, C. Bell, J. Fisher, E. Ingham and R. M. L. Evans, Langmuir, 2005, 21, 3733–3737 CrossRef CAS.
- S. G. Zhang and M. Altman, React. Funct. Polym., 1999, 41, 91–102 CrossRef CAS.
- S. G. Zhang, D. M. Marini, W. Hwang and S. Santoso, Curr. Opin. Chem. Biol., 2002, 6, 865–871 CrossRef CAS.
- M. J. Krysmann, V. Castelletto, A. Kelarakis, I. W. Hamley, R. A. Hule and D. J. Pochan, Biochemistry, 2008, 47, 4597–4605 CrossRef CAS.
- C. Whitehouse, J. Y. Fang, A. Aggeli, M. Bell, R. Brydson, C. W. G. Fishwick, J. R. Henderson, C. M. Knobler, R. W. Owens, N. H. Thomson, D. A. Smith and N. Boden, Angew. Chem., Int. Ed., 2005, 44, 1965–1968 CrossRef CAS.
- M. Bergkvist, J. Carlsson and S. Oscarsson, J. Biomed. Mater. Res., Part A, 2003, 64A, 349–356 CrossRef CAS.
- F. Tanaka and T. Koga, Bull. Chem. Soc. Jpn., 2001, 74, 201–215 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2009 |
Click here to see how this site uses Cookies. View our privacy policy here. 

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600×) onto Kodak SO-163 film. Images were subsequently scanned using a UMAX2000 transmission scanner providing a specimen level increment of 0.366 nm pixel−1.
600×) onto Kodak SO-163 film. Images were subsequently scanned using a UMAX2000 transmission scanner providing a specimen level increment of 0.366 nm pixel−1.




![Kratky [q2IA(q)vs. q] plot of the intensity scattered at room temperature by 10 (○) and 80 (●) mg ml−1AEAEAKAK solutions and 10 (◇) and 40 (◆) mg ml−1AEAKAEAK solutions prepared in D2O.](/image/article/2009/SM/b811288f/b811288f-f2.gif)

![ln[qI(q)]
vs. q2 plot of the intensity scattered at room temperature by 10 (○) and 80 (●) mg ml−1AEAEAKAK solutions prepared in D2O. Dotted lines represent the best fit obtained using eqn (7) (see text for details).](/image/article/2009/SM/b811288f/b811288f-f3.gif)



![Kratky [q2IA(q)vs. q] plot of the intensity scattered at room temperature by 10 (○) and 80 (●) mg ml−1AEAEAKAK solutions prepared in D2O. Dotted lines represent the best fit obtained using eqn (10) (see text for details).](/image/article/2009/SM/b811288f/b811288f-f4.gif)






![Kratky [q2IA(q)vs. q] plot of the intensity scattered at room temperature for: left 2 (◇) and 5 (○) mg ml−1FEFEFKFK solutions and right 2 (◆) and 5 (○) mg ml−1FEFEFKFK solutions prepared in pure D2O. Dotted lines represent the best fit obtained using eqn (10) (see text for details).](/image/article/2009/SM/b811288f/b811288f-f10.gif)