Nanoscale thermodynamic study on phase transformation in the nanocrystalline Sm2Co17 alloy
Wenwu
Xu
a,
Xiaoyan
Song
*a,
Nianduan
Lu
a,
Martin
Seyring
b and
Markus
Rettenmayr
b
aCollege of Materials Science and Engineering, Key Laboratory of Advanced Functional Materials, Ministry of Education of China, Beijing University of Technology, Beijing 100124, China. E-mail: xysong@bjut.edu.cn.; Fax: +86 10 6739 2311; Tel: +86 10 6739 2311
bInstitute of Materials Science and Technology, Metallic Materials, Friedrich-Schiller-University Jena, Jena D-07743, Germany
First published on 30th September 2009
Abstract
The characteristics of phase transformation in nanocrystalline alloys were studied both theoretically and experimentally from the viewpoint of thermodynamics. With a developed thermodynamic model, the dependence of phase stability and phase transformation tendency on the temperature and the nanograin size were calculated for the nanocrystalline Sm2Co17 alloy. It is thermodynamically predicted that the critical grain size for the phase transformation between hexagonal and rhombohedral nanocrystalline Sm2Co17 phases increases with increasing temperature. When the grain size is reduced to below 30 nm, the hexagonal Sm2Co17 phase can stay stable at room temperature, which is a stable phase only at temperatures above 1520 K in the conventional polycrystalline alloys. A series of experiments were performed to investigate the correlation between the phase constitution and the grain structure in the nanocrystalline Sm2Co17 alloy with different grain size levels. The experimental results agree well with the thermodynamic predictions of the grain-size dependence of the room-temperature phase stability. It is proposed that at a given temperature the thermodynamic properties, as well as the phase stability and phase transformation behavior of the nanocrystalline alloys, are modulated by the variation of nanograin size, i.e. the grain size effects on the structure and energy state of the nanograin boundaries.
1 Introduction
As compared with coarse-grained polycrystalline alloys, nanocrystalline alloys have a much larger volume fraction of interfaces, e.g. grain boundaries, phase boundaries, and domain interfaces. Owing to their special structures, nanocrystalline alloys consisting of either a single phase or multiple phases exhibit distinctly different physical, chemical, and mechanical properties from those of the coarse-grained alloys with the same composition.1–3 However, it was found that when the nanograin size increases to greater than a critical value, the nanostructure may evolve unstably and abrupt changes in thermal stability and phase stability of nanomaterials can occur.4 Consequently, the advanced properties of the material may deteriorate due to the destabilization of the nanostructure.Phase transformations induced by changes in nanograin size have been reported for a variety of nanocrystalline materials synthesized by different methods, e.g. Mo–Si,5 Ga–Sb,6 Ti–Al,7 Fe–Cr–Ni and Fe–Mn,8 and Cd–Se.9 A typical example is that the room-temperature phase in the nanocrystalline Ni–Ti shape memory alloy, prepared by high-pressure torsion, transforms in the sequence B2-austenite → R-phase → B19′-martensite with increasing nanograin size.10 From the viewpoint of thermodynamics, the long-range disordered arrangement of atoms at the nanograin boundaries influences the configurational and vibrational entropy and also the enthalpy of the nanomaterial.11 Therefore, the thermodynamic properties of nanocrystalline materials cannot be accurately described by the classic thermodynamic models in which the fundamental functions were derived without taking into account the effects of internal boundaries, which certainly applies for coarse-grained polycrystalline materials. In order to understand the thermal properties hence the related functional and structural properties of nanocrystalline materials more profoundly, it is very necessary to develop a nanoscale thermodynamic model. A variety of thermodynamic approaches12–14 have been proposed for nanocrystalline materials in recent years. It is noticed that these approaches are mainly correlated with the energy state of the free surface, which applies properly for nanopowder materials. Very recently, a few theoretical studies focusing on thermodynamic descriptions for nanocrystalline metals15,16 have been reported. However, nanoscale thermodynamic calculations, as well as their application to nanocrystalline alloy systems, are very limited in the literature so far. In particular, quantitative thermodynamic descriptions of the phase transformation behavior of nanocrystalline alloys have been rarely reported.
In this paper, we aim to develop the thermodynamic description for the phase transformation characteristics of nanocrystalline alloys. As reported in our previous work,17 we discovered an abnormal phase stability in the nanocrystalline Sm2Co17 alloy, i.e. a hexagonal Th2Ni17-type crystal structure (2 : 17 H phase) exists stably at room temperature instead of a rhombohedral Th2Zn17-type crystal structure (2 :1 7 R phase), which is well known as the stable room-temperature phase in the conventional polycrystalline Sm2Co17 alloy. Accordingly, using the nanocrystalline Sm2Co17 alloy system as an example, we studied the phase stability and the phase transformation behavior of nanocrystalline alloys both thermodynamically and experimentally.
2 Thermodynamic model for nanocrystalline alloys
2.1 Nanoscale thermodynamic functions
Structurally, nanocrystalline alloys consist of two kinds of regions: the nanometer-sized crystallines (nanograin interior), and the nanograin boundaries between adjacent nanocrystals.18 Atoms at nanograin boundaries and inside nanocrystals have different effects on the thermodynamic properties of the nanocrystalline alloy due to their different structure and energy states. To describe the structural characteristics of nanograin boundaries, Wagner19 and Fecht20 proposed a “dilated crystal” model, where a nanograin boundary is equivalent to a dilated crystal with the same crystallographic structure as the nanograin interior, but has an expanded unit cell. Based on the dilated crystal assumption, the dependence of the thermodynamic properties of nanograin boundaries on the structure state and the grain size is possible to described quantitatively. Firstly, a concept of “excess volume” at the nanograin boundary, when compared with the perfect crystal, was introduced to characterize the structure feature of nanograin boundaries, which was defined as,19 ΔV = (Vb/V0) − 1, where Vb is the primitive cell volume at nanograin boundary, Vb = 4πrb3/3; V0 is the primitive cell volume in nanograin interior, which is taken as equal to that in the perfect crystal at equilibrium state, V0 = 4πr30/3; rb and r0 are the Wigner–Seitz radii at the nanograin boundary and in the nanograin interior, respectively. Apparently, ΔV characterizes the deviation of the nanograin boundary structure with respect to the perfect crystal. The excess volume ΔV, which is directly related to the nanograin size, is the most significant intrinsic parameter that affects the thermal properties of nanograin boundaries, as has been shown theoretically in the literature.4,19–21Based on the theory of mean-field approximation,22 for a binary nanocrystalline alloy, the primitive cell volume can be taken as the sum of fractions of each constituent, i.e.
| V0 = x1V1 + x2V2 | (1) |
According to the dilated crystal model, the thermal features of the nanograin boundary are equivalent to those of the dilated crystal with the same excess volume. Thus, the fundamental thermodynamic functions of nanograin boundaries, i.e. the excess enthalpy Hb, the excess entropy Sb, and the excess Gibbs free energy Gb per atom are given by21,23
| Hb(Vb,T) = E + P(Vb,T)Vb | (2) |
| Sb(Vb,T) = CVγ(Vb,T)ln(Vb/V0) | (3) |
| Gb(Vb,T) = Hb(Vb,T) + CV(T − TR) − T[Sb(Vb,T) + CVln(T − TR)] | (4) |
Considering different effects of atoms at nanograin boundaries and in nanograin interiors on the thermodynamic properties of the nanocrystalline alloy, we introduce the atomic fraction at nanograin boundaries, xb,27 in the expressions of thermodynamic functions of the nanocrystalline alloy:
| H = NAxbHb(ΔV,T) + (1 − xb)Hi(T) | (5) |
| S = NAxbSb(ΔV,T) + (1 − xb)Si(T) | (6) |
| G = NAxbGb(ΔV,T) + (1 − xb)Gi(T) | (7) |
To summarize, the fundamental thermodynamic functions of the nanograin boundaries, as well as the whole nanocrystalline alloy, can be described as functions of excess volume ΔV and temperature T by eqns (2)–(7). By the above model, the thermodynamic properties, the phase stability, and the phase transformation characteristics of nanocrystalline alloys, can be quantitatively studied.
2.2 Relationship between nanograin size and excess volume
Although it has been recognized that the excess volume ΔV increases with decreasing nanograin size d, no precisely quantitative relationship between d and ΔV has been reported so far. In recent years, some approximation models for this relationship have been developed. The simplest approximation proposed by Chattopadhyay29 is | (8) |
In their model, ΔV is equal to the fraction of the excess surface area of the grain boundary, where d2D is the diameter of the equivalent circular area of the grain and h is the thickness of the grain boundary. Concerning this approximation, Song4 proposed that ΔV can be better estimated if the three-dimensional grain size, e.g. the diameter of the equivalent spherical volume, d, is used. For the space-filling nanograin structure, when the share of interface between neighboring nanograins is taken into account, the excess volume at the boundary of a nanograin may be expressed as
 | (9) |
 | (10) |
A nanograin is assumed to have a sphere shape with a diameter of d. A nanograin boundary, shared by two neighboring grains, has a thickness of 2δ. Thus, the core of a nanograin (the nanograin interior or the nanocrystal) has a diameter of d − 2δ. δ is assumed to be equivalent to two atom layers and to remain the same when the nanograin size changes or the phase transformation takes place. The volume fraction of the nanograin boundary, fb, can be estimated as
 | (11) |
The fraction of atoms at the nanograin boundary, xb, is then given by
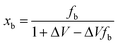 | (12) |
Thus, the molar volume of the nanocrystalline alloy, Vncmol, is expressed as
| Vncmol = NA[(1 − xb) Vi + xbVb] | (13) |
The molar volume of a nanocrystalline alloy can be calculated by the following equation,30 using lattice constants that can be obtained from X-ray diffraction (XRD) measurements on the prepared nanocrystalline sample,
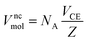 | (14) |
 , a and c are the lattice constants), and Z is the number of atoms per unit cell.
, a and c are the lattice constants), and Z is the number of atoms per unit cell.
The lattice constants and the average grain size of the nanocrystalline alloy were obtained using the following approaches. For the single-phased nanocrystalline Sm2Co17 samples, with the XRD data as the input, the lattice constants and the average crystallite sizes are calculated by the software Jade 5.031 in which the modified Scherer formula32 was embedded. On the other hand, the average grain sizes of the nanocrystalline Sm2Co17 samples consisting of either a single-phase or multiple phases were measured by the linear intercept method4 on the TEM images. Due to the negligible thickness of the nanograin boundary (e.g. 2δ = 1.1680 nm as estimated from the Wigner–Seitz radius) as compared with the nanograin size (d = 10–100 nm), the calculated average crystallite size of the nanocrystalline sample by the modified Scherer formula is considered to be approximately equivalent to the average nanograin size measured on the TEM images. By combining the calculations with the modified Scherer formula based on the XRD data with the measurements on the TEM images, the average grain sizes of the nanocrystalline Sm2Co17 samples can be obtained with good precision.
In summary, by combining eqns (9)–(13) with eqn (14), one can calculate the excess volume corresponding to a given nanograin size. Based on this approach, we obtained three values for the excess volume by measuring the average nanograin sizes and the lattice constants on the three single-phase samples of the prepared nanocrystalline Sm2Co17 alloy, the results including the reliability factor – the Smith and Snyder figure of merit33FN – are listed in Table 1.
| Phase | Average nanograin size d/nm (±10−2-10−1) | Lattice constants/Å (±10−4-10−3) | Smith and Snyder figure of merit, FN | Excess volume ΔV (±10−4-10−3) | |
|---|---|---|---|---|---|
| a | c | ||||
| 2 : 17 H | 15 | 8.7171 | 7.9347 | F 10 = 17.1(18) | 0.3113 |
| 2 : 17 H | 25 | 8.5362 | 8.0125 | F 11 = 11.4(20) | 0.1743 |
| 2 : 17 R | 80 | 8.3889 | 12.2312 | F 9 = 15.3(18) | 0.0452 |
Based on the three pairs of values of ΔV and d as listed in Table 1, the fitting parameters A, B and C in eqn (10) can be determined. Therefore, the excess volume ΔV as a function of the nanograin size d in nanocrystalline Sm2Co17 alloy is derived as
 | (15) |
The above relationship between excess volume and nanograin size is demonstrated in Fig. 1, in comparison with the function in eqn (9) with ρb/ρi = 0.8 as used in the literature.4 It can be seen that the deviation increases when the nanograin size decreases to below approximately 30 nm. Therefore, the dependence of ρb/ρi on the nanograin size should be considered.
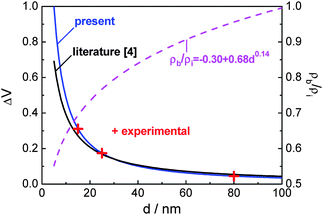 | ||
| Fig. 1 The deduced relationship between the excess volume ΔV and the nanograin size d, and the relative distribution density of atoms at the nanograin boundary and in the nanograin interior ρb/ρi as a function of the nanograin size for the nanocrystalline Sm2Co17 alloy. | ||
3 Thermodynamic calculations and predictions
3.1 Dependence of Gibbs free energy on grain size
To apply the nanoscale thermodynamic model described in Section 2 in the nanocrystalline Sm2Co17 alloy system, as a first step the input parameters for the thermodynamic calculations should be determined. The related input parameters were used referring to the literature,34–39 as listed in Table 2.Based on the model calculations, the thermodynamic properties of the nanocrystalline Sm2Co17 alloy can be characterized, hence the phase stability and the tendency of phase transformation in the alloy may be predicted by the criterion of the minimum Gibbs free energy.40Fig. 2 shows the calculated Gibbs free energy differences of the two phases, i.e. the hexagonal Th2Ni17-type Sm2Co17 (2 : 17 H phase) and the rhombohedral Th2Zn17-type Sm2Co17 (2 : 17 R phase), as a function of the nanograin size at different temperatures. As can be seen in Fig. 2, the values of ΔGH–R reduce with the decrease of nanograin size at given temperatures, which implies that the degree of phase stability of nanocrystalline 2 : 17 H increases with the decrease of nanograin size at a constant temperature. Moreover, it is observed that the nanograin size corresponding to ΔGH–R = 0, i.e. the critical nanograin size for the phase transformation, increases with increasing the temperature. As indicated in Fig. 2, at temperatures of 300 K, 600 K, 900 K and 1200K, the critical nanograin sizes for the phase transformations between 2 : 17H and 2 : 17R are about 30 nm, 33 nm, 39 nm and 54 nm, respectively.
 | ||
| Fig. 2 Calculated Gibbs free energy differences, ΔGH–R, between hexagonal and rhombohedral Sm2Co17 phases as a function of nanograin size at different temperatures. | ||
According to the thermodynamic analysis in the case of the nanocrystalline Sm2Co17 alloy, it is shown that the degree of phase stability, as well as the phase transformation tendency, is dependent distinctly on the grain size of the nanocrystalline alloy. In nanocrystalline alloys, with the decrease of the grain size, especially to below a few tens of nanometres, the volume fraction of the grain boundaries is significantly increased. The nanograin boundary atoms, which have the disordered or short-range ordered arrangement, play an increasingly important role in the changes of the entropy, enthalpy, and the free energy of the nanocrystalline alloy with the decrease of the grain size. Therefore, the thermodynamic properties of the nanocrystalline alloy are modulated by variations in the nanograin size, i.e. the grain size effects on the structure and energy states of the nanograin boundaries.
3.2 Room-temperature phase stability
In order to study the stability of different phases at room temperature in the nanocrystalline Sm2Co17 alloy system, the Gibbs free energies of the nanocrystalline 2 : 17 H and 2 : 17 R phases at a temperature of 300 K were calculated, the results are shown in Fig. 3. | ||
| Fig. 3 Calculated Gibbs free energies of the nanocrystalline 2 : 17 H and 2 : 17 R phases as a function of the nanograin size at a temperature of 300 K (the inset showing local enlargement at the intersection point). | ||
Fig. 3 demonstrates that at room temperature, the Gibbs free energies of both nanocrystalline 2 : 17 H and 2 : 17 R phases increase with the decrease of the nanograin size. The two Gibbs free energy curves intersect at a grain size of about 30 nm, indicating a critical state of phase transformation between 2 : 17 H and 2 : 17 R structures. This means that the ultrafine nanocrystalline Sm2Co17 alloy (with grain size smaller than 30 nm) will have a hexagonal structure at room temperature, while the coarser nanocrystalline (with the grain size larger than 30 nm) or the submicro-scaled and polycrystalline Sm2Co17 alloys will have a rhombohedral crystal structure at room temperature. In contrast to the conventional polycrystalline Sm2Co17 alloys which have the hexagonal crystal structure only at temperatures above 1520 K, in the nanocrystalline alloy the 2 : 17 H phase can exist stably at room temperature when the grain size is reduced to below the critical value. Therefore, the nanocrystalline alloy exhibits distinctly different phase stability and phase transformation characteristics at room temperature as compared with the conventional polycrystalline alloy with the same composition
4 Experimental investigation
Since the single-phase Sm2Co17 nanocrystalline alloy is the matrix used to develop the nanocrystalline Sm2Co17-type permanent magnets,41,42 it is of great scientific interests and technological importance to investigate the phase transformation characteristics of the nanocrystalline Sm2Co17 alloy. To verify the thermodynamic predictions of the phase transformation behavior in the nanocrystalline Sm2Co17 alloy system, we prepared the nanocrystalline Sm2Co17 bulk samples with different average grain sizes, and investigated their microstructures and phase constitutions at room temperature.Firstly, the coarse-grained polycrystalline Sm2Co17 ingot was prepared by induction-melting Sm (99.99%) and Co (99.99%) in a vacuum furnace. The ingot was annealed for 24 h at 1320 °C in argon gas to obtain the homogeneous single-phase Sm2Co17 alloy. Then the Sm2Co17 ingot was crushed into the coarse powder, and sealed in a vial in a glove box filled with argon gas. The powder was subjected to high-energy ball milling, from which the amorphous Sm–Co alloy powder was obtained. The concurrent consolidation and crystallization of the amorphous powder were carried out by the spark plasma sintering (SPS) technique at a temperature of about 1000 K in a system filled with highly purified argon gas.
To obtain different levels of the average grain size of the nanocrystalline alloy, the as-SPSed sample was cut into three parts, labeled with A, B and C, respectively. The samples B and C were sealed in the quartz tubes filled with argon gas then annealed for 1 h at the temperatures of 973 K and 1073 K, respectively, and were subsequently cooled down naturally to room temperature. The phase constitutions of the above three samples were detected by XRD, and the microstructures of the three samples were observed by TEM, the results are shown in Figs. 4 and 5, respectively.
 | ||
| Fig. 4 XRD patterns of nanocrystalline Sm2Co17 samples prepared with different treatments: (A) as-SPSed sample, (B) annealed at 973 K for 1 h using the as-SPSed sample as the starting material, (C) annealed at 1073 K for 1 h using the as-SPSed sample as the starting material. | ||
 | ||
| Fig. 5 TEM images and SAED patterns of nanocrystalline Sm2Co17 samples prepared with different treatments: (a) as-SPSed sample, (b) annealed at 973 K for 1 h using the as-SPSed sample as the starting material, (c) annealed at 1073 K for 1 h using the as-SPSed sample as the starting material. | ||
As shown by curve (A) in Fig. 4, together with the selected-area electron diffraction (SAED) pattern shown in Fig. 5a, the sample A (as-SPSed) has a single Sm2Co17 phase with the hexagonal Th2Ni17-type crystal structure (2 : 17 H) at room temperature. By combining the estimation using the modified Scherer formula based on the XRD data with the measurements on the TEM images (an example shown in Fig. 5a), the average grain size of sample A was obtained to be about 15 nm. It is found that sample B (annealed at 973 K using the as-SPSed sample as the starting material) has the coexisting 2 : 17 H and 2 : 17 R phases at room temperature (as indicated by the curve (B) in Fig. 4 and the SAED pattern and its indexing in Fig. 5b). For sample B with a double-phase microstructure, it is not accurate to use the Scherer formula to estimate the grain size of the material. In this case, the linear intercept method was used to measure the grain sizes in the TEM images, and an average grain size of about 45 nm was obtained for sample B. Sample C (annealed at 1073 K using the as-SPSed sample as the starting material) has a single phase of 2 : 17 R at room temperature (as indicated by the curve (C) in Fig. 4 and the SAED pattern and its indexing in Fig. 5c), and the average grain size was obtained as about 80 nm by the same method as used for sample A.
As shown by the experimental results, at room temperature, the as-SPSed nanocrystalline Sm2Co17 alloy with an average grain size of 15 nm has the single 2 : 17 H phase. Applying the newly developed method for the measurement of the nanograin size distribution,43 we obtained that the as-SPSed nanocrystalline Sm2Co17 sample has a grain size distribution in a range of 5–25 nm. This experimental finding validates the model prediction in Section 3.3, i.e. when the grain size is smaller than the critical value of 30 nm, the nanocrystalline Sm2Co17 has a stable 2 : 17 H phase instead of a 2 : 17 R phase as in the conventional polycrystalline Sm2Co17 alloy at room temperature.
In the experiment, the nanocrystalline Sm2Co17 alloy with an average grain size of about 45 nm and a grain size distribution of 15–80 nm (a relatively higher number fraction of grains in a range of 20–40 nm, see Fig. 5b) consists of 2 : 17 H and 2 : 17 R phases at room temperature. While the nanograins with the grain size smaller than the critical value of 30 nm have the hexagonal structure, the grains larger than 30 nm have the rhombohedral structure. The appearance of the coexisting 2 : 17 H and 2 : 17 R phases is attributed to the nanograin size distribution hence its effect on the phase stability in the nanocrystalline Sm2Co17 alloy. When the average grain size increases to 80 nm with a grain size distribution of 50–115 nm, the Sm2Co17 alloy has the single 2 : 17 R phase at room temperature. This confirms the thermodynamic calculation on the room-temperature phase stability in the nanocrystalline Sm2Co17 alloy with the grain size larger than the critical value. Therefore, the experimental results on the room-temperature phase constitutions in the three samples with different grain size levels agree well with the model predictions demonstrated in Section 3.3. It is reasonably concluded that the nanograin growth due to the annealing treatment causes the changes in the energy and structure states of the nanocrystalline phases, hence results in the change of the phase stability in a coarser nanograin structure at room temperature.
5 Conclusions
In this paper we developed a thermodynamic model that describes quantitatively the phase transformation characteristics of the nanocrystalline Sm2Co17 alloys. The experiments concerning preparation and characterization of nanocrystalline Sm2Co17 alloys with different grain size levels were performed to verify the thermodynamic calculations. The conclusions are drawn as follows:(1) By deducing the relationship between the excess volume at nanograin boundaries and the nanograin size, the Gibbs free energy of nanocrystalline alloy as a function of temperature and nanograin size is distinctly determined.
(2) The thermodynamic calculations indicate an apparent deviation on phase stability and phase transformation tendency between nanocrystalline and conventional polycrystalline alloys. Using Sm2Co17 alloy as an example, the present thermodynamic model predicted the characteristics of phase transformations between hexagonal and rhombohedral 2 : 17 phases at a series of temperatures. The critical nanograin size for the phase transformation increases with increasing temperature.
(3) The experimental results, that with the increase of nanograin size, the phase constitution at room temperature in nanocrystalline Sm2Co17 alloys transforms from a single hexagonal phase to coexisting hexagonal and rhombohedral phases then to a single rhombohedral phase, confirm the thermodynamic predictions on the room-temperature phase stability of the nanocrystalline Sm2Co17 alloy.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant no. 50671001 & 50871001), the Program for New Century Excellent Talents in University (NCET-2006-0182), and the Doctorate Foundation of Chinese Education Ministry (20070005010).References
- E. Botcharova, J. Freudenberger and L. Schultz, Acta Mater., 2006, 54, 3333 CrossRef CAS.
- T. T. Sasaki, T. Mukai and K. Hono, Scr. Mater., 2007, 57, 189–192 CrossRef CAS.
- Y. Nakamoto, M. Yuasa, Y. Q. Chen, H. Kusuda and M. Mabuchi, Scr. Mater., 2008, 58, 731–734 CrossRef CAS.
- X. Y. Song, J. X. Zhang, L. M. Li, K. Y. Yang and G. Q. Liu, Acta Mater., 2006, 54, 5541 CrossRef CAS.
- P. C. Kang and Z. D. Yin, Nanotechnology, 2004, 15, 851–855 CrossRef CAS.
- C. E. M. Campos, J. C. de Lima, T. A. Grandi, J. P. Itié, A. Polian, J. C. Chervin, P. S. Pizani and E. B. Saitovich, J. Phys.: Condens. Matter, 2008, 20, 275212 CrossRef.
- N. Forouzanmehr, F. Karimzadeh and M. H. Enayati, J. Alloys Compd., 2009, 471, 93–97 CrossRef CAS.
- B. Efros, V. Pilyugin, A. Patselov, S. Gladkovskii, N. Efros, L. Loladze and V. Varyukhin, Mater. Sci. Eng., A, 2009, 503, 114–117 CrossRef.
- M. Grünwald and C. Dellago, Nano Lett., 2009, 9, 2099–2102 CrossRef.
- T. Waitz, V. Kazykhanov and H. P. Karnthaler, Acta Mater., 2004, 52, 137–147 CrossRef CAS.
- F. Gartner, R. Bormann, R. Birringer and A. Tschope, Scr. Mater., 1996, 35, 805 CrossRef.
- H. Hasegawa, Prog. Mater. Sci., 2007, 52, 333–351 CrossRef CAS.
- W. H. Luo, W. Y. Hu and S. F. Xiao, J. Phys. Chem. C, 2008, 112, 2359–2369 CrossRef CAS.
- H. Yildirim, A. Kara and T. S. Rahman, J. Phys.: Condens. Matter, 2009, 21, 084220 CrossRef.
- W. Qin, T. Nagase and Y. Umakoshi, J. Appl. Phys., 2007, 102, 124303 CrossRef.
- F. Sommer, R. N. Singh and E. J. Mittemeijer, J. Alloys Compd., 2009, 467, 142–153 CrossRef CAS.
- X. Y. Song, N. D. Lu, M. Seyring, M. Rettenmayr, W. W. Xu, Z. X. Zhang and J. X. Zhang, Appl. Phys. Lett., 2009, 94, 023102 CrossRef.
- H. Gleiter, Acta Mater., 2000, 48, 1 CrossRef CAS.
- M. Wagner, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 635 CrossRef.
- J. H. Fecht, Phys. Rev. Lett., 1990, 65, 610 CrossRef.
- Q. P. Meng, N. Zhou, Y. Rong, S. Chen and T. Y. Hsu, Acta Mater., 2002, 50, 4563 CrossRef CAS.
- J. Park and J. Lee, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2008, 32, 135 Search PubMed.
- H. J. Fecht, Acta Metall. Mater., 1990, 38, 1927 CrossRef CAS.
- J. H. Rose, J. Ferrante and J. R. Smith, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1835 CrossRef CAS.
- P. Vinet, J. R. Smith, J. Ferrante and J. R. Rose, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 1945 CrossRef CAS.
- W. W. Xu, X. Y. Song, E. D. Li, J. Wei and J. X. Zhang, J. Appl. Phys., 2009, 105, 104310 CrossRef.
- X. Y. Song, J. P. Gao and J. X. Zhang, Acta Phys. Sin., 2005, 54, 1313 Search PubMed.
- A. T. Dinsdale, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 1991, 15, 317 Search PubMed.
- P. P. Chattopadhyay, P. M. Nambissan, S. K. Pabi and I. Manna, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 054107 CrossRef.
- T. D. Shen, J. Z. Zhang and Y. S. Zhao, Acta Mater., 2008, 56, 3663 CrossRef CAS.
- Jade 5.0, XRD Pattern Processing, Materials Data Inc.Livermore, CA, 1999 Search PubMed.
- A. W. Burton, K. Ong, T. Rea and I. Y. Chan, Microporous Mesoporous Mater., 2009, 117, 75 CrossRef CAS.
- G. S. Smith and P. L. Snyder, J. Appl. Crystallogr., 1979, 12, 60 CrossRef CAS.
- C. Kittel, in Introduction to Solid State Physics, 7th edn, John Wiley & Sons, New York, 1996, pp. 7–9 Search PubMed.
- S. Q. Xu, Shanghai Metals, 1981, 2, 62 Search PubMed.
- J. J. Xu, Z. Y. Deng and T. J. Zhang, in Physical Properties of Metals, Shanghai Scientific & Technical Publishers, Shanghai, 1988, pp. 97–98 Search PubMed.
- S. Tian, X. C. Li and B. S. Li, in Metallic Physical Property, National Defence Industry Press, Beijing, 2000, pp. 64–65 Search PubMed.
- X. M. Tao, Y. F. Ouyang, H. S. Liu, F. J. Zeng, Y. P. Feng and Z. P. Jin, Phys. B, 2007, 399, 27–32 CrossRef CAS.
- Y. G. Zhang, Y. F. Han and G. L. Chen, in Intermetallic Structural Material, National Defence Industry Press, Beijing, 2001, pp. 325–326 Search PubMed.
- R. J. Silbey and R. A. Alberty, in Physical Chemistry, 3rd edn, John Wiley & Sons, New York, 2000, pp. 106–116 Search PubMed.
- M. Yue, J. X. Zhang, D. T. Zhang, L. J. Pan and X. B. Liu, Appl. Phys. Lett., 2007, 90, 242506 CrossRef.
- G. Sreenivasulu, R. Gopalan, V. Chandrasekaran, G. Markandeyulu, K. G. Suresh and B. S. Murty, Nanotechnology, 2008, 19, 335701 CrossRef.
- M. Seyring, X. Y. Song, A. Chuvilin, U. Kaiser and M. Rettenmayr, J. Mater. Res., 2009, 24, 342–346 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2009 |
