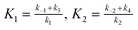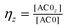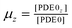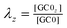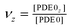Crosstalk between G-protein and Ca2+ pathways switches intracellularcAMP levels
Najl V.
Valeyev
*a,
Pat
Heslop-Harrison
b,
Ian
Postlethwaite
a,
Antonina N.
Gizatullina
c,
Nikolay V.
Kotov
c and
Declan G.
Bates
a
aSystems Biology Lab, Department of Engineering, University of Leicester, University Road, Leicester, UK LE1 7RH. E-mail: najl.valeyev@googlemail.com; Tel: +44 (0)7817 068953
bSystems Biology Lab, Department of Biology, University of Leicester, University Road, Leicester, UK LE1 7RH
cBiophysics & Bionics Lab, Department of Physics, Kazan State University, 420008, Kazan, Russia
First published on 27th October 2008
Abstract
Cyclic adenosine monophosphate and cyclic guanosine monophosphate are universal intracellular messengers whose concentrations are regulated by molecular networks comprised of different isoforms of the synthases adenylate cyclase or guanylate cyclase and the phosphodiesterases which degrade these compounds. In this paper, we employ a systems biology approach to develop mathematical models of these networks that, for the first time, take into account the different biochemical properties of the isoforms involved. To investigate the mechanisms underlying the joint regulation of cAMP and cGMP, we apply our models to analyse the regulation of cilia beat frequency in Paramecium by Ca2+. Based on our analysis of these models, we propose that the diversity of isoform combinations that occurs in living cells provides an explanation for the huge variety of intracellular processes that are dependent on these networks. The inclusion of both G-proteinreceptor and Ca2+-dependent regulation of AC in our models allows us to propose a new explanation for the switching properties of G-protein subunits involved in nucleotide regulation. Analysis of the models suggests that, depending on whether the G-protein subunit is bound to AC, Ca2+ can either activate or inhibit AC in a concentration-dependent manner. The resulting analysis provides an explanation for previous experimental results that showed that alterations in Ca2+ concentrations can either increase or decrease cilia beat frequency over particular Ca2+ concentration ranges.
Introduction
Cyclic 3′,5′ adenosine monophosphate (cAMP) and cyclic 3′,5′ guanosine monophosphate (cGMP) were first identified as intracellular mediators in the 1950s.1 Intracellular signalling via the cAMP and cGMPnucleotides is involved in many areas of animal cell biology and is an important area of research. Conceptual models of cAMP concentration regulation have undergone significant changes in recent years as more details of the role of adenylate cyclases (ACs) and cyclic nucleotide phosphodiesterase (PDE) in cAMP regulation have been reported.2–4 Both these enzymes exhibit a continuum of isoforms with unique biochemical properties, which are expressed in various combinations within both single and multicellular organisms. Such isoforms are also sometimes referred to as gene products,5 and are expressed by somewhat different gene groups or may arise from the same gene by alternative splicing.Dictyostelium cells contain three distinct AC isoforms6 and mammalian cells can express ten different major AC gene isoforms.5 As well as having different structures and biochemical properties, it is now well-established that different AC gene products can be either activated or inhibited by G-protein7 and Ca2+ pathways.8 The ten AC genes can be divided into five families according to their structural and activation properties.5 The Ca2+–CaM activated isoforms are ACI, ACIII and ACVIII. ACII, ACIV and ACVII are activated by Gβγ. ACV and ACVI are inhibited by Gαi isoforms (Gα0, Gαi1, Gαi2, Gαi3, and Gαz,) and Ca2+ ions. There is an ongoing debate as to whether the ACV and ACVI isoforms are inhibited by Ca2+ directly or via CaM.9 The last membrane-bound ACIX isoform is the most divergent from the other eight membrane-bound isoforms. The last soluble isoform is similar to the AC found in Anabaena.10
In combination with synthesis by AC and guanylate cyclase, PDEs regulate the levels of cAMP and cGMP by degradation of the cyclic molecules, and these enzymes are expressed in a wide range of organisms: Trypanosoma,11,12Dictyostelium,13Drosophila14 and Homo sapiens.15,16 Eleven families of PDE in various species, each containing several isoforms with diverse structures and biochemical properties, have now been identified in the literature.17 The calcium and calmodulin-dependent PDEI family was one of the first to be identified.18 The specific property of PDEII enzymes is that they are activated by cGMP binding.19cAMP hydrolysis by the PDEIII family, unlike in the case of PDEII, is inhibited by cGMP. PDEIV, PDEVII and PDEVIII are highly sensitive to cAMP as a substrate, with Km being of the order of magnitude of 1μM and lower.20–22 PDEV was originally identified in platelets23 and later become a target for a number of drugs regulating vascular smooth muscle contraction.24,25 PDEV is characterised by relative specificity to cGMP rather than to cAMP. PDEVI is also known as a photoreceptorphosphodiesterase due to its expression in mammalian retina. PDEIX has the highest affinity for cGMP and has been proposed as a regulator of cGMP signaling.26,27 PDEX is not as well characterized as some other PDE families. However, it has been reported that PDEX is more cAMP rather than cGMP specific.28 PDEXI is the most recently discovered phosphodiesterase29 and has been reported to hydrolyse both cAMP and cGMP without any preference for either nucleotide.
It is now well established that many of the intracellular effects of cAMP are mediated by cAMP-dependent kinase (PKA). PKA catalyzes the transfer of the terminal phosphate group from ATP to serines and threonines of target proteins, hence modulating their activity. The phosphorylation of different substrates by PKA in various cells certainly provides a partial explanation for the variety of cAMP effects in different cellular systems. In this paper, we use a structural systems biology approach to further investigate this issue, and propose that the multitude of AC, GC and PDEgene group products which may occur in living cells provides another important mechanism for cAMP concentration-dependent differential regulation of intracellular events. The proposed approach can therefore be regarded as a natural extension of previous approaches to modelling cAMP regulation,30,31 which allows us to generate isoform specific cAMP concentration profiles and study isoform specific regulatory effects.
An important, but perhaps insufficiently recognized, problem in nucleotide signalling is the convergence and mutual influence of Ca2+ and G-protein pathways on cAMP production. It is not clear to what extent each of these pathways contributes to the shaping of the output AC response and subsequent modulation of the cAMP-dependent effects across the cell. Previous mathematical modelling studies have largely focused on the separate effects of either G-protein or Ca2+ signals on cAMP production.4,31–36 We aimed here to develop a model to include the effects of AC regulation by both Ca2+ and G-protein dependent signals and thus to elucidate the interplay between these two major pathways modulating AC, and hence cAMP, concentrations within the framework of the network shown in Fig. 1. By analysing this model, we are able to predict various potential outputs for cAMP dependence on Ca2+ and G-protein signals and we can thus compare the model predictions for nucleotide signalling with a number of experimental studies, in order to identify potential cellular mechanisms governing the interplay between Ca2+ and G-protein pathways. In this study, we decided to select a number of AC isoforms that have been elucidated experimentally and represent different types of concentration profiles: activation, inhibition, bell-shaped dependence and reverse bell shaped dependence.
 | ||
| Fig. 1 Signalling network for intracellularcAMP regulation: cyclic AMP is synthesised by AC and hydrolysed by PDE enzymes. The activities of ACs are regulated by Ca2+via CaM proteins as well as by G-protein subunits. PDE is activated by intracellularCa2+ concentration via CaM. The level of cAMP is regulated by extracellular signals through the GPCRs as well as by intracellularCa2+ variations. | ||
cGMP acts as a second messenger in a similar way to cyclic AMP, but exhibits several notable differences. In particular, significant activity of cGMP is observed at higher Ca2+ concentrations.37cGMP synthesis is catalyzed by GC, which converts GTP to cGMP, and is hydrolysed by cyclic nucleotide phosphodiesterases (PDE I–IV) into 5′-GMP. Both cGMP and cAMP have been reported to be involved in cell migration and chemotaxis mechanisms in unicellular organisms such as Dictyostelium38–40 and Paramecium.41–43 Currently, however, there is limited understanding of the nature and extent of crosstalk between these two pathways. To investigate this issue, we aimed to develop a model incorporating Ca2+ dependent alterations of both cAMP and cGMP. The model predictions are tested against multiple sets of experimental data on the complementary roles of cAMP and cGMP-dependent cilia beat in Paramecium, and allow us to propose a new explanation for how intracilia Ca2+ and nucleotide concentration alterations translate to cilia beat frequency and the movement that defines the trajectory of Paramecium motion.
Results
Isoform-specific modelling reveals the diversity of cAMP concentration profiles
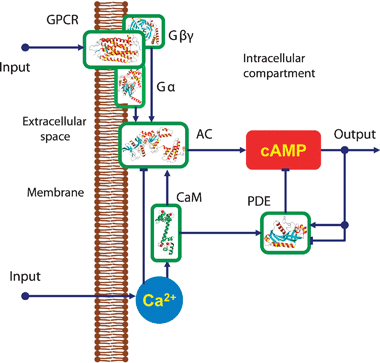
Our isoform-based model predicts that the differences in cAMP profiles among various cell types are at least partly due to the many different combinations of AC and PDE isoforms expressed in particular types of cells and tissues. Various combinations of AC and PDE isoforms, each with their own unique biochemical properties, can provide a multitude of cell specific concentration profiles. In this section, we demonstrate how the AC and PDE pairs regulated by Ca2+ and G-protein subunits form cAMP concentration profiles (Fig. 1) and tune physiological effects. Model predictions for ACI, ACII and PDEI isoform activation (Fig. 2A) by Ca2+ are compared against experimental data from the literature44,45 in Fig. 2B. The combination of ACI and ACII with PDEI in our model allows quantitative predictions concerning intracellularcAMP concentrations to be made. Eqn (6) and (7) (see Experimental) have been employed to combine the Ca2+–CaM-dependent PDEI isoform with the Ca2+-dependent AC isoforms. Fig. 2C–H show the resulting intracellularcAMP concentration profiles predicted by the model. In addition to the clear dependence of cAMP levels on the unique biochemical properties of the AC and PDE isoforms, the shape of the cAMP concentration profile is seen to be highly sensitive to the values of the CaM-AC dissociation constants. Indeed, variation of these parameters in the model resulted in dramatic alterations in cAMP profiles even for the same AC and PDE isoforms (Fig. 2C–2H). The same ACI and PDEI enzyme pair revealed variable steady-state cAMP concentration profiles when the CaM–PDEI dissociation constants were equal to 0.02 μM, 10 nM and 1 μM on Fig. 2C, 2D, and 2E, respectively. Similarly the same variability of the CaM–PDEI equilibrium dissociation constants produced qualitatively different cAMP concentration profiles for the ACII and PDEI enzymes on Fig. 2F, 2G, and 2H.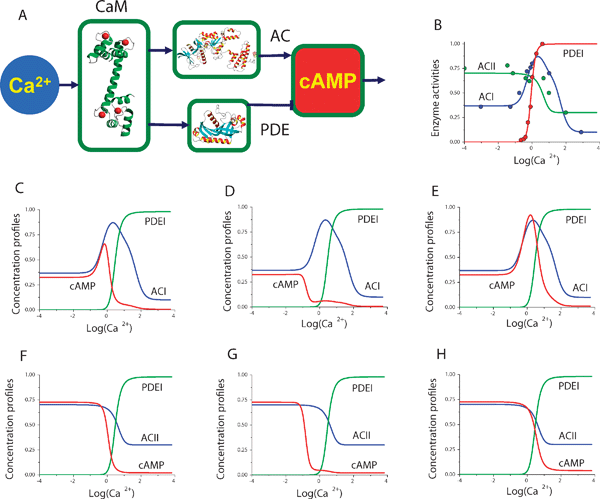 | ||
| Fig. 2 Model predictions of cAMP dependence on Ca2+ concentration: (A) Schematic diagram of cAMP regulation by Ca2+via the CaM, AC and PDE proteins. (B) Data for ACI, ACII and PDEI isoforms from44,45 shown as circles. The solid line in each case shows the model dependence on Ca2+. The ACI–PDEI and ACII–PDEI isoform pairs are used to study the cyclic AMP concentration profiles. The steady-state cAMP dependence on Ca2+ concentration is predicted for the ACI–PDEI enzyme pair (C, D and E) and for the ACII–PDEI pair (F, G and H). The equilibrium dissociation constant for CaM–PDEI interaction has been set equal to: 0.02 μM (B, E), 10 nM (C, F), and 1 μM (D, G). The model predictions illustrate how the diverse range of cAMP concentration profiles may be achieved due to the combinations of AC and PDE isoforms with unique biochemical properties. | ||
Some AC isoforms interact with G-protein subunits that transmit extracellular signals viaG-protein coupled receptors (Fig. 3A). We used our model to analyse the intracellularcAMP concentration dependence as a function of these G-protein signals. Fig. 3B compares the model responses against experimental data for the ACI and ACII regulation curves by G-protein subunits. Since the G-protein mediated signals do not always assume simultaneous Ca2+ stimulation, we have chosen to use the steady-state level of Ca2+-dependent PDEI activity in combination with G-protein activated AC isoforms shown in Fig. 3B. Fig. 3C–E shows the range of intracellularcAMP concentration profiles achieved by the G-protein mediated signals. The data suggests that G-protein mediated signals can cause intracellularcAMP concentration to decrease (Fig. 3D), increase (Fig. 3E), or even exhibit a reversed bell-shaped dependence (Fig. 3C).
 | ||
| Fig. 3 Model predictions of cAMP dependence on G-protein subunit concentrations: (A) Schematic diagram of cAMP regulation by G-protein subunits via the AC isoforms. (B) The dependence of ACI, ACII and PDEI isoforms activity on G-protein subunits from7 shown as circles. The solid line in each case shows the model prediction. The model predictions for combinations of ACI regulated by Gα, Gβγ subunits and ACII with PDE fixed at a basal activity level suggest that extracellular signals via the GPCRs can form a range of intracellularcAMP concentration profiles: reversed bell-shape (C), inhibition (D) or activation (E). | ||
Interactions between G-protein and Ca2+/CaM signalling pathways switch cAMP concentrations
We next employed our model to investigate the level of interaction between the G-protein and Ca2+ signalling pathways. As discussed above, AC can be activated by Ca2+–CaM complexes as well as by G-protein subunits. While the dose-dependent responses have been characterized for both Ca2+ and G-protein pathways, it is not always clear if and how interactions between these two different pathways occur. Since both Ca2+ and G-protein mediated signals can activate or inactivate AC, it is of interest to establish what state the AC is likely to be at if there is an inhibition signal through the G-protein and activation signal via the Ca2+ pathway.Building on work on nucleotide signalling showing that AC was activated by G-protein subunits,35,46,47 it was found that there are many other regulators of AC with various activation patterns. In addition to regulation by G-protein subunits, the activities of AC are also modulated by Ca2+, phosphorylation, glycosylation and many other regulatory phenomena.48 An interesting example of a molecular system with joint Ca2+-CaM and G-protein dependent AC regulation is the network underlying cAMP production in Dictyostelium.49 Indeed, in these cells the interplay between Ca2+ and GPCR induced signals appears to govern the direction and the rate of migration in chemotaxis.50Fig. 4A shows a schematic diagram for AC interactions with Ca2+, Ca2+/CaM and with G-protein subunits. Although AC has two ATP binding domains, it has been shown that these domains are inactive separately and require dimerization for AC activity.51 This fact allows us to introduce a simplification and consider a model of AC with one catalytic centre that describes the activity of the two domains. The multiple G-protein subunits (15α, 5β and 13γ) together with the nine membrane bound AC isoforms raise the issue of selectivity between the interacting partners.52 We showed previously that structural selectivity can be complemented by ligand concentration-based selective target activation.53 In this case, however, the selectivity of the regulation achieved appears to be due to the combination of signals from separate pathways. For example, G-protein subunit binding may inhibit or activate AC, depending on the AC isoform and the subunit. At the same time, the binding of the same subunit, in combination with AC phosphorylation or by binding to a Ca2+–CaM pair, may cause a different degree of AC activity, produce more or less cAMP and as a result induce a different intracellular effect. In order to investigate the relationship and the influence of the two regulatory pathways, we analysed an example of the Ca2+–CaM and G-protein subunit interactions with AC. In the most general case there is no strong reason to assume that the actual activity of AC is simply the sum or multiplication of activities mediated by the G-protein subunits and Ca2+–CaM separately. In other words, binding of one of the modulators to the AC is likely to have an impact on the overall molecular conformation and may thus lead to alterations in its affinity to another modulator. Since the AC activity may not be just a linear combination of the G-protein and Ca2+ pathway induced signals, we considered the overall state of the AC molecules and employed mathematical modelling to analyse a range of potential outcomes.
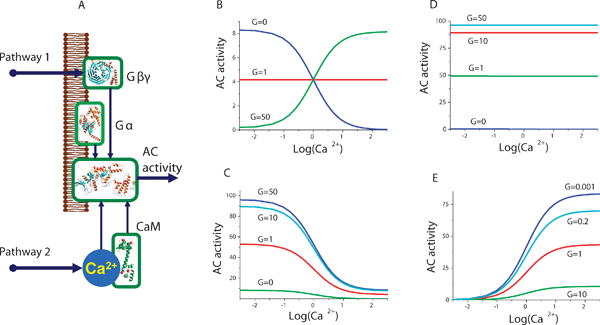 | ||
| Fig. 4 AC regulation by Ca2+ and G-protein pathways: (A) Schematic representation of the AC activity regulation network. Various AC isoforms are affected by Ca2+ and G-protein pathway signals according to their unique structures and corresponding biochemical properties. The model elucidates the link between the effect of Ca2+ and G-proteins on cAMP production via the regulation of AC. The model predicts four different potential scenarios for AC regulation by Ca2+ in the presence of G-protein subunits. (B) G-proteins may possess switching functionality. The model predicts that AC is inhibited by Ca2+ in the absence of G-proteins but can become insensitive to Ca2+ alterations when the number of G-protein subunits increases. Further increase of G-protein subunits produces a switching effect so that AC is now activated by Ca2+. The analysis of other potential scenarios for the interactions of G-protein and Ca2+ pathways reveals that AC can be completely insensitive to Ca2+ (D) or Ca2+ can inhibit (C) or activate (E) AC, over the full physiological range of G-protein subunit concentrations. | ||
Fig. 4 shows model predictions for the variety of AC activation modes by Ca2+ in different conformational states. The results of this analysis suggest that Ca2+ can be either an activator or inhibitor of AC, depending on the AC conformation in the complex with G-protein subunits. The binding of G-proteins alters the conformation of the molecule, changes the Ca2+, Ca2+–CaM and substrate interaction constants with AC and thereby modulates the activity state. The predicted probabilities for AC molecules to be in complexes with G-protein subunits and Ca2+–CaM complexes are shown in Fig. 4B as a function of Ca2+ concentration. As shown in Fig. 4, the proportion of non Ca2+/CaM bound AC species decreases with the elevation of Ca2+ concentration, whereas the proportion of other species gradually increases. The sum of the activities for individual AC species is represented in Fig. 4C with low and high concentrations of G-protein subunits. The model predicts that the switch between Ca2+-dependent activation and inhibition of AC is due to the interaction with G-proteins. G-protein subunits shift the balance between the number of AC conformations which increase with Ca2+ and the number of those that decrease with Ca2+. Thus, Ca2+ signals can both activate or inhibit AC depending on the presence or absence of specific G-protein subunits. The difference between the AC isoforms in terms of their Ca2+ and G-protein mediated properties appears to be in the variability of affinity constant pairs to the substrate and to the G-protein subunits. Fig. 4B, 4C, 4D and 4E show alternative combinations of dissociation constants of AC to both substrates and G-proteins. An interesting finding is that the model predicts that there can exist cases where Ca2+ always inhibits (Fig. 4C), does not affect (Fig. 4D), or always activates (Fig. 4E) AC molecules. At the same time, the G-protein mediated signals modulate the amplitude of the Ca2+-dependent responses. Effectively, G-protein subunits define the state of the AC, depending on which cAMP production can be either Ca2+ inhibited (Fig. 4C), Ca2+ independent (Fig. 4D) or Ca2+ activated (Fig. 4E).
Complementary regulation of cilia beat frequency by cAMP and cGMP
The steady-state concentration of cGMP as a function of Ca2+ concentration predicted by eqn (8) in our model (see Experimental) has been validated against the experimental data from.37 It is clear from the experimental data that some GC and PDE isoform pairs also produce a bell-shaped dependence of cGMP on Ca2+ concentration, in a similar way as AC and PDE do with cAMP. However, the peak cGMP concentration is reached at a significantly higher value of Ca2+ compared to the maximum cAMP concentration (Fig. 5B). This similarity in the shape of the concentration-dependent curves and at the same time the difference in the Ca2+ concentration corresponding to the highest nucleotide levels is rather intriguing, and may shed light on the mechanisms involved in synchronised intracellularnucleotide signalling.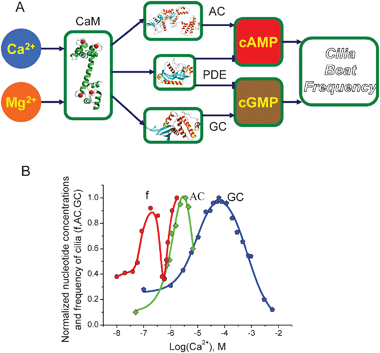 | ||
| Fig. 5 Cilia beat frequency dependence on Ca2+ concentration in Paramecium: (A) Schematic diagram representing the molecular network regulating CBF. Dynein subunits responsible for creating cilia movement are phosphorylated by cAMP and cGMP-dependent kinases. The levels of cAMP and cGMP are regulated by AC, GC, and PDE. The activities of these enzymes are regulated by CaM in a Ca2+-dependent manner. Mg2+ binds competitively to the Ca2+ binding sites on CaM. (B) The comparison of the nucleotide concentrations and the CBF dependence on Ca2+ concentrations. The data for CBF,61 AC69 and GC37 is shown as circles, squares, and pentagons, respectively. Both experimental data and the model predictions suggest that CBF almost superimposes on the sum of AC and GC steady-state curves. The only difference is the shift along the Ca2+ concentration, which can be explained by the difference in Mg2+ concentration at which the experiments took place. | ||
To investigate the issue of joint regulation by cAMP and cGMP, we considered an experimental system that requires the alteration of both cAMP and cGMPnucleotides in a Ca2+-dependent manner. Multiple studies have found that cilia beat frequency (CBF) is regulated by cAMPphosphorylation of dynein subunits.41,54,55cGMP-dependent kinase has also been shown to be involved in CBF regulation.56–58Ca2+ shapes both cAMP and cGMP intracilia concentrations and it is well established that it controls the cilia beat.59 In Paramecium, elevation of Ca2+ is reported to decrease cilia beat to the point at which the direction of beat is reversed.60 However, a further rise in Ca2+ leads to increased CBF,61 and the results of this study generally revealed a highly complex CBF dependence on the Ca2+ concentration. In mammals, increases in Ca2+ concentration almost always intensify cilia beat62–65 and reduced Ca2+ appears to diminish CBF.64 In spite of these and other experimental studies, there still appears to be considerable disagreement on the precise mechanisms of Ca2+ action in this system.56,66
We have used the mathematical model for Ca2+-dependent cAMP and cGMP metabolism developed in this study to investigate the underlying molecular mechanism of CBF regulation in Paramecium. The model predictions for cAMP and cGMP concentration (Fig. 5B) according to eqn (6) and (8) were superimposed on one graph (Fig. 5B) and compared with the experimentally measured dependence of CBF on Ca2+ concentration in Paramecium cells. Previous studies have already demonstrated how phosphorylation of dynein subunits by cAMP- and cGMP-dependent enzymes translates into cilia movement.67,68 Here we compare the nucleotide concentrations in comparison with CBF, presuming that the degree of cilia movement is proportional to the nucleotide concentration, via the phosphorylation of dynein protein by protein kinases.
The superimposition of the sum of the cAMP and cGMP concentration profiles predicted by the model and the CBF as a function of Ca2+ reveals a striking overlay of the two pieces of data. The only difference is the shift along the Ca2+ concentration. This difference can be explained by the fact that the Mg2+ concentrations used in the sets of experiments were significantly different. It has been shown before that Mg2+ ions can competitively bind to the same Ca2+ binding sites of CaM protein and make it require higher Ca2+ concentrations to achieve the same effects. With the amendment to Mg2+ concentration, the sum of the nucleotides closely reproduces the CBF dependence on intracilia Ca2+ concentration. This observation, emerging from the combination of the nucleotide model predictions with experimental data, provides an alternative to the previously discussed roles of cAMP and cGMP in cilia beat. First, the model clarifies how and why the alterations of Ca2+ concentrations can both increase or decrease CBF at specific Ca2+ concentration ranges. Second, it is reasonable to suggest that cAMP and cGMP operate in combination, rather than having unique and separate roles in CBF.
Discussion
This study elucidates some fundamental properties of the cAMP and cGMP regulatory systems using a structural systems biology approach. Our model allows a detailed analysis of the AC, GC and PDE isoform specific nucleotide distribution as a function of intracellularCa2+ concentration and G-protein subunits. This analysis in turn allows us to distinguish the diverse modes of cAMP concentration regulation emerging from combinations of AC and PDE isoforms with unique structural properties (Fig. 2 and 3). The possibility of inhibition, bell-shaped, reverse bell-shaped and sigmoidal saturation of cAMP as a function of intracellularCa2+ concentration suggests a potential explanation for mechanisms of intracellular selective cAMP-dependent signalling. In a previous work, we demonstrated that conformation-specific target activation is a mechanism for selective activation of multiple targets by multisite proteins.53 The non-bound, intermediate and fully saturated multisite protein conformations are mostly present at different ranges of Ca2+ concentration. In the case of nucleotide signalling, the predicted and observed concentration profiles as a function of Ca2+ and G-protein subunits (Fig. 4) can be interpreted as a mechanism for selective nucleotide signalling. Given that the cAMP-dependent PKA kinase phosphorylates so many different targets, a fundamental question arises as to how it targets its phosphorylation targets selectively. Structural studies demonstrate complementary protein surfaces are responsible for docking and phosphorylation but do not explain why different proteins or phosphorylation sites would be phosphorylated separately by the same cAMP-dependent PKA kinase. PKA has two cAMP binding sites and according to our previous work it could be selectively active to its phosphorylation targets in a complex with variable numbers of cAMP molecules bound. The diversity of possible cAMP concentration profiles demonstrated by this study provides additional potential mechanisms for selective regulation.The model predictions for simultaneous AC activation by both Ca2+ and G-proteins illuminate the impact of these two signals on cAMP concentration. We investigated potential scenarios of Ca2+ influence on the AC enzymatic activity in the presence and absence of G-protein subunits. The experimental data suggest that both Ca2+ and G-protein subunits may act as either inhibitors or activators of AC under different conditions (Fig. 4). Our mathematical modelling-based analysis shows that one potential possibility is that the state of AC changes when G-protein subunits bind to the molecule. Fig. 3B and 3C show that Ca2+ can modulate AC enzymatic activity in activatory or inhibitory fashion depending on whether G-protein subunits are bound to the AC protein. It has been proposed that multiple regulators of AC form patterns resulting in variability of AC activity.3,48 Here we demonstrate the underlying mechanism and effects of Ca2+ and G-proteins on cAMP concentration via the AC regulation. The resulting analysis allows us to propose a new explanation for the switching properties of G-protein subunits involved in nucleotide regulation. In particular, we show that, depending on whether the G-protein subunit is bound to AC, Ca2+ can either activate or inhibit AC in a concentration-dependent manner, in agreement with recent experimental results.3,4
The nature of the complementary regulation of cilia beat frequency in Paramecium cells by cAMP and cGMP has also been clarified by our study. While it has been known for some time that both nucleotides are required for cilia beat, little has been known about the level and nature of interaction between them. Our mathematical model allowed us to link both the nucleotide alterations with recorded CBF as a function of Ca2+ concentration (Fig. 5). The action of Ca2+ is translated into cilia movement via the sum of cAMP and cGMP bell-shaped concentration profiles with maximum concentrations. The trick here is that physiological intracilia concentration varies mostly between the peaks of cAMP and cGMP, effectively forming the reversed bell-shaped dependence of CBF on Ca2+ concentration. This result resolves the seeming inconsistency between reports suggesting that increasing Ca2+ may increase or decrease CBF. Thus, the underlying mechanism of cilia movement in Paramecium represents an interesting example of complementary roles in nucleotide-dependent regulation, and also proposes an explanation for how intracilia Ca2+ and nucleotide concentration alterations translate to cilia movement, hence defining the trajectory of Paramecium motion.
The models presented suggest how the diversity of isoforms of PDE, AC and GC within a single organism can give rise to precise regulation of cellular activity and address the paradox that alterations in Ca2+ concentrations can either increase or decrease outputs over similar Ca2+ concentration ranges depending on the cellular state. The model should be able to help interpret the extraordinary evolutionary diversity, including the absence, of PDE, AC and GC proteins, and the complementary functions of different isoforms. It may also be valuable in revealing adverse or unexpected cellular responses to drugs or other inhibitors which, because of the multiple isoforms and complex interactions of these proteins related to signal-response proteins, may be otherwise unpredictable and hard to measure experimentally.
Experimental
The model for intracellularcAMP metabolism
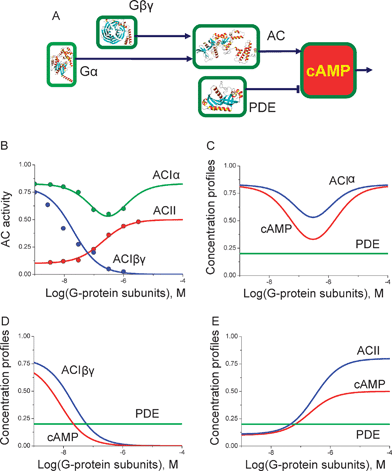
Fig. 1 provides a schematic outline of the network regulating cAMP concentration that is considered in our model. The cAMP production rate is proportional to the concentration of AC molecules in the active state that form complexes with adenosine triphosphate (ATP) and hydrolyse ATP to cAMP. At the same time, PDE molecules constantly bind to cAMP and degrade the phosphodiester bond, thereby converting cAMP into inactive 5′AMP. The intracellular level of cAMP is defined by the concentrations of AC and PDE isoforms in the active state and their enzymatic activities. The major regulators of AC are Ca2+ and signals mediated viaG-protein coupled receptors. Various AC isoforms have unique characteristics in terms of their dependence on both Ca2+ and G-proteins. Some of them are directly inhibited by Ca2+, whereas other AC isoform activities are regulated by Ca2+via calmodulin (CaM). The main activity regulator for cAMP hydrolysing PDE isoform I is a Ca2+–CaM pair. In our model, the law of mass action has been applied to derive a model based on measurable parameters for the dependence of cAMP levels on the AC and PDE enzymes. The chemical reactions underlying cAMP production and further hydrolysis are given by: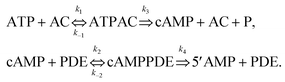 | (1) |
The reduced system of kinetic equations for the chemical reactions in eqn (1) is given by:
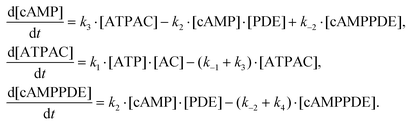 | (2) |
| [PDE] + [cAMPPDE] = [PDE*] [AC] + [ATPAC] = [AC*] | (3) |
Assuming that the alterations of [ATPAC] and [cAMPPDE] complex concentrations are relatively small, and applying the quasi-stationary approximation to eqn (2), we derive:
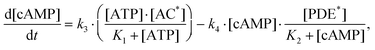 | (4) |
.
Given that [ATP]>>K1 in real cells (the ATP concentration is usually of the order of mM, whereas K1 is of the order of μM), eqn (4) can be transformed to the following form:
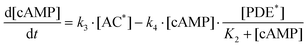 | (5) |
 | (6) |
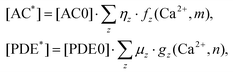 | (7) |
and
are the fractions of each isoform of AC and PDE. The dependence of the AC and PDE activities on Ca2+ is separated from the G-protein dependence, which is denoted in the above equations by m and n for AC and PDE, respectively.
Similarly, in steady-state, cGMP concentration can be represented explicitly as a function of GC and PDE isoform concentrations and activities by:
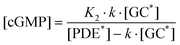 | (8) |
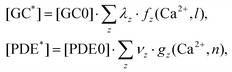 | (9) |
and
are the fractions of each isoform of GC and PDE. The dependence of the GC and PDE activities on Ca2+ is separated from the G-protein dependence, which is denoted in the above equations by l and n for GC and PDE, respectively.
The model for interactions between G-protein and Ca2+/CaM signalling pathways
The “state” or activity of each AC molecule has been represented in our mathematical model as follows. In order to cover all potential combinations, we assume that the molecule can be in four different states with diverse ratios of dissociation constants:| 1. v0 = 0.1, k0 = 1, 2. v1 = 100, k1 = 1, 3. v2 = 1, k2 = 10, 4. v3 = 10, k3 = 0.1. | (10) |
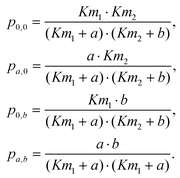 | (11) |
The rate of cAMP production by AC in each of the different states is given by:
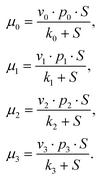 | (12) |
The full activity of the molecule is given by:
| M = μ0 + μ1 + μ2 + μ3 | (13) |
| cAMP | cyclic 3′,5′ adenosine monophosphate |
| cGMP | cyclic 3′,5′ guanosine monophosphate |
| GC | guanylate cyclase |
| PKA | cAMP-dependent kinase |
| CBF | cilia beat frequency |
| AC | adenylate cyclase |
| PDE | phosphodiesterase |
| ATP | adenosine triphosphate |
Acknowledgements
This work was carried out under EPSRC platform grant (EP/D029937/1), BBSRC grant (BB/D015340/1) and an RFBR grant.References
- T. M. Konijn, Cyclic AMP as a First Messenger, Raven Press Books, Ltd, New York, 1972 Search PubMed.
- S. Bader, A. Kortholt and P. J. Van Haastert, Biochem. J., 2007, 402, 153–161 CrossRef CAS.
- D. Willoughby and D. M. Cooper, Physiol. Rev., 2007, 87, 965–1010 CrossRef CAS.
- D. Willoughby and D. M. Cooper, J. Cell Sci., 2006, 119, 828–836 CrossRef CAS.
- R. K. Sunahara and R. Taussig, Mol. Interventions, 2002, 2, 168–184 CrossRef CAS.
- E. Alvarez-Curto, K. E. Weening and P. Schaap, Biochem. J., 2007, 401, 309–316 CrossRef CAS.
- R. Taussig, W. J. Tang, J. R. Hepler and A. G. Gilman, J. Biol. Chem., 1994, 269, 6093–6100 CAS.
- D. M. Cooper, Biochem. J., 2003, 375, 517–529 CrossRef CAS.
- C. Gu and D. M. Cooper, J. Biol. Chem., 2000, 275, 6980–6986 CrossRef CAS.
- J. Buck, M. L. Sinclair, L. Schapal, M. J. Cann and L. R. Levin, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 79–84 CrossRef CAS.
- R. Zoraghi, S. Kunz, K. Gong and T. Seebeck, J. Biol. Chem., 2001, 276, 11559–11566 CrossRef CAS.
- A. Rascon, S. H. Soderling, J. B. Schaefer and J. A. Beavo, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4714–4719 CrossRef CAS.
- H. Kuwayama, H. Snippe, M. Derks, J. Roelofs and P. J. Van Haastert, Biochem. J., 2001, 353, 635–644 CrossRef CAS.
- A. Nighorn, M. J. Healy and R. L. Davis, Neuron, 1991, 6, 455–467 CrossRef CAS.
- D. R. Repaske, J. V. Swinnen, S. L. Jin, J. J. Van Wyk and M. Conti, J. Biol. Chem., 1992, 267, 18683–18688 CAS.
- X. Jiang, J. Li, M. Paskind and P. M. Epstein, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 11236–11241 CrossRef CAS.
- A. T. Bender and J. A. Beavo, Pharmacol. Rev., 2006, 58, 488–520 CrossRef CAS.
- W. Y. Cheung, J. Biol. Chem., 1971, 246, 2859–2869 CAS.
- T. J. Martins, M. C. Mumby and J. A. Beavo, J. Biol. Chem., 1982, 257, 1973–1979 CAS.
- D. A. Fisher, J. F. Smith, J. S. Pillar, S. H. St Denis and J. B. Cheng, Biochem. Biophys. Res. Commun., 1998, 246, 570–577 CrossRef CAS.
- M. Salanova, S. C. Jin and M. Conti, Methods, 1998, 14, 55–64 CrossRef CAS.
- T. Sasaki, J. Kotera and K. Omori, Biochem. J., 2002, 361, 211–220 CrossRef CAS.
- J. F. Coquil, D. J. Franks, J. N. Wells, M. Dupuis and P. Hamet, Biochim. Biophys. Acta, 1980, 631, 148–165 CrossRef CAS.
- E. Fung, R. R. Fiscus, A. P. Yim, G. D. Angelini and A. A. Arifi, Chest, 2005, 128, 3065–3073 CrossRef CAS.
- G. Ravipati, J. A. McClung, W. S. Aronow, S. J. Peterson and W. H. Frishman, Cardiol. Rev., 2007, 15, 76–86 Search PubMed.
- W. C. van Staveren, J. Glick, M. Markerink-van Ittersum, M. Shimizu, J. A. Beavo, H. W. Steinbusch and J. de Vente, J. Neurocytol., 2002, 31, 729–741 CrossRef CAS.
- S. G. Andreeva, P. Dikkes, P. M. Epstein and P. A. Rosenberg, J. Neurosci., 2001, 21, 9068–9076 CAS.
- M. Gross-Langenhoff, K. Hofbauer, J. Weber, A. Schultz and J. E. Schultz, J. Biol. Chem., 2006, 281, 2841–2846 CAS.
- L. Fawcett, R. Baxendale, P. Stacey, C. McGrouther, I. Harrow, S. Soderling, J. Hetman, J. A. Beavo and S. C. Phillips, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 3702–3707 CrossRef CAS.
- M. Maeda, S. Lu, G. Shaulsky, Y. Miyazaki, H. Kuwayama, Y. Tanaka, A. Kuspa and W. F. Loomis, Science, 2004, 304, 875–878 CrossRef CAS.
- M. T. Laub and W. F. Loomis, Mol. Biol. Cell, 1998, 9, 3521–3532 CAS.
- D. P. Dougherty, G. A. Wright and A. C. Yew, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10415–10420 CrossRef CAS.
- R. Valkema and P. J. Van Haastert, Mol. Biol. Cell, 1994, 5, 575–585 CAS.
- Y. V. Gorbunova and N. C. Spitzer, Nature, 2002, 418, 93–96 CrossRef CAS.
- A. G. Gilman, Adv Second Messenger Phosphoprotein. Res., 1990, 24, 51–57 Search PubMed.
- A. G. Gilman, Biosci. Rep., 1995, 15, 65–97 CrossRef CAS.
- S. Klumpp, G. Kleefeld and J. E. Schultz, J. Biol. Chem., 1983, 258, 12455–12459 CAS.
- R. Meili, C. Ellsworth, S. Lee, T. B. Reddy, H. Ma and R. A. Firtel, EMBO J., 1999, 18, 2092–2105 CrossRef CAS.
- G. N. Europe-Finner and P. C. Newell, Biochem. Biophys. Res. Commun., 1985, 130, 1115–1122 CrossRef CAS.
- G. N. Europe Finner, H. S. Tillinghast, Jr, S. J. McRobbie and P. C. Newell, J. Cell Sci., 1985, 79, 151–160 CAS.
- M. Salathe, Annu. Rev. Physiol., 2007, 69, 401–422 CrossRef CAS.
- F. Hofmann, J. Biol. Chem., 2005, 280, 1–4 CAS.
- K. Hasegawa, H. Kikuchi, S. Ishizaki, A. Tamura, Y. Tsukahara, Y. Nakaoka, E. Iwai and T. Sato, J. Cell Sci., 1999, 112(Pt 2), 201–207 CAS.
- J. L. Guillou, H. Nakata and D. M. Cooper, J. Biol. Chem., 1999, 274, 35539–35545 CrossRef CAS.
- R. K. Sharma and J. Kalra, Biochem. J., 1994, 299(Pt 1), 97–100 CAS.
- W. F. Simonds, Trends Pharmacol. Sci., 1999, 20, 66–73 CrossRef CAS.
- V. J. Watts, J. Pharmacol. Exp. Ther., 2002, 302, 1–7 CrossRef CAS.
- R. Taussig and A. G. Gilman, J. Biol. Chem., 1995, 270, 1–4 CrossRef CAS.
- T. Nebl, M. Kotsifas, P. Schaap and P. R. Fisher, J. Muscle Res. Cell Motil., 2002, 23, 853–865 CrossRef CAS.
- W. Korohoda, Z. Madeja and J. Sroka, Cell Motil. Cytoskeleton, 2002, 53, 1–25 CrossRef CAS.
- J. J. Tesmer, R. K. Sunahara, A. G. Gilman and S. R. Sprang, Science, 1997, 278, 1907–1916 CrossRef CAS.
- N. Wettschureck and S. Offermanns, Physiol. Rev., 2005, 85, 1159–1204 CrossRef CAS.
- N. V. Valeyev, P. Heslop-Harrison, I. Postlethwaite, N. V. Kotov and D. B. Bates, Mol. Biosyst., 2008, 4, 66–73 RSC.
- T. Hamasaki, T. J. Murtaugh, B. H. Satir and P. Satir, Cell Motil. Cytoskeleton, 1989, 12, 1–11 CrossRef CAS.
- T. Hamasaki, K. Barkalow, J. Richmond and P. Satir, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 7918–7922 CrossRef CAS.
- N. Uzlaner and Z. Priel, J. Physiol., 1999, 516(Pt 1), 179–190 CAS.
- C. A. Geary, C. W. Davis, A. M. Paradiso and R. C. Boucher, Am. J. Physiol., 1995, 268, L1021–1028 CAS.
- R. Kissmehl, T. P. Kruger, T. Treptau, M. Froissard and H. Plattner, Eukaryotic Cell, 2006, 5, 77–91 CrossRef CAS.
- T. A. Wyatt, M. A. Forget, J. M. Adams and J. H. Sisson, Am. J. Physiol.: Lung Cell. Mol. Physiol., 2005, 288, L546–551 CrossRef CAS.
- Y. Naito and H. Kaneko, Science, 1972, 176, 523–524 CrossRef CAS.
- Y. Nakaoka, H. Tanaka and F. Oosawa, J. Cell Sci., 1984, 65, 223–231 CAS.
- A. B. Lansley, M. J. Sanderson and E. R. Dirksen, Am. J. Physiol., 1992, 263, L232–242 CAS.
- P. R. Girard and J. R. Kennedy, Eur. J. Cell Biol., 1986, 40, 203–209 CAS.
- M. Salathe and R. J. Bookman, J. Cell Sci., 1995, 108(Pt 2), 431–440 CAS.
- P. Verdugo, Nature, 1980, 283, 764–765 CrossRef CAS.
- L. Zhang and M. J. Sanderson, J. Physiol., 2003, 551, 765–776 CAS.
- N. V. Kotov, A. M. Volchenko, D. A. Davydov, E. K. Kostyleva, I. Sadykov and K. V. Platov, Biofizika, 2000, 45, 514–519 CAS.
- N. V. Kotov, V. V. Miroshnikov and I. D. Iudin, Biofizika, 1992, 37, 301–305 CAS.
- M. C. Gustin and D. L. Nelson, Biochem. J., 1987, 246, 337–345 CAS.
| This journal is © The Royal Society of Chemistry 2009 |