Towards a catalogue of glow discharge emission spectra
Zdeněk
Weiss
*a,
Edward B. M.
Steers
b,
Petr
Šmíd†
b and
Volker
Hoffmann
c
aLECO Instrumente Plzeň spol. s r.o., Plaská 66, 323 25, Plzeň, Czech Republic. E-mail: weissz@leco.cz
bLondon Metropolitan University, 166-220 Holloway Road, London, UK N7 8DB
cLeibniz Institute for Solid State and Materials Research Dresden, Helmholtzstraße 20, 01069, Dresden, Germany
First published on 16th October 2008
Abstract
Work has started on a new catalogue of glow discharge spectra. The motivation for this project, the contents of the future catalogue and its intended use are discussed, together with the methodology of the measurements, strategies for data acquisition and data processing. A high resolution Fourier transform (FT) spectrometer and two commercial CCD spectrometers will be used to collect the spectra. Preliminary data are presented for iron, showing the comparison of the CCD and FT spectra and the distribution of wavelength intervals between adjacent lines. Another example, concerning sensitive lines of copper, shows a possible use of the future catalogue to identify and evaluate line interferences and select the most suitable analytical lines for a given application.
1. Introduction
Glow discharge optical emission spectroscopy (GD-OES)1,2 is a well-established method for accurate analysis of metals and alloys and depth profiling of various surface-modified materials, thick layers and thin film systems. For successful work with modern GD-OES spectrometers with CCD detectors, allowing a fast registration of continuous spectra over wide wavelength ranges, a reliable catalogue of glow discharge spectra is needed. The only systematic reference work of this kind is a collection of photoplates from the early seventies3 published by E.W. Salpeter in collaboration with the company RSV Präzisionsmessgeräte GmbH. That work is not easily accessible to the general public and in many respects is insufficient for the current needs. Other common spectral tables and databases such as the NIST database,4 the Kurucz database,5 the Payling–Larkins tables,6 the Vienna Atomic Line Database,7 the tables by Striganov and Sventinskij8 and the PLASUS database9 are either based on measurements made with sources other than the glow discharge or on calculated intensities, assuming a quasi-equilibrium plasma with certain excitation/ionization temperature. Neither of these approaches works satisfactorily for the glow discharge, because, in glow discharge, populations of excited levels depend strongly on interactions of the sputtered atoms with atoms and ions of the discharge gas. An example of such an interaction is a process called asymmetric charge transfer,10 selectively populating certain excited levels of the analyte ions. As a result, glow discharge spectra differ significantly from the spectra excited e.g. by spark or arc and intensities of some lines in glow discharge sources differ by orders of magnitude from what can be found in the spectral databases mentioned above.Because of these reasons, work aimed at producing a new catalogue of glow discharge spectra has started. The concept is to collect GD-OES spectra of the elements in the Grimm-type glow discharge in argon and convert them into lists of observed emission lines with their relative strengths. This project is one of the topics to be solved in the framework of the Analytical Glow Discharge Network “GLADNET”,11,12 a Marie Curie Research Training Network (RTN) funded by the EC under its Sixth Framework Programme (FP6).
2. Methodology and the anticipated contents of the catalogue
2.1. General
The future catalogue will be based on experimental data, i.e., the spectra will have to be collected, individual emission lines identified and described in a suitable way. A convenient way of presenting information about relative strengths of individual lines in GD-OES is by using the emission yields rather than raw intensities, because emission yields provide a more general description than raw intensities measured for a given material. In particular, emission yields provide a convenient platform for comparing relative strengths of lines belonging to different elements. According to the standard model of GD-OES,13 the emission intensity Iλ(E),M of a line λ(E) of an element E in the analysis of a material M depends on the concentration cE,M of the element E and the sputtering rate qM of that material:| Iλ(E),M = Rλ(E)cE,MqM | (1) |
Glow discharge spectra depend strongly on the discharge gas and to some extent also on the operating conditions. Sputtering rates and emission yields are subject to variations with the discharge current and voltage, as described in ref. 1 and 2. For the catalogue, it was proposed to collect the spectra using a Grimm-type source1,2 with a 4 mm internal diameter anode, operating in the dc mode with constant voltage and constant current at 700 V, 20 mA in argon. This experimental setup is common in analytical practice and reflects also a convention, used in many commercial instruments, according to which these conditions are used as the ‘reference’ conditions for calibration.
An essential step will be to produce for each spectrum a list of all observed lines together with their intensities. In order to obtain ‘true’ emission yields, not affected by the optical system of the spectrometer, intensity response of each instrument will have to be calibrated with calibrated standard lamps. The spectra are represented in a format specific for each instrument and suitable software is needed to produce lists of observed lines from the raw spectral data. A very large number of spectral lines will have to be processed. A compiled list of all observed lines for each element, together with the corresponding emission yields, will be intended to become the basis of the future catalogue. Further physical characteristics of the lines such as term identification, energy of the levels involved, transition probabilities, etc., will be added, depending on the time and resources available for this project. Two different types of instruments will be used: a Fourier transform (FT) spectrometer and two CCD spectrometers. The CCD instruments are easy to operate and can collect data from a large number of samples within a reasonably short period of time. They are routinely used for analytical applications and the data collected on them reflect well what is needed in analytical practice. On the other hand, the Fourier transform spectrometer (FTS) provides a much better resolution and enables unambiguous identification of observed lines.
2.2. The CCD spectra
Two CCD instruments with a similar resolution will be used in this project: LECO GDS500A in the LECO Applications Centre, Prague, operates in the range 165 to 464 nm and is designed for a routine analytical work. An Echelle CCD spectrometer ARYELLE200 (LTB Lasertechnik Berlin GmbH., Germany) in the Leibniz-Institut für Festkörper- und Werkstoffforschung Dresden (IFW), with the range 200–750 nm, is a general-purpose instrument and the spectra will be collected using a stand-alone Grimm-type glow discharge source. These two instruments have a similar resolution and complementary wavelength ranges and can collect relatively easily and quickly spectra of pure elements and selected alloys, to determine emission yields and describe the intensity response of self-absorbed lines.The LECO GDS500A spectrometer is based on the ‘centred sphere’ optics.14 In this optical setup, the spectrum is focused on a plane, unlike e.g. in the more common Paschen–Runge polychromators. This suits better the CCD array detectors which are planar structures. Two identical spectra corresponding to the first positive and first negative diffraction orders are focused on the focal plane on opposite sides of the entrance slit and each spectrum is recorded by a pair of CCD arrays. The dispersive focal length is 225 mm, spectral resolution is 70 pm and the reciprocal linear dispersion is 26 pm pixel−1. The relative sensitivity at different wavelengths, i.e., the instrument function w(λ) of this spectrometer between 350 and 464 nm was determined using a calibrated tungsten halogen lamp and is shown in Fig. 1. Its discontinuity at the wavelength of 387.9 nm is caused by a different sensitivity of the two CCD arrays involved and/or the different radiation fluxes in the negative and the positive order. The observed variations of the instrument function are most likely caused by interference from reflections at the front and back of a layer covering an optical element of the system, probably the CCD arrays.
 | ||
| Fig. 1 Instrument function w(λ) of the LECO GDS500A spectrometer in the range of 350–460 nm. | ||
The wavelength scale of the CCD arrays is calibrated using a set of known lines existing in the spectrum. Individual lines in the spectrum are then characterized acccording to the following model, reflecting the intensity distribution in the focal plane of the spectrometer and also the broadening phenomena in the CCD array:15 The intensity–wavelength distribution generated in the focal plane by a monochromatic spectral line is represented by Gaussian function, and, because of the discrete character of the detector, this distribution is sampled (integrated) by individual cells of the CCD array. Suppose now that every pixel has a width d, of which g is the width of the non-sensitive area separating it from the next pixel. The lateral coordinate x can be chosen so that the active area of the nth pixel extends from the position x = nd to x = (n + 1)d − g. If x0 is the position corresponding to the central wavelength λ0 of a spectral line with an intensity I0, intensities generated by the spectral line in the pixels close to x0 are
 | (2) |
 | (3) |
 | (4) |
The signal recorded by a CCD detector is proportional to the light intensity and the integration time. The signal-integration time proportionality was experimentally verified for the LECO GDS500A spectrometer. To extend the dynamic range, each spectrum is recorded five times, with sampling rates (integration times) differing by a factor of 4 between each two consecutive acquisitions. Thus the resulting (composite) spectrum consists of five components (individual spectra), each measured with a 4 times higher sensitivity than the preceding one. The number of individual collections averaged for each component is inversely proportional to the integration time. Each of the 5 components of the CCD spectrum is processed separately, the lists of lines found in each component are combined and the resulting intensity of each line is calculated as average of its intensities in such components of the spectrum in which the line is stronger than a given threshold but not saturated. An example of the resulting data is given in Table 1. This particular data acquisition strategy is statistically robust, but not optimized for the best possible precision of intensities.
| Rel. sensitivity: | 1 | 4 | 16 | 64 | 256 | The resulting intensity |
|---|---|---|---|---|---|---|
| λ/nm | Intensities in individual components of the spectrum | |||||
| a “sat” stands for a saturated pixel at the particular wavelength, a blank cell means that the corresponding intensity was below the selected threshold. | ||||||
| 232.738 | 0.212 | 0.236 | sat | sat | 0.224 | |
| 232.940 | 0.031 | 0.035 | 0.033 | |||
| 233.136 | 0.185 | 0.185 | sat | sat | 0.185 | |
| 233.279 | 0.588 | 0.631 | 0.619 | sat | sat | 0.613 |
| 233.799 | 0.391 | 0.429 | sat | sat | 0.410 | |
| 233.964 | 0.087 | 0.063 | sat | 0.075 | ||
| 234.044 | 0.064 | 0.049 | sat | 0.056 | ||
The ARYELLE20016 is an echelle spectrometer with a focal length of 200 mm and an aperture of f/10. It has a chromatic resolving power of 9000, resulting in spectral resolution of 22–83 pm. It is equipped with a thermoelectrically cooled CCD array detector with 1024 × 1024 pixels, 13 × 13 mm2 image area (DV434, Andor Technology PLC, Belfast, Northern Ireland). Light from a stand-alone Grimm-type glow discharge source is coupled to the spectrometer by optical fibre. The wavelength scale is calibrated using the mercury lamp and data processing is carried out by a dedicated program (Sophi for ARYELLE). For the purpose of the catalogue, our intention is to treat the spectral data resulting from this program similarly as it was described above for the GDS500A.
2.3. The FT spectra
High resolution and a very accurate wavelength determination are two major features of FT spectra that make FTS data very useful for unambiguous identification of the lines that cannot be resolved by the CCD instruments. The high resolution FT spectrometer at Blackett Laboratory, Imperial College, London, is based on the Michelson interferometer; details of this instrument can be found elsewhere.17 It can operate in the range from ∼137 nm to > 800 nm, with the best available resolution of ∼0.035 cm−1 which gives the chromatic resolving power of 1.4 × 106 and resolution of 0.14 pm at 200 nm. Normally, a lower resolving power is used to achieve the maximum light throughput and line profiles with a very small contribution from the instrumental function (a sin x/x function showing the effect known as ‘ringing’).The wavelength spectral range of the FT spectrometer can be relatively large; it is determined by the frequency with which the interferogram is sampled, and the alias chosen.18 Furthermore, in order to suppress a fold-back of lines from adjacent aliases and to eliminate a contribution to the overall noise from the radiation from outside the spectral range of interest, a combination of appropriate optical filters and PMTs has to be used. In our previous experiments, we have been using four separate wavelength ranges which overlap partially—see Table 2. The overlapping of the spectral ranges is important because the intensity response in each spectral range falls off towards its limits (no signal outside the spectral range) and the lines at the limits would not be recorded if there was no overlap.
| FSR/cm−1 | Alias | Alias range/cm−1 | Filters | PMT | Actual wavelength range/nm |
|---|---|---|---|---|---|
| a A very narrow band filter to reduce the background signal produced by scattered laser light. | |||||
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–64 000–64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
R1220 | 160–290 | |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–40 000–40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
UG5 | 1P28 | 280–405 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–34 000–34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
WG295 | 1P28 | 300–550 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–22 000–22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
NOTCH a + LP47 | R928 | 470–850 |
Since the intensity response in each spectrum is wavelength dependent because of the variation of the PMT efficiency and the optical filter transparency, intensity calibration using appropriate intensity standards (tungsten and deuterium lamps) is necessary. FTS has a linear wavenumber scale which is derived from the intervals at which the interferogram is sampled. The sampling intervals are determined by the fringes of a stabilised He–Ne laser. In theory, the laser wavelength can be used for absolute wavenumber calibration. In practice, there is always a small angular difference between the source and the laser beams through the interferometer, so that the wavenumber calibration is not absolute. However, from our experience, the wavelength determination is very accurate and no correction in wavenumber scale is usually needed.
The interferogram recorded with equal positive and negative optical path differences is the Fourier transform of the source spectral distribution. Therefore, an inverse Fourier transform is carried out to produce the spectrum.18 Computer programs commonly used for this are those by J. W. Brault, DECOMP19 and its successors GREMLIN and XGREMLIN. After the transform, a list of lines from the spectrum is produced in one of these programs. This ‘line list’ contains information about wavenumbers, wavelengths, the intensities and the widths of all lines which have their intensity stronger than a specified threshold.
Because of the high resolving power of the FT instrument, true line profiles can be observed, including e.g. hyperfine structure and self-reversal. Therefore, the intensity measurements have to be made with special care. In general, each line which shows no hyperfine structure or self-reversal can be expressed as a convolution of Gaussian, Lorentzian and instrumental functions. To fit a Voigt profile to the line and subtract the contribution from the instrumental function is a complex procedure. Such procedure is essential only when e.g. Doppler line width needs to be measured. For the purpose of the intensity measurements in this work, either a peak value (for the lines which do not show any hyperfine structure or self-reversal), or the area under the line calculated based on a Gaussian fit or a spline fit will be used.
Another important feature of FTS is how the noise is transformed from an interferogram to a spectrum. In FTS, all spectral elements contribute to the overall noise and this noise is distributed throughout the entire spectrum Therefore, if the source spectrum contains one strong line with the intensity fluctuation e.g. 1%, the resulting level of the noise in the transformed spectrum due to this fluctuation can be quite significant for weaker lines present in the spectrum, and those weak lines can have a very low signal-to-noise ratio. In some cases, it may be possible to optimise the noise level by filtering out such strong lines (spectra with and without those lines are recorded). This can be done by adjusting the spectral range in combination with appropriate optical filters. The noise in the spectrum can be also reduced by adding several separate scans together, so called co-adding. The gain in the signal-to-noise ratio will increase as the square root of the number of co-adds.
2.4. Comparison of the FT- and CCD spectra
To prepare methodology for the actual measurements and get some real data on which the software for producing the catalogue can be developed and tested, the following experiment was made. Spectrum of pure iron was measured on both spectrometers with Grimm-type sources in argon at the following conditions: 700 V, 20 mA, 4 mm anode (the LECO CCD instrument) and 700V, 80 mA, 8 mm anode (the FTS instrument). The same portion of both spectra, ranging from 213 to 287 nm, was then processed, lists of lines were produced from both sets of data and compared. In the CCD spectrum, 349 lines were found and in the FT spectrum 457 lines. To compare both spectra based on individual lines, a set of ‘clean’ lines that can be individually characterized on the CCD spectrometer was selected, in the following way: a line is considered ‘clean’ if no other line with an intensity greater than 10% of the intensity of the examined line exists in its vicinity, closer than Δλ = 0.078 nm from its central wavelength. This Δλ corresponds to 3 pixels and is close to the resolution of the instrument. Such lines were identified based on the FTS list of lines. It should be noted that the information from the FTS data was used here a posteriori, i.e., only to filter the original CCD list of lines. The procedure reduced the original set to 140 ‘clean’ lines. In this respect, it is interesting to show the distribution of wavelength intervals separating adjacent lines in the spectrum, as resulting from the original FTS list of lines (Fig. 2). This very rich portion of the Fe spectrum (mostly Fe II lines) was deliberately used to test the procedures intended for the catalogue. In the spectra of many other elements, the relative proportion of ‘clean’ lines will be higher. The classes in the histogram in Fig. 2 were chosen arbitrarily. This histogram shows only separation of the adjacent lines. Whether or not a specific line can be reasonably well characterized in the CCD spectrum depends also on how strong the adjacent line is. Nevertheless, it is clear that a significant part of the spectrum can be well described only with the FTS instrument. | ||
| Fig. 2 Distribution of wavelength intervals separating adjacent lines in the FT spectrum of iron in an argon discharge between 213 and 287 nm (histogram): e.g., 84 wavelength intervals between adjacent lines are wider than 0.010 nm and narrower than 0.030 nm. The total number of intervals is 456. | ||
Comparison of the FT and the CCD spectra on the set of ‘clean’ lines gave the following results: concerning the central wavelengths of individual lines, Fig. 3 shows a histogram of the deviations of the central wavelengths in the CCD list, relative to the corresponding central wavelengths in the FTS data, and Fig. 4 shows the corresponding cumulative distribution function. From Fig. 4, it is apparent that, for more than 50% of the lines, central wavelengths reported in the CCD data are within the interval of ±3 pm from the correct value. Considering that the criterion for selecting the ‘clean’ lines was not very strict, and, consequently, overlapping lines were not completely avoided, this performance is very good for an instrument with a specified resolution of 0.070 nm. This justifies the use of the data processing procedure as described in section 2.2. Concerning the intensities, comparison between the CCD and the FT spectra is given in Fig. 5. The correlation can be also considered satisfactory, taking into account that the intensity response of neither of the two instruments was calibrated in this spectral range and the intensities are linked randomly to the wavelengths. Also, the CCD data came from two different CCD arrays, one recording the first negative order and the other the first positive order, whilst each array provided signal for a part of the described spectral range. Finally, the spectral sources were not the same, the source used for the FTS measurements had twice as large anode diameter than that in the CCD spectrometer but the sample surface current densities were the same.
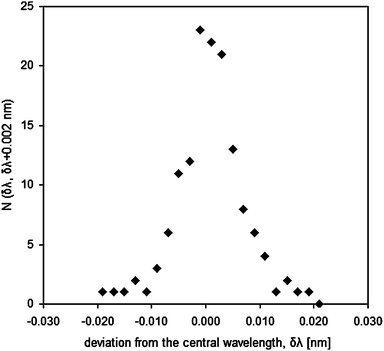 | ||
| Fig. 3 Histogram showing the number of ‘clean’ lines for which the difference between their central wavelengths, as calculated from the CCD spectrum, and the correct values from the FTS data is in the interval (δλ, δλ + 0.002 nm). | ||
 | ||
| Fig. 4 The portion of ‘clean’ lines having the deviations of the central wavelength, as resulting from the CCD spectrum, smaller than δλ from the correct value (corresponds to Fig. 3). | ||
 | ||
| Fig. 5 Comparison of intensities of the ‘clean’ lines in the FT and the CCD spectrum. | ||
3. The use of the catalogue in analytical applications: an example
An obvious use of the catalogue will be searching for emission lines of an element to be analyzed that are not affected by line interferences from the matrix elements. Line interferences can be corrected for by subtracting from the total measured intensity the contribution of the interfering line of another element, but, even so, sensitivity of the analysis will be reduced by the noise associated with that interfering line. Magnitude of a line interference can be expressed in the following way: Suppose that a line λ(E) of an element E has an interference from a line λ(F) of another element, F, having the same wavelength. Then the total intensity measured at that wavelength will be according to eqn (1)| Iλ,M = Rλ(E)cE,MqM + Rλ(F)cF,MqM | (5) |
 | (6) |
 | (7) |
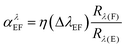 | (8) |
As an example, analysis of copper in steels, nickel alloys and cobalt alloys can be mentioned. Such materials may contain relatively high concentrations of some alloying elements with rich spectra, such as W, Mo, Cr, V. In Table 3, the most sensitive lines of copper are listed, together with some observed line interferences caused by matrix elements relevant to these materials. The interference factors αλEF and the wavelength differences ΔλEF between those copper lines and the corresponding interfering lines are given. The interference factors come from measurements made on the GDS500A spectrometer. Such data make it possible to optimize automatically selection of analytical line(s) in the analysis of specific material, depending on which alloying elements have been detected at which concentrations. Emission yields listed in Table 3 are not corrected for the instrument function and therefore provide only an approximate comparison of relative sensitivities of these lines in the glow discharge. The interference factors αλEF, however, do not depend on the instrument function w(λ) and should be similar for all instruments on which the particular line interference is unresolved, i.e., for instruments collecting all the light from the interfering line in the spectral window of the analytical line. The most sensitive copper line observed is the Cu II line at 224.700 nm. However, it is excited predominantly by charge transfer with argon ions,10 is therefore very sensitive to the presence of hydrogen in the sample or plasma gas20 and may be subject also to another excitation-related matrix effects.21 Factors like this should be also considered when evaluating candidate analytical lines for a given application, in addition to their strengths and existing spectral interferences.
| Line | R a (arb. units) | Line interferences: αλEF (top, bold), ΔλEF/nmb (bottom) | ||||
|---|---|---|---|---|---|---|
| Fe | Ni | Co | W | Mo | ||
| a emission yields of the copper lines: the data were not corrected for the instrument function. b ΔλEF are the differences between the wavelengths of the Cu lines, as listed in column 1, and wavelengths of the adjacent lines of the interfering elements found in the database.9 Hyperfine structure and any broadening of the lines involved is not included. | ||||||
| Cu II, 224.700 nm | 4.4 | 0.52 × 10−3 | 95 × 10−3 | 0.38 × 10−3 | 5.5 × 10−3 | |
| −0.008 | 0.023 | −0.013 | −0.006 | |||
| Cu I, 324.754 nm | 2.1 | 1.6 × 10−3 | 2.5 × 10−3 | 1.7 × 10−3 | ||
| 0.015 | −0.009 | 0.007 | ||||
| Cu I, 327.396 nm | 1.25 | 0.38 × 10−3 | 2.6 × 10−3 | |||
| 0.007 | −0.002 | |||||
| 0.008 | 0.005 | |||||
Another task that can be solved using the catalogue is the selection of lines for depth profile analysis on CCD instruments. Because the signal detected by a CCD array can be controlled only by integration time, there will be always tradeoff between the sampling rate and sensitivity for a given line. Sampling rate determines the time resolution in depth profiling, and, consequently, the thickness of the layers present in the sample that can be recognized as individual layers. Then the task arises of choosing such analytical lines that would fit to the selected sampling rate, i.e., that would not be too strong to become saturated, and, at the same time, not too weak to provide an acceptable signal-to-noise ratio. Such lines can be selected based on their emission yields listed in the catalogue. It is also likely that, for some elements, different lines will be used at different depths, because, e.g., in the analysis of a coating system, concentrations of some elements are changing by orders of magnitude between individual layers or between the coating and the substrate.
4. Conclusions
The task to set up a catalogue of spectra differs from more common work in spectroscopy by the fact that, instead of dealing with a pre-selected, limited set of lines that are interesting for an application or a fundamental study, the goal is to find, identify and characterize virtually all measurable lines appearing in the spectrum. This requires, besides other things, special means of data processing, oriented to searching for lines in the spectra and to manipulation of large lists of lines. All the procedures must reflect the performance of the instruments used. Because of the extent of the work, the experiments should be carefully planned and the methodology clarified before the work starts. The goal of this paper is to prepare the ground for the project, analyze its feasibility and identify possible obstacles. The combination of a high resolution FT spectrometer and two commercial CCD spectrometers is a good combination for this task.References
- N. Jakubowski, A. Bogaerts and V. Hoffmann, Glow discharges in emission and mass spectrometry, in Atomic Spectroscopy in Elemental Analysis, ed. M. Cullen, Blackwell Publishing, Sheffield, 2003 Search PubMed.
- Glow Discharge Plasmas in Analytical Spectroscopy, ed. R. K. Marcus and J. A. C. Broekaert, Wiley, Chichester, 2003 Search PubMed.
- E. W. Salpeter, Spektren in der Glimmentladung von 1500 bis 4000Å, Specola Vaticana, Città del Vaticano: 1. Teil (1971) - Fe, Co, Cr, Mo, Nb, Ni, Ta, Ti; 2. Teil (1971) - Edelgasse; 3. Teil (1972) - Fe, Cu–Be, Ca–Si, Hg–Zn, Pb–Bi, Sb–S, Sn–As, Mg–Cd; 4. Teil (1972) - Fe, Ag, Au, Ir, Pd, Pt, Rh, Ru; 5. Teil (1973) - Fe, Al, Hf, Mn, Se–Te, V, W, Zr Search PubMed.
- Yu. Ralchenko, A. E. Kramida, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (version 3.1.5), 2008 [Online]. Available: http://physics.nist.gov/asd3 [2008, April 20]. National Institute of Standards and Technology, Gaithersburg, MD Search PubMed.
- 1995 Atomic Line Data (R.L. Kurucz and B. Bell) Kurucz CD-ROM No. 23. Cambridge, MA, Smithsonian Astrophysical Observatory, http://cfa-www.harvard.edu/amdata/ampdata/kurucz23/sekur.html.
- R. Payling and P. L. Larkins, Optical Emission Lines of the Elements, John Wiley and Sons Ltd., 1999 Search PubMed.
- Vienna Atomic Line Database (VALD) at http://ams.astro.univie.ac.at/%E2%88%BCvald/.
- A. R. Striganov and N. S. Sventitskij, Tables of Spectral Lines of Neutral and Ionized Atoms, Plenum Data Corporation, New York, 1968 Search PubMed.
- PLASUS SpecLine, Version 1.32, PLASUS Ingenieurbüro, Königsbrunn, Germany, 2001, see also http://www.plasus.de Search PubMed.
- E. B. M. Steers, Charge transfer excitation in glow discharge sources: The spectra of titanium and copper with neon, argon and krypton as the plasma gas, J. Anal. At. Spectrom., 1997, 12, 1033–1040 RSC.
- N. Jakubowski, E. Steers and A. Tempez, Glow and Glory, J. Anal. At. Spectrom., 2007, 22, 715–721 RSC.
- GLADNET website http://www.gladnet.eu/.
- Z. Weiss, Emission yields and the standard model in glow discharge optical emission spectroscopy: Links to the underlying physics and analytical interpretation of the experimental data, Spectrochim. Acta, Part B, 2006, 61, 121–131 CrossRef.
- K. A. Marshall and P. M. Willis, Centered sphere spectrometer, US Pat., 6023330 Search PubMed.
- Z. Weiss, Characterization of spectral lines in optical emission spectra measured by CCD detectors, J. Anal. At. Spectrom., 2005, 20, 1–2 RSC.
- Information at http://www.ltb-berlin.de/aryelle200.html.
- J. C. Pickering, High resolution Fourier transform spectroscopy with the Imperial College (IC) UV-FT spectrometer and its applications to astrophysics and atmospheric physics: a review, Vib. Spectrosc., 2002, 29, 27–43 CrossRef CAS.
- A. P. Thorne, U. Litzen and S. Johansson, Spectrophysics: Principles and Applications, Springer Verlag, 1999 Search PubMed.
- J. W. Brault, High precision Fourier transform spectrometry: The critical role of phase corrections, Mikrochim. Acta, 1987, 93, 215–227 CrossRef.
- V.-D. Hodoroaba, V. Hoffmann, E. B. M. Steers and K. Wetzig, Emission spectra of copper and argon in an argon glow discharge containing small quantities of hydrogen, J. Anal. At. Spectrom., 2000, 15, 951–958 RSC.
- Z. Weiss, Glow discharge excitation and matrix effects in the Zn–Al–Cu system in argon and neon, Spectrochim. Acta, Part B, 2007, 62, 787–798 CrossRef.
Footnote |
| † Present address: AQura GmbH, Rodenbacher Chaussee 4, 63457 Hanau, Germany. |
| This journal is © The Royal Society of Chemistry 2009 |
