Laser ablation inductively coupled plasma mass spectrometry—current shortcomings, practical suggestions for improving performance, and experiments to guide future development

Abstract

Experimental parameters and processes important in laser ablation such as the wavelength, fluence and pulse width of the laser, the form of the ablation cell, the cell gas, the particle transport and atomization in the ICP have an impact on the analytical performance of laser ablation inductively coupled mass spectrometry. The paper discusses the influence of the aforementioned parameters and processes on LA-ICP-MS and presents proposals to map out strategies for optimum LA-ICP-MS analyses. Additionally, experiments are identified which still need to be done for better understanding of the relevant processes and further improvement of the analytical performance of the technique.

---

Carmen C. Garcia

Carmen Garcia obtained her PhD in 2003 in analytical chemistry at the University of Malaga. In 2005, she joined ISAS in Dortmund, where she is currently working as a Postdoc.

Helmut Lindner

Helmut Lindner obtained his PhD at ISAS in 2008. Currently, he is working as a Postdoc in the PLASMANT group of the University of Antwerp in Belgium.

Kay Niemax

Kay Niemax is Director at ISAS and Full Professor for Physics at the Technische Universität Dortmund, Germany. His current fields of research are plasma and laser spectrochemistry.

---

Introduction

Laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) is a widely used technique for direct analysis of solid samples.^1–5 In principle, LA-ICP-MS can be applied to different matrices such as metal, glass, ceramic, meteorites, plant material, or biological tissue. However, the choice of experimental parameters, such as wavelength, pulse width, pulse frequency, focus position and fluence of the laser, the gas in the ablation cell, the geometry of the cell and of the particle transport system, has to be made in a strategic way. For example, the strategies will differ considerably if the average elemental concentrations of samples or the elemental distribution of inhomogeneous samples have to be measured. A sophisticated strategy is even more important if, for any reason, the optimum experimental parameters or the most appropriate instrumentation cannot be used or is not available. The present paper is not a review on the field of LA-ICP-MS and does not claim to be complete. It is rather an attempt to give a couple of hints and ‘recipes’ on how to adapt the experimental parameters to the analytical problem in an effective way.

The paper takes into account the results and personal experience of the authors and their colleagues gained during a three year research project sounding out the feasibility of femtosecond-LA-ICP-MS analysis with calibration by non-matrix matched standards. However, the scope of the paper will also cover laser ablation with nanosecond lasers since, because of economic reasons, ns lasers are still more often used for LA in analytical laboratories. Important topics will be elemental fractionation observed in LA processes, generation of particles and their spatial distribution in ablation cells, size distribution and composition of the particles, and aerosol transport to the ICP as well as particle atomization in the ICP.

In addition, the present paper also identifies open questions and presents proposals for experiments which still need to be made for better understanding of the different processes involved in the technique in order to develop strategies for improving the analytical performance of LA-ICP-MS.

Ideal and real conditions in LA-ICP-MS

The following ideal conditions would be required for optimum bulk analyses of homogeneous samples by LA-ICP-MS (see Fig. 1):

1. The pulsed laser removes mass from the sample which forms particles having in total the same stoichiometric composition as the sample. The sample is chemically unchanged by the ablation process. No ablated material is re-deposited onto the surface of the original sample.

2. The mass ablated forms particles which are transported without any loss from the place of ablation, the ablation cell, through the transport tube and the injector of the ICP-torch into the plasma.

3. The particles are completely atomized and ionized in the ICP without affecting the plasma parameters.

If these three conditions are fulfilled the element ion ratios measured by ICP-MS are measures of the elemental concentration ratios in the sample. Therefore, quantification can be made by comparing the recorded element ratios of the sample of interest with the respective ratios measured in homogeneous standard reference samples. In this case, the matrices can be very different. They should only contain the elements of interest. It means that the assumed ideal LA-ICP-MS conditions allow the use of non-matrix matched standards for calibration.

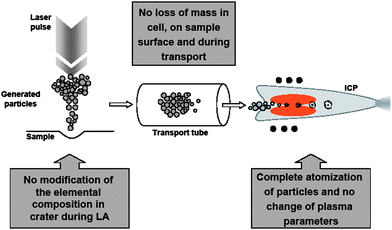Fig. 1 Idealized conditions for LA-ICP-MS analyses.

Unfortunately, the real conditions in LA-ICP-MS can be far from the ideal requirements listed above. The degree of deviation depends on the choice of experimental parameters, i.e., the experimental parameters have to be carefully optimized taking into account the instrumental boundary conditions given by the laser system, the gas, the ablation cell, and the ICP instrument. Such optimizations require:

1. information on the physical–chemical nature of the sample, such as major constituents, homogeneity and morphology,

2. some understanding of laser interaction with materials and the ablation processes,

3. knowledge about the formation processes and the spatial distribution of particles in the ablation cell which are both dependent on laser fluence, laser wavelength and in-cell carrier gas,

4. the proper choice of ablation cell and particle transport system for the particular analytical application of LA-ICP-MS (bulk analysis, microanalysis, depth profiling, etc.),

5. information on the particle size distributions applying suitable on-line measurements, such as optical laser scattering or differential mobility analysis, and

6. knowledge on the atomization capability of the ICP for particles of different size, material and composition.

The ablation process and preferential elemental ablation

The physical background of the laser ablation process has been described in many original papers, in reviews and text books (see, for example, ref. 6–10). Laser ablation is a very complex process which has been treated theoretically using different approximations taking into account the expected dominant physical processes for particular experimental parameters (pulse length, fluence, wavelength, physical properties of matrix, etc.). In recent years, the theory of fs laser interaction with solids and the ablation mechanism has been the focus of interest.^9–13 However, one can state that the main processes are still under controversial discussion and the laser ablation theories present an insular and incoherent picture. Further work has to be invested to formulate the physics and simulate the processes of laser ablation in a way that theoretical predictions are in agreement with experimental data for all matrices. For the user of LA-ICP-MS it is of particular interest that theory can model LA of multi-element samples, since so far there are no theoretical attempts which take chemical compositions of laser probed samples into account.

In LA intense laser radiation is directed onto the sample where it is absorbed in single and multi-photon processes by electrons in the surface layer. Subsequently the energy is transferred to other electrons in the sample. High energy electrons leave the sample surface or diffuse into deeper layers of the sample. Typical electron penetration depths are of the order of 100 nm. While the electrons are thermalizing in the femtosecond (fs) time domain, heating and thermalization of the heavier atoms by electron collisions require time durations in the picosecond (ps) range. Explosive-like ablation of the affected sample layer follows if the amount of absorbed and transferred energy surpasses a matrix-specific value (ablation threshold). The mass propagation in a buffer gas is similar to the blast of an atomic bomb explosion from ground. After being stopped by the in-cell gas, the material is distributed ‘mushroom cloud’-like, as has been demonstrated by imaging the optical plasma emission or by laser scattering on the particles generated (see below). We will see that such a ‘mushroom cloud’-like mass propagation mode is desirable for optimization of the LA-ICP-MS since particle loss due to re-deposition on the sample surface near to the laser crater is small. Unfortunately, there is another very different mass propagation mode which can cause high particle losses. Here, material propagation is more horizontal than vertical in respect to the sample surface, which favours particle deposition. Undesirable horizontal propagation is enforced by strong plasma breakdown in the gas above the sample. A hypothesis for the reason of the breakdown, a proposal for an experiment to prove the hypothesis, and experimental actions to avoid or reduce the effect of plasma breakdown in the gas are discussed below.

Helium and argon at atmospheric pressure are applied as in-cell and particle carrier gas in LA-ICP-MS. The gas has a significant impact on the analytical performance of the technique since it determines the maximum material expansion after the ablation event and has influence on the transport properties of particles. Furthermore, plasma breakdowns with subsequent plasma shielding and modified spatial material expansion are more probable for gases with low ionization energy. Therefore, helium is the preferred in-cell gas in LA-ICP-MS.

Another very important parameter is the pulse length of the laser. Very short laser pulses, e.g., 100 fs pulses directly deposit their energy in the sample while longer laser pulses may also heat the expanding plasma by inverse Bremsstrahlung. At high laser fluence, plasma heating can be so effective that the electron density in the plasma increases to values which make the plasma opaque and reduce the interaction of the laser with the sample. As a result less mass is ablated from the sample. The LA-ICP-MS detection efficiency is further reduced if there is additionally a significant change from the vertical to the horizontal material expansion with particle deposition.

A second, pulse length dependent process which can have significant influence on LA-ICP-MS analysis is heat transfer from the laser-material interaction region into the sample. Depending on the thermal properties of the sample and the length of the laser pulse more or less melting is produced in the laser crater. Melting not only dislocates elements from their original position, a drawback for any analysis where spatial element distributions are of interest (e.g., in microanalysis or depth profiling), but is also a source for fractional evaporation of volatile elements isolated and delayed from the ablation event and the formation of particles. Thermally evaporated elements form very small clusters which tend to get lost by diffusion and deposition to the walls. For example, the depletion of volatile elements has been demonstrated in our laboratory by analysing the melt ejected from a brass crater in ns-LA.¹⁴ Instead of 1.54, the Cu/Zn ratio in the bulk, the ratio in the melt was about 2 due to preferential evaporation of the element with higher volatility, Zn.

In general, analytical problems due to melt formation may arise if the interaction time between the laser and material is long and the melting point of the sample is low. This means, lasers with very short pulse length, e.g. fs lasers, should be preferably used if available since the interaction time with the sample is shorter than the electron–phonon coupling time (> 1 ps). On the other hand, the laser fluence should be reduced to a tolerable level to avoid extensive melting in the crater if lasers with longer pulse lengths, e.g., ns lasers, are the only ones available. In the case of bulk analysis, the fluence should be lowered by defocusing the laser beam. It is recommended to set the focus of the laser beam below the sample surface in order to reduce the probability of plasma breakdown and shielding in the gas above the laser crater (see below).

Elemental fractionation during and immediately after laser-material interaction

In general, elemental fractionation in LA is the preferential ablation of particular elements in the sample. One type of elemental fractionation has already been mentioned in the preceding section, the atomic evaporation of volatile elements from crater melt. The other type of preferential elemental ablation can be observed during and immediately after the laser shot. It will be the focus of this section.

Elemental fractionation is a very important process which occurs in the analysis of almost all samples, independently of whether fs lasers^15–17 or ns lasers^18–21 are applied. It is particularly strong if the laser fluences are near the ablation threshold.^15–17,20 Recently,¹⁷ it has been shown by shot-to-shot fs-LA-ICP-MS measurements of multi-element glass and different binary samples that the element ratios in the mass ablated change monotonically from shot to shot until they approach asymptotic ratios. The same asymptotic ratio can be reached applying more or fewer shots if the laser fluence is reduced or increased, respectively. The monotonic, fluence dependent shot-to-shot variation and the approach of the asymptotic element ratios can be described in a consistent way by a recursion formula for any fluence, taking into account the element ratio variation measured at a selected fluence.¹⁷ It is important to note that the measured asymptotic element ratios are measures of the element ratios in the samples, the basic requirement for LA-ICP spectrometry with calibration by non-matrix matched standards^15,22 as outlined in the section on ideal LA-ICP-MS conditions. Therefore, ablation under asymptotic element ratio conditions can be regarded as stoichiometric ablation.¹⁷ Complementary to the element composition in the ablated mass, the element composition in the affected thin layer of the crater bottom is changing as shown for brass and GaAs samples. At stoichiometric ablation, the element compositions in the bottom layers reach equilibrium values which are different from the composition of the bulk. The average thickness of the modified layer was found to be of the order of 30–50 nm. It has to be noted that the effect of elemental fractionation in the first shots is usually not seen clearly since typical LA-ICP-MS measurements are made with laser frequencies of ∼20 Hz and relatively large ablation cells. Under such experimental conditions the particles are filling the ablation cell in order to record smooth signals (see below). Therefore, fractionation can only be observed if the laser fluence is so low that many laser shots are required to reach stoichiometric ablation conditions.^15–17,22

Furthermore, it was speculated that there is a correlation between elemental fractionation and the ionization energies of the elements studied. With the exception of the Cr/Fe ratio measured in a Cr–Fe binary sample, which showed a slightly deviant behaviour, elements with lower ionization energy appeared to be preferentially ablated or depleted in the crater bottom. It was hypothesized that Coulomb interaction is responsible for the observed elemental fractionation. Just after multi-photon absorption of the fs laser pulse in the layer given by the optical penetration depth, extremely hot electrons are leaving the sample with high velocity or penetrating into deeper layers. The affected sample layer can be regarded as a very dense plasma equalizing its ionization temperature within 1 ps, leaving element ion concentrations according to their ionization energies. Repulsive and attractive Coulomb interactions between element ions in the dense plasma layer and between the element ion and the electrons outside the sample (ambipolar diffusion^23,24), respectively, are assumed to be responsible for element de-mixing and preferential ablation of elements with lower ionization energy. The hypothesis is supported by earlier fs-LA-ICP-MS experiments on glass samples¹⁶ showing ionization energy dependent fractionation of Pb/U and no or only very minor fractionation of the elements U/Th, which have almost the same ionization energy.

In the meantime, the attention of the authors of the elemental fractionation paper¹⁷ was called to recent publications (see ref. 25 and references therein) on fs laser-produced, very dense plasma layers. Here it is assumed, and by the sole detection of XUV transitions of the innermost electrons of the corresponding element atoms shown, that the atoms in the interaction layer are free and ionized by what is called ‘pressure ionization’, a reduction of the ionization energy due to the extremely high density of charged particles in the plasma layer. Physically this is similar to the reduction of the ionization potential observed in dc arcs at high gas pressure.²⁶ In fact, pressure ionization with subsequent very rapid di-electronic recombination would form a kind of ionization equilibrium in the very dense plasma layer before it starts to expand. Moreover, the authors of ref. 25 even discuss the possibility of Local Thermodynamic Equilibrium (LTE) conditions in the plasma layer which require, however, a sufficiently high electron density in the plasma. This has to be carefully reconsidered and if possible measured by appropriate techniques.

It has to be stressed again that currently there are no theories which include the effect of preferential ablation. Understanding and modelling of these processes are essential not only for LA-ICP-MS but also for other fields of application such as surface modification by lasers in material science. Therefore, it is an important task in the near future to consider all possible realistic processes which can theoretically describe the measured elemental fractionation effects.

Strategies to reduce elemental fractionation in LA-ICP-MS

Elemental fractionation is no problem for bulk analysis if equilibrium conditions between ablated mass and modified element composition in the crater are achieved with a few laser shots only. At worst, the ion signals at the beginning of LA-ICP-MS should be disregarded because of possible impact of elemental fractionation.

However, elemental fractionation can be a significant problem if single shot analyses, such as micro-analyses or depth-profiling of samples with high spatial resolution, have to be performed. Here, the spatial information on element distribution is difficult to evaluate without previous knowledge about micro-heterogeneities of the sample.

In general, the influence of elemental fractionation in LA can be reduced in laser ablation if laser fluences well above the ablation threshold of the respective sample are applied. This applies for fs- as well as ns-LA. However, evaporation and diffusion losses of volatile elements from crater melt, a problem typical for ns-LA and metallic samples with low melting temperature, can hardly be suppressed. It can be reduced by keeping the volume of melt small, e.g., by low fluence and low pulse frequency.

Experiments and theoretical modelling still to be done

1. Further experiments on elemental fractionation have to be made, in particular with more elements of a variety of ionization energies.

2. The assumed effect of ionization energy dependent element ion concentration in the plasma laser created by the laser and de-mixing of elements by Coulomb forces should be included in theoretical treatments of LA in order to account for elemental fractionation.

Spatial distribution and element composition of laser produced particles

The elemental composition of laser produced particles is dependent on particle size. A first hint was given by a simple experiment performed in our laboratory some time ago.²⁷ Brass and steel samples were ablated by a ns laser (Nd:YAG, λ = 1.06 µm) and measured by ICP-MS. After the respective experiments were finished, the transport tube to the ICP was cut into equal parts and the deposited mass was analysed. It turned out that (i) there was more mass deposited in the first sections of the tube than in the others downstream, obviously due to predominant settling of larger particles, and (ii) in particular for brass, the element composition of the mass deposited in the first part of the tube was different from the composition found in the other sections, where the deposition of larger particles was less probable. These qualitative findings were confirmed by impactor measurements of ns and fs laser generated particles of brass.²⁸ The brass particles <100 nm showed an excess of Zn while there was more Cu than Zn in the larger particles. Obviously, the higher Cu concentration in large particles was either due to incompletely atomized brass droplets, which appeared as a second maximum in the mass distribution in dependence on particle diameter (see ref. 28) or to a longer growth after early nucleation from the vapour phase, favouring the low vapour pressure element Cu at the beginning of growth process. The very small particles predominantly produced by condensation from the vapour phase at later times should then have an excess of the high vapour pressure element Zn. Even stronger differences in element ratios as a function of particle diameter were found in fs laser generated particles from glass.²⁹

Spatial particle distributions above the sample immediately after laser ablation

As discussed before, the propagation of the laser ablated mass is vertical to the sample surface forming a spatial ‘mushroom cloud’-like particle distribution at optimum analytical conditions. The size of the ‘mushroom cloud’ is dependent on the in-cell gas used. It is larger in He than Ar since the frictional coefficients of the gases are different. Fig. 2a shows the particle distribution after fs-LA of brass in He measured by light scattering with a delay of 200 µs.³⁰ Such particle distribution is almost perfect for further gas transport to the ICP. However, particle distributions can be very different as shown in Fig. 2b. In this case the distribution was measured after ns-LA of brass in Ar. The modified distribution is a result of a plasma breakdown in the gas above the crater. The breakdown with strong plasma heating is changing the expansion from the vertical to the more horizontal mode which results in an increase of particle loss near the crater. Furthermore, particle distributions near the surface are unfavourable for gas transport since the gas velocity near the surface is low.

Fig. 2 Spatial particle distribution after fs and ns laser ablation of brass in He (a) and Ar (b), respectively, measured by light scattering (from ref. 30, reprinted with permission from Spectrochim. Acta, Part B, 2007, 62, 20). Exposures (c) and (d) taken from ref. 40 (reprinted with permission from Appl. Spectrosc., 2001, 55, 1297) show the spatial emission intensities of the Cu 521.8 nm line immediately after ns-LA of copper with (c) and without (d) orthogonal pre-pulse plasma breakdown in air.

It has to be noted that vertical expansion can even be achieved by NIR ns-LA in Ar if the laser fluence is low, e.g., by focusing the beam below the surface of the sample,³⁰ lowering the fluence by attenuation of the pulse, or by choosing shorter laser wavelengths. On the other hand, deviation from the vertical particle distribution can also be observed in UV fs-LA in Ar if the laser beam is tightly focused onto the sample.³⁰ In the latter case, strong particle deposition can be observed as shown in Fig. 3a. Note, that there is practically no particle deposition at the same focus conditions if He instead of Ar is used as in-cell gas at otherwise unchanged experimental conditions (see Fig. 3b). However, particle deposition can also be significantly reduced in Ar if the fs laser beam is focused below the surface (see Fig. 3c). This is an indication that the particle distribution is predominantly vertical in Ar when the fs laser beam is focused below the surface as shown also by laser scattering.³⁰ The importance of the focus position in LA was highlighted recently.³¹ It was also shown that more mass is ablated if the laser beam is defocused, which is a further advantage in bulk analysis by LA-ICP-MS since micro-inhomogeneities are averaged if crater diameters are larger.

Fig. 3 SEM pictures of laser craters in brass produced by 32 shots by a focused near-IR femtosecond laser in Ar and He. The bottom picture displays a crater obtained with a defocused laser beam (focus below the surface of the sample).

A very important, often ignored point is particle initiated plasma breakdown in the gas above the sample. Airborne particles left from preceding shots reduce the breakdown threshold.^32,33 As shown above, plasma breakdown can affect the particle distribution after the ablation causing an increase of particle deposition near the crater. Particle triggered breakdown is depending on number, size and position of the particles in the focused laser beam. It can be avoided if the particles are rapidly removed from the focus region by gas transport. In any case, the laser pulse frequency has to be adapted to the time of particle removal. Pulse frequency dependent particle re-deposition was recently demonstrated.³⁴

Here, it has to be noted that particularly in ns-LA variations of the spatial particle distribution due to particle induced plasma breakdown may also lead to changes of the plasma shielding conditions from shot to shot. It is likely that these effects have a significant influence on the reproducibility in LA-ICP-MS. However, this has to be studied experimentally.

Different actions can be taken to avoid particle induced breakdown. They are listed in the strategy inset below. For example, in-cell gases with a high breakdown threshold should be used, the laser fluence near the sample surface should be kept low (never focus the laser beam above the sample!), and, of course, airborne particles left from preceding shots should be rapidly removed from the focus region by gas flow. Note that the gas flow near the sample surface is usually low. Therefore, particle removal not only make demands on gas flow velocity and laser pulse frequency, it is also an issue if the crater aspect ratio (crater depth to crater diameter) is large since airborne particles remaining in the crater volume are difficult to remove by gas transport.

Recently¹⁷ the morphology and element composition in brass and GaAs craters were studied by scanning electron microscopy (SEM) and electron microprobe X-ray analysis, respectively. It was found that the roughness of the crater bottom increased in fs-LA when more shots or higher fluences were applied. Fig. 4 shows a SEM picture of a crater bottom in brass produced by 16 shots of a NIR fs laser and a laser fluence of 0.8 J cm⁻². We can see frozen brass droplets which were solidified just at the moment of leaving the crater. On average, the diameter of the re-solidified droplets was smaller or larger when fewer or more shots with the same fluence were applied, respectively. Similar solid droplet sizes can be obtained with more shots at lower fluence or fewer at much larger fluence, respectively. Therefore, it is likely that the particle size distribution of individual fs laser shots depends on shot number, showing a larger fraction of big particles at high shot numbers than at the first laser shots. This might have an impact on the analytical data in LA-ICP-MS since the element composition of particles is size dependent and larger particles can be more easily lost during gas transport to the ICP (see below). Indications for a change in the particle size distribution in dependence on shot number have already been found.³⁵ However, additional measurements of the size dependent element composition of particles and the dependence on shot number of a fs laser needs to be made. It has to be noted that the particle size distribution in ns-LA also changes with shot number, but in a different way than in fs-LA. For example, Kuhn and Günther³⁶ found fewer larger particles at higher shot number. However, it has to be pointed out that the bottom of a ns laser produced crater is less structured than the crater bottom after fs laser application (see Fig. 4).

Fig. 4 SEM photograph of the bottom layer of a brass crater produced by 10 fs laser shots (fluence: 0.8 J cm⁻²). The uprising, re-solidified droplets have typical diameters up to about 300 nm.

It is known from laser induced breakdown measurements (LIBS) with ns lasers that the atomization efficiency is high^14,37,38 and the ablated mass propagates vertically with respect to the surface of the sample³⁹ if LA is performed at reduced gas pressure or density. The spatial distribution of free, light emitting atoms (Cu) after LA of copper at reduced gas density can be seen in Fig. 2c, which is taken from ref. 40. The reduced gas density (air) above the sample was produced by a pre-pulse breakdown applying a ns laser. Note that the spatial distribution of light emitting atoms in the double-pulse experiment is qualitatively similar to the particle distribution in fs-LA of brass in He measured by laser scattering (Fig. 2a). On the other hand, the spatial mass distribution measured by atomic line emission after ns-LA in air without gas density reduction by pre-pulse breakdown (Fig. 2d) is similar to the particle distribution observed in ns-LA of brass at 1 atm of Ar (see Fig. 2b).

The particle size distribution in orthogonal pre-pulse LA applying ns lasers was recently measured using a low-pressure impactor.¹⁴ It was shown that such an arrangement generates a very large mass fraction as ultrafine particles (<5 nm) and almost no big particles in comparison with ns-LA without pre-pulse where the large particles represent a very large fraction of the total mass ablated. The production of ultrafine particles is favoured by the unhindered and wider expansion of material in orthogonal pre-pulse ns-LA (see Fig. 2c) and the additional atomization by the diluted gas plasma above the sample before final condensation.¹⁴ Unfortunately, ns-LA with orthogonal pre-pulse breakdown is unsuitable for LA-ICP-MS because of the large fraction of the ultrafine particles which is expected to be partly lost by diffusion during gas transport to the ICP (see below). However, it would be interesting to apply the technique of orthogonal pre-pulse breakdown with ns lasers in fs-LA using Ar as in-cell gas. A lower Ar density created by the pre-pulse breakdown would reduce the risk of serious plasma breakdowns by fs laser pulses in the gas above the sample and, therefore, also of modified spatial particle distributions. Maybe, even particles in the gas above the sample left from preceding shots will have a smaller influence. However, this has to be carefully investigated (see inset with proposed experiments).

Online control of particle size distribution in LA-ICP-MS

It would be beneficial to routinely measure the particle size distribution in LA-ICP-MS during analysis. Online techniques which can be applied are, e.g., optical laser scattering or differential mobility analysis.⁴¹ However, optical emission spectrometry can also be used to measure the relative frequency of big particles produced in the ablation process.⁴² Online detection allows one to optimize the particle production for gas transport by variation of laser fluence, focus position and gas flow during measurement. A diminishment of the relative frequency of large particles is not only beneficial for more efficient mass transport but would also reduce the ‘noise’ in ICP-MS signals since large particles are generating spikes. This is also the reason why noisier signals are recorded in ns-LA-ICP-MS than in fs-LA-ICP-MS⁴² where finer particles are produced.

The formation of agglomerates

Airborne nano-particles which collide tend to form agglomerates.⁴⁴ This particularly happens in the ‘mushroom clouds’ of laser produced particles (see Fig. 2a), as shown, e.g., in ref. 43 where the particles and agglomerates were collected on filters and inspected by SEM. Very often, agglomerates are loosely bound and may partially fall to pieces on the way into the ICP, in particular, if there are sharp turnarounds in the gas transport which release the larger heavier particles in the agglomerate due to inertial force. However, sometimes particles in agglomerates are also glued to each other. This can occur if the particles are not completely solid during formation of agglomerates. The appearance of loosely or strongly bound, hard agglomerates is dependent on the matrix ablated and the laser applied.⁴⁵ Strongly bound agglomerates are predominantly found in ns-LA of metals while loosely bound agglomerates are mainly seen in fs-LA. Note, that large and heavy strongly bound agglomerates can get lost by inertial or gravitational settling during transport to the ICP.

Strategies for optimum ablation and particle production in LA-ICP-MS

It is important to avoid plasma breakdown in the gas above the sample because it may change the propagation of the mass ablated and results in significant particle loss by deposition on the surface near to the crater.

Nanosecond laser ablation

1. Helium instead of argon should be used as in-cell gas because of the high plasma breakdown threshold.

2. Lasers with pulse widths <10 ns rather than >10 ns should be applied.

3. The laser fluence has to be adapted to the matrix by reduction of the laser power or, if possible, by defocusing. The focus position should be slightly below the surface of the sample which is also favourable in bulk analysis since a larger laser beam is ablating more mass and inhomogeneous element distributions in samples are averaged.

4. Airborne particles from the preceding laser shots should be removed from the focus region by gas flow because they can initiate plasma breakdowns in the gas above the sample. Laser repetition frequency has to be adapted to the particle residence time above the sample. Laser pulse frequencies larger than ∼10 Hz should not been applied unless special ablation cells with very short particle washout time are used.

5. Crater aspect ratios (depth/diameter) should be kept small since it is difficult to remove particles from preceding shots by gas flow from the crater volume.

6. If possible, online control of particle size distribution by laser scattering, differential mobility analysis, or optical emission spectrometry is recommended in order to reduce the number of large particles by proper alignment of laser focus, pulse power and gas flow.

Femtosecond laser ablation

1. Points 2–6 listed for nanosecond laser ablation also apply to fs-LA.

Experiments still to be done

1. Study of spatial particle distribution after particle induced breakdown in the cell gas. Such experiments require the measurement of the spatial particle distribution after one single shot (see, e.g., Fig. 2a) and after the nth shot at laser pulse frequency and gas transport where particles from the preceding shot are still in the focus region above the crater.

2. Experimental investigation of laser pulse frequency dependent effects on the particle size distribution, which is expected to vary with pulse frequency.

3. Study of the particle size distribution dependence on the shot number. In particular the fraction of larger particles is expected to increase with shot number in fs-LA. Since large particles are subject to gravitational and inertial losses (see next section) systematic, laser pulse frequency dependent errors can be expected.

4. fs-LA-ICP-MS with pre-pulse plasma breakdown in Ar generated by an orthogonal ns laser beam above the crater. The pre-pulse plasma reduces the gas density above the sample and thus hampers fs laser induced gas breakdown. It is likely that the particle size distribution and element composition produced by such ns fs double pulse arrangement is not very different from single shot fs-LA. This hypothesis has to be proved experimentally.

Particle transport

Particle transport is one of the crucial processes in LA-ICP-MS. Having in mind that the element composition of particles is size dependent, any particle loss during gas transport will have an impact on the analysis.

There are several mechanisms which account for particle transport by a flowing gas. First, there is friction which moves the particles with the flow, and there are ‘loss mechanisms’ such as diffusion and gravitational and inertial motions. Further forces having an impact on particle movements are electrical forces and thermophoretic forces. However, the latter become important only if electrical fields or high thermal gradients, respectively, are present in the transport path, which is usually not the case in LA-ICP-MS.

Diffusion becomes important for particles smaller than the mean free path of atoms of the gas used. At room temperature and atmospheric pressure, the mean free path in helium is ∼200 nm, while it is ∼72 nm in argon.⁴⁶ The smaller the particle the more pronounced is the diffusion effect. The gravitational force is important for particles in the µm size range. It gives rise to settling of particles during transport, in particular, if the transport tube is horizontally aligned and the gravitational drop distance (tube diameter) small. Gravitational losses are less important for vertically arranged tubes and upstream gas flow because the friction force may exceed the gravitational force. For usual flow rates (∼1 L min⁻¹), particle diameters (≤5–10 µm) and inner tube diameters (≤5 mm) this is usually achieved.⁴⁴

Fig. 5 shows calculated transport losses in a 1 m long horizontal tube taking into account diffusion and gravitational losses and the formulas given in the text book of Baron and Willeke.⁴⁴ The inner diameter of the tube and the gas flow rate (He or Ar) were assumed to be 4 mm and 1 L min⁻¹, respectively. As one can see, almost loss-free transport can be achieved with particles >10 nm and <2 µm. In fs-LA, most of the mass ablated is represented by particles well inside this size-range while in ns-LA often a larger fraction of big particles is generated (see section on particle production) which can increase mass loss during transport. In orthogonal pre-pulse ns-LA the particles are very small (see section on particle production) which would boost the problem of diffusion losses for such experimental arrangement in LA-ICP-MS.

Fig. 5 Theoretical transport loss of spherical particles in a horizontal tube (length: 1 m, inner diameter: 4 mm) with argon and helium as transport gases (flow rate: 1 L min⁻¹) in dependence on particle diameter.

Inertial forces become important if there are turnarounds in the transport arrangement. The inertial force can exceed the gravitational force but it is more dependent on the actual geometry and gas flow rates. If we take, for example, the 1 m long tube with 4 mm inner diameter used in our horizontal tube arrangement above, coil it with a radius of 5 cm and substitute the gravitational acceleration in the calculations above by the inertial acceleration v²/r, the upper ‘cut-off’ diameter for 20% transport loss is reduced from 2 µm (gravitation) to 800 nm (inertia).

Particle transport efficiency

The mass transport efficiency of particles generated by fs-LA in He was recently measured in our laboratory applying a low pressure impactor for particle sampling.⁴⁷ The statements made in the preceding section on particle transport were fully verified. The fs-LA transport efficiency was found to be relatively large (about 77% with error bars of −9 and +19%) in comparison with ns-LA (typically 20–60%, depending on the matrix).^48,49 Within the limits of experimental errors the transport efficiency in fs-LA was independent of the cell used. The same was found with Ar as in-cell and transport gas.⁵⁰ The absolute transport efficiency for near infrared fs-LA in Ar is slightly smaller than in He (about 75% with uncertainties of −9 and +19%).³¹ It has to be stressed that plasma breakdown in the gas above the sample was avoided by putting the focus below the surface of the sample. As discussed in the chapter on spatial particle distribution in LA, a plasma breakdown in the gas, particularly in Ar, can change the particle propagation towards the surface favouring particle settling near the crater. It is recommended to check the magnitude of particle deposition, e.g. by a good optical microscope or better by SEM, as shown in Fig. 3.

Elemental fractionation in single shot laser ablation due to particle transport

Small particles follow turbulences in the gas transport systems easier than the larger ones, i.e. they will arrive slightly delayed in comparison with larger particles if there are regions of turbulence on the way to the ICP.⁵¹ As a consequence, element ratios measured by single shot LA-ICP-MS may change with time if the element composition of the particles is size-dependent. This effect is shown in Fig. 6 where the averaged Cu/Zn ratio of 10 single fs laser shots on brass is displayed. The bigger particles have a higher Cu/Zn ratio than the smaller particles²⁸ and arrive earlier because there were gas turbulences in our transport system⁵¹ on the way to the ICP. The measurements were made with a sampling tube ablation cell⁴⁷ having a very short washout time. There is a clear change of the Cu/Zn ratio from ∼16 to ∼8 due to the dispersion in particle transport although the error bar is increasing to larger values for t > 0.4 s. The increase is not only due to the weak Cu and Zn signals at t > 0.4 s delivered by the sampling tube ablation cell, but also to the atomization of single large Cu enriched particles which were occasionally released from the tube walls.

Fig. 6 Transport induced elemental fractionation in fs-LA-ICP-MS of brass. The time dependent Cu/Zn ratio was calculated from 10 averaged Cu and Zn signals measured with a sampling tube ablation cell⁴⁷ in Ar. The error bars are given by dashed curves. The peaks at 0.38, 0.48, 0.50 and 0.55 are due to individual measurements where single Cu-enriched larger particles most likely released from the walls arrived in the ICP.

As a consequence of particle transport dependent elemental fractionation, high precision element ratio measurements by single laser shot sampling can be affected. Therefore, it is recommended to measure integral element signals rather than peak signals if high accuracy and precision are required in analyses.

Strategies for optimum particle transport and small systematic errors

1. To keep particle loss during transport small

—the tube length should be as short as possible to have small gravitational losses.

—narrow turnarounds should be avoided to lessen inertial loss of large particles.

—the gas flow through a tube with fixed inner diameter has to be sufficiently high.

2. Turbulences in the gas flow should be avoided if LA-ICP-MS is used for single shot analysis since turbulences lengthen the particle washout time and can cause elemental fractionation by particle size dependent transport.

3. Integral instead of peak signals should be measured in single shot LA-ICP-MS analysis to account for particle transport induced elemental fractionation in order to improve the accuracy and precision of element ratio measurements by LA-ICP-MS.

Experiments still to be done

1. Further careful experiments are required to study quantitatively and in more detail the transport induced, particle size dependent element fractionation and its impact on precision and accuracy of element ratio measurements by LA-ICP-MS.

2. It is interesting to measure the transport properties (loss and transport induced dispersion) of loosely and strongly bound agglomerates and their impact on LA-ICP-MS analyses. Such investigations can, e.g., be made with tailored agglomerates made from sets of mono-disperse particles of known sizes.

Ablation cells for bulk and single shot analyses

Shape, peak intensity and total duration of LA-ICP-MS signals generated by single laser shots depend on the in-cell gas and its flow mode (laminar or turbulent) as well as on the volume and form of the ablation cell used. A very important, strategic parameter is the so-called ‘effective volume’, V_e. It is the partial volume of the ablation cell and the volume of the transport tubes that will be filled with laser generated particles during the transport.⁵² The effective volume could be, for example, the transport volume of a mushroom-like particle cloud, as shown in Fig. 2a, through the cell plus the corresponding volume of the transport tubes to the ICP. Note that the effective volume is usually smaller than the volume of the ablation cell, in particular, when large ablation cells are used.

Let us start with an effective volume that is the same as the total volume V of the cell. Furthermore, we assume that the particles are homogeneously distributed in the cell after ablation. Note, that such condition can be approximately achieved if there are strong gas turbulences in the cell generated, for example, by a nozzle at the gas inlet.⁴⁷ The particle mass leaving the cell with a gas flow is proportional to the mass which is still in the cell. Therefore, we will get an exponential decay of the ICP-MS signal with a decay constant τ given by the ratio V/V_p where V_p is the transport gas flow rate.⁵²

In case the particles are not fully distributed in the ablation cell (V_e < V) a laminar gas flow through the cell will sweep the particles directly through the gas outlet into the transport tube and the half-width of the ICP-MS signal will be usually shorter than for V_e = V. The signal is even not changed significantly if the gas outlet of the cell is very narrow.⁴⁷ However, not all particles will leave the cell immediately. This holds in particular for particles which were very near to the crater and the sample after ablation and for those which experience any turbulent flow in the cell. These particles stay longer inside the cell and, thus, lengthen the time for complete particle washout. The time for complete washout is comparable to the respective washout time observed with homogeneously distributed particles as described above.

The effective volume depends on the position of ablation. It will be smaller if the particles are generated near the outlet of the cell than far away. Therefore, the peak height and length of an ICP-MS signal also depends on the place of ablation as sketched in Fig. 7a and b for a large ablation cell. Ablation near the exit produces short and high signals while the signals are longer with smaller peak if the distance to the exit is larger. It means that the detection power is dependent on the position of laser sampling. This aspect is in particular important if LA-ICP-MS is used for 2D element mapping of samples, such as biological tissue or gel electrophoresis plates which usually need large ablation cells.

Fig. 7 (a) and (b) Position dependent signal response in a large ablation cell. (c) Position independent ablation, applying a sampling tube ablation cell.

Another aspect is that the laser pulse frequency used in 2D mapping is limited by the residence time of particles in the ablation cell. Particles from a particular shot have to be out of the ablation cell before the next shot can be applied in order to avoid overlapping signals and thus a degradation of the spatial resolution. In case the effective volume depends on the ablation position an additional adjustment of the laser pulse frequency to the position of ablation would be required which is disturbing.

In order to obtain the shortest time for complete washout and the maximum peak signal, the cell volume in which the particles can disperse should be as small as possible. In that case, the signal is dominated by the lengths of the transport tubes and the gas velocity therein. Let us assume a homogeneous distribution of transportable particles in a very thin volume across the transport tube at t₀ and a laminar gas flow through the transport tube having the length L. The parabolic flow pattern in the tube will result in a prolongation of the signal S(t) measured at the end of the tube. As shown in ref. 51, S(t) ∝ L²/(v̄²t³), where v̄ is the average gas velocity of the parabolic flow in the tube. However, it has to be noted that laser produced particles are usually not homogeneously distributed across the transport tube^52,53 and the transport tubes including the injector of the ICP torch usually do not have the same diameter, which both have impact on the length of the signal.

A very simple ablation cell that comes close to the ideal ablation cell for single shot analyses is sketched in Fig. 7c. Here, the mass is directly ablated into the transport tube which is in contact with the sample. The transport gas enters the tube from an ambient gas reservoir through notches. Such sampling tube ablation cells have been used, e.g., in ref. 47, 48, 54. Note that the LA-ICP-MS signal is independent of the position of ablation if the sample is moved by a xy-translator unit in respect to laser beam, focusing lens and sampling tube which are fixed in space. Recently, the particle transport from the sampling tube ablation cell, through the transport tubes and the injector into the ICP has been calculated by numerical simulation⁵¹ in order to find the optimum experimental parameters for LA-ICP-MS application.

The sampling tube ablation cell is recommended, particularly for rapid depth profiling and 2D mapping. It provides high spatial resolution in both types of analysis since the laser pulse frequency can be high without having memory effects (particles) from preceding shots. However, the authors believe that sampling tube ablation cells have also advantages for bulk analysis because particle induced plasma breakdown in the gas above the sample and, therefore, variations of the spatial particle distribution just after ablation are unlikely. However, an additional, separate cell with turbulent gas flow downstream to the ICP would be required if a sampling tube cell is applied in bulk analyses. This second cell will mix the particles from several shots. The mixing will not only smooth the otherwise spike-shaped ICP-MS signal but also average the element signals if there are spatial inhomogeneities in the sample.

Strategies for choosing the ablation cell

Bulk analyses:

The volume of the ablation cell should be much larger than the volume including the laser produced particles just after ablation. It is recommended to distribute the particles reasonably homogeneously in the cell volume by turbulent flow, not only to get a smooth ICP-MS signal at usual laser pulse frequencies but also to average element signals from successive shots on samples with inhomogeneous element distributions. However, the particle density in the gas volume just above the crater should be as low as possible to reduce the probability of particle induced plasma breakdown in the in-cell gas.

Single shot analyses:

The use of an ablation cell with very small volume having a very short washout time for all particles is recommended. It allows the use of high laser pulse frequencies, for example, for 2D element mapping or depth profiling. The sampling tube ablation cell offers these advantages. Furthermore, the shape of the LA-ICP-MS signals is independent of the position of laser sampling if a sampling tube ablation cell is applied.

Experiments still to be done

An arrangement of sampling tube ablation cell and turbulent cell downstream to the ICP is proposed for bulk analyses. The sampling tube ablation cell is suitable for high laser pulse frequencies without particle induced plasma breakdown above the sample while the turbulent cell mixing particles from consecutive shots is for smoothening of the signal and for averaging element signal variations due to element inhomogeneities in the sample.

Atomization and ionization in the ICP

The particles generated by LA and transported into the ICP should be completely atomized and should not affect the plasma parameters at the sampling cone of the mass spectrometer. The consequence of incomplete atomization is always an ionization temperature which is matrix dependent. However, even when all particles are atomized, the ionization temperature at the location of ion extraction can also be affected if too many particles are simultaneously introduced into the ICP. The ICP has to be sufficiently robust for particle mass load. The robustness of the ICP against mass load can be checked in a simple way. Mass load effects can be neglected if the integrated ion signals are independent of the sampling position in a large ablation cell. Ablation near the outlet generates short, high signals (high mass load), while the signals are smaller and longer (low mass load) if the ablation position is far from the outlet, as shown in Fig. 7a and b. However, mass load effects can also be investigated if ablation cells with different washout times are applied. For example, in a recent paper on relative transport efficiency in fs-LA-ICP-MS applying very different ablation cells the integral signals were found to be independent of the ablation cell used.⁴⁷ Such results can be taken as evidence that mass load effects could be neglected in that particular experiment.

Recent experiments^55,56 have shown that incompletely atomized larger particles may contribute to systematic errors in LA-ICP-MS analyses. Data should be evaluated with care if the LA-ICP-MS signal is very spiky since this is a sign of excessive introduction of big particles into the ICP. Signals with many spikes are more likely seen in ns-LA-ICP-MS where more bigger particles are produced than in fs-LA-ICP-MS.^28,43

It is evident that there has to be a maximum size for complete particle atomization which depends on the particle-plasma interaction time (typically 1–3 ms) and the thermal properties of the elements and their compounds in the particles. Fig. 8 shows the emission intensities of the Si(I) 288 and 263 nm lines measured simultaneously end-on when hardly vaporizable, monodisperse SiO₂ particles of 1 µm diameter were introduced into the ICP. Taking into account the excitation energies and the transition probabilities of the lines, the temporal change of the excitation temperature can approximately be derived from Boltzmann plots. The local cooling of the plasma due to the evaporation of the particle can clearly be seen in Fig. 8. It should be kept in mind that the measured excitation temperature is an average temperature from the plasma volume where free, excited Si atoms are present. The intensity and temperature data tell us that the evaporation of the particle is obviously incomplete. The excitation temperature is still changing when the line intensities have their maxima. Therefore, the criterion for complete atomization of single particles and the necessary plasma temperature equilibration can be formulated as follows:

Particles are fully atomized in ICPs if the intensity ratios of ion and neutral lines, having different excitation energies and measured by end-on OES, are approximately constant at times where the individual intensities are still near to their maximum values.

Fig. 8 Emission intensities of the Si(I) lines at 288 and 263 nm measured with 1 µm SiO₂ particles by end-on observation and the excitation temperature showing the local cooling of the ICP by the evaporation process (from unpublished work⁵⁰).

At complete evaporation and steady state conditions, ion signals in LA-ICP-MS are expected to be proportional to the respective element masses of the particles, and their ratios are a function of the plasma ionization temperature at the location of ion extraction unless the evaporated mass of all particles affects the plasma parameters.

The atomization of single particles during their transit through the ICP have been studied, e.g. by the research groups of Olesik^57,58 and Houk.⁵⁹ Such investigations have to be continued for better understanding of particle–plasma interaction processes. Furthermore, such experiments will not only give answers on the plasma load effects but also on the mutual interaction of elements in the small sub-volumes of the ICP where particles vaporize (matrix effects).

One can certainly expect that too many, not completely atomized big particles will have measurable affects on the plasma parameters. However, the effect might be negligible if more than 95% of the mass is carried by particles with diameters below 600 nm as it can be achieved in fs-LA. Such particles should be completely atomized. Otherwise, non-matrix matched calibration with brass, aluminium and glass samples as shown recently by fs-LA-ICP-MS/OES^15,22 should not be possible. However, recent investigations on fractionation effects by plasma loads in fs-LA-ICP-MS¹⁶ seem to contradict that statement. The authors found significant fractionation effects when they diluted the particles produced by fs-LA. It is not unlikely that the commercial particle diluter used in that experiment and in further experiment on mass load effects in ns-LA-ICP-MS⁶⁰ had an effect on the particle size distribution and, because element compositions in particles are size dependent, also on the measured element ratios. The principle of particle dilution, used in the instrument which was applied in ref. 16, 60, is based on a rotating disk with cavities which separates a channel with the original aerosol distribution from a second channel with the diluted distribution. The dilution depends on the rotation frequency, the number and volume of the cavities, as well as the gas flow. One might expect preferential separation of the very small particles since the rotating disk creates turbulences and the smaller particles can better follow turbulent gas flows (see above). At least the Zn/Cu ratio, which showed a strong dependence on the dilution factor in ref. 16, seems to indicate a non-perfect dilution over the whole size range. However, this should be investigated carefully, for example, by low pressure impaction and analysis of the original and diluted aerosols.

Strategies to avoid mass load effects in LA-ICP-MS

The laser ablation parameters (fluence, focus position) affecting the total particle mass and size distribution should be controlled by online measurements or at least by monitoring and reducing the particle induced spikes in the LA-ICP-MS signal.

Experiments still to be done

1. The atomization of single particles needs to be further investigated by optical emission spectrometry or, if higher detection sensitivity is required, by laser induced fluorescence,

(a) to find the maximum particle diameter of different matrices for complete evaporation.

(b) to study the mutual interaction of different elements in the vapour clouds of the atomized particle.

(c) to measure the influence of an increasing particle flow on the plasma parameters in order to determine the limits given by plasma load effects.

2. A study of the effect of rotating disk diluters on the particle size distribution is suggested, because it cannot be excluded that the variations of element ratios recently measured by LA-ICP-MS are rather due to changes in the relative particle size distribution than to mass load effects.

Conclusion

Despite the fact that LA-ICP-MS is an accepted and established analytical method, there are several strategies which have the potential to improve the analytical performance of the technique. Some of these outlined in the present paper are summarized for ns- and fs-LA in Tables 1 and 2 at a glance. However, the present paper also highlights several questions which are still open and which should be answered for better understanding of the processes involved in LA-ICP-MS. Experiments have been identified in the hope that interested colleagues and research groups feel that it is worthwhile to take up some of the proposals and perform the experiments.

Table 1 Recommended experimental parameters and conditions for LA-ICP-MS

	Wavelength	In-cell gas	Laser fluence	Laser pulse frequency
ns laser	Short wavelengths are preferred to avoid strong heating of the material plume and plasma shielding	Plasma shielding and plasma breakdown in gas less severe in He than Ar	Should be kept as low as possible by defocusing to avoid extensive melting by heat transfer and plasma shielding and breakdown; focus below sample surface	Low: has to be adapted to the removal time of airborne particles above crater to improve sampling statistics and to the tolerable thermal stress of the matrix (melting)
fs laser	No heating of plasma plume and no plasma shielding by any wavelength	He and Ar are good as in-cell gases; no plasma shielding and no plasma breakdown	Should be well above ablation threshold to reduce elemental fractionation; focus below surface is recommended to avoid particle initiated plasma breakdown in gas above sample	Relatively low: has to be adapted to the removal time of airborne particles above crater to avoid particle initiated breakdown in gas and to improve statistics

---

Table 2 Recommended experimental conditions for the most common applications of LA-ICP-MS

	Preferred cell volume	Gas flow	Spatial dependence of signal peak and shape
Bulk analysis	Large	Turbulent	Not important
Single shot analysis e.g., microanalysis or depth profiling	Small	Laminar or turbulent; high gas flow for fast particle transport	Important: no spatial dependence of signal peak and shape required
2D element mapping	Small	Laminar or turbulent; high gas flow for fast particle transport	Important: no spatial dependence of signal peak and shape required

---

Acknowledgements

The authors gratefully acknowledge financial support by the Deutsche Forschungsgemeinschaft (NI 185/37: fs-LA-ICP-spectrometry) as well as by the Ministry of Innovation, Science, Research and Technology of the state Northrhine-Westphalia and the Ministry of Education and Research of the Federal Republic of Germany.

References

1. A. Montaser, Inductively Coupled Plasma Mass Spectrometry, Wiley-VCH, New York, 1998.
2. R. E. Russo, X. Mao, H. Liu, J. Gonzales and S. S. Mao, Talanta, 2002, 57, 425.
3. D. Günther and B. Hattendorf, Trends Anal. Chem., 2005, 24, 255.
4. B. Fernández, F. Claverie, C. Pécheyran and O. F. X. Donard, Trends Anal. Chem., 2007, 26, 951.
5. J. Koch and D. Günther, Anal. Bioanal. Chem., 2007, 387, 149.
6. J. F. Ready, Effects of High-Power Laser Radiation, Academic Press, New York, 1971.
7. D. Bäuerle, Laser Processing and Chemistry, Springer, New York, 2000.
8. Laser Ablation and its Applications, Springer Series in Optical Sciences, ed. C. R. Phipps, Springer, New York, 2006.
9. S. I. Anisimov and B. S. Luk'yanchuk, Phys. Usp., 2002, 45, 293.
10. P. Gibbon, Short Pulse Laser Interaction with Matter – An Introduction, Imperial College Press, London, 2005.
11. E. G. Gamaly, A. V. Rode and B. Luther-Davies, Phys. Plasmas, 2002, 9, 949.
12. N. M. Bulgakova, R. Stoian, A. Rosenfeld, I. V. Hertel and E. E. B. Campbell, Phys, Rev. B, 2004, 69 054102.
13. J. Osterholz, F. Brandl, T. Fischer, D. Hemmes, M. Cerchez, G. Pretzler, O. Willi and S. J. Rose, Phys. Rev. Lett., 2006, 96, 085002.
14. H. Lindner, J. Koch and K. Niemax, Anal. Chem., 2005, 77, 7528.
15. Q. Z. Bian, C. C. Garcia, J. Koch and K. Niemax, J. Anal. At. Spectrom., 2006, 21, 187.
16. J. Koch, M. Wälle, J. Pisonero and D. Günther, J. Anal. At. Spectrom., 2006, 21, 932.
17. C. C. Garcia, H. Lindner and K. Niemax, J. Anal. At. Spectrom., 2008, 23, 470.
18. E. F. Cromwell and P. Arrowsmith, Anal. Chem., 1995, 67, 131.
19. X. L. Mao, A. C. Ciocan and R. E. Russo, Appl. Spectrosc., 1998, 52, 913.
20. D. Figg and M. S. Kahr, Appl. Spectrosc., 1997, 51, 1185.
21. Z. Chen, J. Anal. At. Spectrom., 1999, 14, 1823.
22. Q. Z. Bian, J. Koch, H. Lindner, H. Berndt, R. Hergenröder and K. Niemax, J. Anal. At. Spectrom., 2005, 20, 736.
23. S. Amoruso, X. Wang, C. Altucci, C. de Lisio, M. Armenante, R. Bruzzese, N. Spinelli and R. Velotta, Appl. Surf. Sci., 2002, 186, 358.
24. O. Albert, S. Roger, Y. Glinec, J. C. Loulergue, J. Etchepare, C. Boulmer-Leborgne, J. Perrière and E. Millon, Appl. Phys. A, 2003, 76, 319.
25. J. Osterholz, F. Brandl, T. Fischer, D. Hemmers, M. Cerchez, G. Pretzler, O. Willi and S. J. Rose, Phys. Rev. Lett., 2006, 96 085002.
26. W. Lochte-Holtgreven, Plasma Diagnostics, North-Holland, Amsterdam, 1968.
27. J. Koch, I. Feldmann, N. Jakubowski and K. Niemax, Spectrochim. Acta, Part B, 2002, 57, 975.
28. J. Koch, A. von Bohlen, R. Hergenröder and K. Niemax, J. Anal. At. Spectrom., 2004, 19, 267.
29. J. Koch, H. Lindner, A. von Bohlen, R. Hergenröder and K. Niemax, J. Anal. At. Spectrom., 2005, 20, 901.
30. J. Koch, S. Schlamp, T. Rösgen, D. Fliegel and D. Günther, Spectrochim. Acta, Part B, 2007, 62, 20.
31. C. C. Garcia, M. Wälle, H. Lindner, J. Koch, K. Niemax and D. Günther, Spectrochim. Acta, Part B, 2008, 63, 271.
32. D. E. Lencioni, Appl. Phys. Lett., 1973, 23, 12.
33. D. C. Smith and R. T. Brown, J. Appl. Phys., 1975, 46, 1146.
34. J. J. Gonzales, A. Fernandez, D. Oropeza, X. L. Mao and R. E. Russo, Spectrochim. Acta, Part B, 2008, 63, 277.
35. S. H. Jeong, O. V. Borisov, J. H. Yoo, X. L. Mao and R. E. Russo, Anal. Chem., 1999, 71, 5123.
36. H. R. Kuhn and D. Günther, J. Anal. At. Spectrom., 2004, 19, 1158.
37. F. Leis, W. Sdorra, J. B. Ko and K. Niemax, Mikrochim. Acta, 1989, II, 185.
38. K. Niemax, Fresenius’ J. Anal. Chem., 2001, 370, 332.
39. W. Sdorra and K. Niemax, Spectrochim. Acta, Part B, 1990, 45, 917.
40. D. N. Stratis, K. L. Eland and S. M. Angel, Appl. Spectrosc., 2001, 55, 1297.
41. H. R. Kuhn, D. Günther, J. Koch, R. Hergenröder, K. Niemax and M. Kalberer, J. Anal. At. Spectrom., 2005, 20, 894.
42. M. Miclea, C. C. Garcia, I. Exius, H. Lindner and K. Niemax, Spectrochim. Acta, Part B, 2006, 61, 361.
43. C. Liu, X. L. Mao, S. S. Mao, X. Zeng, R. Greif and R. E. Russo, Anal. Chem., 2004, 76, 379.
44. P. A. Baron and K. Willeke, Aerosol Measurements: Principles, Techniques and Applications, John Wiley & Sons, New York, 2001.
45. J. J. Gonzalez, C. Liu, S.-B. Wen, X. L. Mao and R. E. Russo, Talanta, 2007, 73, 567 and 577.
46. Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, FL, 2003.
47. C. C. Garcia, H. Lindner and K. Niemax, Spectrochim. Acta, Part B, 2007, 62, 13.
48. P. Arrowsmith and S. K. Hughes, Appl. Spectrosc., 1988, 42, 1231.
49. Y. Huang, Y. Shibata and M. Morita, Anal. Chem., 1993, 65, 2999.
50. ISAS, Dortmund, unpublished.
51. D. Autrique, A. Bogaerts, H. Lindner, C. C. Garcia and K. Niemax, Spectrochim. Acta, Part B, 2008, 63, 257.
52. M. Baerns, H. Hofmann and A. Renken, Chemische Reaktionstechnik, Wiley-VCH, Weinheim, 2004.
53. J. Koch, M. Wälle, R. Dietiker and D. Günther, Anal. Chem., 2008, 80, 915.
54. J. Uebbing, A. Ciocan and K. Niemax, Spectrochim. Acta, Part B, 1992, 47, 601.
55. M. Guillong and D. Günther, J. Anal. At. Spectrom., 2002, 17, 831.
56. D. B. Aeschliman, S. J. Bajic, D. P. Baldwin and R. S. Houk, J. Anal. At. Spectrom., 2003, 18, 1008.
57. J. W. Olesik and S. E. Hobbs, Anal. Chem., 1994, 66, 3371.
58. J. W. Olesik, Appl. Spectrosc., 1997, 51, 158A.
59. D. C. Perdian, S. J. Bajic, D. P. Baldwin and R. S. Houk, J. Anal. At. Spectrom., 2008, 23, 325 and 336.
60. I. Kroslakova and D. Günther, J. Anal. At. Spectrom., 2007, 22, 51.

---