The energy penalty of post-combustion CO2 capture & storage and its implications for retrofitting the U.S. installed base
Kurt Zenz
House
a,
Charles F.
Harvey
b,
Michael J.
Aziz
c and
Daniel P.
Schrag
a
aDepartment of Earth & Planetary Sciences, Harvard University, 202 River Street, Cambridge, MA 02139, USA
bDepartment of Civil & Environmental Science, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139-4307, USA
cSchool of Engineering & Applied Science, Harvard University, 29 Oxford Street, Cambridge, MA 02138, USA
First published on 23rd January 2009
Abstract
A review of the literature has found a factor of 4 spread in the estimated values of the energy penalty for post-combustion capture and storage of CO2 from pulverized-coal (PC) fired power plants. We elucidate the cause of that spread by deriving an analytic relationship for the energy penalty from thermodynamic principles and by identifying which variables are most difficult to constrain. We define the energy penalty for CCS to be the fraction of fuel that must be dedicated to CCS for a fixed quantity of work output. That penalty can manifest itself as either the additional fuel required to maintain a power plant's output or the loss of output for a constant fuel input. Of the 17 parameters that constitute the energy penalty, only the fraction of available waste heat that is recovered for use and the 2nd-law separation efficiency are poorly constrained. We provide an absolute lower bound for the energy penalty of ∼11%, and we demonstrate to what degree increasing the fraction of available-waste-heat recovery can reduce the energy penalty from the higher values reported. It is further argued that an energy penalty of ∼40% will be easily achieved while one of ∼29% represents a decent target value. Furthermore, we analyze the distribution of PC plants in the U.S. and calculate a distribution for the additional fuel required to operate all these plants with CO2 capture and storage (CCS).
 Kurt Zenz House | Kurt Zenz House received his PhD in Geosciences from Harvard University in 2008 for work On the Physics & Chemistry of Carbon Dioxide Capture & Storage in Terrestrial & Marine Environments. House studies and develops methods for large-scale capture and storage of human-made carbon dioxide. He recently patented electrochemical weathering, a novel process that expedites the ocean's natural ability to absorb carbon dioxide, and cofounded a venture-capital-backed alternative-energy company. Additionally, he cofounded the Harvard Energy Journal Club to facilitate cross-disciplinary discussions about energy technology; in 2008 Esquire magazine featured him among its “Best and Brightest”. |
Broader contextWe derive an analytic relationship for the energy penalty from thermodynamic principles, and we apply that relationship to the installed base of U.S. coal-fired power plants to determine the energetic requirements of retrofitting that base for CCS. Pulverized-coal (PC) facilities compose over 95% of the CO2 produced by U.S. coal-fired power plants. It is unlikely that either national or global CO2 emissions can be substantially reduced without either shutting down or retrofitting these plants for CCS. The economics of CCS from PC power plants depend, to a large degree, on the thermodynamic work required to capture and store the CO2. The data demonstrate that—under reasonable assumptions—retrofitting the most efficient 10% of existing plants will offset 30% more CO2 per unit of additional fuel than retrofitting the least efficient 10% of plants. Indeed, CCS on the least-efficient plants may not make economic sense compared with building new capacity and shutting down the least efficient plants. Finally, we show that a reduction in electrical power demand by between 15% and 20%, combined with retrofitting existing plants for CCS, would lower CO2 emissions from electricity production by ∼65% if the newly liberated power were used for CCS. |
Introduction
Global carbon dioxide (CO2) emissions have accelerated from 1.1%/yr in the 1990's to over 3%/yr since 2000.1 Those continued growth rates would result in global CO2 emissions of ∼40 GtCO2/yr and ∼100 GtCO2/yr by 2050, respectively. Stabilizing atmospheric CO2 concentration below 550 ppm, however, requires emissions to essentially stay flat for the next 42 years.2 CO2 capture and storage (CCS) is a promising technology that has the potential to address the ∼40% of emission emanating from large-point sources such as power plants.3 CCS for existing plants involves separating the CO2 from the plant's flue gas, compressing the CO2 for pipeline transport, and injecting the CO2 into a geologic formation where it is intended to remain for millennia.The U.S. has 1493 coal-fired power plants that constitute 336 gigawatts (GW) of rated power generation capacity. Nearly all of these plants involve pulverized-coal (PC) combustion, where the coal is pulverized such that over 98% of it is less than 300 µm,4 and then it is combusted in air at atmospheric pressure. In 2006, these plants composed about 70% of U.S. fossil-fuel derived electricity and about 50% of total electricity production.5 To produce that electricity, the plants burned ∼930 million tonnes of coal and produced ∼1.9 gigatonnes (Gt) of CO2, about 1/3 of total U.S. emissions.6 In addition, PC power constitutes well over 90% of coal-fired power in the world.4 The dominance of PC power plants makes significant reduction in national or global CO2 emissions from power-plants dependent on either shutting down a substantial fraction of the existing PC plants or retrofitting those plants for post-combustion capture and storage.
Each of the CCS steps—separation, compression, transport, and storage—requires work. To perform that work, a fraction of the fuel input must be dedicated to CCS. That fuel requirement constitutes the CCS energy penalty. The energy penalty can be realized as either additional fuel input to maintain the baseline power output or as reduced power output for a constant fuel input. Several studies have estimated the energy penalty for PC plants, but these estimates differ between studies by nearly a factor of 4 (Fig. 1).7–18
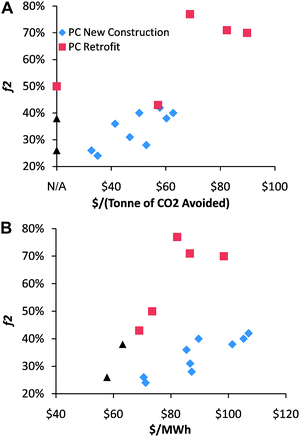 | ||
| Fig. 1 (A) Published values for the additional fuel required to maintain constant electric with CCS and the cost of CO2 avoided in 2007 US dollars7–18 for post-combustion capture and storage from pulverized coal plants. The blue diamonds are for new construction projects, the red squares are for retrofits, and the black triangles are for retrofits with boiler upgrades. The horizontal intercept—labeled N/A—is for three studies that estimated the energy penalty but not the cost of the CO2 avoided. (B) Values from the same studies of the CCS energy penalty and the levelized cost of electricity in constant 2007 dollars from the CCS power plant. Note that while the cost of CO2 avoided is much higher for PC retrofits than for new projects, the levelized cost electricity is essentially the same in both cases. | ||
In this paper, we calculate the thermodynamic work required for the various steps of CCS. We elucidate the cause of the spread in previously estimated energy penalties by deriving an analytic relationship for the energy penalty from first principles and by identifying which of the variables are most difficult to constrain. We show that the energy penalty associated with capturing and storing all the CO2 generated by U.S. PC plants will require either burning an additional ∼400–600 million tonnes of coal per year or building an additional ∼100 GW of CO2-free baseload power. In the latter scenario, the additional baseload power would be required to make up for the reduced power output of the retrofitted PC plants. It should be noted that separate end-use efficiency improvements could serve to offset the CCS energy penalty. In the discussion, we apply our analysis to the actual U.S. fleet of PC power plants. Since the energy penalty is a function of the power-plant's baseline efficiency, then we derive the expected distribution of energy penalties that would result from retrofitting the U.S. installed base of PC plants.
Minimum work required to sequester CO2
We first derive the lower bound for the work required to capture and store CO2 from a PC plant. Throughout this section, we neglect frictional losses in both pipeline transport and resistance to flow through geologic formations. Those losses are addressed later. For the calculation of this ideal limit, the work to store CO2 is described in three steps (Fig. 2): (1) The work required to separate the CO2 from the mixture of gases in power-plant flue gas; (2) the work to compress the CO2 for transport and injection at hydrostatic pressure (pipeline pressure is typically ∼14 MPa and hydrostatic pressure in reservoirs is roughly 1 MPa per 100 meters of depth);19 (3) the work required to emplace the CO2 at depth, displacing denser groundwater upward. Each step is required to overcome particular physical barriers: separation overcomes entropy; compression to pipeline and hydrostatic pressure overcomes pressure; and emplacing beneath the groundwater overcomes gravity and surface tension.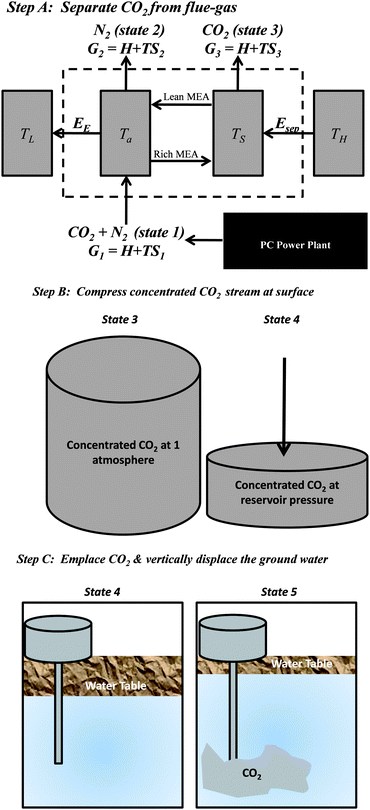 | ||
| Fig. 2 Step (A): The first panel depicts our idealized model of a temperature-swing separation system. State 1 features the flue gas mixture, which enters the absorber at temperature Ta, where it reacts with the solvent (e.g., monoethanolamine), and state 3 is the concentrated stream of CO2 leaving the thermally activated stripper unit at temperature TS. Esep is the primary energy required for separation; TH, TS, Ta, and TL are the temperatures of the boiler, the stripper, the absorber, and the environment. G1 is the free energy of the mixed state of the gases while G2 and G3 are the free energy of the concentrated N2 and CO2 streams, respectively. Step (B): The second panel depicts the compression to the initial pore-pressure. Step (C): Once the pressure of the CO2 at the bottom of the well equals the pore pressure, then it must be pushed into the reservoir. If we ignore viscous drag, then the minimum work required in step C (Wc) is the sum of the work required to lift the water table and the work required to overcome the capillary pressure of the CO2–H2O interface. The capillary pressure is several orders of magnitude smaller than the work required to lift the water table. The work required to lift the water table is independent of the size of the domain and the geometry of the injected CO2 plume. If CO2 were injected beneath twice the land area, then the change in potential energy would not change because a greater quantity of water would be lifted a corresponding smaller distance. | ||
Our analysis follows carbon through the process of oxidation to CO2 in a power plant to storage in a geologic formation. As such, we have defined 6 different chemical and physical states during this process:
State 0: Reduced carbon in the plant's combustor
State 1: Dilute CO2 mixed with N2 and H2O in the flue gas
State 2: Concentrated N2 stream at low pressure that has been separated from the flue gas
State 3: Concentrated CO2 stream at low absolute pressure exiting the separation process
State 4: Concentrated CO2 stream compressed for injection at the surface
State 5: Concentrated CO2 stream emplaced beneath the pore water in the geologic formation
The process of sequestering CO2 requires the input of work to transfer the system from state 1 to states 2 and 3, from state 3 to state 4, and from state 4 to state 5. We have labeled the work required for these three transitions: Wa, Wb, and Wc.
W a (from state 1 to states 2 and 3)
Flue gas emitted from typical coal-burning power plants contain ∼78% N2 from the atmosphere, ∼15% CO2 from the oxidation of the carbon in the hydrocarbon, and ∼7% water from both the oxidation of hydrogen in the coal and the vaporization of water that was adsorbed on the coal. Removing H2O from the flue gas is—in principle—thermodynamically favorable because H2O condenses at surface conditions indicating the enthalpy change of separation is not zero. In the thermodynamic limit, the minimum work to separate the flue gas into one concentrated CO2 stream and one concentrated N2 stream is the difference in the thermodynamic availability before and after separation. For an isothermal and isobaric process, the work equals the change in free energy before and after separation:
| Wmin = −dG | (1) |
For the separation, we employ the ideal gas assumption as the pressure is near atmospheric and N2 and CO2 do not chemically interact. The mole fraction of N2 and CO2 in the fully mixed state is XN1 and XC1. After the separation, the mole fraction in state 2 (low CO2) are XN2 and XC2, and the mole fractions for state 3 (high CO2) are XN3 and XC3.
The partial molar Gibbs energy for each gas in an ideal mixture is given by:20
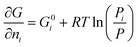 | (2) |
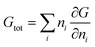 | (3) |
If we assume that none of the states are completely pure (i.e., Xij > 0 for all i and j), then the previous equation will determine the free energy of each state. The minimum work to change a system's state is given by the change in free energy between those states:
| W = ΔGsep = (G2 + G3) − G1 | (4) |
To calculate the minimum work required to transfer the system from state 1 into the distinct states 2 and 3, we calculate the free energy of each state:
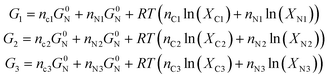 | (5) |
So, the minimum required work is:
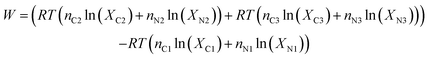 | (6) |
And the work per mole of CO2 in the flue gas is:
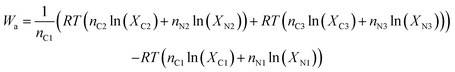 | (7) |
The number of parameters can be reduced by substituting the definition of the mole fraction into eqn (6), and the minimum work required to isothermally separate an ideal gas mixture into two ideal gas mixtures of different concentrations (Wa) is given by:
 | (8) |
W b (from state 3 to state 4)
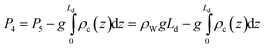 | (9) |
The minimum work required to compress the concentrated CO2 stream from state 3 to state 4 (Wb) is given by the reversible isothermal compression:
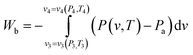 | (10) |
W c (from state 4 to state 5)
The work required to vertically displace the ground water is equal to the volume of ground water displaced times the well-head pressure:
| Wc1 = (P4 − Pa)v4 | (11) |
In the limiting case of zero viscous drag, the minimum value of Wc1 occurs when P4 equals the hydrostatic pressure of the ground water at the well-head. For typical values, Wc1 equals ∼1–2 kJ/(mol CO2).
In addition, work is required to create the interfacial surface between the CO2 and the pore-water because, on the injection time-scale, the CO2 acts primarily as an immiscible phase.21 The interfacial surface tension between supercritical CO2 and water at the relevant conditions is ∼0.02 J/m2,22 and the work required to increase the surface area goes as the interfacial surface tension (γ) and the change in surface area of the interface:
| Wc2 = γdA = ΔVΔPcap | (12) |
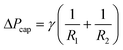 | (13) |
The total compression work is the sum of Wb and Wc, where Wc is the sum of Wc1 and Wc2. By the reverse integration by parts:
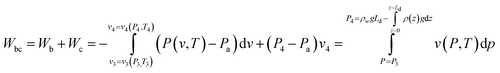 | (14) |
| Wbc = nC3((hC4 − hC3) − T0(sC4 − sC3)) + nN3((hN4 − hN3) − T0(sN4 − sN3)) | (15) |
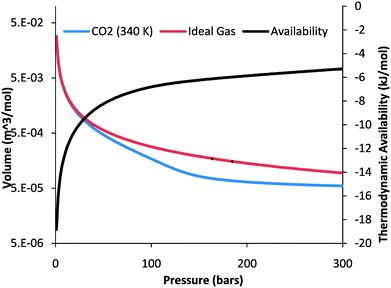 | ||
| Fig. 3 The left-hand vertical axis is for the volume–pressure curves of an ideal gas and pure CO2 at 340 K. The non-ideal behavior of CO2 at above ∼70 bars indicates that less work is required to fully compress CO2 than would be required to compress an ideal gas. The right-hand vertical axis depicts the thermodynamic availability of a pure CO2 phase as a function of pressure at 340 K. The definite integral of the volume–pressure curve between two pressures equals the state change in thermodynamic availability between those same two pressures. | ||
A different approach to ascertain the work required to emplace the CO2 below the pore water is to calculate the change in gravitational potential energy between state 4 and state 5. The total turbine shaft work is then the sum of Wb and the change in gravitational potential energy:
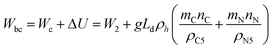 | (16) |
Eqn (14), (15), and (16) all yield the same value for Wbc, the minimum possible work. It should be noted that this lower limit depends on the depth of injection, but it is independent of the reservoir geometry and area [see Fig. 2(c)]. That is to say that creating sufficient pore-space for a given volume of CO2 in a reservoir with smaller area requires greater vertical displacement of less pore-water while emplacing the CO2 into a reservoir with larger area requires less vertical displacement of more pore-water. The displaced volume and the required work are the same in both cases.
Friction. The energetic calculations are now extended to include friction associated with transport and storage. As the CO2 is transported from the injection zone to the storage site, viscous drag within the pipeline decreases the fluid pressure. The pressure drop in a pipeline is given by:
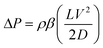 | (17) |
Friction is encountered again when CO2 is injected into the formation and work is required to compress the pore-fluid and expand the pore-space. That work dissipates into friction, which is manifest in elevated injection pressure requiring additional compression work (Wb and Wc). The frictional loss is larger for high rates of flow – so the compression work is greater for faster injection. But, storage within the reservoir reduces work by slowing down flow.
Induced fracturing, however, limits reservoir pressures to the formation's least compressive stress.27 The fracture threshold is predominately determined by the least compressive stress. If the vertical stress, which is often near lithostatic pressure, is the weakest stress, then horizontal fractures will form and accommodate the injected CO2. It is more likely, however, that one of the horizontal stresses is the weakest indicating that vertical fractures are most likely.28
In any case, the pressure and the required work are bounded by pressure-induced fracturing. Prior to having reached fracture pressure, however, additional compression work is required to maintain the constant flow of CO2 into the formation. Over the lifetime of the injection, the reservoir pressures can increase from the hydrostatic pressure of the formation to the fracture pressure, which is ∼1.4–2.0 times the hydrostatic pressure.27
The additional compression work required (i.e., the increase in Wb) to accommodate the increased reservoir pressure is small compared with the initial compression as the CO2 pressure–volume curve (Fig. 3) flattens out significantly above 100 bars. On the other hand, the additional work required to emplace the CO2 beneath the pore-water by pushing the fluid into the reservoir (i.e., the increase in Wc) is on the same order as the initial work Wc. That is because eqn (11) is linear in pressure, and the fracture pressure is about twice the initial hydrostatic pressure. Specifically, Wb changes from ∼12 kJ/(mol CO2) initially to 13 kJ/(mol CO2) once fracture pressure is reached, while Wc changes from 1 kJ/mol to ∼2 kJ/mol. Thus, the friction related work increases Wbc by ∼15%.
Primary energy required and waste heat recovery
The minimum total work required to separate, compress, transport, and store a unit of CO2 produced from a power plant is:| Wtot = Wa + Wb + Wc | (18) |
Performing work Wa, Wb, and Wc, requires primary energy Ea, Eb, and Ec. Calculating ES—the sum of Ea, Eb, and Ec—requires determining the theoretical limit for each conversion of primary energy to work. Subsequently, we extend our calculations to consider reasonable upper bounds on efficiencies, and hence reasonable lower bounds for the energy penalty.
E a
A well developed technology for post-combustion separation of CO2 from flue gas is the temperature-swing system with the solvent monothenolamine (MEA).29Ea is not set by the enthalpy of desorption because nearly the same quantity of heat is generated during the exothermic absorption as the endothermic desorption. Rather, Ea is set by the 2nd-law of thermodynamics, which limits the efficiency of any heat-to-work conversion.20 Therefore, Ea is given by Wa over the product of the ideal heat-to-work conversion efficiency for separation (ηsideal) and the 2nd-law efficiency of the actual separation process (ηs2nd):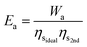 | (19) |
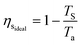 | (20) |
Temperature-swing separation systems—like MEA—often work at low temperatures.29 For that reason, harnessing low-temperature waste heat for this type of separation is practical, and as such, the additional primary energy required for separation, Esep, is lower than Ea. If the quantity of waste heat that can—in principle—be used for separation is Ew, then and the primary energy required from additional combustion of fuel is:
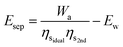 | (21) |
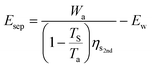 | (22) |
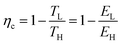 | (23) |
The actual power plant efficiency (ηpp) is given by:
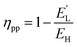 | (24) |
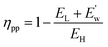 | (25) |
Solving for E′wwith the above 3 equations yields:
| E′w= EH(ηc − ηpp) | (26) |
Eqn (26) gives the total waste heat produced by irreversible processes (or inefficiencies) within the plant by a power plant. E′w, however, is greater than Ew—the available waste—because temperature-swing separation systems have a minimum temperature at which heat can be used. The stripper accepts heat at or above TS while the absorber dumps heat to the environment (or the condenser) at or above TL (Fig. 2). As such, waste heat can only be utilized if it is greater than TS. The fraction of available waste heat (ηw) approaches zero as TS approaches TH. Likewise, ηw approaches 1 as TS approaches TL. There is limited published data on the temperature distribution of power-plant waste heat. For that reason, a linear temperature distribution between TL and TH was assumed. Such a waste–heat distribution yields:
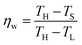 | (27) |
Careful research is needed to more accurately access the waste–heat distributions. Such work would be very valuable, but also very difficult as it would require detailed engineering studies of existing power-plants. The goal of this study is to constrain what is physically possible given actual and theoretical power plant efficiencies.
Given our assumed waste–heat distribution, the quantity of available waste heat is:
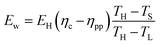 | (28) |
Or,
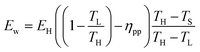 | (29) |
Only a fraction of the available waste heat, however, will actually be harnessed. Therefore, we introduce a new variable (ηw2nd), which is the 2nd-law efficiency (i.e., the fraction of maximum possible) of the waste heat recovery, and therefore, the total quantity of waste heat that is actually recovered for productive us is:
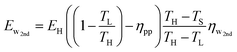 | (30) |
Combining eqn (21) and (30) yields the additional primary energy required to perform Wa for a temperature-swing separation process:
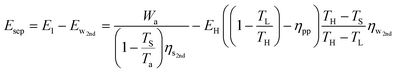 | (31) |
E b and Ec
The primary energy required for compression depends on the efficiency of the turbine to produce shaft work and the 2nd-law efficiency of the compressors themselves. No waste heat is allocated to compression as that would require building a more efficient power plant. Therefore: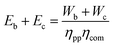 | (32) |
The re-compression necessary to overcome pipeline and reservoir friction will be powered by either natural-gas from a parallel pipeline or electricity from the grid. Calculating the associated CO2 emissions requires either the efficiency of natural gas compressors or the collective efficiency of grid power with respect to CO2 emissions (i.e., all the electric power produced over all the thermal power from CO2 production). Assuming the CO2 is not transported more than a few hundred kilometers, the primary energy calculated from such values increases Ebc by less than 10%
Adding eqn (31) and (32), we arrive at the lower limit of the total primary energy used by a temperature-swing separation system for CO2 sequestration:
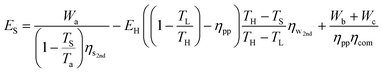 | (33) |
For non-temperature-swing separation systems—such as membranes or pressure-swing absorption systems—waste heat is not useful because the separation work is a parasitic load on the power-plant turbine. As such, ES is:
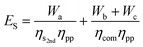 | (34) |
The energy penalty
The energy penalty, f1, is the fraction of the fuel that must be dedicated to CCS activities for a given quantity of fuel input (EH):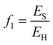 | (35) |
If the quantity of fuel is fixed, then the energy penalty is manifest in the reduction of the plant's power output. The new power output per unit fuel is:
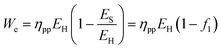 | (36) |
If, on the other hand, the power output is fixed, then the energy penalty is manifest as the increase in fuel necessary to maintain that constant power output. This additional fuel requirement is expressed as the ratio of the fuel for CCS (ES) to the fuel that produces power output (EH − ES). Thus, the fraction of additional fuel required to maintain the constant power output associated with EH is:
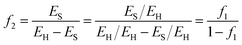 | (37) |
This additional fuel requirement can also derived as the geometric sum of the energy penalty. The additional fuel required to sequester the CO2 produced for a unit of power generation is f1, but in burning this fuel, more CO2 is produced that requires (f1)2 additional fuel to sequester, which in turn requires more fuel, ad infinitum, to give the sum of the infinite geometric series:
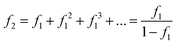 | (38) |
By combining eqn (33) with eqn (35), the energy penalty (f1) and the additional fuel requirement (f2) for a temperature-swing separation system can be written in terms of basic system parameters as well as the minimum work required for separation and compression:
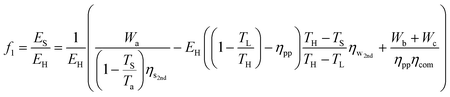 | (39) |
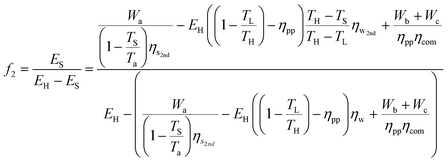 | (40) |
Discussion
The lower bound of the total CCS work—for a 2 km injection—with perfect 2nd-law efficiencies for all three steps is Wabc = ∼24 kJ/(mol of CO2), where Wa, Wb, and Wc equal ∼ 9, 13, and 2 kJ/(mol CO2). Eqn (33) and (34) convert the work lower bound to the primary energy lower bound for temperature-swing separation systems and pressure-swing separation systems, respectively. For a pressure-swing separation process with perfect compression and perfect separation, the ideal primary energy requirement for the total installed base would be ∼75 kJ/(mol CO2), which implies an f1 of ∼19% and an f2 of 23% (assuming EH ∼ 400 kJ/(mol CO2)). For a temperature-swing separation process, the minimum primary energy requirement corresponds to the case when sufficient waste heat is harnessed for complete separation. In such an ideal case, the minimum energy requirement would be ∼45 kJ/(mol CO2), implying an f1 of ∼11% and an f2 of ∼13%.Table 1 reveals the end-member cases for post-combustion capture and storage between the thermodynamic lower-bound and values being reported for current technology. From these values, it is clear that the energy penalties achieved from temperature-swing separation systems are more uncertain, but also that waste–heat recovery offers a significant opportunity to decrease the energy penalty.
| Pressure-swing separation | Temperature-swing separation | |
|---|---|---|
| Lower bound (ηpp = 33%, ηcom = 100%, ηs2nd = 100%, ηw2nd = 100%, TS = 390 K) | E S = ∼75 kJ/(mol CO2) | E S = ∼43 kJ/(mol CO2) |
| f 1 = ∼19%, f2 = ∼23% | f 1= ∼11%, f2 = ∼13% | |
| Easily achieved (ηpp = 33%, ηcom = 65%, ηs2nd = 50%, ηw2nd = 0%, TS = 390 K) | E S = ∼130 kJ/(mol CO2) | E S = ∼160 kJ/(mol CO2) |
| f 1 = ∼33%, f2 = ∼48% | f 1 = ∼40%, f2 = ∼67% | |
| 33% available-waste-heat recovery (ηpp = 33%, ηcom = 65%, ηs2nd = 60%, ηw2nd = 33%, TS = 390 K) | E S = ∼130 kJ/(mol CO2) | E S = ∼116 kJ/(mol CO2) |
| f 1 = ∼33%, f2 = ∼48% | f 1 = ∼29%, f2 = ∼41% |
The thermodynamic limit for sequestration with a temperature-swing separation system indicates that capturing and storing all the CO2 generated from current U.S. PC plants while delivering the same power output would require—at the very least—consuming an additional ∼120 million tonnes of coal annually. If, on the other hand, the energy penalty were incurred by decreasing the electrical work output—rather than increasing the fuel consumption—then the electrical work output of the U.S. coal fleet will drop by—at the very least—∼37 GW. That means that either an additional 37 GW of base-load CO2-free power have to be built, or national electricity use would have to be reduced by 37 GW.
The energy penalty for post-combustion capture and storage of PC power-plant CO2 has been estimated by several different studies.7–18 A review of that literature demonstrates a relationship between the energy penalty and the economics of CCS (Fig. 1); it also reveals a significant spread between the various published estimates of the energy penalty. The reviewed studies of PC retrofits include only small amounts of waste–heat recovery, and the associated f2 values are between 43% and 77%, which indicate ηs2nd values of ∼40%–60% (Fig. 1). Analysis of eqn (39) and (40) provides insight into that spread as well as into future CCS development.
Eqn (40) depends on 17 parameters, yet in practice only two of them—the fraction of available waste heat that is actually recovered (ηw2nd) and the 2nd-law separation efficiency (ηs2nd)—are poorly constrained (ηpp varies significantly, but it is well constrained). Fig. 4 reveals how f2 depends on these poorly constrained parameters.
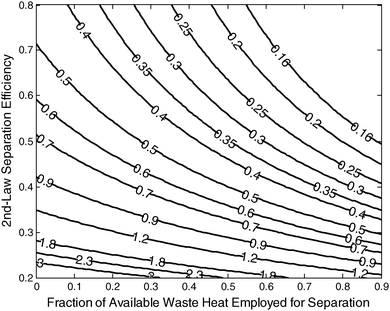 | ||
| Fig. 4 The additional fuel requirement (f2) for coal-fired power plants employing a MEA separation system. The horizontal axis is the fraction of available available-waste heat employed for separation, and the vertical axis is the 2nd-law efficiency of the separation process (ηs2nd). For these calculations, the stripper temperature (TS) = 390 K, the absorber temperature (Ta) = 310 K, the power plant efficiency = 33% (ηpp), the isothermal compressor efficiency = 65% (ηcom), the highest turbine temperature (TH) = 1000 K, and the environmental temperature (TL) = 300 K). | ||
New construction projects have two distinct advantages; first, the power plants themselves—having supercritical or ultra-supercritical steam cycles—are more efficient which results in a lower energy penalty since the primary energy required for compression is function of ηpp; and second, new construction projects can more easily be designed to utilize low-grade waste heat for CO2 separation. The absolute value of the contour slopes in Fig. 4 are mostly less than 1, which indicates that f2 is generally more sensitive to changes of ηs2nd than to changes of ηw2nd. Since current systems already achieve ηs2nd values in the range of ∼40%–60%,29ηw2nd represents the most potential for improvement as the contour slopes are significantly steeper for ηs2nd values above ∼50%.
The energy penalty—as derived in this paper—can be used to calculate the optimal values for various independent variables. For instance, Wa and Wbc depend on the degree of separation in opposite directions. Zero separation minimizes Wa, but it maximizes Wbc. The same is true—naturally—for Ea and Ebc. Fig. 5 shows the optimal separation as a function of the fraction of flue-gas CO2 that is emitted to the atmosphere.
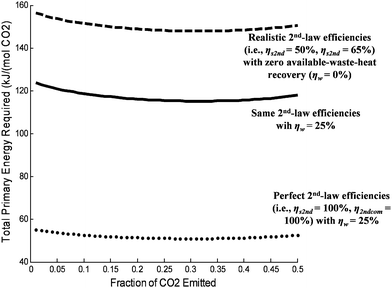 | ||
| Fig. 5 The optimal degree of temperature-swing separation (TS = 390 K) as measured by the fraction of CO2 that is emitted (i.e., not stored) per unit primary energy (Etot) required for CCS. In all cases, it was assumed that 99% of the N2 in the flue-gas was emitted to the atmosphere. The optimal separation fraction does not change much with efficiency scenarios. Indeed, it is clear from this figure that modest improvements in available waste–heat recovery and 2nd-law efficiencies will reduce the energy penalty significantly more than optimizing the fraction of CO2 that is captured. | ||
The stripper temperature is another parameter for optimization as TS affects f1 in two different directions. The ideal separation efficiency increases with TS (eqn (20)), but the quantity of available waste heat decreases with TS (eqn (27)). MEA strippers operate at ∼390 K, and research is ongoing to identify new absorption materials—such as ionic liquids32—that can operate at higher temperatures with the goal of increasing the heat to work conversion efficiency. Due to the decrease in available waste heat, however, these efforts might be limited in their potential. For typical efficiency and waste–heat recovery values, increasing the Ts beyond ∼500 K might not be helpful because the loss of available waste heat compensates for the increase in separation efficiency [Fig. 6(a)]. Indeed, given the likelihood that the waste–heat temperature distribution is more skewed toward lower temperatures than the linear distribution assumed here, it is probable that the optimal Ts is below 500 K, suggesting that current systems are operating near the optimal Ts. That assumes, however, that effective engineering can harness the available waste heat.
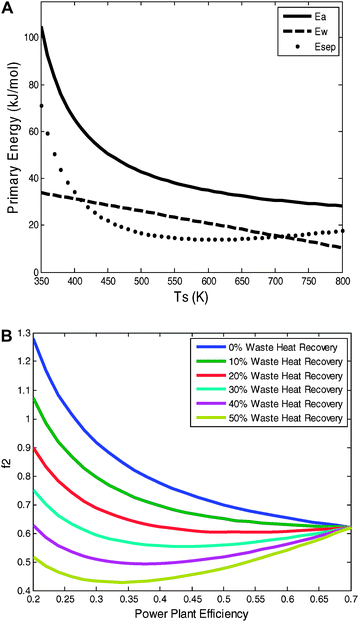 | ||
| Fig. 6 (A) The potential for waste–heat recovery as a function of the stripper temperature. If the fraction of available-waste–heat recovery is significantly large, then due to the decrease in available waste heat, finding materials that absorb CO2 and are stable at higher temperatures than MEA will not help beyond ∼500 K as the loss available waste heat compensates for the increase separation efficiency (ηs2nd = 40%, ηw2nd = 25%). (B) The additional fuel requirement (f2) depends on the power-plant efficiency in two ways: Ebc decreases as ηpp increases, but Ea can actually decrease as ηpp increases because the available waste heat decreases as ηpp increases. f2 monotonically decreases for available-waste-heat recovery fractions of below ∼30%. At values greater than 30%, however, f2 is minimized for particular power-plant efficiencies. If available waste heat recovery rates can exceed 30%, then it may not be beneficial to target efficient plants for CCS retrofits. | ||
Sensitivity analysis on the total energy penalty is performed by varying the power-plant efficiency. The additional fuel requirement (f2) depends on the power-plant efficiency in two ways: Ebc decreases as ηpp increases, but Ea can actually decrease as ηpp increases because the available waste heat decreases as ηpp increases. Fig. 6(b) shows f2 as a function of ηpp, and that figure demonstrates that f2 is minimized for particular power-plant efficiencies. If available waste heat recovery rates can exceed 30%, then it may not be beneficial to target inefficient plants for CCS retrofits.
The reviewed studies also indicate significant differences in the energy penalty between new construction projects and retrofits. Those differences are primarily driven by 3 factors that are made clear from our analysis of the energy penalty: (1) the degree of available-waste-heat recovery (ηw2nd), (2) the baseline power plant efficiency (ηpp), and (3) the 2nd-law separation efficiency (ηs2nd). All the studies of new construction projects involve either supercritical or ultra-super critical cycles whose superior plant efficiencies result in lower energy penalties than subcritical cycles. In addition, waste–heat recovery for separation is easier to implement in new construction projects than in retrofits.
The U.S. installed base of PC plants has a total thermal efficiency (ηpp) of 33%. Fig. 7(a) shows the distribution of thermal efficiencies for the installed base of PC plants.33
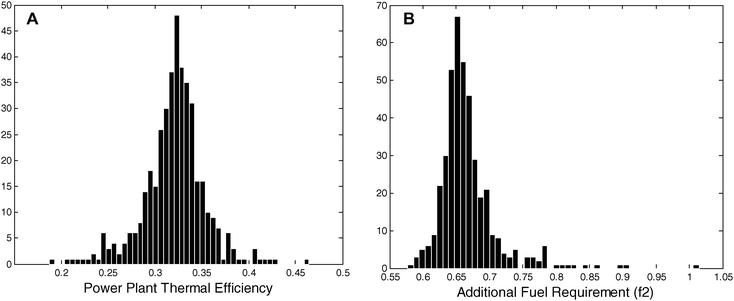 | ||
| Fig. 7 (A) The thermal efficiency distribution of an ensemble of 420 large U.S. coal-fired power plants. These plants produced the equivalent of 218 GW of constant electric power in 2007 constituting 96% of all U.S. coal-fired power output. (B) The distribution of additional fuel requirements (f2) is calculated from the power-plant efficiency distribution. From this distribution, the total additional fuel required is calculated to be 530 million tonnes of coal. These calculations assume, ηs2nd = 40%, ηw2nd = 20%, ηcom = 65%, and the national average coal heat content (25 GJ/(tonne)). | ||
In 2007, the most efficient plant recorded a thermal efficiency of 46.4% while the least efficient plant recorded a value 18.7%. The energy penalties (f1) to capture and store the CO2 from those two plants with a modern temperature-swing separation system are 34% and 52%, respectively. From the distribution of thermal efficiencies, f1 and the additional fuel requirement (f2) associated with converting all or some of the U.S. coal-fleet to CCS can be calculated.
Fig. 7(b) shows the distribution of f2 for the U.S. installed base with 20% available-waste-heat recovery. That distribution yields a spread in Esep between 78 and 96 kJ/mol because less efficient plants have more available waste heat. Fig. 7(b) shows the corresponding f2 distribution, which spreads from 0.57 to 1.01 with a mean value of 0.66 and standard deviation of 0.05. Converting the entire PC installed base to CCS while keeping its electrical work output constant would require an additional ∼460 million tonnes of coal annually (assuming an average energy content of 25 GJ/(tonne coal)). Alternatively, the energy penalty could be manifest in a decreased plant output. In that case, the power output of the U.S. coal fleet would drop by ∼78 GW.
Under the 20% available-waste-heat recovery assumption, the difference between retrofitting the most efficient plants for CCS and retrofitting the least efficient plants is significant [Fig. 7(b)]. If the 10 most efficient plants were retrofitted to capture and store 80% of their CO2, then an additional 6.5 million tonnes of coal would be required and 27 million tonnes of CO2 emissions would be eliminated annually. Thus, the CO2 abatement effectiveness (i.e., the mass ratio of CO2 eliminated to additional coal required) for the top 10 plants is 4.1. On the other hand, retrofitting the 10 least efficient plants would require 2.4 million tonnes of additional coal and would only eliminate 6.8 million tonnes of CO2 annually yielding a CO2 abatement effectiveness of 2.8. Thus, retrofitting the 10 most efficient PC plants for CCS would eliminate 46% more CO2 emissions per unit of additional coal than retrofitting the 10 least efficient plants.
These calculations were repeated for the most and least efficient 10% and 25% of current PC plants (Table 2). The columns in Table 2 reveal how the CO2 abatement effectiveness depends on the fraction of available-waste heat that is recovered from retrofitting a particular ensemble of the most efficient plants versus the equivalent ensemble of least efficient plants.
| CO2 abatement effectiveness (ηw2nd = 0%) | CO2 abatement effectiveness (ηw2nd = 20%) | CO2 abatement effectiveness (ηw2nd = 40%) | |
|---|---|---|---|
| Top 2% (top 10) | 3.3 | 4.1 | 5.3 |
| Top 10% | 3.1 | 4.0 | 5.2 |
| Top 25% | 3.0 | 3.9 | 5.1 |
| Bottom 25% | 2.6 | 3.4 | 4.6 |
| Bottom 10% | 2.4 | 3.1 | 4.5 |
| Bottom 2% (bottom 10) | 2.1 | 2.8 | 4.0 |
The dependence of the energy penalty and the CO2 abatement effectiveness on base-line efficiency derives from the primary energy required for compression and from the available waste heat. More efficient power-plants have lower Ebc values, but they also have less available waste heat. Fig. 6(b) reveals the sensitivity of f2 to both ηpp and ηw2nd. That figure indicates that once ηw2nd exceeds 50%, f2 is essentially independent of power-plant efficiency. On the other hand, if ηw2nd = 0%, then both Table 2 (column 4) and Fig. 6(b) reveal that retrofitting the most efficient plants is a substantially more effective method of CO2 emission abatement. Table 2 reveals a narrowing of the CO2 abatement effectiveness with increasing available-waste-heat recovery, but even in the high ηw scenario, retrofitting the most efficient PC plants is nevertheless measurably more effective than retrofitting the least efficient plants.
The financial costs of CCS are tightly related to the energy penalty (Fig. 1). Indeed, it is worth noting in Fig. 1 that while new PC construction appear superior to PC retrofits when measured by the common metric of dollars per tonne of CO2 avoided (Fig. 1(a)), retrofits and new construction are about equal when measured by the more relevant metric of cost of electricity from a CCS power plant (Fig. 1(b)). That is partially the result of lower fixed costs associated with plants that have been fully or partially amortized.
The correlation between the costs of CCS and the energy penalty coupled with the variance in expected energy penalties (Fig. 7(b)) suggests an optimal CCS deployment strategy. The cheapest path to drastically reduce CO2 emissions from electricity production will combine the selective retrofitting of the most efficient PC plants with the closing of the least efficient plants. Overall, our analysis strongly suggests that the supply curve for retrofitting PC plants for CCS is a function of the power-plant's baseline thermal efficiency.
It should be noted, however, that the relationship between base-line efficiency and the energy penalty assumes that the power plant itself is providing the compression work. Other configurations are possible. For example, a dedicated natural-gas-fired compressor or even a wind turbine could provide the necessary compression work. In those scenarios, f1 would manifest as the reduced power output from either natural gas or wind; f2, however, would be lower because the CO2 intensity of both gas and wind are lower than that of coal.
To demonstrate the potential value of available-waste-heat recovery, we calculate f2 for the entire U.S. coal fleet with and without 1/3 available-waste-heat recovery. Retrofitting the entire U.S. coal fleet with zero available-waste-heat recovery would require additional ∼600 million tonnes of coal annually. If, on the other hand, 1/3 of the available waste heat were productively used for separation, then the additional fuel requirement would drop from ∼600 million to ∼390 million tonnes of coal annually. Alternatively, if the energy penalty were manifest in a reduced power output, then with zero available-waste-heat recovery an additional ∼92 GW of CO2-free base-load power would be required to make up for the decrease in power output. With 1/3 available-waste-heat recovery, however, the additional power requirement would drop from ∼91 GW to ∼69 GW.
Improving end-use electrical efficiency is an additional path through which the CCS energy penalty could be offset. This path is intriguing because the total U.S. smoothed power output was ∼472 GW in 2007,34 indicating that increasing end-use electrical efficiency of between 15% and 20% would be sufficient to make up for the decrease in power output after retrofitting the installed PC base for CCS. That would yield a ∼65% reduction in CO2 emissions from the power sector while not requiring any additional power-generation capacity to be build or any additional coal to be burned. The remaining 35% would come primarily from natural gas as well as a little from coal as we assumed 80% CO2 capture. This approach may be feasible as California has been able to keep its per capita electricity use constant for the past 30 years, while average per capita electricity use in U.S. grew by nearly 50%.35
Conclusion
Achieving substantial reductions in CO2 emissions requires either shutting down a large fraction of the current installed base of coal-fired power plants or retrofitting those plants for CCS. Previous studies have estimated that the additional fuel required (f2) to maintain constant work output for a PC retrofit is between ∼50% and 80%. An analysis of the thermodynamic limit indicates those values might be improved by harnessing more of the available waste heat and by improving the 2nd-law efficiency of temperature-swing separation systems. It appears difficult, however, to improve f2 for post-combustion capture to below ∼25% in practice. Our most likely efficiency scenario indicates that offsetting the energy penalty incurred from capturing and storing 80% of the U.S. coal fleet's CO2 emissions will require either an additional ∼390–600 million tonnes of coal, an additional ∼69–92 gigawatts of CO2-free-baseload power, or a 15%–20% reduction in overall electricity use.Nomenclature list with some characteristic values
| W a | The work required to separate the CO2 from the flue gas [thermodynamic limit∼9 kJ/mol] |
| W b | The work required to compress the concentrated CO2 from atmospheric to reservoir pressure [thermodynamic limit ∼13 kJ/mol] |
| W c1 | The work required to vertically displace groundwater [thermodynamic limit ∼1–2 kJ/mol] |
| W c2 | The work required to generate a interface between CO2 and the pore-water [thermodynamic limit <1 kJ/mol] |
| W c | W c1 + Wc2 [thermodynamic limit ∼2 kJ/mol] |
| W e | Power plant work output after the addition of CCS |
| W tot | W a + Wb + Wc [kJ/mol] |
| W ab | W a + Wb [kJ/mol] |
| W bc | W b + Wc [kJ/mol] |
| E a | The primary energy required to separate the CO2 from the flue gas [kJ] |
| E b | The primary energy required to compress the concentrated CO2 to reservoir pressure [kJ] |
| E c | The primary energy required to emplace compressed CO2 into the geologic formation [kJ] |
| E sep | The incremental primary energy required to separate CO2 from the flue [kJ] |
| E S | The total primary energy required for sequestration [kJ] |
| E w | The quantity of waste heat that can—in principle—be used in separation [kJ] |
| E′w | The total waste heat produced [kJ] |
| E L | The minimum quantity of heat transferred to the environment [kJ] |
| E′L | The actual quantity of heat transferred to the environment [kJ] |
| E H | The primary energy content of the fuel [kJ] |
| η sideal | Ideal separation efficiency (ηpp * ηcom for pressure swing, ∼30% for temperature swing) |
| η s2nd | 2nd-law separation efficiency (∼50%) |
| η c | The power-plant Carnot efficiency (∼70%) |
| η pp | The power plant efficiency (25%–45%) |
| η com | Isothermal compression efficiency (65%) |
| X Ni | The mole fraction of N2 in state i (state 1: ∼80%) |
| X Ci | The mole fraction of CO2 in state i (state 1: ∼12%) |
| n Ci | The number of moles of CO2 in state i (state 1: ∼0.12 moles CO2 per mole of flue gas) |
| n Ni | The number of moles of N2 in state i (state 1: ∼0.80 moles N2 per mole of flue gas) |
| P i | The pressure of state i [Pa] (∼105 Pa at the surface, ∼107 Pa in the reservoir) |
| g | The gravitational acceleration [m/(s2)] |
| L d | The depth of CO2 injection [∼1000 m] |
| L | Length of pipeline |
| ρ W | The density of H2O [∼kg/m3] (∼1000 kg/m3) |
| ρ Ci | The density of CO2 in state i [kg/m3] (∼2 kg/m3 at the surface, ∼400–600 kg/(m3) in the reservoir) |
| ρ Ni | The density of N2 in state i [kg/m3] (∼1.2 kg/m3) |
| h Ci | The molar enthalpy of CO2 in state i [kJ/mol] |
| h Ni | The molar enthalpy of N2 in state i [kJ/mol] |
| s Ci | The molar entropy of CO2 in state i [kJ/(K mol)] |
| s Ni | The molar entropy of N2 in state i [kJ/(K mol)] |
| m C | The molar mass of CO2 [kg/mol] |
| m N | The molar mass of N2 [kg/mol] |
| T a | Temperature of the MEA absorber unit [∼320–350 K] |
| T S | Temperature of the MEA stripper unit [∼400 K] |
| T L | Temperature of the environment [∼293 K] |
| T H | Temperature of the steam working fluid [∼1000 K] |
| f 1 | The energy penalty |
| f 2 | The fraction of additional fuel required to maintain the constant power output |
| V | Total swept out pore volume [m3] |
| v i | Molar volume of state i [m3/mol] |
| G | The Gibbs free energy [kJ] |
References
- M. R. Raupach, G. Marland, P. Ciais, C. Le Quéré, J. G. Canadell, G. Klepper and C. B. Field, Global and regional drivers of accelerating CO2 emissions, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(24), 10288–10293 CrossRef CAS.
- S. Pacala and R. Socolow, Stabilization Wedges: Solving the Climate Problem for the next 50 Years with Current Technologies, Science, 2004, 305(5686), 968–972 CrossRef CAS.
- E. Rubin, L. Meyer, and H. de Coninck, IPCC Special Report on Carbon Dioxide Capture and Storage: Prepared by Working Group III of the Intergovernmental Panel on Climate Change, Intergovernmental Panel on Climate Change, Cambridge, UK, 2005 Search PubMed.
- IEA, Pulverized Coal Combustion, International Energy Agency, 2008 Search PubMed.
- EIA, Net Generation by Energy Source by Type of Producer, Energy Information Agency, 2007 Search PubMed.
- EIA, Emissions of Greenhouse Gases Report, Energy Information Agency, US Department of Energy, Washington DC, USA, 2007 Search PubMed.
- J. Gibbins, R. I. Crane, D. Lambropoulos, C. Booth, C. A. Roberts and M. LordMaximising the effectiveness of post-combustion CO2 capture systems, in Proceedings of the 7th International Conference on Greenhouse Gas Control Technologies, Elsevier Science, Vancouver, BC, Canada, 2005 Search PubMed.
- D. Singh, E. Croiset, P. L. Douglas and M. A. Douglas, Techno-economic study of CO2 capture from an existing coal-fired power plant: MEA scrubbing vs. O2/CO2 recycle combustion, Energy Convers. Manage., 2003, 44(19), 3073–3091 CrossRef CAS.
- D. R. Simbeck and M. McDonald, Existing coal power plant retrofit CO2 control options analysis, in Proceedings of the 5th International Conference on Greenhouse Gas Control Technologies, CSIRO Publishing, Cairns, Australia, 2000 Search PubMed.
- A. Roa and E. Rubin, A Technical, Economic, and Environmental Assessment of Amine-Based CO2 Capture Technology for Power Plant Greenhouse Gas Control, Environ. Sci. Technol., 2002, 36, 4467–4475 CrossRef CAS.
- C. Chen, A. B. Rao, and E. S. Rubin, Comparative assessment of CO2 capture options for existing coal-fired power plants, in Second National Conference on Carbon Sequestration, Alexandria, VA, 2003 Search PubMed.
- Parsons, Updated cost and performance estimates for fossil fuel power plants with CO2 removal, Parsons Infrastructure & Technology Group, Palo Alto, CA, 2002 Search PubMed.
- Alstom, Engineering feasibility and economics of CO2 capture on an existing coal-fired power plant, Alstom Power and US Department of Energy, National Energy Technology Laboratory, Columbus, OH, 2001 Search PubMed.
- D. R. Simbeck, New power plant CO2 mitigation costs, SFA Pacific, Inc., Mountain View, CA, 2002 Search PubMed.
- IEA, Improvements in power generation with post-combustion capture of CO2, International Energy Agency, Cheltenham, UK, 2004 Search PubMed.
- E. L. Parson, W. W. Shelton, and J. L. Lyons, Advanced fossil power systems comparison study, National Energy Technology Laboratory, US Department of Energy, Morgantown, WV, 2002 Search PubMed.
- E. S. Rubin and A. B. Rao, Uncertainties in CO2 capture and sequestration costs, in Proceedings of the 6th International Conference on Greenhouse Gas Control Technologies, Elsevier Science, Kyoto, Japan, 2003 Search PubMed.
- R. Stobbs and P. Clark. Canadian Clean Power Coalition: The Evaluation of Options for CO2 Capture From Existing and New Coal-Fired Power Plants, in Proceedings of the 7th International Conference on Greenhouse Gas Control Technologies, Elsevier Science, Vancouver, Canada, 2005 Search PubMed.
- K. Thambimuthu, M. Soltanieh and J. C. Abanades, Capture of CO2, in IPCC, 2005: IPCC Special Report on Carbon Dioxide Capture and Storage. Prepared by Working Group III of the Intergovernmental Panel on Climate Change, Intergovernmental Panel on Climate Change, Cambridge, UK, 2005 Search PubMed.
- D. Gaskell, Introduction to the Thermodynamics of Materials, Taylor & Francis, Washington DC, USA, 1995, pp. 219–264 Search PubMed.
- W. Gunter, S. Bachu and S. Benson, The role of hydrogeological and geochemical trapping in sedimentary basins for secure geological storage of carbon dioxide, Geological Society: Special Publications, London, UK, 2004, 233, pp. 129–145 Search PubMed.
- P. Chiquet, J.-L. Daridon, D. Broseta and S. Thibeau, CO2/water interfacial tensions under pressure and temperature conditions of CO2 geological storage, Energy Convers, Manage., 2007, 48(3), 736–744 CrossRef CAS.
- P.-G. de Gennes, F. Brochard-Wyart and D. Quere, Capillary and Wetting Phenomena, Springer, New York, NY, 2003 Search PubMed.
- A. Dandekar, Petroleum Reservoir Rock and Fluid Properties, CRC, Wiley, 2006, p. 488 Search PubMed.
- R. Sonntag, C. Borgnakke and G. J. Van Wylen, Fundamentals of Thermodynamics, Wiley, 2002 Search PubMed.
- E. W. McAllister, Pipeline Rules of Thumb Handbook: A Manual of Quick, Accurate Solutions to Everyday Pipeline Engineering Problems, Gulf Professional Publishing, San Francisco, CA, 2005, 6th edn Search PubMed.
- K. Z. House, C. Harvey and D. Schrag, Pressure dissipation as a limiting resource for geologic storage of CO2, 2008, in preparation.
- M. K. Hubbert and D. G. Willis, Mechanics of hydraulic fracturing, Mem. Am. Assoc. Pet. Geol., 1972, 18, 239–257 Search PubMed.
- B. A. Oyenekan, Modeling of Strippers for CO2 Capture by Aqueous Amines, Department of Chemical Engineering, The University of Texas at Austin, Austin, Texas, 2007 Search PubMed.
- E. W. Lemmon, M. O. McLinden and D. G. Friend, Thermophysical Properties of Fluid Systems, in NIST Chemistry WebBook, ed.P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg, MD, 2005 Search PubMed.
- Ramgen, Ramgen CO2 Compressor - Technical Specifications, 2007 [cited 2007; Available from: http://www.ramgen.com/files/Ramgen%20CO2%20Compressor%20Technology%20Summary%2008-21-07.pdf Search PubMed.
- J. Tang, W. Sun, H. Tang, M. Radosz and Y. Shen, Enhanced CO2 Absorption of Polyionic Liquids, Macromolecules, 2005, 38, 2037–2039 CrossRef CAS.
- EIA, EIA-906/920 database, Energy Information Agency, Washington DC, USA, 2007 Search PubMed.
- EIA, Net Generation by Energy Source by Type of Producer, Energy Information Administration (EIA), Washington DC, USA, 2007 Search PubMed.
- NRC, Energy Research at DOE: Was It Worth It?Energy Efficiency and Fossil Energy Research 1978 to 2000, Committee on Benefits of DOE R&D on Energy Efficiency and Fossil Energy, National Research Council, Washington DC, USA, 2004 Search PubMed.
| This journal is © The Royal Society of Chemistry 2009 |
