5,5′-Dicyano-2,2′-bithiophene and 3,3′-dicyanobiphenyl: off-axis rod-like ligands for silver(I)

Abstract

The two ligands 3,3′-dicyanobiphenyl (3) and 5,5′-dicyano-2,2′-bithiophene (4) are geometrically similar but give rise to different coordination compounds when reacted with silver(I) salts. The crystal structures of 3·AgClO₄ and 3·AgBF₄ have 1 : 1 ligand : cation ratios, while 4₂·ClO₄ and 4₂·BF₄ have 2 : 1 ligand : cation ratios. These ratios for the solid-state materials were constant, even when different stoichiometric ratios were used in the reaction vessels. The structures of these four coordination compounds are presented and the reasons for the difference in the coordination environments discussed with reference to IR spectroscopic and DFT computational results.

---

Introduction

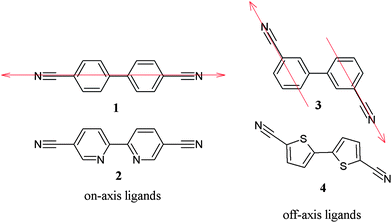
The node-and-spacer method of crystal engineering is widely used to generate solid-state structures that are predictable based on the preferred geometry of the metal (cation) node and the structure of the ligand spacer.¹ When the cation has no geometric preference, e.g. for a d¹⁰ electronic configuration, the three-dimensional geometry of the solid will be determined by other factors acting in concert. For such materials, changes in the solvent, counterion, and stoichiometry of the ligand can have a dramatic impact on the crystal structure.

Silver(I) is a typical d¹⁰ metal cation. In coordination compounds it can have virtually any geometry, from linear to octahedral. Ligands can range from the very strong (e.g., phosphine donors^2–5) to the very weak (e.g., sulfonate donors^6–8). The most common donor atom for silver(I), though, is nitrogen.^9,10 Of this subset, the nitrile group is an especially favoured donor unit, because of the wide variety of organic nitriles available. Ligands range from very flexible alkyl-bridged dinitriles,^11,12 to rigidly trigonal 1,3,5-trisubstituted phenyl trinitriles.¹³

We are interested in exploring rod-like dinitrile ligands with potential additional binding sites in the bridge. Rod-like ligands can be on-axis or off-axis, as demonstrated in Scheme 1 for the 4,4′-biphenyl 1 (on-axis) and 3,3′-biphenyl 3 (off-axis) bridges. On-axis ligands are more common, examples of which include the seminal dinitrile 1, and also 2, which contains a bipyridine bridge. Silver(I) compounds containing ligand 1 range from linear coordination polymers¹⁴ to three-dimensional diamondoid networks,¹⁵ depending on the solvents, counterions, stoichiometry, etc. For ligand 2, the dinitriles form a one-dimensional coordination polymer with Ag⁺, but in this case the bipyridyl moiety also binds to the cation to cross-link the polymer chains.¹⁶

Scheme 1

In contrast, 3 and 4 (5,5′-dicyano-2,2′-bithiophene) are off-axis ligands. The sulfur atoms in the thiophene rings of 4 are potential secondary binding sites, although there are many examples where binding between metals and thiophene sulfurs does not occur, even when the ligand geometry should allow for such an interaction.^2,17–19 Thus, we have embarked on the synthesis of silver(I) coordination compounds of the off-axis rod-like ligands 3 and 4. These two ligands are putatively the same shape, while having different donor characteristics. We present herein the crystal structures for several compounds, comparing the structures formed using ligands 3 and 4 in a variety of solvents and with a variety of silver(I) counterions.

Synthesis and characterisation

Synthesis and IR characterisation

Both 3²⁰ and 4,^21,22 are known compounds. We used alternate syntheses for each, however. Ligand 3 is conveniently synthesised by homocoupling m-bromobenzonitrile in the presence of Ni(PPh₃)₄.²³ Ligand 4 is synthesised by converting dibromobithiophene²⁴ to 4 by refluxing in quinoline with copper(I) cyanide.²⁵ Both ligands were purified by recrystallisation followed by vacuum sublimation, repeating if necessary until the NMR was clear of any impurities.

Coordination compounds of silver(I) with the ligands 3 and 4 were generated by sealing the two solids (ligand and silver(I) salt, 1 : 1 molar ratio) in a glass tube with an appropriate solvent. The contents were heated to 100 °C until the solids dissolved, and were then cooled to room temperature at the rate of 1° h⁻¹ using a programmable tube furnace. Alcoholic and chlorinated solvents are unsuitable, as reaction between the silver(I) and solvent causes a black decomposition product. We therefore limited ourselves to aromatic solvents (benzene, toluene, nitrobenzene, etc.) and acetonitrile. The latter was also discovered to be unsuitable as the nitrile group on the acetonitrile competes with the ligand, leading to partial or no reaction between the cation and the ligand; this result is unsurprising considering the large number of alkyl nitriles that are known to bind to silver(I).^11,26–30 Solids were isolated by cutting open the tubes and characterised by the infrared absorption frequency of the nitrile.

Table 1 summarises the results for complexes using 3 as the ligand. The anions are arranged in the table from most coordinating to least coordinating (using an order determined by others^31,32). All combinations of ligand and solvent gave a reaction, although it was only partial in some cases and in other cases decomposition (black powder) occurred. Crystalline solids were stable for short periods in the air, but did tend to pick up atmospheric water (at least on the surface) upon prolonged exposure. There is no photodegradation, even after several months under ambient light in the laboratory.

Table 1 IR frequencies for the nitrile (C≡N) stretch of the coordination compounds 3·AgX (ligand 3 has a frequency of 2229 cm⁻¹)

Anion (X)	BF4^−	ClO4^−	PF6^−	SbF6^−	CF3SO3^−	NO3^−
Solvent
benzene	2274 + 2263	2258	2257 + SM	insol.	2257	2249 + SM
toluene	2272	2255	decomp.	decomp.	2256	decomp.
CH3CN	---	2260 + SM	---	SM	---	---

---

We have previously published the results of the reaction of 4 with some silver(I) cations.³³Table 2 presents our new results. As was found in the earlier work, only some of the new combinations of anion and solvent yielded coordination compounds (the lack of reactivity is explained below).

Table 2 IR frequencies for the nitrile (C≡N) stretch of the coordination compounds 4·AgX (ligand 4 has a frequency of 2220 cm⁻¹)

Anion (X)	BF4^−	ClO4^−	PF6^−	SbF6^−	CF3SO3^−	NO3^−
a From ref. 33. b A vibrational frequency of 2205 cm^−1 has been reported for this compound,^33 which was a shift of +10 from the ligand frequency of 2195 cm^−1; on the instrument used for this paper, the ligand frequency is 2220 cm^−1, so the frequency in this table has been entered as 2220 + 10 = 2230 cm^−1. c The same shift was observed for crystals of this compound grown in o-, m-, and p-xylene.
Solvent
benzene	insol.	2250	SM ^a	insol.	2230^ab	SM ^a
toluene	2230	2231	SM ^a	SM ^a	SM ^a	SM ^a
CH3CN	---	SM	SM ^a	SM ^a	SM ^a	SM ^a
CH2Cl2	---	decomp.	SM	SM	SM	SM
DMSO	---	decomp.	---	decomp.	decomp.	decomp.
CH3NO2	---	decomp.	---	decomp.	decomp.	decomp.
C6H5NO2	2229	2230^c	---	2233	high sol.	decomp.

---

For both ligands, the IR stretching frequency increases upon coordination. The lone pair on the nitrile group is in a weakly σ* (antibonding) orbital, so donation from this orbital to the metal centre should cause such an increase. Since a metal-to-ligand charge transfer back-bond would populate a π* orbital causing a decrease in stretching frequency, the opposite of our observation, it would seem to be of little importance. This is confirmed by DFT calculations (see below).

We have solved the crystal structures of several combinations of ligand, solvent, and counterion. The crystallographic data is summarised in Table 3, and discussed in detail immediately below.

Table 3 Crystallographic and refinement data

Compound	4	3·AgClO4 (C6H6 solvate)	3·AgBF4 (0.5 C7H8 solvate)	4 2·AgClO4	4 2·AgBF4
Chemical formula	C10H4N2S2	C20H14AgClN2O4	C17.5H12AgBF4N2	C20H8AgClN4O4S4	C20H8AgBF4N4S4
Mr/g mol^−1	216.27	489.65	445.00	639.86	627.22
Crystal system	P1̄	P21/c	P21/c	P4/n	P4/n
Space group	Triclinic	Monoclinic	Monoclinic	Tetragonal	Tetragonal
μ(Mo Kα)/mm^−1	0.531	1.226	1.275	1.358	1.285
a/D	3.8090(2)	7.4242(6)	8.8779(14)	13.834(5)	13.6376(19)
b/D	7.4518(4)	19.9968(17)	14.465(2)	13.834(5)	13.6376(19)
c/D	8.2086(5)	12.8576(10)	13.422(2)	6.162(4)	6.2054(17)
α/°	87.9360(10)	90	90	90	90
β/°	85.4850(10)	92.527(2)	108.114(3)	90	90
γ/°	82.1260(10)	90	90	90	90
V/D^3	230.00(2)	1907.0(3)	1638.1(4)	1179(1)	1154.1(4)
Z	1	4	4	2	2
D c/g cm^−1	1.561	1.705	1.821	1.802	1.805
T/K	173(2)	296(2)	200(2)	296(2)	200(2)
F(000)	110	976	892	632	616
θ range/°	3.67 to 26.46	2.93 to 29.99	2.79 to 30.56	3.62 to 29.99	3.28 to 27.99
R, wR [I > 2σ(I)]	0.0236, 0.0604	0.0422, 0.0894	0.0384, 0.0950	0.0299, 0.0715	0.0400, 0.0866
R, wR (all data) Reflections	2744	18166	18925	10613	10648
collected	947	5548	5016	1699	1398
unique	889	4476	4475	1480	1233
observed

---

Crystal structures of silver(I) complexes containing the ligand 3

The majority of silver(I) salts reacted completely to give a coordination compound with 3, but in many cases the resultant material was microcrystalline at best. Crystals large enough for single-crystal X-ray analysis were formed when the anions ClO₄⁻ and BF₄⁻ were used. These are both on the low end of donor strength, and they both have high symmetry and similar sizes. The structure of 3·AgClO₄ (benzene solvate) is shown in Fig. 1 and that of 3·AgBF₄ (modeled with one half a toluene molecule per formula unit) in Fig. 2 (top). The most obvious difference is that the ClO₄⁻ anion is coordinating in its structure,^34,35 while the BF₄⁻ anion is not. Otherwise, the gross features of the two structures are similar.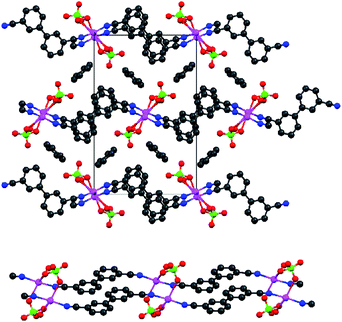

Fig. 1 Two views of the structure of 3·ClO₄ (benzene solvate). Top: The full structure viewed down the crystallographic a axis. Bottom: The paired one-dimensional coordination polymer, bridged by ClO₄⁻ anions. Colour scheme: grey = C, blue = N, pink = Ag, red = O, green = Cl.

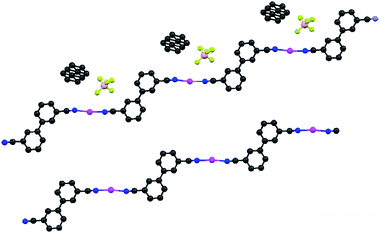Fig. 2 Comparison of the structures of 3·AgBF₄ and 3·AgClO₄, emphasising the stepped structure of the coordination polymer. Top: Full structure of 3·AgBF₄ (0.5 toluene solvate); the toluene is disordered. Bottom: One strand of 3·ClO₄ with solvate and anion removed. Colour scheme is the same as in Fig. 1 (peach = B, yellow–green = F).

The ligand 3 is in the anti (or transoid) conformation, leading to a stepped 1D coordination polymer. Fig. 2 is drawn to emphasize this feature. Adjacent polymers are not intertwined, which can occur, e.g., with the off-axis rod-like nitrile 3,3′-dicyanodiphenylacetylene.³⁶ Both complexes of 3 contain disordered molecules of solvent. The N–Ag–N bond angles are not quite linear (172.8° for the BF₄⁻ species and 170.3° for the ClO₄⁻ species). The silver(I) centre in 3·AgClO₄ is roughly square planar, which allows the near linear coordination to 3 (the remaining two vertices of the square are used by the two bridging ClO₄⁻ anions). The two phenyl rings in the biphenyl bridge are nearly coplanar in 3·AgClO₄ (<2° torsion angle), but considerably more twisted in 3·AgBF₄ (just under 30°). Presumably the angles are due to packing effects. In the only other crystal structure containing 3 of which we are aware, a cocrystal containing 3 and tetramethylimidazolium, the rings are essentially coplanar.²⁰ This cocrystal contains isolated nitriles (not coordinated nor H-bonded) with a C–N bond distance of 1.172 Å. The coordinated C–N distance in 3 is 1.140 Å for the ClO₄⁻salt. The BF₄⁻salt has two crystallographically inequivalent nitriles with bond lengths 1.140 and 1.133 Å. The shortened distances are consistent with the increase in the IR stretching frequency noted above.

Although Ag⁺–Ag⁺ contacts are weak (certainly weaker than for aurophilic bonds^37–39), they can exert a structural effect in the solid state.^36,40–42 In our case, however, argentophilic interactions cannot be invoked; the closest Ag⁺–Ag⁺ contact in 3·ClO₄ is 3.42 Å, which is the same as the sum of the van der Waals radii.⁴³ The closest separation in 3·BF₄ is slightly longer at 3.51 Å. The benzene rings of the ligand are packed in a slipped π-stack in 3·ClO₄. In the BF₄⁻salt, the benzene rings of the ligands are slipped more, so that each π-systems is over the CN–Ag–NC portion of the molecule below it.

Crystal structure of the ligand 4

As shown in Table 2, not all combinations of 4 and silver salts give a coordination compound. When no reaction occurs, in many cases, uncoordinated ligand is isolated as crystalline needles from the reaction mixture. This lack of reactivity can be explained by the competition between formation of nitrile-silver(I) bonds and interligand hydrogen bonds—the strength of this 2-bond interligand interaction is apparently of very similar magnitude to that of a 1-bond CN–Ag⁺ interaction. After collection of many data sets, a suitable crystal structure was determined for the uncoordinated ligand 4 (crystals grown by slow cooling of a toluene solution). Each molecule of 4 is planar with the rings mutually anti to each other (the torsion angle between the rings is exactly 180° as the molecule lies on an inversion centre).

As shown in Fig. 3, the structure contains pairwise hydrogen bonds. The two H-bonds are crystallographically equivalent, with a distance of 2.593 Å and a C–N⋯H bond angle of 127.28°. This pairwise H-bond is geometrically similar to those found in the higher-order oligothiophenes (C₄H₂S)_n(CN)₂ (n = 3–5)⁴⁴ and in p-dicyanobenzene.⁴⁵ The H-bond in 3 is shorter and presumably stronger than the average H-bond in these species (e.g., the CN⋯H distances are 2.688 and 2.711 Å in (C₄H₂S)₄(CN)₂ and 1,4-C₆H₄(CN)₂, respectively); however, it is not the shortest ever observed for oligothiophene nitriles ((C₄H₂S)₃(CN)₂ has six crystallographically independent H-bonds, the shortest of which is 2.420 Å, although the average of these six bonds is longer than the H-bond in 3 at 2.64 Å).

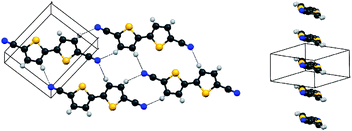Fig. 3 Structure of 4. Left: Viewed to illustrate the intermolecular hydrogen-bond network. Right: Viewed to show π-stacks. Colours as in Fig. 1 (yellow = S).

Nitrile-substituted oligomers have been considered as potential n-type semiconducting materials for use in transistor devices.^46,47 In this context, the structure of 4 is interesting as the molecules pack in a slipped π-stack, considered the preferred packing motif for maximum mobility.^48–50 Unfortunately, the intrinsic conductivity of bithiophenes is normally too low for devices, and the closest S⋯S contacts in 4 are over 3.8 Å, well outside the van der Waals contact distance of 3.6 Å.

Crystal structures of silver(I) complexes containing the ligand 4

In spite of the fact that the ligand : cation stoichiometry in the reaction tube was 1 : 1, the coordination compounds formed by 4 with AgBF₄ and AgClO₄ have 2 : 1 ligand : cation ratios. The two compounds 4₂·AgBF₄ and 4₂·AgClO₄ are isomorphous, crystallising in the tetragonal space groupP4/n, shown in Fig. 4 (viewed down the crystallographic c axis). The structure is a “squashed” diamondoid structure with disordered anions encased in the pores created by the cation-ligand network (only one network is present, there is no interpenetration). The distance between consecutive silver(I) cations is the same as that between consecutive central atoms of the anion (6.205 Å for B, 6.162 Å for Cl), which is also the length of the c axis. Presumably the lattice is compressed to optimally accommodate the anion. The C≡N bond distance does not change (within experimental error) upon coordination with the metal (although, as mentioned above, the IR stretch suggests the bond strengthens slightly). There is only one crystallographically independent thiophene ring, nitrile, silver cation, and anion due to the 4/n symmetry. Similarly, the two rings of 4 are exactly anti (torsion angle of 180°).

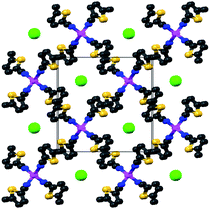Fig. 4 Structure of 4₂·AgX (X⁻ = ClO₄⁻ or BF₄⁻) viewed down the crystallographic c axis. The counterions are represented as the large green spheres. Other colours are as in Fig. 1 (yellow = sulfur).

Neither anion is coordinating, nor is there any solvent encapsulated in the lattice. There are no Ag⁺–S contacts with the thiophene sulfurs, nor are there any argentophilic bonds. This structure is remarkably reproducible from a number of different solvents. Crystals of 4₂·AgClO₄ grown in nitrobenzene, and in o-, m- and p-xylene, all formed this structure (crystallographic diffraction data were collected on crystals grown from each solvent, but were not fully refined once it became clear the crystals were identical). Attempts to generate a similar 2 : 1 complex with ligand 3, by using a 2 : 1 stoichiometric ratio in the reaction vessel, failed. The only crystalline material recovered were 1 : 1 complexes that were, by IR and combustion analysis, the same complexes generated in the 1 : 1 reactions.

Discussion

Nitrile–silver(I) interactions are not particularly strong (weaker than the phosphine equivalent, for example), and bithiophene-bridged ligands are weaker donors than biphenyl- or bipyridyl-bridged dinitriles. This is illustrated in Tables 1 and 2 - coordination compounds of 3 had significantly larger shifts in the IR stretching frequency than did compounds of 4, indicating a stronger σ-donation. Similarly, 3 gave a reaction with all the tested silver(I) salts in all solvents except acetonitrile (where the nitrile on the solvent competes with the ligand). In contrast, only a few combinations of salt and solvent gave a coordination compound with 4. In cases where no reaction took place, the ligand itself crystallised, meaning the combined total of the interligand hydrogen bonds are very close in energy to the combined total of nitrile–silver(I) bonds. Phenyl nitriles have the same type of interligand hydrogen bonds in the solid state,^45,51 but they do not appear to compete successfully with the nitrile–silver(I) interactions. The “partial” reactions of ligand 3 (see Table 1) may indicate some weakness in the phenylnitrile–silver(I) bond, but could also result from non-optimised stoichiometries (presumably there is excess ligand once the preferred silver(I) coordination compound is formed). We are working on optimising crystal-growth conditions for these combinations to see if this is the case.

Density functional theory (DFT) calculations were performed on benzonitrile- and cyanothienyl-ligated silver(I) molecules to understand the bonding in these complexes. Organonitrile–silver(I) complexes have been the subject of a previous computational analysis⁵² and we have employed the same computational approach with identical results for the simplest benzonitrile-silver(I) complexes. The results for the model compounds (PhCN)₂Ag⁺ and (TCN)₂Ag⁺ (Ph = phenyl and T = thienyl) are given in Table 4. Fig. 5 shows the localised orbitals and their electron populations, obtained using the NBO method,⁵³ in the silver(I)-nitrile complexes along with change in population from the isolated species. An analysis of the orbitals and interaction energies verifies that the nitrile–silver(I) bond is predominantly a donation from the nitrile lone pair into the s and p_z orbitals on the silver(I), with practically no backbonding to the nitrile π* orbital. The orbital “CN lp” (Fig. 5, top) has a node between the C and the N of the nitrile (i.e. is antibonding) and loses 0.10 e⁻ upon complexation. The computed nitrile stretching frequencies (Table 4) reflect this decrease in orbital population. The frequency is calculated to increase upon coordination to Ag⁺. For (PhCN)₂Ag⁺ it increases 20 cm⁻¹ relative to PhCN, and 16 cm⁻¹ for (TCN)₂Ag⁺ over TCN. This matches the experimental trend that the increase in IR frequency is larger for coordination compounds of 3 than for compounds of 4.

Table 4 Selected properties of L₂Ag⁺ gas-phase complexes obtained at the B3LYP/dzvp model chemistry

	L = PhCN	L = TCN
a The change in value from the uncomplexed ligand in parenthesis. b Ag^+ + 2L 6 L2Ag^+ complexation reaction in the gas phase at 298 K. c See Fig. 5 for graphical representation of localized interacting orbitals.
r CN/Å	1.162 (−0.004)^a	1.164 (−0.003)^a
r n –Ag^+/Å	2.163	2.162
ν CN/cm^−1	2342 (+20)^a	2329 (+16)^a
q Ag^+ /e^−	0.822	0.824
ΔGcomplex/kcal mol^−1^b	−68.74	−67.59
NBO Orbital Interaction energies kcal^−1 mol^−1^c
CN lp → Ag^+ 5s	29.88	29.71
CN lp → Ag^+ pz	9.18	9.17
Ag^+ dxz → CN π2*	1.74	1.70
Ag^+ dyz → CN π1*	1.88	1.93

---

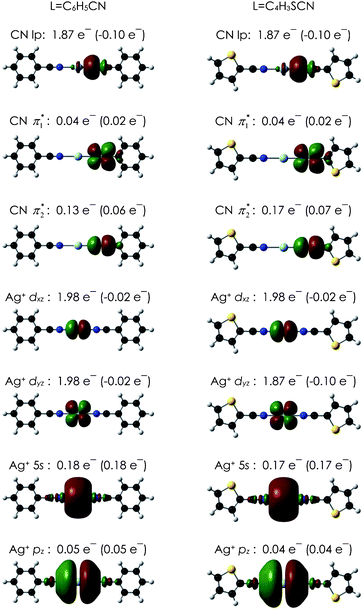Fig. 5 Graphical representation of the localized natural bond orbitals in L₂Ag⁺ obtained at the B3LYP/dzvp model chemistry corresponding to the interactions given in Table 4 along with the occupancy and change in occupancy, in parentheses, upon complexation.

The relative weakness of 4 as a ligand is also illustrated in the coordination compounds that have been crystallographically characterised. In 3·AgBF₄ only two nitrile-Ag⁺ contacts are needed to satisfy the Ag⁺ centre, and there are no solvent or anion coordinations. In 4₂·AgBF₄, on the other hand, the Ag⁺ requires four nitriles to satisfy its coordination sphere, even though the stoichiometry of the reaction from which the crystals were grown was not 2 : 1.

There is no compelling energetic reason why 3 should not also form a 4-coordinate (2 : 1) compound. DFT calculations (Table 5) suggest that there is little difference in energy between two-coordinate coordination compounds based on the nature of the aromatic ring. Certainly, (TCN)₂Ag⁺ has a slightly lower formation energy but the difference is small. Similarly, although the stabilisation per nitrile is less for a four-coordinate species, the overall formation energy for (TCN)₄Ag⁺ and (PhCN)₄Ag⁺ are very similar.

Table 5 Gas-phase (B3LYP/dzvp, 298 K) free energies (in kcal mol⁻¹) for the sequential complexation reactions: AgL_(n−1)⁺ + L → AgL_n⁺

n	L = PhCN	L = TCN
1	−38.94	−37.72
2	−29.80	−29.87
3	−4.37	−3.05
4	−8.80	−10.23

---

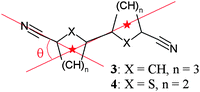
Thus, we conclude the four-coordinate equivalents using ligand 3 are not formed for steric reasons. Crowding at the metal centre is not the problem, as four phenyl nitriles can fit around silver(I), which is demonstrated for the complex 1₂·AgPF₆.¹⁵ There is so much room in that structure, in fact, that it has several interpenetrating adamantoid networks. Similarly, compounds of 4 can fit four aromatic nitriles around the Ag⁺, although now there is only enough room for one independent network. There is enough space in the lattice to incorporate the (non-coordinating) counterion in the channels formed by the distorted-diamondoid network. Thus, the space in the lattice has decreased, as a consequence of the collapsing of the off-axis angle (the angle of intersection between the centroid–centroid axis and the nitrile C≡N axis, Scheme 2). On changing from ligand 1 to ligand 4, the angle changes from 0 to 33°, pinching off the potential for open space in the structure. In 3 the angle is even sharper at 60°, and presumably this wouldn't even allow space for counterions in a tetragonal structure with a 4-coordinate Ag⁺ centre.

Scheme 2

Experimental details

All silver(I) salts, copper(I) cyanide, 2-bromothiophene, and m-bromobenzonitrile were purchased from Sigma-Aldrich and used as received. Dichloromethane, benzene, and acetonitrile were purchased from Caledon and purified by passage through an alumina column under nitrogen. Toluene was purchased from EMD Chemicals and purified in the same manner. Dimethylsulfoxide (DMSO, Caledon), nitrobenzene (Fisher), nitromethane (Caledon), and quinoline (Aldrich) were distilled followed by drying over Linde 4Å molecular sieves (Aldrich). Dimethylformamide (DMF, Caledon) was dried over sieves without distillation. Triphenylphosphine, nickel(II) chloride, and zinc powder were purchased from Aldrich and dried in a vacuum desiccator over P₂O₅ (Aldrich) for 16 h. N-Bromosuccinimide (NBS) (Aldrich) was recrystallised from water. Bithiophene was synthesised by a Kumada coupling^54,55 with 2-bromothiophene. Bromination using NBS in DMF (to create 5,5′-dibromobithiophene) followed the literature method.²⁴

Nuclear magnetic resonance (NMR) spectra were recorded on a Varian Unity Inova 500 at room temperature; chemical shifts are reported in ppm referenced to TMS added to the solvent. Infrared absorption spectra were recorded as nujol mulls on a Nicolet 380 FT-IR spectrometer; vibrational frequencies are reported as wavenumbers (cm⁻¹), with an experimental resolution of 1 cm⁻¹. Combustion analyses were performed on a CEC (SCP) 240-XA Analyzer. Gradient vacuum sublimations and crystal growth for X-ray crystallography were performed on an Applied Test Systems model 3210 split tube furnace attached to a series 2404 3-zone temperature control system. Melting points were recorded on an Electrothermal 9100 apparatus and are uncorrected.

Synthesis of biphenyl-3,3′-dicarbonitrile (3)

An alternate synthesis to the known compound^20,56 is given. The catalyst Ni(PPh₃)₄ was generated as previously described²³ by heating a mixture of triphenylphosphine (1.25 g, 4.8 mmol), nickel(II) chloride (0.078, 0.6 mmol), and zinc powder (1.25 g, 19 mmol) in 20 mL DMF to 50 °C under an atmosphere of N₂ (Schlenk line) until the mixture turned the characteristic deep red colour of Ni(0). m-Bromobenzonitrile (2.00 g, 11 mmol) was added and the mixture stirred at 50 °C for 4 h. The resultant solution was filtered and 50 mL of chloroform was added to the filtrate. Washing with 1 M HCl and rotary evaporation yielded crude 3, which was twice purified by gradient vacuum sublimation in a tube furnace (120–80 °C) to yield 0.96 g (4.6 mmol, 85%) of pure 3. Mp 189–191 °C. ¹H NMR (CDCl₃), δ = 7.85 (m, 1H), 7.80 (d of m, ³J = 8.0 Hz, 1H), 7.72 (d of m, ³J = 8.0 Hz, 1H), 7.62 (dd, ³J = 8.0 Hz, 1H). IR 3067 (w), 2229 (s), 789 (s), 687 (s).

Synthesis of 2,2′-bithiophene-5,5′-dicarbonitrile (4)

An alternate synthesis is given to the previously published route.²¹Copper(I) cyanide (6.8 g, 76 mmol) and 5,5′-dibromobithiophene (9.0 g, 28 mmol) were refluxed in 50 mL of quinoline for 3 h. After adding 100 mL of 1 M HCl and filtering, the crude 4 was recrystallised from chlorobenzene and purified by gradient vacuum sublimation in a tube furnace (150–90 °C) to yield 1.5 g (6.9 mmol, 25%) of pure 4. Mp 252–254 °C. ¹H NMR (CDCl₃), δ = 7.59 (d, ³J = 4.5 Hz, 2H), 7.26 (d, 2H). IR 3093 (w), 3074 (w), 2220 (s), 1295 (w), 1215 (w), 1158 (w), 1059 (w), 884 (w), 812 (m), 721 (s). Crystals suitable for X-ray analysis were grown from toluene.

General procedure for reaction of 3 with AgX

Ligand 3 (20 mg, 0.098 mmol) and an equimolar amount of AgBF₄ (19 mg), AgClO₄ (20 mg), AgPF₆ (25 mg), AgSbF₆ (33 mg), AgCF₃SO₃ (25 mg), or AgNO₃ (17 mg) were added to a flame-dried Pyrex reaction tube (home-made, approximately 20 mm diameter by 10 cm long). A dried solvent (benzene, toluene, or acetonitrile) was added (20 mL) and the tube subjected to one freeze-pump-thaw cycle before being sealed under vacuum. The tube was heated to 100 °C until 3 and the silver(I) salt had dissolved. The tube was then cooled to room temperature in a tube furnace, at a rate of 1° h⁻¹. Crystals were harvested in the air, but were left in the mother liquor until transferred to oil (for crystallography) or dried under N₂ (for IR or CHN analysis).

Characterisation of 3·AgClO₄CC₆H₆. IR 3077 (w), 2258 (s), 1575 (w), 1175 (w), 1063 (s, br), 928 (m), 885 (m), 788 (s), 697 (s), 621 (s). Anal. calcd. for C₂₀H₁₄AgClN₂O₄: C, 49.1; H, 2.9; N, 5.7. Found: C, 48.0; H, 2.9; N, 5.2%.

Characterisation of 3·AgBF₄C(C₇H₈)_0.5. IR 3079 (w), 2272 (s), 1177 (m), 1059 (s), 800 (m), 755 (m), 687 (m). Anal. calcd. for C_17.5H₁₂AgBF₄N₂: C, 47.2; H, 2.7; N, 6.3. Found: C, 46.7, H, 2.7; N, 5.9%.

General procedure for reaction of 4 with AgX

Ligand 4 (20 mg, 0.093 mmol) and an equimolar amount of AgBF₄ (18 mg), AgClO₄ (19 mg), AgPF₆ (24 mg), AgSbF₆ (32 mg), AgCF₃SO₃ (24 mg), or AgNO₃ (16 mg) were added to a flame-dried reaction tube. Dried solvent (20 mL) was added and the tube subjected to one freeze-pump-thaw cycle before being sealed under vacuum. The tube was heated to 100 °C until 4 and the silver(I) salt had dissolved. The tube was then cooled to room temperature in a tube furnace, at a rate of 1 °C h⁻¹. Crystals were harvested in the air, but were left in the mother liquor until transferred to oil (for crystallography) or dried under N₂ (for IR or CHN analysis).

Characterisation of 4₂·AgClO₄. Data for crystals grown from p-xylene are reported. Crystals grown from o-xylene, m-xylene, and nitrobenzene had identical crystal structures and similar IR and combustion data. IR 3092 (w), 3074 (w), 2231 (s), 1297 (m), 1211 (w), 1099 (s), 887 (w), 811 (s), 721 (w). Anal. calcd. for C₂₀H₈AgClN₄O₄S₄: C, 37.5; H, 1.3; N, 8.8. Found C, 37.1, H, 1.5; N, 8.6%.

Characterisation of 4₂·AgBF₄. Crystals grown from nitrobenzene. IR 3094 (w), 2229 (s), 1426 (s), 1298 (m), 1211 (w), 1102 (m), 1069 (s), 1059 (s), 888 (w), 811 (m). Anal. calcd. for C₂₀H₈AgBF₄N₄S₄: C, 38.3; H, 1.2; N, 8.9. Found C, 37.6, H, 1.5; N, 8.9%.

Computational methods

Molecular orbital calculations were performed using Gaussian 03.⁵⁷ All structures were optimised by DFT using the B3LYP hybrid method^58–60 and the DZVP basis set.⁶¹ Critical points were characterised by harmonic frequency calculations and shown to be minima. Corrections for basis set superposition errors (BSSE) were not performed, as it has been previously shown for Ag⁺-nitrile calculations that these errors are consistent and small.⁵² The NBO program⁵³ was used to transform the molecular orbitals into localized terms corresponding to one-centre (lone pair) and two centre (bond) descriptions. This localized description was then used to assess the interaction energies of the fragments in the complex.

X-Ray crystallography

Single-crystal data were collected using the Smart Apex CCD (Bruker) equipped with an area detector utilizing graphite-monochromated Mo Kα radiation (λ = 0.71073 Å). For 3·AgClO₄CC₆H₆ and 4₂·AgBF₄, four sets of 600 frames at different ϕ angles, 0, 90, 180 and 270° were measured with exposure times of 30 second per frame and omega scan of 0.3°. For 4₂·AgClO₄, three sets of 600 frames at different ϕ angles, 0, 90, and 180° were measured with exposure times of 20 second per frame and omega scan of 0.36°. The data were corrected for Lorentz and polarization effects. Absorption corrections were based on fitting a function to the empirical transmission surface as sampled by multiple equivalent measurements of numerous reflections using the scale function of the APEX II software.

The space groups for all compounds were determined on the basis of the systematic absences using symmetry and space group of the APEX II package. Structure solution and refinement using the SHELXTL package of APEX II were successful in the chosen centrosymmetric space groups. The structure solution via direct method led to the identification of the heavy atoms and the refinement on F² using least-square method resulted in good R values. Full details of the structures have been deposited with the Cambridge Crystallographic Data Centre as CDCC 692771–692775. This information may be obtained free of charge viahttp://www.ccdc.cam.ac.uk/data_request/cif.

Full data sets were collected for 4₂·AgClO₄ on crystals grown from o-, m-, and p-xylene, and from nitrobenzene. The unit cells for all four crystals were identical; the data set from p-xylene was chosen for a full refinement. This structure has a disordered ClO₄⁻ (O4 partially occupies two sites O4A and O4B); six restraints are used in the refinement, i.e., O4A and O4B have the same temperature factors Uij (U11, U22, U33, U12, U13, U23). Similarly for 4₂·AgBF₄, the fluorine atom F4 is disordered and F4A and F4B have the same temperature factors Uij (U11, U22, U33, U12, U13, U23).

Conclusions

Although the two ligands 3 and 4 are putatively the same geometry, viz. off-axis rod-like, they give very different crystal structures when bound to silver(I). A combination of electronic and steric factors limits the ligand 3 to a two-coordinate compound with silver(I), while ligand 4 is limited to tetra-coordination. There is a small difference in the binding energy of the two ligands, 4 being weaker, so a four-coordinate species is required. Otherwise, the stronger interligand hydrogen bond will cause precipitation of the ligand by itself. For ligand 3, the energetics of the bond are such that coordination compounds are always favoured over ligand precipitation. A four-coordinate species is not favourable due to the sharp off-axis angle that does not leave room for the counterions in the tetragonal/tetrahedral structure. Thus, only a 2-coordinate Ag⁺ is formed with ligand 3, giving 1-dimensional coordination polymers. On the other hand, 4 only creates an extended 3-D structure with non-coordinating anions/solvents. The latter structure is remarkably consistent, forming from a number of solvents and with both anions tested here. DFT calculations verify the IR spectroscopic observation that the nitrile–silver(I) bond is primarily a σ-symmetry lone-pair donation from the nitrile to the cation with no significant π-backbonding from the silver(I) to the nitrile.

Acknowledgements

Funding was provided by the Research Corporation's Cottrell College Science Award program and by Lakehead University. Thanks are due to Mr Ian S. Morgan for assistance with a Cambridge Crystallographic Database search.

References

1. B. Moulton and M. J. Zaworotko, Chem. Rev., 2001, 101, 1629.
2. B.-L. Chen, K.-F. Mok and S.-C. Ng, J. Chem. Soc., Dalton Trans., 1998, 4035.
3. C. W. Liu, B.-J. Liaw, L.-S. Liou and J.-C. Wang, Chem. Commun., 2005, 1983.
4. E. Fournier, F. Lebrun, M. Drouin, A. Decken and P. D. Harvey, Inorg. Chem., 2004, 43, 3127.
5. C.-M. Che, M.-C. Tse, M. C. W. Chan, K.-K. Cheung, D. L. Phillips and K. H. Leung, J. Am. Chem. Soc., 2000, 122, 2464.
6. A. P. Côté and G. K. H. Shimizu, Inorg. Chem., 2004, 43, 6663.
7. D. J. Hoffart, S. A. Dalrymple and G. K. H. Shimizu, Inorg. Chem., 2005, 44, 8868.
8. H.-Y. Liu, H. Wu, J.-F. Ma, S.-Y. Song, J. Yang, Y.-Y. Liu and Z.-M. Su, Inorg. Chem., 2007, 46, 7299.
9. C.-L. Chen, B.-S. Kang and C.-Y. Su, Aust. J. Chem., 2006, 59, 3.
10. A. N. Khlobystov, A. J. Blake, N. R. Champness, D. A. Lemonovskii, A. G. Majouga, N. V. Zyk and M. Schröder, Coord. Chem. Rev., 2001, 222, 155.
11. L. Carlucci, G. Ciani, D. M. Proserpio and S. Rizzato, CrystEngComm, 2002, 4, 413.
12. J. Bourlier, M. W. Hosseini, J.-M. Planeix and N. Kyritsakas, New J. Chem., 2007, 31, 25.
13. Z. Xu, S. Lee, Y.-H. Kiang, A. B. Mallik, N. Tsomaia and K. T. Mueller, Adv. Mater., 2001, 13, 637.
14. G. B. Gardner, D. Venkataraman, J. S. Moore and S. Lee, Nature, 1995, 374, 792.
15. K. A. Hirsch, D. Venkataraman, S. R. Wilson, J. S. Moore and S. Lee, J. Chem. Soc., Chem. Commun., 1995, 2199.
16. H.-P. Wu, C. Janiak, G. Rheinwald and H. Lang, J. Chem. Soc., Dalton Trans., 1999, 183.
17. M. G. B. Drew, C. J. Harding, O. W. Howarth, Q. Lu, D. J. Marss, G. G. Morgan, V. McKee and J. Nelson, J. Chem. Soc., Dalton Trans., 1996, 3021.
18. Y.-B. Dong, Y. Geng, J.-F. Ma and R.-Q. Huang, Organometallics, 2006, 25, 447.
19. L. Zhao and T. C. W. Mak, Organometallics, 2007, 26, 4439.
20. K. Ono, T. Iwao, H. Uchiumi, T. Suzuki, M. Tomura, M. Ohkita and K. Saito, Bull. Chem. Soc. Jpn., 2005, 78, 867.
21. G. F. Pedulli, M. Tiecco, M. Guerra, G. Martelli and P. Zanirato, J. Chem. Soc., Perkin Trans., 1978, 2, 212.
22. A. W. Cordes, R. C. Haddon, C. D. MacKinnon, R. T. Oakley, G. W. Patenaude, R. W. Reed, T. Rietveld and K. E. Vajda, Inorg. Chem., 1996, 35, 7626.
23. I. Colon and D. R. Kelsey, J. Org. Chem., 1986, 51, 2627.
24. P. Bäuerle, F. Würthner, G. Götz and F. Effenberger, Synthesis, 1993, 1099.
25. C. Paulmier, J. Morel, P. Pastour and D. Semard, Bull. Soc. Chim. Fr., 1969, 2511.
26. L. Carlucci, G. Ciani, P. Macchi, D. M. Proserpio and S. Rizzato, Chem.–Eur. J., 1999, 5, 237.
27. L. Carlucci, G. Ciani, D. M. Proserpio and S. Rizzato, Chem.–Eur. J., 2002, 8, 1520.
28. A. Westcott, N. Whitford and M. J. Hardie, Inorg. Chem., 2004, 43, 3663.
29. M. N. Kozlova, S. Ferlay, S. E. Solovieva, I. S. Antipin, A. I. Konovalov, N. Kyritsakas and M. W. Hosseini, Dalton Trans., 2007, 5126.
30. E. D. Genuis, J. A. Kelly, M. Patel, R. McDonald, M. J. Ferguson and G. Greidanus-Strom, Inorg. Chem., 2008, 47, 6184.
31. O.-S. Jung, Y. J. Kim, Y.-A. Lee, K.-M. Park and S. S. Lee, Inorg. Chem., 2003, 42, 844.
32. X.-D. Chen and T. C. W. Mak, Chem. Commun., 2005, 3529.
33. W. A. Sears, M. L. Hudolin, H. A. Jenkins, R. C. Mawhinney and C. D. MacKinnon, J. Coord. Chem., 2008, 61, 825.
34. Y.-B. Dong, Y. Geng, J.-P. Ma and R.-Q. Huang, Inorg. Chem., 2005, 44, 1693.
35. J.-R. Li, X.-H. Bu, J. Jiao, W.-P. Du, X.-H. Xu and R.-H. Zhang, Dalton Trans., 2005, 464.
36. K. A. Hirsch, S. R. Wilson and J. S. Moore, Inorg. Chem., 1997, 36, 2960.
37. A. Codina, E. J. Fernández, P. G. Jones, A. Laguna, J. M. López-de-Luzuriaga, M. Monge, M. E. Olmos, J. Pérez and M. A. Rodríguez, J. Am. Chem. Soc., 2002, 124, 6781.
38. M. Bardaji and A. Laguna, J. Chem. Educ., 1999, 76, 201.
39. S.-L. Zheng, C. L. Nygren, M. Messerschmidt and P. Coppens, Chem. Commun., 2006, 3711.
40. I. Kalf, M. Braun, Y. Wang and U. Englert, CrystEngComm, 2006, 8, 916.
41. B.-F. Fei, W.-Y. Sun, T. Okamura, W.-X. Tang and N. Ueyama, New J. Chem., 2001, 25, 210.
42. S.-L. Zheng, A. Volkov, C. L. Nygren and P. Coppens, Chem.–Eur. J., 2007, 13, 8583.
43. A. Bondi, J. Phys. Chem., 1964, 68, 441.
44. T. M. Barclay, A. W. Cordes, C. D. MacKinnon, R. T. Oakley and R. W. Reed, Chem. Mater., 1997, 9, 981.
45. U. Drück and W. Littke, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 3095.
46. A. Yassar, F. Demanze, A. Jaafari, M. El Idrissi and C. Coupry, Adv. Funct. Mater., 2002, 12, 699.
47. M.-Y. Kuo, H.-Y. Chen and I. Chao, Chem.–Eur. J., 2007, 13, 4750.
48. X. Gao, W. Wu, Y. Liu, W. Qiu, X. Sun, G. Yu and D. Zhu, Chem. Commun., 2006, 2750.
49. P. Gao, D. Beckmann, H. N. Tsao, X. Feng, V. Enkelmann, W. Pisula and K. Müllen, Chem. Commun., 2008, 1548.
50. S. Ando, J. Nishida, H. Tada, Y. Inoue, S. Tokito and Y. Yamashita, J. Am. Chem. Soc., 2005, 127, 5336.
51. H. Guth, G. Heger and U. Drück, Z. Kristallogr., 1982, 159, 185.
52. T. Shoeib, H. El Aribi, K. W. M. Siu and A. C. Hopkinson, J. Phys. Chem. A, 2001, 105, 710.
53. NBO, Version 5.0, E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, and F. Weinhold, Theoretical Chemistry Institute, University of Wisconson, Madison WI, 2001.
54. K. Tamao, K. Sumitani, Y. Kisio, M. Zembayashi, A. Fujioka, S. Kodama, I. Nakajima, A. Minato and M. Kumada, Bull. Chem. Soc. Jpn., 1976, 49, 1958.
55. K. Tamao, S. Kodama, I. Nakajima and M. Kumada, Tetrahedron, 1982, 38, 3347.
56. H. Kageyama, O. Furusawa and Y. Kimura, Chem. Express, 1991, 6, 229.
57. Gaussian 03, Revision E.01, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. V. Jr., K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople, Gaussian Inc., Wallingford CT, 2004.
58. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
59. A. D. Becke, Phys. Rev., 1988, A38, 3098.
60. C. Lee, W. Yang and R. G. Parr, Phys. Rev., 1988, B37, 785.
61. N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, Can. J. Chem., 1992, 70, 560.

---

Footnote

† CCDC reference numbers 692771–692775. For crystallographic data in CIF or other electronic format see DOI: 10.1039/b810479d

---