Crumpled surface structures
Douglas P.
Holmes
,
Michal
Ursiny
and
Alfred J.
Crosby
*
Polymer Science & Engineering, University of Massachusetts, 120 Governors Dr., Amherst, MA, USA. E-mail: crosby@mail.pse.umass.edu; Fax: +1 413-545-0082; Tel: +1 413-577-1313
First published on 5th November 2007
Abstract
We present a scalable patterning method based on surface plate buckling, or crumpling, to generate a variety of topographies that can dynamically change shape and aspect ratio in response to stimuli.
The topographic control of pattern features is of great interest for a range of applications including the generation of ultrahydrophobic surfaces,1 microfluidic devices,2,3 and the control and tuning of adhesion.4,5 In these areas, surface patterning is achieved by a variety of techniques including: photolithography,6 imprint lithography,7,8ion beam patterning,9 surface wrinkling,10–13 and stereo lithography.14 We present an alternative, simple patterning technique to generate various surface topographies using classical plate buckling, or confined crumpling. Specifically, the buckling of circular plates leads to the preparation of microstructures with rotational symmetry (spherical microlenses), tri-fold symmetry, and quad-fold symmetry (Fig. 1) with predictable aspect ratios. The geometry of the structures depends on the plates' material properties and geometry, and the applied force during preparation. This approach leads to patterns that are difficult, if not impossible, to achieve with other methods. Additionally, these patterns demonstrate dynamic, or responsive behavior.
 | ||
| Fig. 1 (a) A schematic illustrating an array of individual circular plates and plate buckling from applied compressive strain. (b) The microstructure morphology as the applied biaxial strain is increased. (c) Confocal microscopy images of spherical and bifurcated shells. | ||
To fabricate the surface patterns, we use the biaxial compression of an array of circular plates (Fig. 1a) to generate microstructured surfaces. The fabrication method is based on earlier work by our group.15 In this paper, we use crosslinked poly(dimethylsiloxane) (PDMS) (Sylgard 184™) to generate the surface patterns, but this technique can be extended to a variety of materials. We take a micromolded PDMS substrate with an array of circular surface depressions, inflate it, and bond a thin film of crosslinked PDMS (∼20 μm) over it. Upon deflation of the PDMS substrate, an equibiaxial compressive stress is generated at the edges of the circular plates. Compressive stresses exceeding a critical value cause the plates to buckle, thus creating a surface array of microstructures (Fig. 2). This patterning technique is simple, tunable to smaller length scales, and applicable to a wide range of materials.
 | ||
| Fig. 2 Buckling schematic illustrating various plate buckling possibilities, where (a) illustrates a plate that buckles to form an axisymmetric, spherical shell, and (b) shows spherical shells that have bifurcated and exhibit circumferential waves, or folds dictated by the packing density of the shells. SEM images of spherical and nonaxisymmetric shells are presented in (a) and (b). | ||
Applying a compressive or tensile force to a confined thin plate can lead to either buckling,16 wrinkling,17 or crumpling.18 For a thin plate, the equilibrium shape is determined by a balance of the elastic plate's bending and stretching energy since the in-plane strain is minimal for a thin geometry. The stretching energy scales linearly with the plate thickness, t, while the bending energy scales as t3, therefore as the plate thickness decreases, the stretching energy term dominates and the plate bends significantly to reduce the in-plane strain.19 As a result, the circular plates buckle under lateral compression and form equilibrium structures with high curvatures, due to the plate's preference for bending.
The specific topography, or shape, of the microstructures is determined by the initial geometry and material properties of each plate, and the applied biaxial strain (Fig. 1). The plate stiffness, D is given by:16
 | (1) |
 | (2) |
 | (3) |
The critical strain required to buckle a circular plate is dependent on k, which can be determined through classical plate theory. From classical plate theory, the equilibrium equation of a circular plate is:16,20
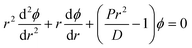 | (4) |
| kJ0(k) − (1 −ν)J1(k) = 0 | (5) |
Assuming ν≈ 0.49 for PDMS, k = 2.16 for the first buckling mode of a simply supported circular plate under biaxial compression. This value is used in eqn (3) to determine the strain required for the first mode of buckling for a circular plate of a given geometry, which is plotted as a solid line in Fig. 3b. The data below this line did not buckle while the data points above it did exhibit buckling. The aspect ratio of the shells, i.e. ratio of shell height (h) to final hole radius, (a), can be approximated by conservation of surface area15 (Fig. 3a):
 | (6) |
 | ||
| Fig. 3 (a) The prediction of aspect ratio from the applied biaxial strain on the surface of the substrate. (b) A phase map demonstrating the buckling modes of a circular plate under compression. In region iii the ratio of plate thickness to radius is too high to buckle, as predicted by classical plate theory, in region ii the plates buckle and form axisymmetric, spherical shells, while in region i the spherical shells bifurcate to form nonaxisymmetric geometry. The dashed line separating regions i and ii was determined empirically. The open circles represent experimental data for plates that did not buckle, the filled circles represent plates that buckled to form spherical microlenses, and the triangles indicate shells that bifurcated into nonaxisymmetric microstructures. (c) A schematic illustrating regions i, ii, iii. | ||
According to classical theory,16,20 this assumption should be valid for thin plates, where t/2ai < 0.1, which is accurate for all the circular plates that exhibited buckling. Here, the strain is defined as the biaxial surface strain of the depression covered substrate. As ε increases, eqn (6) continues to predict the microstructure aspect ratio, but the shape of the microstructure deviates from the lowest buckling mode, i.e. spherical shell. Shells exhibiting these stable, nonaxisymmetric buckling modes are depicted in Fig. 1 and Fig. 2b, where shells have three or four lobes in the circumferential direction.
Due to the boundary condition of asymmetric bonding at the plates' edges, and the change in volume in the encapsulated microwells, buckling always produces structures with a convex shape. During fabrication, the volume enclosed beneath the microstructures changes. Assuming ideal gases, the pressure change is given by Δp = Patm(Vi/Vf− 1), where Δp is the change in pressure, Patm is the atmospheric pressure, and Vi and Vf are the initial and final volumes. If the structures form in a concave state, the volume of the encapsulated microwells decreases, leading to a pressure increase. This pressure increase always exceeds the pressure decrease associated with the convex structure formation, thus convex formation is preferential. Although the concavity of the structures is impacted by this pressure difference, the resultant shape is not significantly affected. For our microstructures, Δp/E≈ 10−4–10−2, making the effect of pressure change on the buckled plate geometry negligible for these materials. This relationship suggests that for softer materials or shallower hole depths, the pressure change may impact the resultant geometry.
In Fig. 3b, a phase diagram illustrates the applied biaxial compressive strains that cause non-spherical geometries for circular plates with different t/ai. The data above the dashed line exhibit nonaxisymmetric geometries, while the data for circular plates in between the dashed and solid lines buckle and form axisymmetric spherical shells. The dashed line in Fig. 3b is empirical, but some insight into the onset and shape of the nonaxisymmetric shells can be gained by considering the bifurcation of a spherical shell. At an applied ε, a spherical shell is created with h/a defined by eqn (6). In this initial state, the base edge of the shell is resisting an applied bending moment related to a, ε, and E. As Shilkrut numerically demonstrated,21 for spherical shells of h/t≤ 3, the applied bending moment is resisted by a stable surface of constant curvature. For spherical shells with h/t > 6, the applied bending moment leads to the bifurcation and secondary buckling of the spherical shell, causing a break in asymmetry.21,22 This bifurcation leads to local bending to minimize in-plane strain, causing waves in the circumferential direction, and effectively resists the applied bending moment. The shape of the bifurcated shell is related to the surface metric tensor determination of the Gaussian curvature, similar to discussions by Klein et al. for elastic sheets.19
Additionally, the geometry of our bifurcated shells is determined by the packing density and configuration of the patterned surface. In the case of hexagonally packed circular plates, the bifurcation of an individual spherical shell creates a microstructure with inflection points, creating a tri-fold symmetry (Fig. 1). This geometry influences the orientation of the shell's nearest neighbors. The shells couple together and the stress concentration from each of the three buckle folds of a single shell directs the inflection points of its nearest neighbor (Fig. 2). The geometric coupling of these shells is also evident when the shells exhibit a four-fold symmetry. Again, the stress concentration from the folds of the shell directs the inflection points of its nearest neighbors. This suggests a method for controlling the long-range order of these patterned features using defects to template order.
By changing strain through environmental triggers, the relationship between shell geometry and strain defines a responsive surface of microstructures that can dynamically change their shape. Depending on the material properties of the patterned surface, a variety of stimuli can be used to change the strain applied to the shell structures. As one example, we use swelling of the PDMS network with hexane to change the applied strain. When a hexane droplet is added to the surface of initially spherical shells (Fig. 4a-ii), the thin film shell swells initially, but is laterally confined by the edges of the unswollen hole below it, to which it is bound. This lateral confinement increases the compressive strain along the edge of the shell, which from eqn (6) increases the height of the shell when a remains constant. Since the change in film thickness is negligible, the shell transitions through a bifurcation point to form a stable, nonaxisymmetric geometry (Fig. 4b-ii). Upon evaporation of the solvent, the shell returns to its initial, spherical geometry. The swelling time required to induce this change is on the order of seconds.
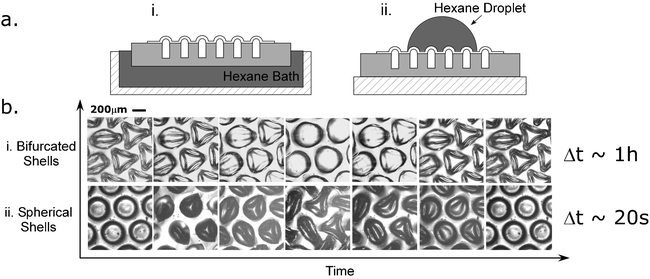 | ||
| Fig. 4 A schematic illustrating two (i and ii) manners of responsive behavior in the microstructures. b-i. The responsiveness of convex shells that are initially nonaxisymmetric and form spherical shells as the substrate swells with hexane. b-ii. Shells that are initially spherical bifurcate to form nonaxisymmetric geometries when the shells are swollen with hexane. | ||
The reverse topographical change can occur by changing the diameter of the hole below an initially nonaxisymmetric shell structure. To demonstrate this change, we swelled the PDMS substrate below the thin film shell with hexane to increase the hole diameter (Fig. 4a-i). This increase in a causes a decrease in the compressive biaxial strain along the edge of the shell, which in turn decreases the height of the shell to achieve an h/t value where an axisymmetric shell can resist the bending moment in a stable manner (Fig. 4a-ii). Therefore, the initially nonaxisymmetric shell forms a spherical shell geometry. The timescale for this process is approximately an hour as the entire PDMS substrate needs to swell before the shell layer. This process allows the surface to return to its initial topography once the hexane evaporates.
In summary, we have presented a simple, scalable patterning method to generate a variety of controlled, tunable surface topographies that would be difficult, if not impossible, to achieve using current fabrication techniques. The geometry of these microstructures can be understood using classical plate buckling and shell theory and can be tuned by varying the plate's geometry, material properties, and applied biaxial strain. The resulting surface patterns can dynamically and reversibly change shape and aspect ratio by changing the strain applied to the shell structures. This surface patterning strategy offers a novel approach for fabrication of the next generation of surface patterns, especially in the context of responsive materials.
Experimental
For fabrication of patterned features, PDMS substrate, and microstructures refer to reference 15. The film thickness in microstructure fabrication was varied from 9 μm to 55 μm, and was measured by stylus profilometry (Veeco Dektak 3 Stylus Profilometer). The microstructure height was measure by observing the contact of a glass probe controlled by a sub-nanometre precision inchworm actuator (Exfo Burleigh IW-812) with the shell surface viaoptical microscopy (Ziess, Variotech). Geometry of the convex and concave shells was examined by scanning electron microscopy (JOEL 6320FXV FESEM, SEI mode, 10 kV, gold-coated) and confocal microscopy (Leica Confocal Optical Microscope).Swelling of the PDMS thin film was done by depositing a 10 μl droplet of hexane (VWR) onto the surface of spherical microlens. The swelling of the PDMS substrate was done in a bath of hexane, and the substrate was swollen to equilibrium.
Acknowledgements
Funding for this work was provided by the Army Research Office Young Investigator Program as well as the NSF-MRSEC REU Program. The authors acknowledge NSF-MRSEC Central Facilities for use of their SEM and Confocal Microscope.Notes and references
- L. C. Gao and T. J. McCarthy, Langmuir, 2006, 22, 2966–2967 CrossRef CAS.
- S. R. Quake and A. Scherer, Science, 2000, 290, 1536–1540 CrossRef CAS.
- T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Phys. Rev. Lett., 2001, 86, 4163–4166 CrossRef CAS.
- A. Jagota and S. J. Bennison, Am. Zool., 2001, 41, 1483–1483 Search PubMed.
- A. J. Crosby, M. Hageman and A. Duncan, Langmuir, 2005, 21, 11738–11743 CrossRef CAS.
- P. Rai-Choudhury, Handbook of Microlithography, Micromachining, and Microfabrication, SPIE Opt. Engineer. Press, Bellingham, WA, 1997 Search PubMed.
- Y. N. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184 CrossRef CAS.
- S. Y. Chou, P. R. Krauss and P. J. Renstrom, J. Vac. Sci. Technol., B, 1996, 14, 4129–4133 CrossRef CAS.
- S. Rusponi, G. Costantini, F. B. de Mongeot, C. Boragno and U. Valbusa, Appl. Phys. Lett., 1999, 75, 3318–3320 CrossRef CAS.
- T. Tanaka, S. T. Sun, Y. Hirokawa, S. Katayama, J. Kucera, Y. Hirose and T. Amiya, Nature, 1987, 325, 796–798 CrossRef CAS.
- E. S. Matsuo and T. Tanaka, Nature, 1992, 358, 482–485 CrossRef CAS.
- N. Bowden, S. Brittain, A. G. Evans, J. W. Hutchinson and G. M. Whitesides, Nature, 1998, 393, 146–149 CrossRef CAS.
- E. P. Chan and A. J. Crosby, Adv. Mater., 2006, 18, 3238–3242 CrossRef CAS.
- P. Dario, M. C. Carrozza, N. Croce, M. C. Montesi and M. Cocco, J. Micromech. Microeng., 1995, 5, 64–71 CrossRef.
- D. P. Holmes and A. J. Crosby, Adv. Mater., 2007, 19, 3589–3593 CrossRef.
- S. P. Timoshenko and J. M. Gere, Theory of Elastic Stability, McGraw-Hill Book Company, New York, 2nd edn, 1961 Search PubMed.
- E. Cerda, K. Ravi-Chandar and L. Mahadevan, Nature, 2002, 419, 579–580 CrossRef CAS.
- E. M. Kramer and T. A. Witten, Phys. Rev. Lett., 1997, 78, 1303–1306 CrossRef CAS.
- Y. Klein, E. Efrati and E. Sharon, Science, 2007, 315, 1116–1120 CrossRef CAS.
- P. S. Bulson, The Stability of Flat Plates, Chatto & Windus, London, 1970 Search PubMed.
- D. Shilkrut, Stability of Nonlinear Shells, Elsevier, London, 2002 Search PubMed.
- M. Ortiz and G. Gioia, J. Mech. Phys. Solids, 1994, 42, 531–559 CrossRef.
| This journal is © The Royal Society of Chemistry 2008 |
