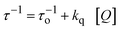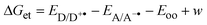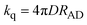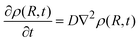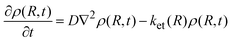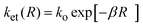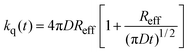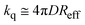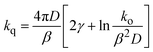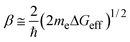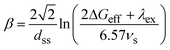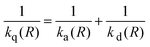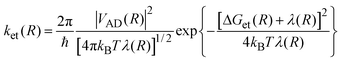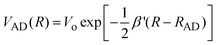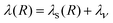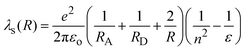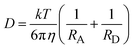Free energy dependence of the diffusion-limited quenching rate constants in photoinduced electron transfer processes†
Received
11th June 2007
, Accepted 29th October 2007
First published on 14th November 2007
Abstract
Electron-transfer rate constants were determined by means of lifetime measurements for the fluorescence quenching of 9,10-dicyanoanthracene by aromatic amines and methoxybenzenes as electron donors, and for the quenching of the synthetic dyeseosin Y and phenosafranine by a series of p-benzoquinones as electron acceptors. All determinations were carried out in acetonitrile at 298 K. The quenching rate constants (kq) in the region of –1.9 eV < ΔGet < –0.2 eV do not decrease as predicted by Marcus theory, but they show a small increase with decreasing ΔGet. Although this behaviour is in qualitative agreement with the current theories for reactive systems in the diffusion limit region, a closer analysis of the experimental data showed that several aspects of the dependence of the kq on ΔGet are not entirely explained, suggesting that new, refined theoretical models may be required.
Introduction
Since the pioneering work of Rehm and Weller1 it was generally accepted that the electron transfer (ET) fluorescence quenching rate constants (kq) reached a diffusion-limited plateau in the exothermic region (ΔGet < –0.2 eV) and decreased as the ET driving force becomes positive. However, the lack of an inverted region at large negative ΔGet, as predicted by Marcus theory,2,3 represented for many years an intriguing dilemma which understanding demanded significant experimental and theoretical efforts.4–9
Several explanations have been given for the absence of the inverted region in fluid media10 and among them, the dependence of the ET rate constants (ket) on the electron donor (D)/electron acceptor (A) separation distance (R) was particularly successful. According to this interpretation the plateau reached at large negative ΔGet is related to the solvent reorganization energy being an increasing function of R (see, for instance, eqn (17) below). This notion is illustrated in Scheme 1.
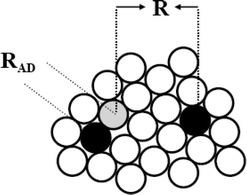 |
| | Scheme 1 Simplified 2D model for intermolecular ET. The reaction between an electron donor molecule (grey sphere) and electron acceptors (black spheres) surrounded by solvent molecules (open spheres) can occur at variable distances. | |
ET reactions can produce diverse ionic species that differ in their degree of solvation such as contact (CRIP) and solvent separated (SSRIP) radical ion pairs. CRIP arise from neutral A/D precursors that have diffused to the contact distance (RAD = RA + RD), while SSRIP can be formed (trough a solvent-mediated superexchange coupling mechanism) from a wide distribution of A/D pairs in which the reactants are at variable distances (R).11 In Marcus theory, the largest rate for ET reaction is attained when ΔGet + λ = 0. Hence, for an ET reaction falling in the inverted region (i.e., ΔGet + λ < 0) there is a significant probability for the process to take place from the solvent separated A/D pairs. These species are characterized by a larger A/D separation and therefore, by a larger solvent reorganization energy. Another consequence of this interpretation is that the effective A/D separation distance (Reff) at which the ET reaction takes place should increase with decreasing ΔGet.
One of the most frequent systems used to investigate the kinetics of ET reactions at large negative ΔGet was the quenching of anthracenecarbonitriles by electron donors. These systems were first studied by Eriksen and Foote12 and more recently by Jacques and Allonas13,14 and Niwa et al.15,16 by means of stationary fluorescence measurements. In these studies, the experimental Stern–Volmer plots show a positive deviation at high quencher concentrations. From the analysis of the curvature of the plots the ET effective distance (Reff), the mutual A/D diffusion coefficient (D) and the intrinsic rate constant for ET (ket) can be extracted. These studies confirmed the apparent increase of the Reff with decreasing ΔGet.
On the other hand, direct measurement of the quenching rate constant kq by means of time resolved fluorescence experiments is much less frequent, in particular, in the investigation of the dependence kq on ΔGet in the region of high ET exergonicity.17–19
We report here a time resolved fluorescence study of the quenching of the singlet excited state of 1,9-dicyanoanthracene (DCA) by aromatic amines and methoxybenzenes, and the quenching of the synthetic dyeseosin Y (Eos) and phenosafranine (PS) by a series of p-benzoquinones. All experiments were performed in acetonitrile at 298 K. The quenchers were chosen in order that the driving force of the ET processes were in the region of –1.9 < ΔGet < –0.2 eV. It was found that, in all cases, the kq increase linearly with decreasing ΔGet. It was also observed that each fluorophore/quenchers system follows a particular relationship with the ET driving force. The experimental data are analyzed using the current theories for diffusion-mediated ET reactions.
Experimental
1,9-Dicyanoanthracene (DCA), phenosafranine (PS) and eosin Y (Eos) were obtained from Aldrich and used without further purification. The electron donors N,N,N′,N′-tetramethyl-(p-phenylenediamine) (TMPD), N,N,N′,N′-tetramethylbenzidine (TMBZ), p-anisidine, p-toluidine, 1,2,4-trimethoxybenzene, 1,4-dimethoxybenzene, 1,2-dimethoxy benzene and anisole were all commercially available and were purified by standard procedures. The acceptors p-benzoquinone, chloro-p-benzoquinone, p-methylquinone, 2,6-dimethylbenzoquinone and duroquinone were obtained from Aldrich and were purified by sublimation. Acetonitrile (HPLC grade) was from Sintorgan.
Fluorescence lifetime measurements were carried out with the time correlated single photon counting technique using an Edinburgh Instruments OB-900 equipment. All measurements were carried out in air equilibrated acetonitrile solutions at 25 ± 0.1 °C.
Results
Table 1 collects some relevant electrochemical and photophysical parameters of the fluorophores involved in this study. The structure of the fluorophores is given in Chart 1 in the annexed Electronic Supporting Information, ESI.†
| Fluorophore |
E
D/D+˙/V |
E
A
/A
–˙/V |
E
00/eV |
τ
o
/nsa |
|
The reported uncertainties correspond to one standard deviation calculated from five independent determinations.
Values obtained from reference12.
Ref. 20.
Ref. 21.
|
|
1,9-Dicyanoanthracene
b |
— |
–0.98 |
2.89 |
12.71 ± 0.03 |
|
Phenosafranine
c |
+1.30 |
–0.67 |
2.34 |
3.52 ± 0.02 |
|
Eosin
Y
d |
+0.80 |
— |
2.31 |
3.99 ± 0.04 |
In all cases, the emission of the fluorophores in air equilibrated acetonitrile solutions (at 298 K) decays monoexponentially. The experimental lifetimes (τo) are collected in Table 1. As expected, the emission decay times of the fluorophores decrease with increasing concentration of the quenchers. No deviation from a single exponential decay law could be detected even at the larger concentrations of the quenchers employed ([Q] ≤ 0.02 M). The χ2 of the fitting were always in the range of 1.05–1.20; and applying bi-exponential or non-exponential (Föster-like) decay models to the analysis of the emission decays do not lead to significant improvements of χ2 or residuals plots.
The bimolecular quenching rate constants (kq) were obtained according to eqn (1):
| | 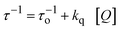 | (1) |
where
τ stands for the fluorescence decay time measured in the presence of the quencher. The plots according to
eqn (1) were linear with correlation coefficients (
R) better than 0.999 (even for
τo/
τ >7.0). The emission decay of DCA in the presence of TMPD 0.02 and three plots according to
eqn (1) are shown in the ESI.
† The quenching rate constants (
kq) measured for all the systems studied are collected in
Tables 2–4. The values for the PS/D are given in
Table 1 in the ESI.
†
Table 2 Bimolecular rate constants (kq) for the quenching of the singlet excited state of DCA by aromatic electron donors in acetonitrile at 298 K and exponential decay constant β calculated according eqn (11)
Assuming that the quenching processes studied involve a single type of ET reactions,22 the free Gibb energy changes for the ET processes (ΔGet) can be calculated according to:1
| | 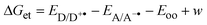 | (2) |
where
w =
z1z2e2/
εRAD represents the free energy gained by bringing the formed ions (with charges
z1 and
z2) from infinite to the contact distance
RAD in a medium of static dielectric constant
ε. Taking a mean value of
RAD ∼0.6 nm and +1 and –1 for the charges of the radical ions (
z1z2 = –1) a value of ∼ –0.064 eV is calculated for the Coulombic term in
acetonitrile. For the systems PS/A and Eos/A, the Coulombic terms were calculated taking into account that the products
z1z2 are –2 and +1, respectively. The redox potentials of the quenchers were taken from several sources.
23–25 The values of Δ
Get calculated according
eqn (2) are also given in
Tables 2–4.
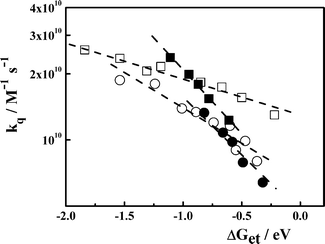
When the experimental kq in Table 2–4, Table 1-SI† and the Rehm and Weller data are represented together vs. ΔGet they show an acceptable correlation within the usual scatter observed in these types of free energy correlation plots (see, Fig. 3-SI, ESI †). However, a closer inspection of our data (Fig. 1) shows that the kq increase with decreasing ΔGet and also, that each fluorophore/quenchers system follows its own relationship with the ET driving force.
Discussion
Let us assume a quenching process that can occur at the encounter A/D separation distance, RAD, exclusively. In such case, the theoretical limit for a diffusional controlled quenching rate constant is given by| | 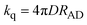 | (3) |
Eqn (3) is the Smoluchovsky's result26 for the long time limit solution of the diffusion equation
| | 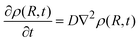 | (4) |
where
ρ(
R,
t) = [
Q]/[
Qo] stands for the density distribution of the quencher (A or D) about the fluorophore. However, for diffusional processes where A and D can react over a distance greater than the encounter separation,
eqn (4) is modified to
8,27| | 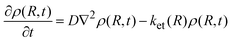 | (5) |
where
ket(
R) represents the distance dependent ET rate constant. In the simplest formulation possible, this can be written as
| | 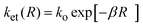 | (6) |
where
β stands for the exponential decay constant and
R ≥
RAD. Solving simultaneously
eqn (5) and
(6), the rate constant for concurrent diffusion/ET reaction,
kq(
t), is obtained
| | 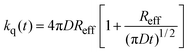 | (7) |
which in the long time limit (
t > 0.1 ns) simplifies to:
| | 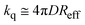 | (8) |
Since in our experimental conditions (and resolution of our instrumental) the emission decays can be fitted to a single exponential model, the results can be analyzed according to eqn (8). The values of Reff for the DCA/donor system calculated from the experimental kq in Table 1 and assuming D ∼ 3.3 × 10–9 m2 s–1 (vide infra) are in good agreement with the values estimated from steady-state fluorescence measurements reported by Jacques and Allonas13 and Niwa et al.15,16
In turns, Reff and kq can be related to the parameters in eqn (6) by 27
| | 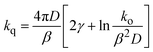 | (9) |
where
γ is the Euler's constant (0.5772). In principle,
eqn (9) could be used to rationalize the dependence of
kq on Δ
Get, provided that
D and the dependence of
β and
ko on Δ
Get were known. Considering that the quenchers chosen are similar in sizes and shapes, it seems reasonable to assume that
D is nearly constant throughout each particular correlation in
Fig. 1. Hence, the slopes of the plots must be related to the variation of
β or
ko (or both). The exponential factor
β in
eqn (6) is given by the Gamow's factor
28,29| | 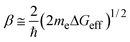 | (10) |
where
me stands for the electronic mass and Δ
Geff represents the effective tunneling barrier. Δ
Geff is related to the adiabatic energy gap for the electron transfer (or hole transfer) from the reactants to the
solvent molecules. Approximated values ofΔ
Geff can be estimated from the ionization potentials and electronic affinities of the reactants and
solvent,
30 or directly from their redox potentials. Recently, Kobori
et al.31 proposed an alternative model for explaining the dependence of
β on Δ
Geff. According to these authors,
β is given by
| | 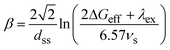 | (11) |
where
dss is the center-to-center distance between the nearest neighbor
solvent molecules in the condense medium,
λex is the total (
solvent plus internal) reorganization energy of the superexchange ET process and
νs represents the solute–
solvent and/or the
solvent–
solvent electronic coupling which, by simplicity, were assumed to be the same. Taking a value of
λex = 1 eV mol
–1, Kobori
et al. used
eqn (11) to fit a series of
β values measured for several A/D systems in fluid and frozen media using
νs as an adjustable parameter. The best value of
νs was found to be ∼850 cm
–1; which as pointed out by the same authors, appears to be excessively large considering that it represents the electronic coupling between randomly oriented
solvent molecules. We used
eqn (10) and
(11) to estimate approximated values of
β for the systems studied. Details of these calculations are given in the ESI.
† The values of
β calculated from Kobori's equation are collected in
Tables 2–4. The values of
β are ∼6–7 nm
–1 for the Eos and
PS/A systems and ∼10 nm
–1 for DCA and
PS/D systems. These values are in good agreement with previously reported values of
β ≈ (3–10) nm
–1.
32 The
β calculated from Gamow's equation are just about twice those estimated from
eqn (11).
As it may be concluded from the analysis above, the estimated β are constant within each particular system in Fig. 1, and therefore, β cannot be the main responsible for the observed dependence of kq on ΔGet. Consequently, everything points to ko as being the factor controlling the variation of kq. This result is not unexpected taking into consideration that ko involves the ET Franck–Condon factor; which in turns, depends on ΔGet and on the reorganization energy of the system. Assuming values of ∼1 eV and ∼0.4 eV for the solvent and A/D internal reorganization energies (vide infra), most of the A/D systems studied should be in the normal Marcus's region and therefore, an increase of ko with decreasing ΔGetis expected.
An alternative explanation for the dependence of kq on ΔGet may be given in terms of the model developed by Tachiya and Murata.9 Hug and Marciniak10 analyzed Rehm and Weller1 data using this model and found that it satisfactorily explains the dependence of kq on ΔGet in the diffusion-controlled limit. According to Tachiya and Murata, the second-order quenching rate constant kq(R) can be expressed as
| | 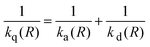 | (12) |
where
ka(
R) represents the second-order ET rate constant
33| | 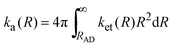 | (13) |
and
kd(
R) is the diffusion-limited rate constant. In
eqn (13),
ket(
R)represents the distance dependent rate constant for the ET as given by the semi-classical version of the ET theories:
| | 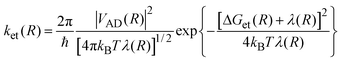 | (14) |
where
| | 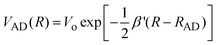 | (15) |
is the distance dependent electronic coupling
matrix element. The reorganization energy has two contributions:
| | 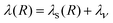 | (16) |
In eqn (16), λs(R) accounts for the solvent reorganization energy and λν is the internal reorganization energy of the reactants. λs(R) can be calculated according to
| | 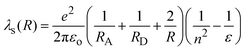 | (17) |
where
εois the permittivity of vacuum, and
n2and
ε represents the refraction index and the static dielectric constant of the
solvent, respectively.
According to Tachiya and Murata,9 the diffusion-limited rate constant, kd(R), is given by
| | 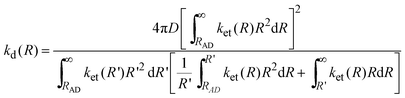 | (18) |
The value of kd(R)can be calculated numerically using the Simpson's rule algorithm, but such computation requires the knowledge of many parameters that characterize the A/D systems. Approximated values for RA and RD, required for the calculation of λs(R), were estimated following Zissimos et al.34 The calculated values are: DCA 0.37 nm, PS 0.41 nm, Eos 0.48 nm, and 0.31 and 0.27 nm as the average values for the aromatic donors and quinine quenchers, respectively. Approximated values for λν were obtained from molecular orbital calculations.35,36 The estimated contributions of the donors (λνD) and acceptors (λνA) to λν are summarized in Table 1-SI.† The value λν for each fluorophore/quencher system was obtained by addition of the donor and acceptor contributions. The free Gibbs ET energy change ΔGet depends on R as shown in eqn (2). The molecular radii were also used to estimate mutual A/D diffusion coefficients (D) from the Stokes–Einstein equation:
| | 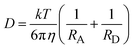 | (19) |
Taking η = 0.346 cp for the viscosity of the solvent at 298 K, values of ∼3.3 × 10–9 m2 s–1 (DCA/D), 3.2 × 10–9 m2 s–1 (PS/D), 3.5 × 10–9 m2 s–1 (PS/A) and 3.3 × 10–9 m2 s–1 (Eos/A), were calculated. The values estimated for the DCA/D systems are in good agreement with the average of the experimental D reported by Jacques and Allonas13 for the same systems.
The solid curve in Fig. 2 corresponds to the fitting of the experimental kq measured for DCA/donors system to eqn (12), taking rA = 0.37 nm, rD = 0.31 nm, λν = 0.37 eV, Vo = 100 cm–1, β′ = 10 nm–1 and D as an adjustable parameter. The value of D ∼ 4.0 × 10–9 m2 s–1, which provided the best fit of the experimental data, is similar to that calculated for the DCA/donors system from the Stokes–Einstein equation. As it may be concluded from Fig. 2, although the theoretical curve predicts correctly the increase of kq with decreasing ΔGet, the fit is just fair. Similar results were found for the PS/D system (Fig. 4-SI).† However, for the systems Eos/A and PS/A we were not able to find a realistic set of parameters (Vo and D) to fit the experimental kq.37
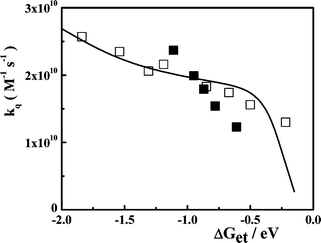 |
| | Fig. 2 Experimental kq for the quenching of DCA emission by electron donors (□) and eosin Y by electron acceptors (■). The solid line corresponds to the simulation of the second order diffusion-mediated electron transfer rate constant according to the model developed by Tachiya and Murata.9 The parameters used for the simulation are: RA = 0.37 nm, RD = 0.31 nm, λν = 0.37 eV, Vo = 100 cm–1, β′ = 10 nm–1 and D = 4.0 × 10–9 m2 s–1. | |
The main inconvenient found for fitting the experimental kq to eqn (12) is related to the uncertainties on RAD. Although, this can be considered just as a “technical” problem, it has clear mechanistic implications. For instance, an inspection of the values of Reff (and D) reported for the DCA/donor systems by Jacques and Allonas13 and Niwa et al.15,16 shows that the experimental Reff measured for the less exothermic reactions approach to those expected for exciplex (CRIP) formation, i.e. ∼ 0.35–0.42 nm. These Reffvalues are consistent with the expected inter-planar aromatic-aromatic A/D separation of the systems studied and they are considerably smaller than the “contact” separation distance (RAD) calculated from the reactant's volumes. Niwa et al.16 proposed that this behavior obeys to a change in the ET reaction mechanism occurring around ΔGet ∼ –0.5 eV. In the strongly exothermic region (ΔGet < –0.5 eV) the ET reaction produces SSRIPs, while the reaction goes via exciplex formation at ΔGet > –0.5 eV. Similar conclusions were reached by Gould et al.38 in the study of the quenching of tetracyanoanthracene and DCA by alkylbenzenes, although these authors proposed a branched mechanisms in which the relative importance of the SSRIP/exciplex reaction routes is a continuous function of ΔGet. These mechanistic complications are not being taken into account by the models used here for interpreting the dependence of kqon the ET driving force.9 In Tachiya and Murata models9,11 the CRIP species are treated as weakly interacting radical ion pairs at a contact distance (assumed to be the sum of the reactants radii, typically 0.6 nm). Although these parameters may be appropriated for describing the A/D systems discussed by these authors,11 they can hardly be used for characterizing exciplexes. In addition, it seems clear that alternative models, particularly those which consider the reactants and solvent molecules as discrete entities,39 may have better chances to explain this discontinuity (or branch) in the ET mechanism.
Summary
ET quenching rate constants obtained by direct measurement of the decay of the excited fluorophore, produced results in line with the predictions of current theories for reactive systems in the diffusion limit region. The rate constants increase with decreasing ΔGet in all the range explored. However, a detailed analysis showed that some aspects of the dependence of the rate constants on the driving force are not fully explained, suggesting that new, refined theoretical models may be required.
Acknowledgements
The authors thank to Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET-Argentina), Agencia Nacional de Promoción Científica (FONCYT-Argentina) and Secretaría de Ciencia y Técnica de la Universidad Nacional de Río Cuarto for the financial support.
References
- D. Rehm and A. Weller, Isr. J. Chem., 1970, 8, 259 CAS.
- R. A. Marcus, Discuss. Faraday Soc., 1960, 29, 21 RSC.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155 CrossRef CAS.
- G. L. Closs, L. T. Calcatera, N. J. Green, K. W. Penfield and J. R. Miller, J. Phys. Chem., 1986, 90, 3673 CrossRef CAS.
- J. R. Miller and J. V. Beitz, J. Chem. Phys., 1981, 74, 6746 CrossRef CAS.
- R. A. Marcus and P. Siders, J. Phys. Chem., 1982, 86, 622 CrossRef CAS.
- A. I. Burshtein, Unified Theory of Photochemical Charge Separation, Adv. Chem. Phys. 2000, 114, 419 Search PubMed.
-
S. A. Rice, Diffusion-Limited Reactions, in Comprehensive Chemical Kinetics, ed. C. F. H. Tipper and R. G. Compton, C. H. Bamford, Elsevier, Amsterdam, 1985, vol. 25, ch. 4 Search PubMed.
- M. Tachiya and S. Murata, J. Phys. Chem., 1992, 96, 8441 CrossRef CAS.
- G. L. Hug and B. Marciniak, J. Phys. Chem., 1995, 99, 1478 CrossRef CAS and references therein.
- S. Murata and M. Tachiya, J. Phys. Chem., 1996, 100, 4064 CrossRef CAS.
- J. Eriksen and C. S. Foote, J. Phys. Chem., 1978, 82, 2659 CrossRef CAS.
- P. Jacques and X. Allonas, Chem. Phys. Lett., 1995, 233, 533 CrossRef CAS.
- X. Allonas and P. Jacques, Chem. Phys., 1997, 215, 371 CrossRef CAS.
- T. Niwa, T. Inada, C. S. Miyazawa, K. Kikuchi, M. Yamauchi, T. Nagata, Y. Takahashi, H. Ikeda and T. Miyashi, J. Am. Chem. Soc., 1999, 121, 7211 CrossRef CAS.
- T. Niwa, K. Kikuchi, N. Matsuita, M. Hayashi, T. Katagiri, Y. Takahashi and T. J. Miyashi, Phys. Chem., 1993, 97, 11960 Search PubMed.
- S. Murata, S. Y. Matsuzaki and M. Tachiya, J. Phys. Chem., 1995, 99, 5354 CrossRef CAS.
- H. L. Tavernier, M. M. Kalashnikov and M. D. Fayer, J. Chem. Phys., 2000, 113, 10191 CrossRef CAS.
- S. Nishikawa, T. Asahi, T. Okada and N. Mataga, Chem. Phys. Lett., 1991, 185, 237 CrossRef CAS.
- S. N. Guha, P. N. Moorthy and J. P. Mittal, Radiat. Phys. Chem., 1992, 39, 183 CrossRef CAS.
- T. Shen, Z.-G. Zhaq, Q. Yu and H.-J. Xu, J. Photochem. Photoibol., A, 1989, 47, 203 Search PubMed.
- Although it is well established that the quenching of all the systems studied takes place through an ET mechanism leading to the formation of free radical ions in solution, other concomitant ET processes (such as the formation of non fluorescent exciplexes, radical ion excited states, etc.) may be also possible. The implications of these alternative reaction channels on the interpretation of the experimental kq have been discussed in detail in ref. 10.
- S. Fukuzumi, S. Koumitsu, K. Hironaka and T. Tanaka, J. Am. Chem. Soc., 1987, 109, 305 CrossRef CAS.
- H. Kim, N. Kitamura, Y. Kawanishi, Y and S. Tazuke, J. Phys. Chem., 1989, 93, 5757 CrossRef CAS.
- M. F. Broglia, S. G. Bertolotti and C. M. Previtali, J. Photochem. Photobiol., A, 2005, 170, 261 CrossRef CAS.
- M. Smoluchowski, Z. Phys. Chem., 1917, 92, 129 Search PubMed.
- B. Sipp and R. Voltz, J. Chem. Phys., 1983, 79, 434 CrossRef CAS.
- G. Gamow, Z. Phys., 1928, 51, 204.
- H. M. McConnell, J. Phys. Chem., 1961, 35, 508 CrossRef CAS.
- M. B. Zimmt and D. H. Waldeck, J. Phys. Chem., 2003, 107, 3580 Search PubMed.
- Y. Kobori, T. Yago, K. Akiyama, S. Tero-Kobota, H. Sato, F. Hirata and J. R. Norris, Jr., J. Phys. Chem. B, 2004, 108, 10226 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265 CAS.
- M. Doi, Chem. Phys., 1975, 11, 115 CrossRef.
- Y. H. Zhao, M. H. Abraham and A. M. Zissimos, J. Org. Chem., 2003, 68, 7368 CrossRef CAS.
- S. F. Nelsen, S. C. Blacktock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677 CrossRef CAS.
- G. Cosa and C. A. Chesta, J. Phys. Chem., 1997, 101, 4922 Search PubMed.
- For the systems Eos/A and PS/A different combinations of Vo (between 50–150 cm–1) and β (2–15 nm–1) were used as fixed parameters for fitting the experimental kq to eqn (12). However, none of the combinations allows reproducing satisfactorily the pronounced slopes of the plots in Fig. 2.
- I. R. Gould, R. H. Young, L. J. Mueller and S. Farid, J. Am. Chem. Soc., 1994, 116, 8176 CrossRef CAS.
- M. Hilczer and M. Tachiya, J. Mol. Liq., 1995, 64, 113 CrossRef CAS and references therein.
Footnote |
| † Electronic supplementary information (ESI) available: Chart 1, Fig. 1–4SI, and Tables 1–6SI. See DOI: 10.1039/b708797g |
|
| This journal is © The Royal Society of Chemistry and Owner Societies 2008 |
Click here to see how this site uses Cookies. View our privacy policy here.